斜拉桥的结构体系一般有漂浮体系、半漂浮体系和塔梁固结体系[1].随着斜拉桥跨径增大以及一些地区抗震要求,大跨径斜拉桥经常采用漂浮体系或半漂浮体系结构形式.为了降低地震荷载效应,通常会选择在塔梁处设计一定约束.国内外学者也不断的研究出弹性连接装置和黏滞阻尼器等塔梁连接方式.文献[2]对某标准斜拉桥比较了半主动刚度阻尼器、半主动摩擦阻尼器、被动阻尼器混合连接方式的减震效果.文献[3]采用铅芯橡胶支座作为被动控制元件配合理想的水压激励器作为主动控制元件协同工作,获得了相对理想的减震效果.苏通大桥作为主跨长达1 088 m的超大跨度斜拉桥,在设计过程中分别比较了地震响应几个关键参数后,最终确定选择大型黏滞阻尼器作为苏通大桥的塔梁纵向约束方式[4],并分别在两个塔梁位置附近各安装了4个大型阻尼器.
塔梁连接阻尼器在桥梁的正常养护运营过程中是一个长期服役的构件.这种黏滞阻尼器正常工作中要承受非常大的压力,因此对加工材料、加工工艺的要求都非常高[5].大型阻尼器经常会出现油缸漏油导致阻尼性能大幅减退,未达到使用寿命而导致被迫更换的情况在国内外也屡见不鲜,浪费了大量的人力物力.
目前针对这种大型阻尼器研究中,大多数学者将研究重点放在实验室中研究阻尼器本身的性能[6-7],并在有限元模型中模拟地震状态下的抗震性能[8-9],而在实桥中关于阻尼器使用情况和效果缺少有利的数据支撑.本文针对实桥大型塔梁阻尼器,采用基于振动响应参数识别的方法,获取阻尼器的实际性能参数,相关研究可为桥梁关键附属设施的养护管理提供参考.
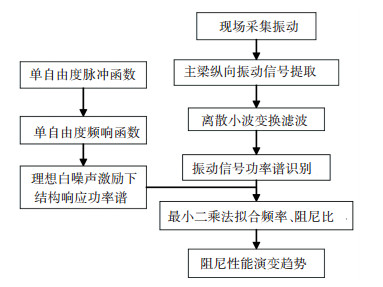
1 塔梁阻尼器实际性能参数识别基本流程本文首先将斜拉桥纵向一阶振动简化为单自由度线性系统,并推导出在理想白噪声激励下的结构振动响应功率谱.现场对阻尼器开展振动响应实测,采用基于小波变换的滤波方法,将主梁的纵向振动低频数据进行提取,并进行振动功率谱识别.同时将现场试验识别的功率谱与推导的公式进行参数拟合,获得纵向一阶振动的近似频率和阻尼比.经过长时段的多次重复试验,预测出塔梁阻尼器的性能变化趋势,具体步骤如图 1所示.
|
图 1 本文的技术路线 Fig. 1 Technical route of this study |
大跨度斜拉桥塔梁连接处设置黏滞阻尼器是典型的局部阻尼非线性增大问题.研究参考文献[10-11]等的单自由度评价模型思路,应用附加阻尼比的概念,近似以线弹性体系代替设置了黏滞阻尼器的非线性体系,经换算后的两种体系具有相同的耗能能力.
在简化为线弹性体系后,根据文献[12]提出的单自由度模型一阶纵飘振型简化方法,将全桥简化为以桥塔的抗推刚度为纵向刚度,主梁质量与堆聚于塔顶的桥塔参与质量为等效质量的单自由度弹性装置.把环境对主梁的随机激励等效成白噪声激励,在此基础上可通过随机振动理论获取结构白噪声机理下响应功率谱.
2.1 频率响应函数考虑单自由度线性振动系统,其运动方程为
| $ m\ddot Y\left( t \right) + c\dot Y\left( t \right) + kY\left( t \right) = X\left( t \right), $ | (1) |
| $ Y\left( 0 \right) = \dot Y\left( 0 \right) = 0. $ | (2) |
式中:m为质量,c阻尼系数,k为系统刚度.式(1)可改写成无量纲形式,即
| $ \ddot h\left( t \right) + 2\xi {\omega _0}\dot h\left( t \right) + {\omega _0}^2h\left( t \right) = \frac{1}{m}\delta \left( t \right), $ | (3) |
其中
设结构响应Y(t)=H(ω)eiωt,则式(3)可化为
| $ \left[ {{{\left( {{\rm{i}}\omega } \right)}^2} + 2\xi {\omega _0}\left( {{\rm{i}}\omega } \right) + {\omega _0}^2} \right]H\left( \omega \right){{\rm{e}}^{{\rm{i}}\omega t}} = {{\rm{e}}^{{\rm{i}}\omega t}} \cdot \frac{1}{m}, $ | (4) |
式中
| $ H\left( \omega \right) = \frac{1}{m}\frac{1}{{\left( {{\omega _0}^2 - {\omega ^2}} \right) + 2{\rm{i}}\xi {\omega _0}\omega }}, $ | (5) |
其中H(ω)为复值函数,相应的幅值与相位分别为
| $ \left| {H\left( \omega \right)} \right| = \frac{1}{m}\frac{1}{{\sqrt {{{\left( {{\omega _0}^2 - {\omega ^2}} \right)}^2} + {{\left( {2\xi {\omega _0}\omega } \right)}^2}} }}, $ | (6) |
| $ \psi = {\tan ^{ - 1}}\left\{ {\frac{{2\xi \omega /{\omega _0}}}{{1 - {{\left( {\omega /{\omega _0}} \right)}^2}}}} \right\}. $ | (7) |
在白噪声激励作用下,平稳反应过程Y(t)的自相关函数RY(τ)以及功率谱SY(ω)分别为
| $ \begin{array}{l} {R_Y}\left( \tau \right) = E\left[ {Y\left( t \right)Y\left( {t + \tau } \right)} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;\int_{ - \infty }^{ + \infty } {h\left( u \right)} \int_{ - \infty }^{ + \infty } {h\left( v \right){R_X}\left( {\tau + u - v} \right){\rm{d}}u{\rm{d}}v} , \end{array} $ | (8) |
| $ \begin{array}{l} {S_Y}\left( \omega \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \infty }^{ + \infty } {{R_Y}\left( \tau \right){{\rm{e}}^{ - {\rm{i}}\omega \tau }}{\rm{d}}\tau } = \\ \;\;\;\;\;\;\;\;\;\;\;H\left( { - \omega } \right)H\left( \omega \right){S_X}\left( \omega \right). \end{array} $ | (9) |
考虑到H(-ω)和H(ω)是共轭函数,因此式(9)可进一步改写为
| $ \begin{array}{l} {S_Y}\left( \omega \right) = {\left| {H\left( \omega \right)} \right|^2}{S_X}\left( \omega \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{{S_0}}}{{{m^2}\left[ {{{\left( {{\omega _0}^2 - {\omega ^2}} \right)}^2} + 4{\xi ^2}{\omega _0}^2{\omega ^2}} \right]}}. \end{array} $ | (10) |
故白噪声作用下的响应功率谱,可用未知系数x1、x2、x3表示,即
| $ {S_Y}\left( \omega \right) = \frac{{{x_1}}}{{{{\left( {{x_2}^2 - {\omega ^2}} \right)}^2} + 4{x_3}^2{x_2}^2{\omega ^2}}}, $ | (11) |
相对应加速度功率谱为
| $ {S_{\ddot Y}}\left( \omega \right) = {\omega ^2}{S_{\dot Y}}\left( \omega \right) = {\omega ^4}{S_Y}\left( \omega \right). $ | (12) |
其中x1=S0/m2,x2=ω0=2πf0,x3=ξ,通过对功率谱函数进行x1、x2、x3这3个参数拟合,本文即可以近似得到系统阻尼比.
3 离散小波变换及滤波小波变换的理念,不同于傅里叶变换将信号分解为无限长度的正弦、余弦的函数,它是以一种有限长度的小波,对整个时域上的信号进行的一种变换,其实质为一种小波函数与信号的卷积形式[13-14],即
| $ \left\langle {u,K} \right\rangle = \int_{ - \infty }^\infty {\mathit{u}\left( t \right)K\left( {t,a,b} \right){\rm{d}}t} . $ | (13) |
按照信号特点选定了合理的小波基后,K(t, a, b)可以通过改变小波基ψ(t)的尺度参数a,以及小波在时域上挪动的位置平移参数b得到,并将式(13)改写为
| $ {T_\psi }\left[ u \right]\left( {a,b} \right) = \frac{1}{{\sqrt a }}\int_{ - \infty }^\infty {\mathit{u}\left( t \right)\overline {\psi \left( {\frac{{t - b}}{a}} \right)} {\rm{d}}t} . $ | (14) |
通过小波与时域信号的卷积,能得到信号在整个时域过程中,在不同时间段下不同频率出现的成分大小.
采用离散小波变换,对尺度参数a和平移参数b进行离散化,使得分析十分有效.由于离散小波的小波基函数具有正交性,小波空间中两点之间因冗余度造成的关联得以消除.在信号分解的同时,通过向下采样,使得分解后的信号总长度未发生变化,从而避免了大量数据的冗余,并将信号中的有效成分也能全部保留.
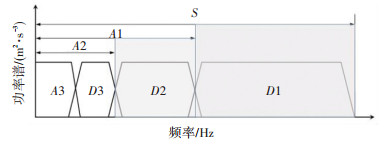
具有正交性的离散小波共有4个滤波器,这4个滤波器能够将信号中的大尺度信息A和小尺度信息D分解,并随后重构.分解滤波器还可以在分解一层的基础上继续分解,从而达到多层分解将频域细化的作用.按照3层分解时,频率的区间可以细化为总频率范围的1/8,如图 2所示.
|
图 2 3层小波分解的频率分布 Fig. 2 Frequency distribution of three-layer wavelet decomposition |
离散小波滤波就是在分解的基础上进行的,如果对分解的信号不加以处理,则重建信号与原始信号一致,也并无滤波效果. 图 3揭示了离散小波滤波的基本流程,在分解后的信号中设置阈值对小波系数进行处理(如将较小的小波系数置为0,较大的削弱或保留),则可以将重构之后的信号中某一频率区间的数据部分滤掉.以本文对超低频信号进行低通滤波为例,将数据进行分解后,对数据中的高频成分处理,再与未做任何处理的低频成分重构,在这一过程中低频成分得以保留,从而达成了低通滤波的目的.

|
图 3 离散小波变换滤波流程图 Fig. 3 Flow diagram of discrete wavelet transform filter |
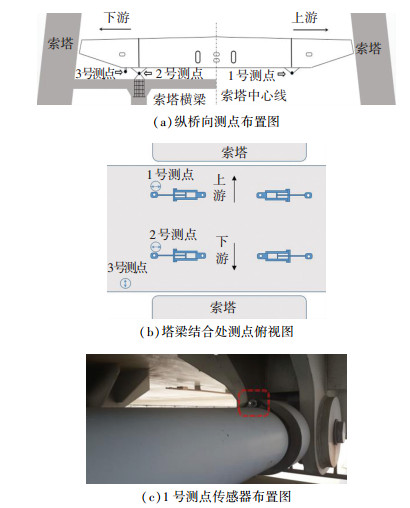
试验选取在温度15~20 ℃,风速3~4级的条件进行,测点位置位于苏通大桥北桥塔北侧的塔梁阻尼器,试验时共设有3个测点,其中1号测点位于上游,2号测点位于下游,传感器安装在与主梁固结的阻尼器活塞杆处,用于测量主梁的纵向振动,3号测点安装在主梁下部构造处,用于测量主梁的横向振动,见图 4.本文主要分析数据来自两个纵桥向的加速度传感器采集的主梁纵桥向随机振动数据.试验选用KD12000L型IC超低频加速度传感器,该加速度传感器具有量程小(0~0.2g)、灵敏度高(20 V/g)的特点,可测的频率范围为0.01~400 Hz.
|
图 4 测点布置 Fig. 4 Measuring point arrangement |
设置采样频率为128 Hz,将采样的时间定为3 600 s.按照同一试验标准,分别在2014年4月17日、2015年4月27日、2016年11月9日,进行3次试验,以观察系统阻尼比随时间的变化趋势.
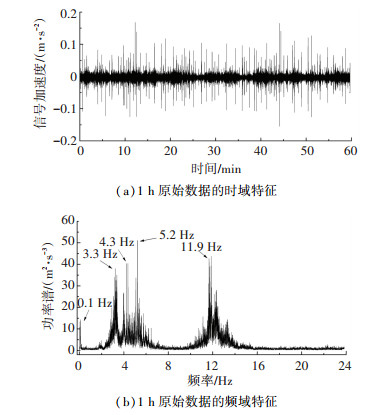
5 数据分析首先分析了原始数据时域的波动情况和频域的功率谱情况. 图 5选取了2014年试验数据,5(a)为时域特征,5(b)为频域特征.从时域角度可以看出振动数据具有较强随机性;频域上反映出在随机环境激励下,有几个频率峰值能量比较集中,第1个峰值就是在贴近0 Hz附近,该频率最接近于主梁一阶纵向振动的频率.在2~6 Hz和10~14 Hz也出现比较明显的能量峰值.根据文献[15-16]研究的车辆振动特性可知,车身的弹跳影响的振动频率一般在1.5~4.9 Hz,车轮跳动的造成的振动频率大约为7.5~19.6 Hz.因此主梁在这两个频率区间的是由车辆振动激励的,可能由于车型、车速、路面情况稍有不同导致主梁振动频率稍有不同.为了更好的提取主梁一阶纵飘振动响应,需采用合理的方法对数据进行处理.
|
图 5 测量原始数据特征 Fig. 5 Characteristics of the measured raw data |
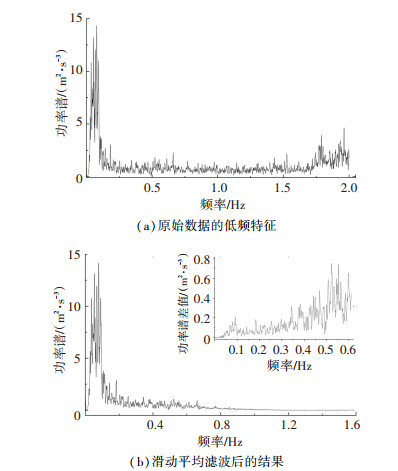
按半漂浮体系设计的苏通大桥主梁出现的第一阶模态是纵飘模态,其频率低于0.1 Hz.如果直接保留2 Hz以下的功率谱,如图 6(a),在所需的频率附近有其他频率成分的干扰,会导致最后的阻尼比拟合受到影响,因此需要适当的滤波方法保留低频数据.
|
图 6 数据低频特征以及滑动平均后的滤波结果 Fig. 6 Low frequency characteristics and the filtered results after moving average |
经典的低频滤波方法有很多,比如限幅滤波法、算数平均滤波法、加权平均滤波法等[17].本文先采用了滑动平均滤波方法,为了达到低于1 Hz滤波区间,选取128个数据作为滑动数据队列,并将滤波结果画在图 6(b).从结果中看出,滑动滤波尽管也能大幅度抑制高频信号,但是对低频信号也有很大的影响,同样会对拟合结果产生一定影响.考虑需要限制高频信号的同时减少对低频信号的影响,采用滤波区间更精准的离散小波变换滤波.
5.2 离散小波变换滤波在分析过程中,首先要选择合适的小波基,为了能够更好的重建信号,选取了具有紧支撑双正交Coiflet小波,Coiflet小波具有更好的对称性,支承长度相对较长,消失矩数目更高[18].
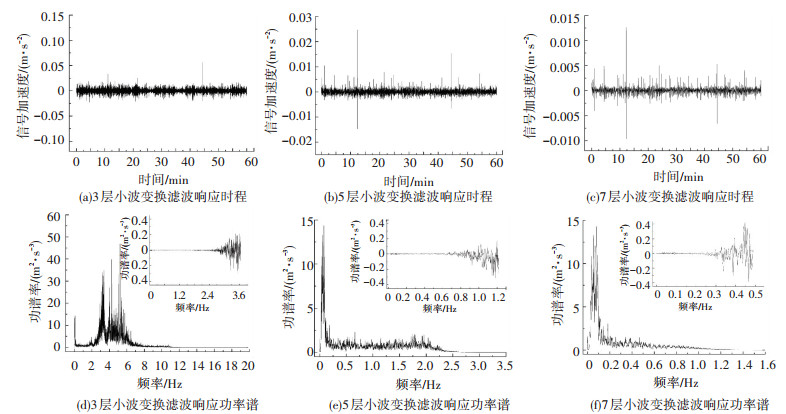
图 7为数据进行了不同层数的Coiflet小波分解,通过层数的增加观察数据在时域和频域下的变化.从图 7中可以看出,随着小波分解层数的逐步增加,时域上看,振动信号中一些幅值较大的非主梁纵飘数据逐渐剔除;频域上看,滤波后低通范围逐渐在减小,由第3层分解后低通的0~12 Hz,变为第5层分解后低通的0~2.5 Hz,再到第7层分解后低通的0~1.2 Hz.同时通过比较与原功率谱的差值,如图 7(d)~7(f)中的功率谱差值变化所示,可以看出,在3层、5层乃至7层分解时,0~0.3 Hz频率范围内的信号功率谱能量滤波变化差值均小于0.05,即小波变换方法滤波对此频段的能量几乎不产生影响,可见该方法对信号的滤波效果较好.
|
图 7 经过不同层小波分解重构滤波后的信号时域和频域的特征变化 Fig. 7 Time and frequency domain characteristics of signal reconstructed with wavelet transform filters of different layers |
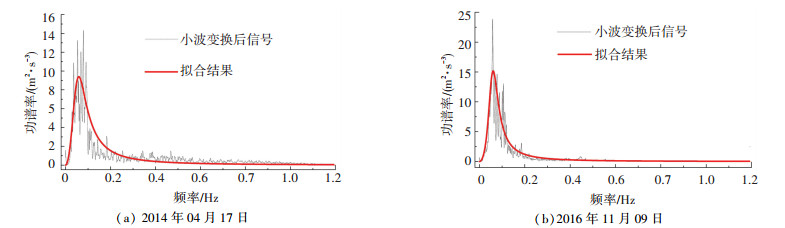
将经7层小波变换滤波后的结构振动响应功率谱按照2.2节中推导的式(11)进行参数拟合.以图 8(a)中2014年测量1号测点数据和图 8(b)中2016年测量的1号测点数据为例,可以看出拟合的曲线与功率谱吻合很好.同时,为了避免一次试验的偏差,本文将两个测点的结果分别计算并取平均值列在表 1中.通过表中的数据可以看出同一个时间段下,一个小时内两个测点的白噪声功率比较接近,而不同的时间段,白噪声的数量略有不同. 3段时间下识别出的主梁一阶纵向振动频率的数值很接近,并且与成桥报告中的一阶纵向频率0.060 Hz[19]和有限元模拟的一阶纵向频率0.063 7 Hz也比较接近,验证了测量数据的正确性.
|
图 8 1号测点2次试验下的数据拟合结果 Fig. 8 Fitted curves of No.1 point data for two experiments |
| 表 1 滤波后一阶纵向频率与阻尼比识别结果 Tab. 1 Identification results of first-order longitudinal vibration frequency and damping ratio |
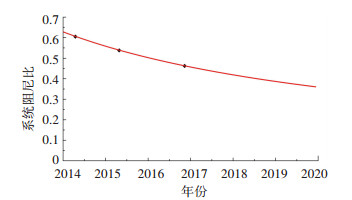
将3次试验的时间为横坐标,识别系统阻尼比为纵坐标,如图 9所示,并用反比例函数对系统阻尼比衰减进行拟合外推,发现阻尼比有不断衰减的趋势,同时衰减速度随着时间推移逐渐减慢.
|
图 9 系统阻尼比外推 Fig. 9 Extrapolation of system damping ratio |
苏通大桥的阻尼器按照Maxwell阻尼模型设计,其阻尼力函数为F=CVα,其中阻尼系数C=3 750 kN、速度指数α=0.4.为了验证整个非线性体系的正确性并对阻尼性能加以研究,利用Midas桥梁有限元计算软件进行模拟.将阻尼器按照实桥位置和实桥参数设置在全桥模型中,对全桥进行纵向正弦振动激励,记录主梁在自由衰减状态下的时程位移响应,并计算出C和α不同取值的工况下主梁纵飘的系统阻尼比.
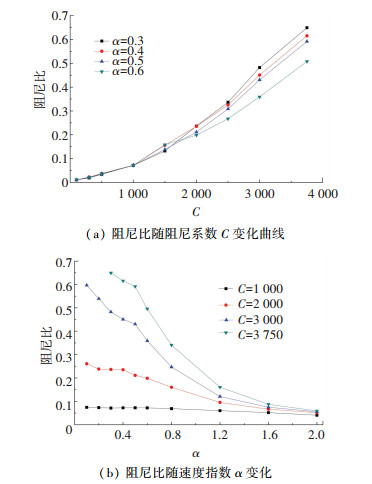
在有限元模型中调整Maxwell阻尼模型的两个参数,系统阻尼比也随之发生变化,将变化趋势画在图 10.从图中可以看出,系统阻尼比随着阻尼系数下降大幅下降,随着速度指数的上升也在逐渐下降.
|
图 10 阻尼比随参数变化 Fig. 10 Damping ratio fluctuations with parameters |
计算结果一方面与识别的系统阻尼比相近,验证了这一体系研究的正确合理性;另一方面可以看出,系统阻尼比下降直接说明决定阻尼器性能的C和α的两大参数与初始状态相比发生了变化,系统阻尼比的下降即代表阻尼器性能也随之衰退.
以目前的数据为基础,塔梁阻尼器阻尼比将在以后的寿命周期内继续衰减.受时间上的约束,本文只选取了3 a的数据进行了比对和预测.在随后的寿命周期内,系统阻尼比的变化趋势是否还以这个速度衰减,需间隔固定的时间采集更多的数据加以支持,才能更加准确的估计阻尼器性能的变化.根据苏通大桥养护管理部门长期对塔梁阻尼器外观的跟踪检查,发现存在少量阻尼器漏油现象,并且在许多桥梁的运营维护中,这一现象极为普遍.因此,本文提供的识别方法能够更好的帮助桥梁的养护管理部门,在外观检查基础上,更为有效的评估阻尼器的实际工作性能.对是否需要进行阻尼器液压油的补充、甚至阻尼器的更换具有重要的指导意义.
6 结论1) 可将大跨度斜拉桥纵向的一阶振动近似等效成为线性单自由度系统,并将环境激励近似为理想白噪声激励,基于所建立的随机白噪声激励下的响应功率谱函数,通过参数拟合方法可以获取系统频率和阻尼比进行识别.
2) 基于离散小波变换的滤波方法,将结构响应随机信号在频率上进行分解与重构,可以有效地保留随机结构响应中的低频振动响应.
3) 通过3 a内多次现场试验,发现系统阻尼比缓慢退化,基于Midas模型的模拟结果表明塔梁阻尼器的性能也在同步退化.以目前的数据分析结果进行外推,可以预测塔梁阻尼器随时间的衰减曲线.
4) 所提出的方法可以很好地对阻尼器性能进行监测,从而能够在塔梁阻尼器性能失效时,及时对其进行维修和更换;在塔梁阻尼器超出使用寿命后,为塔梁阻尼器的更换提供依据.
| [1] |
GEORGAKIS C T, GIMSING N J. Cable supported bridges: Concept and design[M]. 3rd ed. West Sussex: Wiley, 2012: 20.
|
| [2] |
PARK K S, JUNG H J, LEE I W. Hybrid control strategy for seismic protection of a benchmark cable-stayed bridge[J]. Engineering Structures, 2003, 25(4): 405. DOI:10.1016/S0141-0296(02)00182-7 |
| [3] |
AGRAWAL A K, YANG J N, HE W L. Applications of some semi active control systems to benchmark cable-stayed bridge[J]. Journal of Structural Engineering, 2003, 129(7): 884. DOI:10.1061/(ASCE)0733-9445(2003)129:7(884) |
| [4] |
张喜刚, 裴岷山, 袁洪, 等. 苏通大桥主桥结构体系研究[J]. 中国工程科学, 2009, 11(3): 20. ZHANG Xigang, PEI Minshan, YUAN Hong, et al. Study on structural system of Sutong Bridge[J]. Engineering Sciences, 2009, 11(3): 20. DOI:10.3969/j.issn.1009-1742.2009.03.004 |
| [5] |
马良喆, 陈永祁. 对液体粘滞阻尼器动力性能及测试要求的研究及探讨[J]. 建筑结构, 2008, 38(5): 65. MA Liangzhe, CHEN Yongqi. Research and investigation on dynamic performance and testing requirements of liquid viscous dampers[J]. Building Structure, 2008, 38(5): 65. |
| [6] |
Taylor粘滞阻尼器性能试验报告[R].哈尔滨: 哈尔滨工业大学力学与结构实验中心, 2005 Taylorviscous damper performance test report[R] Harbin: Mechanical and Structural Experiment Center, Harbin Institute of Technology, 2005 |
| [7] |
韩万水, 黄平明, 兰燕. 斜拉桥纵向设置粘滞阻尼器参数分析[J]. 地震工程与工程振动, 2005, 25(6): 146. HAN Wanshui, HUANG Pingming, LAN Yan. Parametric analysis of cable-stayed bridge with longitudinal viscous dampers[J]. Journal of Earthquake Engineering and Engineering Vibration, 2005, 25(6): 146. DOI:10.3969/j.issn.1000-1301.2005.06.025 |
| [8] |
聂利英, 郭其远, 李建中. 设置纵向大型液体粘滞阻尼器的大跨斜拉桥主梁纵向运动阻尼水平研究[J]. 工程力学, 2015, 32(9): 141. NIE Liying, GUO Qiyuan, LI Jianzhong. Longitudinal damping level of girder motion of long-span cable stayed bridge with large longitudinal fluid viscous dampers[J]. Engineering Mechanics, 2015, 32(9): 141. DOI:10.6052/j.issn.1000-4750.2014.02.0119 |
| [9] |
焦驰宇, 李建中, 彭天波. 塔梁连接方式对大跨斜拉桥地震反应的影响[J]. 振动与冲击, 2009, 28(10): 179. JIAO Chiyu, LI Jianzhong, PENG Tianbo. Effects of different connecting styles between towers and deck on seismic responses of a long-span cable-stayed bridge[J]. Journal of Vibration and Shock, 2009, 28(10): 179. DOI:10.3969/j.issn.1000-3835.2009.10.036 |
| [10] |
SONEJI B B, JANGID R S. Passive hybrid systems for earthquake protection of cable-stayed bridge[J]. Engineering Structures, 2007, 29(1): 57. |
| [11] |
TERENZI G. Dynamics of SDOF systems with nonlinear viscous damping[J]. Journal of Engineering Mechanics, 1999, 125(8): 956. DOI:10.1061/(ASCE)0733-9399(1999)125:8(956) |
| [12] |
李国豪. 桥梁结构稳定与振动[M]. 北京: 中国铁道出版社, 2002: 123. LI Guohao. Stability and vibration of bridge structure[M]. Beijing: China Railway Publishing House, 2002: 123. |
| [13] |
FUGAL D L. Conceptual wavelets in digital signal processing: An in-depth, practical approach for the non-mathematician[M]. 1st ed. San Diego, California: Space & Signals Technical Publishing, 2009: 87.
|
| [14] |
MALLAT S G. A wavelet tour of signal processing: the sparse way[M]. 3rd ed. Amsterdam: Elsevier/Academic Press, 2009: 12.
|
| [15] |
HONG Hao. Analytical modeling of traffic-induced ground vibrations[J]. Journal of Engineering Mechanics, 1998, 124(8): 921. DOI:10.1061/(ASCE)0733-9399(1998)124:8(921) |
| [16] |
HUNT H. Modeling of road vehicles for calculation of traffic-induced ground vibration as a random process[J]. Journal of Sound & Vibration, 1991, 144(1): 41. |
| [17] |
RIOUL O, VETTERLI M. Wavelets and signal processing[J]. IEEE Signal Processing Magazine, 2002, 8(4): 14. |
| [18] |
张德丰. MATLAB小波分析[M]. 北京: 机械工业出版社, 2009: 76. ZHANG Defeng. MATLAB wavelet analysis[M]. Beijing: China Machine Press, 2009: 76. |
| [19] |
刘剑锋, 张启伟, 章关永.苏通大桥运营阶段动力特性参数变异性研究[C]//第十届全国振动理论及应用学术会议.南京: 南京航空航天大学, 2011: 45 LIU Jianfeng, ZHANG Qiwei, ZHANG Guanyong. Variability in dynamic properties of the Sutong cable-stayed bridge under routine traffic conditions[C]. Proceedings of the 10th National Conference on Vibration Theory and Application. Nanjing: Nanjing University of Aeronautics and Astronautics, 2011: 45 |
 2019, Vol. 51
2019, Vol. 51


