中国现役的钢-混凝土组合梁桥有很多是根据20世纪70年代或80年代初期颁布的设计标准建造的,其设计荷载等级偏低.随着交通量日益增长、重型车辆增多以及超载、超限现象严重,加之钢材腐蚀、混凝土劣化、附属设施病害等因素,早期修建的组合结构桥梁有很多已不能适应现代交通的需求.对这部分桥梁进行加固和修复,提高其承载能力,确保公路交通安全,是目前和今后桥梁工程界面临的主要任务之一.在传统加固方法的基础上,研究开发新的、更有效的加固技术成为国内外桥梁加固领域研究者的工作重点.
碳纤维增强复合材料(CFRP)问世于20世纪60年代,最早应用于航天领域[1].自1991年,瑞士联邦材料实验室(EMPA)首次将CFRP用于Ibach桥加固试验[2]获得成功,从此掀起了碳纤维材料在土木工程中的发展热潮.作为结构加固材料,其高强、轻质、耐腐蚀、抗疲劳性能、施工便捷的优点得到充分发挥[3-4].碳纤维片材(laminate)包括布材(sheet)和板材(plate)两种形式[5],在构件受拉薄弱区直接粘贴碳纤维布的加固方法曾在我国盛行一时,但随着研究深入,逐渐被加固量大、损失率小、性能稳定的碳纤维板所淘汰[6-7].预应力技术能完美匹配高强纤维的力学特点,克服应变滞后的先天性不足,提高材料利用效率.
国内外学者关于上述加固方法开展了一些有益的探索:文献[8]进行了预应力CFRP布加固箱形钢-混凝土组合梁力学性能的理论分析,文献[9]提出了碳纤维片材加固钢-混凝土组合梁承载力极限状态的计算方法,文献[10]进行了CFRP板加固工字形钢-混凝土组合梁的静力性能试验,文献[11]设计和试制了一套适用于钢-混凝土组合梁加固的预应力FRP片材锚具.目前,国内针对预应力碳纤维板加固钢-混凝土组合梁的锚具研究处于起步阶段[12],工艺尚不成熟,相关理论及计算方法亦存在空白.鉴于此,本文开展钢-混凝土组合梁抗弯加固试验,为建立该类桥梁的加固设计方法提供试验依据.
1 试验方案 1.1 试件设计设计5根钢-混凝土组合简支梁缩尺试件,其中1根作为对比试件,不进行加固,其余4根采用预应力碳纤维板加固. 5根试件的原始参数相同:混凝土设计强度为C30,混凝土板宽500 mm,厚80 mm,配置两层Ф8的HPB300纵向钢筋,箍筋为Ф6@100 mm;钢梁牌号为Q235,梁高180 mm,工字钢上翼缘板宽160 mm,下翼缘板宽240 mm,腹板高160 mm,板厚均为10 mm.抗剪连接件为栓钉,钉杆直径13 mm,焊后长度60 mm;栓钉数量按完全抗剪连接设置,纵向等间距100 mm布置29排,每排横向中心距80 mm.试件全长3 200 mm,计算跨径3 000 mm,纯弯段600 mm,剪弯段1 200 mm.预应力碳纤维板宽度50 mm,厚度有2 mm和3 mm两种,粘贴长度1 800 mm.张拉时通过千斤顶的压力传感器和碳纤维板上的应变计双控,加载方式采用四点弯曲,布置情况见图 1.
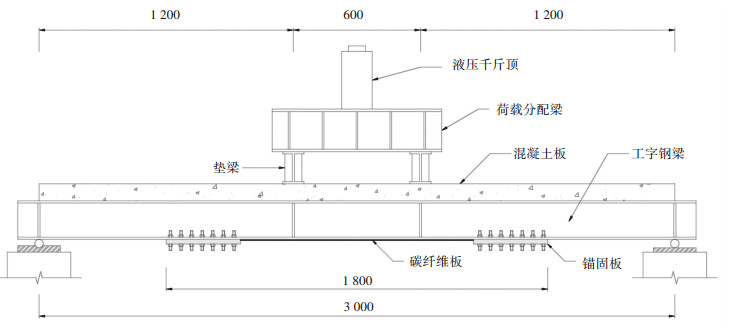
|
图 1 试件加载布置示意图(mm) Fig. 1 Load setup and specimen geometry (mm) |
5根试件编号为US-1、RS-1、RS-2、RS-3、RS-4. US-1为不进行任何加固的对比梁;RS-1采用宽50 mm×厚3 mm的碳纤维板加固,张拉至15%抗拉强度,初始拉力54 kN;RS-2至RS-4均采用宽50 mm×厚2 mm的碳纤维板加固,预应力水平分别为20%、30%、40%,初始拉力分别为48、72、96 kN,参数见表 1.
| 表 1 试件加固设计参数 Tab. 1 Strengthening parameters of test specimens |
锚固装置为课题组研发的用于钢梁锚固的装配式预应力碳纤维板锚固系统,其特点是各个部件构造精巧,便于现场装配;且张拉完成后,张拉组件均可从被加固梁上拆除,仅留一对锚固板在碳纤维板两端永久锚固.锚具尺寸小、张拉空间小,传力模式清晰、重复利用率高.锚固系统整体结构见图 2.

|
图 2 装配式预应力碳纤维板锚固系统 Fig. 2 Fabricated prestressed CFRP plate anchorage system |
经测试,组合梁试件的钢材拉伸屈服强度为283 MPa,混凝土立方体平均抗压强度为37.1 MPa,碳纤维板采用深圳市威士邦公司生产的WSB-TB系列碳纤维板,抗拉强度2 450 MPa,受拉弹性模量1.62×105 MPa,试验中与WSB-QT碳纤维复合板材胶配合使用,该环氧胶的抗拉强度可达到40.3 MPa.各类材料均采用实测结果的平均值计算,见表 2,其中fy为钢梁和钢筋屈服强度,fcu为混凝土立方体抗压强度,ff为碳纤维板抗拉强度.
| 表 2 材料性能 Tab. 2 Material properties |
本文试验的测试内容包括:1)组合梁跨中截面的应变(钢梁、混凝土板、钢筋);2)碳纤维板的纵向拉应变;3)跨中挠度和支座沉降;4)试件的屈服荷载与极限荷载.分别在钢梁上翼缘板顶面、腹板侧面和下翼缘板底面布置2片5 mm×3 mm的电阻应变计,共计6片.在混凝土板顶面布置3片100 mm×3 mm的电阻应变计,侧面布置1片100 mm×3 mm的电阻应变计,共计4片.沿碳纤维板中心线等距离布置3片5 mm×3 mm的电阻应变计,如图 3所示.此外,在跨中截面的纵向钢筋上布置3 mm×2 mm的电阻应变计.百分表安装在试验梁跨中截面下缘和两个支座截面上缘.加载装置采用100 t液压千斤顶,分级、平稳、缓慢加载.应变采集仪为东华DH3816N静态应力应变测试分析系统.

|
图 3 梁截面和碳纤维板测点布置(mm) Fig. 3 Locations of strain gauges on specimen and CFRP plate (mm) |
对比梁US-1在加载过程中钢梁底部首先达到屈服,之后跨中挠度增长速度加快,可观察到试件产生明显的弯曲变形.临近破坏时,混凝土板内受压钢筋屈服,混凝土板侧面出现纵向水平裂缝并逐渐连通扩展,上缘混凝土压碎,向上拱起,直至彻底压溃,停止加载.
加固梁RS-1加载到12 t之后,可听到轻微的环氧胶开裂的声音;加载到24 t之后,可观察到纯弯段碳纤维板与胶层之间出现局部细小的缝隙,同时发出较之前稍大的噼啪声;加载到30 t左右钢梁达到屈服,变形快速发展;加载到44 t时,跨中截面出现混凝土压酥现象,挠度急剧增长,梁整体纵向弯曲很大;荷载接近48 t时,混凝土顶面压碎,碳纤维板随即拉断,断口位于跨中,呈散丝状,两端锚固完好,无滑移迹象,见图 4(a).

|
图 4 预应力碳纤维板断裂/剥离现象 Fig. 4 Rupture and debonding of prestressed CFRP plates |
加固梁RS-2在加载过程中能间歇听到环氧胶开裂的脆响,加载初期不易察觉,至中后期愈发频繁也较之前明显.破坏过程为钢梁率先进入屈服,加载至46 t时混凝土板上缘压碎.试件破坏后经过数秒,碳纤维板从中部剥离,伴随有砰的剧烈响声,两端锚固完好,见图 4(b).
加固梁RS-3和RS-4在加载时同样发出局部轻微的脆响.钢梁下缘先受拉屈服,加载至破坏阶段跨中受压钢筋屈服、混凝土板上缘压碎.随后数秒内,碳纤维板沿横截面拉断,断裂位置靠近锚区,偏离跨中.碳纤维板断口平直光滑,未炸裂散丝,两端锚固完好,见图 4(c)、4(d).
2.2 破坏模式本文的4组加固试验结果表明:组合梁在加载过程中,均为钢梁下翼缘板首先受拉屈服,此后跨中挠度急剧增长;破坏阶段均为混凝土板顶面压碎,截面刚度迅速减小,碳纤维板随之失效.
预应力碳纤维板的破坏模式包括:1)碳纤维板拉断,断口呈散丝状(RS-1):散丝状断裂表明CFRP板受拉均匀,强度得到完全发挥,可视作CFRP板破坏的理想形式. 2)碳纤维板未拉断,于中部剥离(RS-2):环氧胶的弹性模量远小于纤维复合材料,当组合梁纵向弯曲很大时,由于跨中区域胶层较厚,碳纤维板容易在此处产生剥离. 3)碳纤维板拉断,断口呈平坦状(RS-3、RS-4):锚具附近的碳纤维板处于多重应力状态.极限状态下,碳纤维板截面的拉应力和剪应力均较高,最终形成薄弱部位发生横向断裂.
2.3 主要试验结果表 3给出了本文的主要试验结果,其中fc为混凝土轴心抗压强度,σf0为碳纤维板初始应变,Py和Pu分别为试件屈服荷载和极限荷载,ηy和ηu分别为屈服荷载和极限荷载的提高系数,最大跨中挠度wmax和碳纤维应变增量Δσf为试件破坏的前一级加载的实测值.
| 表 3 主要试验结果 Tab. 3 Main test results |
本文试验中,4根预应力碳纤维板加固的钢-混凝土组合梁发生了典型的受弯破坏.预应力碳纤维板的失效几乎与试验梁破坏同时发生,碳纤维板平均拉应变达到极限拉应变的80%以上.此外,试件破坏时整体纵向弯曲明显,受拉区钢梁和混凝土板内受压钢筋均已屈服,证明加固后的钢-混凝土组合梁仍具有较好的延性.
3 试验结果分析 3.1 试件抗弯承载力分析从试验结果可以看到,采用预应力碳纤维板加固钢-混凝土组合梁,对屈服承载力有一定的提高,RS-1至RS-4相较于对比试件分别提高了8%、9%、13%和17%,呈梯度增长,其主要影响因素为预应力水平,即对应15%、20%、30%和40%的初始预应力.极限承载力的主要影响因素为碳纤维板截面面积,即补强材料的使用量.采用厚度2 mm规格碳纤维板提高极限承载力约20%,而采用厚度3 mm规格碳纤维板提高极限承载力约25%.基于可靠的锚固技术,试件破坏时CFRP板已经接近材料的抗拉强度,因此CFRP板的使用量对结构提载起关键作用.
3.2 碳纤维板应变分析在钢-混凝土组合梁屈服之前,碳纤维板的应变增量基本呈线性稳步增长,不同试件之间的应变差异较小.加载至30 t之后,钢梁逐渐进入屈服阶段,变形速度加快,碳纤维板的应变增量变化规律与之相协调,也呈急剧增长的趋势(图 5). RS-1至RS-4碳纤维板的初始应变分别为2 250×10-6、3 105×10-6、4 535×10-6和6 010×10-6,初始应变与应变增量的总和即碳纤维板的实际拉伸应变.实际拉伸应变与理论极限应变的比例分别为78.16%、75.98%、88.79%和86.60%,即碳纤维板的强度利用率.试验数据表明,高强纤维复合材料的抗拉特性在加固钢-混凝土组合梁时能得到充分发挥,在材料利用效率方面具有很大优势.

|
图 5 碳纤维板荷载-应变增量曲线 Fig. 5 Load-strain increment curves of CFRP plates |
图 6描绘了预应力碳纤维板加固试件RS-1至RS-4的跨中截面在不同荷载等级下,沿截面高度的混凝土板及钢梁的应变分布.可以清楚看到,在荷载等级较低时受拉区与受压区各点材料应变基本呈线性分布.当荷载超过36 t后,钢梁屈服、混凝土板内部产生破坏,中性轴位置基本不变,沿截面高度各点应变也近似呈线性分布,表明采用预应力碳纤维板加固的钢-混凝土组合梁的截面应变仍然符合平截面假定.
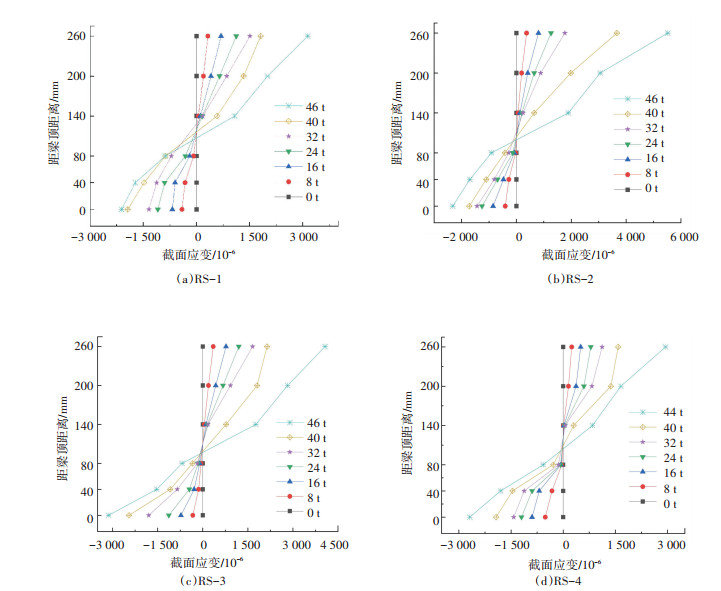
|
图 6 加固试件跨中截面应变分布 Fig. 6 Strain distribution along mid-span section |
图 7为5根试件US-1、RS-1至RS-4跨中截面的荷载-挠度曲线.由试验结果可知,采用预应力碳纤维板加固,对钢-混凝土组合梁的变形有一定的抑制作用.其挠度发展根据斜率不同大致分为两段:钢梁屈服前挠度值基本按线性规律增长,4根加固试件的挠度曲线斜率差异较小,加固试件的变形量均略小于不加固试件的变形量;钢梁屈服后挠度发展显著加快,破坏阶段RS-1至RS-4跨中挠度依次为41.38 mm、37.42 mm、33.46 mm和26.38 mm,表明最大变形量与预应力水平有关,即预应力水平越高,最大变形量越小.
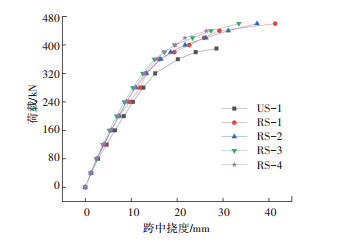
|
图 7 跨中截面荷载-挠度曲线 Fig. 7 Load-deflection curves at mid-span section |
混凝土是一种各向异性的非匀质材料,而钢材可以认为是理想的弹塑性材料,因此组合梁的截面弹性分析只适用于桥梁的正常使用极限状态.钢-混凝土组合梁的截面抗弯承载力可根据其在极限状态下的应力图假设,划分为塑性抗弯承载力和弹塑性抗弯承载力[13].
4.1 塑性抗弯承载力计算钢-混凝土组合梁按塑性方法计算的前提是截面能够形成塑性铰,使得结构能够充分转动和变形,最终形成破坏机构.为保证进行截面塑性计算,其钢材必须是软钢,且翼缘板和腹板的宽厚比应满足《钢-混凝土组合桥梁设计规范》[14]表5.1.1的要求,以避免稳定性破坏先于抗弯破坏.
钢-混凝土组合梁截面塑性抗弯承载力的计算基于如下假设:1)钢梁与混凝土板之间、碳纤维板与钢梁之间的连接可靠,能够保证材料强度充分发挥;2)位于塑性中性轴以下的混凝土受拉开裂,退出工作;3)位于塑性中性轴以上的混凝土,应力达到抗压强度,取矩形应力图计算;4)钢梁的受压区和受拉区均达到屈服强度,应力分布为矩形;5)碳纤维板的应力达到材料的抗拉强度.
在计算截面塑性抗弯承载力时,根据组合梁的塑性中性轴位置x的不同,可分为3种类型截面,见图 8.
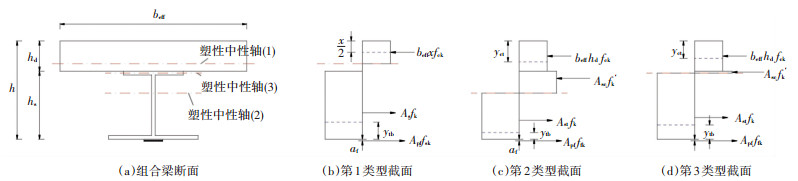
|
图 8 截面塑性抗弯承载力计算图式 Fig. 8 Plastic computing model of composite beam |
组合截面的塑性中性轴位于混凝土翼板内,判断条件为
| $ {b_{{\rm{eff}}}}{h_{\rm{d}}}{f_{{\rm{ck}}}} \ge {A_{\rm{s}}}{f_{\rm{k}}} + {A_{{\rm{pf}}}}{f_{{\rm{fk}}}}, $ | (1) |
加固截面的塑性中性轴位置及塑性抗弯承载力可由下列公式确定:
| $ {b_{{\rm{eff}}}}x{f_{{\rm{ck}}}} = {A_{\rm{s}}}{f_{\rm{k}}} + {A_{{\rm{pf}}}}{f_{{\rm{fk}}}}, $ | (2) |
| $ {M_{{\rm{pu}}}} = \left( {{A_{\rm{s}}}{f_{\rm{k}}} + {A_{{\rm{pf}}}}{f_{{\rm{fk}}}}} \right)\left( {h - {y_{{\rm{tb}}}} - x/2} \right). $ | (3) |
式中:Mpu为加固后组合截面塑性抗弯承载力;beff、hd分别为混凝土板的有效宽度和高度;As、Apf分别为钢梁、碳纤维板的截面面积;fck为混凝土抗压强度标准值;fk为钢梁屈服强度标准值;ffk为碳纤维板的抗拉强度标准值;h为组合梁的高度;ytb为组合截面受拉区合力作用点至钢梁下边缘的距离;af为碳纤维板的截面重心至钢梁下边缘的距离.
4.1.2 第2类型截面(x≥hd+t′)组合截面的塑性中性轴位于钢梁腹板中,判断条件为
| $ {b_{{\rm{eff}}}}{h_{\rm{d}}}{f_{{\rm{ck}}}} + 2{b_{{\rm{su}}}}t'{f_{\rm{k}}} \le {A_{\rm{s}}}{f_{\rm{k}}} + {A_{{\rm{pf}}}}{f_{{\rm{fk}}}}, $ | (4) |
加固截面的塑性中性轴位置及塑性抗弯承载力可由下列公式确定:
| $ \begin{array}{*{20}{c}} {{b_{{\rm{eff}}}}{h_{\rm{d}}}{f_{{\rm{ck}}}} + {b_{{\rm{su}}}}t'{f_{\rm{k}}} + \left( {x - {h_{\rm{d}}} - t'} \right){t_{\rm{w}}}{f_{\rm{k}}} = }\\ {\left( {h - x - t} \right){t_{\rm{w}}}{f_{\rm{k}}} + {b_{{\rm{s}}l}}t{f_{\rm{k}}} + {A_{{\rm{pf}}}}{f_{{\rm{fk}}}},} \end{array} $ | (5) |
| $ {M_{{\rm{pu}}}} = \left( {{A_{{\rm{st}}}}{f_{\rm{k}}} + {A_{{\rm{pf}}}}{f_{{\rm{fk}}}}} \right)\left( {h - {y_{{\rm{tb}}}} - {y_{{\rm{ct}}}}} \right). $ | (6) |
式中:bsu、bsl分别为钢梁上、下翼缘板的宽度;t′、t分别为钢梁上、下翼缘板的厚度;tw为钢梁腹板厚度;Ast为钢梁受拉区面积;yct为组合截面受压区合力作用点至混凝土板上边缘的距离.其他符号意义同前.
4.1.3 第3类型截面(hd < x < hd+t′)此外,还有可能出现塑性中性轴位于钢梁上翼缘板内的情况,判断条件为
| $ {b_{{\rm{eff}}}}{h_{\rm{d}}}{f_{{\rm{ck}}}} < {A_{\rm{s}}}{f_{\rm{k}}} + {A_{{\rm{pf}}}}{f_{{\rm{fk}}}} < {b_{{\rm{eff}}}}{h_{\rm{d}}}{f_{{\rm{ck}}}} + 2{b_{{\rm{su}}}}t'{f_{\rm{k}}}, $ | (7) |
加固截面的塑性中性轴位置及塑性抗弯承载力可由下列公式确定:
| $ {b_{{\rm{eff}}}}{h_{\rm{d}}}{f_{{\rm{ck}}}} + 2{b_{{\rm{su}}}}\left( {x - {h_{\rm{d}}}} \right){f_{\rm{k}}} = {A_{\rm{s}}}{f_{\rm{k}}} + {A_{{\rm{pf}}}}{f_{{\rm{fk}}}}, $ | (8) |
| $ {M_{{\rm{pu}}}} = \left( {{A_{{\rm{st}}}}{f_{\rm{k}}} + {A_{{\rm{pf}}}}{f_{{\rm{fk}}}}} \right)\left( {h - {y_{{\rm{tb}}}} - {y_{{\rm{ct}}}}} \right). $ | (9) |
当组合梁在弹塑性状态下的变形零点c位于钢梁腹板内时,可根据图 9的计算图式建立考虑钢梁弹性核心影响的组合截面抗弯承载力计算方法.计算中以下列基本假设为基础:1)截面应变符合平截面假定;2)钢梁与混凝土板之间、碳纤维板与钢梁之间的连接可靠,能够保证材料强度充分发挥;3)在极限状态下,受压混凝土板上边缘的应变达到其极限压应变εcu;4)受压区混凝土取矩形应力图计算,应力取其抗压强度标准值fck,高度取x=hd;5)将钢梁视为理想的弹塑性体,在极限状态下,钢梁的应力为:当|εs| < fk/Es时,取σs=εsEs,当|εs| ≥fk/Es时,取σs=fk;6)碳纤维板为线弹性材料,其应变取钢梁下翼缘板底面的应变,其应力由胡克定律计算.
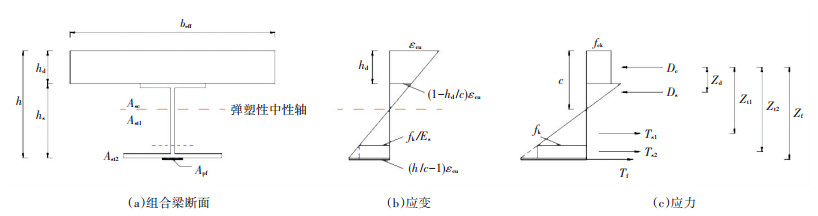
|
图 9 截面弹塑性抗弯承载力计算图式 Fig. 9 Elastic-plastic computing model of composite beam |
根据内力平衡条件可以得到基本方程为
| $ \begin{array}{*{20}{c}} {\sum {N = 0} ,{D_{\rm{c}}} + {D_{\rm{s}}} = {T_{{\rm{s1}}}} + {T_{{\rm{s2}}}} + {T_{\rm{f}}},}\\ {\sum {M = 0} ,\;\;\;\;{M_{{\rm{epu}}}} = - {D_{\rm{s}}}{Z_{\rm{d}}} + {T_{{\rm{s1}}}}{Z_{{\rm{t1}}}} + {T_{{\rm{s2}}}}{Z_{{\rm{t2}}}} + {T_{\rm{f}}}{Z_{\rm{f}}}.} \end{array} $ | (10) |
式中:Mepu为考虑钢梁弹性核心影响的截面抗弯承载力;Dc为受压混凝土合力,Dc=beffhdfck;Ds为受压区钢梁合力,一般情况下钢梁受压区部分均达不到屈服,故取Ds=∫AscσscdAs;Ts1为受拉弹性区钢梁的合力,有Ts1=∫Ast1σstdAs;Ts2为受拉塑性区钢梁的合力,Ts2=fkAst2;Tf为碳纤维板拉应力的合力;Asc为钢梁受压区截面面积;Ast1、Ast2分别为受拉弹性区、受拉塑性区钢梁的截面面积;Zd为受压区钢梁的合力作用点至受压混凝土合力作用点的距离;Zt1、Zt2分别为受拉弹性区、受拉塑性区钢梁合力作用点至受压混凝土合力作用点的距离;Zf为碳纤维板合力作用点至受压混凝土合力作用点的距离.
在上述式中,Ds、Ts1、Ts2和Tf均可利用平截面假设,通过变形零点至上边缘的距离c表示,将其代入式(10)的∑N=0中,即可求得未知数c.这样,面积Asc、Ast1和Ast2即为已知,上述合力及其力臂Zd、Zt1和Zt2亦可求出.将计算结果代入式(10)的∑M=0中,即可求得考虑钢梁弹性核心影响的组合梁弹塑性抗弯承载力Mepu.
4.3 计算结果对比分析根据上述计算方法,以试验的实测值代替公式中的标准值,将本文组合梁试件截面塑性抗弯极限承载力及弹塑性抗弯承载力的理论值与试验值列于表 4.
| 表 4 抗弯极限承载力理论值与试验值对比 Tab. 4 Comparison of analytical values and test results |
塑性理论认为钢梁的受压区和受拉区均已达到完全塑性,其应力沿梁高方向均匀分布,并取矩形应力图计算.事实上,这种假设与实际情况是存在差异的.例如靠近钢梁下翼缘部分的应变较大,可能已经超过屈服应变而进入强化阶段.若不考虑这部分钢材的强化应力,计算结果是偏于安全的.另一方面,在中性轴附近的钢梁应变较小,仍处于弹性阶段.显然,对于弹性核心部分的钢梁,取屈服强度计算其承载力是偏于不安全的.但是这部分合力的力臂很小,对抗弯承载力的影响有限.因此,采用截面塑性计算方法,不仅能简化计算过程,经试验证明亦具有足够的准确性.抗弯极限承载力的理论值与试验值之比大于90%,在工程计算中这种假设是可以接受的.
5 结论1) 预应力碳纤维板加固钢-混凝土组合梁受弯性能试验的研究表明,该加固方法能有效提高钢-混凝土组合梁的抗弯极限承载力,进而提高组合梁的承载能力.建议采用塑性方法计算加固后钢-混凝土组合梁的抗弯极限承载力,试验结果与理论计算吻合良好.
2) 预应力碳纤维板加固法可一定程度上抑制结构变形发展,改善钢-混凝土组合梁的正常使用性能,截面应变分布基本符合平截面假定.
3) 预应力碳纤维板加固钢-混凝土组合梁技术能有效利用纤维复合材料的高抗拉特性.组合梁试件加载至极限状态时,碳纤维板可以达到散丝状断裂,是一种材料利用效率较高的主动加固方法.
4) 预应力碳纤维板加固钢-混凝土组合梁技术须建立在可靠锚具的基础上.试验表明,本文采用的装配式预应力碳纤维板锚固系统在组合梁的破坏阶段仍可保持锚固端完好,锚固装置具有工程应用价值.
| [1] |
李威, 郭权锋. 碳纤维复合材料在航天领域的应用[J]. 中国光学, 2011, 4(3): 201. LI Wei, GUO Quanfeng. Application of carbon fiber composites to cosmonautic fields[J]. Chinese Optics, 2011, 4(3): 201. DOI:10.3969/j.issn.2095-1531.2011.03.001 |
| [2] |
MEIER U. Carbon fiber-reinforced polymers: modern materials in bridge engineering[J]. Structural Engineering International, 1992, 2(1): 7. DOI:10.2749/101686692780617020 |
| [3] |
ASLAM M, SHAFIGH P, JUMAAT M Z, et al. Strengthening of RC beams using prestressed fiber reinforced polymers-A review[J]. Construction and building materials, 2015, 82: 235. DOI:10.1016/j.conbuildmat.2015.02.051 |
| [4] |
岳清瑞, 陈小兵, 牟宏远. 碳纤维材料(CFRP)加固修补混凝土结构新技术[J]. 工业建筑, 1998, 28(11): 1. YUE Qingrui, CHEN Xiaobing, MOU Hongyuan. New technology of carbon fibre reinforced plastics on strengthening & repairing concrete structures[J]. Industrial Construction, 1998, 28(11): 1. DOI:10.3321/j.issn:1000-8993.1998.11.001 |
| [5] |
结构加固修复用碳纤维片材: JG/T 167—2016[S].北京: 中国标准出版社, 2016 Carbon fiber laminate for strengthening and restoring structures: JG/T167—2016[S]. Beijing: Standards Press of China, 2016 |
| [6] |
张树仁. 桥梁病害诊断与加固设计[M]. 北京: 人民交通出版社, 2013: 85. ZHANG Shuren. Disease diagnosis and reinforcement design of bridges[M]. Beijing: China Communications Press, 2013: 85. |
| [7] |
薛伟辰, 曾磊, 谭园. CFRP板加固混凝土梁试验与设计理论[J]. 哈尔滨工业大学学报, 2009, 41(12): 88. XUE Weichen, ZENG Lei, TAN Yuan. Experimental and theoretical studies on concrete beams strengthened with CFRP plates[J]. Journal of Harbin Institute of Technology, 2009, 41(12): 88. DOI:10.3321/j.issn:0367-6234.2009.12.017 |
| [8] |
王德选.预应力CFRP布加固钢箱梁与混凝土组合梁力学性能[D].沈阳: 东北大学, 2009 WANG Dexuan. Mechanical performance of steel-concrete composite beams strengthened with prestressing CFRP sheets[D]. Shenyang: Northeastern University, 2009 http://cdmd.cnki.com.cn/Article/CDMD-10145-2010055512.htm |
| [9] |
荣学亮, 黄侨. 碳纤维加固钢-混凝土组合梁承载力极限状态计算[J]. 科学技术与工程, 2011, 11(27): 6756. RONG Xueliang, HUANG Qiao. Analysis of ultimate load-carrying capacity of strengthening steel-concrete composite beam using carbon fiber[J]. Science Technology and Engineering, 2011, 11(27): 6756. DOI:10.3969/j.issn.1671-1815.2011.27.056 |
| [10] |
AL-SAIDY A H, KLAIBER F W, WIPF T J. Strengthening of steel-concrete composite girders using carbon fiber reinforced polymer plates[J]. Construction and Building Materials, 2007, 21(2): 295. DOI:10.1016/j.conbuildmat.2005.08.018 |
| [11] |
EL-HACHA R, ALY M Y E. Anchorage system to prestress FRP laminates for flexural strengthening of steel-concrete composite girders[J]. Journal of Composites for Construction, 2012, 17(3): 324. |
| [12] |
万世成, 黄侨. 钢梁预应力碳纤维板新型张拉锚具的设计和数值分析[J]. 工业建筑, 2017, 47(12): 181. WAN Shicheng, HUANG Qiao. Structure design and numerical analysis of new anchorage for prestressed CFRP plates in reinforcement of steel girder[J]. Industrial Construction, 2017, 47(12): 181. |
| [13] |
黄侨. 桥梁钢-混凝土组合结构设计原理[M]. 2版. 北京: 人民交通出版社, 2017: 62. HUANG Qiao. Design principle of bridge steel-concrete composite structure[M]. 2nd ed. Beijing: China Communications Press, 2017: 62. |
| [14] |
钢-混凝土组合桥梁设计规范: GB 50917—2013[S].北京: 中国计划出版社, 2013 Code for design of steel and concrete composite bridges: GB 50917—2013[S]. Beijing: China Planning Press, 2013 |
 2019, Vol. 51
2019, Vol. 51


