2. 中交公路规划设计院有限公司, 北京 100088;
3. 交通运输部公路科学研究所, 北京 100088
2. CCCC Highway Consultants Co., Ltd., 100088 Beijing, China;
3. Research Institute of Highway Ministry of Transport, 100088 Beijing, China
研究表明,在纷繁复杂的各类桥梁损毁事故中,桥梁基础冲刷往往是最主要的原因之一.文献[1]与文献[2]在各自研究中给出结论:大约60%的桥梁损毁与基础冲刷有关.随着社会经济的高速发展,越来越多的大跨度缆索支承桥梁建成、通车,尤其是近年来兴建的一系列跨江跨海大桥,大多采用大型群桩基础,而且往往水深桩高.同时水文地址环境比起普通河流更为复杂,水流变化更为激烈,河床中不利于工程的淤质土层更厚.显然,复杂水文环境下的桥梁基础冲刷变化较大,水下支承边界的设计预期与实际情况可能发生明显偏差,从而降低结构的整体稳定性,使得运营期间存在桥梁结构水毁倒塌的可能[1-4].
水下作业仍是既有桥梁基础冲刷检测或监测的主要手段,除了潜水员肉眼观测以外,各种水下监测设备也很常见,包括时域反射技术、FBG传感器、滑动磁环、压力陶瓷传感器、主动温度测试法、以及磁感应传感器等[5-10].但尚存在水下安装操作难、经济性差、无法识别冲刷回填等缺点[11-12].故亟需一种简单便捷的桥梁基础冲刷检测方法,可用于运营阶段的桥梁基础冲刷状态快速检测与长期监测,其判断结果也可作为特定桥梁基础进一步水下检测的理论依据,从而实现大范围区域性的桥梁冲刷状态检测.
事实上,桥梁基础冲刷直接对结构支承边界条件产生影响,可直接改变上部结构的整体刚度以及动力特性.显然,通过跟踪上部结构动力特性来反演桥梁基础的冲刷状态具有理论上的可行性[13-16].但是,桥梁结构实际状态与参数通常未知,同时水下基础、水文环境、地基状况以及三者之间的相互作用异常复杂,难以直接得到与实际桥梁状态相符的冲刷数值模型,更无法以此得到动力特性与冲刷状态之间的理论关系来对运营阶段实际冲刷发展进行预测.所以该类研究现阶段仍仅限于定性分析,同时缺乏实际水下观测数据的验证.
本文提出一种基于实测模态变化的缆索支承桥梁基础冲刷模型更新方法,并在运营阶段的杭州湾大桥桥塔冲刷识别与检测中进行应用.分别于2013年、2016年两次进行环境振动下上部结构加速度数据采集及模态分析,得到对应的结构自振频率与振型;同时建立上、下部结构的数值模型.首先利用冲刷非敏感模态的实测自振频率对数值模型中的桩侧等效弹簧刚度进行模型更新,直至得到与实际相符的桩土边界条件.进而利用冲刷敏感模态自振频率在2013年6月至2016年6月期间的实测变化值,对数值模型中的基础冲刷深度进行模型更新,直至数值模拟变化与实测变化值相一致,从而定量识别出3 a中基础冲刷深度的发展.最后基于杭州湾大桥水下地形测量数据对其识别准确度进行验证,证明了该方法可解决长期以来需要水下作业才能完成桥梁基础冲刷检测的技术难题.
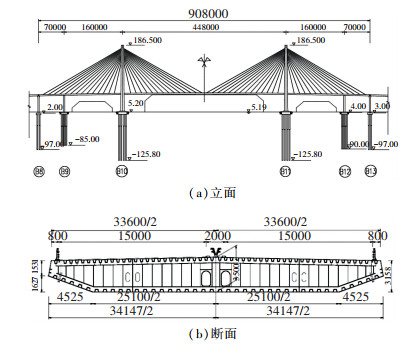
1 桥梁结构基本信息杭州湾大桥横跨我国杭州湾,全长约36 km,其中北航道桥是一座双塔双索面五跨连续半飘浮体系钢箱梁斜拉桥(图 1),桥长928 m,跨径布置为70 m+160 m+448 m+160 m+70 m,桥塔为钻石型塔,桥面以上塔高130.194 m,桥型布置见图 2.

|
图 1 杭州湾大桥北航道桥 Fig. 1 North channel bridge of the Hangzhou Bay Bridge |
|
图 2 桥梁结构布置图(尺寸单位:mm;标高单位:m) Fig. 2 Arrangement of bridge structure (Measurement unit: mm; elevation unit: m) |
主梁采用栓焊扁平钢箱梁,顶宽38.2 m,梁轴线处高3.5 m,不同位置顶板厚分别为14、16、20 mm,底板厚分别为12、14、16 mm,下斜腹板为20 mm,桥面顶板为正交异性板.钢箱梁横隔板标准间距为3.75 m.斜拉索为扇形双索面体系,索面由56对索组成,主梁索间距为15 m.
事实上,由于北航道桥所处杭州湾的水文环境异常复杂,例如:流速急、流向乱、潮汐强、潮差大,海床面泥沙冲淤状态变化迅速,桥墩对水流侵蚀海床的影响更为复杂.桥梁基础局部冲刷对结构安全一直存在潜在隐患,也是相关管理部门的重点关注对象.考虑到该桥已运营多年,桥梁基础(特别是桥塔位置)的冲刷深度可能明显发展.所以,杭州湾大桥北航道桥适合作为本文提出的基于实测模态与模型更新技术的桥梁基础冲刷识别方法的应用对象.
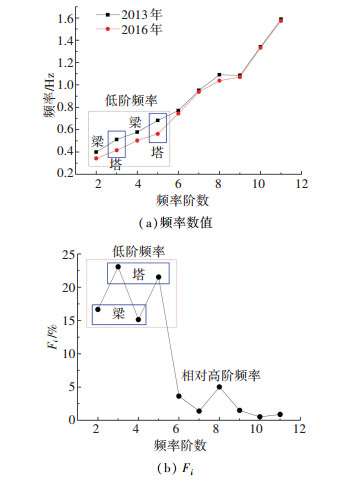
2 环境振动下的实测模态分析在杭州湾大桥北航道桥主梁箱梁内布设竖向加速度传感器共计33个,主要位于靠近腹板及横梁处(半桥);在主塔内布设横向加速度传感器共计18个,主要位于节段间内壁支承结构处.如果承台能够长期露出水面,也可布置加速度传感器于承台表面直接测试基础的振动响应.以大地脉动为环境激励荷载,分别于2013年与2016年针对各测点位置进行了两次现场加速度时程的采集工作.多个传感器分批次同步采集,每一次采集时间为20 min,采集频率为100 Hz,分别记录主梁测试点的竖向加速度时程以及主塔测试点的桥横向加速度时程. 图 3给出2013年与2016年针对杭州湾大桥北航道桥两次现场数据采集得到的前11阶振动模态的固有频率实测值.
|
图 3 2013年与2016年各阶自振频率对比 Fig. 3 Comparison of different natural frequencies from 2013 to 2016 |
从图 3中的对比可以看出,对于第2阶至第5阶的自振频率,不同时期分析结果具有明显差别.另外,基于图 3(a)中虚线框内的局部对比,该差别更显著体现在主塔低阶模态上.若定义固有频率变化率Fi表示频率的变化程度(Fi=Δωi/ωi,其中ωi、Δωi分别为第i阶自振频率以及该阶频率的变化值),并在图 3(b)中给出2013年6月至2016年6月期间各阶频率所对应的Fi数值,可见基于低阶自振频率(第2~5阶)计算得到的3 a(2013年6月至2016年6月)固有频率变化率Fi均大于15%,要明显高于高阶频率所对应的Fi数值(均低于5%).这是因为斜拉桥振动主要以低阶振动为主;又由于冲刷深度直接决定桥塔基础主要边界条件,导致3 a间低阶阵型中桥塔频率变化率要大于主梁变化率.
3 有限元模型构建 3.1 上部结构杭州湾大桥北航道桥上部结构采用ANSYS大型有限元软件进行建模,主梁选取beam4单元.钢箱梁采用高强钢材焊接制成,材料弹性模量为2.1×105 MPa,密度为7 850 kg/m3,泊松比取0.28.主梁采用等截面钢箱梁,截面形式复杂,箱室内包含94个U形肋,且上下分布的U形肋尺寸不同.截面面积为1.754 41 m2,竖向与横向惯性矩分别为3.52、217 m4,抗扭惯性矩为9.86 m4,风嘴总梁宽为37.1 m,梁高为3.5 m.主塔模型采用Beam4单元,选择C50混凝土的材料.弹性模量取3.45×104 MPa,泊松比取0.2,密度取2 420 kg /m3.斜拉索采用Link10单元,材料弹性模量为1.9×105 MPa,密度取钢材密度7 850 kg/m3,泊松比取0.28.各索单元的初应变按设计索力迭代确定,斜拉索弹性模量通过Ernst公式修正.
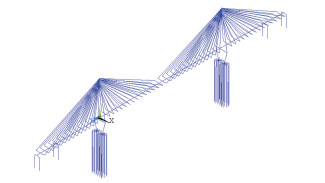
上部结构采用鱼骨法进行建模,主梁为线性单元,其与斜拉索的连接通过与主梁垂直的横梁实现,有限元模型如图 4所示.
|
图 4 全桥有限元模型 Fig. 4 Simulation model of the entire bridge |
水下基础模型采用Beam4单元,选择C30混凝土材料.弹性模量为3.0×104 MPa,泊松比取0.2,密度取2 385 kg/m3.每个主塔下布设桩基础为26个,直径为3.1 m,在标高-35 m处桩直径发生改变,缩小至2.8 m,单桩总长为131 m.
其中,为了模拟桩-土相互作用,在ANSYS有限元模型群桩基础每根单桩的桩身周围,除去承台到河床共约15 m桩身范围内,沿深度每隔0.5 m建立纵桥向与横桥向的水平约束,在桩底建立纵向、横向和竖向3个方向的约束,共233层.所有约束采用Combin14一维弹簧-阻尼器单元,如图 5所示.

|
图 5 桩土效应数值模拟 Fig. 5 Simulation of the pile-soil interaction effects |
桩土效应弹簧单元刚度K按弹性文克尔地基假定进行确定,深度z处桩侧土作用在桩上的水平抗力σz(kN/m)与该深度处桩身横向线位移uz之间的关系符合理想线弹性模型,即
| $ {\sigma _{\rm{z}}} = C{u_z}. $ | (1) |
式中:C为桩侧土水平抗力系数,或称水平基床系数或地基系数(kN/m3);C与深度z的关系采用m法,假定C-z分布模型为线性,按比例系数m(单位为kN/m4)随深度z线性增加,则有
| $ C = mz. $ | (2) |
另外,假设数值模型中冲刷层以下基础从上到下分为n个单元,每个单元的厚度为hj(j=1, 2,…,n),如图 6所示.

|
图 6 桩侧等效弹簧刚度计算图示 Fig. 6 Calculation of equivalent spring stiffness around the pile |
定义深度H处,桩侧土水平抗力系数为C(H),按式(2)得到C(H)=b0mH,其中b0为桩直径.则1号单元的节点1和节点2处桩侧等效弹簧刚度系数K1, 1、K1, 2的计算公式分别为
| $ {K_{1, 1}} = 0.5C({h_1}){h_1}/3 = C({h_1}){h_1}/6, $ | (3) |
| $ {K_{1, 2}} = 0.5C({h_1}){h_1} \cdot 2/3 = C({h_1}){h_1}/3. $ | (4) |
式中h1为1号单元的长度(深度).
而j(j > 1)号单元节点j和节点j+1处桩侧等效弹簧刚度系数Kj, j、Kj, j+1的计算公式分别为
| $ \begin{array}{l} {K_{j, j}} = C\left( {\sum\nolimits_{i = 1}^j {{h_i}} } \right){h_j}/2 + [C\left( {\sum\nolimits_{i = 1}^{j + 1} {{h_i}} } \right) - \\ \;\;\;\;\;\;\;\;\;\;C\left( {\sum\nolimits_{i = 1}^j {{h_i}} } \right)]{h_j}/6, \end{array} $ | (5) |
| $ \begin{array}{l} {K_{j, j + 1}} = C(\sum\nolimits_{i = 1}^j {{h_i}} ){h_j}/2 + [C(\sum\nolimits_{i = 1}^{j + 1} {{h_i}} ) - \\ \;\;\;\;\;\;\;\;\;\;\;\;C(\sum\nolimits_{i = 1}^j {{h_i}} )]{h_j}/3. \end{array} $ | (6) |
式中hj为j号单元的长度(深度).
将相邻两单元同一个节点上的桩侧等效弹簧刚度系数相加,可得到数值模型中各个Combin14一维弹簧-阻尼器单元的刚度取值为
| $ \left\{ \begin{array}{l} {K_1} = {K_{1, 1}}, \\ \cdots \\ {K_j} = {K_{j - 1, j}} + {K_{j, j}}, \\ \cdots \\ {K_{n + 1}} = {K_{n, n + 1}}. \end{array} \right. $ | (7) |
桩侧等效弹簧的刚度直接影响杭州湾大桥北航道桥的基础边界条件,该刚度的变化显然会改变桥梁整体刚度,从而导致动力特性发生变化.本研究通过在数值模型中不断改变桩侧等效弹簧刚度的数值,直至数值分析得到的全桥动力特性理论值与实测值一致,即数值模型中的桩土边界条件最接近于实际情况,来确定数值模型桩侧等效弹簧刚度的准确数值,从而完成桩侧等效弹簧刚度的模型更新工作.但是,由于基础冲刷的存在,桥梁整体刚度不仅由桩侧等效弹簧刚度决定,还会被基础冲刷深度的发展所影响.本研究为规避或尽量减小冲刷发展对全桥整体刚度的影响,在进行桩侧等效弹簧刚度模型更新时,仅选择冲刷非敏感模态作为更新目标进行刚度的更新,来确保更新过程中全桥模态参数的改变仅由唯一因素,即桩侧等效弹簧刚度的数值变化而引起的.
此处若将桥塔视为方向向上的“悬臂梁”,则该“悬臂梁”的动力特性直接与基础边界条件相关,该基础边界条件主要由桩侧土提供的桩-土刚度或冲刷深度决定.或者说,由于桩-土效应与冲刷深度变化对基础边界条件的改变方式不一样,对不同振动模态的影响也会不同.由图 3及相应分析可明显看出,2013年6月至2016年6月虽然发生冲刷,但第6、7、9、10、11阶模态所对应的自振频率并未发生明显变化,故本研究将该桥的第6、7、9、10、11阶模态确定为冲刷非敏感模态(为减少计算量,下文模型更新时仅选择第9、10、11阶模态,即主梁二阶反对称竖弯、主梁四阶正对称竖弯、以及主梁三阶反对称竖弯),它们的频率不会随冲刷深度的改变而发生改变,但却会对桩侧等效弹簧刚度的改变非常敏感.据此,杭州湾大桥北航道桥数值模型中桩侧等效弹簧刚度模型更新的具体步骤如下.
步骤1 根据设计资料,确定主塔下方群桩基础所在处土层分布,将土质相同的区域划分为一层,在桩土效应弹簧刚度计算时,同一层土的m值相同.查阅资料与规范[17],初步拟定各层土m值,见表 1第4列结果.按式(2)~(7)便可得到数值模型中桩侧等效弹簧刚度.
| 表 1 m初始取值与第24次迭代对应的更新数值 Tab. 1 Initial values of m and their updated values at the 24th iteration |
步骤2 以100 kN/m4的调整步长改变各土层m数值,随之调整数值模型中桩侧等效弹簧刚度,进而通过数值分析得到每一次刚度调整所对应的冲刷非敏感模态的自振频率数值.通过不断改变m数值,总共计算了33个工况,对应33种不同m数值的桩土模型.需要说明的是,各层仅采用相同的调整幅度,以达到简化更新过程的目的,在后续研究中将进一步细化.
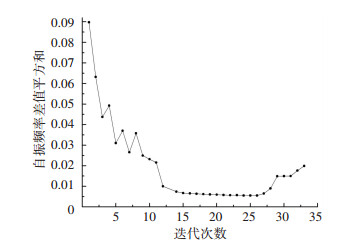
步骤3 计算步骤2得到的不同m数值下冲刷非敏感模态自振频率数值与实测值之间的差值.由于选择第9、10、11阶为冲刷非敏感模态,差值计算时采用以上3阶自振频率计算值与实测值之差的平方和作为两者间差别的定量表述.该差值随m的变化曲线见图 7,图中m以100 kN/m4步长增大.
|
图 7 自振频率差值平方和与迭代次数的关系 Fig. 7 Relationship between the sum of squares of frequency difference and the iteration times |
从图 7可以看出,随着数值模型中各层土m值的不断增大,冲刷非敏感模态(主梁二阶反对称竖弯、主梁四阶正对称竖弯、主梁三阶反对称竖弯)自振频率的数值计算与实测之间的差值平方和不断减小.这说明随各层土m值的增大,正在不断接近实际状况.
图 7还可看出,当各层土m值以100 kN/m4步长迭代至第24次,数值计算与实测的差值平方和达到最小.如果继续提高m值,差值平方和又会迅速增大.这说明继续增加各层土的m值会使基础边界条件又偏离实际情况.所以,迭代至第24次时所对应的的各层土m值最接近实际情况,具体数值见表 1第5列结果.此时,按式(2)~(7),数值模型中桩侧等效弹簧刚度的计算值见表 2(篇幅有限仅给出部分节点的刚度).由于基于实测振动响应数据进行模型更新,更新后m值已自动计入实际下部结构的群桩效应.
| 表 2 桩侧等效弹簧刚度更新值 Tab. 2 Updated equivalent spring stiffness around piles |
至此,通过模型更新得到符合杭州湾大桥北航道桥实际基础边界条件的桩侧等效弹簧刚度,为下一步的冲刷深度更新提供了准确的数值.
5 基础冲刷深度更新一旦确定桩侧等效弹簧刚度的准确数值,便使仅有基础冲刷深度能够显著改变杭州湾大桥北航道桥的动力特性.考虑到同一区域水下地形的变化不会差别太大,可假设两主塔冲刷深度相同.类似地,不断调整上一章节得到的数值模型中的冲刷深度,直至数值分析得到的全桥动力特性理论值与实测值一致,即数值模型中的基础冲刷深度最接近于实际情况,从而完成基础冲刷深度的模型更新工作,得到动力特性测量时对应的杭州湾大桥北航道桥冲刷深度.
同样,由图 3以及上文中针对图 3的分析,可以明显看出,2013年6月至2016年6月期间,第2、3、4、5阶模态所对应的自振频率发生明显变化,即该桥以第2、3、4、5阶模态为冲刷敏感模态(即主梁一阶对称竖弯、主塔一阶反向侧弯、主梁一阶反对称竖弯和主塔一阶同向侧弯),它们的频率随冲刷深度的改变而发生明显改变,却对桩土刚度的变化不敏感.所以本研究以第2、3、4、5阶模态为更新目标进行基础冲刷深度的更新.更新的具体步骤如下.
步骤1 将模型的初始冲刷状态定为2013年杭州湾大桥北航道桥的冲刷状态,即将局部冲刷线处基础标高定为-20.2 m,各土层桩侧等效弹簧刚度K值按上节更新过的K值设置.由于桩侧等效弹簧单元分布为每0.5 m一层,冲刷深度调整步长为0.5 m,共进行40次迭代.
步骤2 随着数值模型中每一次冲刷深度变化的迭代,针对第2、3、4、5阶冲刷敏感模态,分别得到冲刷深度发展d下的自振频率fd与2013年初始状态下自振频率f0之差,即fd-f0.令fd, i与f0, i分别为第i阶模态所对应的冲刷深度发展d以及2013年初始状态下的自振频率,构造新的对应于冲刷深度发展d的综合差值参数Fd=(fd, 2-f0, 2)2+(fd, 3-f0, 3)2+ (fd, 4-f0, 4)2+(fd, 5-f0, 5)2.
步骤3 同理,针对2013年与2016年两次现场实测得到各阶自振频率,亦可得对应于2013年6月至2016年6月实际冲刷深度发展变化的综合差值参数F=(f2016, 2-f2013, 2)2+(f2016, 3-f2013, 3)2+ (f2016, 4-f2013, 4)2+(f2016, 5-f2013, 5)2.其中f2013, i与f2016, i为基于2013年与2016年实测数据进行模态分析得到的第i阶自振频率.
步骤4 将基于数值模型与实测数据分别得到的Fd与F之间的差别与数值模型中冲刷深度更新之间的关系绘于图 8,图中更新步长为0.5 m.
|
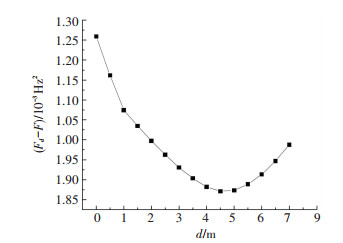
图 8 Fd与F的差值与数值模型冲刷深度的关系 Fig. 8 Relationship between the difference of Fd and F and the scour depth in the simulation model |
由图 8可以看出,在数值模型中的冲刷深度从0 m更新至4.5 m的过程中,第2、3、4、5阶模态(主梁一阶对称竖弯、主塔一阶反向侧弯、主梁一阶反对称竖弯和主塔一阶同向侧弯)的频率变化与基于2013年与2016年实测数据得到的频率变化之间的差别不断减小,表明数值模型中的基础冲刷深度与2013年6月至2016年6月杭州湾大桥北航道桥冲刷发展的实际数值不断接近.而当更新的冲刷深度继续增大时,两者差值又开始不断增大,表明此时模型中的冲刷深度又开始逐渐偏离实际状态.也就是说,数值模型中的基础冲刷深度更新至4.5 m时,数值分析得到的全桥动力特性理论值与实测值最为接近.
另外,表 3给出2016年实测自振频率与两次更新后桥梁模型计算频率在前11阶模态中的对比情况.表中可以看出,经过先后两次模型更新,更新后的计算频率与实测自振频率无论是“冲刷敏感模态”还是“冲刷非敏感模态”均比较接近,不仅证明了所提出的两次模型更新进行冲刷识别方法的科学性,同时也验证了“冲刷敏感”与“冲刷非敏感”模态定义的合理性.
| 表 3 2016年实测自振频率与更新后桥梁模型计算频率对比 Tab. 3 Comparison between natural frequencies from the measurements and the updated model in 2016 |
综上所述,根据上部结构的实测模态变化以及模型更新技术,4.5 m的基础冲刷深度发展最接近于2013年6月至2016年6月所发生的实际情况.也就是说,根据上部结构振动响应,杭州湾大桥北航道桥2013年6月至2016年6月所发生的冲刷深度最终识别为4.5 m.
6 冲刷深度识别验证相关测试部门同时采用多波束测深系统,进行了杭州湾大桥北航道桥水下地形全覆盖的测量工作. 2013年与2016年单侧主塔处水下地形测量标高分别为-20.2、-25.4 m,单侧边墩地形标高分别为-19.4、-23.4 m;故3 a间冲刷发展分别为5.2、4 m.可以看出单侧桥塔包括边墩处冲刷深度变化较为明显,该水下扫描测量数据与本文提出方法的识别结果4.5 m较为接近.
所以,通过实测与识别结果的对比,上文中利用上部结构实测数据分两步依次识别桩土效应以及冲刷深度的识别方法是可行的,识别结果是合理的,且具有较好的识别准确度.
7 结论1) 利用冲刷非敏感模态的实测自振频率对数值模型中的桩侧等效弹簧刚度进行模型更新,可以得到与实际相符的桩土边界条件.
2) 利用冲刷敏感模态的实测自振频率变化值,对有限元模型中的基础冲刷深度进行模型更新,直至数值模拟变化与实测变化值相一致,可以定量识别出桥梁基础冲刷深度的发展数值.
3) 上部结构(主梁、主塔)低阶振动模态对桥塔冲刷的发展更为敏感,高阶振动模态对桩侧等效弹簧刚度的变化更为敏感.
4) 通过与水下地形测试得到的冲刷数据进行对比,可以验证所提出的基于实测模态变化的桥梁基础冲刷识别方法的可行性与识别准确性.
| [1] |
RICHARDSON E V, DAVIS S. Evaluating scour at bridges[R]. Washington DC: ASCE, 2001
|
| [2] |
DENG L, CAI C. Bridge scour: prediction, modeling, monitoring, and countermeasures—review[J]. Practice Periodical on Structural Design and Construction, 2009, 15(2): 125. |
| [3] |
PRENDERGAST L J, GAVIN K. A review of bridge scour monitoring techniques[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2014, 6(2): 138. DOI:10.1016/j.jrmge.2014.01.007 |
| [4] |
XIONG W, TANG P B, KONG B, et al. Computational simulation of live-bed bridge scour considering suspended sediment loads[J]. Journal of Computing in Civil Engineering, ASCE, 2017, 31(5): 04017040. DOI:10.1061/(ASCE)CP.1943-5487.0000689 |
| [5] |
XIONG W, CAI C S, KONG X. Instrumentation design for bridge scour monitoring using fiber Bragg grating sensors[J]. Applied Optics, 2012, 51(5): 547. DOI:10.1364/AO.51.000547 |
| [6] |
LIN Y B, LAI J S, CHANG K C, et al. Using MEMS sensors in the bridge scour monitoring system[J]. Journal of the Chinese Institute of Engineers, 2010, 33(1): 25. DOI:10.1080/02533839.2010.9671593 |
| [7] |
WANG C Y, WANG H L, HO C C. A piezoelectric film type scour monitoring system for bridge pier[J]. Advances in Structural Engineering, 2012, 15(6): 897. DOI:10.1260/1369-4332.15.6.897 |
| [8] |
WU B, CHEN W L, LI H. Real-time monitoring of bridge scouring using ultrasonic sensing technology[C]//Proceeding of SPIE Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems. San Diego, California: The International Society for Optical Engineering, 2012
|
| [9] |
RADCHENKO A, POMMERENKE D, CHEN G D, et al. Real time bridge scour monitoring with magneto-inductive field coupling[C]//Proceeding of SPIE Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems. San Diego, California: The International Society for Optical Engineering, 2013
|
| [10] |
YU X B, YU X. Development and evaluation of an automation algorithm for a time-domain reflectometry bridge scour monitoring system[J]. Canadian Geotechnical Journal, 2011, 48(1): 26. DOI:10.1139/T10-041 |
| [11] |
MILLARD S G, BUNGEY J H, THOMAS C, et al. Assessing bridge pier scour by radar[J]. NDT International, 1998, 31(4): 251. DOI:10.1016/S0963-8695(98)00006-1 |
| [12] |
FALCO F D, MELE R. The monitoring of bridges for scour by sonar and sediment[J]. NDT International, 2002, 35(2): 117. DOI:10.1016/S0963-8695(01)00031-7 |
| [13] |
熊文, 董夏鑫, 唐平波, 等. 基于动力指纹的斜拉桥桥塔冲刷深度识别方法[J]. 湖南大学学报(自然科学版), 2017, 44(11): 1. XIONG Wen, DONG Xiaxin, TANG Pingbo, et al. Identification method for pylon scour depth of cable-stayed bridges by tracing dynamic index[J]. Journal of Hunan University (Natural Science), 2017, 44(11): 1. |
| [14] |
熊文, 邹晨, 叶见曙. 基于动力特性识别的桥墩冲刷状态分析理论[J]. 中国公路学报, 2017, 30(5): 89. XIONG Wen, ZOU Chen, YE Jianshu. Condition assessment of bridge scour by tracing dynamic performance of bridges[J]. China Journal of Highway and Transport, 2017, 30(5): 89. DOI:10.3969/j.issn.1001-7372.2017.05.012 |
| [15] |
李泽新.公路双柱式桥墩健康状态动力评估方法研究[D].北京: 北京交通大学, 2013 LI Zexin. Study on dynamic assessment method for highway bridge double-column piers[D]. Beijing: Beijing Jiaotong University, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10004-1013278913.htm |
| [16] |
FISHER M, ATAMTURKTUR S, KHAN A A. A novel vibration-based monitoring technique for bridge pier and abutment scour[J]. Structural Health Monitoring, 2013, 12(2): 114. DOI:10.1177/1475921713476332 |
| [17] |
API. Recommended practice for planning, designing and constructing fixed offshore platforms-working stress design: RP 2A-WSD[S]. Washington DC: API Publishing Services, 2007
|
 2019, Vol. 51
2019, Vol. 51


