随着社会经济的发展、建桥技术的提高以及新型材料的出现,大跨度桥梁在工程中的应用日益广泛.风荷载对桥梁的结构安全及车辆的运行安全产生了很大的影响,已经成为大跨度桥梁设计中的首要控制因素[1].因而,准确地描述结构所受到的风荷载,对于分析桥梁响应具有重要的工程意义.随机风速场的模拟主要有线性滤波、小波模拟和谐波合成等几种方法.其中,谐波合成法算法简单,理论完善,其样本的高斯特性、均值及相关函数的一致性、均值及相关函数的各态历经特性等都已经得到了数学证明,模拟结果较为可靠[2-5].目前国内外常采用经验谱来进行模拟.然而,统一参数的经验谱难以准确描述不同地区、不同地形条件下的复杂风场.因此,国内外的学者多针对大跨度桥梁进行风速场的实测[6-12],并基于实测数据分析桥址区风场特性.
地处长江下游的沪通大桥,主跨1 092 m,建成后将成为世界上跨度最大的公铁两用斜拉桥.目前,还未有针对沪通大桥的现场风特性实测分析.本文以该桥为工程背景,对桥址区的风速场特性开展测试[13],并基于实测数据的功率谱参数进行全桥三维脉动风速场模拟,是对该大跨度桥进行后期风振分析的基础工作,根据模拟得到的有效的风速时程序列,具有良好的实用效果.
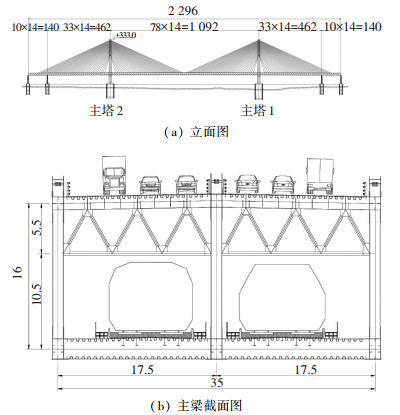
1 沪通大桥风场实测概况 1.1 工程概况沪通大桥桥位区地处长江下游,采用公铁合建方式,主航道桥桥式方案采用双塔斜拉桥布置,主跨跨度1 092 m,主跨两侧各设一个462 m边跨,作为辅助通航孔.为使斜拉桥结构既满足通航又满足结构受力和梁端转角要求,辅助通航孔两侧各增加了140 m的辅助跨,主桥具体孔跨布置为:140 m +462 m +1092 m +462 m +140 m. 图 1中给出了沪通大桥的立面布置图及主梁截面图.
|
图 1 沪通大桥布置(m) Fig. 1 Elevation of the Hutong Bridge (m) |
为真实的获取桥址区的风场情况,综合大桥现场情况,试验选取施工中的北侧主塔1(见图 1)沉井为测点布置地.利用施工中的现有条件,选取施工现场的多个塔吊为风速仪安装测点.
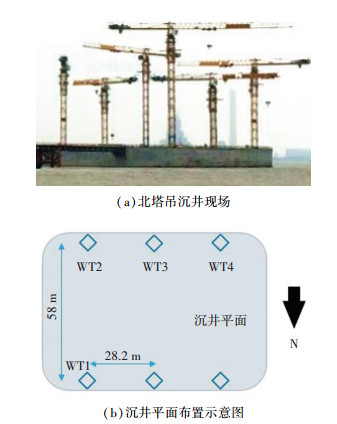
沉井现场及其平面布置如图 2所示.沉井上分布6座塔吊,因施工需求不同而处于不同高度位置,如图 2(a)所示,其平面布置图如图 2(b)所示.其中,南北方向相邻塔吊间距为58 m,东西方向相邻塔吊间距为28.2 m.
|
图 2 北塔沉井现场及平面布置 Fig. 2 Plan view of the north open caisson |
实验将4台风速仪分别布置于4个测点.根据当地气象资料,在实测试验期间(春季),桥址区的风向以东南风为主.因此,选取位于东北角及南端的4台塔吊为测点,可更直接地观测到未受干扰的来流风,受现场施工环境因素影响较小.如图 2(b)所示,WT1-4分别表示4个风速计.其中,WT1和WT2为超声波式风速计,分别位于东侧南北端两塔吊上,WT3和WT4为螺旋桨机械式风速计,分别布置于南端中、西侧塔吊上. 4台风速仪采用统一的安装高度,根据现场实际施工情况,选取距离江面25 m高度处为安装位置.
图 3给出了安装于塔吊上的风速仪现场图,在测点位置,通过三角铁将风速仪伸出塔吊外侧1.5 m远位置处,以减小塔吊遮挡及施工干扰的影响.

|
图 3 实测试验中安装在现场的风速计 Fig. 3 Anemometers installed on the site |
根据当地气象资料,沪通大桥南北连接的张家港市与南通市,每年春季的平均风速较大.根据气象统计,多以4月的平均风速为全年最大值.基于此,结合现场施工条件,本次风场实测试验自2016年4月初开始,至4月末结束,采样期间,4台风速仪采用10 Hz的采样频率,24 h无间断观察并记录风速时程数据,实测试验总时间进程超过400 h.数据通过无线传输装置实时传回数据采集仪.
超声波风速仪可记录风场三维空间方向的风速时程,螺旋桨机械式风速计记录风场水平面内方向的风速时程.
根据中国公路抗风设计规范[14],以10 min为子样本长度,分割整体样本,并剔除不良数据. 4台仪器共得到5 800组有效子样本.对子样本进行风特性分析.
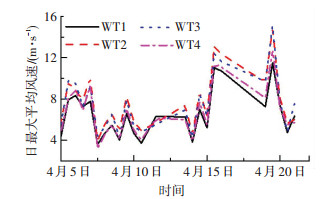
1.3 实测结果分析 1.3.1 平均风特性图 4给出了试验观测时间区间内,由4台风速仪分别记录的每日最大的10 min内平均风速时程曲线.观察曲线可知,4台仪器的时程曲线趋势相同,数值有一定的差异性,可认为4台仪器的观测数据互相验证,为有效的数据样本.
|
图 4 日最大10 min平均风速时程曲线 Fig. 4 Max daily 10-minute-averaged wind velocity histories |
图 5给出了观测期内,每日的平均风向变化曲线.图中竖坐标表示风向,其中,0°,90°及180°分别代表南风、东风和北风.观察可知,4台仪器所获取风向数据的趋势基本一致,数值上有一定的差异性.其中,绝大部分平均风向角处于22.5°~67.5°之间,表征为东南风向(22.5°为东南偏南, 45°为东南, 67.5°为东南偏东).由此可见,在观测期,桥址区风场以东南风为主导风.这一结果,与当地气象报告吻合.

|
图 5 日平均风向角变化曲线 Fig. 5 Mean daily 10-minute-averaged wind directions |
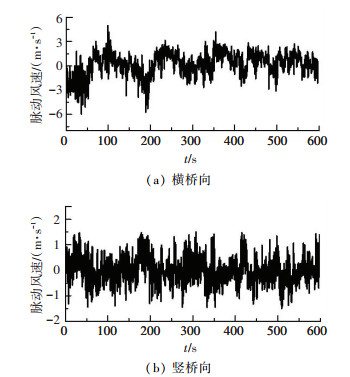
图 6中给出了某日10 min平均风速为12 m/s时的脉动风速时程曲线.观察可知,横桥向的风速脉动幅值约6 m/s,竖桥向的脉动幅值约3 m/s.
|
图 6 某平均风速为12 m/s时的脉动风速时程曲线 Fig. 6 Fluctuating wind velocity histories with averaged wind velocity at 12 m/s |
根据实测数据得到的脉动风时程数据,可以计算实测数据的功率谱,其功率谱密度函数曲线可归总为具有待定参数的数值曲线,其归一化公式分别为
| $ \frac{{n{S_u}}}{{{u_*}^2}} = \frac{{af}}{{{{\left( {1 + bf} \right)}^{5m/3}}}}, $ | (1) |
| $ \frac{{n{S_w}}}{{{u_*}^2}} = \frac{{af}}{{{{\left( {1 + bf} \right)}^{2m}}}}. $ | (2) |
式中:Su和Sw分别表示脉动风的顺风向和竖桥向分量的功率谱密度函数,n为频率,f=nz/V,V为平均风速,z为测点高程,u*为摩擦速度,a,b和m为待拟合确定的参数.
中国公路抗风设计规范[14]中给出的功率谱密度函数公式中,顺风向(横桥向)三参数分别为a = 200,b = 50,m = 1;竖桥向三参数分别为a = 6,b = 4,m = 1.
根据实测谱,可通过拟合运算得到待定参数值.其中,横桥向三参数分别为a = 81.93,b = 49.49,m = 1.02;竖桥向三参数分别为a = 2.51,b = 40.99,m = 0.61.拟合数值结果与规范给出的结果有较大的差异性. 图 7绘制了实测谱、拟合目标谱以及规范谱的对比曲线,观察可知,实测谱与拟合目标谱吻合度较好,而二者与规范谱所得的功率谱密度函数曲线具有一定的差异性.

|
图 7 规范谱、目标谱及实测谱曲线 Fig. 7 Power spectra density (PSD) curves of records, curve fitting results, and the specification values |
从图 7可见,实测谱与目标谱的吻合效果很好,但与规范谱之间有一定的差异性.由于规范给出的参数谱是基于全国范围内多场地、多次风场测试的结果,无法准确地描述具体桥址区的实际气象条件及风场特性.受大桥施工进度的影响,本次观测的时间有限,所获得的有效样本不足以对沪通大桥的近地强风场特性进行完整地描述.但本次观测为后期实现全桥多测点、多维风速场观测奠定了基础,并提供了数据支持.
2 基于观测结果的脉动风速模拟基于某段时间段内的脉动风速时程观测记录X0(t),可通过Fourier变化及相位角转换,构造出一个非平稳随机过程,得到模拟的风速时程序列X(t),可表示为
| $ X\left( t \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \infty }^\infty {\left| {{X_0}\left( \omega \right)\left| {\exp \left\{ {i\left[ {\omega t + {\xi _0}\left( \omega \right) + \varphi \left( \omega \right)} \right]} \right\}{\rm{d}}\omega {\rm{.}}} \right.} \right.} $ | (3) |
式中:X0(ω)为X0(t)的Fourier变换,ξ0(ω)为X0(ω)的相位角,φ(ω)为随机过程.
因ξ0(ω)+φ(ω)是ω的奇函数,式(3)可以改写为
| $ X\left( t \right) = \frac{1}{{\rm{ \mathsf{ π} }}}\int_0^\infty {\left| {{X_0}\left( \omega \right)\left| {\cos \left[ {\omega t + {\xi _0}\left( \omega \right) + \mathit{\Phi }} \right]{\rm{d}}\omega , } \right.} \right.} $ | (4) |
式中Φ为随机变量.
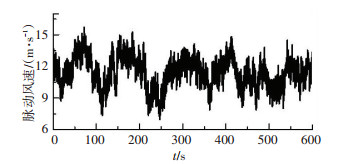
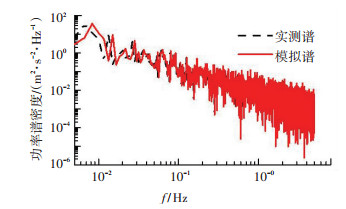
选取沪通大桥风场实测数据中某一平均风速为12 m/s的子样本数据,根据其10 min的脉动风速时程,进行模拟,得到的模拟数据的顺风向时程曲线如图 8所示,模拟脉动风功率谱密度与实测功率谱曲线的对比如图 9所示.
|
图 8 模拟脉动风时程曲线 Fig. 8 The simulated wind velocity history curves |
|
图 9 实测和模拟功率谱曲线 Fig. 9 PSD curves of comparison between records and simulation results |
观察可知,图 8中的模拟风速时程,其平均风速与原实测数据一致,脉动变化基本在6 m/s之内,与实测结果的基本特性一致. 图 9中模拟与实测数据的功率谱密度函数曲线,其变化趋势及数值均较为接近,吻合度较好.但是基于观测记录的直接模拟法因缺少相关性数据,只适用于单一模拟点的风速模拟,而无法应用于空间大跨度的桥梁三维风场模拟.
3 沪通大桥三维风场模拟根据文献[15]提出的基于显式Cholesky分解的快速谱分析法,假定桥面沿水平方向是等高程的,平均风速和风速谱沿桥面不变,任意相邻模拟风速点之间的距离相等.则桥梁第j个节点的横桥向水平和竖桥向垂直分量的时程uj(t)和ωj(t)可以表示为
| $ {u_j}\left( t \right) = \sqrt {2\Delta \omega } \sum\limits_{m = 1}^j {\sum\limits_{k = 1}^N {\sqrt {{S_u}({\omega _{mk}})} } } {G_{jm}}({\omega _{mk}})\cos ({\omega _{mk}}t + {\varphi _{mk}}), $ | (5) |
| $ {\omega _j}\left( t \right) = \sqrt {2\Delta \omega } \sum\limits_{m = 1}^j {\sum\limits_{k = 1}^N {\sqrt {{S_\omega }({\omega _{mk}})} } } {G_{jm}}({\omega _{mk}})\cos ({\omega _{mk}}t + {\varphi _{mk}}). $ | (6) |
式中:Δω为谱线间的频率间隔;N为频率分量的总数;j为桥梁模拟风速点;Su和Sw分别为水平和数值风速自功率谱;φmk为[0, 2π]中平均分布的随机变量;G(ω)为不同风速点之间的相关系数矩阵.
根据沪通大桥的结构特点,将其风场简化为6个独立的一维多变量随机风场,分别为主梁公路桥面横桥向及竖桥向,主梁铁路桥面横桥向及竖桥向、桥塔1横桥向和桥塔2横桥向.
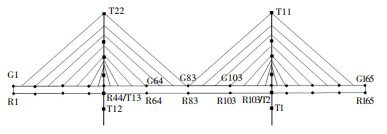
根据主梁桥跨结构特点,以一个桁架节间单元长度为模拟点间隔,主梁从南向北以14 m为间距,在公路及铁路桥面分别等间距分布165个模拟点,其中,公路桥面编号为G1~G165,铁路桥面编号为R1~R165号.根据主塔塔高,每座主塔以30 m高度为间距,自下而上等间距分布11个模拟点,其中,塔1编号为T1~T11,塔2编号为T12~T22.详细编号如图 10所示,图中,黑色圆点表示主梁上的模拟点,黑色方点表示主塔上的模拟点.
|
图 10 沪通大桥三维风场模拟点布置 Fig. 10 Arrangement of simulation points of 3D wind field of Hutong Bridge |
依据图 10所示,主梁自南向北,以14 m为间距设置165个模拟点,对于铁路桥面,模拟点编号为R1~R165.模拟点高程统一采用铁路桥面高度60 m,根据设计资料,桥址区10 m高度处的设计风速取为38 m/s,频率分量总数为1 024,样本时间间隔为0.1 s,采样总时长为100 s.
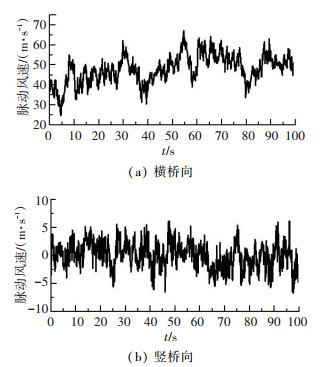
采用谱表示法进行模拟时,采用得到的基于实测数据的功率谱拟合参数. 图 11给出了主梁铁路桥面跨中位置(L/2)处水平横桥向和竖桥向的风速模拟结果. 图 12中给出了主梁铁路桥面L/2跨(R83)、L/4跨(R44)及3L/4跨(R103)三点的功率谱密度函数与目标谱的对比曲线. 图 13中给出了这三点的相关系数曲线.
|
图 11 主梁铁路桥面L/2跨中模拟点瞬时风速时程曲线 Fig. 11 Fluctuating wind velocity histories of mid-span point on railwaydeck |
|
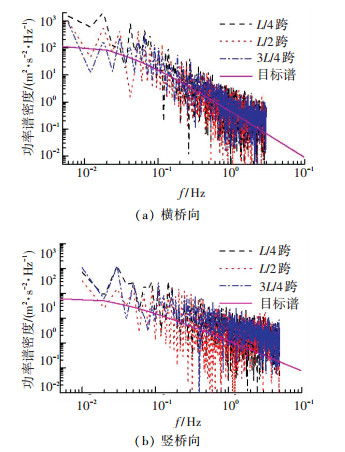
图 12 主梁铁路桥面主跨3处模拟点功率谱密度函数曲线 Fig. 12 PSD curves of three points on railway deck |
|
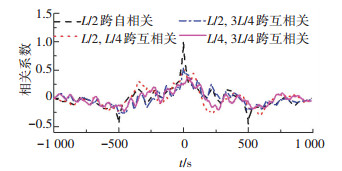
图 13 主梁铁路桥面风场模拟相关系数曲线 Fig. 13 Correlation coefficient curves on railway deck |
观察图 11可知,当主梁高度处平均风速为47.8 m/s时,横桥向脉动风速时程在幅值25 m/s之内波动,竖桥向脉动风速在8 m/s之内波动. 图 12中,三点的功率谱曲线与目标值吻合度较好.根据图 13给出的相关系数曲线,可以看出随着模拟点之间距离的增大,相关系数的值逐渐减小,模拟点之间的相关性降低.
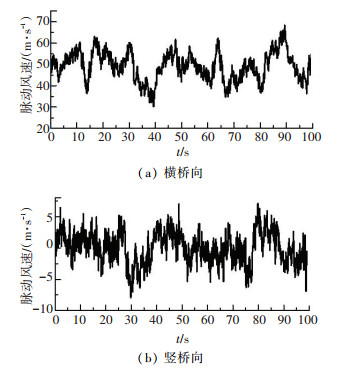
3.1.2 公路桥面依据图 10所示,与铁路桥面基本设定相同,公路桥面模拟点高程统一高度为76 m,编号分别为G1~G165.公路桥面跨中位置处模拟横桥向及竖桥向风速时程结果如图 14所示.根据设计风速的设定,主梁公路桥面高度处平均风速为49.1 m/s时,横桥向脉动风速时程在幅值25 m/s的范围内波动,竖桥向脉动风速在8 m/s的范围内波动.结果表明,公路桥面的模拟结果与铁路桥面相近似.其功率谱密度及相关性分析此处不再赘述.
|
图 14 主梁公路桥面L/2跨中模拟点瞬时风速时程曲线 Fig. 14 Fluctuating wind velocity histories of mid-span point on roadway deck |
根据图 10所示,每座主塔上自下而上设置间距为30 m的11个模拟点,编号分别为T1~T11(塔1),T12~T22(塔2).模拟采用实测数据得到的修正参数目标谱,主塔上高程不同的各个模拟点,根据规范给出的风剖面公式计算平均风速, 即
| $ {{\bar U}_z} = \frac{{\lg {H_z} - \lg {Z_0}}}{{\lg 10 - \lg {Z_0}}}{{\bar U}_{10}}. $ | (5) |
式中:Hz为模拟点所在高程,Z0为地面粗糙度高度,U10为10 m高度处的平均风速,根据设计资料,桥址区10 m高度处的设计风速取为38 m/s.频率分量总数等其他模拟参数定义与主梁模拟相同.
采用谱表示法进行模拟时,采用得到的基于实测数据的功率谱拟合参数. 图 15~17给出了水平横桥向的风速模拟结果.
|
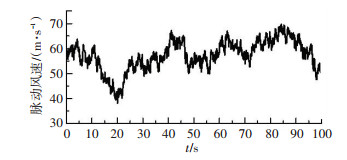
图 15 主塔风场模拟塔顶横桥向瞬时风速时程曲线 Fig. 15 Fluctuating wind velocity histories of tower-top point |
|
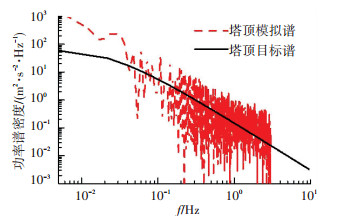
图 16 主塔风场横桥向模拟功率谱密度函数曲线 Fig. 16 PSD curves of three points of the tower |
|
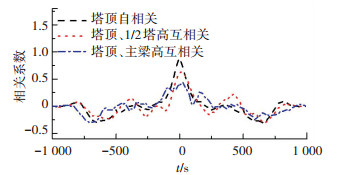
图 17 主塔风场模拟相关系数曲线 Fig. 17 Correlation coefficient curves of the tower |
观察图 15可知,当主塔墩顶处平均风速为57.2 m/s时,横桥向脉动风速时程在幅值30 m/s之内波动.根据图 16,塔顶位置处的模拟点功率谱曲线与目标值吻合度较好. 图 17中观察可知随着模拟点之间距离的增大,相关系数的值逐渐减小.
4 结论1) 对沪通大桥进行了现场风速实测实验,并根据实验数据结果,对桥址区风场特性进行了分析.结果表明:实测风数据与当地气象记录相吻合,印证了实测风速时程数据的有效性.
2) 得到了实测脉动风功率谱的拟合参数,根据此参数,采用基于显式分解的谐波合成法,将沪通大桥的三维脉动风速场简化为多个线状的一维脉动风速场,分别对两座主塔、公路桥面、铁路桥面进行了脉动风时程的数值模拟,并对结果进行了分析.结果表明:采用实测的风速谱参数可以得到有效的大跨度桥梁数值模拟三维脉动风场,其结果与规范给出的统一功率谱有一定的差异性,弥补了规范谱应用于不同地区时的局限性.
3) 得到了基于该地区风场特性的沪通大桥数值模拟风速时程序列,此序列能够更准确地反应桥址区的风场情况,为后期桥梁的风振分析提供了研究基础.
| [1] |
夏禾, 张楠, 郭薇薇, 等. 车桥耦合振动工程[M]. 北京: 科学出版社, 2014: 19. XIA He, ZHANG Nan, GUO Weiwei, et al. Coupling vibrations of train-bridge system[M]. Beijing: Science Press, 2014: 19. |
| [2] |
王浩, 李爱群, 黄瑞新, 等. 基于实测风谱的润扬悬索桥桥址区三维脉动风场模拟[J]. 东南大学学报, 2009, 39(6): 1206. WANG Hao, LI Aiqun, HUANG Ruixin, et al. Digital simulation of 3-dimensional turbulence wind field of Runyang Suspension Bridge based on measured wind spectra[J]. Journal of Southeast University, 2009, 39(6): 1206. DOI:10.3969/j.issn.1001-0505.2009.06.023 |
| [3] |
李永乐, 周述华, 强士中. 大跨度斜拉桥三维脉动风场模拟[J]. 土木工程学报, 2003, 36(10): 60. LI Yongle, ZHOU Shuhua, QIANG Shizhong. Simulation of three-dimensional fluctuating wind field for large span cable-stayed bridge[J]. China Civil Engineering Journal, 2003, 36(10): 60. DOI:10.3321/j.issn:1000-131X.2003.10.012 |
| [4] |
丁泉顺, 陈艾荣, 项海帆. 大跨度桥梁空间脉动风场的计算机模拟[J]. 力学季刊, 2006, 27(2): 184. DI Quanshun, CHEN Airong, XIANG Haifan. Simulation of spatialfluctuating wind field on long span bridges[J]. Chinese Quarterly of Mechanics, 2006, 27(2): 184. DOI:10.3969/j.issn.0254-0053.2006.02.002 |
| [5] |
马麟, 刘健新, 韩万水. 基于改进谐波合成法的杭州湾跨海大桥风场模拟研究[J]. 郑州大学学报(工学版), 2008, 29(1): 56. MA Lin, LIU Jianxin, HAN Wanshui. Wind field simulation of Hangzhou Bay Bridge based on the improved WAWS[J]. Journal of Zhengzhou University (Engineering Science), 2008, 29(1): 56. |
| [6] |
XU Youlin, ZHU Ledong, WONG K Y, et al. Field measurement result of Tsing Ma suspension bridge during Typhoon Victor[J]. Structural Engineering and Mechanics, 2000, 10(6): 454. |
| [7] |
XU Youlin, ZHU Ledong. Buffeting response of long-span cable-supported bridges under skew winds. Part 2:case study[J]. Journal of Sound and Vibration, 2005, 281(3): 675. |
| [8] |
李杏平, 李爱群, 王浩, 等. 基于长期监测数据的苏通大桥桥址区风特性研究[J]. 振动与冲击, 2010, 29(10): 82. LI Xingping, LI Aiqun, WANG Hao, et al. Wind characteristics of Sutong bridge based on long-term monitored data[J]. Journal of Vibration and Shock, 2010, 29(10): 82. DOI:10.3969/j.issn.1000-3835.2010.10.016 |
| [9] |
陈政清, 柳成荫, 倪一清, 等. 洞庭湖大桥拉索风雨振中的风场参数[J]. 铁道科学与工程学报, 2004(1): 52. CHEN Zhengqing, LIU Chengyin, NI Yiqing, et al. Wind parameters in wind-rain induced stay cable vibration on Dongting Lake Bridge[J]. Journal of Railway Science and Engineering, 2004(1): 52. DOI:10.3969/j.issn.1672-7029.2004.01.009 |
| [10] |
胡俊, 欧进萍. 某大跨悬索桥风振响应的现场实测与理论对比分析[J]. 振动与冲击, 2013, 32(11): 149. HU Jun, OU Jinping. Comparison between field measurement and theoretical analysis results for a long-span suspension bridge's wind-induced vibration responses[J]. Journal of Vibration & Shock, 2013, 32(11): 149. DOI:10.3969/j.issn.1000-3835.2013.11.030 |
| [11] |
胡俊, 欧进萍. 基于长期监测数据的某悬索桥桥位近处风场特性分析[J]. 中南大学学报(自然科学版), 2013, 44(7): 2989. HU Jun, OU Jinping. Wind field characteristics analysis at a long-span suspension bridge based on a long-term monitoring data[J]. Journal of Central South University(Science and Technology), 2013, 44(7): 2989. |
| [12] |
黄国庆. 普立特大桥桥位处山区风特性实测研究[J]. 西南交通大学学报, 2016, 51(2): 349. HUANG Guoqing. Field measurement study on wind characteristics at Puli Great Bridge site in mountainous area[J]. Journal of Southwest Jiaotong University, 2016, 51(2): 349. DOI:10.3969/j.issn.0258-2724.2016.02.014 |
| [13] |
XU Man, GUO Weiwei, XIA He, et al. Wind-field measurement of a long-span bridge near Yangtze River estuary[C]//Proceedings of the Twenty-Seventh International Ocean and Polar Engineering Conference. San Francisco: ISOPE, 2017: 1093
|
| [14] |
中华人民共和国交通部.中国公路桥梁抗风设计规范: JTG/T D60-01-2004[S].北京: 人民交通出版社, 2004 The Ministry of Communications of PRC.Wind-resistent design specification for highway bridge: JTG/T D60-01-2004[S]. Beijing: China Communication Press, 2004 |
| [15] |
CAO Yinghong, XIANG Haifan, ZHOU Ying. Simulation of stochastic wind velocity field on long-span bridges[J]. Canadian Metallurgical Quarterly, 2000, 126(1): 1. |
 2019, Vol. 51
2019, Vol. 51


