2. 北京交通大学 交通运输学院, 北京 100044
2. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China
随着我国大城市建设的不断推进, 职住分离的现象越发普遍, 通勤距离不断扩大, 轨道交通和常规公交在通勤出行方式中逐渐占据主导地位.同时, 新规划中居民住宅用地逐渐由分散化向集中化转移.因此, 在城市交通拥堵问题日益凸显的背景下, 研究典型大客流通勤OD间乘客在高峰时段对接运轨道交通的公交线路的选择行为特性, 对于管理者通过运营手段最大化公交网络运输效率具有重要意义.
既有研究中, 对公交线网中乘客出行费用的描述, 均基于一个重要假设, 即所有乘客在车站的等车时间均为发车间隔的一半或是选取随机数[1-4], 不考虑乘客在车站的排队现象, 与实际可能存在一定偏差.对公交车站的排队拥挤及能力限制的研究中, 文献[5]最先考虑拥挤条件下公交车辆能力与乘客等车时间之间的关系, 但其模型缺乏普适性.文献[6-7]用不同的模型描述了拥挤条件下的公交配流问题, 但其模型均假设乘客在车站的等车时间不受乘客流量的影响, 并不能反映实际情况.文献[8]等考虑了乘客在站点的排队延误时间, 但未考虑出发时刻对延误时间的影响.文献[9]考虑了车站排队拥挤现象, 设非延迟乘客和延迟乘客在站点的等待时间分别为发车间隔的一半和1.5倍, 未考虑乘客实际的到站时刻与车辆到达时刻间的动态关系.本文在既有研究的基础上, 考虑了不同出发时刻导致的乘客实际到站时刻与车辆到达时刻间的关系, 对乘客在站点的排队等待过程较为细致的定量描述, 并与既有研究进行对比, 验证了模型的可行性和有效性.
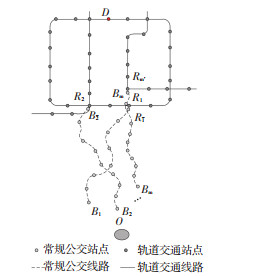
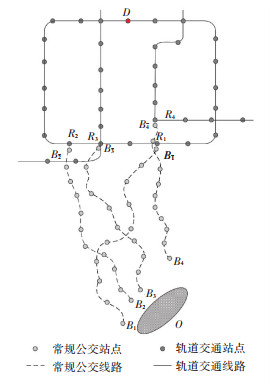
1 构建乘客出行时空网络 1.1 通勤乘客出行网络研究对象为大城市典型通勤OD间、需求为Q的通勤者群体.高峰时段, Q个个体均选择公交换乘轨道的方式, 由O出发, 选择接运范围内m′个轨道交通站点的m条接运公交线路, 由于一个轨道交通站点可能存在多条接运公交线路, 则m≥m′.设个体由O点出发到达公交线路k的上车站点为Bk, k=1, 2, …, m, 下车站点为
|
图 1 通勤出行网络示意图 Fig. 1 Diagram of the commuting travel network |
设Q个个体中, 选择接运公交线路k的乘客数量为qk, 则
|
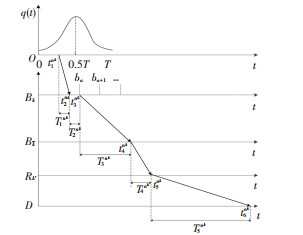
图 2 乘客nk出行时空路径示意图 Fig. 2 Diagram of the travel route of passenger nk |
1) 网络中的重要节点. a)初始节点O表示个体nk的出发节点, 设出发时刻为t1nk.b)公交上车站点Bk表示个体nk由O点出发后到达公交线路k的上车站点.到达Bk的时刻为t2nk, 离开Bk的时刻为t3nk.将t21k时刻后顺序到达Bk的公交车辆分别编号为b1k, b2k, …, bn′k, n′为时段0~T中可到达的公交车辆最大编号, 由时段0~T、公交线路发车间隔fk等因素决定.将t2nk时刻后第1辆到达Bk的公交车辆编号为bak, a=1, 2, …, n′.c)公交下车站点
2) 时空节点间的弧段.a)步行弧T1nk表示个体nk从节点O至Bk的步行时间, T1nk=t2nk-t1nk.b)公交车站排队等待弧T2nk表示个体nk在站点Bk的等待时间, T2nk=t3nk-t2nk.c)接运公交乘车弧T3nk表示个体nk在站点Bk至站点
乘客nk的出行费用wnk由时空网络中的5类弧段所对应的出行时间费用及票价费用组成, 即由弧段T1nk~T5nk所对应的时间费用w1nk~w5nk和公交与轨道交通综合票价费用w6nk组成, 即
| $ {w^{{n^k}}} = w_1^{{n^k}} + w_2^{{n^k}} + w_3^{{n^k}} + w_4^{{n^k}} + w_5^{{n^k}} + w_6^{{n^k}}. $ |
式中:w1nk由乘客从O至Bk的步行距离l1k、乘客步行速度v1及时间费用换算系数λ确定, 即w1nk=λTnk1=λl1k/v1;w2nk由u和时间费用换算系数λ确定, 即w2nk=λTnk2=λu,其中u为乘客在站点候车时间费用函数;w3nk由乘客从站点Bk至
既有文献中对乘客在公交车站的候车时间的描述大多简化为发车间隔的一半.文献[9]假设乘客的到达时间服从均匀分布, 当拥挤存在使乘客无法乘上即将到达的第1辆车, 则其必可乘上第2辆车.定义可乘上第1辆公交车的乘客为非延迟乘客, 其候车时间为0.5fk;因拥挤存在而仅能乘上第2辆车的乘客为延迟乘客, 其候车时间为1.5fk,即
| $ u\left( {{f_k}} \right) = \left\{ \begin{array}{l} 0.5{f_k},q' = 0;\\ 1.5{f_k},q' \ne 0. \end{array} \right. $ |
式中fk为公交发车间隔, q′为延迟乘客数量.
而在实际情况中, 乘客到达时刻是不均匀的, 乘客在车站的候车时间将与出发时刻、到达时刻、公交线路发车间隔、车站排队情况等有关, 将候车时间简化为发车间隔的倍数, 可能导致乘客出行费用与实际存在较大偏差.
2.2.2 本文对候车时间的描述设乘客1k到站点Bk时距离编号为b1k的公交车辆到达站点时间刚好为0.5fk.当乘客步行到达站点Bk时, 需判断该公交站点的节点状态, 并以此对等车时间函数u进行如下描述.
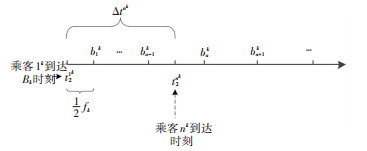
1) 车辆编号的判断.设个体nk步行至站点Bk时距离时刻t21k的时间为Δtnk, Δtnk=t2nk-t21k.乘客到达站点Bk时, 需判断此时即将达到的公交车辆编号bak, 如图 3所示.
|
图 3 乘客nk到达Bk站点状态示意图 Fig. 3 Diagram of the note state when passenger nk arrives at the bus station Bk |
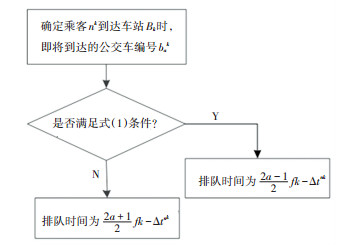
2) 节点状态的判断.除车辆编号外, 乘客到达时, 还应判断该站点的节点状态, 即乘客能够乘上即将到达的第几辆公交车.设μak为到达Bk的公交车bak的满载率.Nnk为0至t2nk时刻到达站点Bk的乘客总数, 包括之前时段Q个个体中选择线路k的人数及由其他出发源出发随机到达该站点的乘客人数.若公交车辆定员均为Z, 公交车辆最大满载率为h, 当乘客能够乘上第1辆即将到达的公交车bak时, 需满足Nnk-(h-μ1k)Z-(h-μ2kZ)-…-(h-μa-1k)Z≤(h-μak)Z.则有节点状态判断过程如图 4所示.因此, 得到u的计算公式为
| $ \begin{array}{l} u\left( {\Delta {t^{{n^k}}},{f_k},a,{N^{{n^k}}},\sum\limits_{j = 1}^{a - 1} {\mu _j^k} ,\mu _a^k,Z,h} \right) = \\ \left\{ \begin{array}{l} \frac{{2a - 1}}{2}{f_k} - \Delta {t^{{n^k}}},{N^{{n^k}}} - \sum\limits_{j = 1}^{a - 1} {\left( {h - \mu _j^k} \right)Z} \le \left( {h - \mu _a^k} \right)Z;\\ \frac{{2a + 1}}{2}{f_k} - \Delta {t^{{n^k}}},{N^{{n^k}}} - \sum\limits_{j = 1}^{a - 1} {\left( {h - \mu _j^k} \right)Z} > \left( {h - \mu _a^k} \right)Z. \end{array} \right. \end{array} $ |
|
图 4 站点状态判断过程流程图 Fig. 4 Flow chart of the judge process for the station state |
其中
为保证无法乘坐即将到达的第1辆公交车的乘客可乘上第2辆车, 上式的约束条件为
| $ \begin{array}{l} {N^{{n^k}}} - \left( {h - \mu _1^k} \right)Z - \left( {h - \mu _2^k} \right)Z - \cdots - \left( {h - \mu _a^k} \right)Z \le \\ \left( {h - \mu _{a + 1}^k} \right)Z. \end{array} $ | (1) |
设乘客从出发源O点相继出发, 设以t为时间步长, 将乘客划分为I份, 分别对数量为Qi的乘客进行I次配流, 且i=1, 2, …, I, Q1+Q2+…+QI=Q.
高峰时期的每个乘客将根据自身经验选择自己认为出行费用最少的公交接驳线路, 线路选择行为依然遵循Wardrop第一原理, 设第i次配流时OD对间公交线路k被选择的概率为αki, 每条线路上分配的流量为gki, 则
| $ \begin{array}{*{20}{c}} {g_k^i = \alpha _k^i{Q_i},\forall k,i;\sum\limits_{k = 1}^m {\alpha _k^i} = 1,\forall i;}\\ {\sum\limits_{k = 1}^m {g_k^i} = {Q_i},\forall i;\sum\limits_{i = 1}^I {{Q_i}} = Q.} \end{array} $ |
运用Logit模型来描述乘客对常规公交线路的选择概率, 即当达到平衡状态时, 第i次配流时OD对间被选择的公交线路k上的乘客流量gki满足
| $ g_k^i = {Q_i} \times \frac{{\exp \left( { - \theta {w_k}} \right)}}{{\sum\limits_{j = 1}^m {\exp \left( { - \theta {w_j}} \right)} }}. $ |
其中θ为描述乘客对网络中路径费用感知程度的系数, θ取值越大, 模型配流的随机性越小, 当θ取值较大时, SUE配流趋近于UE配流[10].
根据文献[10], 构建基于Logit-SUE的公交线路配流模型为
| $ \min Y = \sum\limits_{i = 1}^I {\sum\limits_{k = 1}^m {\int_0^{g_k^i} {{w^{{n^k}}}\left( g \right){\rm{d}}g} } } + \frac{1}{\theta }\sum\limits_{i = 1}^I {\sum\limits_{k = 1}^m {g_k^i\ln g_k^i} } . $ | (1) |
| $ {\rm{s}}.{\rm{t}}.:\sum\limits_{k = 1}^m {g_k^i} = {Q_i}, $ | (2) |
| $ \sum\limits_{i = 1}^I {{Q_i}} = Q, $ | (3) |
| $ g_k^i \ge 0. $ | (4) |
其中优化模型(1)共分为两项, 前一项是对各出行线路的出行费用函数积分求和; 后一项与乘客感知相关.约束(2)为第i次配流的乘客总流量等于第i次配流中选择各路径的乘客流量之和; 约束(3)为第1~I次配流的乘客流量总和等于系统总乘客流量Q.
下面证明模型与SUE条件之间的等价性.首先构造模型的广义拉格朗日函数:
| $ L\left( {g,\kappa } \right) = Y\left( g \right) - \sum\limits_{i = 1}^I {{\kappa _i}\left( {\sum\limits_{k = 1}^m {g_k^i} - {Q_i}} \right)} . $ | (5) |
可写出优化模型(1)~(4)Kuhn-Tucker条件:
| $ g_k^i\left( {{w^{{n^k}}} + \frac{1}{\theta }\left( {\ln g_k^i + 1} \right) - {\kappa _i}} \right) = 0, $ | (6) |
| $ {w^{{n^k}}} + \frac{1}{\theta }\left( {\ln g_k^i + 1} \right) - {\kappa _i} \ge 0, $ |
| $ \sum\limits_{k = 1}^m {g_k^i} = {Q_i},g_k^i \ge 0. $ |
其中κi为对应于式(2)的K-T乘子.
当gki>0时, 式(6)可化简为
| $ {w^{{n^k}}} + \frac{1}{\theta }\left( {\ln g_k^i + 1} \right) - {\kappa _i} = 0,\forall i. $ |
解得gki, 并代入式(2)中, 可得到Logit模型为
| $ g_k^i = {Q_i}\frac{{\exp \left( { - \theta {w^{{n^k}}}} \right)}}{{\sum\limits_{k = 1}^m {\left( { - \theta {w^{{n^k}}}} \right)} }}. $ |
以步长时间t为单位, 对乘客需求Q在出发总时间T内进行T/t次(T/t=I)配流, 每次配流均遵循上述SUE配流模型, 并运用MSA算法进行求解, 最终得到乘客需求Q对m条线路的选择结果.
4 算例分析 4.1 模型参数算例中, 通勤出行网络包含4条接运公交线路, 即m=4, 如图 5所示, 各出行路径基本信息见表 1.
|
图 5 算例中接运网络示意图 Fig. 5 Diagram of the feeder bus network in the case |
| 表 1 4条出行路径信息表 Tab. 1 Input data of the four routes |
根据实地调研结果和文献[11-12], 模型中v1=1.5 m/s, v2=22 km/h, Z=75人, T=30 min.以t=5 min为例, 则I=6;参考既有文献, 算例中, v3=35 km/h[13], h=1[13]; θ=2[10], λ=0.2元/min[13], ε=0.4[14].
4.2 结果与分析分别按本文及文献[9]提出的方法对典型OD下的200个通勤乘客进行流量分配, 由于车辆达到站点的满载率及每个步长内从其他出发源到达站点的乘客数量均是随机的, 因此对此公交出行网络分别进行100次流量分配, 选取100次仿真结果的平均值见表 2.
| 表 2 乘客对不同公交线路的选择概率统计表 Tab. 2 Passenger choice probabilities of different bus lines |
从表 2可知, 本文方法相比既有方法得到的乘客对4条公交线路的选择概率不同, 分别相差-10.7%、5.5%、0.3%、4.9%.以fk=9 min为例, 分析选择概率出现差异的原因.假设乘客在时刻5到达线路4的公交站点, 则两种方法得到的站点候车时间如图 6、7所示.
|
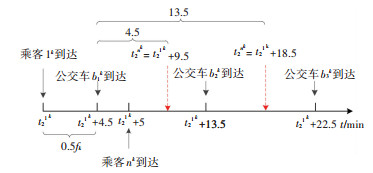
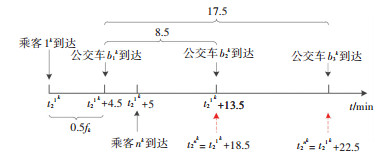
图 7 fk=9 min时本文站点候车时间示意图 Fig. 7 Diagram of waiting time at station in this research (fk=9 min) |
由于乘客1k到达该节点的时刻为t21k, 当fk=9 min时, 公交车b1k到达站点的时刻为t21k+4.5, 公交车b2k到达站点的时刻为t21k+13.5, 公交车b3k到达站点的时刻为t21k+22.5, 以此类推.考虑站点排队及公交车上的乘客满载率前提下, 当乘客在时刻t21k+5到达时, 文献[9]方法:对于非延迟乘客, 其在站点的候车时间为0.5fk, 即4.5 min; 对于延迟乘客, 其在站点的候车时间为1.5fk, 即13.5 min.本文方法:考虑了乘客到达站点的实际时刻与车辆到达时刻间的动态关系, 若乘客可乘上即将到达的第1辆公交车, 其在站点的候车时间实际为8.5 min; 若由于站点及公交车容量限制导致其仅能乘上第2辆公交车时, 其在站点的候车时间则实际为17.5 min.
对于既有方法, 忽略了乘客在公交站点的实际到站时刻与车辆达到时刻间的关系, 采用0.5fk(或1.5fk)简化代替车站等待时间, 即削弱了发车间隔对乘客选择概率的影响程度.本文方法更加细致的刻画了乘客在站点的实际等待时间, 配流结果更符合实际情况.由表 2可知, 本文方法得到的4条接运线路的选择概率p1>p3>p4>p2, 而f1 < f3 < f4 < f2, 可知乘客更倾向于选择发车间隔更小的线路.
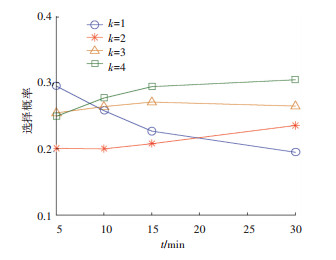
4.3 重要参数灵敏度分析1) t对选择概率的影响.改变t的取值, 研究本文方法中时间步长对接运公交线路乘客选择概率的影响, 如图 8所示.当t由5 min逐渐增加至30 min时, 乘客对接运公交线路的选择概率整体变化较小, 4条接运常规公交线路乘客选择概率随t变化的标准差值分别为0.042、0.016、0.006、0.024, 均小于0.05, t的取值不会引发配流结果较大程度的改变.文中假设乘客在30 min内全部出发, 因此, 当t较小时, 得到更加细化的配流结果, 而当t增加至30 min时, 配流结果与文献[9]一致, 证明了模型的准确性.
|
图 8 t对乘客选择概率的影响 Fig. 8 Effect of t on choice probabilities |
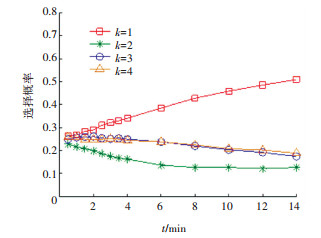
2) θ对选择概率的影响.在乘客流量分配模型中, 参数θ是描述乘客对网络中路径费用感知程度的变量, 其值越大, 乘客的感知结果与实际的路径费用越贴近.θ对接运公交线路乘客选择概率的影响如图 9所示.由图可知, 当θ较小时, 乘客感知到的各接运线路的路径阻抗与其实际阻抗存在一定差距, 配流结果随机性较强; 而随着θ的逐渐增大, 乘客对路径阻抗的感知与现实越来越贴近, 乘客均倾向于选择实际阻抗较小的接运线路, 阻抗较小的线路选择概率逐渐增大, 而阻抗相对较大的线路选择概率则存在逐渐减小的趋势.
|
图 9 θ对乘客选择概率的影响 Fig. 9 Effect of θ on choice probabilities |
1) 模型在大城市典型通勤OD间具有较为广泛的适用性, 考虑乘客在公交站点的排队情况, 从而更加细致地计算乘客在公交站点的等待时间, 将有助于得到更精确的客流分配结果, 为公交管理者更好的规划接运公交线路提供理论依据.
2) 模型中, t的取值变化不会引发配流结果较大程度的改变, t越小, 乘客候车时间的计算结果越贴近现实情况, 当t增大到步长时间内乘客可全部出发时, 配流结果与既有文献一致.
3) 模型中, 当θ较小时, 乘客对阻抗的感知与实际存在一定差距, 配流结果随机性较强; θ越大, 乘客对阻抗的感知越贴近现实, 实际阻抗越小的线路选择概率则越大.
| [1] |
巫威眺, 靳文舟, 魏明, 等. 配合区间车的单线公交组合调度模型[J]. 华南理工大学学报(自然科版), 2012, 40(11): 147. WU Weitiao, JIN Wenzhou, WEI Ming, et al. Mixed scheduling model of single-line bus for zonal vehicles[J]. Journal of South China University of Technology (Natural Science Edition), 2012, 40(11): 147. DOI:10.3969/j.issn.1000-565X.2012.11.022 |
| [2] |
赵淑芝, 刘华胜, 张晓亮, 等. 轨道与常规公交局域换乘网络站点优化模型[J]. 哈尔滨工业大学学报, 2014, 46(12): 96. ZHAO Shuzhi, LIU Huasheng, ZHANG Xiaoliang, et al. Station optimization in local transfer network of rail transit and bus[J]. Journal of Harbin Institute of Technology, 2014, 46(12): 96. DOI:10.11918/j.issn.0367-6234.2014.12.016 |
| [3] |
宗芳, 王琳虹, 贾洪飞. 综合客运枢纽内各方式协调调度模型[J]. 华南理工大学学报(自然科学版), 2010, 38(3): 53. ZONG Fang, WANG Linhong, JIA Hongfei. Heuristic algorithm to solve vehicle routing problem with split pickups and deliveries[J]. Journal of South China University of Technology (Natural Science Edition), 2010, 38(3): 53. DOI:10.3969/j.issn.1000-565X.2010.03.010 |
| [4] |
曾鹦, 李军, 朱晖. 换乘行为影响下的城市公交配流算法[J]. 交通运输工程学报, 2013, 13(4): 70. ZENG Ying, LI Jun, ZHU Hui. Urban public traffic assignment algorithm under influence of transfer behavior[J]. Journal of Traffic and Transportation Engineering, 2013, 13(4): 70. DOI:10.3969/j.issn.1671-1637.2013.04.011 |
| [5] |
LAST A, LEAK S E. Transportation :a bus model[J]. Traffic Engineering and Control, 1976(6): 14. |
| [6] |
SPIESS H, FLORIAN M. Optimal strategies: a new assignment model for transit network[J]. Transportation Research, 1989, 23B: 83. |
| [7] |
NGUYEN S, PALLOTINO S. Equilibrium traffic assignment for large scale transit networks model[J]. European Journal of operation research, 1988, 37: 176. DOI:10.1016/0377-2217(88)90327-X |
| [8] |
宋一凡, 高自友. 能力限制条件下的公交平衡配流模型和求解算法[J]. 铁道学报, 1999, 1(5): 10. SONG Yifan, GAO Ziyou. A transit equilibrium assignment model and algorithm under the condition of capacity constraint[J]. Journal of the China Railway Society, 1999, 1(5): 10. DOI:10.3321/j.issn:1001-8360.1999.05.003 |
| [9] |
高自友, 任华玲, 林兴强. 拥挤条件下公交系统的拟动态均衡配流模型[J]. 交通运输系统工程与信息, 2002, 2(2): 38. GAO Ziyou, REN Hualing, LIN Xingqiang. A time-dependent transit equilibrium assignment model for congested transit network[J]. Journal of Transportation Systems Engineering and Information Technology, 2002, 2(2): 38. DOI:10.3969/j.issn.1009-6744.2002.02.010 |
| [10] |
李远, 四兵锋, 杨小宝, 等. 考虑换乘费用的城市公交网络随机用户均衡配流模型及算法[J]. 系统工程理论与实践, 2014, 34(8): 2127. LI Yuan, SI Bingfeng, YANG Xiaobao, et al. A stochastic user equilibrium model and algorithm for urban transit network with transfer cost[J]. Systems Engineering - Theory & Practice, 2014, 34(8): 2127. DOI:10.12011/1000-6788(2014)8-2127 |
| [11] |
李淑庆, 李哲, 朱文英. 一体化公交网络均衡配流模型[J]. 交通运输工程学报, 2013, 13(1): 62. LI Shuqing, LI Zhe, ZHU Wenying. Equilibrium assignment model of integrated transit network[J]. Journal of Traffic and Transportation Engineering, 2013, 13(1): 62. DOI:10.3969/j.issn.1671-1637.2013.01.010 |
| [12] |
城市建设研究院. 城市公共交通分类标准[M]. 北京: 中国建筑工业出版社, 2007. Urban Construction Design & Research Institute. Standard for classification of urban public transportation[M]. Beijing: China Building Industry Press, 2007. |
| [13] |
孙杨, 孙小年, 孔庆峰, 等. 轨道交通新线投入运营下常规公交网络优化调整方法研究[J]. 铁道学报, 2014, 36(3): 1. SUN Yang, SUN Xiaonian, KONG Qingfeng, et al. Methodology ofbus network optimization and adjustment under operation of new urban rail transit line[J]. Journal of the China Railway Society, 2014, 36(3): 1. DOI:10.3969/j.issn.1001-8360.2014.03.001 |
| [14] |
邵敏华, 李田野, 孙立军. 常规公交乘客对车内拥挤感知阻抗调查与建模[J]. 同济大学学报(自然科学版), 2012, 40(7): 1031. SHAO Minhua, LI Tianye, SUN Lijun. Survey method and model of passengers' cost perception of crowding level in bus[J]. Journal of Tongji University (Natural Science), 2012, 40(7): 1031. DOI:10.3969/j.issn.0253-374x.2012.07.012 |
 2019, Vol. 51
2019, Vol. 51