2. 综合交通大数据应用技术国家工程实验室(西南交通大学),成都 610031
2. National Engineering Laboratory of Integrated Transportation Big Data Application Technology(Southwest Jiaotong University), Chengdu 610031, China
随着社会经济发展,城市规模日益扩张,城市居民出行结构逐渐发生变化,城郊出行需求比例逐步提高,这种现象在大城市中尤为突出.因此,构建合理的城郊公交线网是调节公交出行供需关系的有效手段.
早在1967年,国外学者就对公交线网优化问题进行了初步探索,并构建了公交线网优化模型[1-3].国内对相关研究较国外较晚,如1992年刘清等[4]结合国外研究基础,提出了相应的改进模型和优化算法,王炜[5]为了将公交线网研究的理论方法推广应用到实践中,设计了相应公交规划软件.早期的公交线网优化考虑的因素较少,且假设条件较多,很难用于实际的线网规划.随着实际公交线网设计的需求变化,相关研究逐步转变到了网络层面[6-11].导致传统的解析式算法已很难求解出有效解,而智能算法相比于其他算法对于该问题求解更为有效[12-14].
随着公交线网的设计工作将城郊公交纳入考虑范围,跨区域的城郊公交线网出行具有出发地的客流站点分布密集,而目的地的站点分布较为分散的特征[15].
本文将物流领域hub-spoke和milk-run线路设计理念融入到城郊公交线网规划中.其中milk-run成功应用在汽车零部件配送中,能够有效减少库存[16],而hub-spoke模式作为一种组织结构,能够形成规模优势[17].通过milk-run线路将客流聚集到相应hub站点,然后大客流可以利用直达线路直接从hub站点到达目的地,将有效减少乘客出行时间.
1 构建公交线网优化模型 1.1 模型假设结合文献[18],模型假设条件为:1)假设所规划或优化的公交网络的OD已知;2)优化的公交网络可以使用的车辆总数与现有的公交服务的车辆数量保持一致;3)假设城区站点都有能够满足hub站点选择的条件;4)假设公交车辆运行速度一致.
1.2 概念说明为方便后续模型构建,首先对相关概念说明,如图 1所示为1条由4个站点构成的简单线路,本文将相邻的两个站点之间路段定义为站间路段,站间路段前面站点定义为该站间路段的前端站点,站间路段后面的站点定义为该站间路段的后端站点.在图 1中共有4个站点,3个站间路段分别为站间路段1—2、2—3、3—4,站点1为站间路段1—2的前端站点,站点2为站间路段1—2的后端站点.

|
图 1 四站点的简单线路案例图 Fig. 1 Case diagram of a simple transit route with four stops |
1) 目标函数.通过上述分析,本文所提出的城郊公交线网优化模型以乘客总出行时间最小为优化目标,可以表示为
| $ \min Z = \sum\limits_{o \in {N_c}} {\sum\limits_{d \in {N_d}} {{p_{od}}\left( {{t_{od}} + {w_{od}}} \right)} } . $ | (1) |
式中:Z为目标函数,o, d代表站点编号,No为公交客流起点站集合,Nd为公交客流终点站集合,pod为单位时间内从站点o到站点d的OD量,tod为某位乘客从起点站到终点站所需要花费的在车旅行时间,wod为单某位乘客从起点站到终点站出行过程中所花费的等待时间.
2) 约束条件.约束条件包括:a)载客能力约束; b)车队规模约束;c)变量计算.
为了保证线路配置的车辆数量能够满足乘客出行需求,依据1.2的相关说明,载客能力约束条件为
| $ \max \left( {B_l^m} \right) \le {f_l} \cdot C. $ | (2) |
式中:l为线路编号,m为站间路段编号,Blm为线路l的站间路段m的在车人数,fl为线路l的发车频率,C为单位车辆的载客能力.
式(2)即规划时间段内,一条线路站间路段的最大在车人数不能超过该线路车辆能够提供的最大运输能力.其中,线路站间路段的在车人数计算方式为
| $ B_l^m = \left\{ \begin{array}{l} b_l^m,m = 1;\\ B_l^{m - 1} + b_l^m - a_l^m,2 \le m \le {n_l} - 1. \end{array} \right. $ | (3) |
式中:blm为站间路段m的前端站点上车人数,alm为站间路段m的后端站点下车人数,nl为线路l的站点数量.
车队规模约束是用来保证各线路分配的车辆总数不超过整个网络的可用车辆总数为
| $ \sum\limits_{l \in L} {2{f_l}{T_l}} < V, $ | (4) |
式中L为线路集合,V为车辆总的配置数量,Tl为线路l的单程旅行时间.
变量计算主要是对乘客的出行时间和等待时间的计算,由于所提出的方法中将乘客的等待时间以及在车旅行时间都分为两部分,可以分别表示为
| $ {w_{od}} = w_{oh}^{{h_{od}}} + w_{hd}^{{h_{od}}}, $ | (5) |
| $ {t_{od}} = t_{oh}^{{h_{od}}} + t_{hd}^{{h_{od}}}. $ | (6) |
式中:h为hub站点编号 wohhod为单位人次从站点o到hub站点h的等待时间,whdhod为单位人次在hub站点所需的等待时间,tohhod,thdhod分别为单位人次从起点站点到hub和从hub站点到达目的站点的在车旅行时间.
等待时间与发车频率的关系可以表示为
| $ w_{oh}^{{h_{od}}} = 0.5 \cdot \left( {\frac{1}{{{f_l}}}} \right),\;\;\;\;o,h \in l; $ | (7) |
| $ w_{hd}^{{h_{od}}} = 0.5 \cdot \left( {\frac{1}{{{f_l}}}} \right),\;\;\;\;h,d \in l. $ | (8) |
在车旅行时间和站间运行时间的关系以及与站点停靠时间的关系可以表示为
| $ t_{oh}^{{h_{od}}} = {c_{oh}}{x_{ohl}} + \sum\limits_{o \in {L_o} \cup {L_m},j \ne o \cap j \ne h} {{x_{ojl}}R_{jh}^l\left( {t_{jh}^l + {c_{oj}} + s} \right)} , $ | (9) |
| $ t_{hd}^{{h_{od}}} = {c_{hd}}{x_{hdl}} + \sum\limits_{h \in {L_o} \cup {L_m},j \ne o \cap j \ne d} {{x_{hjl}}R_{jd}^l\left( {t_{jd}^l + {c_{hj}} + s} \right)} . $ | (10) |
式中:coh车辆从起点站点o到hub站点h的平均车旅行时间,xohl为二进制变量,当线路l中包含站点o,且站点o的下一个站点为h时取1,否则取0,Rjhl为二进制变量,当乘客从站点j和站点h可以由线路l完成时取1,否则取0,Lo为所有线路的第一个站点的集合,tjhl为从站点j到站点h采用线路l出行时所花的时间,Lm为所有线路中间停靠的站点集合,s为中间站点平均停靠时间.其中式(9)和式(10)中出现的表示客流是否能够通过线路l实现出行的变量计算方式为
| $ R_{ik}^l = {x_{ikl}} + \sum\limits_{j \in {L_o} \cup {L_m},j \ne i,j \ne k} {{x_{ijl}}R_{jk}^l} . $ | (11) |
为求解该模型,本文设计了如图 2所示的遗传算法,具体步骤如下.

|
图 2 算法流程图 Fig. 2 Flow chart of the proposed algorithm |
步骤1 相关参数的输入.输入的参数包括两方面,一方面是线网数据信息,另一方面是算法参数信息,其中线网数据信息包括站点数量、站间最短距离、站点停靠时间、初始化hub站点数量比例、车辆数量等;算法参数信息包括种群规模、遗传算法的交叉变异概率、最大迭代次数及邻域搜索迭代次数等;
步骤2 初始化hub站点数量及位置.根据线网中公交站点数量以及设置的hub站点比例,如图 3所示,图 3为一二进制编码解,在此解中,站点1、6、7、12、18站点分别被确定为hub站点.

|
图 3 二进制编码解 Fig. 3 Binary code solution |
步骤3 确定hub站点覆盖的附属站点.根据步骤2确定的hub站点位置,依据就近原则确定hub站点的附属站点.
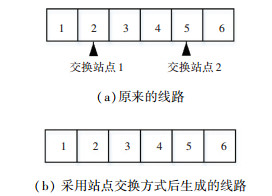
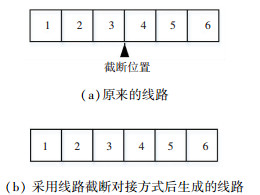
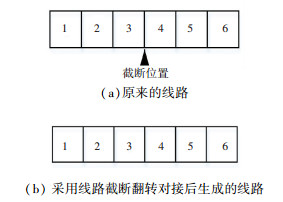
步骤4 确定milk-run线路结构.milk-run初始的线路可以直接通过组合hub站点及其附属站点确定,但此时的milk-run线路可能不是最佳线路布局结构,为确定最佳的milk-run线路结构,使线路运行时间最短,本文设计了如下3种邻域搜索方式,优化milk-run线路结构,其中所设计的改变milk-run的3种线路结构方式,分别如图 4~6所示.站点交换方式为先确定交换的站点对位置,然后进行交换;线路截断对接方式为先确定截断点位置,然后将位置左右两边的序列进行翻转而线路截断翻转对接与线路截断对接类似,不同的是在翻转之前先将截断点左端的序列逆序排列,然后再进行翻转对接.
|
图 4 站点交换改变线路结构方式 Fig. 4 Changing route structure by exchanging stops |
|
图 5 站点截断对接改变线路结构方式 Fig. 5 Changing route structure by stops truncation and joint |
|
图 6 站点截断翻转对接改变线路结构方式 Fig. 6 Changing route structure by stops truncation and reversal joint |
步骤5 分配初始线路车辆数量.得到milk-run线路及hub站点之后,依据总的车队规模为所构成公交线网分配初始车辆数量,其中为了保证载客能力约束条件,车辆分配分为两步,首先计算各线路满足车辆的最少车辆数量,然后再将剩余车辆数量随机分配给各线路.
步骤6 车辆分配数量优化.对各线路分配初始车辆之后,需要对分配方案进行进一步优化,在优化的过程中也采用邻域搜索对车辆规模进行优化,其过程类似于步骤4中milk-run线路局部优化的过程,同样的为了保证载客能力约束条件,参与优化的车辆数只包括第2步分配的剩余车辆数量.
步骤7 计算目标函数.根据所形成的公交线网规划及优化的发车频率对公交线网依据式(1)对目标函数进行计算.
步骤8 交叉变异改变线网结构.依据设定的交叉变异概率,通过个体对之间交叉及单个的变异操作,产生与现有种群规模大小一致的新个体数量,按照步骤3~7计算新个体的目标函数.
步骤9 选择优势个体作为新的种群.将原个体和产生的新个体进行混合,依据目标函数优劣对个体进行排序,选择种群规模大小的优势个体作为新一代种群.
步骤10 终止条件判断.判断迭代次数是否已经达到了设定的最大迭代次数,如果达到则输出最终优化方案,否则返回至步骤3.
3 实际案例及参数灵敏度分析 3.1 案例分析为了验证模型有效性,将该方法应用到文献[15]中的案例,如图 7所示,该区域共有29个公交站点,包括郊区的23个公交站点、城区5个目的地公交站点和1个换乘站点T,现有公交服务体系下总的车辆数量为176辆,站点间运行时间及站点间OD、站间最短运行时间、其中现有的公交服务运营情况见文献[15],同时为保证优化结果与现有的服务水平具有可对比性,将站点停靠时间和文献[15]一致设为1.5 min.

|
图 7 案例站点布局 Fig. 7 Stops layout of the case |
在本案例中,遗传算法参数设置为:种群规模为20个个体、初始hub站点比例为20%、交叉率为0.95、变异率为0.05、最大迭代次数为100代;此外,连续迭代50代值不发生变化时,则停止milk-run线路优化的局部搜索.同样的,对于线路分配也当连续迭代50代值不发生变化时,停止车辆分配局部搜索.其中遗传算法最大迭代次数以及局部搜索代数都是要根据公交线网规模大小确定,本文中具体的参数是依据案例网络多次试验测试的实验结果进行设置.
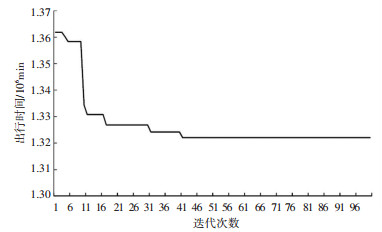
结合案例数据,依据确定的算法设定参数,采用MATLAB编程求解,其中目标函数随着迭代过程的变化如图 8所示,最终优化结果方案的主要信息见表 1.
|
图 8 目标函数随迭代次数增加的变化 Fig. 8 Variation of objective function with the increase of iteration times |
| 表 1 最终优化方案的主要信息 Tab. 1 Main information of the optimized solution |
在优化后的公交服务水平下,乘客总的出行时间为1 322 083 min,与现有的公交服务相比,能够减少乘车总的出行时间达16.26%.说明优化后的结果在不改变现有车辆配置情况下可以有效减少乘客总的出行时间,提高公交服务质量.
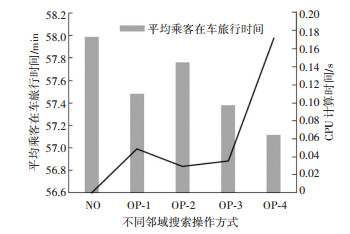
3.2 参数灵敏度分析 3.2.1 算法参数分析在算法设计中,采用了3种邻域搜索方式优化milk-run线路结构,为了探索不同邻域搜索效率,本文随机产生了20个初始解,并对这些初始解单独进行50次不同的邻域搜索方式的迭代优化,然后得到这些初始解的乘客的平均在车旅行时间.如图 9所示的计算结果,其中NO表示没有进行邻域搜索,OP-1、OP-2、OP-3分别表示算法设计过程中单独采用第1种、第2种、第3种邻域搜索的结果,OP-4表示3种邻域搜索进行组合的结果.
|
图 9 不同邻域搜索方式条件下乘客平均在车旅行时间和CPU计算时间 Fig. 9 Average in-vehicle travel time and CPU computation time for different neighborhood search methods |
基于上述测试结果,结合该算法的基本流程是先确定hub站点位置,然后对milk-run线路进行优化,最后分配车辆数量以及后续目标函数计算.本文对算法进行了进一步优化,首先在确定的hub站点和位置条件下解进行初步判定,只对种群中hub站点位置及数量选择较为合适的个体进行后续车辆数量分配和目标函数计算,具体判定方式为
| $ E_u^g \le E_{\lim }^g. $ | (12) |
其中:Eug为第g代且编号为u的个体的在车旅行时间值;Elimg为第g代通过式(12)筛选可以执行后续计算的优势个体的在车旅行时间临界值,即当未经过线路结构优化时乘客的在车旅行时间,需要指出的是由于随着种群迭代次数的增加,种群整体逐步进化,因此Elimg也随着种群变化.
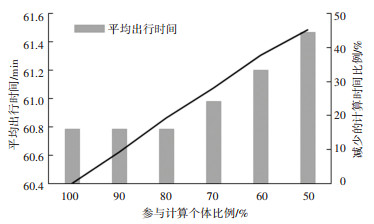
为了验证该参数设置的效果,本文基于同一初始种群进行了数据实验,通过设置不同的Elimg在种群中的取值实现种群中不同比例个体数量参与线路结构优化和发车频率设计,以此得到Elimg的取值与最终优化结果和CPU计算时间的关系,实验结果如图 10所示.
|
图 10 不同Elimg值控制效果 Fig. 10 Control effects of different values of Elimg |
从上图可知,当Elimg与种群中个体Elimg最大值一样时,可以得到最终优化结果,但不能减少CPU计算时间,如果通过Elimg保证参与线路结构优化和发车频率设计的种群个体在90%和80%时,最终优化结果不变,说明当Elimg值与种群中个体的Elimg最大值差距不大时,对优化结果影响较小,且可以节约一定的CPU时间,但随着Elimg控制值过较低时,虽然带来的CPU计算时间显著减少,但会对最终优化结果产生一定的影响.因此,在实际的操作过程中,需要把握Elimg值与最终优化结果的质量和CPU计算时间的关系,可以达到既节约计算时间,又不影响最终优化结果的效果.
3.2.2 设计参数分析1) 客流需求参数.为探索不同客流需求条件下本方法的效果,本文对原有的客流需求进行相应扩大.如图 11所示为客流分别为原客流100%到150%的条件下,通过所提出的方法得到不同客流需求条件下乘客的平均出行时间.通过比较可知,在客流变化的条件下,乘客的平均出行时间基本保持不变,证明了所提出方法鲁棒性.需要说明的是,在客流增加的条件下为了保证载客能力约束条件,本文将原有的车队规模提高了两倍.否则,保持原有的车队规模,当客流需求逐渐增加时,由于现有的车队规模的运输能力不能满足逐步增长的客流,将导致无可行解.

|
图 11 不同客流需求条件下乘客平均出行时间 Fig. 11 Average travel time for different travel demands |
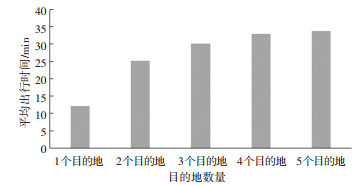
2) 目的地数量参数.不同的规划区域可能存在不同数量的目的地,为了验证所提出的方法在目的地数量变化条件下的应用效果,本文假设案例中目的地数量逐渐变少的情况. 图 12为目的地从1个变到5个时乘客的平均出行时间变化图.从该图可知乘客所到达的目的地越集中,即目的地数量越少,所提出的方法应用效果越好.需要说明的是,在此实验时,为了排除不同目的地距离不同对结果造成的影响,本文假设了所有目的地距离站点T的距离都保持一致.
|
图 12 网络中不同目的地数量条件下乘客平均出行时间 Fig. 12 Average travel time for different destinations in the network |
1) 依据城郊公交出行特征与一般的城区内公交出行特征存在一定的区别,提出了新的城郊公交线网规划模型,是对现有的公交规划模型进行相应的修正和补充,同时提出了相应的遗传算法实现了问题求解,为城郊公交线网规划和优化提供了新的思路.
2) 通过实际案例验证,所提出的采用milk-run和hub-spoke的城郊公交线网设计模式更加符合乘客出行需求,将城区公交客流进行聚集形成规模优化,在不增加车辆配置的前提下,能够有效减少乘客的出行时间.
3) 由于本文采用milk-run和hub站点设计城郊公交线网,所有乘客均需在hub换乘,因此在实际设计规划过程中,应考虑milk-run线路和从hub站点到达郊区目的地的直达线路之间的换乘衔接问题,这也是本文未来进一步需要探究的问题.
4) 通过对相关参数的灵敏度分析,进一步讨论了算法效率以及所提出的方法的应用场景,说明通过合适的Elimg设置,可以在保证解的质量的前提下,提高算法执行效率.所提出的方法在目的地较少的城郊公交网络中对提升公交服务效果更加显著.
| [1] |
LAMPKIN W, SAALMANS P D. The design of routes, service frequencies, and schedules for a municipal bus undertaking: a case study[J]. Operations Research, 1967, 18(4): 375. DOI:10.1057/jors.1967.70 |
| [2] |
NEWELL G F. Dispatching policies for a transportation route[J]. Transportation Science, 1971, 5(1): 91. |
| [3] |
SALZBORN F J M. Optimum bus scheduling[J]. Transportation Science, 1972, 6(2): 137. DOI:10.1287/trsc.6.2.137 |
| [4] |
刘清, 衷仁保, 朱志勇, 谢磊.实现城市公交线网优化的数学模型和广义A*算法[J].系统工程理论与实践, 1992, 2(1): 11 LIU Qing, ZHONG Renbao, ZHU Zhiyong, et al. The mathematical model & extensive algorithm A* for optimization to public traffic network in the city[J]. System Engineering Theory and Practice, 1992, 2(1): 11. http://www.cqvip.com/QK/95538X/199202/906405.html |
| [5] |
王炜. 实用交通网络规划软件系统研制[J]. 中国公路学报, 1992, 2(1): 13. WANG Wei. Research on practical software system of traffic network planning[J]. China Journal of Highway and Transport, 1992, 2(1): 13. |
| [6] |
CONSTANTIN I, FLORIAN M. Optimizing frequencies in a transit network: a nonlinear bi-level programming approach[J]. International Transactions in Operational Research, 1995, 2(2): 149. DOI:10.1111/itor.1995.2.issue-2 |
| [7] |
WAN Q K, LO H K. A mixed integer formulation for multiple-route transit network design[J]. Journal of Mathematical Modelling and Algorithms, 2003, 2(4): 299. DOI:10.1023/B:JMMA.0000020425.99217.cd |
| [8] |
LEE Y J, VUCHIC V R. Transit network design with variable demand[J]. Journal of Transportation Engineering, 2005, 131(1): 1. |
| [9] |
KILIÇ F, GÖK M. A demand based route generation algorithm for public transit network design[J]. Computers & Operations Research, 2014, 51(1): 21. |
| [10] |
蒋阳升, 罗孝羚. 考虑首末站约束和站间客流强度的公交线网优化[J]. 长安大学学报(自然科学版), 2017, 37(1): 106. JIANG Yangsheng, LUO Xiaoling. Optimization of public transit network considering initial and terminal stations location requirements and passenger flow intensity[J]. Journal of Chang'an University (Natural Science Edition), 2017, 37(1): 106. DOI:10.3969/j.issn.1671-8879.2017.01.014 |
| [11] |
魏明, 陈学武, 孙博. 多模式区域公交协调调度模型和算法[J]. 公路交通科技, 2015, 32(4): 136. WEI Ming, CHEN Xuewu, SUN Bo. A model and algorithm of schedule coordination for multi mode regional bus transit[J]. Journal of Highway and Transportation Research and Development, 2015, 32(4): 136. DOI:10.3969/j.issn.1002-0268.2015.04.024 |
| [12] |
BAAJ M H, MAHMASSANI H S. Hybrid route generation heuristic algorithm for the design of transit networks[J]. Transportation Research Part C: Emerging Technologies, 1995, 3(1): 31. DOI:10.1016/0968-090X(94)00011-S |
| [13] |
MARTÍNEZ H, MAUTTONE A, URQUHART M E. Frequency optimization in public transportation systems: Formulation and metaheuristic approach[J]. European Journal of Operational Research, 2014, 236(1): 27. |
| [14] |
WU J, SONG R, WANG Y, et al. Modeling the coordinated operation between bus rapid transit and bus[J]. Mathematical Problems in Engineering, 2015, 2015(1): 1. |
| [15] |
SZETO W Y, WU Y. A simultaneous bus route design and frequency setting problem for Tin Shui Wai, Hong Kong[J]. European Journal of Operational Research, 2011, 209(2): 141. DOI:10.1016/j.ejor.2010.08.020 |
| [16] |
NEMOTO T, HAYASHI K, HASHIMOTO M. Milk-run logistics by Japanese automobile manufacturers in Thailand[J]. Procedia-Social and Behavioral Sciences, 2010, 2(3): 5980. DOI:10.1016/j.sbspro.2010.04.012 |
| [17] |
YANG K, YANG L, GAO Z. Hub-and-spoke network design problem under uncertainty considering financial and service issues: a two-phase approach[J]. Information Sciences, 2017, 402(2017): 15. |
| [18] |
CEDER A. Public transit planning and operation: theory, modelling and practice[M]. Oxford: Elsevier, 2007.
|
 2019, Vol. 51
2019, Vol. 51


