2. 西南交通大学 土木工程学院,成都 610031
2. Civil Engineering School, Southwest Jiaotong University, Chengdu 610031, China
近年来,伴随着中国铁路的持续发展,西部山区已修建了大量的铁路线,如青藏线(全长1956 km, 已通车)、兰渝线(全长873 km,已通车)、兰青铁路(全长188 km,通车)、川藏线(全长1629 km,在建)、青新线(全长1240 km,在建)、成昆复线(全长900 km,在建)、成兰铁路(全长457 km,在建)、西成客专(全长643 km,已通车),为了跨越地形高差大、地震烈度高的西部地区,铁路多跨刚构-连续梁桥被广泛采用,其墩高会随着地形的起伏而发生变化,最大墩高超过100 m,且受地形的影响,墩与墩之间往往高差较大.对于这类典型铁路桥梁,随墩高、跨度的不断增大,桥梁结构的抗震设计将面临众多的技术挑战.此外,西部地区近10 a来地震频发,自汶川地震至今,中国5级以上地震共发生90余次,而大部分地震均发生在西部地区.由于西部很多铁路线跨越高烈度地震区,使得铁路桥梁正面临着地震的严重威胁.然而我国铁路现行桥梁抗震规范并未提出适用于高烈度区桥梁抗震设计和评估的方法[1],因此急需开展西部高烈度区典型铁路桥梁抗震性能评估的工作.
目前地震易损性分析法在桥梁抗震分析领域得到了广泛的应用[2],该方法主要分为3类:经验法[3]、试验法[4]、理论分析法[5].文献[6]于1997年首次提出了结构经验地震易损性曲线的概念,并建立了洛杉矶北岭地震区桥梁结构的经验易损性曲线,文献[7]运用贝叶斯估计法建立了阪神地震区桥梁经验易损性曲线.文献[8]开展了32组桥墩模型振动台试验研究,建立了桥墩试验易损性曲线.文献[9]基于蒙特卡洛法对美国加州典型高速公路桥梁开展了易损性分析.文献[10]基于极大似然估计法建立了西部山区典型简支梁桥地震易损性曲线,评估了桥梁的抗震性能.文献[11]基于云图法对17种矢跨比的圬工拱桥进行了地震易损性分析.文献[12]基于云图法开展了加拿大魁北克地区典型连续梁桥的易损性评估,对比分析了多种减隔震支座对桥梁抗震性能的影响.然而,由于目前桥梁易损性分析中常用的损伤指标(桥墩截面曲率、墩顶位移、截面曲率延性比等)往往只反映桥梁构件单一方向的地震损伤情况,而常用易损性分析方法(云图法、蒙特卡洛法、极大似然估计法)是基于上述这些损伤指标进行推导的,因此目前各国学者开展的地震易损性研究工作主要是针对一维地震作用下的分析研究,而对桥梁三维地震易损性分析研究较少.
本文以西部高烈度区典型铁路4跨刚构-连续梁桥为工程背景,建立桥梁危险构件的三维损伤指标函数,基于可靠度理论和概率统计分析法,建立桥梁三维地震易损性计算分析方法,而后采用云图法验证其正确性和适应性,在此基础上,建立了算例桥危险构件的全视角极坐标空间易损性云图,全面分析评估了桥梁构件的易损性情况及其分布特征.
1 建立桥梁易损构件三维地震损伤指标目前在桥梁易损性分析中,由于易损构件的损伤指标大多反映一维地震损伤状态[2, 10],因此要想实现三维地震下桥梁易损性评估,就必须建立合理有效的三维地震损伤指标,这也是实现三维易损性分析的关键因素之一.而大量实际震害资料[13]及理论分析[1-2, 10]表明:对于大多桥梁结构,在地震动作用下,主梁基本保持线弹性状态,震害主要集中在桥墩和支座构件,因此下文仅针对桥梁易损构件(即桥墩和支座)建立三维地震损伤指标.
1.1 桥墩三维地震弯曲损伤指标由于损伤指标的原因,目前各国学者在进行桥墩易损性分析时,主要开展弯曲破坏的分析研究[2, 10],部分学者虽然开展了桥墩剪切破坏易损性分析[14],但主要是通过计算桥墩剪力,先判断桥墩是否发生剪切破坏,而后将计算结果换算为弯曲破坏的损伤指标来建立易损性曲线.而对于桥墩弯剪破坏的易损性分析研究工作目前甚少,主要是因为墩柱弯剪破坏的分析理论尚不完善[15].因此鉴于目前研究的不足,下文仅针对桥墩三维地震弯曲破坏损伤指标开展研究.
为实现在三维地震作用下桥墩弯曲破坏易损性分析,本文将Bresler[16]提出的钢筋混凝土柱弯曲强度-轴压强度失效屈服面理论引入易损性分析中,为了反映桥墩的延性变形能力,将Bresler所提失效屈服面进行了改进,并基于可靠度理论关于结构功能函数的定义,建立起在三维地震作用下判断钢筋混凝土桥墩发生弯曲破坏的损伤指标函数,即桥墩三维地震弯曲损伤指标为
| $ {Z_i} = f\left( {P,{\varphi _x},{\varphi _y}} \right) = 1 - \left( {{{\left( {\frac{{P - {P_{\rm{c}}}}}{{{P_{\rm{o}}} - {P_{\rm{c}}}}}} \right)}^2} + {{\left( {\frac{{{\varphi _x}}}{{{\varphi _{xu,i}}}}} \right)}^2} + {{\left( {\frac{{{\varphi _y}}}{{{\varphi _{yu,i}}}}} \right)}^2}} \right). $ | (1) |
式中:Po为桥墩截面极限轴压承载力,kN;P为地震作用下桥墩轴压力,kN;Pc为钢筋混凝土桥墩截面发生平衡破坏时(拉、压破坏临界点)对应的轴力,可依据文献[17]求解该值;φxu, i, φyu, i分别为桥墩截面绕x、y轴的曲率变形能力值,可通过弯矩-曲率分析[10]求得,i=1、2、3、4分别对应轻微、中等、严重、完全4种损伤状态;φx、φy分别为桥墩截面绕x、y轴的曲率地震需求值.
1.2 支座三维地震损伤指标为了实现三维地震作用下桥梁支座变形破坏的易损性分析,基于Jangid[18]建立的支座变形滑移准则,建立起三维地震作用下判断支座发生损伤破坏的损伤状态函数,即支座三维地震损伤指标为
| $ {G_i} = g\left( {{S_x},{S_y}} \right) = 1 - \left( {{{\left( {\frac{{{S_x}}}{{S_{x,i}^f}}} \right)}^2} + {{\left( {\frac{{{S_y}}}{{S_{y,i}^y}}} \right)}^2}} \right). $ | (2) |
式中:Sx为支座纵桥向最大地震位移,m;Sy为支座横桥向最大地震位移,m;Sx, if为支座第i种损伤状态对应的纵桥向位移临界值;Sy, if为支座第i种损伤状态对应的横桥向位移临界值.
2 桥梁三维地震作用下易损性分析方法为实现桥梁三维地震作用下的易损性分析评估,本文基于第1节建立的损伤指标,再结合可靠度理论和概率统计分析法,逐步推导建立了桥梁三维易损性分析方法.在这之前先对可靠度理论中的失效概率和可靠指标进行简单介绍,为后续计算理论的推导做铺垫.
2.1 结构失效概率在可靠度理论中,通常采用功能函数反映结构抵抗各类荷载效应的能力.而在地震易损性分析中,功能函数即为第1节建立的损伤指标函数.以桥梁结构为例,假设某桥梁构件的抗震能力为C,地震需求为D,则该构件的损伤指标函数为
| $ Z = C - D. $ | (3) |
故特定强度IM地震作用下,该构件不出现损伤破坏的概率为
| $ {P_{\rm{s}}} = P\left\{ {Z > 0\left| {IM} \right.} \right\} = P\left\{ {C - D > 0\left| {IM} \right.} \right\}. $ | (4) |
假设桥梁构件功能函数的概率密度是fz(z),按照概率论计算原理,则桥梁构件在地震作用下的失效概率(即为地震损伤概率)为
| $ {P_{\rm{f}}} = P\left( {Z < 0} \right) = \int_{ - \infty }^0 {{f_Z}\left( z \right){\rm{d}}z} . $ | (5) |
由于式(3)损伤指标函数Z为二元函数,所以式(5)为两重积分,若损伤指标函数变量更多时,则桥梁构件地震损伤概率将很难通过直接积分法求解.因此,为求解出桥梁构件损伤概率,工程上常运用可靠度理论进行简化计算求解,从而引入可靠指标的概念[19].式(5)给出了桥梁构件地震损伤发生概率的表达式,此时若损伤指标函数Z的概率分布特征已知,假设Z服从正态分布,其均值为μz,标准差为σz,则式(5)可变为
| $ {P_{\rm{f}}} = \int_{ - \infty }^0 {{f_{\rm{z}}}\left( z \right){\rm{d}}z} = \int_{ - \infty }^0 {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}{\sigma _z}} }}\exp \left[ { - \frac{{{{\left( {z - {\mu _z}} \right)}^2}}}{{2\sigma _z^2}}} \right]{\rm{d}}z} . $ | (6) |
将上式进行变换,z=μz+σzt,则dz=σzdt,当z=0时,t=-μz/σz;当z→-∞时,t→-∞,故式(6)变为
| $ {P_{\rm{f}}} = \int_{ - \infty }^{ - {\mu _z}/{\sigma _z}} {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} }}\exp \left( { - \frac{{{t^2}}}{2}} \right){\rm{d}}t} = \mathit{\Phi }\left( { - \frac{{{\mu _{\rm{z}}}}}{{{\sigma _{\rm{z}}}}}} \right) = \mathit{\Phi }\left( { - \beta } \right). $ | (7) |
式中β在可靠度理论中称为结构可靠指标,由上式(7)可知,要求解桥梁地震失效概率,只需求出函数Z的可靠指标β即可.
上述求解可靠指标进而计算失效概率的过程为计算三维地震作用下桥梁构件损伤发生概率提供了很好的思路,因此本文将基于可靠度理论来推导三维地震作用下的易损性分析理论.而由上述分析可知要建立桥梁结构三维地震易损性分析理论,首先需要探讨的是桥梁构件损伤指标函数中指标变量服从怎样的分布特征,以及函数的具体形式,只有明确了函数Z的分布特征和具体形式才能推导出构件地震损伤破坏概率计算理论.
2.3 建立桥梁三维地震易损性计算理论1.1和1.2节提出了桥墩弯曲破坏、支座破坏的损伤指标函数,两损伤指标函数均为多元非线性函数.文献[20]研究表明:在地震作用下桥墩曲率、支座位移等响应是近似服从对数正态分布,并且各指标变量相互独立.但因本文1.1节建立的桥墩损伤指标属于多元非线性函数,其非线性程度较高,这时想要精确计算出指标Z的平均值和标准差是较为困难的,即使可以求解,损伤指标函数也不再服从正态分布.从而不能采用计算可靠指标的方法求解桥梁构件地震损伤概率,为此,本文综合考虑桥墩损伤指标函数的特点,采用工程结构可靠度相关理论和概率统计法,建立了适用于本文所提损伤指标函数的可靠指标计算理论,从而建立了桥梁构件三维易损性分析理论.由于篇幅有限,本文以桥墩弯曲破坏为例,推导建立三维地震作用下桥墩弯曲破坏的易损性计算理论,对于支座构件三维地震易损性计算理论可按桥墩弯曲破坏的计算方法进行推导.
式(1)给出了桥墩弯曲破坏的损伤指标函数,令a1=(Po-Pc)-2,a2=φxu, i-2,a3=φyu, i-2,i=1, …, 4其代表 4种损伤状态.从而式(1)简化为
| $ Z = 1 - {a_1}{\left( {P - {P_{\rm{c}}}} \right)^2} - {a_2}\varphi _x^2 - {a_3}\varphi _y^2. $ | (8) |
假设有N条地震动,其强度指标均为IM,地震动输入方向为竖向+某水平方向,对N条地震动进行非线性时程分析,获得桥墩危险截面各指标变量的抗震需求值为(Pj, φx, j, φy, j)T, j=1, 2, …, N,各指标变量的均值分别为μ1、μ2和μ3,标准差分别为σ1、σ2和σ3.文献[20]研究表明桥墩曲率等指标的地震响应值近似服从对数正态分布.为计算式(8)的可靠指标,采用可靠度理论中的等概率变换原则[21],将式(8)中P、φx和φy转换为标准正态随机变量Y1、Y2和Y3X,则有
| $ \left\{ {\begin{array}{*{20}{c}} {P = \exp \left( {{\mu _{\ln P}} + {Y_1}{\sigma _{\ln P}}} \right),\partial P/\partial {Y_1} = P{\sigma _{\ln P}};}\\ {{\varphi _x} = \exp \left( {{\mu _{\ln \varphi x}} + {Y_2}{\sigma _{\ln \varphi x}}} \right),\partial {\varphi _x}/\partial {Y_2} = {\varphi _x}{\sigma _{\ln \varphi x}};}\\ {{\varphi _y} = \exp \left( {{\mu _{\ln \varphi y}} + {Y_3}{\sigma _{\ln \varphi y}}} \right),\partial {\varphi _y}/\partial {Y_3} = {\varphi _y}{\sigma _{\ln \varphi y}}.} \end{array}} \right. $ | (9) |
式中:
| $ {\mu _{\ln P}} = \ln \left( {{\mu _1}/\sqrt {1 + \delta _P^2} } \right),{\sigma _{\ln P}} = \sqrt {\ln \left( {1 + \delta _P^2} \right)} ,{\delta _P} = {\sigma _1}/{\mu _1}, $ |
| $ {\mu _{\ln \varphi x}} = \ln \left( {{\mu _2}/\sqrt {1 + \delta _{\varphi x}^2} } \right),{\sigma _{\ln \varphi x}} = \sqrt {\ln \left( {1 + \delta _{\varphi x}^2} \right)} ,{\delta _{\varphi x}} = {\sigma _2}/{\mu _2}, $ |
| $ {\mu _{\ln \varphi y}} = \ln \left( {{\mu _3}/\sqrt {1 + \delta _{\varphi y}^2} } \right),{\sigma _{\ln \varphi y}} = \sqrt {\ln \left( {1 + \delta _{\varphi y}^2} \right)} ,{\delta _{\varphi y}} = {\sigma _3}/{\mu _3}. $ |
将桥墩损伤指标函数在标准正态空间内进行变换,则式(8)变为
| $ \begin{array}{l} {g_Y}\left( {{Y_1},{Y_2},{Y_3}} \right) = 1 - {a_1} \times \left( {\exp \left( {{\mu _{\ln P}} + {Y_1}{\sigma _{\ln P}}} \right) - } \right.\\ \;\;\;{\left. {{P_{\rm{c}}}} \right)^2} - {a_2} \times {\left( {\exp \left( {{\mu _{\ln \varphi x}} + {Y_2}{\sigma _{\ln \varphi x}}} \right)} \right)^2} - {a_3} \times \\ \;\;\;{\left( {\exp \left( {{\mu _{\ln \varphi y}} + {Y_3}{\sigma _{\ln \varphi y}}} \right)} \right)^2}. \end{array} $ | (10) |
因损伤指标函数为三元非线性函数,不能直接通过式(7)求解可靠指标和损伤概率,因此需要对损伤指标函数进行适当简化处理,本次采用工程结构可靠度理论,对损伤函数进行简化处理,即对损伤指标函数在其验算点处进行一次泰勒级数展开,为保证展开后函数的计算精度,基于可靠度理论选择在验算点[19]处展开,展开后的函数为线性分布,因各指标变量服从正态分布,故由概率论与数理统计[21]相关理论可知,展开后函数也将服从正态分布.此时假设桥梁结构损伤指标函数的验算点y*=(y1*, y2*, y3*)T已知,则式(10)的一次泰勒展式为
| $ {Z_{\rm{L}}} = {g_Y}\left( {y_1^ * ,y_2^ * ,y_3^ * } \right) + \sum\limits_{i = 1}^3 {\partial {g_Y}\left( {{y^ * }} \right)/\partial {Y_i}\left( {{Y_i} - y_i^* } \right)} . $ | (11) |
求解指标函数ZL的平均值μZL和标准差σZL,可得到指标函数ZL的可靠指标为
| $ {\beta _{\rm{b}}} = \frac{{{\mu _{{Z_{\rm{L}}}}}}}{{{\sigma _{{Z_{\rm{L}}}}}}} = \frac{{{g_Y}\left( {y_1^ * ,y_2^ * ,y_3^ * } \right) + \sum\limits_{i = 1}^3 {\frac{{\partial {g_Y}\left( {{y^ * }} \right)}}{{\partial {Y_i}}}\left( {{\mu _{{Y_i}}} - y_i^ * } \right)} }}{{\sqrt {\sum\limits_{i = 1}^3 {{{\left[ {\frac{{\partial {g_Y}\left( {{y^ * }} \right)}}{{\partial {Y_i}}}{\sigma _{{Y_i}}}} \right]}^2}} } }}. $ | (12) |
对指标函数求偏导数,得
| $ \left\{ \begin{array}{l} \partial {g_Y}\left( {{y^ * }} \right)/\partial {Y_1} = - 2{a_1}\left[ {\exp \left( {{\mu _{\ln P}} + y_1^ * {\sigma _{\ln P}}} \right) - } \right.\\ \;\;\;\;\;\;\;\;\left. {{P_{\rm{c}}}} \right] \times \exp \left( {{\mu _{\ln P}} + y_1^ * {\sigma _{\ln P}}} \right){\sigma _{\ln P}},\\ \partial {g_Y}\left( {{y^ * }} \right)/\partial {Y_2} = - 2{a_2}{\left[ {\exp \left( {{\mu _{\ln \varphi x}} + y_2^ * {\sigma _{\ln \varphi x}}} \right)} \right]^2}{\sigma _{\ln \varphi x}},\\ \partial {g_Y}\left( {{y^ * }} \right)/\partial {Y_3} = - 2{a_3}{\left[ {\exp \left( {{\mu _{\ln \varphi y}} + y_3^ * {\sigma _{\ln \varphi y}}} \right)} \right]^2}{\sigma _{\ln \varphi y}}. \end{array} \right. $ | (13) |
由于桥梁结构地震响应分析的随机性,使得各指标变量验算点y*=(y1*, y2*, y3*)T是未知的,仅仅依靠式(12)并不能直接计算出βb.需要补充其他约束条件.令ZL=0,则表示桥墩构件达到地震损伤破坏临界状态,由可靠指标的几何意义[19]和解析几何相关理论[22]可知,在标准正态空间中,可靠指标与验算点处切线法线的方向余弦的关系为
| $ y_i^ * = {\beta _{\rm{b}}}\cos {\theta _{Yi}} = {\beta _{\rm{b}}}{\alpha _{Yi}},i = 1,2,3; $ | (14) |
| $ {\alpha _{Yi}} = - \left( {\partial {g_Y}\left( {{y^ * }} \right)/\partial {Y_i}} \right)/\left( {\sqrt {\sum\limits_{i = 1}^3 {{{\left[ {\partial {g_Y}\left( {{y^ * }} \right)/\partial {Y_i}} \right]}^2}} } } \right). $ | (15) |
令
| $ \left\{ \begin{array}{l} {\alpha _{{Y_1}}} = 2{a_1}\left[ {\exp \left( {{\mu _{\ln P}} + y_1^ * {\sigma _{\ln P}}} \right) - {P_{\rm{c}}}} \right] \times \\ \;\;\;\;\;\;\;\exp \left( {{\mu _{\ln P}} + y_1^ * {\sigma _{\ln P}}} \right){\sigma _{\ln P}}/S,\\ {\alpha _{{Y_2}}} = \frac{{2{a_2}{{\left[ {\exp \left( {{\mu _{\ln \varphi x}} + y_2^ * {\sigma _{\ln \varphi x}}} \right)} \right]}^2}{\sigma _{\ln \varphi x}}}}{S},\\ {\alpha _{{Y_3}}} = \frac{{2{a_3}{{\left[ {\exp \left( {{\mu _{\ln \varphi y}} + y_3^ * {\sigma _{\ln \varphi y}}} \right)} \right]}^2}{\sigma _{\ln \varphi y}}}}{S}. \end{array} \right. $ | (16) |
由式(12)分析可知,在求解桥墩损伤函数的可靠指标βb时,需确定验算点的数值,而验算点是由式(14)求解得到的,但式(14)又是可靠指标和验算点(反映在式(16)方向余弦值计算式中)的函数,可以看出式(12)、(14)、(16)是相互关联的.故桥梁构件弯曲破坏指标函数的可靠指标和验算点须通过迭代进行求解,具体步骤如下:1)对桥梁有限元模型进行N条地震动作用下的时程分析,提取每组地震时程分析下桥墩危险截面3个指标变量的最大值,求解各指标变量的平均值和标准差,进而计算式(9);2)假设第一次迭代时,验算点取为y*(0)=(0, 0, 0)T;3)将y*(0)、3个指标变量均值和标准差、式(9)代入式(10)和式(13)计算gY和əgY(y*)/əYi;4)将上述计算的gY和əgY(y*)/əYi代入的式(12),计算桥墩可靠指标βb,再由式(16)计算αYi(i=1, 2, 3);5)将以上求解的βb和αYi(i=1, 2, 3)代入式(14),计算新的验算点y*(1);6)判断‖y*(1)-y*(0)‖ < ε是否满足精度要求(ε为设定的容许偏差,这里取1‰),若精度满足要求,则迭代终止,所求βb即为要求的桥墩弯曲破坏的可靠指标,否则令y*(0)=y*(1),转到步骤2)继续迭代计算.
基于上述步骤,可以求解出桥墩地震弯曲破坏的可靠指标,由此便可计算出特定地震强度IM作用下,桥墩易损部位发生弯曲破坏的损伤概率为
| $ P\left\{ {Z \le 0\left| {IM} \right.} \right\} = \mathit{\Phi }\left( { - {\beta _{\rm{b}}}} \right). $ | (17) |
运用上式(17)可求解出地震强度为IM时所对应的桥墩地震损伤概率.按上述计算方法求解各种地震强度作用下桥墩弯曲破坏的损伤概率,便可建立桥墩弯曲破坏的易损性曲线.基于上述求解过程,便可建立任意方向地震作用下桥墩的易损性曲线.
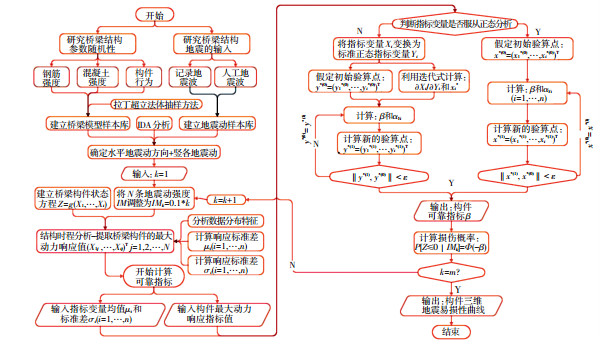
2.4 桥梁构件三维易损性分析方法为实现桥梁构件三维易损性分析,本文将IDA分析法引入2.3节建立的桥梁三维地震易损性计算理论中,提出了桥梁构件三维地震易损性分析方法,具体分析流程详见图 1.
|
图 1 三维地震桥梁构件易损性分析方法 Fig. 1 3D seismic vulnerability analysis method of bridge components |
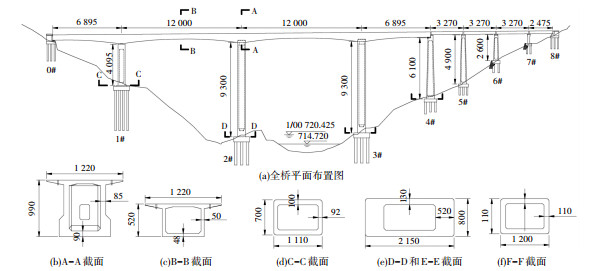
本文以西部山区某典型铁路4跨刚构-连续梁桥为工程背景,跨径布置:68 m+2×120 m+68 m +3×32 m+24 m,上部结构采用预应力混凝土连续箱梁,混凝土强度等级C55;各桥墩为矩形空心墩,1~4#桥墩墩高分别为:40.95、93.0、93.0、61 m,1~3#桥墩混凝土强度等级C40,4#墩混凝土强度等级C35;0#台支座、1#、4#墩支座具体型号如下:TJGZ-LX-Q9000-ZX-e150-0.1g、TJGZ-LX-Q55000ZX-e100-0.1g、TJGZ-LX-Q9000 -ZX-e100-0.1g,图 2给出了全桥总体布置图.
|
图 2 全桥布置示意图(cm) Fig. 2 Schematic diagram of full-bridge layout (cm) |
运用OpenSees有限元分析软件建立全桥模型,采用弹性梁单元模拟主梁;采用弹塑性纤维单元模拟桥墩,并赋予相应的混凝土和钢筋材料本构模型;采用双线性弹塑性单元模拟支座[1];采用6个弹簧单元等效模拟桥梁桩基础,依据文献[23]中附录D方法计算各墩桩基础等效刚度.
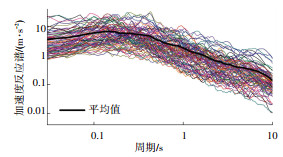
3.2 地震动输入概况 3.2.1 地震动的不确定性因所选算例桥梁位于四川地区,因此本文在选择地震波时考虑选用汶川实测地震波作为易损性分析的输入地震动,这样可保证分析结果与实际相吻合.在充分考虑地震波强度范围和地震记录完整性等因素后,从40个观测站中选取了120条实测地震波,各地震波的加速度反应谱见图 3.基于IDA分析法,对120条地震波的PGA进行调幅处理,从0.1g至1.0g,调幅步长为0.1g,生成1 200组地震波分析样本.
|
图 3 汶川地震120条地震动反应频谱特性图( ξ =0.05) Fig. 3 Spectrum response of the 120 waves in Wenchuan earthquake (ξ=0.05) |
算例桥采用三维地震动输入方式进行易损性分析,即某一水平方向+竖向地震动共同作用来实现三维地震输入.每次分析时,竖向和水平向地震采用同一条地震波,但两条波的峰值加速度PGA各不相同,参照文献[24]第7.1.4条规定,竖向地震的强度取水平向地震强度的65%,即将水平向地震波时程曲线的PGA整体缩放到原来的0.65倍得到竖向地震波.
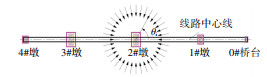
本文考虑37个水平地震动输入方向,在每个水平方向上(同时施加竖向地震动)均运用3.2.1节建立的1200组地震样本进行时程分析,基于分析结果建立对应方向的易损性曲线,具体水平输入方向定义如下:假设水平输入方向与桥梁线路中心线夹角为θ=10°×i,i=0, 1, …, 36,θ为按逆时针转动地震输入角度,具体地震输入方向见图 4.
|
图 4 水平地震输入方向示意图 Fig. 4 Schematic diagram of horizontal seismic input direction |
在三维地震时程分析时,之所以竖向和水平向采用同一条地震波(仅两方向地震动强度不同),主要考虑如下:如果采用3个方向地震波(两水平向+竖向)进行分析,将无法统一表征地震动的强度大小,没有统一的强度指标,则无法绘制易损性曲线,进而无法实现三维易损性分析,故依据文献[24]定义了三维地震动施加方式,并以水平地震动强度值作为三维地震动的强度值.
3.3 桥梁模型参数的不确定性对于典型铁路4跨刚构-连续梁桥,其材料特性及荷载效应的随机性往往直接影响桥梁结构的抗震能力,故在开展易损性分析时,需要考虑结构自身参数随机性的影响.针对典型铁路非规则刚构-连续梁桥的特点,并结合以往的研究成果[1, 25],给出了本文模型桥中考虑的主要结构随机参数及其分布特征值(表 1).采用拉丁超立方体抽样法抽样模型参数,建立120组桥梁分析样本,然后将桥梁样本与地震动样本随机配对,建立地震-桥梁分析样本库,对样本库进行时程分析,基于分析结果便可计算三维地震易损性曲线.
| 表 1 模型桥随机性参数及其分布特征 Tab. 1 Random parameters of the bridge structure and the distribution |
因目前各国学者对桥梁三维地震易损性分析的研究较少,因此无法在三维地震作用下用现有方法来验证本文方法,只能开展一维地震作用下的方法验证.因此为了检验本文算法的正确性,拟采用传统分析方法(云图法),建立纵向地震作用下算例桥梁各构件的易损性曲线,通过比较分析本文方法与传统方法计算结果的差异性,来验证本文方法的正确性.
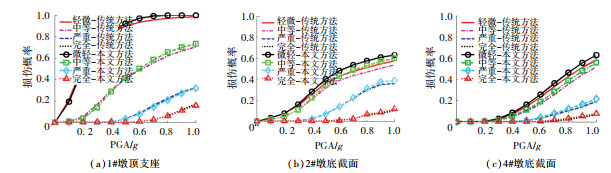
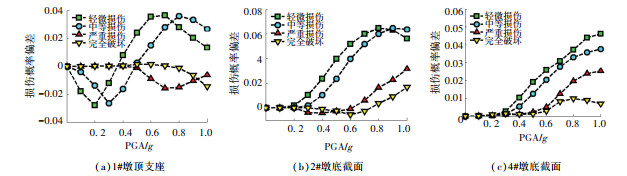
由于篇幅有限,图 5仅给出算例桥部分危险部位(1#墩支座、2#墩底截面、4#墩底截面)两种方法对应的易损性曲线.由图 5分析可知本文方法与传统方法所建易损性曲线较为吻合,两种方法计算结果差异较小,且所建立的易损性曲线变化趋势是一致的,这说明本文所提分析方法计算结果正确.为进一步研究两种方法所得易损性曲线的差异性,图 6给出了两种方法计算结果的偏差走势图,偏差走势图是由本文算法减去传统算法计算结果得到的.
|
图 5 两种分析方法对应的易损性曲线 Fig. 5 Seismic vulnerability curves of the two methods |
|
图 6 两种分析方法对应的概率偏差图 Fig. 6 Probability deviation curves of the two methods |
图 6(a)表明,1#墩顶支座两种方法计算结果偏差较小,轻微损伤出现了最大偏差概率3.7%,轻微、中等损伤的偏差曲线变化规律一致,均为正弦波式的变化趋势.对于严重损伤状态,两种方法最大偏差值为-1.61%,偏差主要集中在0.5g~1.0g.而完全损伤对应的偏差概率近乎为0,综上1#墩顶支座在4种损伤状态下偏差概率均小于4%,两种方法计算结果较为吻合. 图 6(b)表明,2#墩底截面易损概率最大偏差6.42%,出现在轻微损伤状态;轻微、中等损伤状态概率偏差曲线变化趋势一致,即随着PGA的增加是先增大后减小,虽然两种方法偏差达到6.4%,但最大偏差主要集中在很小的范围内(轻微损伤:PGA约为0.7g~0.85g;中等损伤: PGA约为0.85g~1.0g),其他范围内偏差概率较小.对于严重和完全损伤,两种方法所得概率偏差值均小于3%,两种状态偏差曲线变化趋势一致. 图 6(c)表明,在轻微损伤、中等损伤、严重损伤状态下,4#墩底截面最大概率偏差分别为4.59%、3.80%、2.48%,3种状态偏差曲线变化趋势一致,即随着PGA的增大而增大.完全损伤状态的概率偏差小于1%.
基于上述分析可知,对于桥梁各危险构件,本文方法与传统方法建立的易损性曲线变化规律相同,两种方法计算的损伤概率偏差较小,仅2#墩底截面小范围内出现6.42%的偏差,其他构件计算结果均低于5%,依据文献[19]研究表明上述偏差满足工程应用要求.这也说明两种截然不同的分析理论所得计算结果较为一致,即本文所提方法正确.
3.5 桥梁构件三维地震易损性分析基于第2节提出的桥梁三维易损性分析方法,便可建立桥梁各危险部位在不同地震输入方向上的易损性曲线,而后基于各方向的易损性曲线,便可生成桥梁构件全视角的地震易损性云图.
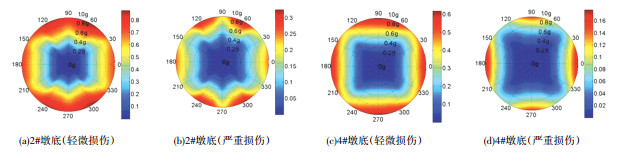
3.5.1 桥墩构件易损性分析由于篇幅有限,图 7仅给出部分桥墩截面发生地震弯曲破坏(轻微和严重损伤)的全视角极坐标空间易损性云图.基于各桥墩截面云图,可获得不同输入方向特定PGA强度地震下桥墩发生地震损伤破坏的概率,能够全方位的评估桥墩抗震性能.此外下文将结合铁路桥梁抗震规范[24],重点评估9度设计地震(PGA为0.4g)和罕遇地震(PGA为0.64g)下的桥梁易损性情况.
|
图 7 桥墩构件全视角极坐标空间易损性云图 Fig. 7 Full-view vulnerability cloud pictures of pier component |
由图 7(a)、7(b)分析表明,三维地震作用下,2#墩底截面在地震输入角为60°、110°、250°、300°左右时,相比其他输入方向更容易发生地震损伤破坏(下文将这些容易发生损伤破坏的地震输入角度称为:最易损输入角),随着地震动强度PGA的逐渐增大,使桥墩出现轻微(或严重)损伤的地震输入方向越来越多,其变化规律是由最易损输入角向两边扩散;对于2#墩底截面,任意输入方向地震作用下,当PGA为0.4g时(9度,设计地震),发生轻微损伤的概率不大于27%,发生严重损伤的概率小于8%;当PGA为0.64g时(9度,罕遇地震),任意方向地震作用下,出现轻微损伤的概率不大于55%,出现严重损伤的概率不大于18%.当PGA为0.64g时,存在4个易损地震输入角区间,即50°~70°、100°~120°、240°~260°、290°~310°,在该区间内,发生轻微损伤的概率均达到55%~58%之间,发生严重损伤的概率均达在18%~21%之间.基于上述分析可知,在地震作用下,2#墩底截面极易发生轻微损伤,最易损输入角为60°、110°、250°、300°.算例桥3#墩易损性分布特征与2#墩相似,这里不再详述.由图 7(c)、7(d)分析表明,4#墩底截面,在三维地震作用下,最易损输入角度为:0°、90°、180°、270°,且90°输入角是最容易发生地震损伤的;在PGA为0.64g时也存在4个易损输入角区间,即为:-10°~10°、70°~110°、170°~190°、260°~280°,地震在该区间内作用时,出现轻微损伤破坏的概率在29%~33%之间,出现严重损伤破坏的概率在6%~7%之间.基于上述分析可知,在PGA为0.64g时,4#墩发生严重损伤破坏的概率不大于7%,这表明4#墩具有一定的抗震延性.
综上所述,对于算例桥各桥墩墩底截面,在PGA为0.64g地震作用下容易出现轻微、中等损伤,但出现严重、完全损伤的概率较低,总的来讲算例桥各墩具有一定的抗震延性.此外由易损性云图分析表明:地震作用下,不同桥墩其最易损地震输入角是各不相同的.尤其是2#墩底截面,最易损输入角为60°、110°、250°、300°,这充分表明:只研究桥梁结构纵、横桥向地震作用下的易损性已无法真实有效地评估桥墩的抗震能力.故开展高烈度地震区典型桥梁三维易损性分析,全面掌握桥梁三维抗震性能至关重要.
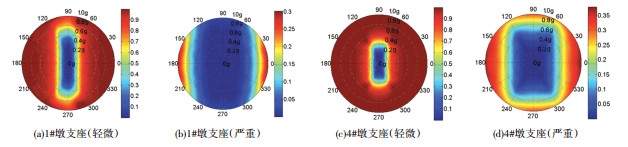
3.5.2 支座构件地震易损性分析由于篇幅有限,图 8给出了1#和4#桥墩支座发生地震损伤破坏(轻微和严重损伤)的全视角极坐标易损性云图.由图 8(a)分析表明,在地震作用下,1#桥墩支座极易发生轻微损伤,其最易损地震输入角度为0o和180°,即纵桥向地震作用下,支座最容易发生地震损伤;当PGA为0.4g(9度,设计地震)时,地震沿-50°~50°和130°~230°方向输入时,支座出现轻微地震损伤的概率大于75%,当PGA为0.64g (9度,罕遇地震)时,地震沿-80°~80°和110°~250°方向输入时,支座出现轻微地震损伤的概率大于80%,中等损伤状态计算结果与轻微损伤接近,这里不再详述.由图 8(b)分析表明,纵向地震作用下,1#墩支座最容易发生严重损伤;当PGA=0.4g时,1#墩支座在任意地震方向作用下,发生严重损伤的概率均小于6%,当PGA为0.64g时,出现严重损伤的概率均小于8%,完全损伤状态的概率则更低.由图 8(c)分析表明,当PGA为0.4g时,4#墩支座任意方向上出现轻微损伤破坏的概率均大于50%;当PGA为0.64g时,4#墩支座任意方向上出现轻微损伤的概率已达到90%以上.由图 8(d)分析表明,对于4#墩支座,当PGA为0.64g时存在两个易损地震输入角区间:-30°~30°和150°~210°,最易损地震输入角为0°和180°,此时这两个区间内发生支座严重损伤的概率在16%~20%,当PGA为1.0g时,这两个区间的严重损伤破坏概率为35%~38%.
|
图 8 支座构件全视角极坐标空间易损性云图 Fig. 8 Full-view vulnerability cloud pictures of bearings |
综上所述,各支座在三维地震作用下,极易发生轻微、中等损伤,在罕遇地震作用下各支座发生完全损伤的概率较低,满足设计要求,保证了主梁不发生落梁震害.
4 结论1) 建立了三维地震作用下的桥梁易损性分析方法.对比分析本文方法与常用方法(云图法)计算结果表明:两种计算方法所得分析结果较为一致,概率偏差均小于6.5%,满足工程应用的精度要求,桥梁构件三维易损性分析方法正确,具有良好的普适性.
2) 算例桥各支座容易发生地震损伤破坏,在设计地震下各支座发生轻微、中等地震损伤破坏的概率均大于50%;各桥墩延性较好,在罕遇地震下发生严重损伤的概率较低,几乎不发生完全损伤破坏,具有良好的抗震性能.
3) 算例桥各构件三维地震易损性分布特征差异较大,2#和3#墩底截面最易损输入角为60°、110°、250°、300°,1#和4#墩底截面最易损输入角为0°、90°、180°、270°,这充分说明仅研究桥梁顺桥向和横桥向地震作用下的易损性情况,已无法真实有效地评估桥梁的实际抗震能力.
4) 全视角极坐标空间易损性云图可直观地了解任意方向特定强度地震作用下桥梁结构发生损伤破坏的概率分布,全面揭示桥梁构件在三维地震作用下的地震损伤破坏分布规律,实现三维地震作用下对桥梁抗震性能的全面分析评估.
| [1] |
董俊, 单德山, 张二华, 等. 非规则连续刚构桥地震易损性分析[J]. 西南交通大学学报, 2015, 50(5): 845. DONG Jun, SHAN Deshan, ZHANG Erhua, et al. Seismic fragility of irregular continuous rigid frame bridge[J]. Journal of Southwest Jiaotong University, 2015, 50(5): 845. DOI:10.3969/j.issn.0258-2724.2015.05.012 |
| [2] |
HWANG H, LIU J B, CHIU Y. Seismic fragility analysis of highway bridges[R]. TN Center for Earthquake Research and Information (Report No.01-06). Memphis: The University of Memphi, 2001
|
| [3] |
DUKES J, DESROCHES R, PADGETT J E. Sensitivity study of design parameters used to develop bridge specific fragility curves[C]//15th World Conference of Earthquake Engineering. Lisbon: Georgia Institute of Technology, 2012
|
| [4] |
VOSOOGHI A, SAⅡDI M S. Experimental fragility curves for seismic response of reinforced concrete bridge columns[J]. ACI Structural Journal, 2012, 109(6): 825. |
| [5] |
DEZFULI F H, ALAM M S. Effect of different steel-reinforced elastomeric isolators on the seismic fragility of a highway bridge[J]. Structural Control and Health Monitoring, 2016, 24(2): 1. |
| [6] |
BASOZ N, KIREMIDJIAN A S. Evaluation of bridge damage data from the Loma Prieta and Northridge California earthquakes[R]. Multidisciplinary Center for Earthquake Engineering Research (Report No. MCEER-98-0004). Buffalo N Y: The State University of New York, 1997
|
| [7] |
KIUREGHIAN A D. Bayesian methods for seismic fragility assessment of lifeline components[J]. Technical Council for Lifeline Earthquake Engineering, ASCE, 2002, 10(1): 61. |
| [8] |
VOSOOGHI A, SAⅡDI M S. Experimental fragility curves for seismic response of reinforced concrete bridge columns[J]. ACI Structural Journal, 2012, 109(6): 825. |
| [9] |
NIELSON B G, DESROCHES R. Seismic fragility methodology for highway bridges using a component level approach[J]. Earthquake Engineering and Structural Dynamics, 2010, 36(6): 823. |
| [10] |
陈力波.汶川地区公路桥梁地震易损性分析研究[D].成都: 西南交通大学, 2012 CHEN Libo. Seismic vulnerability analysis for highway bridges in Wenchuan region[D]. Chengdu: Southwest Jiaotong University, 2012 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2574764 |
| [11] |
ZAMPIERI P, ZANINI M A, FALESCHINI F. Derivation of analytical seismic fragility functions for common masonry bridge types: methodology and application to real cases[J]. Engineering Failure Analysis, 2016, 68(1): 275. |
| [12] |
DEZFULI F H, ALAM M S. Effect of different steel-reinforced elastomeric isolators on the seismic fragility of a highway bridge[J]. Structural Control and Health Monitoring, 2016. |
| [13] |
李乔, 赵世春. 汶川大地震工程震害分析[M]. 成都: 西南交通大学出版社, 2008. LI Qiao, ZHAO Shichun. Analysis of seismic damage of engineering structures in Wenchuan earthquake[M]. Chengdu: Southwest Jiaotong University Press, 2008. |
| [14] |
张菊辉.基于数值模拟的规则梁桥墩柱的地震易损性分析[D].上海: 同济大学, 2006 ZHANG Juhui. Study on seismic vulnerability analysis of normal beam bridge piers based on numerical simulation[J]. Shanghai: Tongji University, 2006 http://d.wanfangdata.com.cn/Thesis/Y1020272 |
| [15] |
SEZEN H, MOEHLE J P. Seismic tests of concrete columns with light transverse reinforcement[J]. ACI, Structural Journal, 2006, 103(6): 842. |
| [16] |
BRESLER B. Reinforced concrete engineering[M]. New York: John Wiley & Sons Press, 1974.
|
| [17] |
PARK R, PAULAY T. Reinforced concrete structures[M]. New York: John Wiley & Sons Press, 1975.
|
| [18] |
JANGID R S. Seismic response of sliding structures to bidirectional earthquake excitation[J]. Earthquake Engineering and Structural Dynamics, 1996, 25(11): 1301. DOI:10.1002/(ISSN)1096-9845 |
| [19] |
贡金鑫. 工程结构可靠度计算方法[M]. 大连: 大连理工大学出版社, 2003. GONG Jinxing. Calculation method of engineering structure reliability[M]. Dalian: Dalian University of Technology Press, 2003. |
| [20] |
冯青海.特大桥梁地震易损性与风险概率分析[D].上海: 同济大学, 2008 FENG Qinghai. Seismic vulnerability and risk probability analysis of large bridge[D]. Shanghai: Tongji University, 2008 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1450111 |
| [21] |
沈恒范. 概率论与数理统计教材[M]. 北京: 高等教育出版社, 2003. SHEN Hengfan. Probability theory & mathematical statistics[M]. Beijing: Higher Education Press, 2003. |
| [22] |
Department of Applied Mathematics, Tongji University. Advanced mathematics(Ⅳ)[M]. Beijing: Higher Education Press, 2014.
|
| [23] |
铁道第三勘察设计院.铁路桥涵地基和基础设计规范: TB 10002.5-2005[S].北京: 中国铁道出版社, 2005 Third Railway Survey and Design Institute Group Corporation. Code for design on subsoil and foundation of railway bridge and culvert: TB 10002.5-2005[S]. Beijing: China Railway Press, 2005 |
| [24] |
铁道第一勘察设计院. GB 20111-2006铁路工程抗震设计规范[S].北京: 中国计划出版社, 2006 First Railway Survey and Design Institute Group Corporation. Code for seismic design of railway engineering: GB20111-2006[S]. Beijing: China Planning Press, 2006 |
| [25] |
董俊, 单德山, 张二华, 等. 非规则桥梁近、远场地震易损性对比分析[J]. 哈尔滨工业大学学报, 2016, 48(3): 159. DONG Jun, SHAN Deshan, ZHANG Erhua, et al. Near and far-field seismic fragility comparative analysis of irregular bridge[J]. Jouranal of Harbin Institute of Technology, 2016, 48(3): 159. |
 2019, Vol. 51
2019, Vol. 51


