有效控制铁路路基填筑压实质量是保证路基运行安全的关键.现行的检测方法由于样本的有限性,很难全面反映整个路基的压实质量,再者检测结果也不能及时获取,不易实现实时反馈.连续压实质量检测技术将振动压路机与土体视为一个动力学系统,通过建立振动轮加速度信号与路基压实状态的关系,实现对整个碾压面压实质量的实时检测[1].常见的压实质量检测参数有:压实计值CMV; 在CMV基础上发展得到的压实指标CCV; 基于土壤—振动轮—机架系统提出的土壤刚度ks; 基于滚动阻力理论开发的机械驱动功率MDP.
在连续压实质量检测过程中,由于检测点数量庞大,将不可避免的产生检测异常值.连续压实检测参数异常值的正确识别及处理,对提高连续压实检测结果的准确性具有重要意义[2].根据异常值的数量及分布范围将其分为两类:一类是单个压实检测值严重偏离近邻点,为单点异常值; 另一类是某区域内连续压实检测数据偏离正常范围,为区域异常值.单点异常值往往是检测设备的系统误差导致的,其结果不能表征该点土体的真实压实状况[3],因此对单点异常值的正确识别和处理尤为重要.
规程[4]规定:单点异常值宜采用拉依达准则(3σ准则)进行识别.但检测值中有多个异常值时,拉依达准则一次只能识别出一个异常值,而且当多个异常值之间互差不满足一定条件时该法则还会失效[5].在一次连续压实质量检测中,往往同时存在多个异常值,上述方法对异常值的识别效率就会十分低下,因此需要寻求更为精确和高效的方法对连续压实检测参数单点异常值进行识别.
文献[6]利用局部平均统计距离法对单点异常值进行识别.文献[7]采用变异系数法对单点异常值进行剔除.然而这些异常值识别方法均未考虑连续压实检测参数的空间分布特征.为弥补传统单点异常值识别方法的不足,本文基于沪昆高铁娄底试验段连续压实检测试验数据,结合地统计学与近邻加权估计法对单点异常值进行识别,并选用最优线性无偏方法—普通克里金插值法对识别出的单点异常值进行处理,以提高连续压实检测结果的精度.
1 连续压实质量检测参数尽管不同的连续压实质量检测参数在计算方法上各不相同,但都是基于压路机—土体动力学系统将振动轮加速度信号转化为表征土体压实状态的指标.故在同一碾压工作面上,不同连续压实质量检测参数的空间分布特征是相仿的.本文以压实计值CMV为例[8],进行单点异常值的识别和处理,计算公式为
| $ {C_{{\rm{MV}}}} = C \times \frac{{{A_{2\Omega }}}}{{{A_\Omega }}}. $ | (1) |
式中:C为常数(通常取300),A2Ω为振动轮竖向加速度的一次谐波振幅,AΩ为加速度的基波振幅.
2 基于自相关距离的近邻加权估计识别法 2.1 半变异函数求解自相关距离连续压实检测参数能够反映一定空间范围内土体的压实状态,其不仅具有随机性还具有一定的结构性. Vanmarcke[9]定义相关距离Lr来描述数据的空间相关性,认为数据在Lr范围内时具有强相关性,而当距离超过Lr时则相关性不显著.本文基于地统计学理论,采用半变异函数计算连续压实检测参数的自相关距离Lr.鉴于半变异函数能同时描述连续压实检测参数的随机性和结构性变化[10],可用其研究连续压实检测参数的空间分布特征.半变异函数的计算公式为
| $ \gamma \left( h \right) = \frac{1}{{2N\left( h \right)}}\sum\limits_{i = 1}^{N\left( h \right)} {{{\left[ {{C_{{\rm{MV}}}}\left( {{x_i}} \right) - {C_{{\rm{MV}}}}\left( {{x_i} + h} \right)} \right]}^2}} . $ | (2) |
式中:h为样本点间距; N(h)为样点对的个数; CMV(xi)、CMV(xi+h)分别为CMV(x)在xi和xi+h处的连续压实质量检测值.
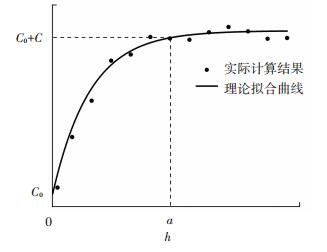
半变异函数γ(h)单调递增,当h大于某一定值a (a>0)时,γ(h)将趋近于定值C0+C,a称为变程(range),即为检测数据在空间上的自相关距离Lr.由于半变异函数的计算结果为散点,为更好地分析检测数据的空间变异特征需要利用数学模型对其进行拟合.本文采用常用的指数模型为
| $ \gamma \left( h \right) = \left\{ \begin{array}{l} 0,\;\;\;\;\left( {h = 0} \right);\\ {C_0} + C\left[ {1 - \exp \left( { - h/a} \right)} \right],\left( {h > 0} \right). \end{array} \right. $ | (3) |
其拟合曲线见图 1.
|
图 1 半变异函数模型 Fig. 1 Semivariogram model |
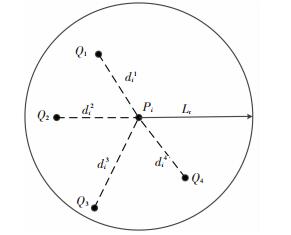
在自相关距离Lr范围内,与待测压实点越邻近的点相关性越强,即数值上越接近待测点值.基于此,利用自相关距离Lr范围内的近邻点来加权估计待测点值,待测点与近邻点位置示意如图 2所示.根据估计值与待测点值的差异大小来识别异常值.异常值识别方法具体如下.
|
图 2 待测点与近邻点的位置示意图 Fig. 2 Diagram of the positions of the measured point and neighbors |
1) 在任意待测压实点Pi(xi, yi)相关距离Lr范围内近邻点Qj的个数为n,近邻点CMV构成的近邻矩阵Ni为
| $ {\mathit{\boldsymbol{N}}_i} = \left| {\begin{array}{*{20}{c}} {{C_{{\rm{M}}{{\rm{V}}_i}}}^1}& \cdots &{{C_{{\rm{M}}{{\rm{V}}_i}}}^{n - 1}}&{{C_{{\rm{M}}{{\rm{V}}_i}}}^n} \end{array}} \right|. $ | (4) |
2) 定义任意点Pi(xi, yi)的近邻加权估计值
| $ \overline {{C_{{\rm{MV}}\;\;i}}} = \sum\limits_{j = 1}^n {\beta _i^j{C_{{\rm{MV}}}}_i^j} , $ | (5) |
| $ \beta _i^j = \frac{{\omega _i^j}}{{\sum\limits_{j = 1}^m {{\omega ^j}} }}, $ | (6) |
| $ \omega _i^j = \exp \left[ { - {{\left( {\frac{{d_i^j}}{{{L_{\rm{r}}}}}} \right)}^2}} \right]. $ | (7) |
式中:
3) 根据计算得到的近邻加权估计值
| $ {\alpha _i} = \frac{{\overline {{C_{{\rm{MV}}\;\;i}}} - {C_{{\rm{MV}}\;\;i}}}}{{{C_{{\rm{MV}}\;\;i}}}}. $ | (8) |
式中αi为异常指数,αlim为异常指数的阈值,当αi>αlim时,则该待测压实点为单点异常值点,αlim的具体取值可利用验证试验获得.
3 普通克里金插值法处理单点异常值将识别出的异常值剔除后会造成部分数据的缺失,为保证数据的完整性和稳定性,需将缺失的数据补齐.利用空间插值法估计缺失数据是处理空间数据的有效方法[12].
克里金插值法不同于常见的空间确定性插值法,如泰森多边形法、立方卷积法等.它是基于变异函数及结构分析理论,对区域化变量进行无偏最优估计的一种方法.不仅克服了空间确定性插值法较少从变量自身出发考虑数据整体分布的缺点,同时还考虑待估点与已知点的相互位置关系,比传统方法更加精确.
普通克里金插值法是克里金插值法中应用最广泛的一种,适用于在区域化变量的数学期望为未知的情况下建立方程.
对于某一压实路段,其连续压实检测参数的数学期望是未知的,故采用普通克里金插值法对单点异常值进行处理.设连续压实质量检测参数CMV的区域化变量CMV(x)满足二阶平稳假设,其数学期望为未知常数,半变异函数γ(h)存在且平稳[13].
现要估计点p0的CMV(p0),待估点p0附近有n个样点pi(i=1, 2, …, n),其观测值为CMV(pi),CMV*(p0)是CMV(p0)的最优无偏估计量,则待估点p0的CMV* (p0)是其自相关距离Lr范围内n个观测值CMV(pi)的线性组合,表示为
| $ {C_{{\rm{MV}}}}^ * \left( {{p_0}} \right) = \sum\limits_{i = 1}^n {{\lambda _i}{C_{{\rm{MV}}}}\left( {{p_i}} \right)} . $ | (9) |
普通克里金插值法的关键在于求解克里金权重系数λi的值,其可由克里金方程组求解.根据无偏性和最优性条件结合半变异函数可推导得到由半变异函数γ(h)表示的普通克里金插值方程组,其矩阵形式表达为
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {\gamma \left( {{p_1},{p_1}} \right)}&{\gamma \left( {{p_1},{p_2}} \right)}& \cdots &{\gamma \left( {{p_1},{p_n}} \right)}&1\\ {\gamma \left( {{p_2},{p_1}} \right)}&{\gamma \left( {{p_2},{p_2}} \right)}& \cdots &{\gamma \left( {{p_2},{p_n}} \right)}&1\\ \vdots&\vdots&\cdots&\vdots&\vdots \\ {\gamma \left( {{p_n},{p_1}} \right)}&{\gamma \left( {{p_n},{p_2}} \right)}& \cdots &{\gamma \left( {{p_n},{p_n}} \right)}&1\\ 1&1&1&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\lambda _1}}\\ {{\lambda _2}}\\ \vdots \\ {{\lambda _n}}\\ \mu \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} {\gamma \left( {{p_1},{p_0}} \right)}\\ {\gamma \left( {{p_1},{p_0}} \right)}\\ \vdots \\ {\gamma \left( {{p_n},{p_0}} \right)}\\ 1 \end{array}} \right],} \end{array} $ | (10) |
| $ \gamma \left( {{p_i},{p_j}} \right) = \gamma \left( {{d_{ij}}} \right), $ | (11) |
| $ {d_{ij}} = \sqrt {{{\left( {{x_i} - {x_j}} \right)}^2} + {{\left( {{y_i} - {y_j}} \right)}^2}} . $ | (12) |
式中γ(pi, pj)为pi和pj两点的半变异函数值,可由两点间空间距离dij经式(3)求得,dij为点pi(xi, yi)和点pj(xj, yj)的空间距离.
4 工程实例验证 4.1 试验概况为验证自相关距离近邻加权估计法以及普通克里金插值在实际连续压实检测过程中对单点异常值识别及处理的适用性,在沪昆高铁娄底试验段进行连续压实质量检测试验.试验段里程为DK107+ 486.02—DK107+578.60,试验段采用A组填料,母岩为砂质板岩,填料物理性质:最大干密度为2.25 g/cm3; 最优含水率为4.22 %; 曲率系数为1.29;不均匀系数为14.65.
试验段采用中联重科YZK25型振动压路机,其技术参数为:工作质量为25 t; 振动轮的直径为1 600 mm,宽度为2 150 mm; 工艺参数的振动频率为28~32 Hz,行驶速度为0~5 km/h,振幅为1.1~2.1 mm.连续压实质量检测设备选用美国Trimble公司的CCS900-CMV采集系统,该检测系统每20 cm采集一次CMV,文中所用CMV数据均由该系统提供. Trimble采集系统如图 3所示.

|
图 3 Trimble CMV采集系统 Fig. 3 Acquisition system of Trimble CMV |
试验段路基的填筑压实严格按照连续压实规程[4]要求进行,填筑层厚度约为30 cm,本压实试验有效碾压面为8 m×20 m的区域,依据振动压路机轮宽将碾压面划分为4条碾压轮迹,即每条碾压轮迹长为20 m宽为2 m,如图 4所示.为减少下卧层刚度不均的影响,每条碾压轮迹选取最后一层最后一遍弱振所采集的CMV数据.

|
图 4 碾压轮迹示意图 Fig. 4 Diagram of rolling wheel traces |
路基压实试验完成后,将4条碾压轨迹采集的数据利用半变异函数计算公式进行分析,并采用指数模型拟合,如图 5所示.模型拟合结果:4条轮迹方差分析中的P值分别为1.736 6×10-5、8.327 2×10-6、4.152 1×10-6、2.621 2×10-6均小于显著性水平0.001(对应置信度为99.9%),表明差异极显著,并且拟合方程的决定系数R2均超过0.9,因此模型拟合效果极好. 4条碾压轨迹的自相关距离Lr分别为2.6、3.5、3.7、3.2 m.

|
图 5 碾压轨迹的半变异函数计算与拟合结果 Fig. 5 Calculation and fitting results of semivariogram |
为验证基于自相关距离的近邻加权估计法能够有效识别连续压实质量检测中出现的异常值.首先利用文献[4]中的拉依达准则(3σ准则)对4条碾压轮迹的CMV数据计算,对异常值进行逐一识别.拉依达准则[14]为:对某一变量进行n次测量,分别为x1,x2,…,xn.若某一数据xk对应的残差vk满足以下条件,则判定xk为异常值,即
| $ \left| {{v_k}} \right| = \left| {{x_k} - \bar x} \right| > 3s, $ | (13) |
式中
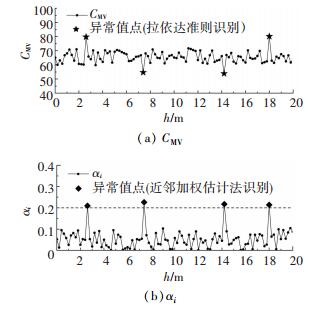
经拉依达准则计算,在4条碾压轮迹中共识别出12个单点异常值(不含12号异常点),识别结果见图 6~9.为验证这些点确系异常值点,按照验收标准[15]的压实要求,检测其地基系数K30和压实系数K.结果表明:这些异常值点处的地基系数K30均大于130 MPa/m,压实系数K均大于0.92,满足施工质量验收要求,确为异常值点,具体试验结果见表 1.
|
图 6 第1条碾压轮迹的CMV及对应异常指数αi Fig. 6 CMV and abnormal index αi of the first roller traces |
|
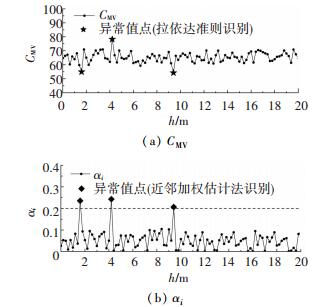
图 7 第2条碾压轮迹的CMV及对应异常指数αi Fig. 7 CMV and abnormal index αi of the second roller traces |
|
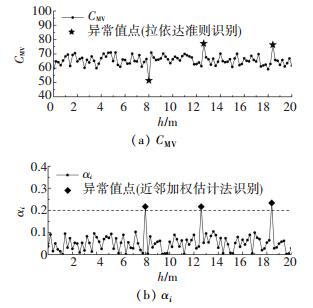
图 8 第3条碾压轮迹的CMV及对应异常指数αi Fig. 8 CMV and abnormal index αi of the third roller traces |
|
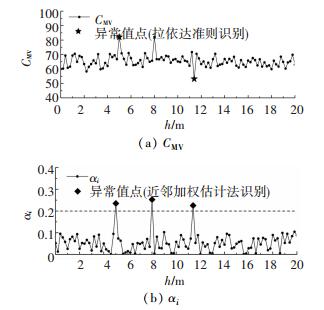
图 9 第4条碾压轮迹的CMV及对应异常指数αi Fig. 9 CMV and abnormal index αi of the fourth roller traces |
| 表 1 异常点的CMV、地基系数K30及异常指数αi Tab. 1 CMV, K30, and abnormal index αi of the outliers |
然后根据半变异函数拟合所得的自相关距离Lr,结合近邻加权估计法对4条碾压轮迹的CMV数据进行批量处理,获得每一CMV检测点的异常指数αi,计算结果见图 6~9.
由图 6~9可知,在4条碾压轮迹中利用拉依达准则识别出的12个单点异常值点所对应的异常指数αi均大于0.2,具体的异常指数αi见表 1.其他正常检测点的异常指数αi集中在0.1及以下,说明异常指数αi在异常值点与正常点存在显著差异,因此异常指数αi可用以表征连续压实质量检测参数的异常程度,根据本次现场压实试验结果,可初步判定连续压实质量检测参数的异常指数阈值αlim为0.2.由以上求解过程可知:αlim的数值仅仅取决于CMV异常值与近邻值的差异大小及两者的空间分布关系,与铁路路基填料性质等因素无关,故可将该方法广泛应用于铁路路基连续压实质量检测参数的单点异常值识别.
在第4条碾压轮迹中位于8.0 m处的12号点的CMV为82.1,而11号异常值点的CMV为82.0,显然12号点也是异常值点.可是12号异常点没有被拉依达准则识别出来,根据拉依达准则的失效条件,当多个异常值的互差太小,而不满足一定条件时,较大的异常值将无法识别[5].因此,在第4条碾压轮迹的异常值识别中拉依达准则出现失效情况,没有识别出全部的异常值.相反,基于自相关距离的近邻加权估计法能准确识别出所有异常值点,且不存在失效的情况,该方法比拉依达准则具有更高的识别准确度.
对比拉依达准则和基于自相关距离的近邻加权估计识别法,拉依达准则每剔除一个异常值就需要重新计算剩余n-1个数据的平均值
对上述13处CMV单点异常值进行剔除,采用普通克里金插值法对异常值点处的数据进行估计补齐.异常值点经拟合处理前后的CMV及其异常指数αi见表 2,原异常值点经处理后的异常指数αi均小于0.2,因此均不属于异常值点.
| 表 2 异常值点处理前后的CMV及异常指数αi Tab. 2 CMV and abnormal index αi before and after outlier processing |
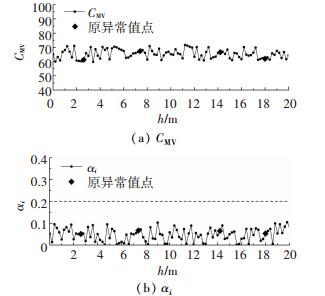
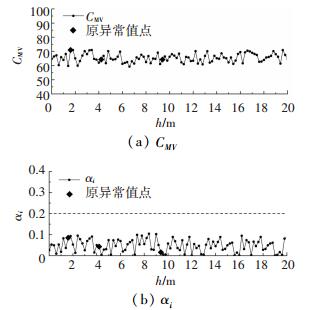
为验证普通克里金插值在连续压实质量检测中对单点异常值处理的适用性,利用拉依达准则对处理后的4条碾压轮迹的CMV再次进行异常值识别,其计算结果表明:数据中未识别出异常值,如图 10~13所示.原异常值点经拟合处理后的异常指数αi均集中分布在0.1及以下,可见普通克里金插值法能够有效的处理连续压实质量检测参数的异常值.
|
图 10 克里金插值处理后第1条碾压轮迹的CMV及对应异常指数αi Fig. 10 CMV and abnormal index αi of the first roller traces after Kriging interpolation |
|
图 11 克里金插值处理后第2条碾压轮迹的CMV及对应异常指数αi Fig. 11 CMV and abnormal index αi of the second roller traces after Kriging interpolation |
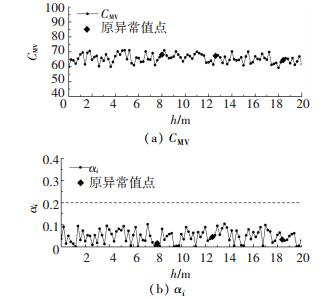
|
图 12 克里金插值处理后第3条碾压轮迹的CMV及对应异常指数αi Fig. 12 CMV and abnormal index αi |

|
图 13 克里金插值处理后第4条碾压轮迹的CMV及对应异常指数αi Fig. 13 CMV and abnormal index αi of the fourth roller traces after Kriging interpolation |
连续压实质量检测参数的均匀性是路基压实质量控制的重要指标之一[16],一般采用变异系数CV来表征数据的均匀程度,即
| $ {C_{\rm{V}}} = \frac{s}{{\bar x}}, $ | (14) |
式中
对克里金插值法处理前后的4条碾压轮迹的CMV进行变异系数CV的求解,具体结果见表 2.通过对比发现:经克里金插值法处理后,4条碾压轮迹CMV的变异系数CV均显著降低,降幅依次为20.97%,14.55%,17.86%,23.81%.可见,采用克里金插值法不仅能够有效处理CMV的异常值,同时还能降低数据的异常系数,提高CMV数据均匀程度.
5 结论1) 采用地统计学中的半变异函数获得连续压实质量检测参数CMV的自相关距离Lr,提出基于自相关距离Lr的近邻加权估计法对单点异常值进行识别.建立异常指数αi作为异常值的判定指标,经试验验证,该方法能够准确识别连续压实检测参数的单点异常值,且当该检测点的异常指数αi超过0.2时,即可判定该检测点为单点异常值点.相比于规范中的拉依达准则,该识别方法更为准确和高效.
2) 普通克里金插值法对CMV异常值的估计充分考虑CMV数据的空间结构关系,能更真实反映待估点处的CMV.选用普通克里金插值法对异常值点的CMV进行估计拟合,处理后原异常值点处的异常指数αi均分布在0.1以下,经拉依达准则验证:估计拟合后的CMV中未出现异常值.
3) 普通克里金插值法对单点异常值的处理能显著降低的CMV数据的变异系数,提高连续压实质量检测参数CMV的均匀性,使得连续压实质量检测参数CMV更加准确地反映路基压实质量.
| [1] |
MOONEY M A. Intelligent soil compaction systems[M]. Washington DC: Transportation Research Board, 2010: 14
|
| [2] |
谭文辉, 王家臣, 周汝弟. 岩体强度参数空间变异性分析[J]. 岩石力学与工程学报, 1999, 18(5): 546. TAN Wenhui, WANG Jiachen, ZHOU Rudi. Spatial variability analysis of rock mass strength parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(5): 546. DOI:10.3321/j.issn:1000-6915.1999.05.012 |
| [3] |
聂志红, 焦倓, 王翔. 基于地统计学方法的铁路路基压实均匀性评价[J]. 中国铁道科学, 2014, 35(5): 1. NIE Zhihong, JIAO Tan, Wang Xiang. Compaction uniformity evaluation of railway subgrade based on geostatistics[J]. China Railway Science, 2014, 35(5): 1. DOI:10.3969/j.issn.1001-4632.2014.05.01 |
| [4] |
铁路路基填筑工程连续压实控制技术规程: TB 10108—2011[S].北京: 中国铁道出版社, 2005 Technical specification for continuous compaction control of fill engineering of railway earth structure: TB10108—2011[S]. Beijing: China Railway Press, 2005 |
| [5] |
毛亚纯, 王恩德, 修春华. 剔除变形监测粗差数据的新方法—数据跳跃法[J]. 东北大学学报(自然科学版), 2011, 32(7): 1020. MAO Yachun, WANG Ende, XIU Chunhua. Datajump method: a new approach to eliminating the deformation monitoring data with gross errors[J]. Journal of Northeastern University (Natural Science), 2011, 32(7): 1020. |
| [6] |
窦鹏, 聂志红, 王翔. 铁路路基压实质量检测指标CMV与Evd的相关性校检[J]. 铁道科学与工程学报, 2014, 11(2): 90. DOU Peng, NIE Zhihong, WANG Xiang. Correlation verification of railway subgrade compaction quality test value between CMV and Evd[J]. Journal of Railway Science and Engineering, 2014, 11(2): 90. DOI:10.3969/j.issn.1672-7029.2014.02.015 |
| [7] |
和民锁.高速铁路路基填筑质量检测方法控制指标及评价体系研究[D].长沙: 中南大学, 2010 HE Minsuo. Research of test methods acceptance criteria and evaluation system for compaction quality of high speed railway subgrade[D]. Changsha: Central South University, 2010 http://d.wanfangdata.com.cn/Thesis/Y1917959 |
| [8] |
THOMPSON M J, WHITE D J. Field calibration and spatial analysis of compactionmonitoring technology measurements[J]. Transportation Research Record: Journal of the Transportation Research Board, 2004(1): 69. DOI:10.3141/2004-08 |
| [9] |
VANMARCKE E H. Probabilistic modeling of soil profiles[J]. Journal of the Geotechnical Engineering Division, 1977, 103(11): 1227. DOI:10.1016/0148-9062(78)90012-8 |
| [10] |
MATHERON G. Principles of geostatistics[J]. Economic Geology, 1963, 58(8): 1246. DOI:10.2113/gsecongeo.58.8.1246 |
| [11] |
李小文, 曹春香, 常超一. 地理学第一定律与时空邻近度的提出[J]. 自然杂志, 2007, 29(2): 69. LI Xiaowen, CAO Chunxiang, CHANG Chaoyi. The first law of geography and spatial temporal proximity[J]. Nature Magazine, 2007, 29(2): 69. DOI:10.3969/j.issn.0253-9608.2007.02.002 |
| [12] |
陈欢.气候资源插值算法在多核环境下的并行计算研究[D].长沙: 湖南大学, 2012 CHEN Huan. Interpolation of climatic resources in multi-core research on parallel computing environment[D]. Changsha: Hunan University, 2012 http://cdmd.cnki.com.cn/Article/CDMD-10532-1013169821.htm |
| [13] |
刘爱利, 王培法, 丁园圆. 地统计学概论[M]. 北京: 科学出版社, 2012: 99. LIU Aili, WANG Peifa, DING Yuanyuan. Geostatistics introduction[M]. Beijing: Science Press, 2012: 99. |
| [14] |
刘瑞民, 王学军, 郑一. 湖泊水质参数空间分析中异常值的识别与处理[J]. 环境科学与技术, 2003, 5(26): 17. LIU Ruimin, WANG Xuejun, ZHENG Yi. Outlieridentification and processing in spatial analysis of water quality parameters of a lake[J]. Environmental Science and Technology, 2003, 5(26): 17. DOI:10.3969/j.issn.1003-6504.2003.05.008 |
| [15] |
高速铁路路基工程施工质量验收标准: TB 10751—2010[S].北京: 中国铁道出版社, 2011 Standard forconstructional quality acceptance of high-speed railway earth structure engineering: TB 10751—2010[S]. Beijing: China Railway Press, 2011 |
| [16] |
聂志红, 焦倓, 王翔. 基于谐波平衡识别法的铁路路基连续压实指标研究[J]. 中国铁道科学, 2016, 37(3): 1. NIE Zhihong, JIAO Tan, WANG Xiang. Study on continuous compaction indicator of railway subgrade based on harmonic balance identification method[J]. China Railway Science, 2016, 37(3): 1. DOI:10.3969/j.issn.1001-4632.2016.03.01 |
 2019, Vol. 51
2019, Vol. 51


