分区段限速作为高速公路常用限速方法之一，往往存在如下问题：限速区段数目过多，频繁换速增加驾驶负担，降低限速遵守率、增大车速离散性、增加行车安全隐患; 部分限速区段因长度过短采取直接与相邻区段合并的方式进行限速，并以安全要求为准则制定合并后区段的限速值，降低高速公路运行效率.本文的研究对象即为高速公路限速区段的安全与效率优化协调设置问题.

限速区段研究方面, 美国德州限速指导意见^[1]中从安全的角度出发，指出当两相邻限速区85%分位车速超过24 km/h时，需设置限速过渡段.文献[2]指出当道路特定点段不能满足法定最高或最低限速时，应采用分区段限速的方法进行限速调整.文献[3]根据道路线形条件，采用聚类分析法对山区公路限速区段组合进行研究，从安全的角度给出多区段组合限速方法.文献[4]根据驾驶人在高速公路不同线形条件下的运行速度、生理和心理变化，提出基于驾驶工作负荷度变化特性的高速公路不同线形组合路段划分标准.文献[5]通过仿真实验等方法提出限速区段及限速区过渡段的设置方法与设计流程.文献[6]通过对国内外道路限速区过渡段的长度计算进行分析，提出适合我国的合理的限速区过渡段长度.文献[7]采用六阶段划分法给出分区段限速设置的指导建议的大体框架.

限速值研究方面，文献[8]采用非线性回归的方法建立运行速度、运行速度差与百万车公里伤亡事故率的关系模型，从安全角度给出不同设计速度下高速公路限速值的确定依据.文献[9]从安全的角度研究高速公路限速值制定，指出高速公路应针对不同的道路条件、交通流状况等条件进行限速和控制.文献[10]通过仿真实验分别确定山区高速公路在弯道路段、长坡路段最优限速值，并提出路面物理设施、路侧电子设施与速度限制措施相结合的限速设计.文献[11]根据安全和效率对限速值变化的灵敏度不同，得到交通事件下高速公路长大下坡处基于安全和效率的限速值.文献[12]等从通行效率的角度，对宏观交通模型METANET进行改进，构建高速公路主线可变限速控制模型.

综述所述，已有限速管理研究中对兼顾安全和效率及驾驶操作舒适性的限速区段协调设置考虑较少，且缺乏具体的分区段限速设置方法.因此，本文综合考虑安全和效率，通过构建高速公路安全指数、效率指数等评价指标模型，提出基于损失时间最小的高速公路分区段限速优化协调模型，并借助理论计算和问卷调查等手段对模型中最小限速区段长度、限速区段数目两参数进行标定.为改善多区段限速高速公路的安全、效率及驾驶舒适性，制定基于安全和效率的高速公路限速区段最优设置方案提供理论依据.

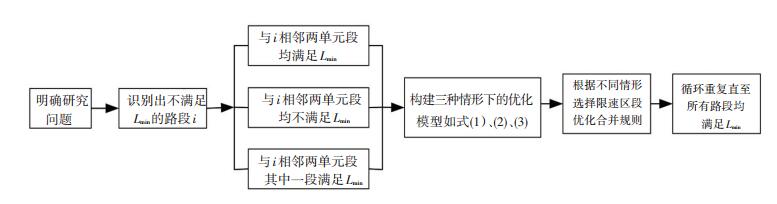
1 安全与效率优化协调模型构建

本文以损失时间最小为原则，在保障安全的前提下兼顾效率，构建基于安全和效率的高速公路限速区段优化协调模型，模型构建流程图如图 1.

1.1 模型要解决的问题

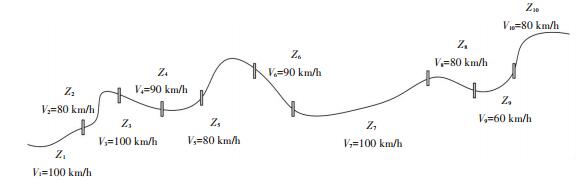
某些线形复杂的分区段限速高速公路限速区段分别为Z₁，Z₂，…，Z_i，…，Z_n，限速值分别为V₁，V₂，…，V_i，…，V_n，如下图 2所示，各区段长度分别为l₁，l₂，…，l_i，…，l_n，其中n≥i=1，2，3，…，道路总长为L.但部分限速区段长度l_i过短，限速区段总数目n过多，使得驾驶人在驾驶过程中需根据限速标志频繁进行减速或加速，增加驾驶负担，当变速频率超过驾驶人心理承受范围时，易促发超速行驶行为，从而降低限速遵守率，影响道路交通安全，或针对路段长度较短不满足最小限速区段长度要求的路段，采取直接与相邻的限速区段合并的措施，并以满足安全要求为准则，选取较低的限速值作为合并后限速区段的限速值，大大降低高速公路运行效率.

1.2 优化模型构建

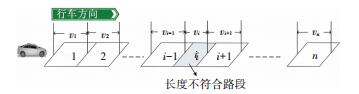
根据不同限速值所需要满足的最小限速区段长度，识别出各限速区段中所有不满足最小限速区段长度要求的路段.以损失时间最小为原则，构建基于安全与效率的高速公路限速区段优化协调控制模型.如下图 3所示，单元段i为不满足最小限速区段长度要求的路段，本文以损失时间最小为原则，分以下3种情形分别构建限速区段优化协调控制模型.

1) 单元段i-1、单元段i+1均满足最小限速区段长度.分别计算单元段i与i-1的一部分合并后的运行时间与合并前的运行时间差值Δt_{i, i-1}，以及单元段i与i+1的一部分合并后的运行时间与合并前的运行时间差值Δt_{i, i+1}，若Δt_{i, i-1}≤Δt_{i, i+1}则单元段i与从i-1上分割的一部分合并，若Δt_{i, i-1}>Δt_{i, i+1}则单元段i与从i+1上分割的一部分合并，合并规则模型为

$ \left\{ \begin{align} &i\cup i-1, \Delta {{t}_{i, i-1}}\le \Delta {{t}_{i, \text{ }i+1}}; \\ &i\cup i+1, \Delta {{t}_{i, \text{ }i-1}}>\Delta {{t}_{i, \text{ }i+1}}. \\ \end{align} \right. $

(1)

式中：$ i\cup i-1$为单元段i与i-1的一部分合并; $i\cup i+1 $为单元段i与i+1的一部分合并; $ \Delta {{t}_{i, i-1}}=\frac{{{l}_{i, \text{ }i-1}}}{{{{{v}'}}_{\text{i}}}}\text{ }~-\text{ }\frac{{{l}_{\text{i }\!\!~\!\!\text{ }}}}{{{v}_{i}}}~, \Delta {{t}_{i, i+1}}=\frac{\text{ }{{l}_{i, \text{ }i-1}}}{{{{{v}'}}_{i}}~}-\frac{{{l}_{i~}}}{{{v}_{i}}}$，其中l_{i, i-1}、l_{i, i+1}分别为单元段i与i-1或i+1的一部分合并后的路段长度，m; l_i为单元段i的初始长度，m; v_i、v'_i分别为单元段i与其他单元段合并前、合并后的路段车辆平均车速，km/h.

2) 单元段i-1、单元段i+1均不满足最小限速区段.分别计算单元段i与i-1合并后运行时间与合并前的运行时间差值Δt_{i, i-1}，以及单元段i与i+1合并后的运行时间与合并前的运行时间差值Δt_{i, i+1}，若Δt_{i, i-1}≤ Δt_{i, i+1}则单元段i与i-1合并，若Δt_{i, i-1}> Δt_{i, i+1}则单元段i与i+1合并，合并规则模型为

$ \left\{ \begin{align} &~i\cup i-1, \Delta {{t}_{i, i-1}}\le \Delta {{t}_{i, i+1}}; \\ &i\cup i+1, \Delta {{t}_{i, i-1}}>\Delta {{t}_{i, i+1}}. \\ \end{align} \right. $

(2)

式中：$ i\cup i-1$为单元段i与i-1合并; $i\cup i+1 $为单元段i与i+1合并; $ \Delta {{t}_{i, i-1}}=\frac{{{l}_{i, i-1}}}{{{{{v}'}}_{i}}~}-\frac{{{l}_{i~}}}{{{v}_{i}}}, \Delta {{t}_{i, i+1}}=~\frac{\Delta {{l}_{i, i-1}}}{{{{{v}'}}_{i}}}-\frac{{{l}_{i~}}}{{{v}_{i}}}$，其中l_{i, i-1}、l_{i, i+1}分别为单元段i与i-1或i+1合并后的路段长度，m.

3) 单元段i-1、单元段i+1一个满足最小限速区段一个不满足最小限速区段，则单元段i直接与不满足最小限速区段长度的单元段合并，合并规则模型为

$ \left\{ \begin{array}{l} i \cup i - 1,{\rm{ }}{l_{i - 1}} \le L_{{\rm{min}}}^{i - 1};\\ i \cup i + 1,{l_{i + 1}} < L_{{\rm{min}}}^{i + 1}. \end{array} \right. $

(3)

式中：l_i-1为单元段i-1实际长度，m; l_i+1为单元段i+1实际长度，m; L_min^i-1为单元段i-1需满足的最小限速区段长度，m; L_minⁱ⁺¹为单元段i+1需满足的最小限速区段长度，m.

限速区段合并过程中，单元段i与其他单元段合并后的车速${{{{v}'}}_{i}}~ $取安全车速，即$ {{{{v}'}}_{i}}=\text{min}\{{{v}_{i}}, \text{ }{{v}_{i-1}}, \text{ }{{v}_{i+1}}\}$.

2 模型参数标定

为确定限速区段优化协调模型运算过程中最小限速区段长度和一定道路长度范围内适当的限速区段数目，本文通过理论计算和问卷调查，分析驾驶人在驾驶过程中所能适应的最小限速区段长度和一定距离内的限速值变化的最大次数.

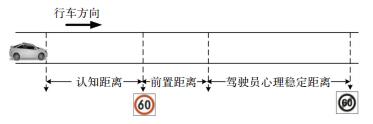
2.1 最小限速区段长度

根据驾驶人认知心理学和对信息的处理特点，在确定限速标志设置位置及限速区段最小长度时，需考虑驾驶人对交通标志的视认、采取行动的整个过程，及进入限速路段后所需满足的心理稳定行驶距离，建立最小限速区段，其组成如图 4^[13]所示.

其中，最小限速区段的长度根据以下因素确定：高速公路自身道路物理条件及驾驶人对限速标志认读过程中所行驶的认知距离、在道路环境变化时为提醒驾驶人及时采取措施将交通标志提前设置在减速点的前置距离、驾驶人在该限速路段行驶时需满足的心理稳定距离.计算公式^[5]为

$ {{L}_{\text{min}}}={{L}_{\text{reco}}}+{{L}_{\text{sign}}}+{{L}_{\text{dri}}}, $

(4)

式中：L_min为理论最小限速区段长度; L_reco为认知距离; L_sign为前置距离; L_dri为稳定距离，m.

经计算分别给出限速值为60~120 km/h对应的限速区段理论最小长度L_min，并以100 m为单位取整得[L_min]，计算结果见表 1.

2.2 限速值最大变化次数

根据调查路段高速公路平均日交通量28 407 veh/d确定总体容量，置信度取95%(置信水平系数K=1.96)、估计样本标准偏差取8、容许误差取2，根据抽样理论计算取整后得最小样本容量n≈195.此问卷调查当日共收集204份有效问卷，满足最小样本容量要求.

问卷内容主要包括两个方面：反映驾驶人和驾驶车辆特征的基本信息，及一定行车距离内驾驶人心理上可接受的变速次数.问卷结果显示：调查对象中性别比例为男性81%、女性19%;驾龄6 a以上、3~6 a、1~3 a、1 a以下的比例分别为54%、15%、16%、15%;在高速公路上行车频率为经常、一般、偶尔、首次的比例分别为40%、46%、13%、1%;小客车、中型车、大型车、汽车列车的比例分别为98.04%、0.49%、0.98%、0.49%.对驾驶人百公里范围内可接受的最大限速值变化次数进行统计，结果如图 5所示.

3 案例分析

完成限速区段优化协调模型参数的标定后，为验证该模型的实施效果，本文以某区段划分较复杂的分区段限速高速公路为论证分析对象.该高速公路采用双向四车道高速公路建设标准，设计行车速度为100 km/h(山岭、重丘区为60~80 km/h).相关数据显示，该段高速公路在2012年—2014年共发生交通事故35起，死亡人数49人，受伤人数43人.其中，事故类型多为追尾碰撞，事故诱发的主要原因多为超速行驶和车速离散性大.限速区段总长度约172.0 km，各限速区段及限速值初始设置情况见表 2.

3.1 限速区段优化协调设置

1) 区段长度判别.根据表 2给出的理论最小限速区段长度值，识别出各限速区段不满足最小限速区段长度的路段的是区段3、区段8、区段10.

2) 区段限速值调整.在确保安全的前提下，限速区段在合并过程中，对于不满足最小限速区段长度要求的单元段i与其他单元段合并后的车速$ {{{{v}'}}_{i}}$取安全车速，即${{{{v}'}}_{i}}=\text{min}\{{{v}_{i-1}}, {{v}_{i}}, \text{ }{{v}_{i+1}}\} $，其中v_i-1、v_i、v_i+1分别为单元段i-1、i、i+1的初始限速值.

3) 区段数目设定.结合问卷调查结果，百公里范围内72%的驾驶人可接受的限速值变化次数为3~5次，所选路段总长约172 km，故在优化计算过程中，限速区段最大设置数目可设置为8.

4) 区段协调计算.依据本文提出的限速区段优化协调控制模型，建立3种情形下的限速区段合并规则：a)单元段i-1、i+1均满足最小限速区段长度.若Δt_{i, i-1}≤Δt_{i, i+1}，则单元段i与i-1的一部分合并，即$ i\cup i-1$; 否则单元段i与i+1的一部分合并，即$ i\cup i+1$. b)单元段i-1、i+1均不满足最小限速区段.若Δt_{i, i-1}≤Δt_{i, i+1}，则单元段i与i-1合并，即$ i\cup i-1$; 否则单元段i与i+1合并，即$ i\cup i+1$. c)单元段i-1、i+1一个满足最小限速区段一个不满足最小限速区段.若${{l}_{i-1}}\le L_{\text{min}}^{i-1} $，则单元段i与i-1合并，即$ i\cup i-1$; 否则单元段i与i+1合并，即$ i\cup i+1$.

根据上述规则建立限速区段优化合并规则，通过VB编程对初始限速区段的设置进行优化协调计算，给出新的限速区段划分方案见表 3.

3.2 优化效果评价 3.2.1 评价指数构建

根据经济学风险与收益原理，可将高速公路安全隐患视为投资风险，用函数f(S)表征; 将高速公路运行效率视为投资收益，用函数f(E)表征.定义(a, b)为理想点，即a=f_max(E), b=f_min(S)时，当a, b分别取极值时，高速公路安全与效率达到理想最优.由于在同一运行规则下安全和效率的对立性质，虽然两个函数不能同时取极值，即达到理想点，但应用欧氏距离最小原理构建单目标线性规划模型，可求得最接近理想点的最优解^[14]，即

$ \text{min}Z=\sqrt{\left[ f\left( {{E}_{i}} \right)\text{ }~-a{{~}^{2}} \right]+{{\left[ f\left( {{S}_{i}}~ \right)\text{ }-b \right]}^{2}}}, $

(5)

式中$f\left( {{E}_{\text{i}}} \right) $、$ f({{S}_{\text{i}}})$分别为第i种限速设置下的综合效率指数、综合安全指数.

1) 综合效率指数.依据Brilon提出的断面通行效率计算指标、叶彭姚提出的断面通行效率定义^[15-16]，以单位时间内通过断面的车辆在该时间段内完成的车公里数表征高速公路综合效率指数，其中q×T可理解为高速公路管理者的期望效益，${\bar{v}} $可理解为高速公路使用者的期望效益，从高速公路管理者和使用者的角度构建综合效率指数评价模型：

$ f\left( E \right)\text{ }=q\times T\times \bar{v}. $

(6)

式中：f(E)综合效率指数; q交通流率，pcu/h; ${\bar{v}} $为平均速度，km/h; T为时间间隔，h.

2) 综合安全指数.根据安全性能函数中年平均日交通量与事故数的关系、速度标准差与事故数的关系^[17-19]，选择平均日交通量、车辆平均速度、车速标准差指标进行合一化处理，构建综合安全指数评价模型：

$ f\left( S \right)={{q}_{\text{AADT}}}\times \bar{v}\times \Delta \bar{v}\text{ }. $

(7)

式中:f(S)为综合安全指数; q_AADT为年平均日交通量，pcu; ${\bar{v}} $为车速标准差，km/h.

3) 综合效率与安全指数标准化.根据量纲属性，在进行目标函数最优值计算前，选用(0, 1)区间变换法对计算得到的综合安全指数$ f({{S}_{i}})$和综合效率指数$ f\left( {{E}_{i}} \right)$进行标准化处理^[20]，即

$ {{x}^{\prime }}=\frac{x-m}{M-m}\text{ }. $

(8)

式中：x^′为无量纲化处理后的值; x为待无量纲化处理的值; m为待无量纲化处理的最小元素值; M为待无量纲化处理的最大元素值.

3.2.2 仿真验证

1) 仿真参数设置.依据建立的安全与效率优化协调评价模型，取平均车速、车速标准差及行车时间作为评价限速区段优化协调控制模型实施效果的表征指标.结合实际道路交通条件，本文采用VISSIM仿真软件分别对限速区段优化前、后车辆的运行情况进行仿真，仿真参数设置如下：车道宽度3.75 m，单向2车道，路段长度172 km; 车长4.11 m，车宽1.5 m，加速度±3.5 m/s²; 单向交通量1 200 pcu/h，期望车速±5 km/h.

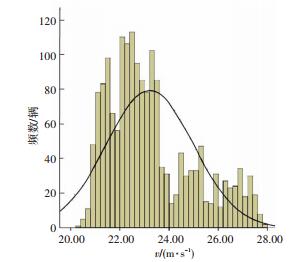
2) 优化前仿真数据分析.根据表 3给出的高速公路初始限速区段设置情况，优化前仿真路段中共设置共设13个限速区段，单向两车道共设置26个数据采集点，经SPSS对仿真输车速数据的统计分析，速度分布如图 6所示，车辆速度分布相对较为离散，速度标准差约为1.97 m/s约等于7.0 km/h.根据在仿真路段其实位置设置的行程时间检测器，获得优化前仿真路段内平均行车时间为7187.1 s.

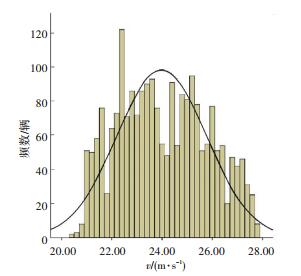
3) 优化后仿真数据分析.根据表 5给出的优化后限速区段设置情况，优化后仿真路段中共设8个限速区段，单向两车道共设置16个数据采集点，经SPSS对仿真输出车速数据的统计分析，速度分布如图 7所示，车辆速度分布相对较均匀，优化后速度标准差约1.12 m/s约等于4.0 km/h.根据在仿真路段起始位置设置的行程时间检测器，获得优化后仿真路段内平均行车时间为7187.1 s

4) 实施效果分析.对仿真数据进行整理和分析，得优化前安全指标q_AADT=7 700 pcu、${\bar{v}} $ =24 m/s、$\Delta \bar{v} $=1.97 m/s，效率指标T=7187.1 s、$ {\bar{v}}$ =24 m/s、q=169.23 pcu/h; 优化后安全指标q_AADT=7 700 pcu、$ {\bar{v}}$=23 m/s、$\Delta {\bar{v}}$=1.12 m/s，效率指标T=7400.1 s、$ {\bar{v}}$=23 m/s、q=220.25 pcu/h.

将上述仿真结果分别代入式(6)、(7)计算得优化前综合安全指数f(S)=3.64×10⁵、综合效率指数f(E)=2.95×10⁷，优化后综合安全指数f(S)=1.98×10⁵、综合效率指数f(E)=3.74×10⁷.经无量纲标准化处理后代入式(5)对比分析，可知优化后高速公路综合安全指数值减小45.51%、综合效率指数值增大26.78%，安全、效率状态向理想点$\left( a, \text{ }b \right)(a={{f}_{\text{max}}}\left( E \right)~~, b={{f}_{\text{min}}}\left( S \right)\text{ }\!\!~\!\!\text{ }) $更加接近，表明优化后的限速区段设置方案使道路的综合交通安全、效率水平得到明显改善.

4 结论

1) 根据最小限速区段理论计算方法得出，当路段限速值分别为60、70、80、90、100、110、120 km/h时，对应的限速区段长度应不小于900、1 000、1 100、2 000、2 200、4 700、5 100 m.根据问卷调查确定驾驶人百公里范围内可接受的限速值变化次数应不超过3~5次.

2) 通过采用基于最小损失时间的限速区段优化协调控制模型对案例高速公路进行限速区段优化协调后，与优化前相比优化后综合安全指数值减小45.51%、综合效率指数值增大26.78%，安全、效率状态向理想点(a, b)更加接近，验证本文所提出的模型算法的实效性，可为制定基于安全和效率的高速公路限速区段优化协调控制提供理论依据.

3) 本文在对比分析限速区段优化前后综合安全、效率指数的变化时，未考虑实际道路物理条件变化，如：道路视距、路面条件等变化时对实际道路通行能力的影响.在后续研究中可根据具体道路实际情况，考虑通行能力的变化进一步完善调整相关参数的设置.