2. 公安部交通管理科学研究所,江苏 无锡 214151
2. Traffic Management Research Institute of the Ministry of Public Security, Wuxi 214151, Jiangsu, China
圆曲线路段是山区公路的事故多发路段,当汽车行驶于圆曲线路段时,容易因侧向失稳引发道路交通事故,而超速行驶又进一步增加了事故风险[1-2].全球每年由超速引发的社会经济成本损失高达400亿美元[3],2016年,我国由超速引发的道路交通事故共6 608起,造成3 332人死亡、6 334人受伤,分别占道路交通事故总数的3.10%、5.28%和2.80%[4].
车速管理和控制是保障公路行车安全的重要手段.由于运行速度、基于专家决策支持系统的限速(如美国联邦公路局研发的USLimits2、澳大利亚道路研究委员会研发的VLIMITS)、公路瓶颈区域的可变限速等限速策略可准确反映驾驶员的车速期望、提高通行效率[5-7],近年来得到了广泛关注.然而,上述策略并未从汽车行驶稳定性出发,对不同路面附着条件下汽车的临界(最高)安全车速进行深入探究,因此,难以有效保障自由流状态下、汽车行驶于山区圆曲线路段时的安全性.
指定设计速度(designated design speed,DS)、推算设计速度(inferred design speed,IS)也是各国交警部门制定限速策略的重要依据[8-9],这两种方法对线形复杂路段的汽车行驶稳定性进行了探讨. DS是依据整条公路中一些对交通安全最不利的地理几何特征(如最小平曲线、最小纵曲线等)设计的临界安全车速. IS由Donnell提出,适用于几何指标大于公路设计速度所对应的最小几何指标的路段的限速,可通过分析行车稳定性、停车视距确定临界安全车速[10]. DS和IS均采用横向力系数为评价指标,以横向力系数与路面摩阻系数的平衡作为汽车侧向失稳条件(认为此时汽车侧滑)[11-12],并据此推算限速值.然而,该计算方法存在以下问题:1)横向力系数仅能反映汽车的轨迹保持能力,无法表征转向稳定性; 2)轮胎是弹性体,其侧偏特性使得汽车完全侧滑之前就已失去了轨迹保持能力,采用侧滑作为临界失稳条件并不准确; 3)为提供较大的安全裕度,选取了较低的路面摩阻系数,因此,限速值为定值,且对于附着系数较高路面偏保守.实际上,路面可提供的最大摩阻系数受附着系数、汽车纵向加(减)速度、纵(横)断面线型影响,限速值应随以上因素的变化而改变.
针对上述问题,本文对汽车侧向失稳模式进行深入分析,依据各失稳模式的安全边界,提出一种圆曲线路段临界安全车速的高精度理论推导方法,从而为山区圆曲线路段限速策略提供可靠的理论依据.首先,将汽车侧向失稳解耦为失去轨迹保持能力、转向失稳、侧翻3种模式,提出各模式下反映汽车安全性的评价指标.其次,基于7自由度非线性整车-圆曲线路段耦合模型,通过理论推导、回归拟合得到汽车轨迹保持能力、转向稳定性安全边界的计算模型.再次,基于Carsim验证不同工况下上述安全边界的准确性.最后,依据上述7自由度车-路耦合模型,通过Simulink仿真得到不同路面附着系数、圆曲线路段设计参数下的限速策略,比较、分析该方法与运行速度、设计速度等限速方法的差异.
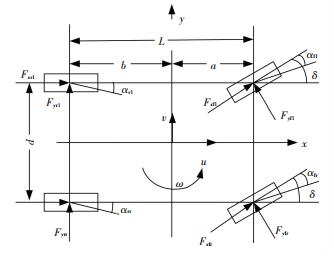
1 7自由度非线性车-路耦合模型 1.1 7自由度整车-圆曲线路段耦合模型在DS、IS限速策略及国内外公路设计规范中,通常采用点-质量车辆模型进行侧向稳定性分析,但该模型仅有一个自由度,无法反映轮胎的非线性特征.为准确分析行驶于设超高圆曲线路段的汽车的侧向失稳模式、推算稳定性指标的安全边界,本文构建了7自由度非线性车-路耦合数学模型,如图 1、2所示.其中7个自由度包括纵向运动、侧向运动、横摆运动和4个车轮的旋转运动[13].
|
图 1 7自由度车-路耦合模型(俯视图) Fig. 1 Vehicle-road model with 7 freedom degrees(plan view) |

|
图 2 7自由度车-路耦合模型(后视图) Fig. 2 Vehicle-road model with 7 freedom degrees(rear view) |
纵向运动、侧向运动和横摆方向的动力学方程分别为
| $ \begin{array}{l} m\left( {\dot u - v\omega } \right) = \left( {{F_{x{\rm{fl}}}} + {F_{x{\rm{fr}}}}} \right)\cos \delta - \left( {{F_{y{\rm{fl}}}} + } \right.\\ \;\;\;\left. {{F_{y{\rm{fr}}}}} \right)\sin \delta + {F_{x{\rm{rl}}}} + {F_{x{\rm{rr}}}}, \end{array} $ | (1) |
| $ \begin{array}{l} m\left( {\dot v + u\omega } \right) = \left( {{F_{x{\rm{fl}}}} + {F_{x{\rm{fr}}}}} \right)\sin \delta + \left( {{F_{y{\rm{fl}}}} + } \right.\\ \;\;\;\left. {{F_{y{\rm{fr}}}}} \right)\cos \delta + {F_{y{\rm{rl}}}} + {F_{y{\rm{rr}}}} + mg\sin \theta , \end{array} $ | (2) |
| $ \begin{array}{l} {I_z}\dot \omega = \left( {{F_{y{\rm{fl}}}} + {F_{y{\rm{fr}}}}} \right)a\cos \delta + \left( {{F_{y{\rm{fl}}}} - {F_{y{\rm{fr}}}}} \right)\frac{d}{2}\sin \delta - \\ \;\;\;\;\left( {{F_{y{\rm{rl}}}} + {F_{y{\rm{rr}}}}} \right)b + \left( {{F_{x{\rm{fl}}}} + {F_{x{\rm{fr}}}}} \right)a\sin \delta - \\ \;\;\;\;\left( {{F_{x{\rm{fl}}}} - {F_{x{\rm{fr}}}}} \right)\frac{d}{2}\cos \delta - \left( {{F_{x{\rm{rl}}}} - {F_{x{\rm{rr}}}}} \right)\frac{d}{2}. \end{array} $ | (3) |
4个车轮的力矩平衡方程为
| $ {J_{\rm{w}}} \cdot {{\dot {\tilde \omega} }_{{\rm{ij}}}} = - {r_{\rm{w}}} \cdot {F_{x{\rm{ij}}}} + {T_{d{\rm{ij}}}} - {T_{b{\rm{ij}}}}. $ | (4) |
式中及图中:m为整车质量; u为汽车质心处纵向速度; v为汽车质心处横向速度; ω为汽车质心处的横摆角速度; Fxij为各车轮纵向力(ij代表fl, fr, rl, rr); Fyij为各车轮侧向力(平行于地面); Fzij为各车轮垂向力; δ为车辆前轮转角; αij为各轮的侧偏角; Iz为整车绕铅垂轴的转动惯量; a、b为整车质心至前、后轴的距离; d为轮距; hg为总质心高度; L为轴距; Jw为车轮的滚动转动惯量;
采用Dugoff模型来描述轮胎-地面间的力学特性[14],αij为
| $ \left\{ \begin{array}{l} {\alpha _{{\rm{fl}}}} = \delta - \arctan \frac{{v + a\omega }}{{u - 0.5d\omega }},\\ {\alpha _{{\rm{fr}}}} = \delta - \arctan \frac{{v + a\omega }}{{u + 0.5d\omega }},\\ {\alpha _{{\rm{rl}}}} = - \arctan \frac{{v - b\omega }}{{u - 0.5d\omega }},\\ {\alpha _{{\rm{rr}}}} = - \arctan \frac{{v - b\omega }}{{u + 0.5d\omega }}. \end{array} \right. $ | (5) |
车轮轮心的纵向速度vij为
| $ \left\{ \begin{array}{l} {v_{{\rm{fl}}}} = \left( {u - 0.5d\omega } \right)\cos \delta + \left( {v + a\omega } \right)\sin \delta ,\\ {v_{{\rm{fr}}}} = \left( {u + 0.5d\omega } \right)\cos \delta + \left( {v + a\omega } \right)\sin \delta ,\\ {v_{{\rm{rl}}}} = u - 0.5d\omega ,\\ {v_{{\rm{rr}}}} = u + 0.5d\omega . \end{array} \right. $ | (6) |
根据式(5)、(6),可求得车轮的滑移率为
| $ {s_{{\rm{ij}}}} = \frac{{{r_{\rm{w}}}{{\tilde \omega }_{{\rm{ij}}}} - {v_{{\rm{ij}}}}\cos {\alpha _{{\rm{ij}}}}}}{{\max \left( {{r_{\rm{w}}}{{\tilde \omega }_{{\rm{ij}}}} - {v_{{\rm{ij}}}}\cos {\alpha _{{\rm{ij}}}}} \right)}}. $ | (7) |
接下来,计算描述轮胎工作点区域的参数λij,即
| $ {\lambda _{{\rm{ij}}}} = \frac{{\varphi {F_{z{\rm{ij}}}}\left( {1 + {s_{{\rm{ij}}}}} \right)}}{{2\sqrt {{{\left( {{k_{x{\rm{ij}}}}{s_{{\rm{ij}}}}} \right)}^2} + {{\left( {{k_{y{\rm{ij}}}}\tan {\alpha _{{\rm{ij}}}}} \right)}^2}} }}. $ | (8) |
其中:λij≥1表示轮胎工作点处于线性区域,λij < 1表示其处于非线性区域; φ为路面附着系数; Fzij为各个轮胎的垂直载荷,忽略汽车转向、加(减)速对Fzij的影响,可得
| $ \left\{ \begin{array}{l} {F_{z{\rm{fl}}}} = {F_{z{\rm{fr}}}} = \frac{{mg}}{2} \cdot \frac{b}{L},\\ {F_{z{\rm{rl}}}} = {F_{z{\rm{rr}}}} = \frac{{mg}}{2} \cdot \frac{a}{L}. \end{array} \right. $ | (9) |
作用于各轮胎的纵向力和侧向力[15]分别为
| $ {F_{x{\rm{ij}}}} = {k_{x{\rm{ij}}}}\frac{{{s_{{\rm{ij}}}}}}{{1 + {s_{{\rm{ij}}}}}}f\left( {{\lambda _{{\rm{ij}}}}} \right), $ | (10) |
| $ {F_{y{\rm{ij}}}} = {k_{y{\rm{ij}}}}\frac{{\tan {\alpha _{{\rm{ij}}}}}}{{1 + {s_{{\rm{ij}}}}}}f\left( {{\lambda _{{\rm{ij}}}}} \right). $ | (11) |
式中kxij、kyij分别为轮胎的纵向、横向刚度,f(λij)定义为
| $ f\left( {{\lambda _{{\rm{ij}}}}} \right) = \left\{ \begin{array}{l} 1,{\lambda _{{\rm{ij}}}} \ge 1;\\ \left( {2 - {\lambda _{{\rm{ij}}}}} \right){\lambda _{{\rm{ij}}}},{\lambda _{{\rm{ij}}}} < 1. \end{array} \right. $ | (12) |
将式(10)、(11)代入式(1)~(4),即可求解7自由度车-路耦合模型.本文依据中国公路常见汽车的外廓尺寸[16],选择Carsim中C级轿车为研究对象,参数分别为m=1 416 kg,a=1 016 mm,b=1 562 mm,d=1 534 mm,Iw=0.9 kg·m2,rw=310 mm,kxfl=117 764.5 N,kxfr=138 355.3 N,kxrl=77 347.1 N,kxrr=97 374.0 N,kyfl=109 400.4 N/rad,kyfr=110 179.2 N/rad,kyrl=72 326.0 N/rad,kyrr=89 722.2 N/rad,d=1 534 mm,hg=540 mm,Ix=606 kg·m2,Iy=1 523 kg·m2,Iy=1 523 kg·m2.
2 汽车侧向稳定性评价指标及其安全边界实际上,当侧向加速度过大时,汽车失稳存在3种模式:转向失稳、失去轨迹保持能力、侧翻.其中,反映转向稳定性的指标为质心的横摆角速度,当横摆角速度过大时,汽车会绕质心垂直轴线快速转动,当横摆角速度过小时,汽车转向不足; 反映汽车轨迹保持能力的指标为轮胎侧偏角,随着侧向加速度的增加,轮胎侧偏角不断增大,进而,轮胎进入非线性区域并接近侧滑极限; 汽车侧翻由过大的侧向加速度带来的载荷转移引起,其动力学机理较复杂,目前常用的简化指标为横向载荷转移率、侧翻剩余时间等[17].
由于本文主要对轿车的限速策略进行研究,而轿车重心较低,当侧向加速度增加时,车辆在侧翻之前已失去轨迹保持能力,即车辆发生侧翻的临界车速高于失去轨迹保持能力时的临界车速.因此,以下仅对转向稳定性、轨迹保持能力的评价指标及其安全边界进行探讨.
2.1 转向稳定性评价指标及其安全边界选取汽车质心的横摆角速度作为转向稳定性评价指标.依据汽车理论,当轮胎侧向力和轮胎侧偏角满足线性关系时,横摆角速度[18]为
| $ \omega = \frac{{u\delta }}{{L\left( {1 + K{u^2}} \right)}}. $ | (13) |
式中K为稳定性因数,计算公式为
| $ K = \frac{m}{{{L^2}}}\left( {\frac{a}{{{k_2}}} - \frac{b}{{{k_1}}}} \right), $ | (14) |
其中k1、k2分别为前、后轴的侧偏刚度,k1=219 579.6 N/rad,k2=162 048.2 N/rad.
式(13)、(14)在平行于地面的侧向加速度ay < 0.4g时很准确
当ay>0.4g,汽车出现转向失稳时对应的横摆角速度安全边界为
| $ {\omega _{\rm{b}}} = \frac{{{u_{\lim }}{\delta _{\lim }}}}{{L\left( {1 + {K_{{\rm{crct}}}}{u_{\lim }}^2} \right)}}. $ | (15) |
式中:ωb为横摆角速度安全边界; ulim为临界车速; δlim为前轮临界转角; Kcrct为修正的稳定性因数,计算公式[19]为
| $ {K_{{\rm{crct}}}} = \frac{m}{{{L^2}}}\left[ {{n_2}\left( {{a_y},\varphi } \right)\frac{a}{{{k_2}}} - {n_1}\left( {{a_y},\varphi } \right)\frac{b}{{{k_1}}}} \right]. $ | (16) |
其中n1(ay, φ)、n2(ay, φ)分别为前、后轴侧偏刚度修正系数,表达式为
| $ {n_i}\left( {{a_y},\varphi } \right) = \left\{ \begin{array}{l} 1,{a_y} < {a_{yi}} < \varphi g;\\ \begin{array}{*{20}{c}} {1 + 20\frac{{b - a}}{b}{{\left( {\frac{{{a_y} - {a_{yi}}}}{g}} \right)}^2},}\\ {{a_{yi}} < {a_y} < \varphi g;} \end{array}\\ \begin{array}{*{20}{c}} {1 + 20\frac{{b - a}}{b}{{\left( {\frac{{\varphi g - {a_{yi}}}}{g}} \right)}^2},}\\ {{a_{yi}} < \varphi g < {a_y};} \end{array}\\ \varphi ,\varphi g \le {\left( {\frac{{\varphi g - {a_{yi}}}}{g}} \right)^2}. \end{array} \right. $ | (17) |
其中i=1、2,ay1、ay2分别为0.4g、0.6g.
接下来,式(15)中的ulim计算公式为
| $ {u_{\lim }} = \sqrt {{a_{y\lim }}R} . $ | (18) |
式中aylim为临界侧向加速度,由图 2可知
| $ m{a_y}\cos \theta - mg\sin \theta \le {\varphi _{\rm{h}}}\left( {m{a_y}\sin \theta + mg\cos \theta } \right). $ | (19) |
式中φh为横向摩阻系数,φh=0.65φ.
由于θ较小,
| $ {a_y} - g{i_{\rm{h}}} \le 0.65\varphi \left( {{a_y}{i_{\rm{h}}} + g} \right). $ | (20) |
因此,有
| $ {a_{y\lim }} = \frac{{0.65\varphi g + g{i_{\rm{h}}}}}{{1 - 0.65\varphi {i_{\rm{h}}}}}. $ | (21) |
接着,δlim的计算公式为
| $ {\delta _{\lim }} = \frac{L}{R} + L{K_{{\rm{crct}}}}{a_{y\lim }}. $ | (22) |
最后,将式(16)、(18)、(22)代入式(15),可求出ωb.
2.2 轨迹保持能力评价指标及其安全边界在车辆稳定性控制领域,通常将质心侧偏角作为稳定性指标之一.但采用质心侧偏角评价轨迹保持能力,存在以下问题:汽车低速行驶时,由于轮胎侧偏角较小,质心侧偏角为正值; 随着车速的增加,轮胎侧偏角增大,质心侧偏角将逐渐减小至零,直至变为负值.其值(或绝对值)不随轨迹保持能力的降低单调变化,故不适宜作为评价指标.
当轮胎侧偏角的绝对值增加时,轨迹保持能力下降,因此,本文采用前轮侧偏角绝对值的均值αf作为轨迹保持能力的评价指标,即
| $ {\alpha _{\rm{f}}} = \left| {{\alpha _{{\rm{fl}}}} + {\alpha _{{\rm{fr}}}}} \right|/2. $ | (23) |
由于很难从数学上准确判定αf的安全边界αflim,在MATLAB/Simulink中构建上述7自由度车-路耦合模型,通过仿真,拟合αflim与路面附着系数φ、超高值ih和圆曲线半径R之间的关系.采用的公路圆曲线路段参数[20]:φ取0.2~0.8;ih分别取4%、6%、8%; R分别取65、150、300 m.车道宽度选用3.50 m.仿真中,当外侧车轮滑出车道时,认为αf到达安全边界. αflim的拟合函数为
| $ \begin{array}{l} {a_{{\rm{f}}\lim }} = - 3.957 + 0.022R + 1.507\varphi + 0.298{i_{\rm{h}}} - \\ \;\;\;\;\;\;\;\;\;3.869 \times {10^{ - 5}}{R^2} - 0.001R\varphi - 0.025R{i_{\rm{h}}} - \\ \;\;\;\;\;\;\;\;\;0.449{\varphi ^2} - 4.368\varphi {i_{\rm{h}}} + 49.234{i_{\rm{h}}}^2, \end{array} $ | (24) |
决定系数R2=0.992,说明拟合精度较高.
3 基于人-车-路高精度动力学模型的汽车侧向安全边界验证为验证ω、αf安全边界的准确性,在Carsim中构建人-车-路高精度动力学仿真模型.其中,驾驶员采用“轨迹跟踪”模型,预瞄时间为2 s[21];仿真车辆为C级轿车,参数见表 1.选取山区二级沥青混凝土公路进行建模,设计速度为80 km/h,圆曲线半径选择最小值300 m,超高值选取最大值4%[20],选取干燥(0.60)、潮湿(0.40)、积雪(0.24)[22-23]作为沥青路面不同天气状况的表现形式.
| 表 1 各指标安全边界准确性验证 Tab. 1 Validation of safety boundaries |
针对上述动力学模型,首先,以圆曲线路段的设计速度(80 km/h)进行仿真,观察本文提出的评价指标、横向力系数f与各自安全边界之间的关系,并与Carsim中车辆的实际运动状态进行比较,验证各指标安全边界的准确性; 如果以设计速度仿真,Carsim中车辆未失稳,采用10 km/h为增幅进行仿真,直至车辆出现失稳.仿真结果见表 1.
对于表 1中的圆曲线路段,《公路工程技术标准》[20]中规定的横向力系数fc为0.13(即横向力系数的安全边界),其值依据设计速度、圆曲线半径、超高值推算得出.因此,当汽车以设计速度80 km/h行驶时,横向力系数刚好达到其安全边界.然而,此时Carsim中车辆未失稳,可见横向力系数的安全边界过于保守.
对于ω,当仿真中的最大值未达到其安全边界时,Carsim车辆模型未激转,反之则发生激转.说明通过ω的安全边界,可以准确判定汽车的转向稳定性.同样,由表中结果可看出,通过αf的安全边界,可准确判定车辆是否失去轨迹保持能力.
4 基于汽车侧向安全边界的公路圆曲线路段限速策略由于ω、αf的安全边界可准确表征汽车的转向稳定性和轨迹保持能力,以设计速度为起始,对7自由度车-路耦合Simulink模型进行仿真; 以1 km/h为间隔增加车速,直至ω、αf中任一指标达到相应的安全边界,此时的仿真车速即为基于汽车侧向安全边界的临界安全车速.选取山区二级公路为研究对象,当设计速度分别为40、60、80 km/h时,分别选取超高值为4%、6%、8%对应的最小半径作为圆曲线路段的半径[20].在不同附着系数下,将本文提出的临界安全车速vs与运行速度v85、设计速度v0进行对比,见表 2.
| 表 2 3种限速策略的比较 Tab. 2 Comparison of three speed limit strategies |
表 2中,运行速度值依据文献[24]中的运行速度计算方法得出,其值均处于相应的最低运行速度和期望速度之间,因此,不需对上述运行速度进行修正.
将设计速度与临界安全车速比较,可以看出:采用设计速度限速可有效保障路面附着系数较低(0.24)时汽车行驶的安全性,但对于潮湿、干燥路面,设计速度的值过于保守,不利于提高公路的通行效率.
表 2中的运行速度为圆曲线路段入口、中点、出口处运行速度的最小值.将运行速度与临界安全车速对比可知,当车辆行驶于干燥路面时,以运行速度限速可保障行车安全; 然而,当行驶于潮湿、积雪路面时,部分圆曲线路段的运行速度超出了临界安全车速,此时应将限速值修正为临界安全车速以下(可向下以10 km/h的倍数取整).在实际操作中,当路面处于潮湿、积雪状态时,可采用可变情报板改变限速值,或采用路表状态提升技术保障行车安全.
5 结论1) 针对横向力系数在汽车侧向稳定性分析中的不足,将汽车侧向失稳状态解耦为失去轨迹保持能力、转向失稳、侧翻3种模式,提出各失稳模式的评价指标.
2) 构建了7自由度非线性整车-圆曲线路段耦合模型,通过理论推导、回归拟合得到汽车轨迹保持能力、转向稳定性指标安全边界的计算模型,并采用Carsim仿真验证了不同工况下各指标安全边界的准确性.
3) 基于汽车侧向安全边界,对7自由度车-路耦合Simulink模型进行仿真,得到不同路面附着系数、圆曲线路段设计参数下的临界安全车速.将临界安全车速与运行速度、设计速度进行对比,结果表明:采用设计速度限速,当路面状况为干燥、潮湿时,限速值过于保守,不利于提高公路的通行效率; 采用运行速度进行限速,对于潮湿、积雪路面,圆曲线路段的运行速度往往大于临界安全车速,需要降低限速值,以保障行车安全.
4) 所提出的限速策略充分考虑了汽车侧向运动的非线性特征和稳定性,可作为其他面向驾驶期望、通行效率山区公路限速策略的有益补充.限于篇幅,本文仅探讨了轿车的限速策略.但对于质心较高的汽车(如SUV、大客车、货车、半挂汽车列车),应将本文提出的失稳模式、安全边界与侧倾稳定性评价指标及其安全边界相结合,制定限速策略,从而保障质心较高汽车的侧向稳定性.
| [1] |
MONTELLA A, PUNZO V, CHIARADONNA S, et al. Point-to-point speed enforcement systems: speed limits design criteria and analysis of drivers' compliance[J]. Transportation Research Part C:Emerging Technologies, 2015, 53(1): 1. DOI:10.1016/j.trc.2015.01.025 |
| [2] |
聂进, 吴京梅, 吴玲涛, 等. 基于行人和自行车交通安全的城市道路限速值研究[J]. 中国公路学报, 2014, 27(7): 91. NIE Jin, WU Jingmei, WU Lingtao, et al. Study on urban road speed limit for pedestrian and bicyclist traffic safety[J]. China Journal of Highway and Transport, 2014, 27(7): 91. DOI:10.3969/j.issn.1001-7372.2014.07.012 |
| [3] |
National Highway Traffic Safety Administration. Traffic safety facts: 2012 data[R]. Washington DC: National Highway Traffic Safety Administration, 2012
|
| [4] |
公安部交通管理局.中华人民共和国道路交通事故统计年报(2016年度)[R].无锡: 公安部交通管理科学研究所, 2017 Traffic Management Bureau, the Public Security Ministry. Annual report on road traffic accidents in the People's Republic of China (2016)[R]. Wuxi: Traffic Management Science Institute of Ministry of Public Security, 2017 |
| [5] |
FITZPATRICK C D, MCKINNON I A, TAINTER F T, et al. The application of continuous speed data for setting rational speed limits and improving roadway safety[J]. Safety Science, 2016, 85: 171. DOI:10.1016/j.ssci.2016.01.020 |
| [6] |
SRINIVASAN R, HARKEY D L, THARPE D, et al. Development of a web-based expert system for setting speed limits in speed zones[C]//Transportation Research Board 87th Annual Meeting. Washington DC: Transportation Research Board, 2008
|
| [7] |
杨庆芳, 马明辉, 梁士栋, 等. 高速公路瓶颈区域可变限速阶梯控制方法[J]. 西南交通大学学报, 2015, 50(2): 354. YANG Qingfang, MA Minghui, LIANG Shidong, et al. Stair-like control strategies of variable speed limit for bottleneck regions on freeway[J]. Journal of Southwest Jiaotong University, 2015, 50(2): 354. DOI:10.3969/j.issn.0258-2724.2015.02.023 |
| [8] |
OH H, MUN S. Design speed based reliability index model for roadway safety evaluation[J]. KSCE Journal of Civil Engineering, 2012, 16(5): 845. DOI:10.1007/s12205-012-1469-9 |
| [9] |
DONNEL E T, HIMES S C, MAHONEY K M, et al. Understanding speed concepts: key definitions and case study examples[J]. Transportation Research Record Journal of the Transportation Research Board, 2009, 45(2120): 3. |
| [10] |
WU K F, DONNELL E, HIMES S, et al. Exploring the association between traffic safety and geometric design consistency based on vehicle speed metrics[J]. Journal of Transportation Engineering, 2013, 139(7): 738. DOI:10.1061/(ASCE)TE.1943-5436.0000553 |
| [11] |
American Association of State Highway Transportation Officials. A policy on geometric design of highways and streets[S]. 6th ed. Washington DC: American Association of State Highway and Transportation Officials, 2011
|
| [12] |
DONNELL E, WOOD J, HIMES S, et al. Use of side friction in horizontal curve design: a margin of safety assessment[J]. Transportation Research Record Journal of the Transportation Research Board, 2016, 2588: 61. DOI:10.3141/2588-07 |
| [13] |
许建, 张政, 李翔, 等. 独立驱动电动汽车横摆力矩的模糊控制算法[J]. 西安交通大学学报, 2014, 48(7): 83. XU Jian, ZHANG Zheng, LI Xiang, et al. A fuzzy control system for the direct yaw moment of 4WD electric vehicles[J]. Journal of Xi'an Jiaotong University, 2014, 48(7): 83. DOI:10.7652/xjtuxb201407015 |
| [14] |
ZHANG B, DU H, LAM J, et al. A novel observer design for simultaneous estimation of vehicle steering angle and sideslip angle[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4357. DOI:10.1109/TIE.2016.2544244 |
| [15] |
郭景华, 罗禹贡, 李克强. 智能车辆运动控制系统协同设计[J]. 清华大学学报(自然科学版), 2015, 55(7): 761. GUO Jinghua, LUO Yugong, LI Keqiang. Collaborative design of a motion control system for intelligent vehicles[J]. Journal of Tsinghua University (Science and Technology), 2015, 55(7): 761. DOI:10.16511/j.cnki.qhdxxb.2015.07.010 |
| [16] |
中国汽车技术研究中心.道路车辆外廓尺寸、轴荷及质量限值: GB 1589—2004[S].北京: 中国标准出版社, 2004 China Automotive Technology Research Center. Outline size, axle load and quality limit of road vehicles: GB 1589—2004[S]. Beijing: China Standard Press, 2004 |
| [17] |
曾小华, 李广含, 宋大凤, 等. 基于遗传算法优化的BP神经网络侧翻预警算法[J]. 华南理工大学学报(自然科学版), 2017, 45(2): 30. ZENG Xiaohua, LI Guanghan, SONG Dafeng, et al. Rollover warning algorithm based on genetic algorithm-optimized BP neural network[J]. Journal of South China University of Technology (Natural Science Edition), 2017, 45(2): 30. DOI:10.3969/j.issn.1000.2017.02.005 |
| [18] |
余志生. 汽车理论[M]. 5版. 北京: 机械工业出版社, 2009: 144. YU Zhisheng. Automotive theory[M]. 5th ed. Beijing: Mechanical Industry Press, 2009: 144. |
| [19] |
CHEN Jie, SONG Jian, LI Liang, et al. A novel pre-control method of vehicle dynamics stability based on critical stable velocity during transient steering maneuvering[J]. Chinese Journal of Mechanical Engineering, 2016, 29(3): 475. DOI:10.3901/CJME.2016.0126.014 |
| [20] |
中华人民共和国交通运输部.公路工程技术标准: JTG B01—2014[S].北京: 人民交通出版社, 2014 The Ministry of Transportation of the People's Republic of China. Technical standard of highway engineering: JTG B01—2014[S]. Beijing: China Communication Press, 2014 |
| [21] |
Mechanical Simulation Corporation, CarSim Reference Manual Version 8.0: Driver Controls[M]. Michigan: Mechanical Simulation Corporation, 2009: 8
|
| [22] |
何杰, 刘霞, 陈一锴, 等. 恶劣天气路面条件对行车安全的影响[J]. 交通运输工程学报, 2011(1): 58. HE Jie, LIU Xia, CHEN Yikai, et al. Influence of road condition on running safety in atrocious weather[J]. Journal of Traffic and Transportation Engineering, 2011(1): 58. DOI:10.3969/j.issn.1671-1637.2011.01.010 |
| [23] |
SALIMI S, NASSIRI S, BAYAT A, et al. Lateral coefficient of friction for characterizing winter road conditions[J]. Canadian Journal of Civil Engineering, 2015, 43(1): 2355. DOI:10.1139/cjce-2015-0222 |
| [24] |
华杰工程咨询有限公司.公路项目安全性评价规范: JTG B05—2015[S].北京: 人民交通出版社股份有限公司, 2016 CHELBI Engineering Consultants, Inc. Specification for highway safety audit: JTG B05—2015[S]. Beijing: China Communication Press, 2015 |
 2019, Vol. 51
2019, Vol. 51


