2. 哈尔滨工业大学 交通科学与工程学院,哈尔滨 150090
2. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China
鉴于城市轨道交通大运量和可以充分利用城市地下空间的特点,其已经成为缓解城市交通问题的有效途径.但在其发展中也暴露出一些问题,如客流预测值与实际情况相差较大,造成资源闲置或供不应求; 城轨快线车站间距小,不能发挥效率优势等.目前,专门对城市轨道交通车站选址的研究相对较少,国外主要从客流预测和车站间距优化(主要是普通公交车站间距)两个方面开展研究,而国内则相对侧重城市轨道交通车站间距优化的研究.文献[1]对美国265个城区进行了研究,发现价格机制和发车间隔对客流量的影响较地理因素、经济水平、人口特征等更直接、显著.文献[2]通过结构方程研究了自变量对客流量的作用及自变量之间的关系.文献[3]基于地形条件的差异对步行、公交吸引力和公交车加速度的影响,研究了公交车站设置问题.文献[4]基于轨道交通与普通公交的合作关系,得到了不同阈值下的优化站间距.文献[5]建立了以居民出行时间最小为目标的市郊铁路站间距优化模型.文献[6]建立了以乘客出行时间成本和车票收入最大化为目标的站间距优化模型.文献[7]以不同地铁线路的效益费用和客流量作为不同方案的对比条件,确定了地铁车站的初步布局方法.但车站间距优化模型得出的一般均为某种特定条件下的优化值,不具有广泛适用性.
本文从客流预测和车站间距两个方面入手,建立双层模型对城市轨道交通车站选址问题进行研究.本文的车站间距优化并非得出某个具体站间距值,而是基于整条线路,以运营成本和出行成本最小化为目标,协调各车站间距.
1 选址模型构建城市轨道交通作为一种公共交通,其社会效益是首要的,即应首先保证乘客选择的公平性,为尽可能多的城市居民提供服务.其次,应考虑其经济属性,本文考虑了乘客和运营两方面的成本,并将二者之和定义为城市轨道交通综合交通成本.良好的车站选址应在保证服务平等性的基础上,使综合交通成本处于较低水平.
1.1 上层模型为确保服务的平等性,首先应确定各车站的客流量特征,即需对候选车站的客流量进行预测.目前,主要采用四阶段法和基于普通最小二乘法的回归模型进行预测.四阶段法虽已得到广泛应用,但其依赖于大量资料,成本高,且主要适用于对大范围区域进行交通预测,而对车站吸引范围规模的研究则不适用.多元回归模型虽使预测成本降低,且能够得到不同变量对客流的影响,但各变量的系数在不同预测单元内均相等,忽略了变量对客流的影响在地理空间上的差异.地理加权回归(geographically weighted regression, GWR)模型适用于解决空间异质性问题,其考虑地理位置属性,基于局部回归对自变量和因变量的关系进行研究,能够体现自变量对因变量的影响在空间上的变化,即对于每一预测单元均能得到一组唯一的系数组合.
1.1.1 影响因素分析已有研究[8]表明,土地使用是决定居民出行生成的核心,且不同土地使用类型会对居民出行强度和出行目的产生影响.结合现有研究和我国土地分类标准,将车站服务范围内的土地类型分为行政管理、教育文化、居住、商业、休闲娱乐和医疗卫生共6类.参考文献[8],以85%的乘客覆盖率确定车站服务范围,本文使用路网距离表示该阈值.在车站服务范围内,乘客选择城市轨道交通出行的概率随其到车站的路网距离增加而呈现降低趋势.即对不同位置的建筑物而言,其对客流的贡献率呈现依路网距离增加而衰减的特征.定义以上6类土地使用类型的建筑实际楼层面积和该衰减规律的乘积为加权楼层面积,表达式为
| $ {A_{{{\rm{w}}_i}}} = D\left( {{L_n}} \right) \cdot {A_i}. $ | (1) |
式中:Awi为建筑i的加权楼层面积,D(Ln)为乘客选择乘坐轨道交通的概率依路网距离的衰减函数,Ai为建筑i的实际楼层面积.
以上,行政管理、教育文化、居住、商业、休闲娱乐和医疗卫生6类土地使用类型的建筑加权楼层面积仅从绝对量上对用地情况进行描述,而未考虑车站吸引范围内不同土地使用类型的搭配对客流量的影响.因此,引入土地使用多样性指数[9],即
| $ {I_{{\rm{lud}}}} = \frac{{ - \sum\limits_{i = 1}^n {{p_i}} \cdot \ln {p_i}}}{{\ln n}}. $ | (2) |
式中pi为第i类用地的楼层面积与各类用地总楼层面积之比,n为不同性质用地的类别数.
公交换乘和“P+R”模式能够延伸车站服务范围,促进多式联运,因此,将车站200 m范围内的接驳公交线路数量和“P+R”设施的有无作为解释变量.
中心度表示某车站与线路中其他车站在物理距离上的联系强度,中心度越高,联系性越强,从而越有可能吸引更多客流,因此,也将其作为解释变量之一.但由于换乘车站客流吸引特征的不同和位置的不确定性,因此,不考虑候选车站.其值大小在(0, 1)内,取值越大,表示车站越靠近线路中心,计算公式为
| $ {I_{{\rm{a}}{{\rm{c}}_i}}} = \frac{{\min \left( {{d_{{n_i}}}} \right)}}{{{d_{{n_i}}}}}. $ | (3) |
式中Iaci为第i个车站的中心度,dni为第i个车站到其他各车站的路网距离之和.
1.1.2 基于GWR的客流量预测模型本文以1 d为单位,预测车站上车乘客量.建立GWR模型之前,需对上述解释变量进行系数显著性检验.此外,共线性变量的存在将使运算结果出现R2偏高的假象.需基于普通最小二乘法,采用方差膨胀因子(VIF)检验自变量的多重共线性.当某自变量的VIF值大于等于10时(严格时,以7.5为标准),认为该自变量与其他自变量之间存在多重共线性,需要剔除.具体的共线性变量需要结合实际情况,根据VIF检验结果进行确定. GWR模型为
| $ {Q_i} = {\beta _{i0}} + \sum\limits_{j = 1}^n {{\beta _{ij}}{x_j}} + {\varepsilon _i}. $ | (4) |
式中:Qi为第i个车站的上车乘客量,xj为上述变量中通过显著性检验和方差膨胀因子检验的第j个解释变量,βij为第i个车站的第j个解释变量的系数,βi0为第i个车站的截距,εi为第i个车站的残差.
GWR模型在运算时,将考虑各回归样本点其某带宽范围内样本点的信息,并根据与其距离大小,对周围样本点的信息设定权重.本文采用适应性核函数确定带宽.计算权重的方法有多种,Gaussian函数法和bi-square法应用最多,本文选用Gaussian函数法对权重进行计算,即
| $ {w_{ij}} = \exp \left( { - {{\left( {\frac{{{d_{ij}}}}{b}} \right)}^2}} \right). $ | (5) |
式中:wij为第j个车站的变量相对于第i个车站的权重,dij为i、j两个车站间的距离,b为限制样本范围的带宽.
所以,在带宽范围内,各位置样本相对回归样本点的权重矩阵为
| $ \mathit{\boldsymbol{W}}\left( i \right) = \left[ {\begin{array}{*{20}{c}} {{w_{i1}}}&{}&{}&{}\\ {}&{{w_{i2}}}&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&{{w_{in}}} \end{array}} \right]. $ | (6) |
式中W(i)为回归样本点i的权重矩阵.
根据加权最小二乘法, 可以得到β(i)的估计向量为
| $ \mathit{\boldsymbol{\hat \beta }}\left( i \right) = {\left[ {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{W}}\left( i \right)\mathit{\boldsymbol{X}}} \right]^{ - 1}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{W}}\left( i \right)\mathit{\boldsymbol{Q}}. $ | (7) |
其中:
| $ \mathit{\boldsymbol{\beta }}\left( i \right) = \left( {{\beta _{i0}},{\beta _{i1}}, \cdots ,{\beta _{in}}} \right), $ | (8) |
| $ \mathit{\boldsymbol{X}}{\rm{ = }}\left[ {{x_1},{x_2}, \cdots ,{x_n}} \right], $ | (9) |
| $ \mathit{\boldsymbol{Q}} = \left[ {{Q_1},{Q_2}, \cdots ,{Q_m}} \right]. $ | (10) |
上层模型以上车乘客量最大为目标函数为
| $ \max {Q_{{\rm{total}}}} = \sum\limits_{i = 1}^n {{Q_i}} \cdot {\zeta _i}. $ | (11) |
式中:Qtotal为各车站上车乘客量之和,ζi为0-1变量,当候选车站i被选中时,其为1,反之为0.
约束条件为
| $ 400 \le S_k^{k - 1} \le 1\;500, $ | (12) |
| $ {N_{\min }} \le \sum\limits_{i = 1}^n {{\zeta _i}} \le {N_{\max }}. $ | (13) |
式中:Skk-1为被选中的相邻车站k-1和k之间的站间距,其中400 m为文献[10]中日本的情况,1 500 m为参考既有线路的最大站间距,Nmin为给定线路按最大站间距可设置的最小车站数,Nmax为给定线路按最小站间距可设置的最大车站数.
1.2 下层模型鉴于不同候选车站上车乘客量的差异,对不同候选车站进行组合,按照乘客出行分布特征,将其分配到其他车站,将导致出行成本的差异,且运营方成本也会不同.合理的车站选址应保证乘客出行成本和运营成本,即城市轨道交通综合交通成本处于较低水平.下层模型基于车站间距优化对综合交通成本进行研究.此站间距优化并非得出某个车站间距最优值,而是基于整条线路,对候选车站进行协调,使各车站间距的组合结果能使综合交通成本处于较低水平.
1.2.1 乘客出行成本以车站i单日上车乘客为研究对象,乘客出行成本包括:步行至车站的时间成本、站内候车时间成本、行程时间成本、离站至目的地的时间成本及车票费用,即
| $ {C_{{{\rm{r}}_i}}} = {C_{{{\rm{f}}_i}}} + {C_{{{\rm{w}}_i}}} + {C_{{{\rm{v}}_i}}} + {C_{{{\rm{l}}_i}}} + {C_{{{\rm{t}}_i}}}. $ | (14) |
式中:Cri为乘客出行成本,Cfi为乘客步行至相应车站的时间成本,Cwi为乘客站内候车时间成本,Cvi为乘客行程时间成本,Cli为乘客离站至目的地的时间成本,Cti为乘客的车票费用.
将车站服务范围以100 m路网距离为单位,分成多个距离带,则步行至车站的时间成本为
| $ {C_{{{\rm{f}}_i}}} = {V_{\rm{f}}}\sum\limits_{j = 1}^n {{Q_{ij}}\frac{{{d_j}}}{{{v_{\rm{r}}}}}} . $ | (15) |
式中:Vf为步行的单位时间价值,Qij为站点i的第j个带宽内每日的客流生成量,dj为第j个带宽的中点与对应车站的路网距离,vr为乘客步行的平均速度.
乘客候车时间主要由发车间隔决定,候车成本为
| $ {C_{{{\rm{w}}_i}}} = {Q_i}{V_{\rm{w}}}{T_{\rm{w}}}. $ | (16) |
式中Vw为乘客候车的单位时间价值,Tw为平均候车时长.
本文假设乘客均匀到达车站,则乘客站内平均等待时间为
| $ {T_{\rm{w}}} = \frac{{\Delta T}}{2}. $ | (17) |
式中ΔT为发车间隔.
行程时间成本为乘客乘坐列车的时间成本,主要由乘客所经过的车站决定,即
| $ {C_{{{\rm{v}}_i}}} = \sum\limits_m {Q_i^j{V_{\rm{v}}}{T_{ij}}} . $ | (18) |
式中:Qij为由车站i上车且到车站j下车的乘客量,Vv为乘客单位行程时间价值,Tij为列车由车站i到车站j的时长.
列车运行时间由牵引时间、惰行时间、制动时间与驻站时间4个部分组成.牵引时间又包括加速运行时间与匀速运行时间.因此,由车站i到车站j的时长为
| $ {T_{ij}} = \sum\limits_{k = 2}^n {\zeta _{ij}^k\left( {T_{\rm{t}}^k + T_{\rm{i}}^k + T_{\rm{b}}^k} \right)} + {n_{ij}}{T_{\rm{s}}}. $ | (19) |
式中:ζijk为二元变量,当乘客在车站i上车、在车站j下车,且经过车站k时,其为1,否则为0,Ttk为列车到达车站k前的牵引时间,Tik为列车到达车站k前的惰行时间,Tbk为列车到达车站k前的制动时间,nij为车站i、j之间的车站数量,Ts为列车驻站时长.
牵引时间Ttk为
| $ T_{\rm{t}}^k = T_{\rm{a}}^k + T_{\rm{c}}^k. $ | (20) |
式中Tak为车辆到达车站k之前的加速时间,Tck为车辆到达车站k之前的匀速运行时间.
本文假设乘客离站至目的地的时间成本与步行至车站的时间成本相同,即
| $ {C_{{{\rm{l}}_i}}} = {C_{{{\rm{f}}_i}}}. $ | (21) |
一般,车票成本由乘客出行经过的车站数决定,即
| $ {C_{{{\rm{t}}_i}}} = \sum\limits_n {Q_i^j} \cdot {P_k} $ | (22) |
式中Pk为车站i、j之间,车站数为k时所对应的车票费用.
综上,单日各车站上车乘客的出行成本之和为
| $ \begin{array}{l} {C_{\rm{r}}} = \sum\limits_{i = 1}^n {\left\{ {2{V_{\rm{f}}}\sum\limits_{j = 1}^n {{Q_{ij}}\frac{{{d_j}}}{{{v_{\rm{r}}}}}} + {Q_i}{V_{\rm{w}}}\frac{{\Delta T}}{2} + } \right.} \\ \;\;\;\;\;\;\;\sum\limits_n {\sum\limits_{k = 2}^n {Q_i^j{V_{\rm{v}}}\left[ {\zeta _{ij}^k\left( {T_{\rm{a}}^k + T_{\rm{c}}^k + T_{\rm{i}}^k + T_{\rm{b}}^k} \right) + {n_{ij}}{T_{\rm{s}}}} \right]} } + \\ \;\;\;\;\;\;\;\left. {\sum\limits_n {Q_i^j{P_k}} } \right\}. \end{array} $ | (23) |
运营成本方面,考虑了列车购置成本、列车上工作人员成本、车队保养成本、站内工作人员成本和牵引能耗成本,以上成本均以单位工作日计算.
不同车站间距组合将导致列车运行周期的差异.在相同发车间隔下,运营周期越长,对车队规模要求越高.列车购置成本为
| $ {C_{\rm{f}}} = {N_{\rm{f}}}{p_{\rm{v}}}. $ | (24) |
式中pv为单位列车组购置费用, Nf为车队规模,车队规模表示为
| $ {N_{\rm{f}}} = \frac{{{T_{\rm{R}}}}}{{\Delta T}}, $ | (25) |
其中TR为列车运行周期.
运行周期TR为列车离开始发站并返回所经过的时长,具体包括列车在各区间的加速运行时长、匀速运行时长、惰行时长、制动时长及在中间车站的驻站时长之和,即
| $ {T_{\rm{R}}} = 2\sum\limits_{k = 2}^n {\left( {T_{\rm{a}}^k + T_{\rm{c}}^k + T_{\rm{i}}^k + T_{\rm{b}}^k} \right)} + \left( {2n - 1} \right){T_{\rm{s}}}. $ | (26) |
列车自购买至达到使用年限,每日使用成本为
| $ {C_{{\rm{vd}}}} = \frac{{\left[ {2\sum\limits_{k = 2}^n {\left( {T_{\rm{a}}^k + T_{\rm{c}}^k + T_{\rm{i}}^k + T_{\rm{b}}^k} \right)} + \left( {2n - 1} \right){T_{\rm{s}}}} \right]{P_{\rm{v}}}\left( {1 - {\delta _{\rm{v}}}} \right)}}{{365 \cdot \Delta T \cdot {n_{\rm{y}}}}}. $ | (27) |
列车上工作人员成本为
| $ {C_{\rm{d}}} = {V_{\rm{d}}} \cdot {n_{\rm{d}}} \cdot {N_{\rm{f}}}. $ | (28) |
式中:Cd为列车上工作人员的单位工作日成本,Vd为列车内工作人员每日平均工资,nd为一个列车组内的工作人员数量.
车队保养成本和站内工作人员成本分别为
| $ {C_{\rm{m}}} = {V_{\rm{m}}} \cdot {N_{\rm{f}}}, $ | (29) |
| $ {C_{\rm{s}}} = {V_{\rm{s}}} \cdot {n_{\rm{s}}} \cdot \sum\limits_{i = 1}^n {{\zeta _i}} . $ | (30) |
式中:Cm为车队保养成本,Vm为单位列车组的保养费用,Cs为站内工作人员成本,Vs为站内工作人员平均工资,ns为各车站工作人员数量平均值.
为简化列车运行特征,假设列车在加速阶段为匀加速.加速运行时间和匀速运行时间分别为
| $ T_{\rm{a}}^k = \sqrt {\frac{{2S_{\rm{a}}^k}}{{{A_{\rm{a}}}}}} . $ | (31) |
| $ T_{\rm{c}}^k = \frac{{S_{\rm{c}}^k}}{{{V_{\max }}}}. $ | (32) |
式中:Sak为到车站k前的加速运行距离,Aa为加速运行阶段的加速度,Sc为到车站k前的匀速运行距离,Vmax为列车最大运行速度.
惰行时间和制动运行时间分别为
| $ T_{\rm{i}}^k = \sqrt {\frac{{2S_{\rm{i}}^k}}{{{A_{\rm{i}}}}}} , $ | (33) |
| $ \begin{array}{l} T_{\rm{b}}^k = \sqrt {\frac{{2S_{\rm{b}}^k}}{{{A_{\rm{b}}}}}} . \end{array} $ | (34) |
式中:Si为到车站k前的惰行距离,Ai为惰行阶段减速度,Sb为到车站k前的制动距离,Ab为制动阶段减速度.
列车编组由动车和拖车构成.其中,动车装有电机,提供动力.在匀加速阶段,由于牵引力恒定,所以发动机为恒转矩工作模式.在匀速运行阶段,由于牵引力和速度均恒定,所以发动机处于恒功率工作模式.在制动阶段,列车优先采用电制动,当速度低于某阈值时,开始采用空气制动.因此,单位列车编组在一个运行周期内实际使用的电能应为牵引消耗电能与再生电能被利用部分的差值,即
| $ \begin{array}{l} {E_{\rm{g}}} = {n_{\rm{g}}}{P_{\rm{e}}}\left[ {{P_{\rm{t}}}\sum\limits_{k = 2}^n {\left( {\frac{{T_{\rm{a}}^k}}{2} + T_{\rm{c}}^k} \right)} - } \right.\\ \;\;\;\;\;\;\left. {{P_{\rm{f}}}\sum\limits_{k = 2}^n {T_{\rm{f}}^k\left( {1 - \delta _{\rm{r}}^k} \right)} } \right]/3\;600. \end{array} $ | (35) |
式中:ng为单位列车编组中动车的数量,Pe为用电单价,Pt为动车电机额定功率,Pf为动车再生电能功率,Tfk为再生电能时间,δrk为电阻制动消耗电能的比例.
再生电能时间Tfk为
| $ T_{\rm{f}}^k = \frac{{{V_{{{\rm{b}}_0}}} - {V_{{{\rm{b}}_{\rm{c}}}}}}}{{{A_{\rm{b}}}}}. $ | (36) |
式中Vb0为制动初始速度,Vbc为由电制动转向空气制动的速度阈值.
考虑到乘客量的增加会使得综合交通成本增大,因此,以单位乘客的综合交通成本作为下层模型的目标函数, 即
| $ \begin{array}{l} {C_{\rm{o}}} = \frac{1}{Q}\left\{ {{P_{\rm{v}}}\left( {1 - {\delta _{\rm{v}}}} \right)\left[ {2\sum\limits_{i = 2}^n {\left( {\sqrt {\frac{{2S_{\rm{a}}^k}}{{{A_{\rm{a}}}}}} + \frac{{S_{\rm{c}}^k}}{{{V_{\max }}}} + \sqrt {\frac{{2S_{\rm{i}}^k}}{{{A_{\rm{i}}}}}} + } \right.} } \right.} \right.\\ \;\;\;\;\;\;\;\left. {\left. {\sqrt {\frac{{2S_{\rm{b}}^k}}{{{A_{\rm{b}}}}}} } \right) + \left( {2n - 1} \right){T_{\rm{s}}}} \right]/\left( {365{n_y}\Delta T} \right) + {N_{\rm{f}}}\left( {{V_{\rm{d}}} \cdot } \right.\\ \;\;\;\;\;\;\;\left. {{n_{\rm{d}}} + {V_{\rm{m}}}} \right) + {n_{\rm{d}}}{n_{\rm{g}}}{P_{\rm{e}}}\frac{{2{T_{\rm{o}}}}}{{\Delta T}}\left[ {{P_{\rm{t}}}\sum\limits_{k = 2}^n {\left( {\frac{{T_{\rm{a}}^k}}{2} + T_{\rm{c}}^k} \right)} - } \right.\\ \;\;\;\;\;\;\;\left. {{P_{\rm{f}}}\sum\limits_{k = 2}^n {T_{\rm{f}}^k\left( {1 - \delta _{\rm{r}}^k} \right)} } \right]/3\;600 + {V_{\rm{s}}} \cdot {n_{\rm{s}}} \cdot \sum\limits_{i = 1}^n {{\zeta _i}} + \\ \;\;\;\;\;\;\;\left. {\sum\limits_{i = 1}^n {{C_{{{\rm{r}}_i}}}} \cdot {\zeta _i}} \right\}. \end{array} $ | (37) |
式中Co为单位乘客综合交通成本,nd为每日发车次数.
约束条件为
| $ \frac{{{T_{\rm{d}}}}}{{{T_{\rm{R}}}}} \cdot {N_{\rm{f}}} \cdot {C_{\rm{u}}} \ge {Q_{{\rm{total}}}}. $ | (38) |
式中Td为城市轨道交通1 d内的运行时间,Cu为一个列车组的容量.
该约束条件能够保证单日城市轨道交通乘客的出行需求得到满足.
考虑到模拟退火算法在运算过程中,需计算之前解和当前解的目标函数之差,且该算法只能用于求解最小值问题,因此,在模拟退火算法编程中将目标函数转化为基于个人的地铁综合交通成本与上车乘客总量的比值,即
| $ \min Z = \frac{{{C_0}}}{Q}. $ | (39) |
双层优化模型求解的难度表现在两方面:其一,双层模型的非凸性使得优化解一般为局部最优解; 其二,双层规划模型为NP-hard问题,传统寻优方法不再适用.而启发式算法,如遗传算法、蚁群算法、禁忌搜索算法、随机搜索算法和模拟退火算法等适用于解决NP-hard问题.然而,前4类算法求解到的基本为局部最优解,其可能和全局最优解相差较大.而模拟退火算法能跳出局部最优,进而可能得到全局最优解.因此,使用该算法对模型进行求解.
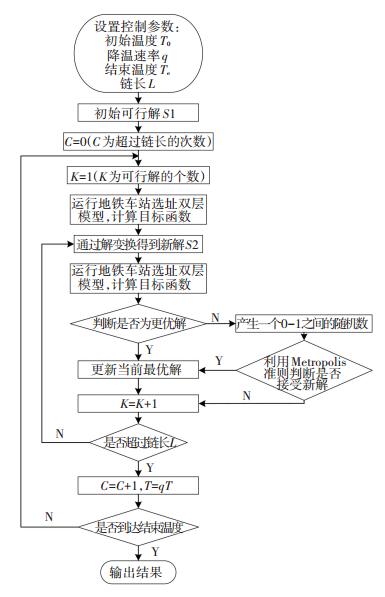
2.2 求解流程如图 1所示为采用模拟退火算法求解车站选址双层模型的基本流程.
|
图 1 基于模拟退火算法的双层车站选址模型求解流程 Fig. 1 Solving process of the bi-level model of stations locating based on simulated annealing algorithm |
模拟退火算法广泛应用于解决组合类问题,通过提高初始温度、改变链长、控制降温速率和调整停止条件等措施,可以改善求解结果.且根据Metropolis准则,其能以某概率接受恶化解的特征,使得该算法能够跳出局部最优.
3 案例分析以哈尔滨地铁1线为例,利用所建立模型对该线路进行重新选址,并将新选址方案和现有车站选址进行对比.
基于ArcGIS10.1,建立了哈尔滨地铁1号线线路、现有车站(由于哈东站和哈南站两个车站主要承担来往火车站的乘客,客流吸引特征与其他车站明显不同,因此,未加以考虑)、车站范围内6类用地性质的建筑的shp文件和乘客步行道路网络数据集,坐标系采用Beijing 1954投影坐标系,并计算了各要素的经纬度.以100 m为间隔设置候选车站,共得到110个候选车站.在ArcGIS环境下,首先基于GWR模块对现有车站上车乘客量进行回归分析,在此基础上,对各候选车站的上车乘客量进行了预测.
3.1 候选车站客流量预测通过乘客出行生成点调查结果,确定使用800 m路网距离作为哈尔滨地铁车站服务范围,其小于经验值800 m欧氏距离.楼层数和用地类型通过百度实景地图获得.表 1所示为通过系数显著性检验和VIF检验所确定的解释变量.需要指出的是,对于哈尔滨地铁1号线,其各车站服务范围内的土地使用多样性和上车乘客量呈负相关,考虑主要原因是当土地使用多样性提高,居民能够在一定范围内满足其生存需求,因此减少了适用于地铁的中远距离出行.
| 表 1 系数显著性及VIF检验结果 Tab. 1 Results of coefficients significance test and VIF test |
基于ArcGIS10.1,运用GWR模型对现有车站的上车乘客量和解释变量进行回归分析,结果显示Adjusted R2为0.81,AIC值为399.01,而基于OLS的多元回归模型其Adjusted R2为0.74,AIC值为399.01.因此,所建立的GWR模型较多元回归模型有更高的解释能力.在此基础上,使用预测模块对候选车站上车乘客量进行预测.表 2为部分车站的预测结果,其中,GWR模型预测结果中的局部R2与一般的全局回归预测模型中的R2有所不同,其一方面能够评价预测结果的优劣,另一方面又能反映模型的稳定性.结果显示,各车站的客流量预测结果的局部R2均在0.9以上,说明预测结果较为理想.
| 表 2 候选车站上车客流量预测结果 Tab. 2 Ridership forecasting results of candidate stations |
参考文献[11-16],对乘客出行成本、乘客出行分布规律、列车运行规律和电机耗电发电参数进行了标定.利用ArcGIS路网分析功能,得到了各候选车站之间的距离和乘客步行距离.由于哈尔滨地铁1号线长度有限,因此,没有考虑候列车上工作人员成本、车队保养成本、站内工作人员成本和列车购置成本的影响.
3.3 求解结果设置模拟退火算法初始温度为50 000、停止温度为100 000,链长为10,降温速率为0.98.在MATLAB R2015a环境下,根据模拟退火算法原理进行编程对模型进行了求解,结果见表 3和图 2~4.
| 表 3 选址结果中的候选车站编号 Tab. 3 Serial numbers of candidate stations in the locating result |
|
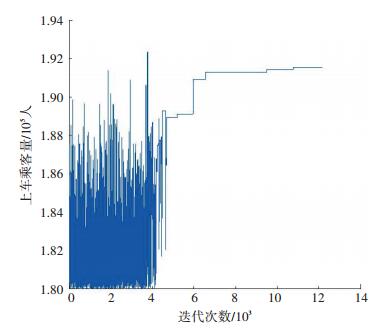
图 2 上车乘客量随迭代次数的变化 Fig. 2 Changes of boardings with iterations |
|
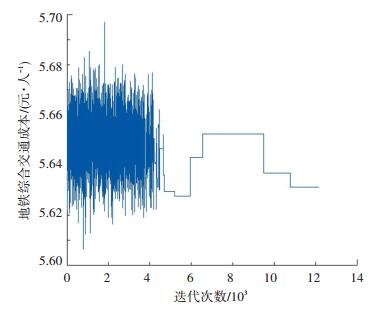
图 3 综合交通成本随迭代次数的变化 Fig. 3 Changes of metro comprehensive cost with iterations |
|
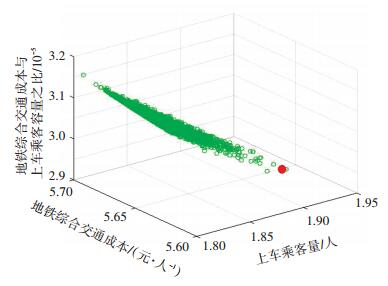
图 4 模拟退火算法解集和最优解 Fig. 4 Solution set and optimal solution of simulated annealing algorithm |
可以看出,在第10 830次迭代运算后,得到了最优车站选址方案.该方案的候选车站编号为3—10—15—19—26—32—36—42—55—61—66—78—82—89—100—108.该候选车站组的上车乘客量之和为191 553人,较现有车站上车乘客量177 010人,增长了14 543人,增长比例为8.2%;牵引能耗成本为15 972元,较现有车站运营成本17 501元,减少了1 529元,减少比例为8.7%.
图 5为新选址方案中各车站上车乘客量和现有车站上车乘客量的比对.可以看出,新选址方案并非每个车站的上车乘客量均大于现有各车站的上车乘客量,其中桦树街车站、烟厂车站、医大一院车站、和兴路车站现有的上车乘客量大于选址优化后的车站上车乘客量.

|
图 5 现有车站选址及优化后的车站选址各车站上车乘客量对比 Fig. 5 Comparison of boardings between the current stations and the optimized stations |
1) 构建了城市轨道交通车站双层选址模型,上层模型以客流量最大为目标,下层模型以综合交通成本最低为目标,给出了基于模拟退火算法的双层车站选址模型求解方法.
2) 考虑车站吸引范围内不同位置建筑单位楼层面积对客流贡献率的影响,和不同解释变量对不同车站客流量影响的差异,建立了基于GWR的客流预测模型,模型预测精度较基于OLS的多元回归模型高.
3) 以哈尔滨为例,运用所建立模型对地铁1号线进行重新选址,结果表明,该双层模型既能够使所选车站的客流量较高,又能使乘客出行成本和运营方成本较少,能够同时保证社会效益和经济效益.
4) 在实际车站选址过程中,还需考虑车站与地面建筑物的关系,尤其是车站对建筑物地下结构稳定性的影响和列车运行对建筑物产生的振动、噪声的影响.此外,还需考虑地下管线和地质水文条件等,下一步研究将对模型进行进一步优化、完善.
| [1] |
TAYLOR B D, MILLER D, ISEKI H, et al. Nature and/or nurture? Analyzing the determinants of transit ridership across US urbanized areas[J]. Transportation Research Part A: Policy & Practice, 2009, 43(1): 60. |
| [2] |
SOHN K, SHIM H. Factors generating boardings atmetro stations in the Seoul metropolitan area[J]. Cities, 2010, 27(5): 358. DOI:10.1016/j.cities.2010.05.001 |
| [3] |
CEDER A, BUTCHER M, WANG L. Optimization of bus stop placement for routes on uneven topography[J]. Transportation Research Part B: Methodological, 2015, 74: 40. DOI:10.1016/j.trb.2015.01.006 |
| [4] |
王芳. 基于出行方式选择的轨道交通站间距确定[J]. 大连交通大学学报, 2011, 32(6): 36. WANG Fang. Spacing determination of rail transit stations based on travel mode choice[J]. Journal of Dalian Jiaotong University, 2011, 32(6): 36. DOI:10.3969/j.issn.1673-9590.2011.06.009 |
| [5] |
贾俊芳, 黄荣松. 基于出行时间最少的市郊铁路合理站间距研究[J]. 交通信息与安全, 2013, 31(5): 74. JIA Junfang, HUANG Rongsong. Minimum travel time-based spacing between suburban railway stations[J]. Journal of Transport Information and Safety, 2013, 31(5): 74. DOI:10.3963/j.issn.1674-4861.2013.05.014 |
| [6] |
左忠义, 赵汉鲲. 城市轨道交通站间距优化研究[J]. 大连交通大学学报, 2014, 35(2): 25. ZUO Zhongyi, ZHAO Hankun. Study on optimal spacing of rail transit station[J]. Journal of Dalian Jiaotong University, 2014, 35(2): 25. DOI:10.3969/j.issn.1673-9590.2014.02.006 |
| [7] |
石瑜.基于GIS的城市地铁站点布设研究[D].石家庄: 石家庄铁道大学, 2014 SHI Yu. Research on the urban metro station layout based on GIS[D]. Shijiazhuang: Shijiazhuang Tiedao University, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10107-1014348369.htm |
| [8] |
ZHAO J, DENG W, SONG Y, et al. Analysis of metro ridership at station level and station-to-station level in Nanjing: an approach based on direct demand models[J]. Transportation, 2014, 41(1): 133. DOI:10.1007/s11116-013-9492-3 |
| [9] |
EWING R, CERVERO R. Travel and the built environment: a meta-analysis[J]. Journal of the American Planning Association, 2010, 76(3): 265. DOI:10.1080/01944361003766766 |
| [10] |
李君, 叶霞飞. 城市轨道交通车站分布方法的研究[J]. 同济大学学报(自然科学版), 2004, 32(8): 1009. LI Jun, YE Xiafei. Studies on distribution of stations of urban mass transit[J]. Journal of Tongji University (Natural Science), 2004, 32(8): 1009. DOI:10.3321/j.issn:0253-374X.2004.08.007 |
| [11] |
秦萍, 陈颖翱, 徐晋涛, 等. 北京居民出行行为分析:时间价值和交通需求弹性估算[J]. 经济地理, 2014, 34(11): 17. QIN Ping, CHEN Ying'ao, XU Jintao, et al. Travel behavior analysis for the residents in Beijing: value of time and travel demand elasticity estimates[J]. Economic Geography, 2014, 34(11): 17. |
| [12] |
鲁钰雯.寒地城市可步行性测度及优化研究[D].哈尔滨: 哈尔滨工业大学, 2017 LU Yuwen.The walkability measurement and optimization study of winter cities[D]. Harbin : Harbin Institute of Technology, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10213-1017738399.htm |
| [13] |
徐威鸿.城市轨道交通系统之复杂网络特征及乘客出行特征研究[D].天津: 天津大学, 2014 XU Weihong. A research on the complex network characteristics of urban railway traffic system and the passenger traffic feature[D]. Tianjin: Tianjin University, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10056-1016188783.htm |
| [14] |
马超云, 毛保华, 梁肖, 等. 地铁列车节能运行惰行控制研究[J]. 交通信息与安全, 2010, 28(2): 37. MA Chaoyun, MAO Baohua, LIANG Xiao, et al. Coast control of urban train movement for energy efficiency[J]. Journal of Transport Information and Safety, 2010, 28(2): 37. DOI:10.3963/j.ISSN1674-4861.2010.02.009 |
| [15] |
杨俭, 李发扬, 宋瑞刚, 等. 城市轨道交通车辆制动能量回收技术现状及研究进展[J]. 铁道学报, 2011, 33(2): 26. YANG Jian, LI Fayang, SONG Ruigang, et al. Review of the utilization of vehicular braking energy in urban railway transportation[J]. Journal of the China Railway Societ, 2011, 33(2): 26. DOI:10.3969/j.issn.1001-8360.2011.02.005 |
| [16] |
尹航, 蒋涛, 张言伟, 等. 列车牵引计算分析及仿真[J]. 大连交通大学学报, 2013, 34(1): 80. YIN Hang, JIANG Tao, ZHANG Yanwei, et al. Analysis and simulation of train traction computation[J]. Journal of Dalian Jiaotong University, 2013, 34(1): 80. DOI:10.3969/j.issn.1673-9590.2013.01.017 |
 2019, Vol. 51
2019, Vol. 51


