2. 江苏省岩土工程技术工程研究中心(河海大学),南京 210098;
3. 浙江省宁波市规划局奉化分局, 浙江 宁波 315500
2. Jiangsu Research Center for Geotechnical Engineering Technology (Hohai University), Nanjing 210098, China;
3. Ningbo Urban and Rural Planning Bureau Fenghua Branch, Ningbo 315500, Zhejiang, China
内涝通常指由于强降水或连续性降水超过城市排水能力致使城市内产生积水灾害的现象[1].一般城市的长时间积水内涝会影响城市交通、城市设施和居民正常生活等.城市内涝风险评估尚处在研究与探索中,内涝灾害风险因子较多,主要包括地面高程、径流系数、排水系统等,而且城市人口居住密度也将与灾害可能造成的损失程度相关联,因此给评估带来了困难.目前内涝程度主要是定性描述,还没有完善的统一的指标体系.内涝程度的评价基本根据积水深度和积水时间(或积水流速)结合经验进行定性的综合评价,不能反映内涝全过程[2].
现有的内涝评估方法和思想主要有历史灾情评估法、情景模拟评估法、指标体系评估法.历史灾情评估法要求有大量历史灾情数据资料,很多城市都难以获得.情景模拟评估法本质就是指标体系评估法,目前已有一系列的水文模拟软件用于内涝灾害情景模拟.较为常用的有SWMM、InfoWorks、GIS、Mike Flood模拟软件[3-7].指标体系评估法是由表征评价对象特点的多个指标构成的有机整体,符合实际情况,目前主要研究重点是风险评价指标体系:文献[8-9]从孕灾环境危险性、承灾体的脆弱性和暴露性3个方面考虑,选取了26个指标构建了英国曼彻斯特市洪水灾害风险评估体系,并借助主成分分析法对曼彻斯特市洪水风险进行了评估,找出了洪水灾害较为严重的区域.文献[10]针对洪水灾害造成的损失,将投影追踪原理与风险指标相结合,提出了一种洪灾风险动态评估模型.该模型采用分析时间数据的评估方法来综合分析评估风险的发展,借助投影追踪理论,应用最优投影矢量计算风险集群式,确认洪水灾害风险水平,并提出局部控制策略.并且以黄山市屯溪区为例,验证模型的准确性,为洪水灾害风险评估提供新的方法.
相比于国外,我国风险评价指标体系的研究也趋于成熟,文献[11]针对我国目前最主要的灾害—洪涝灾害三要素(致灾因子、孕灾环境、承灾体)的作用机理进行了详细的分析,建立了洪灾损失评估模型,并以天津市滨海新区为实例,进行了实际评估与预测.文献[12]在以往洪灾损失评价的基础上,以洪灾损失为核心,建立了洪灾风险评价体系,为洪水管理提供支持,最后结合实际,对评价体系进行了完善.文献[13]从灾害风险表达式出发,概括了洪涝灾害风险评估的内容,并从指标确定及其他角度介绍了洪涝灾害损失评估的内容,为指标体系评估提供指导.文献[14]基于以往内涝灾害风险评估的经验,以北京市为研究对象,构建了基于DEA模型的评价体系,并运用CCR模型对北京市8个城区的内涝风险进行了测度与评价.文献[15]为探究城市洪涝背景下的地区海绵城市潜力评估方法,从海绵城市最具相关的降雨量、水污染、洪涝灾害和生态绿地4个方面展开,构建了海绵城市潜力指标体系.
综合上述已有研究可知,目前的内涝评价方法并不完善.关于内涝程度评价指标,不同学者提出了不同的评价方法和评价指标,还没有形成一个统一的评价体系[16],且大部分研究对象是某个城市或者区域.为了克服不完善的内涝评价指标体系,获得能反映内涝全过程特征的评价方法,本文基于内涝势冲量,提出了一种海绵城市内涝程度评价方法.
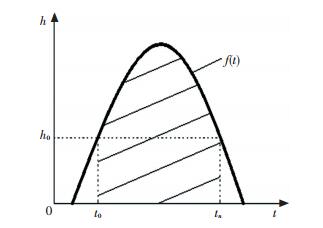
1 基于内涝势冲量的海绵城市内涝程度评价方法 1.1 局部内涝综合指标根据强降雨或连续降雨特点,一般道路或小区积水深度历时曲线如图 1所示,根据规范,当积水深度大于某一值h0(节点根据本地区的历史数据综合考虑给出)时,定义为内涝.因此内涝历时曲线能很好地反映该道路或小区处的内涝严重程度,内涝深度越大、内涝时间越长则内涝越严重.定义图中阴影部分面积, 即内涝曲线与横坐标轴围成的面积为内涝势冲量,阴影部分面积越大则内涝势冲量越大,内涝也越严重.
|
图 1 一般道路或小区积水深度历时曲线 Fig. 1 Duration curve of water depth in general roads or communities |
局部节点的内涝势冲量公式为
| $ \mathit{\Omega } = \int_{{t_0}}^{{t_n}} {f\left( t \right){\rm{d}}t} . $ | (1) |
式中:t0为内涝深度为h0的起始时刻,hn为内涝深度为h0的终止时刻,f(t)为内涝深度历时曲线,t为内涝时长.
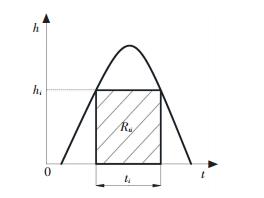
实际内涝深度的历时曲线很复杂,也很难通过积分获得该值,因此根据内涝势冲量特点,建立在某一内涝深度hi时对应的阴影矩形面积为局部节点的内涝程度瞬时指标,如图 2所示,针对某一内涝深度hi,其内涝深度超过hi的持续时长为ti,定义该深度对应时长形成的矩形面积hiti为该点内涝深度为hi的内涝程度瞬时指标,该局部节点的内涝程度瞬时指标RT计算公式为
| $ {R_{\rm{T}}} = {h_i} \cdot {t_i}. $ | (2) |
|
图 2 局部节点的内涝程度瞬时指标示意图 Fig. 2 Diagram of instantaneous index of waterlogging degree of local nodes |
式中hi为内涝深度,ti为内涝深度超过hi的内涝时长.
为了使评价指标更科学,采用无量纲化方法,评价指标值无量纲化后可以更客观地进行评价和运用,无量纲化的局部节点内涝程度瞬时指标RT′计算公式为
| $ {{R'}_{\rm{T}}} = \frac{{{h_i}}}{{h_0^ * }} \cdot \frac{{{t_i}}}{{t_0^ * }}. $ | (3) |
其中h0*为内涝深度基准值,没有特殊要求时,可以根据《城镇内涝防治技术规范》[17]取15 cm,t0*没有特殊要求时,可以取下雨时长.
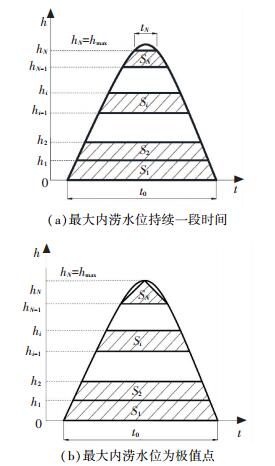
局部内涝瞬时指标计算值只是反映了在该内涝深度下内涝势冲量,不能反映内涝全过程,因此采用梯形面积总和近似内涝全过程的内涝势冲量,(值的大小等于内涝曲线与横轴围成的面积),理论上只要取足够多的内涝瞬时点,误差可趋于无穷小,如图 3所示.根据某内涝点内涝全过程曲线,将最大的内涝深度hmax等分为N份,每份高为Δh,有
| $ \Delta h = \frac{{{h_{\max }}}}{N} = {h_1} - {h_0} = {h_i} - {h_{i - 1}} = \cdots = {h_{N + 1}} - {h_N}, $ | (4) |
|
图 3 内涝全过程的内涝势冲量示意图 Fig. 3 Diagramabout the momentum of waterlogging potential energy of the whole process of waterlogging |
式中i=1, 2, …, N.
采用梯形面积总和近似等于内涝全过程的内涝势冲量,理论上当N趋于无穷大时,内涝水深hi-1和hi在内涝曲线内部围成的梯形面积Si之和趋于内涝曲线构成的内涝势冲量理论值,节点内涝势冲量近似计算公式为
| $ {S_i} = \frac{1}{2}\left( {{h_i} - {h_{i - 1}}} \right)\left( {{t_i} + {t_{i - 1}}} \right),i = 1,2, \cdots ,N. $ | (5) |
因此局部内涝综合指标S#的计算公式近似为
| $ {S^\# } \approx \sum\limits_{i = 1}^N {{S_i}} = \frac{1}{2}\Delta h\left( {{t_0} + {t_N}} \right) + \Delta h \cdot \sum\limits_{i = 1}^{N - 1} {{t_i}} . $ | (6) |
采用无量纲法,定义内涝势冲量为局部内涝综合指标,即
| $ {{S'}_i} = \frac{1}{2}\left( {\frac{{{h_i} - {h_{i - 1}}}}{{h_0^ * }}} \right)\left( {\frac{{{t_i} + {t_{i - 1}}}}{{t_0^ * }}} \right). $ | (7) |
则有无量纲化的局部内涝综合指标RS′为
| $ {{R'}_{\rm{S}}} = \sum\limits_{i = 1}^N {{{S'}_i}} = \frac{1}{2}\frac{{\Delta h}}{{h_0^ * }}\left( {\frac{{{t_0} + {t_N}}}{{t_0^ * }}} \right) + \frac{{\Delta h}}{{h_0^ * }} \times \sum\limits_{i = 1}^{N - 1} {\frac{{{t_i}}}{{t_0^ * }}} . $ | (8) |
根据规范,一般内涝深度大于h0*,内涝时长大于t0*时,定义为内涝(特殊情况也可以取设计需要的h0*和t0*),因此局部内涝综合指标的计算值越大,内涝越严重,按此建立的局部内涝指标概念清晰,并采用无量纲量,容易判断和推广.
1.2 整体内涝综合指标本文建立的内涝势冲量能有效反映内涝全过程的影响,基于内涝势冲量概念构建的内涝程度指标体系能很好反映强降雨过程中城市内涝程度.对于整个区域而言,基于建立的局部内涝点指标体系,建立整体内涝指标,整体内涝程度采用节点内涝程度相对于子汇水区面积的加权平均值和变异系数表示,变异系数描述设计排水条件下内涝局部点之间的内涝局部差异程度,变异系数越大,说明有局部的内涝特别严重应进行重新设计,具体计算方法如下:
假设整体区域有M个点,从整体看,内涝点的程度与内涝的面积也有关,因此建立内涝点整体指标标准值Rj,计算公式为
| $ {R_j} = \frac{{{S_j}}}{{{S_{{\rm{all}}}}}} \times {\left( {{{R'}_{\rm{S}}}} \right)_j}. $ | (9) |
其中:j=1, 2, …, M; Sj为节点j汇水区面积; Sall为总汇水区面积;
因此整体区域内涝实际值为
| $ {R^ * } = \sum\limits_{j = 1}^M {{R_j}} . $ | (10) |
整体区域内涝指标标准值为
| $ \bar R = \frac{{{R^ * }}}{M}. $ | (11) |
整体内涝指标的标准差为
| $ \sigma = \sqrt {\frac{1}{{M - 1}}} \cdot \sqrt {\sum\limits_{j = 1}^M {{{\left( {{R_j} - \bar R} \right)}^2}} } . $ | (12) |
整体内涝指标的变异系数为
| $ {C_{\rm{v}}} = \frac{\sigma }{{\bar R}} \times 100\% . $ | (13) |
平均值反映了整体区域的内涝严重程度,标准差和变异系数反映了内涝的局部分配不均匀性,采用这两个指标进行内涝评价规划更科学,可以为海绵城市规划设计提供优化依据.
2 奉化区中交未来城内涝过程数值模拟 2.1 研究区概况此次规划建设宁波市中交未来城地处奉化区北,规划区域位于剡江、东江之间,县江横穿其中,地势低,历年来常受洪涝灾害影响,属于宁波市奉化区的滞洪区.属亚热带季风性气候,四季分明,温和湿润,降水量1 350~1 600 mm.台风洪涝是主要自然灾害之一.
中交未来城现状用地如图 4所示,由于中交未来城具有“滞洪区”、雨量大的特点,因此内涝问题是中交未来城规划必须克服的难题,有必要利用海绵城市规划理念和方法对规划后的内涝情况进行分析,为设计优化提供指导.

|
图 4 中交未来城现状用地图 Fig. 4 Current situation of land use of Zhongjiao Future City |
SWMM模型是一个目前广泛应用于城市暴雨径流水量、水质的模拟以及洪涝灾害预报的模型,用来模拟研究城市的降雨径流和污染物的运动过程,包括地表径流和排水管网中的水流,雨洪调蓄过程以及水质的评价影响[18].本文根据图 4规划用地性质构建雨洪分析数值模型.
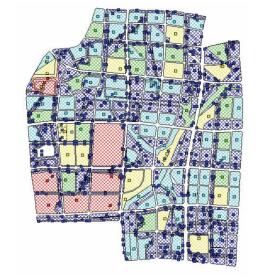
区域内排水管网主要沿主干道路铺设,子流域产生的径流就近排入管网.根据雨水管网、地形、地貌等资料,将研究区概化成1 072个子汇水区域,如图 5所示,共有315条管段、322个管网节点、3个管网末端排放口,如图 6所示.排水管道总长度为161 401.32 m,两节点间管道长度在20~550 m之间.
|
图 5 中交未来城子汇水区概化图 Fig. 5 Generalized map of subcatchment of Zhongjiao Future City |

|
图 6 SWMM中的节点和管网概化图 Fig. 6 Generalized map of nodes and conduits network of SWMM |
1) 子汇水区参数设置.子汇水区的面积大小、漫流宽度、平均坡度、检查井底标高等信息根据规划资料确定,子汇水区的曼宁系数、洼蓄深、不透水区中无洼不透水面积比例等参数按经验取值[19]:商业区、住宅区和其余地块的不渗透性分别取0.95、0.7、0.65;透水区和不透水区的曼宁粗糙系数分别取0.24、0.001 2;透水区和不透水区的洼蓄深分别取5 mm和3 mm; 不透水区中无洼不透水面积比取50%.另外,子汇水区的渗透模型采用霍顿模型,相应的霍顿参数:最大下渗率、最小下渗率、渗透衰减系数分别取76.1 mm/h、3.35 mm/h、3.5 h-1.管道粗糙系数根据材质取0.013.
2) LID措施及其参数.为了有效改善区域生态环境,提高水资源利用率,涵养地下水,在该区域添加LID措施.根据规划资料,LID措施主要有3种:下凹式绿地、绿色屋顶、透水铺装.根据规划,用地为景观绿地、公园绿地性质的子汇水区设置为下凹式绿地; 根据规划,针对商业用地和居住用地设置绿色屋顶; 透水铺装根据规划,取次干道和公共交通场站用地进行设置.布设的下凹式绿地面积为1.68 hm2,滞蓄深度为100 mm; 绿色屋顶的布设总面积为1.24 hm2,排水垫层的厚度为200 mm,孔隙比为0.5,糙率为0.15;透水铺装的面积为1.47 hm2,路面层的厚度为200 mm,孔隙比为0.2,渗透性为0.01;其余的参数参照海绵城市设计指南和相关工程实例[20-23].
2.4 奉化区降雨历时曲线短历时暴雨强度公式采用奉化区水利局统计计算公式, 即
| $ q = \frac{{799.935\left( {1 + 0.75\lg P} \right)}}{{{{\left( {t + 2.08} \right)}^{0.508}}}}. $ | (14) |
式中:q为暴雨强度,L/(s·hm2); t为降雨历时,min; P为重现期,a.
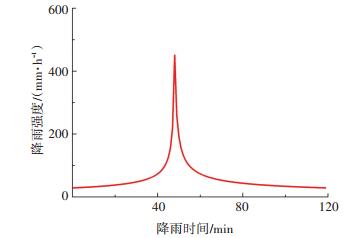
降雨设计历时取120 min,时间间隔为1 min,雨峰相对位置r取0.4.主要分析100 a一遇工况,降雨过程线如图 7所示.
|
图 7 设计降雨过程线 Fig. 7 Process line of design rainfall |
根据建立的中交未来城LID海绵城市数学模型,分析100 a一遇2 h设计标准强暴雨下,局部节点的内涝过程,并利用基于内涝势冲量的海绵城市内涝程度评价方法对模型的内涝情况进行详细的分析评价.
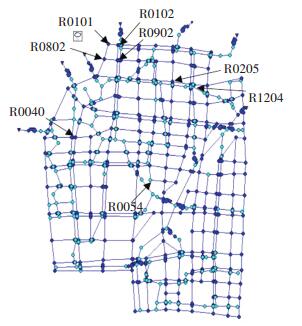
3.1 100 a一遇2 h降雨情况下局部节点内涝过程分析从模拟结果显示,主要有8个节点出现内涝险情,出现严重内涝节点的具体分布如图 8所示,可以发现内涝节点多分布于规划用地的西北区域,即县江上游区域.
|
图 8 模型中内涝严重节点的示意图 Fig. 8 Diagram of severe waterlogging nodes in the model |
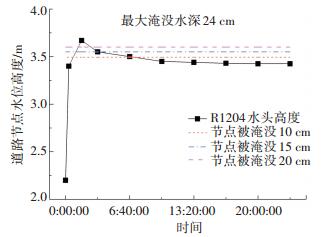
其中节点R1204内涝最严重,其历时过程曲线如图 9,内涝最大深度为3.675 m,路面顶高程为3.425 m,因此内涝最大深度hmax为25 cm(3.675-3.425 = 0.25),将hmax等分为5份,每份高Δh=5 cm.发生内涝的总时间为180 min,内涝5 cm以上持续时间169 min,内涝10 cm以上持续时间108 min,内涝15 cm以上持续时间40 min,内涝20 cm以上持续时间16 min.
|
图 9 节点R1204的内涝历时曲线 Fig. 9 Flood duration curve of node R1204 |
将内涝深度hi=5、10、15、20 cm以及分别对应的内涝时长ti=169、108、40、16 min代入式(3)进行计算,其中h0*根据城镇内涝防治技术规范[17]取15 cm,t0*取降雨时长120 min.通过计算可以得出在100 a一遇2 h降雨情况,R1204在内涝深度5、10、15、20 cm情况下的局部内涝程度瞬时指标分别0.47、0.60、0.33、0.18.
将Δh、hi、ti、h0*、t0*等值代入式(8)进行计算,可得到R1204的局部内涝程度综合指标为0.96.
R1204所对应的子汇水区面积为14.363 6 m2, 内涝节点所对应的的汇水区面积之和为67.612 8 m2,将数据代入式(9)~(11),可计算得出节点R1204整体内涝指标标准值为0.242.
3.2 基于内涝势冲量的内涝程度评价方法对中交未来城内涝程度的评价采用3.1节所介绍的方法,对8个内涝点分别计算其局部内涝程度瞬时指标、局部内涝程度综合指标、整体内涝指标标准值,结果见表 1,其中RT′为无量纲化的局部内涝程度瞬时指标,RS′为无量纲化的局部内涝程度综合指标,
| 表 1 100 a一遇2 h强降雨内涝程度综合指标计算分析 Tab. 1 Calculation and analysis of comprehensive index of waterlogging degree of once-in-a-century heavy rainfall in 2 hours |
根据表 1显示,针对节点R0054和节点R0902,R0054处内涝5 cm时间为183 min,比R0902处长8 min,但R0054处最大内涝深度超过20 cm的持续时间只有2 min,而R0902内涝深度20 cm以上达到10 min,比R0054处长8 min.可以认为R0902的内涝程度比R0054严重.若仅采用某一内涝深度对应的内涝时长这样的瞬时指标来评价节点的内涝程度是不合理的,因为没有考虑时间尺度上的分布,而采用局部内涝综合指标则能在整个降雨历时过程中对节点的内涝程度进行综合评价,该指标将不同内涝深度所对应的内涝时间用冲量的形式进行累加,最终得到的指标值能综合反映该点的内涝过程的特征.前文中提到的R0902的内涝综合指标值为1.160,而R0054的内涝综合指标值为1.138,说明R0902的内涝程度比R0054更加严重,这也与前面的理论分析结果一致.
内涝点整体指标标准值是考虑了断面对应汇水区面积的内涝程度相对值,对于局部内涝点综合指标相近的节点,由于所对应的汇水区面积不相同,因此内涝点整体指标标准值也不同.如R0054、R1204的内涝点综合指标值分别为1.138、1.139,数值接近,而R0054对应汇水区面积为10.046 5 m2,R1204对应的汇水区面积为14.363 6 m2,大于R0054对应的子汇水区面,因此可以认为节点R1204的内涝程度比R0054要严重.而R0054整体指标标准值为0.169,小于R1204对应的整体指标标准值0.242,所以内涝整体指标可以反映内涝点对应的汇水区面积大小对整体内涝程度评价的影响.
目前的内涝点内涝程度评价一般采用国外常用的洪水风险评价标准,主要考虑洪水淹没深度和流速来进行风险程度评估,并以某一深度的瞬时指标来衡量,本质是本文提出的局部内涝瞬时指标,但是这类标准并不能反映内涝的历时全过程,因此没有本评价方法科学.
4 结论1) 针对内涝点空间与历时过程特点,提出了内涝势冲量的概念,基于内涝势冲量,建立了城市局部内涝瞬时指标、局部内涝综合指标、区域整体内涝指标标准值等组成的评价城市内涝程度的指标体系及其具体计算分析方法,该指标体系计算概念明确,计算方法简洁明了,能够快速准确的对内涝程度进行评价.
2) 内涝综合指标将整个降雨历时过程的不同内涝深度和对应的内涝时间用冲量的形式进行累加,与实际情况相符,更能综合反映节点的内涝过程特征.
3) 内涝点整体指标标准值是考虑了断面对应汇水区面积的内涝程度相对值,同时该指标也反映了内涝点对应的汇水区面积大小对整体内涝程度评价的影响,能够真实反映节点内涝情况.通过奉化区中交未来城实际工程,验证了评价方法的合理性.所提出的内涝程度评价方法无论从参数选取还是计算结果与真实案例的对比都更加符合实际情况,在城市规划设计中可供参考.
| [1] |
张炜, 李思敏, 时真男. 我国城市暴雨内涝的成因及其应对策略[J]. 自然灾害学报, 2012, 21(5): 180. ZHANG Wei, LI Simin, SHI Zhennan. Formation causes and coping strategies of urban rainstorm waterlogging in China[J]. Journal of Nature Disasters, 2012, 21(5): 180. |
| [2] |
李保建, 詹健. 基于SWMM模型的南昌市青山湖片区雨洪模拟研究[J]. 工业用水与废水, 2017, 48(5): 33. LI Baojian, ZHAN Jian. Simulation study on rainfall flood of Qingshan Lake area in Nanchang by SWMM model[J]. Industrial Water & Wastewater, 2017, 48(5): 33. DOI:10.3969/j.issn.1009-2455.2017.05.008 |
| [3] |
SUN N, HALL M, HONG B, et al. Impact of SWMM catchment discretization: case study in Syracuse, New York[J]. Journal of Hydrologic Engineering, 2014, 19(1): 223. DOI:10.1061/(ASCE)HE.1943-5584.0000777 |
| [4] |
GIRONAS J, ROESNER L A, ROSSMAN L A, et al. A new applications manual for the storm water management model (SWMM)[J]. Environmental Modelling & Software, 2010, 25(6): 813. |
| [5] |
RUBINATO M, SHUCKSMITH J, SAUL A J, et al. Comparison between InfoWorks hydraulic results and a physical model of an urban drainage system[J]. Water Science & Technology: A Journal of the International Association on Water Pollution Research, 2013, 68(2): 372. |
| [6] |
韩敏, 赵耀.基于MIKE FLOOD和ArcObjects的洪水淹没模拟及可视化[C]//第27届中国控制会议.北京: 北京航空航天大学出版社, 2008 HAN Min, ZHAO Yao. Simulation and visualization of flood submergence based on MIKE FLOOD and ArcObjects[C]//The 27th Chinese Control Conference (International). Beijing: Beihang University Press, 2008 |
| [7] |
PHONG T, RAJIB S, GUILLAUME C, et al. GIS and local knowledge in disaster management: a case study of flood risk mapping in Viet Nam[J]. Disasters, 2010, 33(1): 152. |
| [8] |
XIAO F, MCCALLEY J D. Power system risk assessment and control in a multiobjective framework[J]. IEEE Transactions on Power Systems, 2009, 24(1): 78. DOI:10.1109/TPWRS.2008.2004823 |
| [9] |
ALEKSANDRE K, GINA C. Surface water flooding risk to urban communities: analysis of vulnerability, hazard and exposure[J]. Landscape & Urban Planning, 2011, 103(2): 185. |
| [10] |
ZHAO J, JIN J, GUO Q, et al. Dynamic risk assessment model for flood disaster on a projection pursuit cluster and its application[J]. Stochastic Environmental Research & Risk Assessment, 2014, 28(8): 2175. |
| [11] |
冯平, 崔广涛, 钟昀. 城市洪涝灾害直接经济损失的评估与预测[J]. 水利学报, 2001, 32(8): 64. FENG Ping, CUI Guangtao, ZHONG Yun. On the evaluation and prediction of urban flood economic loss[J]. Journal of Hydraulic Engineering, 2001, 32(8): 64. DOI:10.3321/j.issn:0559-9350.2001.08.012 |
| [12] |
付意成, 魏传江, 王启猛, 等. 区域洪灾风险评价体系研究[J]. 灾害学, 2009, 24(3): 27. FU Yicheng, WEI Chuanjiang, WANG Qimeng, et al. Study on regional flood risk assessment system[J]. Journal of Catastrophology, 2009, 24(3): 27. DOI:10.3969/j.issn.1000-811X.2009.03.006 |
| [13] |
葛鹏, 岳贤平. 洪涝灾害评估研究综述[J]. 南通大学学报(自然科学版), 2012, 11(4): 68. GE Peng, YUE Xianping. Review on assessment of flood and waterlogging disaster[J]. Journal of Nantong University (Natural Science Edition), 2012, 11(4): 68. DOI:10.3969/j.issn.1673-2340.2012.04.014 |
| [14] |
朱文军.北京城区内涝风险评估及控制研究[D].西安: 西安理工大学, 2012 ZHU Wenjun. The risk assessment of waterlogging and the suggestion of management in Beijing city[D]. Xi'an: Xi'an University of Technology, 2012 http://d.wanfangdata.com.cn/Thesis/Y2117693 |
| [15] |
王志杰, 周平, 刘川昆, 等. 海绵城市潜力评估方法及地下排水系统[J]. 哈尔滨工业大学学报, 2018, 50(3): 118. WANG Zhijie, ZHOU Ping, LIU Chuankun, et al. A potential evaluating methods of sponge city and on the underground drainage system[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 118. |
| [16] |
糜宁.小尺度区域内涝风险评价指标体系研究—以湖北郧县老城区为例[D].武汉: 武汉科技大学, 2016 MI Ning. Study of waterlogging risk assessment system in small-scale region—the old city in Yunyang County of Hubei Province as an example[D]. Wuhan: Wuhan University of Science and Technology, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10488-1016101031.htm |
| [17] |
城镇内涝防治技术规范: GB 51222—2017[S].北京: 中国计划出版社, 2017 Technical code for urban flooding prevention and control: GB 51222—2017[S]. Beijing: China Planning Press, 2017 |
| [18] |
余嵘, 赵丹, 刘渊博, 等. SWMM模型中不同LID措施在排水系统模拟中的应用[J]. 中国农村水利水电, 2016(1): 35. YU Rong, ZHAO Dan, LIU Yuanbo, et al. The application of different LID measures of SWMM model in the drainage system in simulation[J]. China Rural Water and Hydropower, 2016(1): 35. DOI:10.3969/j.issn.1007-2284.2016.01.008 |
| [19] |
DIETZ M E, CLAUSEN J C. Stormwater runoff and export changes with development in a traditional and low impact subdivision[J]. Journal of Environmental Management, 2008, 87(4): 560. DOI:10.1016/j.jenvman.2007.03.026 |
| [20] |
HUBER W C, SINGH V P. EPA storm water management model-SWMM[J]. Computer Models of Watershed Hydrology, 1995, 22: 783. |
| [21] |
许萍, 何俊超, 任心欣, 等. 基于SWMM模型的城市道路LID设施设计参数优化研究[J]. 水电能源科学, 2016, 34(2): 21. XU Ping, HE Junchao, REN Xinxin, et al. Optimization of LID design parameters of urban road based on SWMM model[J]. Water Resource and Power, 2016, 34(2): 21. |
| [22] |
张少钦, 吴珊, 李俊. 全局敏感性分析在LID措施选择中的应用研究[J]. 中国给水排水, 2017, 33(19): 125. ZHANG Shaoqin, WU Shan, LI Jun. Application of global sensitivity analysis in selection of LID measures[J]. China Water & Wastewater, 2017, 33(19): 125. |
| [23] |
BEDAN E S, CLAUSEN J C. Stormwater runoff quality and quantity from traditional and low impact development watersheds[J]. JAWRA Journal of the American Water Resources Association, 2010, 45(4): 11. |
 2019, Vol. 51
2019, Vol. 51


