随着陆地资源的减少,海洋资源的探测是21世纪的主要任务,水下航行器是探测海洋资源的主要工具,由于海底环境的复杂性,对航行器提出了高灵活性和可控性能好的要求[1-4].目前国内外大多数水下航行器采用以下几种方式:1)多推进器分布式布局.在航行器上的不同位置安装多个推进器来实现航行器的多自由度操纵运动,可以实现转向和俯仰的姿态调整,可操作性高,运动灵活,因而被广泛应用于机动性要求较高的水下航行器.例如瑞典萨伯公司推出的“双头鹰”水下排雷机器人,能够在零速度和后退运动时实现全向可控,但是有些螺旋桨推进器只有在航行器转向时才启用,平时大多闲置,造成了机构资源的浪费,而且破坏了航行器结构的完整性,增大了水下航行的阻力[5-6].2)矢量喷水推进系统.这种方法通过改变喷水推进器的高速射流方向来改变推力方向,融合了喷水式推进器和推力矢量技术的双重优点,该方法虽有推力损失,但结构简单、易于实现.如新西兰Hamilton公司和瑞典Kamewa公司的各型喷水推进装置[7],其控制主要是通过倒车导向装置和操舵导管的控制,产生不同方向水流的推力,从而使舰艇实现转向、俯仰等运动和姿态[8],但这种系统多用于低自由度的装置,对于高自由度的AUV具有一定技术上的难度,尚无法大量应用[9].3)矢量螺旋桨推进系统.采用单个螺旋桨,通过改变推进器的方向来改变推力方向,从而实现矢量推进.如Cavallo等[10-11]提出的一种基于空间连杆—万向节的全偏转式矢量推进装置;国内中船重工701所也提出了一种类似的全偏转式单回转体矢量推进系统[12-13],这种结构存在自由度冗余,控制相对复杂;山东大学利用3-RRR球面并联机构搭载螺旋桨实现水下机器人的矢量推进[14-15],华中科技大学利用3RPS并联机构,通过液压驱动实现了推进器姿态的矢量调整[16],天津大学在三杆球面机构的基础上进行改进,对一款两自由度并联矢量推进器的运动学、动力学进行了相关理论分析,验证了该型推进器的可行性[17].这3款推进器均采用了作动器外置方式,对推进装置的密封性提出了较高的要求.
基于上述各类水下航行器结构的优缺点,本文提出了一种两自由度、刚度性能良好[18]、作动器可内置、结构简单的矢量推进机构,降低了航行器对水下密封、耐压以及电气性能的要求.通过改变2个移动驱动构件的位置,即可实现AUV尾部螺旋桨的两自由度姿态调整,从而改变推力的方向,实现AUV航向角和俯仰角的快速调整.
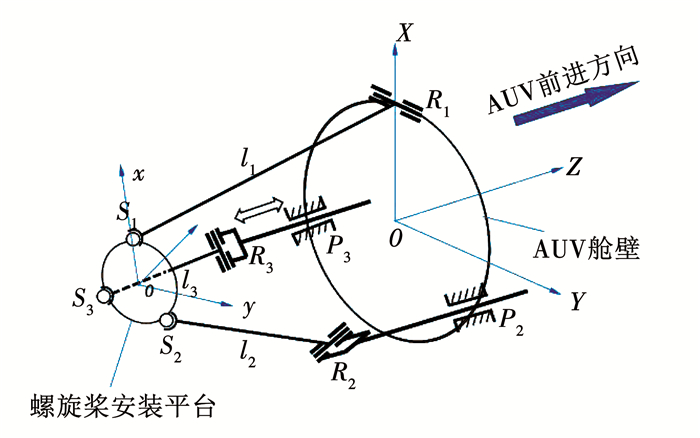
1 矢量推进机构的结构设计为实现螺旋桨的两自由度姿态(俯仰角和航向角)调整,采用如图 1所示的两自由度并联式机构.机构由AUV舱壁通过2条驱动分支(P2R2S2和P3R3S3)、1条从动分支(R1S1),连接螺旋桨的安装平台,其中P、R、S分别为移动副、转动副、球铰,R1S1为定长杆,与转动副R1的轴线垂直,杆长为l1,R2S2和R3S3为定长杆,分别与转动副R2和R3的轴线垂直,杆长相同,分别为l2、l3.为方便运动学分析,建立舱壁坐标系S{O-XYZ},下文简称S系,以舱壁几何中心为坐标系原点,转动副R1(轴线平行于Y轴)、移动副P2和P3(移动方向平行于Z轴),分别以O点为圆心,120°均布,坐标依次为:
| $ \mathit{\boldsymbol{P}}_{R1}^S = {\left[ {R,0,0} \right]^{\rm{T}}}, $ |
| $ \mathit{\boldsymbol{P}}_{R2}^S = {\left[ { - R/2,\sqrt 3 R/2,0} \right]^{\rm{T}}}, $ |
| $ \mathit{\boldsymbol{P}}_{R3}^S = {\left[ { - R/2, - \sqrt 3 R/2,0} \right]^{\rm{T}}}, $ |
|
图 1 两自由度并联式矢量推进机构 Fig. 1 2-DOF parallel vector propulsion mechanism |
式中R为转动副和移动副的分布半径.
建立螺旋桨安装平台坐标系M{o-xyz},下文简称M系,以安装平台中心为坐标系原点,球铰S1,S2和S3分别以o点为圆心,120°均布,坐标依次为:
| $ \mathit{\boldsymbol{P}}_{S1}^M = {\left[ {r,0,0} \right]^{\rm{T}}}, $ |
| $ \mathit{\boldsymbol{P}}_{S2}^M = {\left[ { - r/2,\sqrt 3 r/2,0} \right]^{\rm{T}}}, $ |
| $ \mathit{\boldsymbol{P}}_{S3}^M = {\left[ { - r/2, - \sqrt 3 r/2,0} \right]^{\rm{T}}}, $ |
式中r为球铰分布半径.
作为矢量推进机构,该机构的驱动关节仅为移动副P2和P3,可由位于AUV舱壁内侧的执行系统控制,提供螺旋桨两自由度姿态运动,同时避免了作动器外置于恶劣的海水环境中.
2 推进机构的运动参数分析由于螺旋桨安装平台的运动参数较多且参数之间存在运动耦合,需先进行运动参数间的解耦.
为了方便描述推进机构螺旋桨安装平台M系的姿态,采用Eular姿态角表示,从舱壁坐标系S系重合的初始姿态出发,经过如下旋转次序:
1) 首先绕M系的z轴旋转角度α;
2) 然后绕M系的y轴旋转角度β;
3) 最后再次绕M系的z轴旋转角度γ.
其旋转矩阵为
| $ {\mathit{\boldsymbol{T}}_{SM}} = \left[ {\begin{array}{*{20}{c}} {\cos \alpha \cos \beta \cos \gamma - \sin \alpha \sin \gamma }&{ - \cos \alpha \cos \beta \sin \gamma - \sin\alpha \cos\gamma }&{\cos \alpha \sin \beta }\\ {\sin \alpha \cos \beta \cos \gamma + \cos \alpha \sin \gamma }&{ - \sin \alpha \cos \beta \sin \gamma + \cos \alpha \cos \gamma }&{\sin \alpha \sin \beta }\\ { - \sin \beta \cos \gamma }&{\sin \beta \sin \gamma }&{\cos \beta } \end{array}} \right]. $ | (1) |
式中:α为进动角,为M系的z轴在S系的XOY平面内的投影与x轴的夹角,表示螺旋桨安装平台相对于S系摆动的方位角;β为章动角,为M系z轴与S系z轴之间的夹角,表示安装平台相对于S系,在进动角α方向上的倾斜角度;γ为自旋角,为安装平台绕其z轴作自旋运动的角度,由于前后两次分别绕z轴旋转了α和γ,故安装平台绕z轴的旋转角度为φ=α+γ.
设安装平台M系原点在舱壁S系中的坐标为(xo, yo, zo)T,则螺旋桨安装平台的3个球铰在舱壁坐标系中的空间坐标依次为
| $ \mathit{\boldsymbol{P}}_{Si}^S = {\mathit{\boldsymbol{T}}_{SM}} \cdot \mathit{\boldsymbol{P}}_{Si}^M + {\left[ {{x_o},{y_o},{z_o}} \right]^{\rm{T}}}, $ | (2) |
其中:
| $ \mathit{\boldsymbol{P}}_{S1}^S = \left[ {\begin{array}{*{20}{c}} {r\left( {\cos \alpha \cos \beta \cos \gamma - \sin \alpha \sin \gamma } \right) + {x_o}}\\ {r\left( {\sin \alpha \cos \beta \cos \gamma + \cos \alpha \sin \gamma } \right) + {y_o}}\\ { - r\sin \beta \cos \gamma + {z_o}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{P}}_{S2}^S = \left[ {\begin{array}{*{20}{c}} { - \left( {r/2} \right)\left( {\cos \alpha \cos \beta \cos \gamma - \sin \alpha \sin \gamma } \right) + \left( {\sqrt 3 r/2} \right)\left( { - \cos \alpha \cos \beta \sin \gamma - \sin\alpha \cos\gamma } \right) + {x_o}}\\ { - \left( {r/2} \right)\left( {\sin \alpha \cos \beta \cos \gamma + \cos \alpha \sin \gamma } \right) + \left( {\sqrt 3 r/2} \right)\left( { - \sin \alpha \cos \beta \sin \gamma + \cos \alpha \cos \gamma } \right) + {y_o}}\\ {\left( {r/2} \right)\sin \beta \cos \gamma + \left( {\sqrt 3 r/2} \right)\sin \beta \sin \gamma + {z_o}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{P}}_{S3}^S = \left[ {\begin{array}{*{20}{c}} { - \left( {r/2} \right)\left( {\cos \alpha \cos \beta \cos \gamma - \sin \alpha \sin \gamma } \right) - \left( {\sqrt 3 r/2} \right)\left( { - \cos \alpha \cos \beta \sin \gamma - \sin\alpha \cos\gamma } \right) + {x_o}}\\ { - \left( {r/2} \right)\left( {\sin \alpha \cos \beta \cos \gamma + \cos \alpha \sin \gamma } \right) - \left( {\sqrt 3 r/2} \right)\left( { - \sin \alpha \cos \beta \sin \gamma + \cos \alpha \cos \gamma } \right) + {y_o}}\\ {\left( {r/2} \right)\sin \beta \cos \gamma - \left( {\sqrt 3 r/2} \right)\sin \beta \sin \gamma + {z_o}} \end{array}} \right]. $ |
受转动副R1,R2,R3的约束,3个球铰分别在S系的Y=0、
| $ \mathit{\boldsymbol{P}}_{S1}^S\left( 2 \right) = 0. $ | (3) |
| $ \mathit{\boldsymbol{P}}_{S2}^S\left( 2 \right) = - \sqrt 3 P_{S2}^S\left( 1 \right), $ | (4) |
| $ \mathit{\boldsymbol{P}}_{S3}^S\left( 2 \right) = \sqrt 3 P_{S3}^S\left( 1 \right), $ | (5) |
式(4)、(5)相减,可得
| $ 2{x_o} = r\left( {c\alpha c\beta c\gamma - s\alpha s\gamma + s\alpha c\beta s\gamma - c\alpha c\gamma } \right), $ | (6) |
其中:c=cos,s=sin,文中下同.式(4)、(5)相加,可得
| $ 2{y_o} = r\left( { - 2s\alpha c\beta c\gamma - 2c\alpha s\gamma } \right). $ | (7) |
将式(3)带入式(7),得到:
| $ c\beta \left( {3c\alpha s\gamma + s\alpha c\gamma } \right) + 3s\alpha c\gamma = c\beta \left( { - 2s\alpha c\gamma } \right) - 3c\alpha s\gamma . $ |
可以推导出对于任意一章动角β,需要满足:
| $ \left\{ \begin{array}{l} 3\cos \alpha \sin \gamma = - 3\sin \alpha \cos \gamma ,\\ 3\sin \alpha \cos \gamma = - 3\cos \alpha \sin \gamma , \end{array} \right. $ |
即
| $ \gamma = - \alpha . $ | (8) |
从式(8)可知,螺旋桨安装平台绕M系的z轴的旋转角度为
| $ \varphi = \alpha + \gamma = 0, $ |
将式(8)代入式(6)、(7),可得:
| $ {x_o} = \left( {r/2} \right)\cos \left( {2\alpha } \right)\left( {\cos \beta - 1} \right), $ | (9) |
| $ {y_o} = \left( {r/2} \right)\sin \left( {2\alpha } \right)\left( {1 - \cos \beta } \right). $ | (10) |
由于球铰S1到舱壁坐标系中的转动副R1为一定长度值l1.满足几何关系:
| $ \left\| {{R_1}{S_1}} \right\| = {l_1}. $ | (11) |
设定:
| $ \begin{array}{l} A = r\left( {{{\cos }^2}\alpha \cos \beta + {{\sin }^2}\alpha } \right) + {x_o} - R,\\ B = r\sin \alpha \cos \alpha \left( {\cos \beta - 1} \right) + {y_o}, \end{array} $ |
利用式(11),以及PS1S,可得
| $ {z_o} = r\cos \alpha \sin \beta - \sqrt {{{\left( {{l_1}} \right)}^2} - {A^2} - {B^2}} . $ | (12) |
从式(8)~式(10)、式(12)可知,螺旋桨安装平台的空间位姿参数α和β是独立变量,其余的γ、xo、yo、zo均是独立变量α和β的非线性函数关系.
3 推进机构姿态控制算法为实现螺旋桨姿态的两自由度控制,需要建立螺旋桨安装平台的姿态参数α和β与机构的2驱动关节P2和P3运动量P2R2、P3R3之间的映射模型.
假定螺旋桨安装平台的当前姿态角度为α和β,利用式(9)、(10)、式(12)即可获取螺旋桨的位置参数(xo, yo, zo)T.
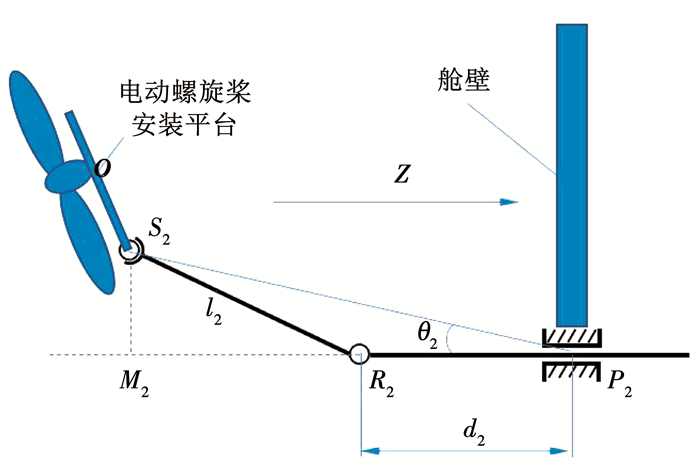
利用式(8)、式(1)、(2)即可获取螺旋桨安装平台的3个球铰在舱壁坐标系中的空间坐标PSiS(i=1, 2, 3).如图 2所示,以驱动支链P2R2S2为例.
|
图 2 驱动支链P2R2S2 Fig. 2 Driving chain P2R2S2 |
利用PS2S、PP2S=(-R/2,
| $ {\mathit{\boldsymbol{S}}_2}{\mathit{\boldsymbol{P}}_2} = \mathit{\boldsymbol{P}}_{P2}^S - \mathit{\boldsymbol{P}}_{S2}^S. $ |
S2P2的投影量M2P2、M2S2依次为:
| $ \begin{array}{*{20}{c}} {{M_2}{P_2} = {\mathit{\boldsymbol{S}}_2}{\mathit{\boldsymbol{P}}_2} \cdot {{\left[ {0,0,1} \right]}^{\rm{T}}} = \left( {\mathit{\boldsymbol{P}}_{P2}^S - \mathit{\boldsymbol{P}}_{S2}^S} \right) \cdot {{\left[ {0,0,1} \right]}^{\rm{T}}},}\\ {{M_2}{S_2} = \sqrt {{{\left( {{S_2}{P_2}} \right)}^2} - {{\left( {{M_2}{P_2}} \right)}^2}} .} \end{array} $ |
进而,可以获取驱动支链P2R2S2的运动输入量为
| $ {d_2} = {R_2}{P_2} = {M_2}{P_2} - \sqrt {{{\left( {{l_2}} \right)}^2} - {{\left( {{M_2}{S_2}} \right)}^2}} , $ |
同理,可以获取驱动支链P3R3S3运动输入量.
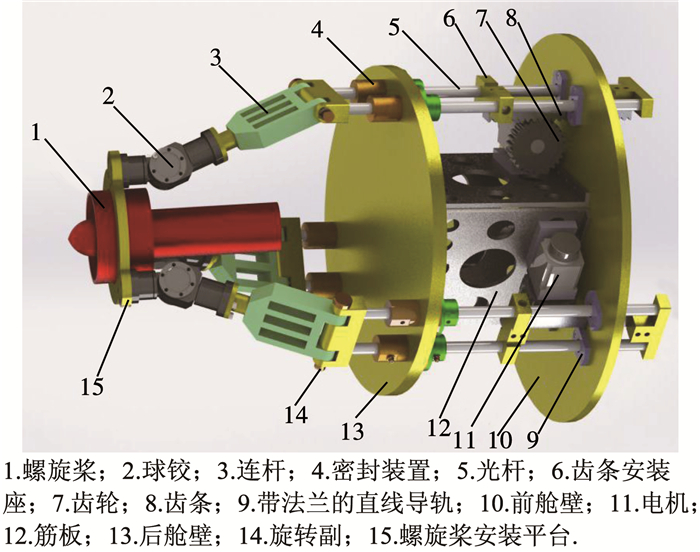
4 模拟仿真分析为验证上述姿态控制算法的正确性,建立两自由度矢量推进系统3D模型,如图 3所示.
|
图 3 两自由度并联矢量式推进机构三维模型 Fig. 3 3D model for 2-DOF propulsion mechanism |
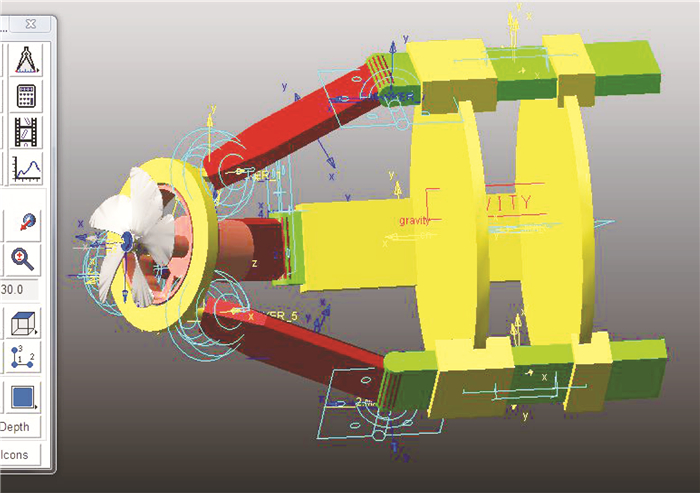
把模型简化之后导入ADAMS运动仿真软件中并添加运动副约束,如图 4所示.
|
图 4 机构的仿真模型 Fig. 4 Simulation model for 2-DOF propulsion mechanism |
进行算法的验证工作,具体方法如下:实现螺旋桨姿态角β=30°;α=0°~360°全向摆动,步长10°;结构参数l1=l2=l3=140 mm,r=75 mm,R=150 mm.利用上述算法借助MATLAB获取螺旋桨不同姿态角对应的驱动参数P2R2、P3R3序列值见表 1,在α=0°~60°时,β=0°~30°以斜率为1/2的趋势均匀增加;α=60°~300°时,β一直保持在30°;α=300°~360°时,β=30°~0°以斜率为-1/2的趋势均匀递减.
| 表 1 螺旋桨不同姿态角对应的驱动参数P2R2、P3R3 Tab. 1 Driving parameters P2R2, P3R3 for different attitude angles |
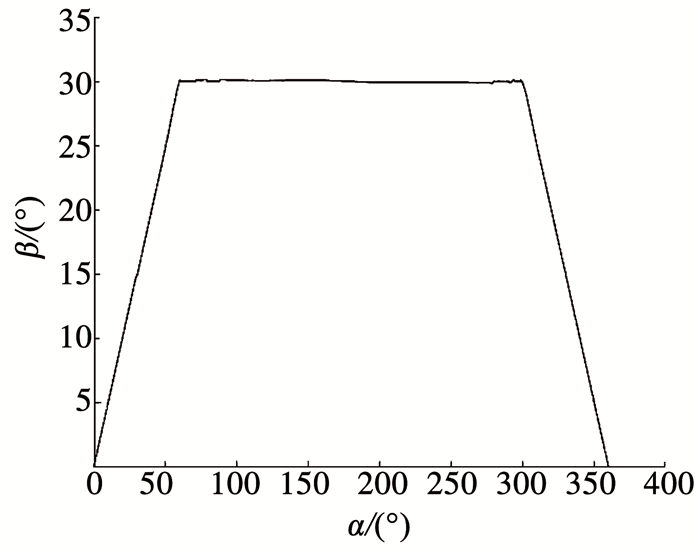
并将驱动长度序列值作为ADAMS运动模型的参数输入,观测螺旋桨的运动姿态,由图 5可知:在α=0°~60°变化时,β=0°~30°以斜率为1/2的趋势均匀增加;α=60°~300°时,β一直保持在30°左右;在α=300°~360°变化时,β=30°~0°以斜率为-1/2的趋势均匀递减.由此,ADAMS仿真出的图线形状与MATLAB中的实验图形吻合,可以验证算法的正确性.在α=60°~300°变化时,β的值会在30°上、下做很小的浮动,这是由于MATLAB在计算杆长时时保留精度与ADAMS进行曲线拟合时所带来的误差引起的.
|
图 5 所求得的β随α变化曲线 Fig. 5 Variation of nutation angle with precession angle |
利用上述结构参数加工并装配出整体的实验平台,实物装置如图 6所示.利用搭建的实验平台可以实现螺旋桨的可控姿态运动,进一步验证了方案的可行性和控制算法的正确性.

|
图 6 搭建的实验平台 Fig. 6 Experimental platform for 2-DOF propulsion mechanism |
1) 针对现有矢量推进机构存在的不足,本文提出了一种作动器可以内置、结构简单的两自由度RS+2PRS并联型矢量推进机构.
2) 结合推进机构自身结构特点,应用ZYZ型Euler角旋转矩阵,解决推进机构的运动参数耦合问题,并建立姿态控制算法,该方法与过程比较快捷.
3) 采用MATLAB和ADAMS联合仿真验证了机构设计与控制算法的正确性,搭建出实验平台,验证了整体方案的可行性.
| [1] |
马伟锋, 胡震. AUV的研究现状与发展趋势[J]. 火力与指挥控制, 2008, 33(6): 10. MA Weifeng, HU Zhen. Current researches and development trend on AUV[J]. Fire Control and Command Control, 2008, 33(6): 10. DOI:10.3969/j.issn.1002-0640.2008.06.003 |
| [2] |
DUBROVIN F S, SCHERBATYUK A F. Studying some algorithms for AUV navigation using a single beacon:the results of simulation and sea trails[J]. Gyroscopy and Navigation, 2016, 7(2): 189. DOI:10.1134/s2075108716020024 |
| [3] |
张铭钧. 水下机器人[M]. 北京: 海洋出版社, 2000. ZHANG Mingjun. Underwater robot[M]. Beijing: China Ocean Press, 2000. |
| [4] |
彭学伦. 水下机器人的研究现状与发展趋势[J]. 机器人技术与应用, 2004(4): 43. PENG Xuelun. Underwater robot research status and development trend[J]. Robot Technique and Application, 2004(4): 43. DOI:10.3969/j.issn.1004-6437.2004.04.008 |
| [5] |
方世鹏.水下矢量推进螺旋桨装置设计与研究[D].长沙: 国防科学技术大学, 2008 FANG Shipeng. Research on submarine thrust-vectoring propulsion device[D]. Changsha: National University of Defence Technology, 2008 http://cdmd.cnki.com.cn/Article/CDMD-90002-2009214204.htm |
| [6] |
高富东, 潘存云, 杨政, 等. 多矢量推进水下航行器6自由度非线性建模与分析[J]. 机械工程学报, 2011, 47(5): 93. GAO Fudong, PAN Cunyun, Yang Zheng. Nonlinear mathematics modeling and analysis of the vectored thruster autonomous underwater vehicle in 6-DOF motions[J]. Journal of Mechanical Engineering, 2011, 47(5): 93. DOI:10.3901/JME.2011.05.093 |
| [7] |
赵涛, 刘明雍, 周良荣. 自主水下航行器的研究现状与挑战[J]. 火力与指挥控制, 2010, 35(6): 1. ZHAO Tao, LIU Mingyong, ZHOU Liangrong. A survey of autonomous underwater vehicle recent advances and future challenges[J]. Fire Control and Command Control, 2010, 35(6): 1. DOI:10.3969/j.issn.1002-0640.2010.06.001 |
| [8] |
王立祥. 喷水推进及喷水推进泵[J]. 通用机械, 2007(10): 12. WANG Lixiang. Water jet propulsion and jet pump[J]. General Machinery, 2007(10): 12. DOI:10.3969/j.issn.1671-7139.2007.10.003 |
| [9] |
张明宇, 林瑞霖, 王永生, 等. 泵喷的三维反问题设计及其与螺旋桨的敞水特性对比[J]. 哈尔滨工程大学学报, 2017, 38(5): 690. ZHANG Mingyu, LIN Ruilin, WANG Yongsheng, et al. 3-D inverse design of pumpjet and comparison with opening water performance of original propeller[J]. Journal of Harbin Engineering University, 2017, 38(5): 690. DOI:10.11990/jheu.201602030 |
| [10] |
CAVALLO E, FILARETOV V F, MICHELINI R C, et al. Path guidance and attitude control of a vectored thruster AUV[C]//Proceedings of the 7th Biennial Conference on Engineering Systems Design and Analysis. Manchester, UK: IEEE, 2011: 325. DOI: 10.1115/esda2004-58196
|
| [11] |
CAVALLO E, MICHELINI R C, FILARETOV V F. Conceptual design of an AUV equipped with a three degrees of freedom vectored thruster[J]. Journal of Intelligent and Robotic Systems, 2010, 39(4): 365. DOI:10.1023/b:jint.0000026081.75417.50 |
| [12] |
龚浩, 吴先用, 黄宇, 等. 一种矢量推进方式下的AUV数学建模[J]. 中国仪器仪表, 2015(8): 41. GONG Hao, WU Xianyong, HUANG Yu, et al. Mathematical modeling of a kind of AUV with vector thruster[J]. China Instrumentation, 2015(8): 41. DOI:10.3969/j.issn.1005-2852.2015.08.008 |
| [13] |
陈路伟, 周朝晖. 矢量推进方式下的自主式水下航行器纵向运动操纵性分析[J]. 船海工程, 2011, 40(2): 119. CHEN Luwei, ZHOU Zhaohui. Maneuverability analysis of vertical movement of the vectored thruster autonomous underwater vehicle[J]. Ship & Ocean Engineering, 2011, 40(2): 119. DOI:10.3963/j.issn.1671-7953.2011.02.033 |
| [14] |
郭楠.水下机器人3-RRR矢量推进球面并联机构的研究[D].威海: 山东大学(威海), 2016 GUO Nan. Research on 3-RRR sphere parallel manipulator with vectored thruster for underwater vehicle[D]. Weihai: Shandong University(Weihai), 2016 http://cdmd.cnki.com.cn/Article/CDMD-10422-1015379804.htm |
| [15] |
ALICI G, SHIRINZADEH B. Topology optimization and singularity analysis of a 3-SPS parallel manipulator with a passive constraining spherical joint[J]. Mechanism and Machine Theory, 2009, 32(2): 215. DOI:10.1016/s0094-114x(3)00116-2 |
| [16] |
BA Xin, LUO Xiaohui, SHI Zhaocun, et al. A vectored water jet propulsion method for autonomous underwater vehicles[J]. Ocean Engineering, 2013, 74: 133. DOI:10.1016/j.oceaneng.2013.10.003 |
| [17] |
郑炎. AUV两自由度并联矢量推进器设计与研究[D].天津: 天津大学, 2015 ZHENG Yan. Design and research of the 2-DOF parallel vectored thruster for AUV[D]. Tianjin: Tianjin University, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10056-1016186794.htm |
| [18] |
曲海波, 梁艺瀚, 方跃法, 等. 4-RRS冗余球面并联机构的静力学与刚度分析[J]. 机械工程学报, 2015, 51(11): 8. QU Haibo, LIANG Yihan, FANG Yuefa, et al. Statics and stiffness analysis of 4-RRS redundant spherical parallel mechanism[J]. Journal of Mechanical Engineering, 2015, 51(11): 8. DOI:10.3901/JME.2015.11.008 |
 2019, Vol. 51
2019, Vol. 51


