2. 哈尔滨理工大学 自动化学院,哈尔滨 150080
2. School of Automation, Harbin University of Science and Technology, Harbin 150080, China
捷联惯导系统(strapdown inertial navigation system,SINS)误差模型本质上是非线性的,当姿态失准角为小角度时可以简化为线性模型处理[1].但是在实际工程中很难保证安装误差角为小角度, 主、子惯导间往往存在较大的安装误差角,因此大失准角情况下的SINS传递对准成为亟待解决的问题[2].大失准角传递对准的特点是非线性误差方程以及非线性滤波算法[3].
可观测性的概念最初是由Kalman为了解决确定性系统的问题而引入的.如果系统的状态能够被过去的观测唯一确定,则称该系统是可观测的[4].可观测性反应了系统利用有限时间内的观测量确定系统状态的能力,在很大程度上决定了状态矢量能否被有效估计,因此在传递对准之前对系统进行可观测性分析是十分必要的[5-7].
线性定常系统的可观测性分析方法已经非常成熟,而非线性系统的可观测度还没有统一的定义,通常的做法是分段线性化后再进行可观测性分析.文献[8]采用了将系统分段线性化后利用分段线性定常系统(piecewise linear constant system,PWCS)和奇异值分解(singular value decomposition, SVD)理论对GPS/SINS超紧组合导航系统进行可观测性分析.文献[9]中同样采用分段线性化的方式研究系统的可观测性.
王丹力等[10]可观测度判断方法只能给出系统的能控能观性以及可控、可观测的状态变量维数;基于奇异值分解的可观测性分析方法能够给出系统可观测的维数以及状态的可观测度,但是不能确定哪些状态是可观测的.文献[11]提出了利用微分几何的方法对非线性系统进行可观测性分析的理论.文献[12-13]将该方法应用于深空自主导航系统的可观测性分析,并根据可观测性分析结果设计了导航方案.本文将从非线性系统的可观测性出发,给出一个系统可观测度的定义以及通过奇异值分解分析状态变量可观测度的方法.
1 SINS非线性误差模型传递对准坐标系的定义:1)理想导航坐标系n(OXnYnZn),本文中指东、北、天地理坐标系.2)子惯导计算导航坐标系n′(OXn′Yn′Zn′).3)主惯导载体坐标系a(OXaYaZa).4)子惯导载体坐标系b(OXbYbZb),a系和b系均定义为右、前、上坐标系,理想情况下两坐标系一致.
其中,n系依次绕Z、X、Y轴转动角度αz、αx、αy可得n′系,定义欧拉角误差为α=[αx αy αz]T,相应的姿态变换矩阵为:
| $ {\mathit{\boldsymbol{C}}_{{\alpha _z}}} = \left[ {\begin{array}{*{20}{c}} {c{\alpha _z}}&{s{\alpha _z}}&0\\ { - s{\alpha _z}}&{c{\alpha _z}}&0\\ 0&0&1 \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{C}}_{{\alpha _x}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{c{\alpha _x}}&{s{\alpha _x}}\\ 0&{ - s{\alpha _x}}&{c{\alpha _x}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{C}}_{{\alpha _y}}} = \left[ {\begin{array}{*{20}{c}} {c{\alpha _y}}&0&{ - s{\alpha _y}}\\ 0&1&0\\ {s{\alpha _y}}&0&{c{\alpha _y}} \end{array}} \right]. $ |
式中:sαz、cαz分别为sin αi和cos αi的简写形式.则n系到n′系的姿态变换矩阵为
| $ \begin{array}{l} \mathit{\boldsymbol{C}}_n^{n'} = {\mathit{\boldsymbol{C}}_{{\alpha _y}}}{\mathit{\boldsymbol{C}}_{{\alpha _x}}}{\mathit{\boldsymbol{C}}_{{\alpha _z}}} = \\ \;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {c{\alpha _y}c{\alpha _z} - s{\alpha _y}s{\alpha _x}s{\alpha _z}}&{c{\alpha _y}s{\alpha _z} + s{\alpha _y}s{\alpha _x}c{\alpha _z}}&{ - s{\alpha _y}c{\alpha _x}}\\ { - c{\alpha _x}s{\alpha _z}}&{c{\alpha _x}c{\alpha _z}}&{s{\alpha _x}}\\ {s{\alpha _y}c{\alpha _z} + c{\alpha _y}s{\alpha _x}s{\alpha _z}}&{s{\alpha _y}s{\alpha _z} - c{\alpha _y}s{\alpha _x}c{\alpha _z}}&{c{\alpha _y}c{\alpha _x}} \end{array}} \right]. \end{array} $ |
设n′系相对于n系的角速度为ωnn′n′,则有
| $ \omega _{nn'}^{n'} = {\mathit{\boldsymbol{C}}_{{\alpha _y}}}{\mathit{\boldsymbol{C}}_{{\alpha _x}}}\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {{{\dot \alpha }_z}} \end{array}} \right] + {\mathit{\boldsymbol{C}}_{{\alpha _y}}}\left[ {\begin{array}{*{20}{c}} {{{\dot \alpha }_x}}\\ 0\\ 0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ {{{\dot \alpha }_y}}\\ 0 \end{array}} \right] = {\mathit{\boldsymbol{C}}_\omega }\dot \alpha , $ |
从而得到欧拉角误差的微分方程为
| $ \dot \alpha = \mathit{\boldsymbol{C}}_\omega ^{ - 1}\omega _{nn'}^{n'}, $ |
则以欧拉角表示的SINS非线性误差模型为[14]
| $ \left\{ \begin{array}{l} \dot \alpha = \mathit{\boldsymbol{C}}_\omega ^{ - 1}\left( {2\omega _{in'}^{n'} + \delta \omega _{in'}^{n'} - \mathit{\boldsymbol{C}}_b^{n'}{\varepsilon ^b}} \right),\\ \delta {V^{n'}} = \left( {\mathit{\boldsymbol{C}}_{n'}^n - I} \right)\mathit{\boldsymbol{C}}_b^{n'}{{\tilde f}^b} - \mathit{\boldsymbol{C}}_{n'}^n\mathit{\boldsymbol{C}}_b^{n'}{\nabla ^b} - \\ \;\;\;\;\;\;\;\;\;\;\left( {2\omega _{ie}^{n'} + \omega _{en'}^{n'}} \right) \times \delta {V^{n'}} - \left( {2\delta \omega _{ie}^{n'} + \delta \omega _{en'}^{n'}} \right) \times {V^{n'}} - \\ \;\;\;\;\;\;\;\;\;\;\left( {2\delta \omega _{ie}^{n'} + \delta \omega _{en'}^{n'}} \right) \times \delta {V^{n'}} + \delta {g^{n'}}, \end{array} \right. $ |
上式为纯捷联惯导误差方程,若将外界参考速度和位置信息引入算法,能够得到更加简洁的方程,称之为阻尼算法.在传递对准中,主惯导的精度至少比子惯导高一个数量级,对于子惯导来说可认为主惯导的导航数据是精确无误的.因此,可采用主惯导阻尼算法进行误差模型的简化.将主惯导解算的相关导航数据带入,SINS基本方程可改写为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot C}}_b^{n'} = \mathit{\boldsymbol{C}}_b^{n'}\left( {\mathit{\boldsymbol{\omega }}_{ib}^b \times } \right) - \left( {\mathit{\boldsymbol{\omega }}_{in,s}^n \times } \right)\mathit{\boldsymbol{C}}_b^{n'},\\ {{\dot V}^{n'}} = \mathit{\boldsymbol{C}}_b^{n'}{f^b} - \left( {2\omega _{ie,s}^n + \omega _{en,s}^n} \right) \times V_s^n + g_s^n, \end{array} \right. $ |
式中,下标为s的表示通过主惯导获得的数据,认为是误差可忽略的.可得相应的阻尼算法下的误差模型为
| $ \left\{ \begin{array}{l} \dot \alpha = \mathit{\boldsymbol{C}}_\omega ^{ - 1}\left( { - {\varepsilon ^{n'}} + \left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{C}}_n^{n'}} \right)\omega _{in'}^{n'}} \right),\\ \delta {V^{n'}} = \left( {\mathit{\boldsymbol{C}}_{n'}^n - \mathit{\boldsymbol{I}}} \right)\mathit{\boldsymbol{C}}_b^{n'}{{\tilde f}^b} - \mathit{\boldsymbol{C}}_{n'}^n\mathit{\boldsymbol{C}}_b^{n'}{\nabla ^b}. \end{array} \right. $ |
传递对准过程中,通常首先将主惯导的姿态、速度、位置等导航信息直接加载到子惯导作为粗对准,而主惯导的姿态信息认为是精确的,因此一般情况下(除高动态等极特殊情况)认为主、子惯导之间的安装误差即为子惯导的初始对准姿态失准角.在实际的工程应用中,水平对准可通过总体安装设计保障,例如将主、子惯导安装面分别调整到与同一基准面水平,从而保证水平失准角为小角度.而方位角的对准就复杂的多,因此可以假设水平失准角是小角度,只考虑大方位失准角的情况时,可将状态方程展开成如下所示的分量形式.
| $ \left\{ \begin{array}{l} {{\dot \alpha }_x} = - s{\alpha _z}{\omega _N} + {\alpha _y}{\omega _U} - \varepsilon _x^{n'},\\ {{\dot \alpha }_y} = \left( {1 - c{\alpha _z}} \right){\omega _N} + {\alpha _x}{\omega _U} - \varepsilon _y^{n'},\\ {{\dot \alpha }_z} = {\alpha _x}c{\alpha _z}{\omega _N} - \varepsilon _z^{n'},\\ \delta \dot V_x^{n'} = \left( {c{\alpha _z} - 1} \right)\tilde f_x^{n'} - s{\alpha _z}\tilde f_y^{n'} + \left( {{\alpha _y}c{\alpha _z} + {\alpha _x}s{\alpha _z}} \right)\tilde f_z^{n'} - c{\alpha _z}\nabla _x^{n'} + s{\alpha _z}\nabla _y^{n'},\\ \delta \dot V_y^{n'} = s{\alpha _z}\tilde f_x^{n'} + \left( {c{\alpha _z} - 1} \right)\tilde f_y^{n'} + \left( {{\alpha _y}s{\alpha _z} - {\alpha _x}c{\alpha _z}} \right)\tilde f_z^{n'} - s{\alpha _z}\nabla _x^{n'} - c{\alpha _z}\nabla _y^{n'}. \end{array} \right. $ |
系统的状态方程为
| $ \mathit{\boldsymbol{\dot X}} = f\left( \mathit{\boldsymbol{X}} \right) + g\left( \mathit{\boldsymbol{W}} \right). $ |
由于纯惯导系统的高度通道是发散的,因此选取的状态变量不包括天向速度误差分量,并将εb和▽b扩展到状态变量中,得到如下10维的状态变量:
| $ \mathit{\boldsymbol{X}} = {\left[ {\begin{array}{*{20}{c}} {{\alpha _x}}&{{\alpha _y}}&{{\alpha _z}}&{\delta V_x^{n'}}&{\delta V_y^{n'}}&{\varepsilon _x^b}&{\varepsilon _y^b}&{\varepsilon _z^b}&{\nabla _x^b}&{\nabla _y^b} \end{array}} \right]^{\rm{T}}}. $ |
速度匹配直接以主、子惯导的速度差值作为观测量得到量测方程为
| $ {\mathit{\boldsymbol{Z}}^v} = {\mathit{\boldsymbol{H}}^v}\mathit{\boldsymbol{X}} + {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^v}. $ |
式中:
姿态匹配以主、子惯导的姿态角差值作为观测量,得到的量测方程为
| $ {\mathit{\boldsymbol{Z}}^\alpha } = {\mathit{\boldsymbol{H}}^\alpha }\mathit{\boldsymbol{X}} + {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^\alpha }. $ |
式中:
与先进行系统线性化再进行可观测性分析的方法不同,本文中直接对非线性系统进行可观测性分析,基于微分几何的非线性系统理论,利用李导数求解非线性系统的可观测性矩阵,并给出系统可观测度的度量方法.
考虑如下非线性系统:
| $ \Sigma :\left\{ \begin{array}{l} \mathit{\boldsymbol{\dot X}} = \mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{X}} \right),\\ \mathit{\boldsymbol{Z}} = h\left( \mathit{\boldsymbol{X}} \right). \end{array} \right. $ |
式中:状态矢量X∈Xn⊂Rn,观测矢量Z⊂Rm,状态方程f和观测方程h为C∞内光滑的解析函数.
定义1 如果对于任意T>0和任意相应的U容许控制u,则
| $ y\left( {t,{x_1},u} \right) = y\left( {t,{x_2},u} \right),\;\;\;\;\;t \in \left[ {0,T} \right], $ |
那么,x1、x2称为U-不可分辨的x0的所有U-不可分辨的点集记作IDU(x0).
定义2 系统∑称为在x0处局部可观测的,当对于x0的任何邻域U,U-不可分割的点集仅仅包含1个点,即IDU(x0)={x0}.若系统在x0处局部弱可观测的,则存在一个x0的邻域U,使得U-不可分辨的点集仅仅包含1个点.
局部可观测性是很强的,因为它意味着全局可观测性.因此,本文主要关注局部弱可观测性.
根据微分几何理论,h沿f的各阶李导数定义为
| $ \left\{ \begin{array}{l} L_f^0h\left( \mathit{\boldsymbol{X}} \right) = h\left( \mathit{\boldsymbol{X}} \right),\\ L_f^kh\left( \mathit{\boldsymbol{X}} \right) = \frac{{\partial \left( {L_f^{k - 1}h\left( \mathit{\boldsymbol{X}} \right)} \right)}}{{\partial \mathit{\boldsymbol{X}}}}f\left( \mathit{\boldsymbol{X}} \right),k = 1,2, \cdots ,n. \end{array} \right. $ |
定义3 系统∑的观测空间H是由{h, Lfh, …, Lfn-1h, …}生成的线性空间,该空间按如下形式定义系统的可观测性分布:
| $ {\rm{d}}\mathit{\boldsymbol{H}}\left( \mathit{\boldsymbol{X}} \right) = {\rm{span}}\left\{ {{\rm{d}}H\left( {{X_0}} \right)\left| {H \in \mathit{\boldsymbol{H}}} \right.} \right\}. $ |
在可观测空间H内,Hn={h, Lfh, …, Lfn-1h}是包含状态和观测变量在内的最小线性空间,并且关于李导数是封闭的.
定理1 对∈Xn,如果dHn满足可观测性秩条件,则称系统∑在X0点是局部弱可观测的.若对于∀X∈Xn,如果dHn都满足可观测性秩条件,则称系统∑是局部弱可观测的.
由dHn定义的非线性系统的可观测矩阵为
| $ \mathit{\boldsymbol{Q}}\left( \mathit{\boldsymbol{X}} \right) = \left[ {\begin{array}{*{20}{c}} {L_f^0h\left( X \right)}\\ {L_f^1h\left( X \right)}\\ \vdots \\ {{\rm{d}}L_f^{n - 1}h\left( X \right)} \end{array}} \right], $ |
定义的系统∑可观测度为
| $ \mathit{\boldsymbol{\delta }}\left( \mathit{\boldsymbol{X}} \right) = \frac{{{\sigma _{\min }}\left( Q \right)}}{{{\sigma _{\max }}\left( Q \right)}}. $ |
为了进一步分析每个系统变量的可观测度,将可观测矩阵Q(X)进行奇异值分解,有Q=USVT.其中,
可观测矩阵的奇异值σi和对应的列向量vi可用来分析状态变量的可观测度.最大奇异值对应的列向量中绝对值最大的数对应的状态是可观测度最高的;最小奇异值对应的列向量中绝对值最大的数的可观测度是最低的[5].
4 SINS的可观测性分析仿真 4.1 仿真条件本文采用摇翼匀速飞行的机动方式进行传递对准仿真.假设飞机以300 m/s的速度匀速向北飞行,并以周期为5 s,幅值为5°的正弦变化规律绕飞机纵轴进行摇翼摆动,滚转角变化规律为
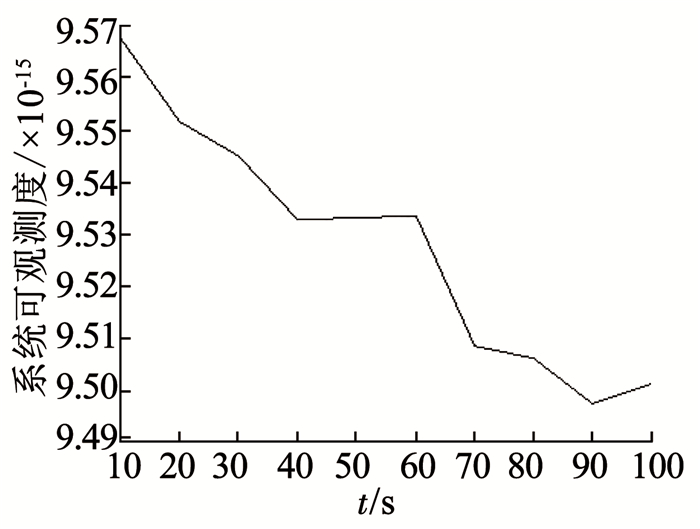
图 1给出了速度匹配时系统可观测度随时间变化曲线,整个仿真过程中系统的可观测度在10-15的量级,也就是说系统的可观测度低,可能存在不能观测的状态变量.由于整个过程中系统的可观测度的比较平稳的,本文选取60 s时系统可观测矩阵为例进行状态变量可观测度的分析,系统可观测矩阵的奇异值分解结果见表 1.
|
图 1 速度匹配系统可观测度随时间变化曲线 Fig. 1 System observability of speed match mode |
| 表 1 60 s时速度匹配可观测矩阵的奇异值 Tab. 1 Observability matrix's singular value of speed match mode at 60 s |
由表 1可以看出,最大的4个奇异值对应的状态变量为αy、αx、εyb、εxb,也就是说水平方向的姿态失准角和陀螺零漂的可观测度是最高的,在滤波过程中可以快速估计出来;数值为1的两个奇异值对应的状态变量为δVxn′和δVyn′,即水平速度误差也是可观测的;下一个奇异值为0.004,对应的状态变量为εzb,由于奇异值很小,认为该状态变量的可观测性很低;最后3个奇异值小于10-10,认为其对应的状态变量是不可观测的,即不可观测的状态变量为▽xb、▽yb和αz.
4.2.2 速度+姿态匹配速度+姿态匹配时系统可观测度随时间变化曲线如图 2所示,系统的可观测度约为0.01,意味着系统是可观测的.同样选取60 s的系统可观测矩阵来分析状态变量的可观测度,系统可观测矩阵的奇异值分解结果见表 2.

|
图 2 速度+姿态匹配系统可观测度随时间变化曲线 Fig. 2 System observability of speed+attitude match mode |
| 表 2 60 s时速度+姿态匹配可观测矩阵的奇异值分解 Tab. 2 Observability matrix's singular value of speed+attitude match mode at 60 s |
由表 2可以看出,最大的4个奇异值对应的状态变量依然是αy、αx、εyb、εxb,并且奇异值要大于速度匹配情况,即水平方向的姿态失准角和陀螺零漂的可观测度在速度加姿态匹配情况下也是最高的,并且可观测度要大于速度匹配情况;数值为1的奇异值增加到4个,对应的状态变量为εzb、δVyn′、δVxn′、αz,相对于速度匹配模式,εzb的可观测性大大提高,同时αz由不可观测变得可观测;最后两个数值为0.1的奇异值对应的状态变量为▽xb和▽yb,而这两个状态变量在速度匹配模式下是不可观测的.
综上所述,速度加姿态匹配模式下系统是局部可观测的,并且状态变量的可观测度相比速度匹配模式有所提高.这与小失准角线性误差模型的可观测度分析结果是一致的.
5 传递对准仿真 5.1 UKF滤波算法本文所涉及到的滤波模型中状态方程为非线性,量测方程为线性定常,即
| $ \left\{ \begin{array}{l} {x_k} = f\left( {{x_{k - 1}}} \right) + g\left( {{x_{k - 1}}} \right){w_{k - 1}},\\ {z_k} = \mathit{\boldsymbol{H}}{x_k} + {v_k}. \end{array} \right. $ |
针对该滤波方程有如下简化的无迹卡尔曼滤波(unscent Kalman filter, UKF)算法[15].
1) 初始化状态变量及其均方差为
| $ {{\hat x}_0} = E\left[ {{x_0}} \right],{\mathit{\boldsymbol{P}}_0} = E\left[ {\left( {{{\hat x}_0} - {x_0}} \right){{\left( {{{\hat x}_0} - {x_0}} \right)}^{\rm{T}}}} \right]. $ |
2) 时间更新为
| $ \left\{ \begin{array}{l} {\chi _{k - 1}} = \left[ {\begin{array}{*{20}{c}} {{{\hat x}_{k - 1}}}&{{{\left[ {{{\hat x}_{k - 1}}} \right]}_L} + \gamma \sqrt {{\mathit{\boldsymbol{P}}_{k - 1}}} }&{{{\left[ {{{\hat x}_{k - 1}}} \right]}_L} - \gamma \sqrt {{\mathit{\boldsymbol{P}}_{k - 1}}} } \end{array}} \right],\\ \chi _{i,k\left| {k - 1} \right.}^ * = f\left( {{\chi _{i,k - 1}}} \right),\\ {{\hat x}_{k\left| {k - 1} \right.}} = \sum\limits_{i = 0}^{2L} {W_i^{\left( m \right)}\chi _{i,k\left| {k - 1} \right.}^ * } ,\\ {\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}} = \sum\limits_{i = 0}^{2L} {W_i^{\left( c \right)}\left( {\chi _{i,k\left| {k - 1} \right.}^ * - {{\hat x}_{k\left| {k - 1} \right.}}} \right){{\left( {\chi _{i,k\left| {k - 1} \right.}^ * - {{\hat x}_{k\left| {k - 1} \right.}}} \right)}^{\rm{T}}}} + \\ \;\;\;\;\;\;\;\;\;\;g\left( {{{\hat x}_{k - 1}}} \right){Q_{k - 1}}g{\left( {{{\hat x}_{k - 1}}} \right)^{\rm{T}}}. \end{array} \right. $ |
3) 量测更新为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{P}}_{{{\hat x}_k}{{\hat z}_k}}} = {\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}}\mathit{\boldsymbol{H}}_k^{\rm{T}},\\ {\mathit{\boldsymbol{P}}_{{{\hat z}_k}{{\hat z}_k}}} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}}\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\mathit{\boldsymbol{R}}_k},\\ {\mathit{\boldsymbol{K}}_k} = {\mathit{\boldsymbol{P}}_{{{\hat x}_k}{{\hat z}_k}}}P_{{{\hat z}_k}{{\hat z}_k}}^{ - 1},\\ {{\hat z}_{k\left| {k - 1} \right.}} = {\mathit{\boldsymbol{H}}_k}{{\hat x}_{k\left| {k - 1} \right.}},\\ {{\hat x}_k} = {{\hat x}_{k\left| {k - 1} \right.}} + {\mathit{\boldsymbol{K}}_k}\left( {{z_k} - {{\hat z}_{k\left| {k - 1} \right.}}} \right),\\ {\mathit{\boldsymbol{P}}_k} = {\mathit{\boldsymbol{P}}_{k\left| {k - 1} \right.}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{P}}_{{{\hat z}_k}{{\hat z}_k}}}K_k^{\rm{T}}. \end{array} \right. $ |
传递对准仿真条件同可观测性分析仿真一致,滤波周期为0.25 s,状态滤波初值均取零,估计误差均方差初值取为
| $ \begin{array}{l} \mathit{\boldsymbol{P}}\left( 0 \right) = {\rm{diag}}\left[ {{{\left( {{1^ \circ }} \right)}^2}{{\left( {{1^ \circ }} \right)}^2}{{\left( {{{15}^ \circ }} \right)}^2}} \right.\\ \;\;\;\;\;\;\;\;\;\;{\left( {0.01\;{\rm{m/s}}} \right)^2}{\left( {0.01\;{\rm{m/s}}} \right)^2}\\ \;\;\;\;\;\;\;\;\;\;{\left( {{{0.01}^ \circ }/{\rm{h}}} \right)^2}{\left( {{{0.01}^ \circ }/{\rm{h}}} \right)^2}{\left( {{{0.01}^ \circ }/{\rm{h}}} \right)^2}\\ \;\;\;\;\;\;\;\;\;\;\left. {{{\left( {10\;{\rm{ \mathsf{ μ} g}}} \right)}^2}{{\left( {10\;{\rm{ \mathsf{ μ} g}}} \right)}^2}} \right], \end{array} $ |
速度匹配法量测噪声方差阵取为
| $ {\mathit{\boldsymbol{R}}^v} = {\rm{diag}}\left[ {\begin{array}{*{20}{c}} {{{\left( {0.01\;{\rm{m/s}}} \right)}^2}}&{{{\left( {0.01\;{\rm{m/s}}} \right)}^2}} \end{array}} \right], $ |
姿态匹配法量测噪声方差阵取为
| $ {\mathit{\boldsymbol{R}}^a} = {\rm{diag}}\left[ {\begin{array}{*{20}{c}} {{{\left( {{1^ \circ }} \right)}^2}}&{{{\left( {{1^ \circ }} \right)}^2}}&{{{\left( {{{15}^ \circ }} \right)}^2}} \end{array}} \right]. $ |
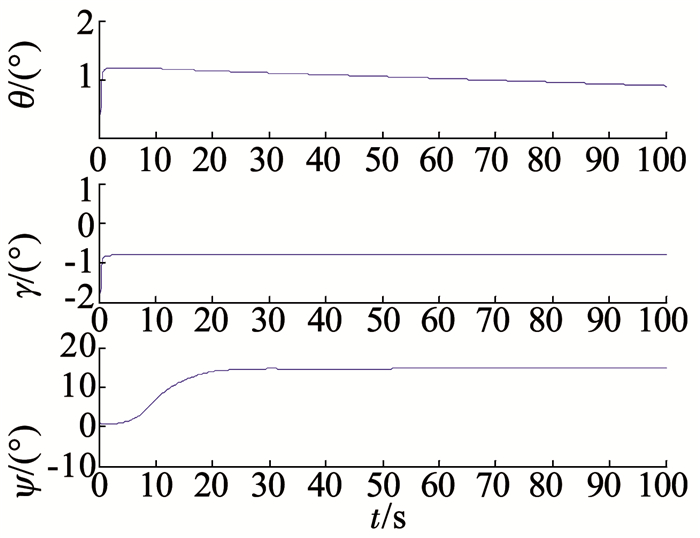
限于篇幅这里只给出姿态失准角的估计结果,如图 3、4所示.可以看出,速度匹配模式下两个水平方向失准角可以很好的估计出来,方位失准角由于不可观测导致基本没有估计结果; 速度+姿态的匹配模式下,3个失准角均可以被估计,水平方向失准角的估计效果要比方位失准角好,这是因为方位失准角的可观测度比水平方向失准角低,并且方位失准角为大失准角非线性更强.

|
图 3 速度匹配传递对准姿态失准角估计结果 Fig. 3 Attitude error estimation of speed match mode |
|
图 4 速度+姿态匹配传递对准姿态失准角估计结果 Fig. 4 Attitude error estimation of speed+attitude match mode |
传递对准的仿真结果与可观测性分析结果一致,证明了该可观测性分析方法的正确有效性.
6 结论1) 利用该方法分析了摇翼匀速飞行状态下SINS大方位失准角传递对准滤波方程的可观测性,具体对速度匹配和速度+姿态匹配两种情况下状态变量的可观测度进行了仿真分析,并通过UKF滤波仿真结果验证了可观测性分析的正确性.
2) 文中给出的可观测性分析方法可直接针对非线性系统进行分析,并同时给出各状态变量的可观测度.不需要将系统分段线性化,也就不需要证明系统方程是否满足PWCS定理,相对PWCS+SVD的可观测性方法更加简捷.
| [1] |
王丹力, 张洪钺. 惯导系统初始对准的非线性滤波算法[J]. 中国惯性技术学报, 1999, 7(3): 17. WANG Danli, ZHANG Hongyue. Nonlinear filtering algorithm for INS initial alignment[J]. Journal of Chinese Inertial Technology, 1999, 7(3): 17. DOI:10.13695/j.cnki.12-1222/o3.1999.03.004 |
| [2] |
杨功流, 王丽芬, 袁二凯, 等. 大方位失准角下舰载机快速传递对准技术[J]. 中国惯性技术学报, 2014, 22(1): 45. YANG Gongliu, WANG Lifen, YUAN Erkai, et al. Rapid transfer alignment of lager misalignment angle for carrier aircrafts[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 45. DOI:10.13695/j.cnki.12-1222/o3.2014.01.010 |
| [3] |
郭子伟, 缪玲娟, 赵洪松, 等. 一种改进的类高斯和粒子滤波在大失准角传递对准中的应用[J]. 航空学报, 2013, 34(1): 164. GUO Ziwei, MIAO Lingjuan, ZHAO Hongsong, et al. Application of an improved Gaussian-like sum particle filter to large misalignment transfer alignment[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(1): 164. DOI:10.7527/S1000-6893.2013.0019 |
| [4] |
刘豹, 唐万生. 现代控制理论[M]. 北京: 机械工业出版社, 2006: 101. LIU Bao, TANG Wansheng. Modern control theory[M]. Beijing: China Machine Press, 2006: 101. |
| [5] |
CHO S Y, LEE H K, LEE H K. Observability and estimation error analysis of the initial fine alignment filter for nonleveling strapdown inertial navigation system[J]. Journal of Dynamic Systems, Measurement, and Control, 2013, 135(2): 021005-1. DOI:10.1115/1.4007552 |
| [6] |
赵琳, 李亮, 孙明, 等. 基于SVD的SINS多位置对准可观测性分析[J]. 中国惯性技术学报, 2008, 16(5): 523. ZHAO Lin, LI Liang, SUN Ming, et al. Analysis on observability of SINS multi-position alignment based on singular value decomposition[J]. Journal of Chinese Inertial Technology, 2008, 16(5): 523. DOI:10.13695/j.cnki.12-1222/o3.2008.05.009 |
| [7] |
张庆, 高延滨, 张勤拓. 机载战术武器传递对准可观测性分析[J]. 华中科技大学学报(自然科学版), 2010, 38(11): 68. ZHANG Qing, GAO Yanbin, ZHANG Qintuo. Analyzing the observability of transfer alignment of airborne tactical weapons[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2010, 38(11): 68. DOI:10.13245/j.hust.2010.11.005 |
| [8] |
周卫东, 蔡佳楠, 孙龙, 等. GPS/SINS超紧组合导航系统可观测性分析[J]. 北京航空航天大学学报, 2013, 39(9): 1157. ZHOU Weidong, CAI Jianian, SUN Long, et al. Observability analysis of GPS/SINS ultra-tightly coupled system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(9): 1157. DOI:10.13700/j.bh.1001-5965.2013.09.006 |
| [9] |
程建华, 陈岱岱, 王冰玉, 等. 基于可观测度分析的传递对准精度评估方法[J]. 系统工程与电子技术, 2015, 37(4): 895. CHENG Jianhua, CHEN Daidai, WANG Bingyu, et al. Approach of transfer alignment accuracy evaluation based on observability degree analysis[J]. Systems Engineering and Electronics, 2015, 37(4): 895. DOI:10.3969/j.issn.1001-506X.2015.04.26 |
| [10] |
王丹力, 张洪钺. 几种可观测性分析方法及在惯导中的应用[J]. 北京航空航天大学学报, 1999, 25(3): 342. WANG Danli, ZHANG Hongyue. Methods for the analysis of observability and their application to INS initial alignment[J]. Journal of Beijing University of Aeronautics and Astronautics, 1999, 25(3): 342. DOI:10.13700/j.bh.1001-5965.1999.03.057 |
| [11] |
HERMANN R, ARTHUR J K. Nonliner controllability and observability[J]. IEEE Transactions on Automatic Control, 1977, 22(5): 728. DOI:10.1109/TAC.1977.1101601 |
| [12] |
YIM J R, CRASSIDIS J L, JUNKINS J L. Autonomous orbit navigation of interplanetary spacecraft[D]. Texas: Texas A & M University, 2002. DOI: 10.2514/6.2000-3936
|
| [13] |
崔平远, 常晓华, 崔祜涛. 基于可观测性分析的深空自主导航方法研究[J]. 宇航学报, 2011, 32(10): 2115. CUI Pingyuan, CHANG Xiaohua, CUI Hutao. Research on observability analysis-based autonomous navigation method for deep space[J]. Journal of Astronautics, 2011, 32(10): 2115. DOI:10.3873/j.issn.1000-1328.2011.10.004 |
| [14] |
梅春波, 秦永元, 游金川. SINS基于非线性量测的大失准角初始对准算法[J]. 宇航学报, 2016, 37(3): 291. MEI Chunbo, QIN Yongyuan, YOU Jinchuan. Nonlinear measurement based SINS initial alignment algorithm under large misalignment angle[J]. Journal of Astronautics, 2016, 37(3): 291. DOI:10.3873/j.issn.1000-1328.2016.03.007 |
| [15] |
严恭敏, 严卫生, 许德民. 简化UKF滤波在SINS大失准角初始对准中的应用[J]. 中国惯性技术学报, 2008, 16(3): 253. YAN Gongmin, YAN Weisheng, XU Demin. Application of simplified UKF in SINS initial alignment for large misalignment angles[J]. Journal of Chinese Inertial Technology, 2008, 16(3): 253. DOI:10.13695/j.cnki.12-1222/o3.2008.03.006 |
 2019, Vol. 51
2019, Vol. 51


