1988年一架波音737飞机因蒙皮搭接处铆钉孔发生了多位置疲劳裂纹,引发了灾难性的事故,多裂纹问题严重威胁飞机结构安全,引起了学术界的重视.目前研究多裂纹结构的数值方法包括边界元法和交替有限法[1],但这些方法要求裂纹尖端的网格或者离散点足够密,裂纹扩展的同时网格或离散点也需要重新划分或布置,导致建模复杂、计算量增大,严重制约了它们在工程中的应用.
为更好地解决裂纹生成和扩展的问题,Silling[2]提出了“近场动力学”(peridynamics)理论.在该理论中,空间中的任意物质点受到一定大小邻域内的其他物质点的作用,其位移积分形式的运动方程不同于传统连续介质力学理论中微分形式的运动方程,有效地避免了裂纹尖端区域的奇异性,在裂纹的模拟上具有显著的优势.同时近场动力学的本构方程里包含了损伤与断裂的描述,裂纹扩展等行为自然发生[3],无需重复划分网格,在疲劳问题的分析中也具有优势.
近场动力学不仅可应用于传统的准静态[4-5]和动态断裂[6-7]等问题的分析中,也可用于描述不同的材料,除了均匀的各向同性材料外[4-5],余音等[8-9]建立了基于PD理论的复合材料模型,Cheng等[10]用PD理论模拟了功能梯度材料的动态断裂,并验证了模型的有效性,顾鑫等[11]则模拟了刚性弹丸侵彻混凝土的裂纹扩展和最终破坏的过程,得到了较好的结果.为突破原有PD理论中材料泊松比存在限制的问题[12],Silling等[13]补充完善了PD理论,提出了“态型近场动力学”(state-based peridynamics).
随着近场动力学相关研究的不断深入,适用于疲劳的PD理论被提出.Oterkus等[14]最早提出的PD疲劳理论能够模拟裂纹扩展阶段,却无法很好地处理裂纹萌生阶段.Silling等[15]在近场动力学中引入了“循环应变”和“剩余寿命”的概念,建立了各向同性材料的疲劳裂纹萌生和扩展理论.Jung等[16-19]在文献[15]提出的疲劳理论的基础上扩展该模型的适用范围至分层混杂材料和复合材料之中.但目前PD疲劳理论相关文献数量极少,均是以键型近场动力学为基础,且并未关注到疲劳问题中材料表面状态对结果的影响以及存在的裂纹闭合等现象.
本文以平面应力问题的常规态型近场动力学理论框架为基础,根据近场动力学疲劳理论,建立可模拟疲劳裂纹萌生与扩展的近场动力学疲劳模型,并依据疲劳工程运算中的“载荷循环分间隔法”[20]对模型的计算流程进行优化.采用该近场动力学疲劳模型,分别对单裂纹平板和多裂纹平板的疲劳破坏过程进行模拟,并将数值模拟计算结果与实验结果进行对比,验证该模型在模拟复杂裂纹的疲劳破坏上的优势与有效性.
1 平面应力问题的OSPD疲劳理论现有文献[14-19]中的PD疲劳理论均以键型PD理论为基础,为突破材料泊松比的限制,且考虑到本文研究的是薄板的疲劳问题,因此在平面应力问题常规态型近场动力学(OSPD)的基础上引入了疲劳模型.
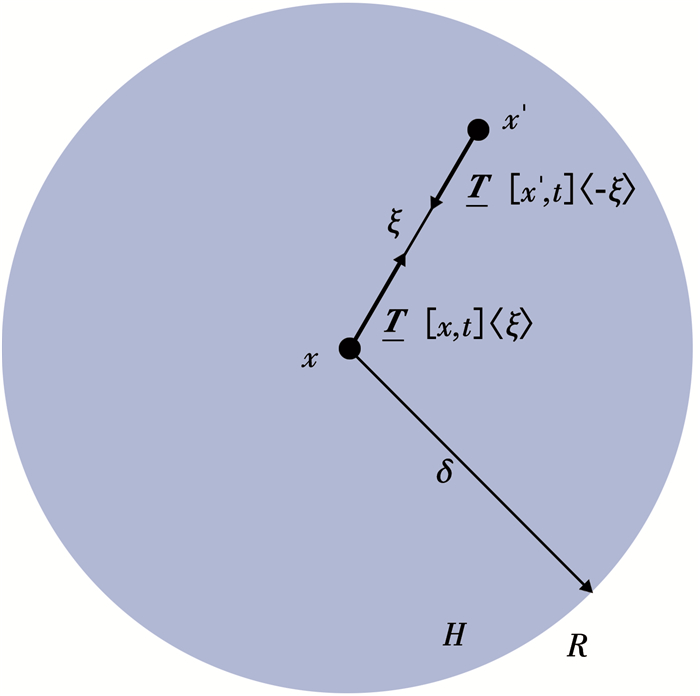
1.1 平面应力问题的OSPD理论如图 1所示,在OSPD中,连续体被离散为一系列的物质点,则点x的运动方程写为
| $ \begin{align} & \rho \left( x \right)\mathit{\boldsymbol{\ddot{u}}}\left( x, t \right)=b\left( x, t \right)+\int_{H}{\left( \mathit{\boldsymbol{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{T}}}\left[ x, t \right]\left\langle \xi \right\rangle\right.}- \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left. \mathit{\boldsymbol{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{T}}}\left[ {x}', t \right]\left\langle -\xi \right\rangle \right)\text{d}{{V}_{{{x}'}}}. \\ \end{align} $ |
|
图 1 OSPD中的力状态 Fig. 1 Force vector state in ordinary state-based peridynamics(OSPD) |
式中:ρ为物质密度; u为物质点位移; b为外载荷密度; H=H(x, δ):{x′∈R:‖x′-x‖≤δ}为物质点x的领域范围; ξ=x-x′为物质点之间的相对位置;T[x, t]〈ξ〉- T[x′, t]〈-ξ〉为点对的相互作用,称之为“键”.
物质点对间的力状态表示为T=tM,其中:M为一个向量状态,表示键变形方向的单位向量;t为一个标量状态,表示力的大小.t的表达式为[21]
| $ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{t}=\frac{2\left( 2v-1 \right)}{\left( v-1 \right)}\left( {k}'\theta -\frac{\alpha }{3}\left( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e}}}^{d}} \right)\cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \right)\frac{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}}{q}+\underline{\alpha \omega }{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e}}}^{d}}, $ |
其中θ、α、k′、ed的表达式分别为:
| $ \theta =\frac{2\left( 2v-1 \right)}{\left( v-1 \right)}\frac{\left( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \right)\cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e}}{q}, $ |
| $ \alpha =\frac{8G}{q}, $ |
| $ {k}'=k+\frac{G{{\left( v+1 \right)}^{2}}}{9{{\left( 2v-1 \right)}^{2}}}, $ |
| $ {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e}}}^{d}}=\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e}-\frac{\underline{\theta x}}{3}. $ |
式中:e为伸长标量状态,表示键变形前后的长度变化;ω为一个与|ξ|有关的标量函数;x为参考位置标量状态;v为泊松比;q为加权体积,其表达式为q=(ωx)·x;G为材料的剪切模量;k为材料的体积模量.
PD理论通过一个标量函数μ来表征键是否断裂,通常认为当键的伸长率超过临界伸长率s0时“键”发生破坏,μ的取值从1变为0,两点之间的相互作用消失:
| $ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{t}=\mu \left[ \frac{2\left( 2v-1 \right)}{\left( v-1 \right)}\left( {k}'\theta -\frac{\alpha }{3}\left( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e}}}^{d}} \right)\cdot \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \right)\frac{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\omega }\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}}{q}+\underline{\alpha \omega }{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{e}}}^{d}} \right]. $ |
通过函数μ定义了PD理论中物质点x处的“损伤指数”,表征物质点x处发生损伤的程度为
| $ \varphi \left( x, t \right)=1-\frac{\int_{H}{\mu \text{d}{{V}_{{{x}'}}}}}{\int_{H}{\text{d}{{V}_{{{x}'}}}}}, $ |
当φ=0时表示材料未发生损伤,φ=1表示材料完全损伤.
1.2 PD疲劳理论PD疲劳理论需要通过对模型的一次准静态分析来处理一次载荷循环,得到这一次载荷循环中键的损伤量.随着循环加载次数的增加,依据疲劳累积损伤定律,键的损伤逐步累积,当达到一定的条件时最终发生键的失效,键不再承载力,从而得到疲劳裂纹的萌生和扩展.
为体现键的损伤,在标量函数μ中引入一个称为“剩余寿命”λ的参数,将μ改写为
| $ \mu \left( \lambda , t \right)=\left\{ \begin{align} &0, s>{{s}_{0}}或\lambda \le 0; \\ &1, 其他. \\ \end{align} \right. $ |
每个键都有各自的剩余寿命λ,λ与循环加载次数N的关系式以及初始值设为:
| $ \frac{\text{d}\lambda }{\text{d}N}\left( N \right)=-A{{\varepsilon }^{p}}, $ | (1) |
| $ \lambda \left( 0 \right)=1. $ | (2) |
式中:ε=|smax-smin|为键的“循环应变”,其中smax、smin分别为在一次载荷循环中某个键的伸长率的最大值和最小值,通过使用准静态分析得到ε;A、p分别为待定的常数,需要与实验数据拟合得到,裂纹萌生阶段和裂纹扩展阶段分别对应不同的A和p.
1.2.1 裂纹萌生阶段在疲劳裂纹萌生阶段,对于整个试件中最大的循环应变,记为ε1,裂纹将从该处生成,将ε1代入式(1)并对式(2)积分,得
| $ {{N}_{1}}=\frac{1}{{{A}_{1}}\varepsilon _{1}^{{{p}_{1}}}}. $ | (3) |
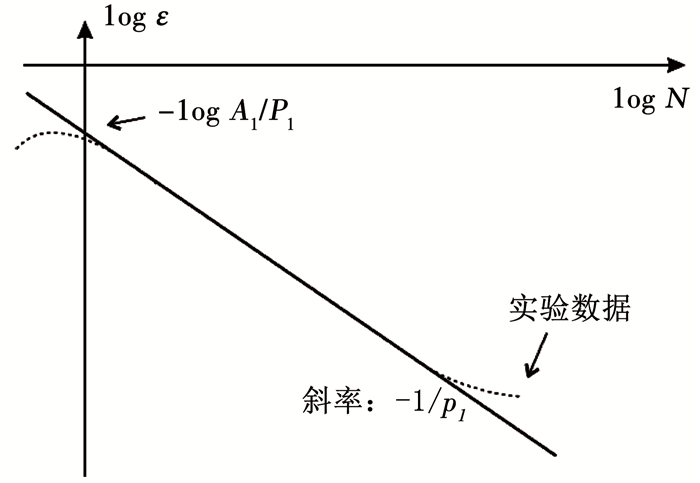
在双对数坐标下,将式(3)与S-N曲线中间段部分拟合,得到适用于该阶段的A和p的值,记做A1和p1,如图 2所示.
|
图 2 与实验数据拟合得到参数 Fig. 2 Constants obtained by fitting with experimental data |
在疲劳的研究中,微观裂纹何时变成宏观裂纹的区分长度需要进行定义,在PD疲劳理论中物质点何时会从裂纹萌生阶段进入裂纹扩展阶段也需要进行定义,文献[15]给出的意见是,当一个物质点x的损伤指数大于0.5时,物质点处于裂纹扩展阶段(否则处于裂纹萌生阶段),计算邻域范围内的键的损伤时,参数选用A2和p2.
在疲劳裂纹扩展阶段,有[15]
| $ \frac{\text{d}a}{\text{d}N}=C\varepsilon _{\text{core}}^{{{p}_{2}}}, C=\beta {{A}_{2}}. $ | (4) |
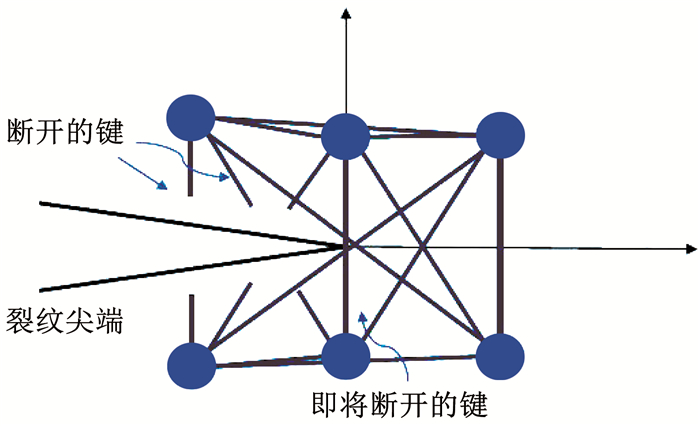
式中:β为一与结构有关的常数,代表结构对应变分布的影响因子;εcore为处于裂纹扩展阶段的物质点x的邻域内最大的循环应变.裂纹尖端附近的简化示意图如图 3所示,因空间中存在的键较多,图 3中只给出了与裂纹扩展有关联的部分键.
|
图 3 裂纹尖端处键示意 Fig. 3 Schematic of bonds near a crack tip |
该式与描述疲劳裂纹扩展规律的Paris公式相似:
| $ \frac{\text{d}a}{\text{d}N}=c\Delta {{K}^{M}}. $ | (5) |
式中:c、M分别为材料相关的常数; ΔK为应力强度因子范围.
根据线弹性断裂力学,ΔK与循环应变成正比[15],因此将式(4)与式(5)进行对比,直接得到p2=M.计算A2的办法为:先给A2随意赋值A′,然后试施加循环载荷,将得到裂纹扩展速率(da/dN)′,因为裂纹扩展速率da/dN与A线性相关,所以将(da/dN)′与实际的裂纹扩展速率da/dN相除,便得到一修正系数,继而得到正确的A2值为
| $ {{A}_{2}}={A}'\frac{\text{d}a/\text{d}N}{{{\left( \text{d}a/\text{d}N \right)}^{\prime }}}. $ |
在疲劳裂纹扩展的计算与模拟中,对每一个载荷循环进行模拟运算会大大增加运算时间.一般采用的方法为“载荷循环分间隔处理法”[20]:给定一个ΔN,一次载荷循环结束后,根据当前计算出的应力强度因子ΔK,在接下来的ΔN次循环中裂纹尖端都是以ΔK进行裂纹扩展的计算而不用重新计算ΔK,随后总循环次数直接增加ΔN.但该方法存在一定的不足,如图 4所示,对于同样的ΔN,在裂纹扩展的前期,裂纹扩展的速度慢,对应的裂纹扩展距离Δa1较小,计算效率较低;而在后期,随着循环次数的增加裂纹扩展速度迅速增长,ΔN次循环中裂纹扩展距离Δa2也迅速变大,会导致误差的成倍上升,出现计算结果不准确的问题.该方法在近场动力学提出前便广泛应用在疲劳裂纹扩展的工程计算和研究中.

|
图 4 a-N曲线 Fig. 4 a-N curve |
在近场动力学中,裂纹扩展是伴随着键的断裂进行的,参考“载荷循环分间隔处理法”的思想,本文通过控制每次断裂的键的数目来达到控制模型计算速度的目的,即建立“断裂键数分间隔处理法”.据此,本文在OSPD疲劳理论中引入一个参量“临界断裂数”nc,构造了PD疲劳理论的计算流程:
1) 初始化模型的所有参数,为一次准静态分析做准备.
2) 如果循环次数N小于设定的最大循环次数Nmax,进行一次准静态分析,得到各个键的伸长率.
3) 在判断键是处于裂纹萌生阶段或者裂纹扩展阶段之后,通过式(1)、(2),分别计算出各个键在一定循环应变下发生断裂所需要的循环次数,在其中筛选出所需循环次数最小的nc个键(不考虑计算效率时最理想的情况为nc=1),同时使这nc个键发生破坏,这nc个键对应的循环次数中最大的记为ΔN1,总循环次数也随之增加ΔN1.
4) 对于其他未发生破坏的键,则将这ΔN1次载荷循环中产生的损伤累积在键中(体现在λ的减小),然后准备进入下一次的准静态分析中.
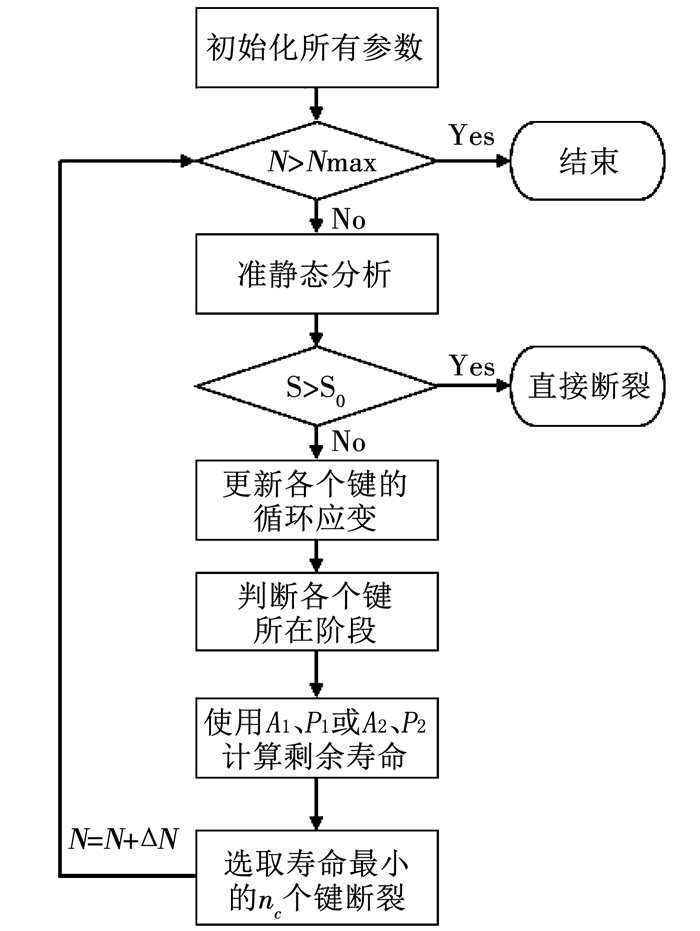
图 5所示的流程图展示了引入“临界断裂数”的近场动力学疲劳理论计算流程.
|
图 5 OSPD疲劳理论计算流程 Fig. 5 Flow chart of OSPD fatigue theory |
以动力松弛法作为方程求解方法,在平面应力问题的OSPD疲劳理论、断裂键数分间隔处理法的基础之上,编写了基于平面应力问题OSPD疲劳理论的计算程序.
3.1 单边裂纹板的疲劳破坏模拟以单边裂纹板为对象,比较不同的nc的取值下疲劳裂纹扩展的情况.模型被均匀离散为一系列物质点,物质点间距为Δx=0.5 mm,邻域范围按建议[22]取δ=3Δx,时间步长Δt=1 s.模型参数如下:1)几何参数.长宽分别为102、50 mm,缺口位于平板上侧中间位置,长10 mm、宽2 mm;2)材料参数.弹性模量取为450 00 MPa,泊松比v取为0.2;3)PD疲劳参数则取A1=1.05×105, p1=3.4, A2=1.80×106, p2=3.0;4)模型左端固定,右端施加拉力,载荷最大值为21.5 MPa,应力比取R=0.
如图 6所示分别为nc取15、25、50、100时(其中nc=50、100时前两次计算取nc=25),裂纹扩展一定距离后的结果,其中红色最深处表示损伤指数为1,蓝色最深处为0,白色区域为裂纹.该模型一共存在557 368个键,表 1展示了每个nc占模型所有键数目的比例以及裂纹扩展9 mm的循环加载次数N,随着nc的增大,次数N也增大,损伤指数大于0的物质点的范围的大小(在本文中这个范围称为裂纹路径精准度,因为损伤范围越小,得到的裂纹路径越精准)也影响着N变动的幅度.nc为15时生成的裂纹较细,而nc为25、50时裂纹粗细基本一致,导致后者N的变动幅度更小(14.28%>13.86%).

|
图 6 取不同nc时的疲劳裂纹扩展 Fig. 6 Fatigue crack propagation with different nc |
| 表 1 不同nc占总键数的比例 Tab. 1 The proportion of nc in bonds number |
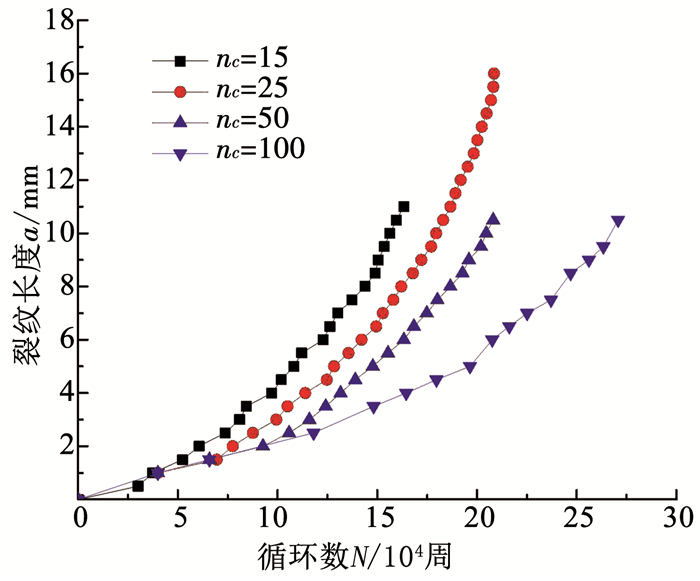
图 7展示了不同nc值时单边裂纹板疲劳扩展的a-N曲线,裂纹扩展后期数据点更密集,避免了后期误差较大的问题,相应地前期的误差变大,但可以考虑在前几次准静态过程中取更小的nc来修正(如本例中nc=50、100时前两次取nc=25).对比图 6,若只为了得到较好的裂纹路径精准度,nc取25即足够.在实际应用中,通过A和p的取值,不同nc对应的a-N曲线偏差对实际计算没有影响.
|
图 7 取不同nc时的a-N曲线 Fig. 7 a-N curve with different nc |
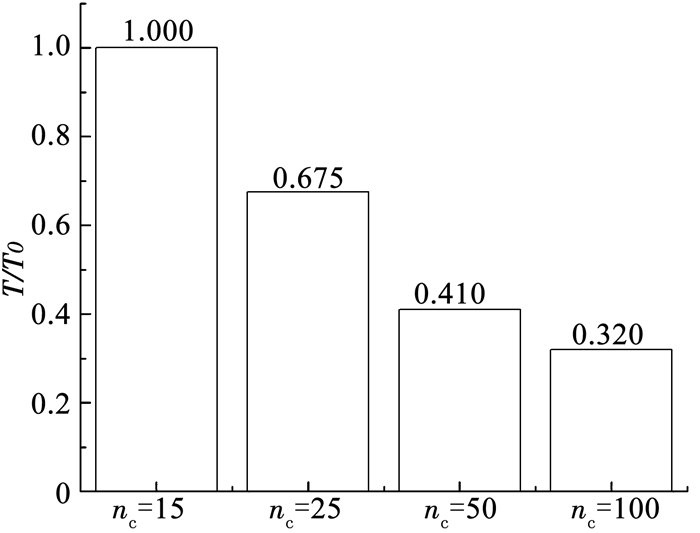
图 8则展示了不同nc值下裂纹扩展9 mm所需要的计算时间T(以T0表示当nc=15时的时间),随着nc值的增大,模型运行时间显著减少,nc值越大运行时间减少幅度越小,这也与nc值更大时疲劳裂纹更粗有关.从结果中比较可知,对于本模型,当nc=25时,在保证较好的裂纹图像的同时,也一定程度上提升了计算速度.
|
图 8 裂纹扩展相同距离程序运行所需时间 Fig. 8 Program runtime of same crack propagation distance |
广布疲劳裂纹问题中需要考虑各个生成的裂纹之间的相互影响,而近场动力学中裂纹的生成被蕴含在本构方程中,能自然的描述裂纹的生成和扩展,不必选用不同的断裂判据,在材料的冲击损伤、动态断裂等复杂问题中具有先天的优势,为此建立一个多裂纹板的平面应力下OSPD疲劳模型,对其进行了模拟.
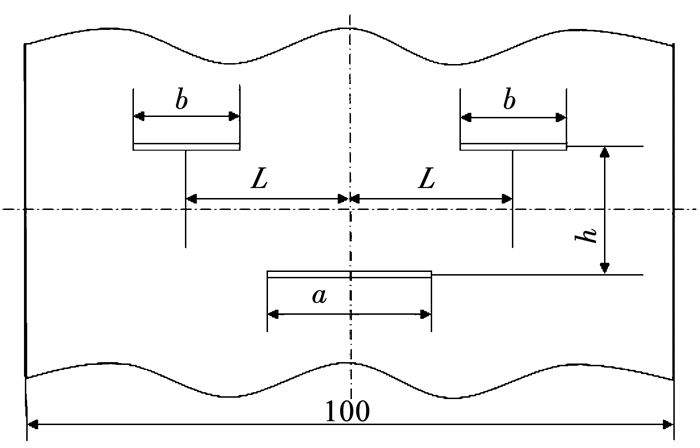
首先对非共线多裂纹板的拉伸破坏进行分析.模型物质点间距Δx=1 mm,邻域范围δ=3Δx,时间步长Δt=1 s;材料为2024-T3铝合金,该材料的弹性模量为724 00 MPa,泊松比0.33;试件尺寸为250 mm×100 mm×1.44 mm,如图 9所示,其中a=20 mm,b=16 mm,L=10 mm,h=15 mm.试件一端固定一端施加载荷直至破坏.
|
图 9 模型尺寸示意 Fig. 9 Schematic model |
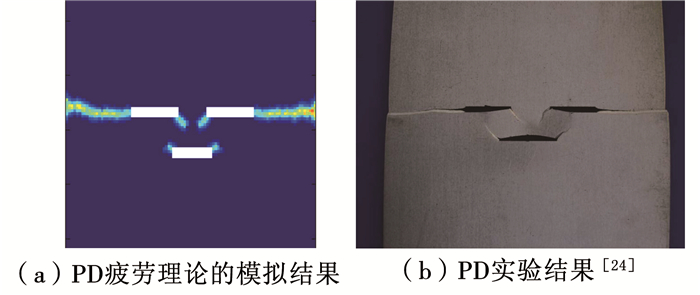
该材料的临界伸长率通过文献[23]的方法计算得到为6.5×10-3.多裂纹板拉伸破坏最终形式的模拟和实验结果如图 10所示,定性地来看,裂纹生成的位置与裂纹扩展的方向与文献[24]中的实验结果基本一致.上侧的两条裂纹向两端扩展,使得多裂纹板最终发生破坏,上侧的两条裂纹之间虽有生成裂纹,但并未连通.
|
图 10 多裂纹板的拉伸破坏 Fig. 10 Tensile failure of panel with multiple cracks |
之后进行非共线多裂纹板的疲劳破坏分析,试件尺寸、材料等参数与上述一致,疲劳载荷的平均载荷6.5 kN,载荷幅值5.5 kN.
因薄板内已存在初始裂纹,初始裂纹尖端附近的点直接进入裂纹扩展阶段.根据文献[24]中的实验结果以及裂纹扩展阶段中所述方法,设置的相关参数为:1)nc=25, A2=76, p2=2.1;2)nc=50, A2=59, p2=2.1.
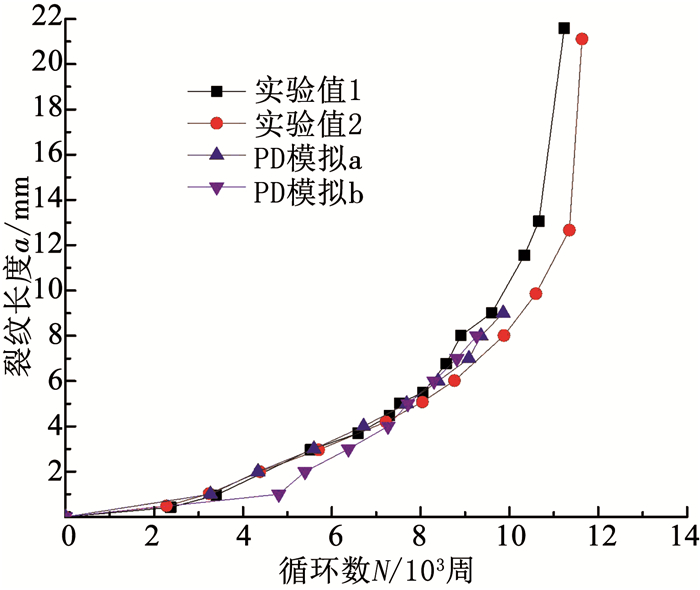
将此时的模拟结果与实验结果作对比,得到如图 11所示的裂纹扩展长度a(以初始裂纹外侧端部作为起点)和循环次数N的关系曲线,可见PD疲劳理论不需额外设置断裂判据,便能较好的拟合复杂裂纹网络的疲劳破坏实验结果,在裂纹扩展初期,nc=25的曲线与实验值更贴近,nc=50的曲线有些许偏离,但在裂纹扩展后期,两者之间差距已经很小,如果在nc=50的前几次计算中取更小的值,则曲线更贴近.而在计算时间上,PD模拟b相比PD模拟a则减少了约45%.
|
图 11 裂纹长度a-循环次数N关系 Fig. 11 a-N curve |
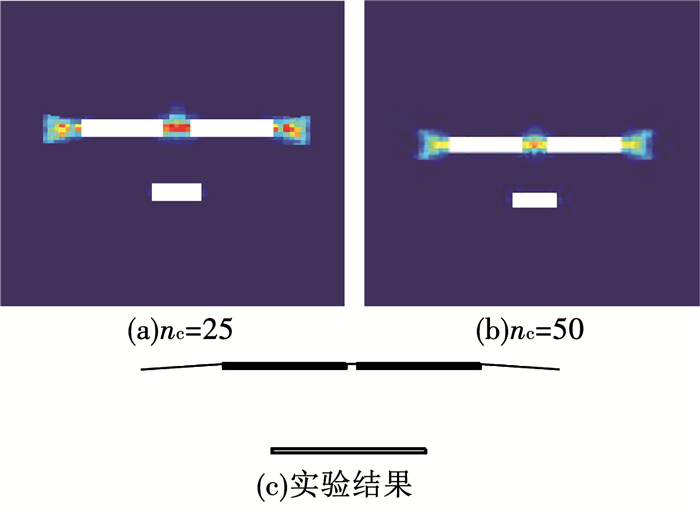
再从裂纹扩展路径上来看,如图 12所示,试件疲劳破坏的形式已经与拉伸破坏有很明显的不同.PD疲劳理论的模拟结果与实验结果的裂纹扩展路径基本保持一致,位于上方的两条裂纹在中间发生连通,两端向外扩展,位于下方的初始缺陷的尖端虽有少量键断裂,但未继续扩展.对于不同的nc,两者皆能正确的模拟出裂纹的扩展路径.
|
图 12 多裂纹板的疲劳破坏实验结果示意[24] Fig. 12 Fatigue failure of panel with multiple cracks |
1) 在近场动力学理论中,本构方程里包含了损伤与断裂的描述,因此裂纹的萌生、扩展、连通在模拟过程中都能自然的发生,且不必在模型中预制裂纹,也不用提出任何断裂准则,相比传统方法具有优势.
2) 本文以平面应力的常规态型近场动力学为基础,模拟了非共线多裂纹板在疲劳载荷作用下的裂纹扩展行为,在不同的“临界断裂数”的情况下,模拟得到的a-N曲线均能较好的拟合实验值.结果表明,在常规态型近场动力学的框架下,近场动力学疲劳理论在模拟复杂裂纹网络的疲劳破坏上是一种有效的工具.
3) 结果表明,通过采用“断裂键数分间隔处理法”,并选取合适的“临界断裂数”的方式,可以在一定程度上提高近场动力学疲劳理论的数值模拟的计算速度.
| [1] |
徐武.飞机结构多位置损伤分析的权函数法与剩余强度预测[D].上海: 上海交通大学, 2012 XU Wu. Weight function method for aircraft structure multiple site damage analyses and residual strength prediction[D]. Shanghai: Shanghai Jiao Tong University, 2012 http://cpfd.cnki.com.cn/Article/CPFDTOTAL-AGLU201211002149.htm |
| [2] |
SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1): 175. DOI:10.1016/S0022-5096(99)00029-0 |
| [3] |
乔丕忠, 张勇, 张恒, 等. 近场动力学研究进展[J]. 力学季刊, 2017, 38(1): 1. QIAO Pizhong, ZHANG Yong, ZHANG Heng, et al. A review on advances in peridynamics[J]. Chinese Quarterly of Mechanics, 2017, 38(1): 1. DOI:10.15959/j.cnki.0254-0053.2017.01.001 |
| [4] |
KILIC B, MADENCI E. An adaptive dynamic relaxation method for quasi-static simulations using the peridynamic theory[J]. Theoretical and Applied Fracture Mechanics, 2010, 53(3): 194. DOI:10.1016/j.tafmec.2010.08.001 |
| [5] |
HUANG Dan, LU Guangda, QIAO Pizhong. An improved peridynamic approach for quasi-static elastic deformation and brittle fracture analysis[J]. International Journal of Mechanical Sciences, 2015, 94-95: 111. DOI:10.1016/j.ijmecsci.2015.02.018 |
| [6] |
HU Wenke, HA Y D, BOBARU F. Peridynamic model for dynamic fracture in unidirectional fiber-reinforced composites[J]. Computer Methods in Applied Mechanics & Engineering, 2012, 217-220: 247. DOI:10.1016/j.cma.2012.01.016 |
| [7] |
HA Y D, BOBARU F. Studies of dynamic crack propagation and crack branching with peridynamics[J]. International Journal of Fracture, 2010, 162(1/2): 229. DOI:10.1007/s10704-010-9442-4 |
| [8] |
刘肃肃, 余音. 复材非线性及渐进损伤的态型近场动力学模拟[J]. 浙江大学学报(工学版), 2016, 50(5): 993. LIU Susu, YU Yin. State-based peridynamic modeling of nonlinear behavior and progressive damage of composites[J]. Journal of Zhejiang University (Engineering Science), 2016, 50(5): 993. DOI:10.3785/j.issn.1008-973X.2016.05.025 |
| [9] |
HU Yile, YU Yin, WANG Hai. Peridynamic analytical method for progressive damage in notched composite laminates[J]. Composite Structures, 2014, 108(1): 801. DOI:10.1016/j.compstruct.2013.10.018 |
| [10] |
CHENG Zhanqi, ZHANG Guanfeng, WANG Yenan, et al. A peridynamic model for dynamic fracture in functionally graded materials[J]. Composite Structures, 2015, 133: 529. DOI:10.1016/j.compstruct.2015.07.047 |
| [11] |
顾鑫, 章青, 黄丹. 基于近场动力学方法的混凝土板侵彻问题研究[J]. 振动与冲击, 2015, 35(6): 52. GU Xin, ZHANG Qing, HUANG Dan. Peridynamics used in solving penetration problem of concrete slabs[J]. Journal of Vibration and Shock, 2015, 35(6): 52. DOI:10.13465/j.cnki.jvs.2016.06.009 |
| [12] |
黄丹, 章青, 乔丕忠, 等. 近场动力学方法及其应用[J]. 力学进展, 2010, 40(4): 448. HUANG Dan, ZHANG Qing, QIAO Pizhong, et al. A review on peridynamic(PD) method and its applications[J]. Advances in Mechanics, 2010, 40(4): 448. |
| [13] |
SILLING S A, EPTON M, WECKNER O, et al. Peridynamic states and constitutive modeling[J]. Journal of Elasticity, 2007, 88(2): 151. DOI:10.1007/s10659-007-9125-1 |
| [14] |
OTERKUS E, GUVEN I, MADENCI E. Fatigue failure model with peridynamic theory[C]//Proceedings of the 12th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm). Las Vegas, NV: IEEE, 2010. DOI: 10.1109/ITHERM.2010.5501273
|
| [15] |
SILLING S A, ASKARI A. Peridynamic model for fatigue cracking: SAND2014-18590[R]. Albuquerque, NM: Sandia National Laboratory Report, 2014
|
| [16] |
JUNG J Y, SEOK J. Fatigue crack growth analysis in layered heterogeneous material systems using peridynamic approach[J]. Composite Structure, 2016, 152: 403. DOI:10.1016/j.compstruct.2016.05.077 |
| [17] |
ZHANG Guanfeng, LE Quang, LOGHIN A, et al. Validation of a peridynamic model for fatigue cracking[J]. Engineering Fracture Mechanics, 2016, 162: 76. DOI:10.1016/j.engfracmech.2016.05.008 |
| [18] |
HU Yile, MADENCI E. Peridynamics for fatigue life and residual strength prediction of composite laminates[J]. Composite Structure, 2017, 160: 169. DOI:10.1016/j.compstruct.2016.10.010 |
| [19] |
ZACCARIOTTO M, SAREGO G, DIPASQUALE D, et al. Simulation of fatigue crack growth in heterogeneous material with peridynamics[C]//Proceeding of the 21st European Conference on Fracture(ECF21). Catania: [s.n.], 2016
|
| [20] |
应中伟, 冯蕴雯, 薛小锋, 等. 改进的载荷循环分间隔法计算工程中MSD裂纹疲劳扩展问题[J]. 航空学报, 2008, 29(4): 898. YING Zhongwei, FENG Yunwen, XUE Xiaofeng, et al. Improved division of cyclic loading method for MSD fatigue crack growth in engineering[J]. Acta Aeronautica ET Astronautica Sinica, 2008, 29(4): 898. DOI:10.3321/j.issn:1000-6893.2008.04.021 |
| [21] |
LE Q V, CHAN W K, SCHWARTZ J. A two-dimensional ordinary, state-based peridynamic model for linearly elastic solids[J]. International Journal for Numerical Methods in Engineering, 2014, 98(8): 547. DOI:10.1002/nme.4642 |
| [22] |
SILLING S A, ASKARI E. A meshfree method based on the peridynamics model of solid mechanics[J]. Computers and Structures, 2005, 83(17/18): 1526. DOI:10.1016/j.compstruc.2004.11.026 |
| [23] |
GERSTLE W H, SAU N, SAKHAVAND N. On peridynamic computational simulation of concrete structures[J]. ACI Special Publication, 2009, 245. |
| [24] |
张松林.多裂纹板破坏过程模拟及寿命预计[D].南京: 南京航空航天大学, 2006 ZHANG Songlin. Crack growth simulation and fatigue life predication of panels containing multiple cracks[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2006 http://cdmd.cnki.com.cn/Article/CDMD-10287-2007194174.htm |
 2019, Vol. 51
2019, Vol. 51


