2. 水声对抗技术重点实验室(中国船舶工业系统工程研究院),北京 100094
2. Science and Technology on Underwater Acoustic Antagonizing Laboratory(CSSC), Beijing 100094, China
水下滑翔机是一种通过调节重、浮力来实行上升、下潜运动的新型海洋探测平台,能够高效地完成海洋环境参数收集任务[1].从理论上讲,滑翔机的升力越大,阻力越小,滑翔机在单个滑翔周期内将具有更远的航程,其滑翔效率就越高[2-3].因此,在设计水下滑翔机的水动力外形时[4],经常将升阻比作为设计指标[5].
水下滑翔机一般由主体和两侧翼板组成,其升力主要由两侧翼板提供,传统的水下滑翔机为单翼设计,升阻比不高[6].为了进一步提高水下滑翔机的升阻特性,本文将航空领域的联翼布局[7-9]与水下滑翔机相结合,重点研究了联翼布局的初始外形设计、平面形状的参数化建模和Kriging代理模型结合EGO算法[10]的优化过程,设计出了联翼式水下滑翔机外形.
1 初始外形设计 1.1 主体外形为了与单翼水下滑翔机进行对比,联翼式水下滑翔机的主体外形与slocum滑翔机[11]保持一致,主体长度1 788 mm,最大直径210 mm,主体两端采用椭球形线型,头部段长度210 mm,尾部段长度378 mm.有关该主体的主要尺寸以及相关参数见表 1.
| 表 1 主体外形参数表 Tab. 1 Main body shape parameter |
联翼布局主要有3种不同的布局形式,分别为正交错、负交错和联尾翼布局. 3种外形选取相同的机翼展长、弦长、后掠角以及截面形状,仅改变前后翼的连接方式.表 2给出了3种水下滑翔机模型的联翼布局方式和基本参数,图 1~3给出了3种联翼布局水下滑翔机的三维模型.

|
图 1 正交错布局 Fig. 1 Positive staggered layout |

|
图 2 负交错布局图 Fig. 2 Negative staggered layout |

|
图 3 联尾翼布局 Fig. 3 Combined empennage layout |
| 表 2 3种联翼布局形式水下滑翔机的基本参数 Tab. 2 Essential parameters of three kinds of joined wing layout underwater gliders |
3种布局形式中,正交错布局是带后掠角的前翼在主体水平对称面以上,带前掠角的后翼在主体水平对称面以下的布局形式,如图 1所示.负交错布局是带后掠角的前翼在主体水平对称面以下,带前掠角的后翼在主体水平对称面以上的布局形式,如图 2所示.上述两种布局形式,前、后翼的高度差设定为120 mm.联尾翼布局是一种特殊的负交错布局形式,不同在于其后翼翼根与尾翼相连接,前后翼翼根的高度差为180 mm,如图 3所示.
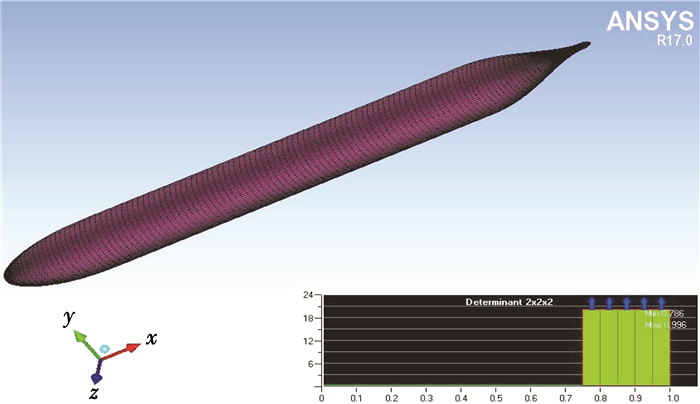
1.3 数值方法的验证为了保证本文数值结果的准确性,需要对运用到的数值方法[12-13]进行有效性验证.由于水下滑翔机的具体实验数据较少,本文以Huang等[14]的雷体实验模型为例进行数值方法的验证.为了确保本文数值计算结果的准确性,采用相同的数值计算方法与该实验数据进行了对比分析.该实验目的是测量一个雷体在水下的压力分布情况,实验模型长2.91 m,最大直径为0.28 m,雷诺数为9.3×106.数值计算中雷体网格划分采用结构化网格,网格总数为534 285,网格质量大于0.75.图 4、5分别展示了尾部的边界层网格和雷体的整体网格.

|
图 4 雷体尾部的边界层网格图 Fig. 4 Detailed grids of the boundary layers of the tail of mine |
|
图 5 雷体整体网格及网格质量图 Fig. 5 Whole grid and grid quality of mine |
图 6为通过CFD软件得到的仿真结果与实验结果的对比情况,CP为压力系数,X/L为雷体测量点的位置分布情况(实验测量值为X/L>0.65的压力分布).从图 6中可以看出,当X/L>0.85时,仿真计算与实验测量得到压力系数表现出了高度的一致性;在X/L < 0.75时,仿真计算的结果虽然与实验结果有一定的差异,但差距很小.压力分布的具体数据见表 3.对比结果表明,数值计算结果与实验结果十分接近,两者都具有相似的压力分布轨迹,从而证明了本文所采用的数值方法的有效性.

|
图 6 仿真计算和实验测量下雷体的压力分布图 Fig. 6 Pressure distribution of mine under simulation and experiment |
| 表 3 数值计算和实验测量得到的压力分布具体数据 Tab. 3 Specific data of the pressure distribution of mine under simulation and experiment |
由于滑翔机左右对称,所以取1/2模型,建立流场域,划分网格进行计算.采用六面体结构化网格进行流场域网格划分,整体网格数量在120~180万之间,在滑翔机表面采用了O-Block进行网格加密.图 7、8分别展示了流场域的网格划分情况及滑翔机表面结构化网格.

|
图 7 流场域结构化网格 Fig. 7 Structured grid of flow field |

|
图 8 滑翔机表面结构化网格 Fig. 8 Structured grid of underwater glider surface |
对表 4中的3种联翼式水下滑翔机模型进行CFD仿真计算,航速取0.35 m/s,攻角取0°、1°、3°、5°、7°、9°、11°、13°、15°、17°、19°共11种不同情况进行数值计算,并与Slocum进行对比,重点关注升力、升阻比与表面压力分布等情况.
| 表 4 不同模型的最大升阻比对比 Tab. 4 Comparison of maximum lift drag ratio of different models |
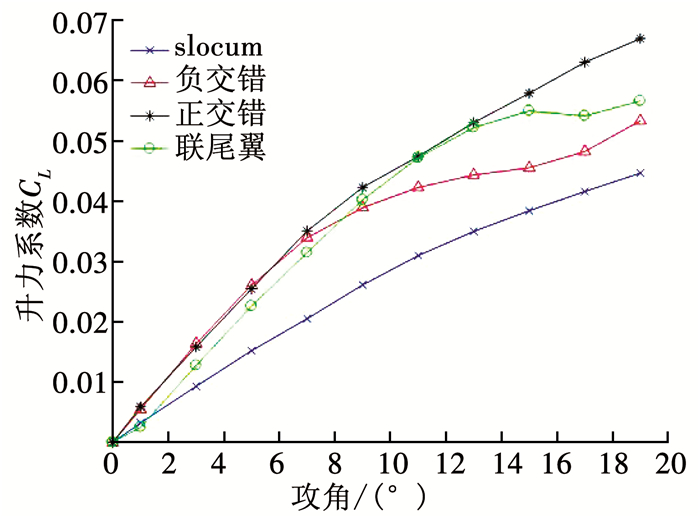
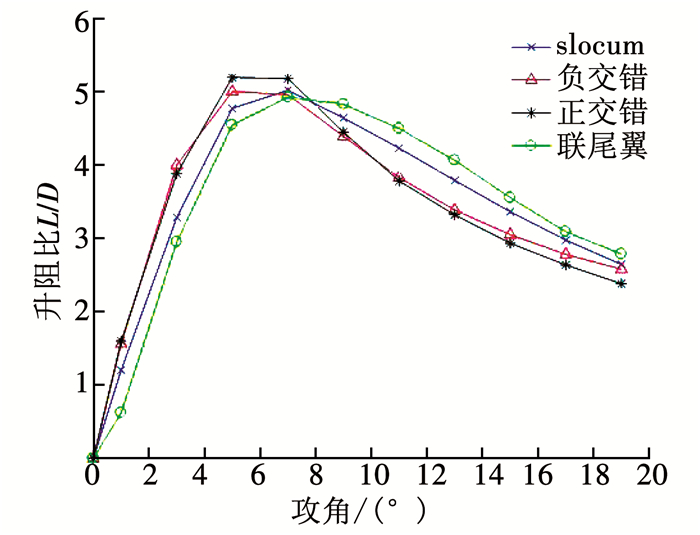
将通过CFD计算得到的升力系数和升阻比汇总并绘制成随攻角的变化曲线图,如图 9、10所示.由图 9可知,升力系数将随着攻角的增大而增大.其中,采用联翼布局的3种滑翔机的升力特性明显好于slocum单翼滑翔机.由图 10可知,随攻角的增大,4种模型的升阻比均呈现先迅速增大后缓慢减小变化规律,且都在5°~7°攻角范围达到最大升阻比.由表 4可知,正交错布局的最大升阻比为5.193 4,大于其他布局方式.联尾翼布局的最大升阻比为4.924 8,小于其他布局方式.
|
图 9 升力系数随α的变化曲线 Fig. 9 Variation curve of the lift coefficient with the attack angle |
|
图 10 升阻比随α的变化曲线 Fig. 10 Variation curve of the lift drag ratio coefficient with the attack angle |
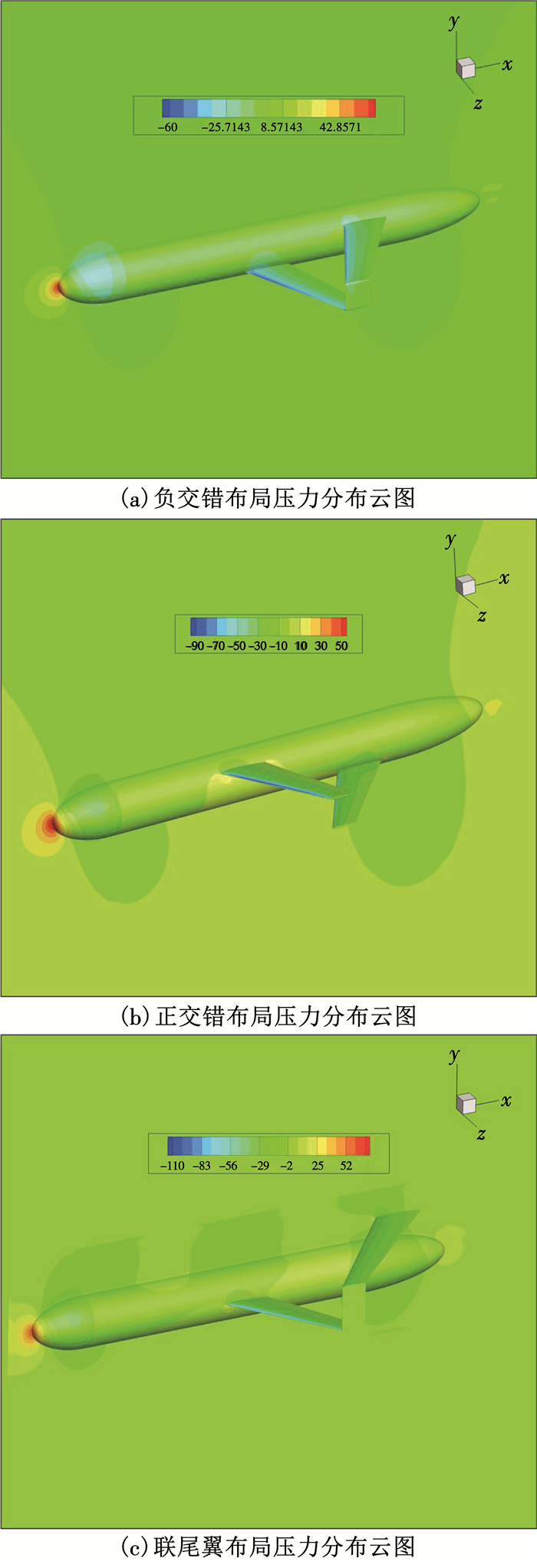
图 11给出了不同联翼布局方式的水下滑翔机在5°攻角下的表面压力分布情况.可以看出,3种联翼布局的表面压力分布情况基本相同,正交错布局的表面压力分布最为均匀,机身和机翼都呈现出明显且均匀的压力梯度,而在相同条件下,机身表面的压力分布越均匀,机体的升力就越大,并且诱导阻力就越小.另外,3种模型的对称面压力分布的主要不同之处在于中间连接翼的位置以及尾部的高压区,而正交错布局压力最小,并且分布集中.
|
图 11 3种布局的压力分布云图 Fig. 11 Pressure distribution cloud map of three kinds of layouts |
综上所述,考虑到正交错布局升阻性能是最好的.为此,本文将在正交错布局的基础上进行联翼式水下滑翔机参数化建模和外形优化设计研究,从而进一步提高这种布局下的水下滑翔机的升阻比.
2 参数化建模水下滑翔机的外形参数化建模是将水下滑翔机的一些外形变量以参数的形式赋值,在不改变模型拓扑结构的情况下,考虑各部分之间的位置关系,利用参数值驱动外形的特征尺寸,快速生成联翼式水下滑翔机的外形模型图.
2.1 基于CST的翼型参数化方法CST参数化方法是一种基于分类函数/形状函数变换的参数化表示方法,近年来在翼型参数化设计中得到广泛应用CST参数化方法包含一个类函数和一个形状函数,类函数用来确定所表示翼型的种类,形状函数用来具体描述翼型的形状.CST参数化方法的优点是参数数量少,而且生成的翼型具有很高的精度.CST参数化方法下的翼型可以表示如下:
| $ Y=C\left( x \right)S\left( x \right)+T\left( x \right). $ | (1) |
式中:C(x)为类函数(class function);S(x)为形状函数(shape function);T(x)为厚度函数.
本文选取联翼式水下滑翔机的初始翼型为NACA0008,拟采用10变量的CST参数化方法对该翼型进行线性拟合,以期提高翼型的拟合精度.
2.2 描形参数化方法平面形状是联翼式水下滑翔机在水平面的投影形状,该投影形状包含了水下滑翔机最丰富的形状要素,如展长、弦长、后掠角、前掠角、机翼安装位置等.由于正交错联翼布局形式,所以其平面形状可以分解为机身主体,机翼和翼梢端板.
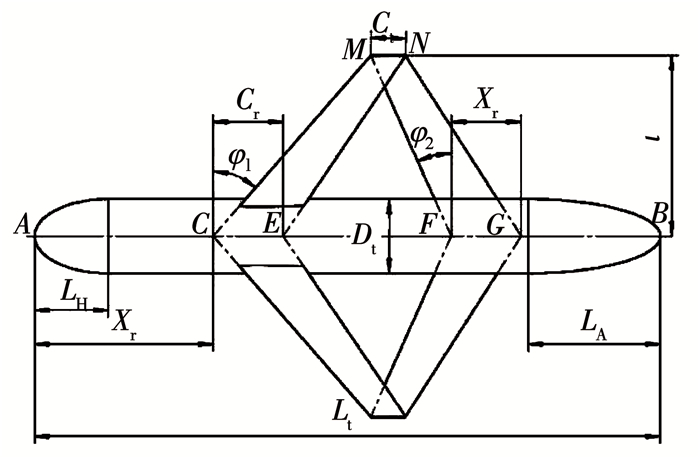
平面几何参数中,主体几何参数由长度Lt,直径Dt,头部段长度LH,尾部段长度LA确定,头尾部线型采用Slocum滑翔机的1/4椭圆线型.平面几何参数中包含了主要的两翼参数,包括两翼的半展长l,前翼的后掠角φ1,后翼前掠角φ2,前翼距头部的距离Xr,以及前后翼的翼根弦长Cr和翼梢弦长Ct,如图 12所示.
|
图 12 联翼式水下滑翔机俯视平面外形参数 Fig. 12 Overlook plane shape parameter of joined-wing underwater glider |
Kriging代理模型[15]在给出设计空间中某一点的预测值的同时也给出了该点的预测方差,预测方差的大小表征了该点预测值的不确定性.而预测方差的大小与预测点所在区域中样本点的疏密程度相关,因此,在预测方差较大的区域加入新的样本点,可以有效地提高Kriging模型的精度,从而提高优化结果的可信度.
对水下滑翔机的外形优化是以水下滑翔机的最大升阻比为优化目标,该数学模型可以表示为
优化目标:
约束条件:
| $ \begin{array}{l} 2.5 \le \lambda \le 5.0, \\ 0 \le {\varphi _1} \le 45, \\ 0.15 \le {x_{\rm{r}}} \le 0.50, \\ 20 \le h \le 200, \\ 1 \le \eta \le 2. \end{array} $ | (2) |
式中:λ为联翼式水下滑翔机的展弦比;φ1为前翼后掠角;h为前后翼高度差;xr=Xr/L为前翼相对于水下滑翔机头部的位置;η为翼根与翼梢之比.
本文通过采用基于Kriging代理模型的高效全局优化算法(efficient global optimization,EGO)[6]优化联翼式水下滑翔机的升阻比.该方法通过最大化一个期望增加函数(expected improvement)来更新样本点,在考虑代理模型最优位置的同时能够探索设计空间的未知区域.期望增加函数表达式为
| $ \begin{array}{l} E\left[ {I\left( x \right)} \right] = \left[ {\hat y - {{\left( {L/D} \right)}_{\max }}} \right] \cdot \mathit{\Phi } \cdot \left[ {\frac{{\hat y - {{\left( {L/D} \right)}_{\max }}}}{s}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;s \cdot \varphi \left[ {\frac{{\hat y - {{\left( {L/D} \right)}_{\max }}}}{s}} \right]. \end{array} $ | (3) |
该问题的收敛条件为
| $ E{I_{{\rm{MAX}}}} \le 0.5\% . $ |
优化过程主要包括以下几个步骤:
1) 初始样本点采取.通常取初始采样的个数满足N>10m(m为变量维数),从优化变量设置可知,本文优化是五维空间寻优问题,因此运用最优拉丁超立方法抽取50组样本点,经仿真计算得到对应的升阻比响应值.
2) 构建Kriging模型.根据采样点及仿真结果构建Kriging代理模型.
3) 迭代寻优.使用遗传算法寻得改善期望(EI(x))的最大值点,将该点作为采样点计算得到响应值,不断更新Kriging代理模型,直到EImax≤0.5%,即达到停止准则,迭代截至.加点具体数据见表 5.
| 表 5 添加样本后的升阻比 Tab. 5 Lift drag ratio after adding samples |
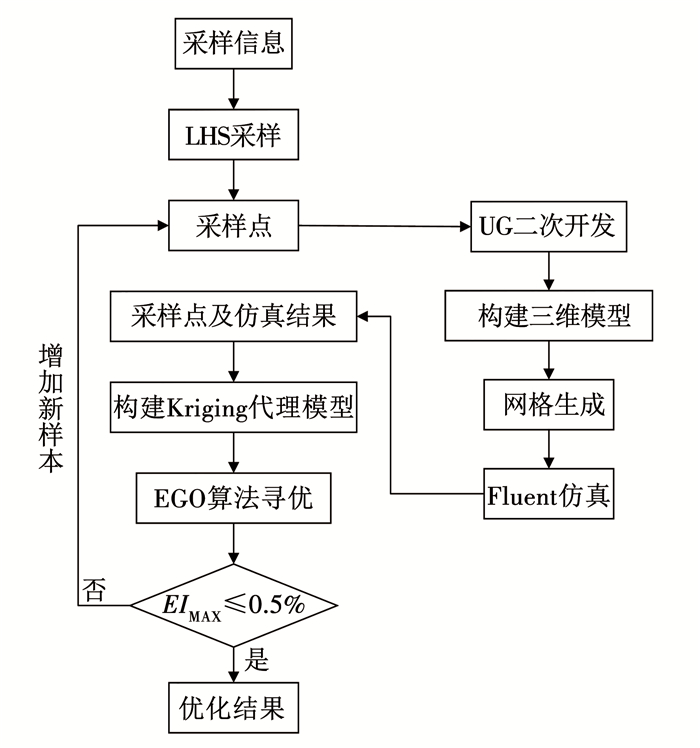
整体优化流程如图 13所示.
|
图 13 优化流程 Fig. 13 Optimization process |
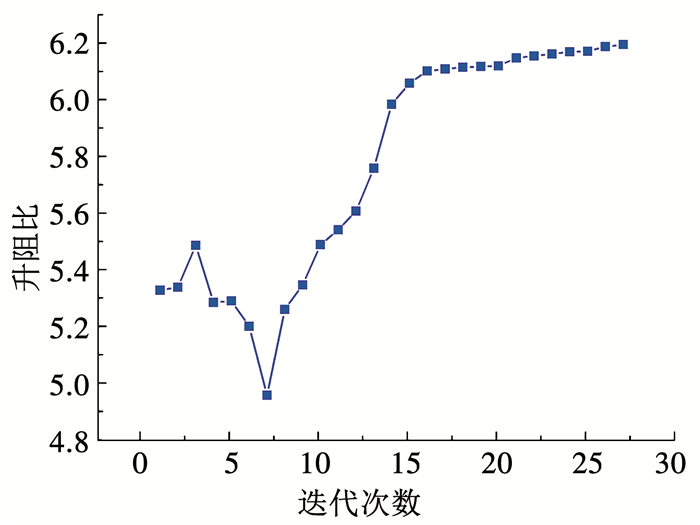
本文中优化迭代过程如图 14所示.在初始样本点数为50的情况下,模型经过27次迭代后达到停止准则,优化结果见表 6.寻优得到的联翼布局外形水下滑翔机最大升阻比为6.195.优化外形与初始外形相比升阻比提高了18.42%,与slocum滑翔机相比提高了23.45%.
|
图 14 EGO加点过程示意 Fig. 14 EGO addition process |
| 表 6 优化结果 Tab. 6 Optimization results |
图 15给出了优化后的外形.从图 15中可以看出,相比于初始设计,优化后的联翼布局外形有明显的变化,具体表现为前翼后掠角和后翼前掠角变小、展弦比变小、两翼高度差变小、根梢比变小等特点,联翼布局中两翼相对位置更紧凑.

|
图 15 优化后的水下滑翔机外形图 Fig. 15 Optimized profile of underwater glider |
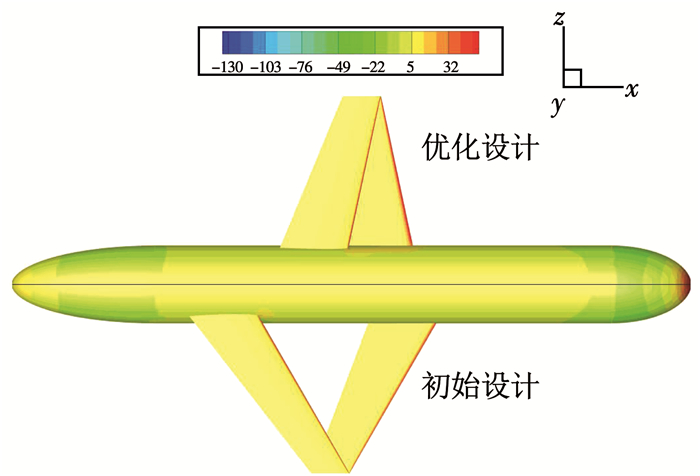
图 16、17给出了联翼式水下滑翔机的初始设计与优化后的上、下表面压力分布情况.从图 16、17中可以看出:两者的主体头部和尾部的压力分布较为相似,整个滑翔机机翼前缘压力小,后缘压力大,整体压力呈从前缘到后缘的递增式分布,最低压区集中在两个机翼前缘中部靠近翼根的位置,分布长度约占半展长的2/3.由机翼与主体连接部分压力分布看,优化后的翼根附近的机身低压区域分布比优化前的初始设计更加均匀,而且,优化后的机翼前缘低压区压力值明显小于初始设计,这会使机翼产生更大的升力.

|
图 16 上表面压力分布对比 Fig. 16 Comparison of upper surface pressure distribution |
|
图 17 下表面压力分布对比 Fig. 17 Comparison of lower surface pressure distribution |
1) 本文将航空领域先进的联翼式布局运用到水下滑翔机的外形优化设计中,针对不同联翼布局模型进行了对比分析,选择升阻比最大的正交错布局作为初始外形布局.
2) 通过运用CST参数化方法和描形参数化方法分别对水下滑翔机的翼型和整体外形进行参数化建模.
3) 构建了Kriging代理模型,并结合EGO算法对水下滑翔机的外形进行了优化设计,相比于初始外形,优化后的联翼布局的外形更加合理.
4) 联翼式水下滑翔机较传统的单翼水下滑翔机(slocum)而言,联翼式水下滑翔机具有优良的升阻特性.研究成果对提高水下滑翔机的滑翔性能提供了一种新思路和途径.
| [1] |
WOOD S, ALLEN T, KUHN S, et al. The development of an autonomous underwater powered glider for deep-sea biological, chemical and physical oceanography[C]//Oceans. Aberdeen, UK: IEEE, 2007. DOI: 10.1109/OCEANSE.2007.4302217
|
| [2] |
李志伟, 崔维成. 水下滑翔机水动力外形研究综述[J]. 船舶力学, 2012, 16(7): 829. LI Zhiwei, CUI Weicheng. Overview on the hydrodynamic performance of underwater gliders[J]. Journal of Ship Mechanics, 2012, 16(7): 829. DOI:10.3969/j.issn.1007-7294.2012.07.014 |
| [3] |
程雪梅. 水下滑翔机研究进展及关键技术[J]. 鱼雷技术, 2009, 17(6): 1. CHENG Xuemei. Development and key technologies of autonomous underwater glider[J]. Torpedo Technology, 2009, 17(6): 1. DOI:10.3969/j.issn.1673-1948.2009.06.001 |
| [4] |
曾庆礼, 张宇文, 赵加鹏. 水下滑翔机总体设计与运动分析[J]. 计算机仿真, 2010, 27(1): 1. ZENG Qingli, ZHANG Yuwen, ZHAO Jiapeng. Design and hydrodynamic analysis of underwater glider[J]. Computer Simulation, 2010, 27(1): 1. DOI:10.3969/j.issn.1006-9348.2010.01.009 |
| [5] |
BHATTA P, LEONARD N E. A lyapunov function for vehicles with lift and drag: stability of gliding[C]//Proceedings of the 43rd Conference on Decision and Control(CDC). Nassau, Bahamas: IEEE, 2004: 4101. DOI: 10.1109/CDC.2004.1429394
|
| [6] |
SUN Chunya, SONG Baowei, WANG Peng, et al. Shape optimization of blended-wing-body underwater glider by using gliding range as the optimization target[J]. International Journal of Naval Architecture & Ocean Engineering, 2017, 9(6): 693. DOI:10.1109/j.ijnaoe.016.12.003 |
| [7] |
WOLKOVITCH J. The joined wing-an overview[J]. Journal of Aircraft, 1986, 23(3): 161. DOI:10.2514/3.45285 |
| [8] |
LAMBERT L A, COOPER J E, NANGIA R K. Buckling alleviation for joined-wing aircraft[C]//Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston, VA: AIAA, 2016, 53(3): 811. DOI: 10.2514/6.2015-1187
|
| [9] |
郑诚行. 连翼布局飞机及探测无人机研究进展[J]. 飞行力学, 2006, 24(4): 1. ZHENG Chengxing. Research and development on joined wing aircraft and sensorcraft[J]. Flight Dynamics, 2006, 24(4): 1. DOI:10.3969/j.issn.1002-0853.2006.04.001 |
| [10] |
JONES D R. Efficient global optimization of expensive black-box functions[J]. Journal of Global Optimization, 1998, 13(4): 455. DOI:10.1023/A:1008306431147 |
| [11] |
WEBB D C, SIMONETTI P J, JONES C P. Slocum: an underwater glider propelled by environmental energy[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 447. DOI:10.1109/48.972077 |
| [12] |
宋保维, 温在顶, 曹永辉. 水下滑翔机外形设计与运动仿真[J]. 计算机仿真, 2011, 28(11): 157. SONG Baowei, WEN Zaiding, CAO Yonghui. Research on movement simulation of underwater gliders[J]. Computer Simulation, 2011, 28(11): 157. DOI:10.3969/j.issn.1006-9348.2011.11.038 |
| [13] |
景思睿, 张鸣远. 流体力学[M]. 西安: 西安交通大学出版社, 2001. JING Sirui, ZHANG Mingyuan. Hydromechanics[M]. Xi'an: Xi'an Jiaotong University Press, 2001. |
| [14] |
HUANG T T, COX D B. Interaction afterbody boundary layer and propeller[C]//Proceedings of the Symposium on Hydrodynamics of the Ship and Offshore Propulsion Systems. Høvik Outside, Oslo: [s.l.], 1977: 2
|
| [15] |
谷海涛, 林扬, 胡志强, 等. 基于代理模型的水下滑翔机机翼设计优化方法[J]. 机械工程学报, 2009, 45(12): 7. GU Haitao, LIN Yang, HU Zhiqiang, et al. Surrogate models based optimization methods for the design of underwater glider wing[J]. Journal of Mechanical Engineering, 2009, 45(12): 7. DOI:10.3901/JME.2009.12.007 |
 2019, Vol. 51
2019, Vol. 51


