近年来，数个国际研究小组通过微压缩实验发现^[1]，微纳尺度金属单晶柱体的塑性应变会发生多次间歇性突变^[2].此外，随着材料外部几何特征尺寸的减小，应变突变(strain burst，也称应变突跳^[3])现象会愈发明显, 这使得应力与位移控制下的应力-应变曲线分别呈现出锯齿状和阶梯状变化^[4].这种特殊的变形行为给微尺度晶体材料的塑性加工成形与力学性能评估带来新的问题.

然而，微小结构的设计工作载荷通常会超过弹性极限^[1]，这就需要准确掌握它们在外载荷下的塑性响应.近期发展的间歇性晶体塑性理论模型^[5-6]能够较为准确合理地描述金属单晶阶梯状变形行为，但难以适用于锯齿状行为分析.

基于上述研究背景，在连续化晶体塑性理论框架下^[7]，建立了能够比较准确可靠描述微尺度(间歇性)锯齿状变形行为的塑性本构理论模型，据此分析了位移控制下IN718合金单晶微柱体的轴向力学响应.研究结果将对相关微纳器件的高性能设计、制备与安全使用有着重要的科学意义和支撑作用.同时，通过构建微尺度锯齿状塑性本构模型，可为经典晶体塑性理论在亚微米尺度领域的发展提供进一步的理论支撑.

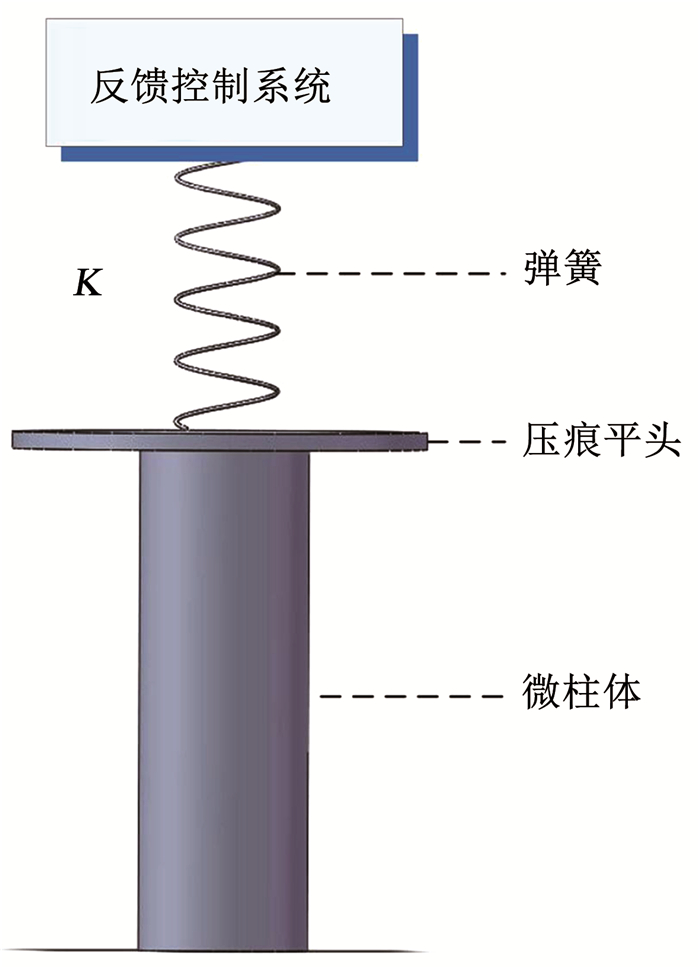
1 锯齿状塑性行为的力学分析模型

微压缩实验是研究微尺度晶体材料塑性变形行为的重要方法之一.基于微压缩实验加载原理^[8]，图 1绘制了微柱体轴向加载过程的简化示意图.在位移控制下，当压痕平头位移与纳米压痕系统预设位移不一致时，系统中的闭环反馈控制系统(closed-loop feedback control system)会通过调节弹簧(具有有限刚度K)的伸缩来控制压痕平头的位移，从而使其达到系统预设位移值^[9].

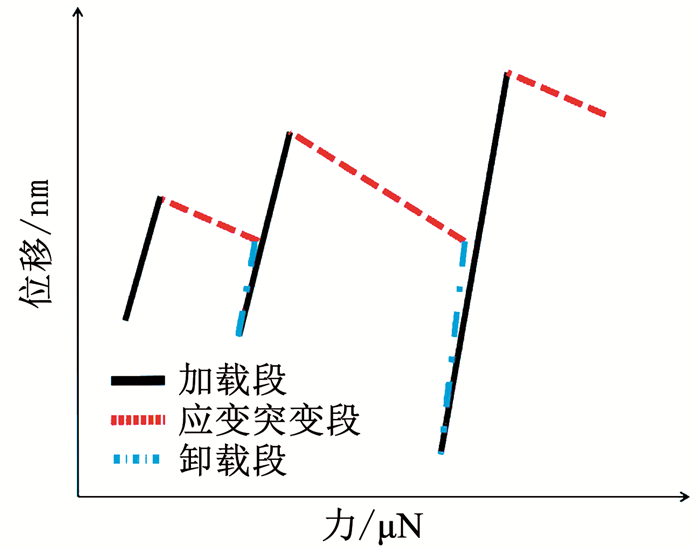
图 2显示了(位移控制下)微柱体锯齿状载荷-位移曲线示意图.从图 2中可以看出，典型的微柱体锯齿状塑性流动过程主要由3类变形阶段构成：加载段、应变突变段与卸载段.在轴向加载过程中，当微柱体内力能够平衡压痕系统施加的外力时，微柱体变形处于一个准静态的加载阶段，当材料内应力无法平衡来自加载段持续增加的外载荷时，其塑性应变则会发生突变.此时，微柱体顶端位移出现突然下沉，导致弹簧急剧伸长，继而降低了作用于顶端的外载荷(如图 1所示).由于应变突变导致微柱体顶端位移与压痕系统预设位移发生了偏离，闭环控制系统会通过收缩弹簧长度以实现两者位移的同步.在此过程中，作用于微柱体顶端的外载荷会急剧减少，微柱体变形也因此处于卸载阶段(如图 2所示).

2 锯齿状晶体塑性理论模型

为了实现对常规塑性理论应用范围的重构和扩展，建立可靠合理地锯齿状晶体塑性理论模型，文中仅考虑几何特征尺寸大于数微米的晶体材料，以此确保均匀位错结构假设的合理性^[7].

2.1 晶体塑性理论本构模型

小变形下的晶体材料应变张量率${\dot \varepsilon _{ij}}$为

$ {\dot \varepsilon _{ij}} = \dot \varepsilon _{ij}^e + \dot \varepsilon _{ij}^p, $

式中上标“e”、“p”分别为晶体材料的弹性变形与塑性变形部分.根据晶体变形几何学分析^[10]，其塑性变形可表述为

$ \dot \varepsilon _{ij}^p = \frac{1}{2}\sum\limits_{\alpha = 1}^n {{{\dot \gamma }_\alpha }\left( {s_i^\alpha m_j^\alpha + m_i^\alpha s_j^\alpha } \right)} . $

式中：${{{\dot \gamma }_\alpha }}$为α滑移系的剪切应变率；n为滑移系个数；s^α、m^α分别为滑移方向与法向矢量.

根据Hooke定律，晶体材料弹性变形关系式为

$ \dot \varepsilon _{ij}^e = C_{ijkl}^{ - 1}:{{\dot \sigma }_{kl}}. $

(1)

式中：σ为Euler应力；C_ijkl为弹性模量系数.针对IN718立方晶体，其独立弹性模量常数仅为3个(C₁₁、C₁₂、C₄₄).

如图 2所示，锯齿状塑性流动过程主要由3类变形阶段构成：加载段、应变突变段与卸载段，它们在以下数学表述中分别采用上标l，b，u表示.针对应变突变行为，该阶段的应力变化率为

$ \dot \sigma _{ij}^b = {C_{ijkl}}\left( {{{\dot \varepsilon }_{ij}} - \sum\limits_{\alpha = 1}^n {\dot \gamma _\alpha ^bP_{ij}^\alpha } } \right), $

(2)

式中${\dot \gamma _\alpha ^b}$为应变突变发生过时α滑移系产生的剪切应变率.一般来说，晶体材料应变突变是内部位错系统结构崩塌引发的^[11]，因而涉及群体位错的移动，总体塑性变形率较大，微柱体变形刚度降低.

针对晶体材料变形加载阶段，其应力变化率可表述为

$ \dot \sigma _{ij}^1 = {C_{ijkl}}\left( {{{\dot \varepsilon }_{ij}} - \sum\limits_{\alpha = 1}^n {\dot \gamma _\alpha ^1P_{ij}^\alpha } } \right), $

(3)

式中${\dot \gamma _\alpha ^1}$为加载过程中的剪切应变率.加载阶段仅涉及少量位错运动，内部位错构形保持相对稳定，总体塑性变形率较小，微柱体变形刚度值非常接近于弹性变形刚度值.

在晶体材料变形进入卸载段后，处于弹性变形线性阶段，其应力变化率则为

$ \dot \sigma _{ij}^u = - {C_{ijkl}}{{\dot \varepsilon }_{ij}}. $

2.2 流动法则

针对应变突变段与加载段，每个滑移系的剪切速率${{\dot \gamma }^\alpha }$可采用幂率表述形式^[6]:

$ {{\dot \gamma }_\alpha } = {{\dot \gamma }_0}{\rm{sign}}\left( {{\tau _\alpha }/{g_\alpha }} \right){\left( {{\tau _\alpha }/{g_\alpha }} \right)^m}. $

(4)

式中：${{\dot \gamma }_0}$为参考应变率，通常取值1.0×10^-3s^-1；m为率敏感指数，是一个拟合参数；τ_α为滑移系α的临界剪切分解应力为

$ {{\dot \tau }_\alpha } = P_{ij}^\alpha {{\dot \sigma }_{ij}}. $

(5)

式(4)中的g^α为某一时刻滑移系α的应变硬化强度.其演化规律为^[12]

$ {{\dot g}_\alpha } = \sum\limits_{\beta = 1}^n {{h_{\alpha \beta }}\left| {{{\dot \gamma }_\alpha }} \right|} , {h_{\alpha \beta }} = q{h_{\alpha \alpha }}. $

(6)

式中：q为潜硬化比率，一般取1≤q≤1.4^[12].h_αα为自滑移系数，采用由文献[12]提出的PAN硬化模型^[12]为

$ {h_{\alpha \alpha }} = {h_0}\sec {h^2}\left| {\frac{{{h_0}\gamma }}{{{g_{\rm{s}}} - {g_0}}}} \right|. $

式中：h₀为金属晶体的初始屈服时的硬化模量；g₀为初始屈服时的临界分切应力；g_s为饱和流动分切应力.它们都是材料常数，需通过试验结合数值模拟试算得到；γ为所有滑移系累积剪切应变之和.

需要说明的是，虽然包括式(4)~(6)在内的等式具有与加载段相同的函数关系式，但它们所表述的物理意义不同^[6].其中，加载段的剪切率变化是在整体位错构形保持相对稳定、变化较小情况下发生，其值较小；应变突变剪切率变化是在位错系统结构发生破坏，并且重新组合情况下发生.由于涉及群体位错移动，其值一般较大.为了反映这两个阶段塑性变形率特征的变化与差异，定义各段的平均剪切滑移率为^[5].

$ {{{\dot{\bar{\gamma }}}}_{\alpha }}=\left( 1-\xi \right){{{\dot{\gamma }}}_{\alpha }}+\xi \dot{\gamma }_{\alpha }^{+}\left( t+\Delta t \right). $

式中：${{{\dot{\bar{\gamma }}}}_{\alpha }}$为Δt增量步内的平均剪切应变率；上标“+”为加载段或者应变突变段的初始剪切滑移率；ξ为量纲一的常数，一般取0.1≤ξ≤0.3.当ξ取较小值时，应变突变段发生时会出现高应变率，而加载段出现低应变率，这与实验观察到的现象是非常一致的.在上述式中，当加载段发生时, Δt=T^l, T^l为加载段持续时间；当应变发生突变时，Δt=T^b，T^b为应变突变持续时间.

2.3 应变突变的判定

由于应变突变与加载段的应力应变关系式较为相近，需要将它们区分开来，以便选择对应阶段的边界条件，进而提出各阶段的塑性边值问题.在晶体塑性理论框架下，可通过系统二阶功${W_2} = \int_V {{{\dot \sigma }_{ij}}{{\dot \varepsilon }_{ij}}{\rm{d}}V} $的正负变化来甄别应变突变的发生，即当W₂满足条件^[13]：

$ {W_2} > 0, $

时，则表明材料的变形是一个加载过程.而当W₂满足条件：

$ {W_2} \le 0, $

时，则表明材料在塑性变形过程中发生了一次应变突变事件.

3 锯齿状塑性行为的微边界条件 3.1 加载段

微柱体顶端与压痕平头运动始终保持同步，为一个恒应变率的加载过程.微柱体顶端的位移变化率在该阶段内满足:

$ {{\dot u}^l} = {{\dot u}_0}. $

式中：u为边界位移；${{\dot u}_0}$为纳米压痕系统预设的位移变化率.

3.2 应变突变

如果从整个应变突变变形过程考虑，轴向突变位移u^b一般服从具有截断项的幂指数分布^[14]:

$ {u^b} = A, P\left( A \right) \sim {A^{ - \tau }}\exp \left[ { - {{\left( {A/{A_{\max }}} \right)}^2}} \right]. $

(7)

式中：A_max为突变位移截断(cut-off)值；τ为标度指数(scaling exponent)，取值1.35^[15].采用线性转换(transformation method)方法^[16]，可以近似预测A的大小：

$ A = {\left[ {r\left( {A_0^{1 - \tau } - A_{\min }^{1 - \tau }} \right) + A_{\min }^{1 - \tau }} \right]^{\frac{1}{{1 - \tau }}}}. $

(8)

式中：r为服从[0, 1]均匀分布的随机数；A_min为幂律下限^[15]; A₀为幂律上限，可通过试验结合数值模拟试算得到.

此外，应变突变随机应变突变的持续时间范围通常需要一个速度临界阀值来界定^[17].若设压痕系统预设位移率${{\dot u}_0}$为该临界阀值，则在应变突变结束时刻，微柱体的轴向位移率应该满足：

$ {{\dot u}^b}\left| {_{\Delta t = {T^b}}} \right. = {{\dot u}_0}, $

式中Δt=T^b为应变突变的结束时刻.

3.3 卸载段

该阶段结束时，微柱体变形再次进入加载阶段, 此时微柱体位移重新与纳米压痕系统位移保持同步.在卸载持续时间T^u内，卸载位移u^u满足：

$ {u^b} - {u^u} = \left( {{T^b} + {T^u}} \right){{\dot u}_0}. $

(9)

考察两个准静态加载段之间微柱体顶端外力变化f^b+u，则有以下关系式成立：

$ {f^{b + u}} = - K\left( {{u^b} - {u^u}} \right). $

4 算例 4.1 模型参数标定

锯齿状晶体塑性本构理论需要定义的模型参数包括：式(2)、(3)中的3个弹性常数C₁₁、C₁₂、C₄₄分别取值259.6 GPa、179 GPa以及109.6 GPa^[18]；式(1)中的参考应变率一般取值${{{\dot \gamma }_0}}$=1.0×10^-3s^-1；式(4)的中的率敏感指数m取值0.003^[6]；式(7)中的幂律下限值A_min≈1.0×10^-9nm^[15]；式(9)中的弹簧刚度K=10 μN/nm^[18]；式(6)中的材料参数h₀，g₀，g_s与式(7)中的幂律上限值A₀均需通过试验结合数值模拟试算得到，它们对应不同晶体取向的值列于表 1.式(8)的预设位移率${{\dot u}_0}$为12 nm/s.

4.2 单滑移取向

图 3显示了直径D=5 μm、具有单滑移取向[216]金属微圆柱体的轴向压缩示意图.该取向的主滑移系为[011](111)，斯密特因子为0.448.应用上述理论模型，模拟了位移加载条件下(${{\dot \varepsilon }_0}$=1.0× 10^-3s^-1)微柱体单轴压缩过程，获得的应力-应变曲线如图 3所示.从图 3中可以看出，微柱体轴向力学响应出现了应力随应变增加而增加、应力随应变减小而减小以及应力随应变增加而降低3种变形方式.其中，第1种变形方式由于变形刚度与弹性加载刚度相同，因此可确定其为弹性卸载变形；针对第2种变形方式，由于变形刚度非常类似与初始弹性变形刚度，且应力随应变增加而显著增加，因此可确定其为加载段变形.

针对最后一种应力随应变增加而降低的变形行为，图 4绘制了该行为在轴向压缩部分变形段内对应的轴向平均位移率.从图 4中可以看出，应力随应变增加而降低时，微柱体轴向平均速度显著大于压痕系统的预设位移率${{\dot u}_0}$=12 nm/s，可以认定微柱体应变发生了突变.因此，图 3显示的轴向锯齿状变形行为则具体包含了应力随应变增加而升高的斜坡加载段、应力随应变增加而降低的应变突变，以及应力随应变减小而减小的应变突变3种变形方式，这与微压缩实验^[6]观察到的现象是一致的.此外，从图 4中还可以发现锯齿状塑性变形主要通过单一应变突变事件来实现，这与力控制下应变突变连续发生的阶梯状变形方式有着显著的不同^[5].

为了验证模型的合理性，图 3也显示了与上述微柱体尺寸相对应的实验测试结果^[18].通过与实验结果比较可以发现，模型预测结果和实验结果是比较一致的.从模拟结果和实验测试曲线的高度相似的塑性流动行为来看，可以认为计算结果是合理的.需要说明的是，针对同一尺寸模拟对象，即使使用完全相同的参数，在不同时刻得到的应力-应变曲线是不完全相同的，这主要是因为模型中考虑了位移突变幅值的随机性因素.

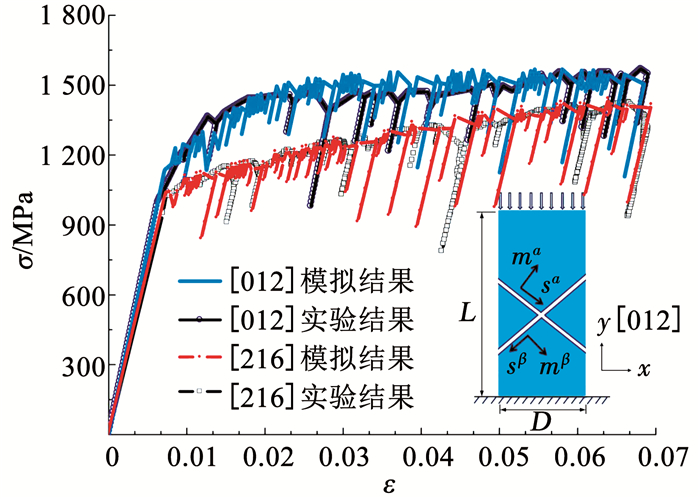
4.3 双滑移取向

[012]取向IN718合金单晶微柱体具有两个主滑移系：[101](111)与[101](111)，施密特因子均为0.49.应用理论模型分析了具有该取向、直径为5 μm微柱体的单轴压缩过程，获得的应力-应变曲线如图 5所示.从图 5中可以看出，微柱体塑性变形呈现出较为显著的锯齿状变化，这与图 5中显示的实际测试结果是非常相似的.此外，图 5中还显示了与双滑移取向直径相同的单滑移取向[216]金属微圆柱体的轴向压缩结果，两者计算过程中采用的材料参数相同，见表 1.对比结果发现，双滑移取向微柱体流动应力明显高于单滑移取向的对应值，原因在于双滑移开动增强了两个滑移系之间的位错交互作用，进而提高了微柱体应变强化效应.

5 结论

1) 提出了反映微尺度锯齿状变形行为的“变形块-弹簧”力学分析模型，在连续介质框架内建立了描述该行为的微尺度晶体塑性本构关系.

2) 提出的本构模型能够较为合理地描述微尺度晶体材料锯齿状变形行为，这为基于连续介质力学的晶体塑性理论在亚微米尺度领域的发展提供进一步的理论支撑.

3) 力控制下微柱体塑性变形主要通过一系列的应变突变行为来实现的，而位移控制下的微柱体塑性变形主要通过单一应变突变事件来实现.