为了有效利用定量信息和专家提供的不完整的或不确定的信息,对复杂问题进行建模,Yang等[1]提出了基于证据推理算法的置信规则库推理方法(belief rule-base inference methodology using the evidential reasoning approach,RIMER).RIMER融合了D-S证据理论、决策理论、模糊理论和传统IF-THEN规则库的知识,能够对带有含糊或模糊不确定性、不完整或概率不确定性以及非线性特征的数据进行建模.目前,RIMER已经在石油管道检漏[2-3]、故障诊断[4-8]、意图识别[9-10]、装备能力评估[11-13]等领域得到广泛应用.
RIMER主要包括知识的表达和知识的推理.其中,知识的表达是通过置信规则库(belief rule-base,BRB)系统来实现的,而知识的推理是利用证据推理(evidential reasoning,ER)算法来进行.由于专家经验的不确定性,初始建立的BRB系统往往是不准确的.为此,可以利用得到的数据集,结合参数训练的方法对BRB系统的推理参数进行优化.目前,对于RIMER的研究也主要集中在这一领域.包括Yang等[14]提出用Matlab中的FMINCON函数进行参数训练;常瑞、吴伟昆等[15-16]基于优化步长和梯度法进行置信规则库参数学习;苏群等[17]利用变速粒子群算法来优化置信规则库参数;杨慧等[18]利用改进粒子群算法对置信规则库参数进行训练.然而,在故障诊断和装备能力评估的实际操作过程中,由于人为失误、操作过程不规范、关键参数难获取等方方面面的原因[19],常常出现输入信息不完整、与置信规则前件无法匹配、从而导致BRB系统不能正常使用的情况.而且BRB系统一经建立,输入参数的个数就固定了,在实际运用的过程中适应性不强.如何根据不完整的输入信息进行置信规则库推理,成为亟待解决的问题,而目前在这方面的研究还比较少.
基于此,本文受抽样思想[20-22]的启发,提出了一种输入信息不完整的置信规则库推理方法.首先,根据经验或历史数据获取前提条件属性分布情况;然后对于缺失的前提条件属性,依据其分布情况,进行分层抽样[23-25],确定多个抽样值;接下来将每个抽样值与已有的前提条件属性组合成多个完整的输入,并分别利用ER算法进行推理;最后将所有输入的推理结果利用ER算法进行二次融合,得到最终的结论.在实验部分引入发动机故障诊断的置信规则库,通过仿真数据与其他几种方法进行对比,验证本文方法的有效性.
1 RIMER方法 1.1 置信规则库表示置信规则是根据IF-THEN规则发展而来,引入了分布式置信框架和权重参数.其中BRB系统中的第k条规则表示如下:
| $ $ |
Rk:if x1 is A1k∧x2 is A2k∧…∧xM is AMk,
Then {(D1, β1, k), (D2, β2, k), …, (DN, βN, k),
With a rule weight θk and attribute weight δ1, δ2, …, δM.
式中:xi(i=1, 2, …, M)为第i个前提属性, 其中M为前提属性的个数;Aik为第k条规则第i个输入的参考值; Di(i=1, 2, …, N)为结果属性的第i个评价等级,其中N为评价等级的个数;βi, k为第k条规则中第i个评价等级的置信度,k=1, 2, …, L, 其中L为BRB中置信规则的个数;θk为规则权重; δi为前提属性权重.
1.2 置信规则库推理方法 1.2.1 置信规则激活权重的计算输入信息x对k条规则的激活权重可以通过下式来计算,即
| $ {\omega _k} = \frac{{{\theta _k}\prod\limits_{i = 1}^M {{{\left( {\alpha _i^k} \right)}^{{{\bar \delta }_i}}}} }}{{\sum\limits_{l = 1}^L {{\theta _l}\prod\limits_{i = 1}^M {{{\left( {\alpha _i^l} \right)}^{{{\bar \delta }_i}}}} } }}. $ |
式中:ωk∈[0, 1],k=1, 2, …, L; αik(i=1, 2, …, M)为在第k条规则中第i个输入xi相对于参考值Aik的置信度.
1.2.2 ER算法融合当计算出规则的激活程度后,就可以利用ER算法将BRB中的规则进行融合.首先,将结果属性中的置信度转化为基本概率质量:
| $ {m_{j, k}} = {\omega _k}{\beta _{j, k}}, $ | (1) |
| $ {m_{D, k}} = 1 - {\omega _k}\sum\limits_{j = 1}^N {{\beta _{j, k}}}, $ | (2) |
| $ {{\bar m}_{D, k}} = 1 - {\omega _k}, $ | (3) |
| ${{\tilde m}_{D, k}} = {\omega _k}\left( {1 - \sum\limits_{j = 1}^N {{\beta _{j, k}}} } \right). $ | (4) |
式中:mj, k为相对于评价结果Dj的基本概率设置; mD, k为相对于集合D的基本概率设置,也就是未设置给任意评价结果的基本概率,mD, k=mD, k+
然后,利用ER解析算法对L条规则进行融合,公式如下:
| $ \begin{array}{l} {{\hat \beta }_j} = \frac{{\mu \times \left[{\prod\limits_{k = 1}^L {({\omega _k}{\beta _{j, k}} + 1-{\omega _k}\sum\limits_{i = 1}^N {{\beta _{i, k}}} } } \right]}}{{1 - \mu \times \left[{\prod\limits_{k = 1}^L {\left( {1-{\omega _k}} \right)} } \right]}} - \\ \;\;\;\;\;\;\;\;\;\frac{{\mu \times \left[{\prod\limits_{k = 1}^L {(1-{\omega _k}\sum\limits_{j = 1}^N {{\beta _{i, k}}} } } \right]}}{{1 - \mu \times \left[{\prod\limits_{k = 1}^L {\left( {1-{\omega _k}} \right)} } \right]}}, \end{array} $ | (5) |
| $ \begin{array}{l} \mu = \left[{\sum\limits_{j = 1}^N {\prod\limits_{k = 1}^L {({\omega _k}{\beta _{j, k}} + 1-{\omega _k}\sum\limits_{j = 1}^N {{\beta _{i, k}}-} } } } \right.\\ \;\;\;\;\;\;{\left. {\left( {N-1} \right)\prod\limits_{k = 1}^L {\left( {1 - {\omega _k}\sum\limits_{i = 1}^N {{\beta _{i, k}}} } \right)} } \right]^{ - 1}}, \end{array} $ | (6) |
式中
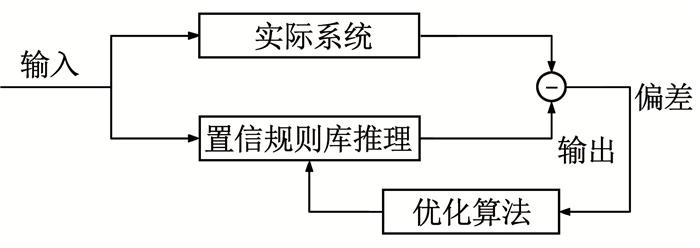
为了提高推理精度,可以利用训练数据在已有置信规则库的基础上对推理参数进行优化,主要优化的推理参数是规则权重以及前提属性权重.基于置信规则库的推理类似于人的推理过程,可以同时综合考虑多条规则,最后推理出的决策结果带有置信度分布特点.规则权重以及规则前提属性权重会影响到推理结果的精度,在提取得到的初始置信规则库基础上,进一步利用训练数据优化推理参数,从而提高推理的精度,过程如图 1所示.
|
图 1 置信规则库参数优化图 Fig. 1 Parameter optimization diagram of belief rule-base |
在实际的系统中,由于性能演变的规律性[26],收集到的参数通常也会存在一定的分布规律.参数的分布规律可以通过经验或者历史数据统计来获取,本文主要介绍数据统计的方法.
假设历史数据集为X,需要统计前提条件属性x1的分布情况,具体过程如下:首先,通过排序,求出X中前提条件属性x1的最大值x1max和最小值x1min,并得到数据分布的范围为
| $ {L_1} = {x_{{\rm{1max}}}} - {x_{{\rm{1min}}}}, $ |
接下来确定分割的区间个数d1,并计算得到每个区间的长度为
| ${l_1} = {L_1}/{d_1}, $ |
据此固定每个区间的范围为[x1min, x1min+l1), [x1min+ l1, x1min+2l1), …, [x1min+(d1-1)l1, x1max].其中,d1的值要根据历史数据的密集程度来进行确定,使得区间的大小更加合理.最后通过统计落在每个区间的数据个数,得出通过数据估计的分布情况.
根据大数定律可知,当数据量足够大时,事件出现的频率将无限接近于其概率.因此,如果历史数据量足够大,通过历史数据来统计得到前提条件的分布情况是合理的.
2.2 通过分层抽样组合成多个输入获取前提条件属性的分布情况后,接下来通过分层抽样的方法对缺失的条件属性进行补充.数据的分布情况通常有两种表现形式,一种是分布函数,这也是分布情况最一般的表示方法;另一种是未能获取分布函数的情况下,通过统计方法估计的分布情况.接下来将分别说明两种情况下抽样的过程.
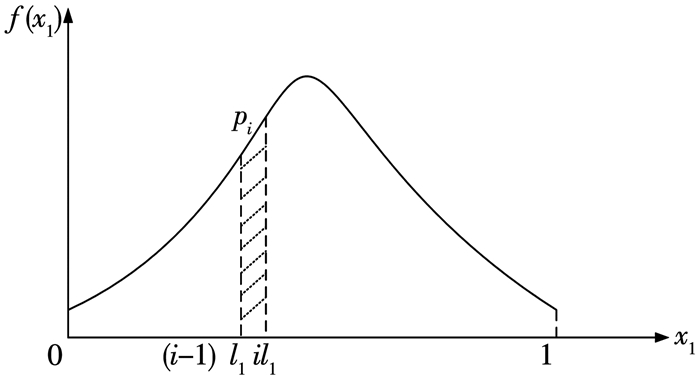
2.2.1 利用分布函数进行分层抽样假设输入的前提属性为X=[x1, x2, …, xM],x1因为某些原因未能获取,但是根据历史经验,得知x1服从[0, 1]上的分布,分布函数为F(x1),其概率密度函数f(x1)如图 2所示.
|
图 2 概率密度函数图 Fig. 2 Probability density function diagram |
分层抽样的过程主要包括以下步骤:首先,确定抽样层数和抽样区间长度l1,从而固定每个抽样区间的范围; 然后,根据x1的概率密度函数求出
| $ {p_i} = \int_{\left( {i - 1} \right){l_1}}^{i{l_1}} {f\left( {{x_1}} \right){\rm{d}}{\mathit{x}_1} = F\left( {i{l_1}} \right) - F\left( {\left( {i - 1} \right){l_1}} \right), } $ |
式中pi为第i个抽样区间[(i-1)l1, l1)与概率密度函数所包围的区域面积,即落在该抽样区间的概率.由此计算得到的pi通常不是整数,但在后续的步骤中,每个区间需要确定一个整数值,从而分开进行推理.为此,设置一个常数K,将pi整数化为
| $ {s_i} = {\rm{round}}(K_{pi}), $ |
si即为每个抽样区间的抽样数.其中,K的取值需要尽量满足:
| $ \mathop {{\rm{min}}}\limits_K \left\{ {\sum {\left| {K{p_i}- {\rm{round}}\left( {K{p_i}} \right)} \right|} {\rm{ }}} \right\}. $ | (7) |
为简便起见,将中间值作为每个抽样区间的抽样值,即
| $x_1^j = x_1^{j + 1} = \cdots x_1^{j + {s_i}} = \left( {i- 1} \right){l_1} + 1/2{l_1}. $ |
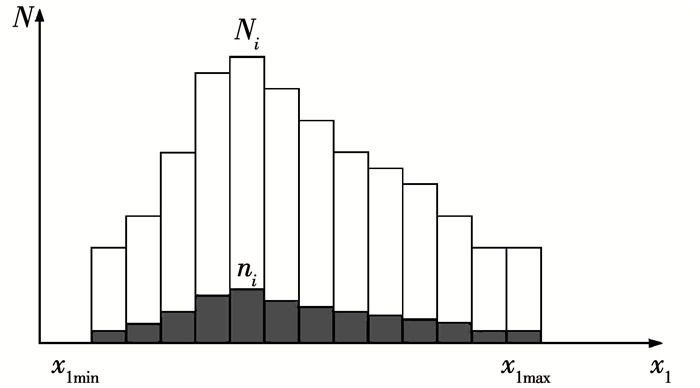
如果是利用统计方法获取的参数分布情况,则可以直接利用统计中所用的区间进行抽样.假设通过统计得到的参数分布如图 3所示.
|
图 3 统计的参数分布图 Fig. 3 Statistical parameter distribution diagram |
图 3中Ni为第i个抽样区间[x1min+(i-1)l1, x1min+il1)统计得到的数据个数.考虑到计算的复杂度,每个抽样区间的抽样数不能太多.为此设置一个常数C,并计算得到抽样数为
| $ {s_i} = {\rm{round}}({N_i}/C), $ |
常数C需要满足:
| $ \mathop {{\rm{min}}}\limits_C \left\{ {\sum {{N_i}/C - {\rm{round}}\left( {{N_i}/C} \right)} } \right\}, $ |
得到抽样数后,取抽样区间的中间值作为抽样值为
| $ x_1^j = x_1^{j + 1} = \cdots x_1^{j + {s_i}} = {x_{1\min }} + \left( {i - 1} \right){l_1} + 1/2{l_1}. $ |
对于缺失的前提条件属性,通过分层抽样的方法得到多个抽样值后,将其与其他已知的前提条件属性组合成多个输入,然后分别利用置信规则库推理方法进行推理,最后利用ER算法将所有推理结论进行二次融合,具体过程如图 4所示.

|
图 4 推理过程图 Fig. 4 Inference process diagram |
首先,由分层抽样得到x1的多个抽样值{x11, x12, x13, …, x1j, …},与其他已知前提条件属性组合成多个输入:
| $ \begin{array}{*{20}{c}} {({x^1}_1, {x_2}, \cdots, {x_M}), ({x^2}_1, {x_2}, \cdots, {x_M}), \cdots, }\\ {({x^j}_1, {x_2}, \cdots, {x_M}), \cdots .} \end{array} $ |
对于每一个输入分别按照置信规则库的推理方法进行推理,即计算激活程度、与置信规则库中的规则进行匹配、利用ER算法进行证据融合,得到带有置信度的评价结果{(Di, βi), i=1, 2, …, N}.
最后,将所有输入的推理结果再次利用ER算法进行融合,具体过程见式(1)~(6).在计算过程中,激活权重ωk设为同一个值,没有偏好.
| $ {\omega _k} = 1/\sum {{s_i}.} $ |
式中si为每个抽样区间的抽样数.
2.4 部分参数确定在分层抽样过程中为了后续步骤的顺利进行,设置了两个参数K和C对抽样数进行取整操作.在尽量满足取整误差最小的情况下,K和C的值依然不能唯一确定.因此,可以利用部分已知数据,将最后的推理误差作为这两个参数的评价标准,对其进行进一步明确.
对于参数K,是将每个抽样区间的概率进行整数化,K的值越大,越能在推理过程中充分反映前提条件属性的分布情况.但是,K的值过大,会在一定程度上增加算法的计算复杂度.为此,将二次融合后的推理结论{(Di, βi), i=1, 2, …, N}与真实数据中的结论对比,得到推理误差为
| $ \varepsilon = \sqrt {\sum\limits_{i = 1}^N {{{\left( {{\beta _i} - {\beta _0}} \right)}^2}} } . $ |
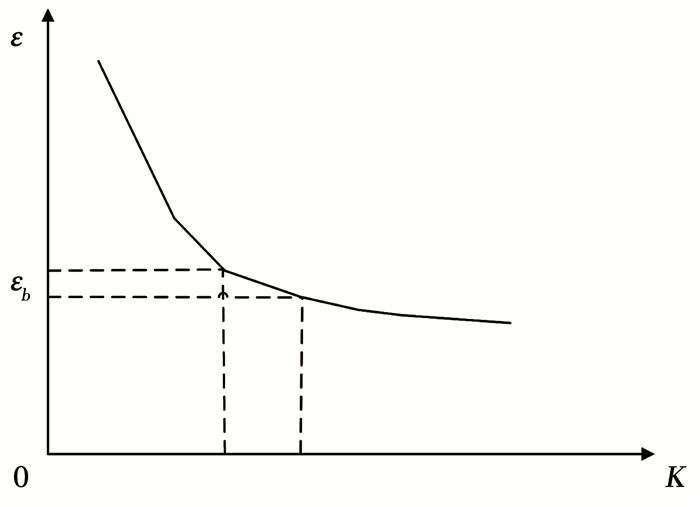
根据K和推理误差的对应关系,可以大致得到如图 5的一条曲线.
|
图 5 推理误差变化图 Fig. 5 Variation of the inference error |
随着K的增大,推理误差ε逐渐减小,但是减小的幅度也越来越小,同时,K值的增大给计算复杂度带来的困难更加明显.为了平衡两者的关系,设置一个误差容忍限度εb.当两个相邻的K值对应的推理误差的差值小于εb,则K不继续增大.
类似的,对于参数C,C越小,越能反映前提条件属性的分布情况.引入推理误差ε作为C的评价标准,并设置误差容忍限度εb将C进行确定.
对于前提属性分布中的抽样区间数d1,也可以利用类似的方法进行优化,从而使d1的值更加合理.
3 实验验证 3.1 实验准备为了验证本文方法的有效性,选取汽车发动机故障诊断的实例[4]进行仿真实验.该实例以进气压力、转速和喷油器喷油时间3个参数作为输入前提条件属性,正常怠速不稳工况状态和进气系统漏气、怠速电机不工作及某缸喷油器堵塞这4种情况作为输出评价等级.3个前提条件属性的参考值设置见表 1~3.
| 表 1 进气压力参考值 Tab. 1 The reference value of intake pressure |
| 表 2 转速参考值 Tab. 2 The reference value of rotate speed |
| 表 3 喷油器喷油时间参考值 Tab. 3 The reference value of fuel injection time |
在文献[4]中,确定好初始置信规则后,利用Matlab中的多目标优化函数fminmax对置信规则库的规则权重进行了优化,训练后的置信规则库,见表 4.
| 表 4 训练后的置信规则库 Tab. 4 Belief rule-base after training |
对于汽车发动机故障实例,文献中只提供了24组数据,难以将本文方法进行实施.而且由于数据的缺乏,局部数据难以反映整体的分布情况,使得本文方法的真正效果不能充分体现.因此,本文通过随机产生输入的前提条件属性,然后将这些前期条件属性输入BRB系统,推理得出评价结果,从而得到仿真数据.
为了检验本文方法对不同分布情况的适应性,在随机生成3个前提条件输入时,使其服从一定的分布.利用Matlab提供的rand()和randn()函数,生成随机数,将其做一定的变换改变其分布情况,并将其组合为输入向量[x1, x2, x3].将这些输入向量利用已经建立好的BRB系统进行推理,得到带有置信度的评价结果{(D1, β1), (D2, β2), (D3, β3), (D4, β4)}.将输入向量和评价结果一一对应起来,由此得到仿真数据.
3.2 实验过程及结果获得仿真数据后,假设部分数据缺失,使得输入信息不完整,难以简单地通过BRB系统进行推理.为此,实验中通过统计分布、抽样、置信规则库推理、ER二次融合等过程,产生利用不完整输入的得到的评价结果{(D′1, β′1), (D′2, β′2), (D′3, β′3), (D′4, β′4)},并与仿真数据中的评价结果比较,得到推理误差为

|
图 6 实验过程图 Fig. 6 Experimental process |
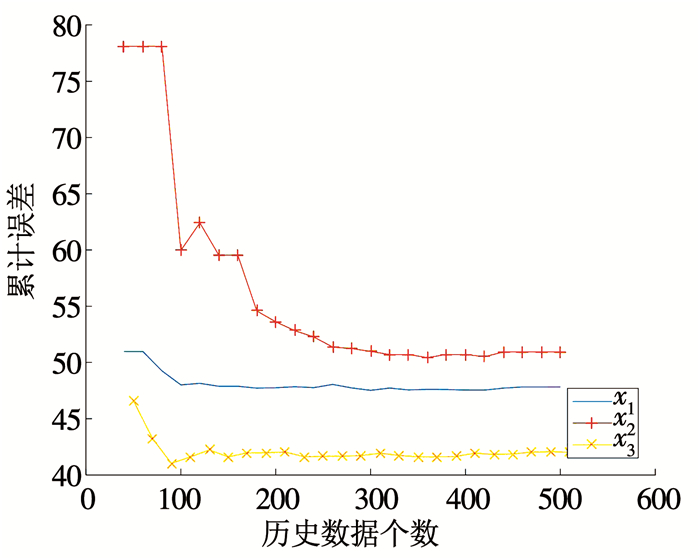
由于实验中前提条件属性的分布情况是通过数据统计的方法来获取的,历史数据个数会在一定程度上对实验结果产生影响.因此,先对历史数据个数这个关键因素进行实验分析.设置多组实验,假设分别有50、100、150个数据缺失了一个前提条件属性,并对3个前提条件属性x1、x2、x3分别进行实验.通过不同数量的历史数据估计其分布情况,然后利用本文中的方法进行推理,最终得到推理误差.为了便于观察,实验中将所有数据的推理误差进行求和,得到累计误差,实验结果如图 7~9所示.通过图 7~9中结果可以看出,3个条件属性都体现出类似的趋势.当历史数据个数较少时,累计误差较大,随着历史数据个数的增多,累计误差逐渐减小,最终趋于一个稳定状态.通过进一步分析得到,当历史数据个数高于缺失数据量的两倍时,累计误差基本趋于稳定.

|
图 7 50组缺失数据累计误差图 Fig. 7 Cumulative error diagram of 50 missing data |

|
图 8 100组缺失数据累计误差图 Fig. 8 Cumulative error diagram of 100 missing data |
|
图 9 150组缺失数据累计误差图 Fig. 9 Cumulative error diagram of 150 missing data |
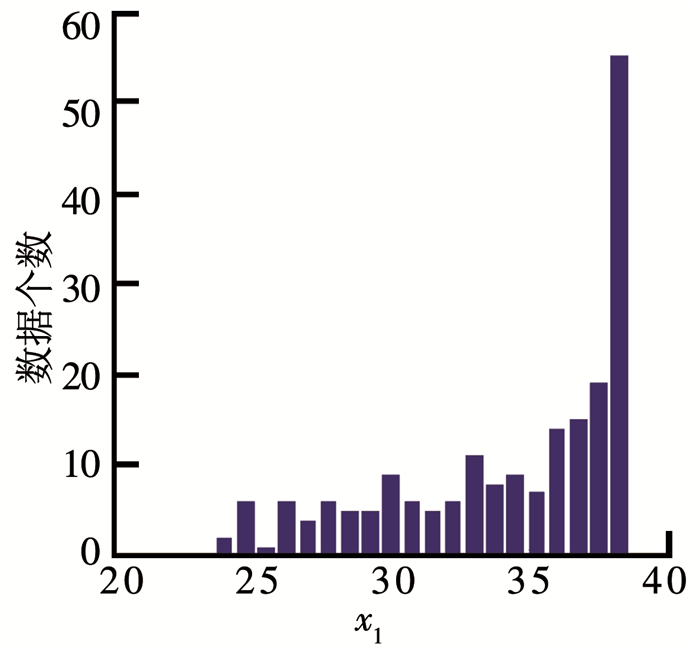
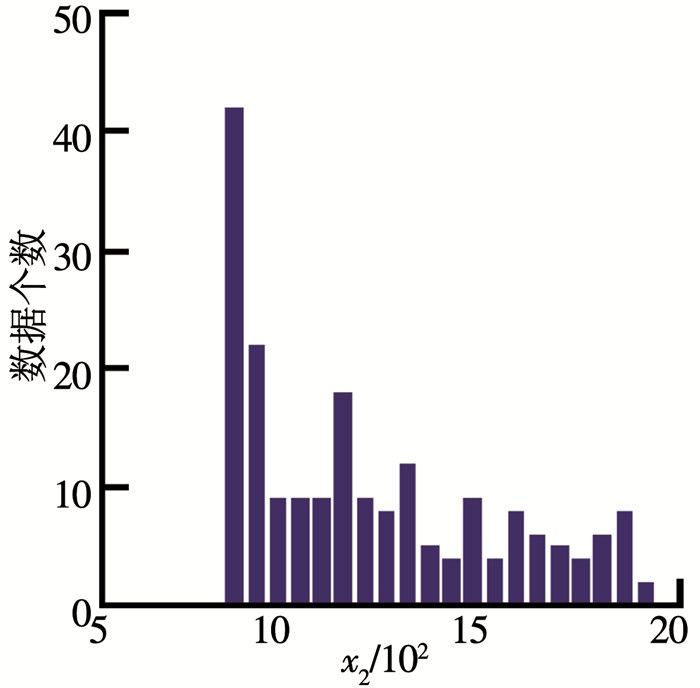
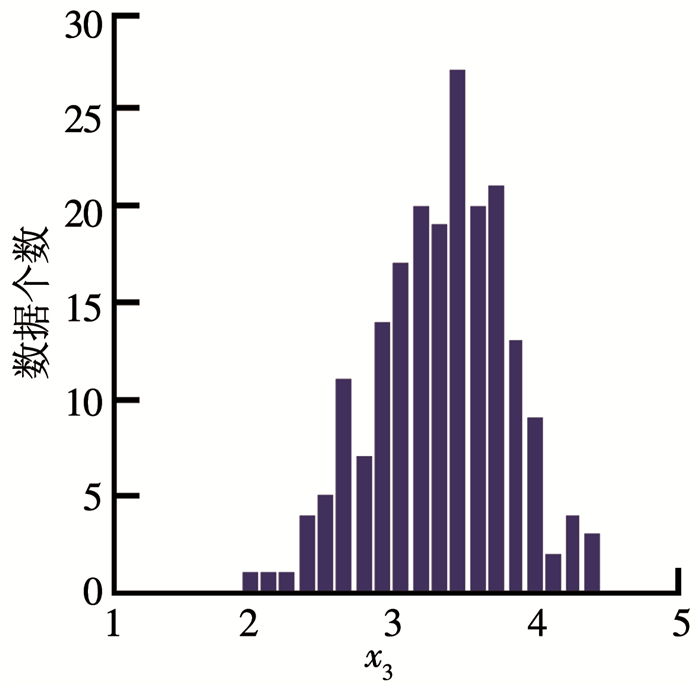
根据上面的实验结论,利用300组仿真数据,对3个不同分布情况的条件属性进一步进行实验分析.具体实验中,假设对于前100组数据缺失了第1个前提条件属性x1,101~200组数据缺失了第2个前提条件属性x2,201~300组数据缺失了第3个前提条件属性x3.然后分别通过统计剩余200组数据来估计前提条件属性的分布情况,统计结果如图 10~12所示.
|
图 10 x1的分布情况 Fig. 10 Distribution of x1 |
|
图 11 x2的分布情况 Fig. 11 Distribution of x2 |
|
图 12 x3的分布情况 Fig. 12 Distribution of x3 |
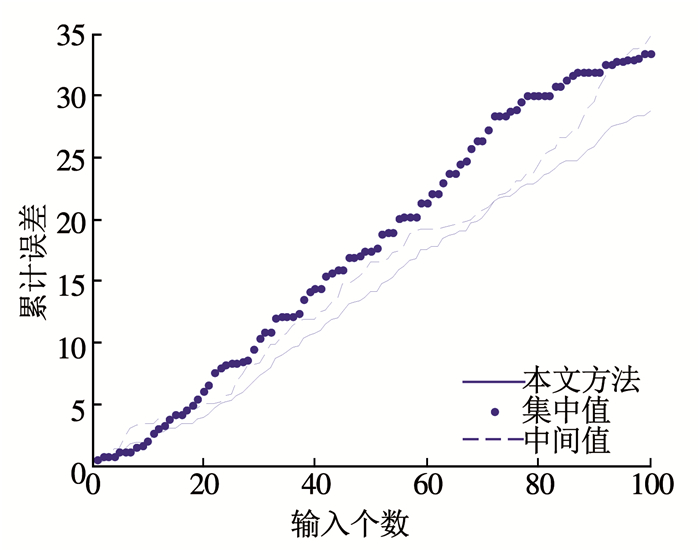
为了验证本文方法的优越性,采用其他两种方法与其进行对比:1)对于缺失的前提条件属性,借鉴统计学中众数的概念[27-28],选取历史数据中分布最密集的区域中间值对缺失属性进行补充,然后利用BRB系统推理得到评价结果.这种方法反映了历史数据的“多数水平”; 2)选取历史数据的中间值对缺失属性进行补充[29],然后利用BRB系统进行推理,体现了历史数据的“中间水平”.3种方法的累计误差如图 13~15所示.
|
图 13 x1的3种方法累计误差图 Fig. 13 Cumulative error diagram of three methods about x1 |

|
图 14 x2的3种方法累计误差图 Fig. 14 Cumulative error diagram of three methods about x2 |

|
图 15 x3的3种方法累计误差图 Fig. 15 Cumulative error diagram of three methods about x3 |
从图 13~15可以看出,本文方法在不同分布情况下得到的推理结果累计误差都明显小于其他两种方法,这在一定程度上反映了本文方法在数据特征提取上的优势.另外,对于汽车发动机故障诊断实例,规则库中的规则数只有27条,对于不同输入的结果区分度还不够大.对于其他规则库庞大的系统,本文方法将能够更好地体现其优越性.
4 结论1) 本文针对实际工程中参数收集困难,导致输入信息不完整、BRB系统难以正常运行的问题,提出一种基于不完整输入信息的推理方法.实验结果表明, 在有充足的历史数据时,本文方法能够大大减少推理误差.
2) 经过多组实验发现,本文方法对于不同的分布情况都有很好的适应性,给不完整输入信息的置信规则库推理提供了一种新思路.
3) 本文方法适用于前提条件属性是独立分布的情况,如何根据不同前提条件属性之间的关联关系估计得到缺失属性,有待进一步研究.
| [1] |
YANG Jianbo, LIU Jun, WANG Jin, et al. Belief rule-base inference methodology using the evidential reasoning approach-RIMER[J]. IEEE Transactions on Systems Man and Cybernetics Part A: Systems and Humans, 2006, 36(2): 266. DOI:10.1109/TSMCA.2005.851270 |
| [2] |
XU Dongling, LIU Jun, YANG Jianbo, et al. Inference and learning methodology of belief-rule-based expert system for pipeline leak detection[J]. Expert Systems with Applications, 2007, 32(1): 103. DOI:10.1016/j.eswa.2005.11.015 |
| [3] |
ZHOU Zhijie, HU Changhua, YANG Jianbo, et al. Online updating belief rule based system for pipeline leak detection under expert intervention[J]. Expert Systems with Applications, 2009, 36(4): 7700. DOI:10.1016/j.eswa.2008.09.032 |
| [4] |
张伟, 石菖蒲, 胡昌华, 等. 基于置信规则库专家系统的发动机故障诊断[J]. 系统仿真技术, 2011, 7(1): 11. ZHANG Wei, SHI Changpu, HU Changhua, et al. Fault diagnosis of engine based on RIMER expert system[J]. System Simulation Technology, 2011, 7(1): 11. DOI:10.3969/j.issn.1673-1964.2011.01.003 |
| [5] |
张邦成, 尹晓静, 王占礼, 等. 利用置信规则库的数控机床伺服系统故障诊断[J]. 振动、测试与诊断, 2013, 33(4): 694. ZHANG Bangcheng, YIN Xiaojing, WANG Zhanli, et al. Fault diagnosis of CNC Servo system based on the belief rule base[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(4): 694. DOI:10.3969/j.issn.1004-6801.2013.04.027 |
| [6] |
徐晓滨, 汪艳辉, 文成林, 等. 基于置信规则库推理的轨道高低不平顺检测方法[J]. 铁道学报, 2014, 36(12): 70. XU Xiaobin, WANG Yanhui, WEN Chenglin, et al. Track vertical irregularity detection based on inference of belief rule base[J]. Journal of the China Railway Society, 2014, 36(12): 70. DOI:10.3969/j.issn.1001-8360.2014.12.012 |
| [7] |
钱虹, 马萃萃. 基于事件触发机制的核电站智能诊断专家系统置信规则库的研究[J]. 原子能科学技术, 2017, 51(3): 485. QIAN Hong, MA Cuicui. Research on belief rule base of intelligent diagnosis expert system based on event-triggering mechanism in nuclear power plant[J]. Atomic Energy Science and Technology, 2017, 51(3): 485. DOI:10.7538/yzk.2017.51.03.0485 |
| [8] |
王力, 周志杰, 胡昌华, 等. 基于置信规则和证据推理的超声检测缺陷识别[J]. 中国测试, 2017, 43(4): 6. WANG Li, ZHOU Zhijie, HU Changhua, et al. Ultrasonic testing defect recognition based on belief-rule-base and evidential reasoning[J]. China Measurement & Test, 2017, 43(4): 6. DOI:10.11857/j.issn.1674-5124.2017.04.002 |
| [9] |
和钰, 常雷雷, 姜江, 等. 基于置信规则库的防空目标意图识别方法[J]. 火力与指挥控制, 2017, 42(9): 7. HE Yu, CHANG Leilei, JIANG Jiang, et al. Intension identification in air defense based on belief rule base expert system under expert guidance[J]. Fire Control & Command Control, 2017, 42(9): 7. DOI:10.3969/j.issn.1002-0640.2017.09.002 |
| [10] |
万平, 吴超仲, 林英姿, 等. 基于置信规则库的驾驶人愤怒情绪识别模型[J]. 交通运输系统工程与信息, 2015, 15(5): 96. WAN Ping, WU Chaozhong, LIN Yingzi, et al. A recognition model of driving anger based on belief rule base[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(5): 96. DOI:10.3969/j.issn.1009-6744.2015.05.014 |
| [11] |
尹德进, 王宏力. 不确定信息下基于证据推理的武器系统戒备率评估方法[J]. 战术导弹技术, 2011(2): 62. YIN Dejin, WANG Hongli. An evidential reasoning approach for alert rate assessment of missile weapon system under uncertainty[J]. Tactical Missile Technology, 2011(2): 62. DOI:10.16358/j.issn.1009-1300.2011.02.023 |
| [12] |
SOLIC K, OCEVCIC H, GOLUB M. The information systems' security level assessment model based on an ontology and evidential reasoning approach[M]. Oxford, UK: Elsevier Advanced Technology Publications, 2015. DOI:10.1016/j.cose.2015.08.004
|
| [13] |
刘佳俊, 胡昌华, 周志杰, 等. 基于证据推理和置信规则库的装备寿命评估[J]. 控制理论与应用, 2015, 32(2): 231. LIU Jiajun, HU Changhua, ZHOU Zhijie, et al. Life assessment approach of equipment based on belief-rule-base and evidential reasoning[J]. Control Theory & Applications, 2015, 32(2): 231. DOI:10.7641/CTA.2015.40406 |
| [14] |
YANG Jianbo, LIU Jun, XU Dongling, et al. Optimization models for training belief-rule-based systems[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2007, 37(4): 569. DOI:10.1109/tsmca.2007.897606 |
| [15] |
常瑞, 张速. 基于优化步长和梯度法的置信规则库参数学习方法[J]. 华北水利水电学院学报, 2011, 32(1): 154. CHANG Rui, ZHANG Su. An algorithm for training parameters in belief rule-bases based on gradient methods with optimization step size[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power, 2011, 32(1): 154. DOI:10.3969/j.issn.1002-5634.2011.01.044 |
| [16] |
吴伟昆, 杨隆浩, 傅仰耿, 等. 基于加速梯度求法的置信规则库参数训练方法[J]. 计算机科学与探索, 2014, 8(8): 989. WU Weikun, YANG Longhao, FU Yanggeng, et al. Parameter training approach for belief rule base using the accelerating of gradient algorithm[J]. Journal of Frontiers of Computer Science and Technology, 2014, 8(8): 989. DOI:10.3778/j.issn.1673-9418.1403061 |
| [17] |
苏群, 杨隆浩, 傅仰耿, 等. 基于变速粒子群优化的置信规则库参数训练方法[J]. 计算机应用, 2014, 34(8): 2161. SU Qun, YANG Longhao, FU Yanggeng, et al. Parameter training approach based on variable particle swarm optimization for belief rule base[J]. Journal of Computer Applications, 2014, 34(8): 2161. DOI:10.11772/j.issn.1001-9081.2014.08.2161 |
| [18] |
杨慧, 吴沛泽, 倪继良, 等. 基于改进粒子群置信规则库参数训练算法[J]. 计算机工程与设计, 2017, 38(2): 400. YANG Hui, WU Peize, NI Jiliang, et al. Belief rule base parameter training approach based on improved particle swarm optimization[J]. Computer Engineering and Design, 2017, 38(2): 400. DOI:10.16208/j.issn1000-7024.2017.02.023 |
| [19] |
李浩. 准则权重信息不完全的证据推理多属性决策算法[J]. 火力与指挥控制, 2015, 40(1): 12. LI Hao. Evidence reasoning algorithm for multi-criteria decision-making with incomplete attribute weight information[J]. Fire Control & Command Control, 2015, 40(1): 12. DOI:10.3969/j.issn.1002-0640.2015.01.004 |
| [20] |
伊鹏, 钱坤, 黄万伟, 等. 基于抽样流长与完全抽样阈值的异常流自适应抽样算法[J]. 电子与信息学报, 2015, 37(7): 1606. YI Peng, QIAN Kun, HUANG Wanwei, et al. Adaptive flow sampling algorithm based on sampled packets and force sampling threshold S towards anomaly detection[J]. Journal of Electronics & Information Technology, 2015, 37(7): 1606. DOI:10.11999/JEIT141379 |
| [21] |
彭寒梅, 曹一家, 黄小庆, 等. 基于组合抽样的含分布式电源随机潮流计算[J]. 电力自动化设备, 2014, 34(5): 28. PENG Hanmei, CAO Yijia, HUANG Xiaoqing, et al. Probabilistic load flow calculation based on combination sampling for power system containing distributed generations[J]. Electric Power Automation Equipment, 2014, 34(5): 28. DOI:10.3969/j.issn.1006-6047.2014.05.004 |
| [22] |
张焕雪, 李强子, 文宁, 等. 农作物种植面积遥感抽样调查的误差影响因素分析[J]. 农业工程学报, 2014, 30(13): 176. ZHANG Huanxue, LI Qiangzi, WEN Ning, et al. Analysis on estimation accuracy of crop area caused by spatial sampling factors based on remote sensing data[J]. Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(13): 176. DOI:10.3969/j.issn.1002-6819.2014.13.022 |
| [23] |
黄江宁, 郭瑞鹏, 赵舫, 等. 电力系统可靠性评估中的分层均匀抽样法[J]. 电力系统自动化, 2012, 36(20): 19. HUANG Jiangning, GUO Ruipeng, ZHAO Fang, et al. Stratified uniform sampling method for power system reliability evaluation[J]. Automation of Electric Power Systems, 2012, 36(20): 19. DOI:10.3969/j.issn.1000-1026.2012.20.004 |
| [24] |
江俊彦, 彭智勇, 吴小莹, 等. 基于分层抽样的重叠深网数据源选择[J]. 软件学报, 2017, 28(5): 1271. JIANG Junyan, PENG Zhiyong, WU Xiaoying, et al. Overlapping deep Web data source selection based on stratified sampling[J]. Journal of Software, 2017, 28(5): 1271. DOI:10.13328/j.cnki.jos.005105 |
| [25] |
胡莹, 邵春福, 王书灵, 等. 基于经济计量回归模型的车辆能耗分层抽样方法研究[J]. 交通运输系统工程与信息, 2017, 17(6): 70. HU Ying, SHAO Chunfu, WANG Shuling, et al. Vehicle energy-consumption stratified sampling survey based on econometrics regression model[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(6): 70. DOI:10.16097/j.cnki.1009-6744.2017.06.011 |
| [26] |
邵文东, 胡海滨, 周国东. 我国货车主型转向架服役性能演变规律的研究[J]. 铁道车辆, 2016, 54(10): 12. SHAO Wendong, HU Haibin, ZHOU Guodong. Research on evolution law of the service performance of main type freight car bogies in China[J]. Rolling Stock, 2016, 54(10): 12. DOI:10.3969/j.issn.1002-7602.2016.10.003 |
| [27] |
郑月萍. 算术平均数、众数、中位数三者关系质疑[J]. 广东技术师范学院学报, 2001(2): 97. ZHENG Yueping. Question to the relationship among arithmetic average, mode and medium[J]. Journal of Guangdong Polytechnic Normal University, 2001(2): 97. DOI:10.3969/j.issn.1672-402X.2001.02.022 |
| [28] |
徐景范. 中位数、算术平均数和众数关系之我见[J]. 统计与咨询, 1999(4): 17. XU Jingfan. A view on the relationship among medium, arithmetic overage, and mode[J]. Tongjiyuzixun, 1999(4): 17. |
| [29] |
程国. 基于中间值的最大间距准则特征提取方法[J]. 甘肃科学学报, 2014, 26(4): 21. CHENG Guo. Extraction of maximum margin criterion features based on median[J]. Journal of Gansu Sciences, 2014, 26(4): 21. DOI:10.3969/j.issn.1004-0366.2014.04.006 |
 2019, Vol. 51
2019, Vol. 51


