除进样压力外,被动式微混合器不需要其他的外部激励,更适合集成在微全分析系统芯片上,与其他功能模块一起实现痕量试样的快速检测[1].不过在结构特征尺寸为0.1 μm~1 mm的μTAS芯片上,流体一般在低雷诺数Re的层流条件下运动,因此需要借助特殊的微结构对流体进行操作,达到提高混合效率的目的[2].T-型和Y-型混合器是结构最简单的被动式混合器[3-4],主要利用分子间的扩散运动实现混合,其混合效率与混合距离都难以满足μTAS芯片的需求.在微结构内增加障碍物可以有效改善混合效率[5],但障碍物使得进样压力大幅下降,将影响混合器后级的功能模块工作.依据Fick定律设计的分流汇合式混合器,将流体分割成多个薄层后再重新汇合[6],多次重复后虽能够获得理想的混合效率,然而过长的混合距离导致其仍不适合集成在μTAS芯片上.
处于混沌运动下的微流体,不仅保持了流速低、压降小等层流基本特征,其扩散特性更接近湍流状态,因此对混合效率的提升明显[7].Stroock等[8]设计的Staggered herringbone mixer(SHM)混合器,利用微沟道底部的交错式结构在低雷诺数条件下可以诱发混沌流.Song等[9]对SHM进行了优化设计,用二维结构代替了的三维结构,在降低制备难度的同时进一步提高了混合效率.然而优化后的SHM仍需经15次循环(混合距离为27 mm),方可达到满意的混合效果.Wiggins等[10]指出依据“面包师变换”(baker map)数学模型,对流体进行“挤压拉伸”和“切割堆叠”操作,多次重复后也可成功诱发混沌流.Carrière[11]使用有限元方法分析了“面包师变换”过程中混沌流产生的机理,验证了该模型用于微混合器设计的可行性.Yasui等[12]根据“面包师变换”成功制备了微混合器,经过10次“挤压拉伸”和“切割堆叠”操作后,在10.4 mm距离内即可达到满意的混合效果.Neerincx等[13]设计的半并行结构“面包师”微混合器,可同时对流体进行多次“切割堆叠”操作,使混合效率呈指数级增长.但是对流体进行“切割堆叠”操作需要复杂的微结构[14],因此在体积有限的μTAS芯片上集成“面包师”微混合器非常困难.
Smale[15]提出的“马蹄变换”(horseshoe transformation)也是一个可以在连续系统内部诱发混沌流的数学模型,变换过程中用“弯曲折叠”操作代替了“切割堆叠”操作,如果将其应用于微混合器的设计可以大幅降制备及集成难度.本文借助符号动力学系统对“马蹄变换”过程中混沌流的产生机理进行了研究,随后建立数值仿真模型证明了仿照“马蹄变换”过程设计的微混合器中存在混沌流,最后在PMMA基底材料上制备得到了微混合器样片并对其性能进行验证.
1 马蹄变换原理如图 1所示的“马蹄变换”,把混沌流的产生过程归结为一个二维映射,首先将混合单元(图 1中的虚线方框)内的“液体”挤压拉伸,随后通过“弯曲折叠”将“挤压拉伸”后溢出的“液体”再塞回混合单元,多次重复上述操作即可诱发混沌流.

|
图 1 马蹄变换示意 Fig. 1 Schematic of Horseshoe Transformation |
利用符号动力系统可以给出“马蹄变换”过程的数学描述,并证明变换后混沌流的存在.如图 1(a)所示,H0、H1分别为混合单元(U)内待混合的两种“液体”,初始状态下水平放置的H0、H1可用下式表示:
| $ \begin{array}{l} {H_0} = \left\{ {\left( {x, y} \right) \in U|0 \le x \le 1, 0 \le y \le 1/\mu } \right\}, \\ {H_1} = \left\{ {\left( {x, y} \right) \in U|0 \le x \le 1, 1 - \frac{1}{\mu } \le y \le 1} \right\}. \end{array} $ |
随后如图 1(b)所示,对水平“液体”H0、H1进行“挤压拉伸”操作,使“液体”H0、H1在x方向上收缩λ,在y方向上伸展μ.操作后得到的竖直“液体”可用下式中雅可比行列式表示:
| $\begin{array}{l} {H_0}\left( {\begin{array}{*{20}{c}} x\\ y \end{array}} \right) = \left( {\begin{array}{*{20}{c}} \lambda &0\\ 0&\mu \end{array}} \right)\left( {\begin{array}{*{20}{c}} x\\ y \end{array}} \right), \\ {H_1}\left( {\begin{array}{*{20}{c}} x\\ y \end{array}} \right) = \left( {\begin{array}{*{20}{c}} { - \lambda }&0\\ 0&{ - \mu } \end{array}} \right)\left( {\begin{array}{*{20}{c}} x\\ y \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 1\\ \mu \end{array}} \right), \left( {0 < \lambda < \frac{1}{2}, \mu > 2} \right). \end{array} $ | (1) |
接下来如图 1(c)所示,对竖直“液体”H0、H1进行“弯曲折叠”操作,将“挤压拉伸”后溢出的“液体”塞回混合单元U内部.操作后得到的“液体”V0、V1可表示为以下映射f(H0)和f(H1):
| $\begin{array}{l} \ \ {V_0} = f\left( {{H_0}} \right) = \left\{ {\left( {x, y} \right) \in U|0 \le x \le \lambda, 0 \le y \le 1} \right\}, \\ {V_1} = f\left( {{H_1}} \right) = \left\{ {\left( {x, y} \right) \in U|1 - \lambda \le x \le 1, 0 \le y \le 1} \right\}. \end{array} $ |
经“挤压拉伸”和“弯曲折叠”操作后混合单元内的“液体”可用集合Vi=f(Hi)∩U(i=0, 1)表示.利用同样的方法可以构造出如图 1(d)所示的逆变换:H1=f-1(V0)和H2=f-1(V1).逆变换集合可表示为:Hi=f-1(Vi)∩U(i=0, 1).如图 1(e)所示的变换f(U)与其逆变换f-1(U)的交集可用下式表示:
| $ \begin{array}{l} {\mathit{\Lambda }_1} = {\rm{ }}{f^{ - 1}}\left( U \right) \cap U \cap {f^{1}}\left( U \right) = \\ \;\;\;\;\;\;\;\;\left[{\left( {{H_0}, {V_0}} \right), \left( {{H_0}, {V_1}} \right), \left( {{H_1}, {V_0}} \right), \left( {{H_1}, {V_1}} \right)} \right]. \end{array} $ |
当i→∞时,图 1(f)中的小方块将收缩为点,但仍将一直留在混合单元内部.由此可以构造出一个如下式所示的i次迭代序列Λ为
| $ \begin{array}{l} \mathit{\Lambda } = \cdots {f^{ - i}}\left( U \right) \cap \cdots {f^{ - 1}}\left( U \right) \cap U \cap f\left( U \right) \cdots \cap {f^i}\left( U \right) = \\ \;\;\;\;\;\;\bigcap\limits_{i = - \infty }^\infty {{f^i}\left( U \right)} . \end{array} $ |
可见,如图 1所示的“马蹄变换”过程可以等价为一个建立在不变集Λ上的符号动力学系统(f, Λ).经“马蹄变换”后,混合单元内的“液体”是否产生混沌流的问题就转化为证明系统(f, Λ)是否具有混沌性的问题.李雅普诺夫指数(Lyapunovexponent)是判断系统内任意点(x, y)混沌性的重要依据,其正负表明了系统是否具有混沌性.根据式(1)给出的“马蹄变换”过程中任意点(x, y)雅可比行列式,系统(f, Λ)的两个李雅普诺夫指数(li)可用下式计算得到:
| $ {l_1} = {\rm{ln}}\left| \lambda \right|{\rm{ }}, {l_2} = {\rm{ln}}\left| \mu \right|. $ |
由于|μ|>2,则ln|μ|>0,因此经马蹄变换后系统具有混沌性.
2 微混合器设计与制备基于“马蹄变换”的微混合器设计流程如图 2所示.当两种液体在T-型微沟道内相遇时,沟道的宽度由4 mm变为0.2 mm,满足“马蹄变换”的“挤压”操作中0<λ<1/2条件;同时沟道的高度由0.2 mm变为0.5 mm,满足“马蹄变换”的“拉伸”操作中μ>2条件.对“挤压拉伸”后的液体沿x轴正、负向分别进行“弯曲折叠”并令液体重新汇合,满足变换过程中的“弯曲折叠”与“逆变换-交集”操作.重复上述混合单元结构3次以增强变换后诱发出的混沌流,即可得到有效混合距离为13 mm的微混合器.

|
图 2 基于马蹄变换的微混合器设计流程 Fig. 2 Mixer design based on Horseshoe Transformation |
依据图 2中的设计,采用超精密雕刻机在聚甲基丙烯酸甲酯(polymethyl methacrylate, PMMA)基底材料上制作微结构,随后使用有机溶剂混溶浸泡法进行键合[16],得到的微混合器芯片如图 3所示.
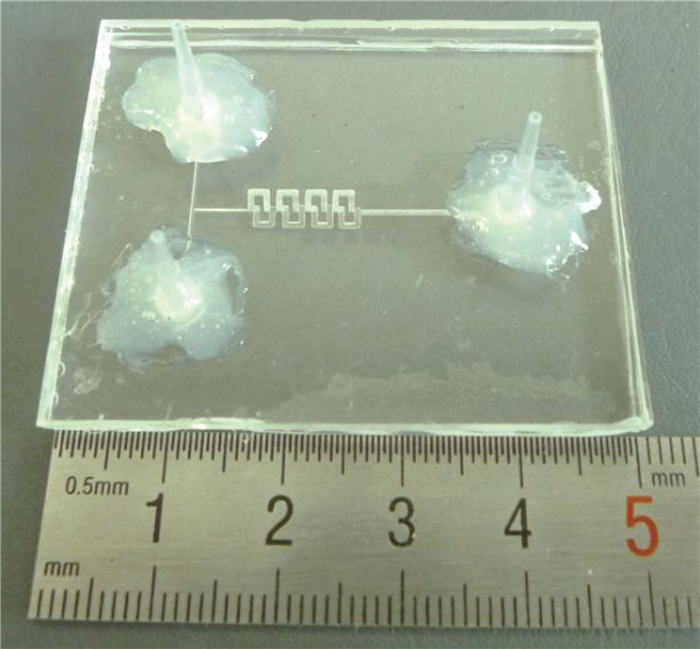
|
图 3 基于马蹄变换的微混合器芯片 Fig. 3 Mixer chip based on Horseshoe Transformation |
以纳维-斯托克斯方程和传质扩散方程为基础,利用COMSOL Multiphysics软件建立数值仿真模型.当液体密度(ρ)为1×103 kg/m3,混合单元结构特征尺度(L)为5×10-4 m,流速(u)为2×10-3 m/s,液体的动力黏滞系数(η)取1×10-3 Pa·s时,根据下式计算出雷诺数Re=1≪2 300,可见微混合器内的流体运动在典型的层流状态下, 如
| $ Re = \frac{{\rho uL}}{\eta }. $ |
当Re=1.0时微混合器的表面、截面质量分数云图及等质量分数线分布如图 4所示.图中的红色代表质量分数为0 mol/L的液体,蓝色代表质量分数为1 mol/L的液体,红色与蓝色之间的颜色梯度代表了液体均匀程度.A-E截面分别选取在T-型进液沟道出口以及4个混合单元出口处,截面中等质量分数线的质量分数差为0.01 mol/L.从表面云图中可以看出,经过微混合器后红、蓝两色间的颜色梯度迅速减小,并在第4个混合单元处趋于一致,表明两种液体间的质量分数差正在缩小.从截面云图A及其等质量分数线中可以看出,经T-型进液沟道“挤压拉伸”后的两色液体间的界面仍然清晰且等质量分数线非常密集,表明单独的“挤压拉伸”操作对混合促进作用并不明显.从截面云图B及其等质量分数线中可以看出,经第1次“弯曲折叠”和“逆变换-交集”操作后,两色液体间的界面已经模糊不清且等质量分数线数量减少明显,表明上述操作对混合的促进作用显著.而从截面云图D及其等质量分数线中可以看出,重复进行“弯曲折叠”和“逆变换-交集”操作4次后,两色液体间的界面已经彻底消失且等质量分数线也仅剩4条,表明在混合器出口处,液体质量分数已经趋近一致.

|
图 4 微混合器表面、截面质量分数云图及等质量分数线分布图 Fig. 4 Surface mass fraction, cross-sectional mass fraction, and contour line distribution |
为精确研究基于“马蹄变换”的微混合器性能,根据下式计算4个混合单元在“弯曲折叠”操作前和操作后的质量分数方差σ.式中,N=9为截面中采样点数量,9个采样点平均分布在截面的两个对角线上;Ci为截面中采样点的实际质量分数;C为采样截面平均质量分数,当两种液体质量分数分别为0、1 mol/L时,C=0.5 mol/L.
| $ \sigma = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{C_i} - \bar C} \right)}^2}} } . $ | (2) |
当Re=1.0时混合单元内部的质量分数方差曲线如图 5所示.从图 5中可以看出,每经过一个混合单元,液体的混合效果都得到明显的改善.在混合单元A中,未进行“弯曲折叠”操作时,截面2的质量分数方差(σA2=0.610)明显小于截面1的质量分数方差(σA1=0.679).这是由于在液体到达截面2之前不仅经过了更长的混合距离,而且其方向随扭曲的沟道发生了连续变化(+y→+z; +z→+x),由此产生的Dean流可以促进混合效率提升[17].当液体经“弯曲折叠”操作后,质量分数方差迅速下降,但截面4的质量分数方差(σA4=0.448)仍明显小于截面3的质量分数方差(σA3=0.491).因此当分层“弯曲折叠”的液体在截面5处汇合时,其质量分数方差(σA5=0.464)与截面4相比有小幅升高.混合单元B、C、D内部的质量分数方差曲线趋势与混合单元A类似,不过变化范围进一步缩小.在混合器出口处的质量分数方差(σD5=0.093)小于0.1,混合效果已经比较理想.
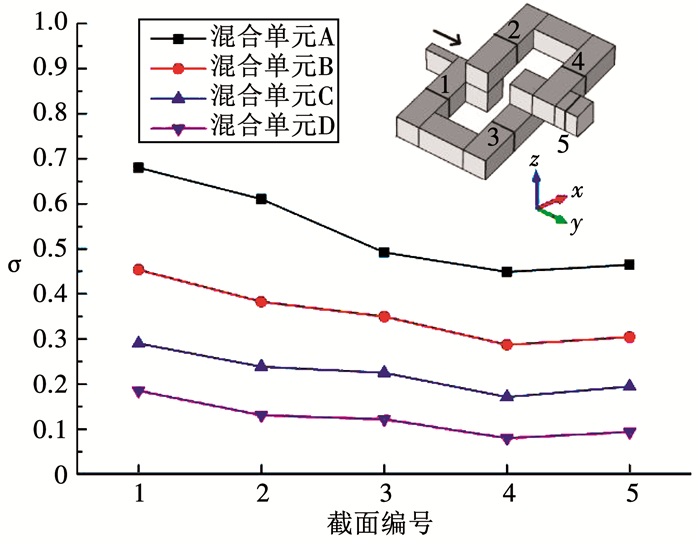
|
图 5 混合单元内部质量分数方差曲线 Fig. 5 Mass fraction variance curve in mixing unit |
混合单元内部的质量分数方差曲线虽然说明依据“马蹄变换”设计的微混合器能够取得满意效果,但并未证明微混合器内部是否有混沌流产生.为此图 6中给出了不同雷诺数下微混合器的浓度方差曲线,图 6中的取样截面为4个混合单元的出口处,既图 5中的截面5.
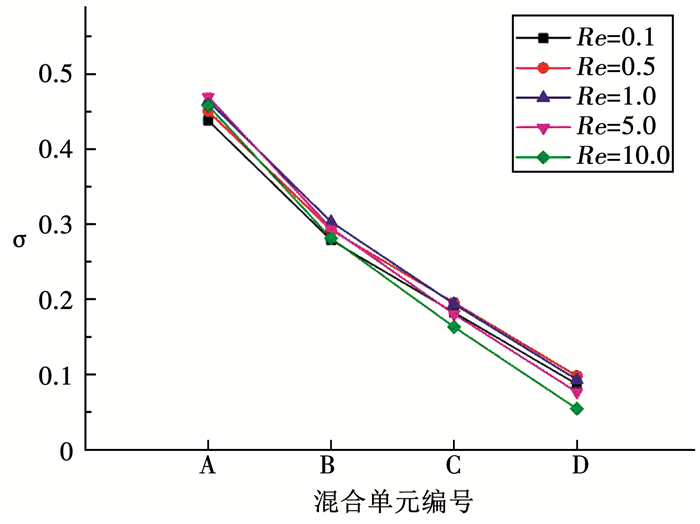
|
图 6 不同雷诺数时混合器的质量分数方差曲线 Fig. 6 Mass fraction variance curves for mixer at different Re |
从图 6中可以看出,当Re<1.0时混合器的质量分数方差曲线与液体流速成反比关系.当Re=0.1时,液体的流速(u)为2×10-4 m/s,混合单元结构特征尺度(L)为5×10-4 m,液体的扩散系数(D)为1×10-9 m2/s,依据式(2)计算出流体的佩克莱数(Peclet number, Pe), Pe=1.可见,此时混合器内的传质过程主要由分子扩散运动决定,而分子扩散运动速度则与待混合液体间的接触面积及接触时间相关.当混合单元结构一定时,液体间的接触面积不会发生变化,因此接触时间越长,分子扩散运动越充分.当流速增加时,两种液体在混合单元内的接触时间缩短,混合效果自然下降.
| $ Pe = \frac{{uL}}{D}. $ |
当Re=1.0时,经过混合单元A和混合单元B后,液体的质量分数方差为σ=0.303仍高于Re=0.5时的0.292,但经过混合单元C后,液体的质量分数方差为0.193已经与Re=0.5时的0.195相当;而经过混合单元D后,液体的质量分数方差为0.093已经小于Re=0.5时的0.098,质量分数方差曲线的变化趋势发生了翻转.此时,依据式(2)计算得到的Pe=10.0,可见混合器内的传质过程由扩散和混沌流共同决定,且随着Pe数的增大,扩散传质的比例减少,混沌流传质的比例增加.当Re>1.0时,质量分数方差曲线与液体流速成正比关系.在Re=10.0时,质量分数方差为0.054已经小于Re=0.1时的0.087,不仅混合效果进一步改善,而且混合效率也得到提升.这时计算得到的Pe=100,混合器内的传质过程主要由混沌流决定,液体的质量分数方差在混沌流的作用下加速下降.
3.2 混合器实验测试分别配置质量分数为1 mol/L的异硫氰酸荧光素(fluorescein isothiocyanate, FITC)和罗丹明B(Rhodamine B)作为示踪剂.以注射泵为动力(设置流速为2×10-3 m/s,此时Re=1),利用荧光显微镜观察混合器内的液体混合情况,并使用ImageJ软件完成CCD截图处理,得到了如图 7所示的可视化测试照片.从图 7中可以看出,在混合器单元A中,两种示踪剂的界面分明而且颜色也比较鲜艳;在混合器单元B中,两种示踪计的界面已经开始模糊,颜色也不再鲜艳;在混合器单元C中,两种示踪剂的界面已经不易分辨而且黄色占据了主导地位;在混合器单元D中,示踪剂基本成黄色,界面几乎消失.混合器的可视化测试结果与数值仿真中的表面云图一致,说明经过4个混合单元后,液体的质量分数趋于一致.

|
图 7 微混合器可视化测试照片 Fig. 7 Photos of micromixer visual test |
在室温下配制不同pH的缓冲液:邻苯二甲酸氢钾(0.05 mol/L,pH=4.01)、混合磷酸盐(0.025 mol/L,pH=6.86)、硼砂(0.01 mol/L,pH=9.18)用来精确测试混合器的性能.取等体积(10 ml)上述缓冲液,利用涡旋搅拌器使其两两均匀混合后,得到的对照溶液组成及pH见表 1.
| 表 1 对照溶液组成及pH Tab. 1 Composition of reference solutions and pH |
随后以双通道注射泵为动力,在微混合器两个进液口通入不同pH的缓冲液,利用酸度计测量出口的pH变化情况.为保证结果的一致性和准确性,在缓冲液通入1 min后开始测量且重复进行3次,得到的Re与混合溶液pH关系曲线如图 8所示.从图 8中可以看出,3种缓冲溶液组合的pH均随Re变化而在标定的对照值以上波动,当Re<0.5时,随着Re的增加,混合器出口处的pH逐步远离对照值,表明混合效果正在下降;当Re≥1.0时,随着Re的增加,混合器出口处的pH逐步接近对照值,表明混合效果正在改善.可见,混合器出口处pH的变化趋势与图 6中Re与σ关系曲线一致,再次说明当混合器中液体的流速较低时,扩散传质起主导作用,此时两种液体的接触时间因流速的升高而减少,进而导致混合效果下降;随着流速的增加,混沌流传质将在混合过程中起主导作用,此时混沌流因流速的升高而增强,进而将改善混合效果.
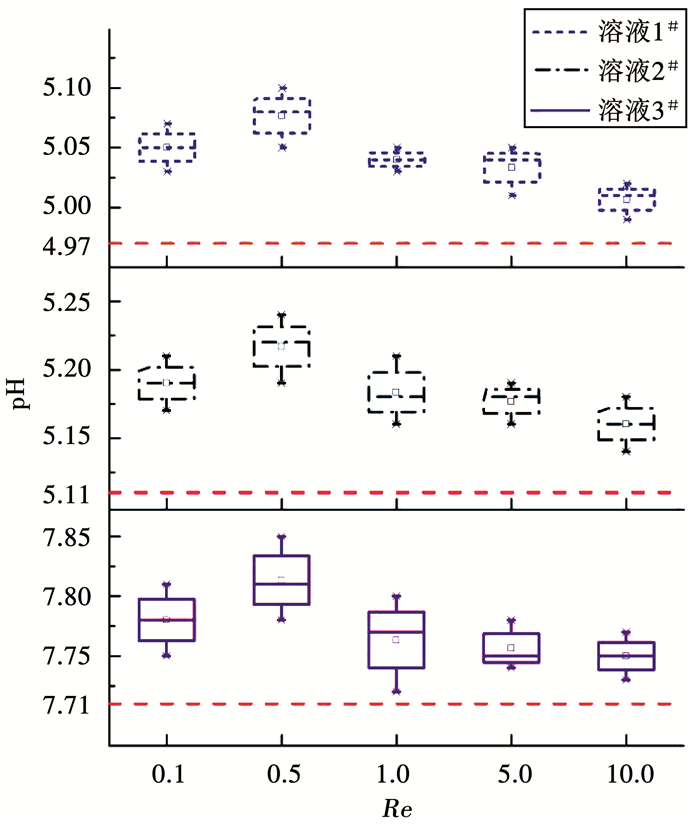
|
图 8 Re与pH关系曲线 Fig. 8 Solution pH versus Re |
1) 依据“马蹄变换”的几何图形,利用符号动力学理论证明了当满足“挤压”幅度0<λ<1/2且“拉伸”幅度μ>2时,变换能够成功诱发混沌流.随后按照“马蹄变换”步骤及条件,设计了由4个混合单元组成,总长度为13 mm的微混合器结构.
2) 数值仿真及佩克莱数计算结果表明:当Re<1.0时扩散传质为促进混合的主要因素,质量分数方差与液体流速成反比关系;当Re=1.0时,传质过程由扩散和混沌流共同决定,且随着流速的增加混沌流逐步成为促进混合的主要因素,质量分数方差与流速的关系发生翻转;当Re>1.0时混沌流成为促进混合的主要因素,质量分数方差与液体流速成正比关系;当Re=10.0时,质量分数方差σ=0.054,接近均匀混合.
3) 可视化测试结果以及不同pH试样混合测试结果表明基于马蹄变换设计并制备的微混合器能够产生混沌流且实际效果理想.
| [1] |
HESSEL V, LÖWE H, SCHÖNFELD F. Micromixers-a review on passive and active mixing principles[J]. Chemical Engineering Science, 2005, 60(8/9): 2479. DOI:10.1016/j.ces.2004.11.033 |
| [2] |
MEIJER H E H, SINGH M K, KANG T G, et al. Passive and active mixing in microfluidic devices[J]. Macromolecular Symposia, 2010, 279(1): 201. DOI:10.1002/masy.200950530 |
| [3] |
赵玉潮, 应盈, 陈光文, 等. T形微混合器内的混合特性[J]. 化工学报, 2006, 57(8): 1884. ZHAO Yuchao, YING Ying, CHEN Guangwen, et al. Characterization of micro-mixing in T-shaped micro-mixer[J]. Journal of Chemical Industry and Engineering, 2006, 57(8): 1884. DOI:10.3321/j.issn:0438-1157.2006.08.023 |
| [4] |
CHEN Zhuo, ZHANG Ruiqi, WANG Xiaona. CFD study of flow-diffusion process in Y-shape micromixer[J]. Journal of Central South University, 2016, 23(4): 969. DOI:10.1007/s11771-016-3144-7 |
| [5] |
LI Tiechuan, CHEN Xueye. Numerical investigation of 3D novel chaotic micromixers with obstacles[J]. International Journal of Heat and Mass Transfer, 2017, 115: 278. DOI:10.1016/j.ijheatmasstransfer.2017.07.067 |
| [6] |
HUSAIN A, KHAN F A, HUDA N, et al. Mixing performance of split-and-recombine micromixer with offset inlets[J]. Microsystem Technologies, 2018, 24(3): 1511. DOI:10.1007/s00542-017-3516-4 |
| [7] |
XIE Tingliang, XU Cong. Numerical and experimental investigations of chaotic mixing behavior in an oscillating feedback micromixer[J]. Chemical Engineering Science, 2017, 171: 303. DOI:10.1016/j.ces.2017.05.040 |
| [8] |
STROOCK A D, DERTINGER S K W, AJDARI A, et al. Chaotic mixer for microchannels[J]. Science, 2002, 295(5555): 647. DOI:10.1126/science.1066238 |
| [9] |
SONG Hongjun, YIN Xiezhen, BENNETT D J. Optimization analysis of the staggered herringbone micromixer based on the slip-driven method[J]. Chemical Engineering Research and Design, 2008, 86(8): 883. DOI:10.1016/j.cherd.2008.03.015 |
| [10] |
WIGGINS S, OTTINO J M. Foundations of chaotic mixing: one contribution of 11 to a Theme 'Transport and mixing at the microscale'[J]. Royal Society of London Transactions Series A, 2004, 362(1818): 937. DOI:10.1098/rsta.2003.1356 |
| [11] |
CARRIÈRE P. On a three-dimensional implementation of the baker's transformation[J]. Physics of Fluids, 2007, 19(11): 937. DOI:10.1063/1.2804959 |
| [12] |
YASUI T, OMOTO Y, OSATO K, et al. Microfluidic Baker's transformation device for three-dimensional rapid mixing[J]. Lab on A Chip, 2011, 11(19): 3356. DOI:10.1039/c1lc20342h |
| [13] |
NEERINCX P E, DENTENEER R P J, PEELEN S, et al. Compact mixing using multiple splitting, stretching, and recombining flows[J]. Macromolecular Materials and Engineering, 2011, 296(3/4): 349. DOI:10.1002/mame.201000338 |
| [14] |
WANG Ruijin, LIJIN Beiqi, SHI Dongdong, et al. Investigation on the splitting-merging passive micromixer based on Baker's transformation[J]. Sensors and Actuators B: Chemical, 2017, 249: 395. DOI:10.1016/j.snb.2017.04.087 |
| [15] |
SMALE S. Finding a horseshoe on the beaches of Rio[J]. The Mathematical Intelligencer, 1998, 20(1): 39. DOI:10.1007/BF03024399 |
| [16] |
ZHANG He, LIU Xiaowei, TIAN Li, et al. Miscible organic solvents soak bonding method use in a PMMA multilayer microfluidic device[J]. Micromachines, 2014, 5(4): 1416. DOI:10.3390/mi5041416 |
| [17] |
YANG Jun, QI Li, CHEN Yi, et al. Design and fabrication of a three dimensional spiral micromixer[J]. Chinese Journal of Chemistry, 2013, 31(2): 209. DOI:10.1002/cjoc.201200922 |
 2019, Vol. 51
2019, Vol. 51


