无人机空战态势评估是指利用自身雷达、传感器和地面雷达搜集到的信息,通过对其分析使自身具备感知当前或下一时刻空战态势的能力[1],这也是无人机自主空战决策的重要依据.最主要的因素是无人机所携带的武器,其他因素也是通过直接或者间接影响武器使用继而影响空战态势.随着三代空空导弹技术的成熟应用,四代空空导弹研制应用,其性能由一代空空导弹的尾后小角度攻击提升为全向攻击[2].文献[3]利用神经网络对空战样本进行学习,避免人为设置权重.文献[4]提出动态贝叶斯网络(bayesian network, BN)的方法,容错性较好,但并不能保证态势评估的准确度.决策树[5](decision tree, DC)是一种优秀的分类方法,已经在数据挖掘[6]、复杂碳酸盐岩岩性[7]、癌症分析[8]等方面广泛应用.
通过上述分析,本文提出一种基于决策树模型的空战态势评估方法(situation assessment based on decision tree, SADT),构造出不同的分类指标,作为决策树分支走向的依据,态势评估过程更加贴近实际空战.其次,在决策树的空白分支部分,引入反推理机制,利用已知相邻分支、同等级节点的标签结果,推理出与其相反的结论,符合人类行为认知模式.态势估计常用的方法是贝叶斯推理方法[9],就是在不完全情报下,对部分未知的状态用主观概率估计,然后用贝叶斯公式对发生概率进行修正.空战仿真结果表明,相比于贝叶斯推理的方法,本文方法用时更少、可靠性更强.
1 空战态势描述 1.1 态势结果分类无人机与有人机一样,在高空对抗时会出现各种态势,但是可以简单归结为4种典型态势[10], 如图 1所示.在采用SADT对空战态势进行评估时,4种态势作为决策树分类的结果进行输出.
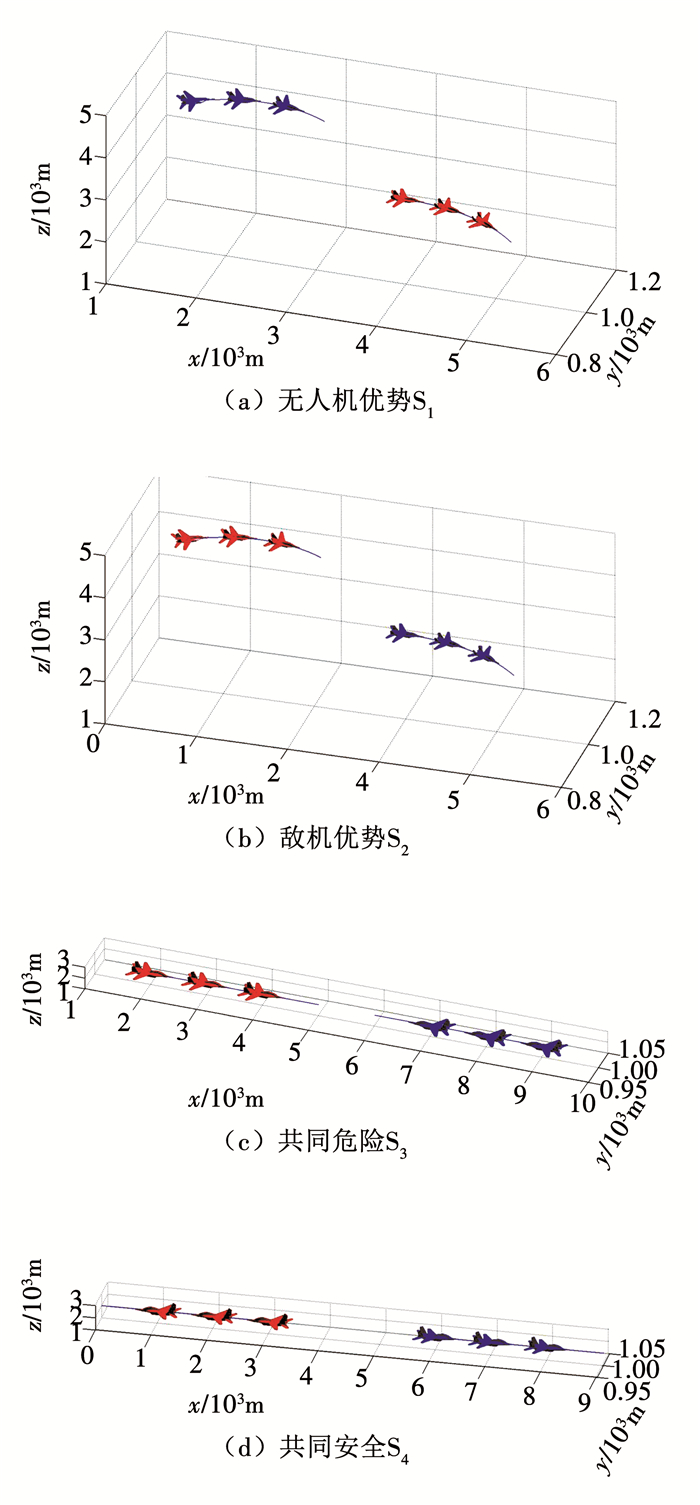
|
图 1 空战态势分类 Fig. 1 Air combat situation classification |
武器作战效能直接影响空战态势结果的划分,无人机与敌机的状态参数,直接或者间接影响双方的武器作战效能的发挥[11].无人机与敌机的相对位置关系如图 2所示.
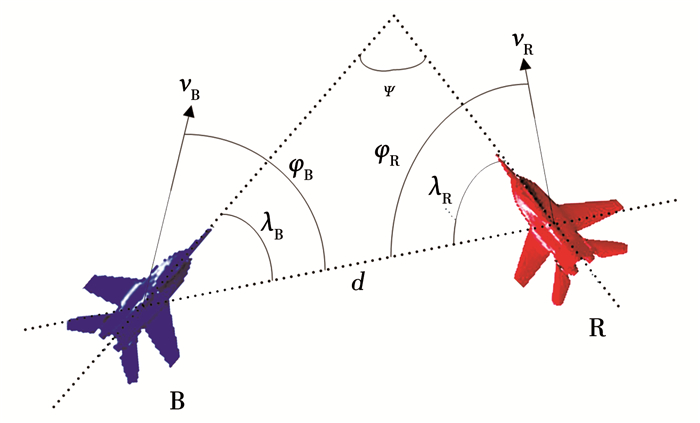
|
图 2 两机相对位置关系 Fig. 2 Relative position between the UAV and enemy |
图 2中:v为飞行速度; λ为目标方位角; φ为偏航角; B为蓝色无人机; R为红色敌机; d为相对距离.空战态势具有很强的相对性,即无人机的优势同时也是敌机的劣势.通过对比相同状态参量下,无人机与敌机的评价指标值的大小,构建对应的空战态势分类指标.以下分类指标都是以无人机视角建立.同样的方法可以类推以敌机的视角建立.
1.3 高度分类指标具备高度优势时将会拥有范围更广的攻击区,但是,高度差过大,空空导弹需要在垂直方位上进行大的过载机动,并且不同大气层之间的空气密度将会影响其飞行轨迹平稳性,命中概率下降[12].因此,在一定的高度差高度优势是呈现上升趋势,高度差继续增加,优势反而下降.基于上述分析,高度分类指标构建如
| $ {T_{\rm{h}}} = {{\rm{e}}^{ - \frac{{{{^{(h - {h_{\rm{k}}})}}^2}}}{{{h_{\rm{k}}}}}}}. $ |
式中:h为两机实际高度差, 设置范围为±1 000 m; hk为理想高度差, 范围为100~1 000 m,在h等于理想高度差时空空导弹的作战效能最佳.高度分类指标如图 3所示.
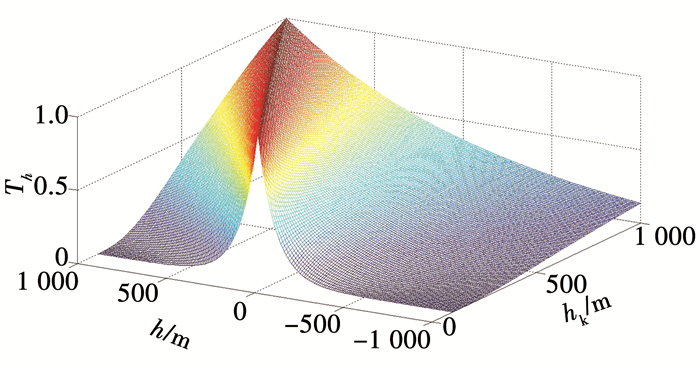
|
图 3 高度分类指标曲面 Fig. 3 Classified index surface of heiqht |
空空导弹的初速度越大, 攻击区的范围越广,命中对手的概率也会增加.但是速度过大将会带来其他问题,如转弯半径增大、油耗增多、压缩飞行员反应时间等[13].因此,无人机的理想速度是在一定的范围内高于敌机速度,无人机速度过小或者过大都将导致速度分类指标下降.基于上述分析,速度分类指标为
| $ {T_v} = \frac{1}{3}\frac{{{v_1}}}{{2{v_2}}}{{\rm{e}}^{ - \frac{{\left| {{v_1} - 2{v_2}} \right|}}{{{v_1}}}}}. $ |
式中:v1为无人机速度;v2为敌机速度,无人机速度范围[200 m/s, 100 m/s], 敌机速度范围[200 m/s, 500 m/s].无人机速度等于2倍敌机速度时分类指标达到最大值, 如图 4所示.
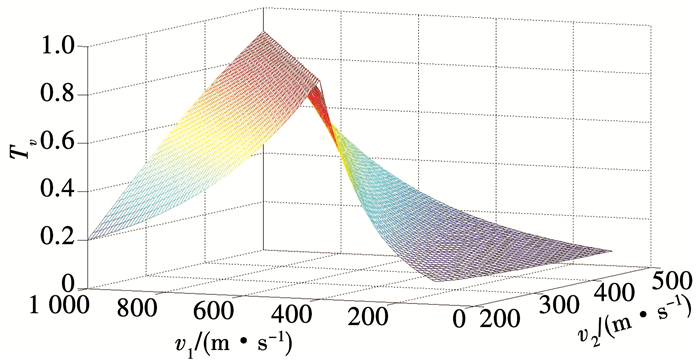
|
图 4 速度分类指标曲面 Fig. 4 Classified index surface of velocity |
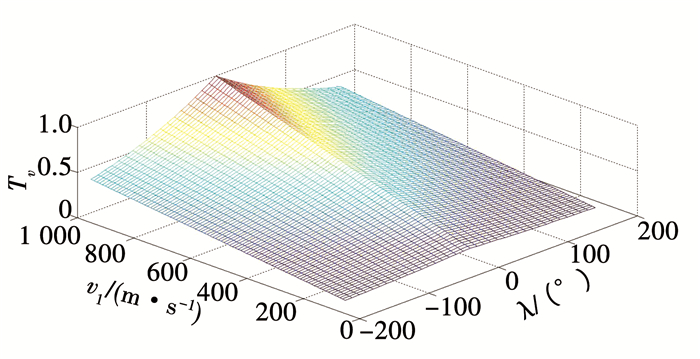
第三代空空导弹具有较大的离轴发射、全向攻击能力,传统的角度优势数学模型已经不能反映这种特性.目标方位角较大时,无人机依然有能力进入攻击区,构成发射条件,空空导弹需要做大过载机动;目标方位角较小时,导弹在传统优势的基础上全向进攻,命中率极大.根据上述分析,构建角度分类指标为
| $ {T_{\rm{o}}} = \frac{{{v_1}}}{{1\;000}}{{\rm{e}}^{ - \frac{{\left| \lambda \right|}}{{180}}}}. $ |
式中:v1为无人机的速度, 假定飞行速度范围[100 m/s, 1 000 m/s];λ为目标方位角,角度范围[-180°, 180°],角度分类指标如图 5所示.
|
图 5 角度分类指标曲面 Fig. 5 Classified index surface of angle |
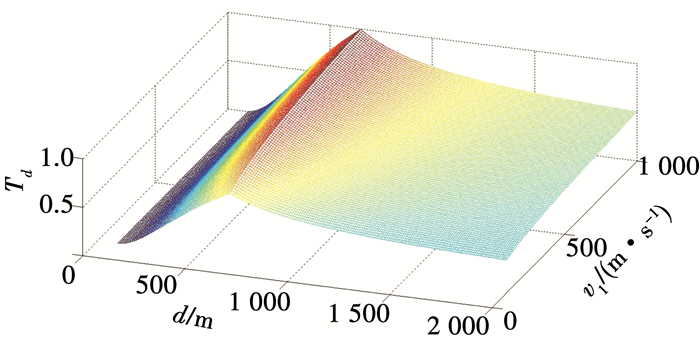
根据无人机与敌机之间的距离,可以将无人机的位置分为攻击区之外和攻击区之内.攻击区之外可以分为攻击区远边界一侧和攻击区近边界一侧;攻击区之内又分为不可逃逸区之内和不可逃逸区之外,不可逃逸区是处于攻击区内部,属于击中目标概率较大的区域.因此构建距离分类指标为
| $ {T_{\rm{d}}} = \left\{ \begin{array}{l} 0, d < {d_1};\\ v{e^{ - \frac{{\left| {2d - {d_1} - {d_2}} \right|}}{2}}}, {d_1} < d < {d_2};\\ 0, d > {d_2}. \end{array} \right. $ |
式中:d1为攻击区近边界;d2为攻击区的远边界,攻击区中间位置为不可逃逸区,空空导弹攻击区范围[200 m, 2 000 m], 得到距离分类指标如图 6所示.
|
图 6 距离分类指标曲面 Fig. 6 Classified index surface of distance |
决策树分类法类似于树的结构,由根到叶的顺序进行划分,包含一个根节点、若干个内部节点和叶节点.SADT中叶节点对应态势评估结果,其他节点对应状态参量.前一节点为父节点,被划分为若干个子节点,依据已经构建的分类指标进行父节点的划分.具体表述为分别从无人机与敌机的视角在同一状态参量下进行分类指标的计算,根据二者对比的大小进行分类,例如:
| $\begin{array}{l} {E_h} = \left\{ \begin{array}{l} 1, {T_h} > T_h^e;\\ 0, {T_h} < T_h^e. \end{array} \right.\;\;\;\;{E_v} = \left\{ \begin{array}{l} 1, {T_v} > T_v^e;\\ 0, {T_v} < T_v^e. \end{array} \right.\\ {E_o} = \left\{ \begin{array}{l} 1, {T_o} > T_o^e;\\ 0, {T_o} < T_o^e. \end{array} \right.\;\;\;\;{E_d} = \left\{ \begin{array}{l} 1, {T_d} > T_d^e;\\ 0, {T_d} < T_d^e. \end{array} \right. \end{array} $ |
通过一定数量的训练样本生成SADT,训练样本中包含双方的空战状态参量、分类指标值、对比结果.利用先验知识构建决策树,获得的分类模型高效、合理.空战态势数据集见表 1.
| 表 1 空战态势数据集 Tab. 1 Data collection of air combat situation |
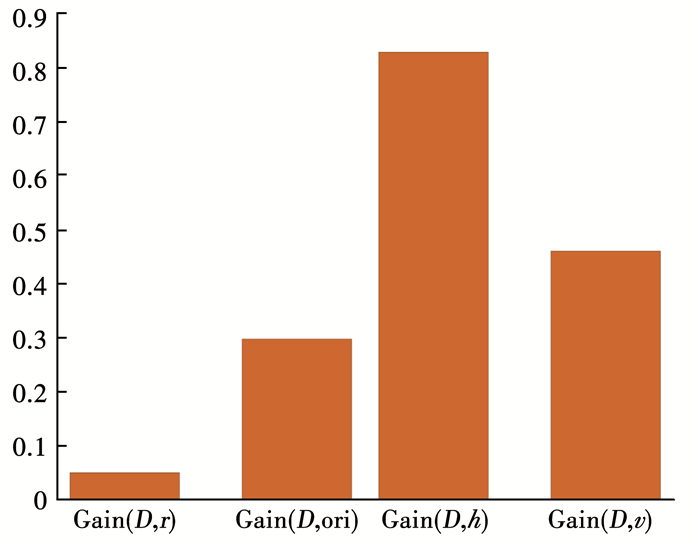
SADT中有4个节点测试属性:无人机与敌机之间高度、速度、角度和距离分类指标的对比.随着划分的不断进行,分支节点包含的样本尽可能属于同一类型,即节点纯度越来越高[14].因此,结合空战数据集,需要对4个测试属性进行排序.信息增益是衡量集合纯度的一种方法.结合空战数据集,计算每个测试属性的信息增益[15],按照不同属性信息增益的大小进行排序.如
| $ {\rm{Gain}}\left( {\mathit{\boldsymbol{D}}, a} \right) = {\rm{Ent}}\left( \mathit{\boldsymbol{D}} \right) - \sum\limits_{v = 1}^2 {\frac{{\left| {{\mathit{\boldsymbol{D}}^{\rm{v}}}} \right|}}{{\left| \mathit{\boldsymbol{D}} \right|}}{\rm{Ent}}({\mathit{\boldsymbol{D}}^{\rm{v}}})} . $ |
式中:a为某个属性,其可能取值为{0, 1},用a对当前数据集D进行划分,会产生2个分支节点,每个分支节点包含数据集D在属性a上取值为0或1的样本,记为Dv.如
| $ {\rm{Ent}}\left( \mathit{\boldsymbol{D}} \right) = - \sum\limits_{k = 1}^{\left| 4 \right|} {{p_k}{\rm{lo}}{{\rm{g}}_2}{p_k}.} $ |
式中:pk为数据集D中第k类样本所占比例(k=1, 2, 3, …, |y|).
经过计算4个属性的信息增益,如图 7所示,高度分类指标的对比信息增益最大,因此被选为根节点.
|
图 7 节点属性信息增益柱状对比 Fig. 7 Histogram of the node attribution gain |
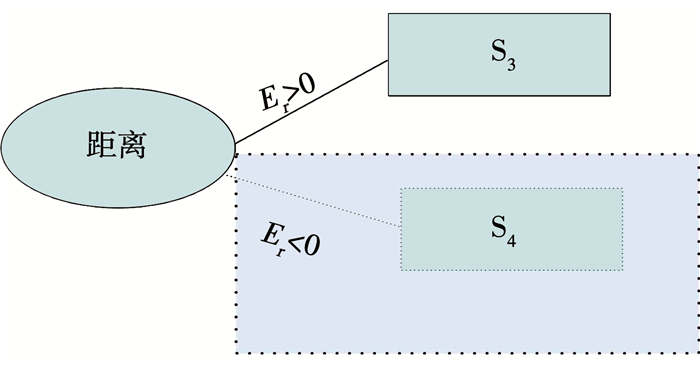
SADT中4个属性的等级顺序依次是高度分类指标对比、速度分类指标对比、角度分类指标对比、距离分类指标对比.通过上述建立SADT节点分类规则,在样本基础上,经过计算4个属性的信息增益,对节点属性进行排序.整体SADT结构如图 8所示.根据样本构建的决策树不能涵盖所有的空战信息,对于缺失分支部分引入反推理规则,如在节点属性距离分类指标对比中,缺失Er<0的分支,如图 9所示.在属于同一个父节点的两个子节点,未知节点的推理结果与已知节点的推理结果相反,即S1对应S2, S3对应S4.反推理机制符合人类的认知模式,在对未知事物进行判断时,已知事物的属性是决策的依据.

|
图 8 SADT结构图 Fig. 8 Structure chart of SADT |
|
图 9 SADT中反推理机制 Fig. 9 Anti-reasoning rule in SADT |
SADT吸收了决策树快速直接的优点,模型简单、参数少、运算速度快,在空战仿真时进行实时评估,方法的具体步骤如下.
Step 1 根据样本数据对节点属性进行排序,建立推理规则,构建完整SADT模型.
Step 2 时间初始化,将空战过程划分为时间序列,在SADT中输入时间序列片断内空战双方的状态参数.
Step 3 计算当前两机的4种分类指标,判断分类走向是否属于已有的分支,如果属于已有分支,则转至步骤5)输出对应的态势结果,如果不属于,则转至步骤4)反推理.
Step 4 对同一个父节点的相邻节点进行分类得到镜像态势,将镜像态势反变换后输出,存储在态势变量序列P.
Step 5 将态势分类结果输出并储存在态势变量序列P.
3 仿真校验通过对空战场景仿真,采用SADT方法和贝叶斯推理方法分别进行态势估计,并对结果分析对比.仿真平台环境硬件为Inter(R)Core(TM)i5-6500, CPU, 3.20 GHz, 4 GB RAM, Win7操作系统,仿真软件为MATLAB R2013a.为充分验证所提方法的有效性,排除随机性和偶然性,在一对一空战、二对一空战、一对二空战和二对二空战模式下的不同场景,分别进行实验.对每个场景下的实验结果进行统计分析,实验仿真空战参数初值见表 2.
| 表 2 空战参数初始化 Tab. 2 Air combat parameters initialization |
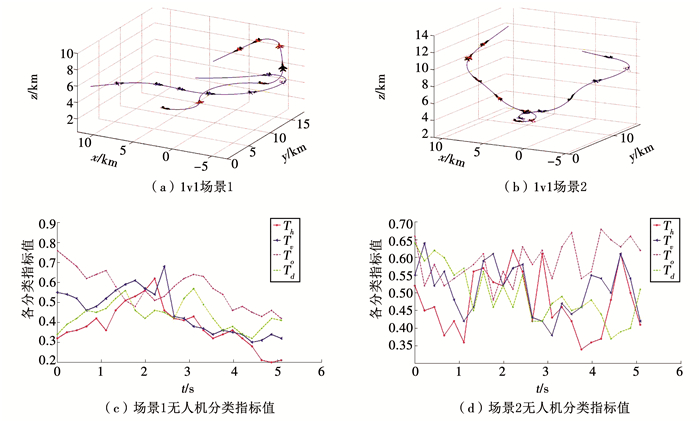
在图 10(a)中的空战仿真初期,无人机处于敌机尾部,占据角度优势.随后敌机以S机动试图摆脱无人机,造成无人机角度优势下降,但获得高度优势.在图 10(b)部分,无人机与敌机纠缠在一起,处于相互危险的态势.空战态势将空战过程按时间序列划分,每组序列生成一个态势.将实际分析结果分别与SADT和BN方法评估的态势结果进行对比,采用SADT方法评估准确度稳定在80%,贝叶斯推理方法的准确度也能够达到80%,但预测结果没有可预见性.SADT方法在两个场景中的预测时间分别为5.36、5.39 s; BN方法预测时间分别为12.51、11.63 s.SADT方法在1v1模式下的预测精度和时间都要优于BN方法.
|
图 10 空战1v1模式 Fig. 10 Air combat one-to-one mode |
| 表 3 1v1场景下两种方法对比结果 Tab. 3 One-to-one classification results under two methods |
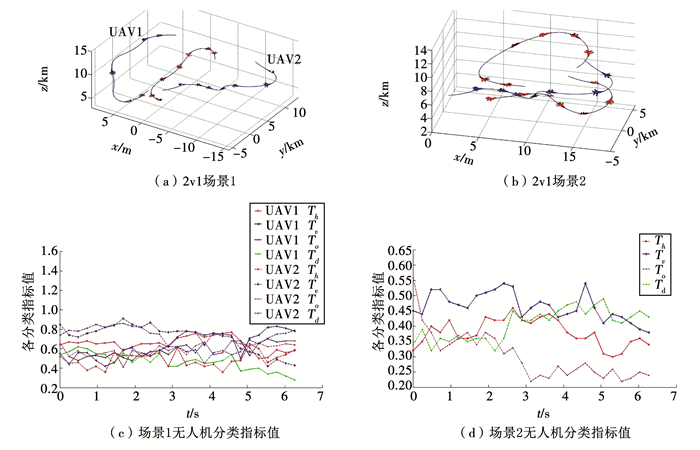
图 11(a)是两架无人机与一架敌机进行对抗的场景,在空战初期,敌机虽然数量少,但是占据角度优势,因此冒险发动进攻.无人机随后分别向不同的方向机动以发挥数量优势.敌机选择爬升继续对无人机2进攻,无人机1在脱逃后掉头爬升,以更高的位置向敌机进攻.因此无人机1最后获得优势态势,无人机2获得劣势态势.图 11(b)中是一架无人机与两架敌机格斗的空战仿真,无人机速度远大于敌机速度.表 4给出了两种方法态势评估结果,在SADT在2v1模式下的准确度与1v1模式下的准确度相差不大, BN方法预测准确度稳定,但是效果不理想.SADT方法的准确度为80%,在两种场景下的用时分别为6.43、6.28 s,而同样情况下,BN方法的准确度为60%,用时分别为13.64、12.74 s.
|
图 11 空战2v1模式 Fig. 11 Air combat two-to-one mode |
| 表 4 2v1场景下两种方法对比结果 Tab. 4 Two-to-one classification results under two methods |
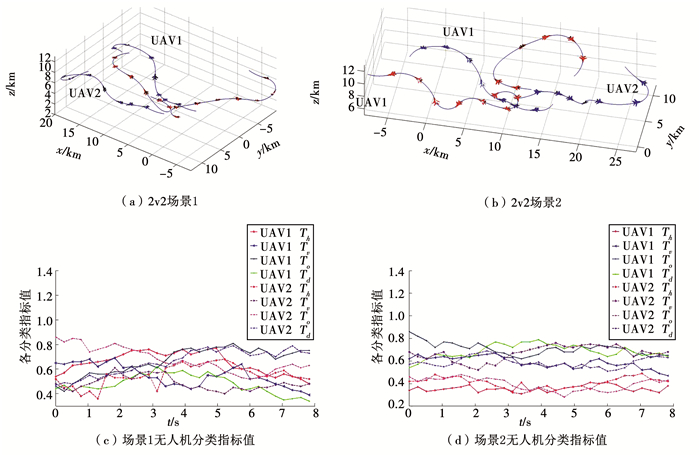
如图 12(a)所示,空战初期无人机1与敌机相向飞行,其中一架敌机以最大加速转弯掉头,进而爬升抢占高位,无人机1也进行高空占位,最后两机又形成攻击态势.在图 12(b)中,无人机与敌机相互纠结在一起,无人机1对其中一架敌机进行追击,敌机进行低速Yo-Yo试图让无人机1超越自己,无人机1通过爬升降低自身速度并保持能量,最后俯冲达到构成武器发射条件.分析SADT和BN的态势评估结果,在复杂的态势下,SADT的评估依据建立的4种分类指标,包含影响空战态势的主要方面,准确度没有降低. BN方法在复杂的态势环境下,缺乏先验经验的指导,评估结果的准确度下降.在场景1中,SADT方法的准确度为80%,用时为7.85 s,而同样情况下,BN方法的准确度为60%,用时为15.38 s;在场景2中,SADT方法的准确度为80%,用时为7.92 s,而同样情况下,BN方法的准确度为40%,用时为13.46 s.
|
图 12 空战2v2模式 Fig. 12 Air combat two-to-two mode |
| 表 5 2v2场景下两种方法对比结果 Tab. 5 Two-to-two classification results under two methods |
为充分验证本文所提方法的有效性,在1v1、2v1和2v2空战模式下,与BN方法分别在两个场景下进行了对比研究,仿真结果表明SADT方法在解决空战态势估计问题时的准确度要高于BN方法,评估时间小于BN方法的评估时间,充分验证了所提方法的高效性.
4 结论1) 通过建立优势指标函数作为决策树推理的规则,完善了推理的准确性和合理性.
2) 在空战态势的评估过程中,采用决策树理论对态势分类,优化了整个结算过程和步骤,提高了对结果的分类的科学性和说服力.
3) 对不同的的态势结果进行分类对比,验证了决策树态势分类方法的优越性和实用性.
| [1] |
张彬超, 寇雅楠, 邬蒙, 等. 基于深度置信网络的空战态势评估[J]. 北京航空航天大学学报, 2017, 43(7): 1450. ZHANG Binchao, KOU Yanan, WU Meng, et al. Close-range air combat situation assessment using deep belief network[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(7): 1450. DOI:10.13700/j.bh.1001-5965.2016.0956 |
| [2] |
KARELAHTI J, VIRTANEN K, RAIVIO T. Game optimal support time of a medium range air-to-air missile[J]. Journal of Guidance Control Dynamics, 2006, 29(5): 1061. DOI:10.2514/1.17910 |
| [3] |
YOON S, LEE S H. ANN-based evaluation model of combat situation to predict the progress of simulated combat training[J]. Journal of the Korea Society of Computer and Information, 2017, 22(7): 31. |
| [4] |
孟光磊, 马晓玉, 刘昕, 等. 基于混合动态贝叶斯网的无人机空战态势评估[J]. 指挥控制与仿真, 2017, 39(4): 1. MENG Guanglei, MA Xiaoyu, LIU Xin, et al. Situation assessment for unmanned aerial vehicles air combat based on hybrid bayesion network[J]. Command Control & Simulation, 2017, 39(4): 1. DOI:10.3969/j.issn.1673-3819.2017.04.001 |
| [5] |
WU C C, CHEN Y L, LIU Y H, et al. Decision tree induction with a constrained number of leaf nodes[J]. Applied Intelligence, 2016, 45(3): 673. DOI:10.1007/s10489-016-0785-z |
| [6] |
王文霞. 数据挖掘中改进的C4.5决策树分类算法[J]. 吉林大学学报(理学版), 2017, 55(5): 1274. WANG Wenxia. Improved C4.5 decision tree classification algorithm in data mining[J]. Journal of Jilin University(Science Edition), 2017, 55(5): 1274. DOI:10.13413/j.cnki.jdxblxb.2017.05.42 |
| [7] |
王振洲, 张春雷, 高世臣. 利用决策树方法识别复杂碳酸盐岩岩性——以苏里格气田苏东41-33区块为例[J]. 油气地质与采收率, 2017, 24(6): 25. WANG Zhenzhou, ZHANG Chunlei, GAO Shichen. Lithology identification of complex carbonate rocks based on decision tree method: an example from block sudong 41-33 in sulige gas field[J]. Petroleum Geology and Recovery Efficiency, 2017, 24(6): 25. DOI:10.13673/j.cnki.cn37-1359/te.2017.06.004 |
| [8] |
TSAI M H, WANG H C, LEE G W, et al. A decision tree based classifier to analyze human ovarian cancer cDNA microarray datasets[J]. Journal of Medical Systems, 2016, 40(1): 21. DOI:10.1007/s10916-015-0361-9 |
| [9] |
XUAN Yongbo, HUANG Changqiang, LI Wangxi. Air combat situation assessment by gray fuzzy Bayesian network[J]. Applied mechanics & Materials, 2011, 69(69): 114. DOI:10.4028/www.scientific.net/AMM.69.114 |
| [10] |
孟光磊, 龚红光. 基于混合贝叶斯网的空战目标威胁评估方法[J]. 系统工程与电子技术, 2010, 32(11): 2398. MENG Guanglei, GONG Hongguang. Threat assessment of aerial targets based on hybrid bayesian network[J]. Systems Engineering and Electronics, 2010, 32(11): 2398. DOI:10.3969/j.issn.1001-506X.2010.11.31 |
| [11] |
顾佼佼, 刘卫华, 姜文志. 基于攻击区和杀伤概率的视距内空战态势评估[J]. 系统工程与电子技术, 2015, 37(6): 1306. GU Jiaojiao, LIU Weihua, Jiang Wenzhi. WVR air combat situation assessment mode based on weapon engagement zone and kill probability[J]. Systems Engineering and Electronics, 2015, 37(6): 1306. DOI:10.3969/j.issn.1001-506X.2015.06.13 |
| [12] |
MENON P K A, BRIGGS M M. Near optimal midcourse guidance for air to air missiles[J]. Journal of Guidance Control and Dynamics, 1990, 13(4): 596. DOI:10.2514/3.25375 |
| [13] |
AUSTIN F, CARBONE G, HINZ H, et al. Game theory for automated maneuvering during air to air combat[J]. Journal of Guidance Control & Dynamics, 1990, 13(6): 1143. DOI:10.2514/3.20590 |
| [14] |
石红姣. 基于改进随机决策树算法的分布式数据挖掘[J]. 计算机与数据工程, 2017, 45(9): 1802. SHI Hongjiao. Distributed data mining based on improved random decision tree algorithm[J]. Computer & Digital Engineering, 2017, 45(9): 1802. DOI:10.3969/j.issn.1672-9722.2017.09.024 |
| [15] |
ZHANG Le, SUANTHAN P N. Oblique decision tree ensemble via multisurface proximal support vector machine[J]. IEEE Transactions on Cybernetics, 2015, 45(10): 2165. DOI:10.1109/TCYB.2014.2366468 |
 2019, Vol. 51
2019, Vol. 51


