在研究实际问题时,经常会遇到研究对象处于动态复杂的环境中,导致构建模型中的参数难以确定,这种现象称之为非决定性现象.非决定性现象主要分为两类,一类是随机现象,一类是基于专家信度的现象.为更好地研究第2类非决定性现象, 陈孝伟等[1]先后对不确定理论进行深入的研究,不断丰富和完善不确定理论,在2010年形成了一个成熟的、完备的数学系统.
在不确定基础理论研究方面,定义了不确定测度、不确定变量、独立性、数字特征及运算法则[1]、不确定分布函数及逆分布函数[2-3]、不确定集合[4]等基本概念,并在此基础上,对不确定微积分[5]、不确定差分方程[6]、不确定分布拟合、不确定规划[7-8]等领域进行了深入地分析和研究,为进一步研究不确定理论奠定了基础.并且不确定理论在解决风险分析[9-10]、股票交易[11]等问题时效果很好.
在应用研究方面,不确定理论在金融、管理、军事等领域应用广泛.但仍存在一些问题,其中最主要的问题是分布拟合后缺乏检验手段.不确定变量及其分布是应用研究的基础,不确定统计理论给出了收集专家经验数据的方法[1],介绍了基于专家经验数据,利用最小二乘法[12]、Delphi法[13]、矩估计法[14]等拟合不确定分布函数的方法,但在不确定统计理论中并没有针对分布拟合检验的研究.文献[15-16]研究了机器路径问题,将工作的处理时间作为不确定变量,利用专家经验数据拟合了不确定变量服从的分布函数;文献[17]基于不确定理论解决了数据缺失条件下可修复系统冗余分配问题,文中构建的不确定多目标规划模型中将部件的修复率、故障率等参数作为不确定变量,并且在案例中直接给定了不确定变量服从的不确定分布函数;文献[18-19]讨论了不确定环境下多目标股票交易问题,模型中均将交易价格、供应量和需求量作为不确定变量,处理不确定变量时直接给定了不确定分布函数.此外,还有许多文献在应用研究中注重如何根据专家经验数据拟合得到不确定分布,却忽略了对拟合的不确定分布进行检验.因此,本文主要讨论如何对拟合的不确定分布进行检验.
不确定理论与随机理论最主要的区别有:1)不确定理论中的乘积测度与概率论中概率乘积测度运算法则不同,在不确定理论中,若干独立事件同时发生的不确定测度是对每个事件发生不确定测度取最小;2)不确定理论不满足可加性公理.基于上述两点,难以将随机理论中关于分布拟合检验的方法推广到不确定理论,即在不确定理论中无法定义一个检验统计量,使其在某种条件下满足皮尔逊定理.因此,本文从其他途径提出了检验分布拟合有效性的方法.
1 不确定分布特征函数 1.1 不确定分布特征函数的定义随机分布的特征函数具有一些性质能够简化某些定理证明及数字特征的计算.因此,本文借助随机分布的特征函数,定义了不确定分布的特征函数,并给出了计算公式.
定义1[1] 函数Φ:R→[0, 1],是一个不确定分布,当且仅当它是一个不满足Φ(x)≡1或Φ(x)≡0的单调增函数.
定义2[1] 设Φ(x)是不确定变量ξ的不确定分布,如果Φ(x)在集合上{x|0Φ(x)<1}是连续严格单调递增的,且
定义3 不确定变量ξ服从正则不确定分布Φ(x),称φ(t)=E(eitξ), -∞<t<+∞为不确定分布Φ(x)或不确定变量ξ的特征函数.其中,E(·)为不确定变量ξ的期望值;t为实数;i为虚数单位.
根据不确定理论中关于期望的计算法则,不确定分布Φ(x)的特征函数的计算式为
| $ \begin{array}{l} \varphi \left( t \right) = \int_{ - \infty }^{ + \infty } {{{\rm{e}}^{{\rm{i}}tx}}{\rm{d}}\mathit{\Phi }\left( x \right)} = \\ \;\;\;\;\;\;\;\;\;\;\int_0^1 {{{\rm{e}}^{{\rm{i}}t\mathit{\Phi } - 1\left( \alpha \right)}}{\rm{d}}\alpha } , - \infty < t < + \infty , \end{array} $ | (1) |
由此可见,不确定变量的特征函数取决于不确定变量服从的分布函数.因此,不确定变量特征函数也称为不确定分布特征函数.
1.2 几种典型不确定分布的特征函数不确定理论中常用的不确定分布有线性、之字形和对数正态等不确定分布函数.根据不确定分布特征函数的定义和式(1),可得如下推论.
推论1 不确定变量ξ服从线性不确定分布
证明 根据文献[1],线性不确定分布
| $ \begin{array}{l} \varphi \left( t \right) = \int_0^1 {{{\rm{e}}^{{\rm{i}}t\mathit{\Phi } - 1\left( \alpha \right)}}{\rm{d}}\alpha } = \int_0^1 {{{\rm{e}}^{{\rm{i}}t\left( {a + \left( {b - a} \right)\alpha } \right)}}{\rm{d}}\alpha } = \\ \;\;\;\;\;\;\;\;\;\;\int_0^1 {{{\rm{e}}^{{\rm{i}}ta}} \cdot {{\rm{e}}^{{\rm{i}}t\left( {b - a} \right)\alpha }}{\rm{d}}\alpha } = \frac{{{{\rm{e}}^{{\rm{i}}bt}} - {{\rm{e}}^{{\rm{i}}at}}}}{{{\rm{i}}\left( {b - a} \right)t}}, \end{array} $ |
证毕.
推论2 不确定变量ξ服从之字形不确定分布
证明 根据文献[1],之字形不确定分布的逆分布为
| $ \begin{array}{l} \varphi \left( t \right) = \int_0^1 {{{\rm{e}}^{{\rm{i}}t\mathit{\Phi } - 1\left( \alpha \right)}}{\rm{d}}\alpha } = \\ \;\;\;\;\;\;\;\;\;\;\int_0^{0.5} {{{\rm{e}}^{{\rm{i}}t\left( {a + 2\left( {b - a} \right)\alpha } \right)}}{\rm{d}}\alpha } + \int_{0.5}^{1.0} {{{\rm{e}}^{{\rm{i}}t\left( {\left( {2b - c} \right) + 2\left( {c - b} \right)\alpha } \right)}}{\rm{d}}\alpha } = \\ \;\;\;\;\;\;\;\;\;\;{{\rm{e}}^{{\rm{i}}t\alpha }} \cdot \frac{{{{\rm{e}}^{2{\rm{i}}t\left( {b - a} \right)\alpha }}}}{{2{\rm{i}}\left( {b - a} \right)t}}\left| {_0^{0.5}} \right. + {{\rm{e}}^{{\rm{i}}t\left( {2b - c} \right)}} \cdot \frac{{{{\rm{e}}^{2{\rm{i}}t\left( {c - b} \right)\alpha }}}}{{2{\rm{i}}\left( {c - b} \right)t}}\left| {_0^{1.0}} \right. = \\ \;\;\;\;\;\;\;\;\;\;\frac{{{{\rm{e}}^{{\rm{i}}bt}} - {{\rm{e}}^{{\rm{i}}at}}}}{{2{\rm{i}}\left( {b - a} \right)t}} + \frac{{{{\rm{e}}^{{\rm{i}}ct}} - {{\rm{e}}^{{\rm{i}}bt}}}}{{2{\rm{i}}\left( {c - b} \right)t}}, \end{array} $ |
证毕.
推论3 不确定变量ξ服从经验不确定分布,则其特征函数为
| $ \varphi \left( t \right) = \sum\limits_{j = 1}^{n - 1} {\frac{{\left( {{\alpha _{j + 1}} - {\alpha _j}} \right)\left( {{{\rm{e}}^{{x_{j + 1}}{\rm{i}}t}} - {{\rm{e}}^{{x_j}{\rm{i}}t}}} \right)}}{{{\rm{i}}\left( {{x_{j + 1}} - {x_j}} \right)t}}} . $ |
证明 根据文献[1],经验不确定分布的逆分布为
| $ \begin{array}{l} \varphi \left( t \right) = \int_0^1 {{{\rm{e}}^{{\rm{i}}t\mathit{\Phi } - 1\left( \alpha \right)}}{\rm{d}}\alpha } = \sum\limits_{j = 1}^{n - 1} {\int_{{\alpha _j}}^{{\alpha _{j + 1}}} {{{\rm{e}}^{{\rm{i}}t\left( {{x_j} + \frac{{\left( {{x_{j + 1}} - {x_j}} \right)\left( {\alpha - {\alpha _j}} \right)}}{{{\alpha _{j + 1}} - {\alpha _j}}}} \right)}}{\rm{d}}\alpha } } = \\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^{n - 1} {\int_{{\alpha _j}}^{{\alpha _{j + 1}}} {{{\rm{e}}^{{\rm{i}}t\left( {\frac{{\left( {{x_{j + 1}} - {x_j}} \right)\alpha }}{{{\alpha _{j + 1}} - {\alpha _j}}} + \frac{{{x_j}{\alpha _j} + 1 - {x_{j + 1}}{\alpha _j}}}{{{\alpha _{j + 1}} - {\alpha _j}}}} \right)}}{\rm{d}}\alpha } } = \\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^{n - 1} {\frac{{\left( {{\alpha _{j + 1}} - {\alpha _j}} \right)\left( {{{\rm{e}}^{{\rm{i}}t{x_{j + 1}}}} - {{\rm{e}}^{{\rm{i}}t{x_j}}}} \right)}}{{{\rm{i}}\left( {{x_{j + 1}} - {x_j}} \right)t}}} , \end{array} $ |
证毕.
推论4 不确定变量ξ服从对数正态不确定分布
证明 根据文献[1],对数正态不确定分布
| $ \varphi \left( t \right) = \int_0^1 {{{\rm{e}}^{{\rm{i}}t\mathit{\Phi } - 1\left( \alpha \right)}}{\rm{d}}\alpha } = \int_0^1 {{{\rm{e}}^{\frac{{{\rm{i}}t\alpha }}{{1 - \alpha }}}}{\rm{d}}\alpha } = \int_0^1 {{{\rm{e}}^{ - {\rm{i}}t}} \cdot {{\rm{e}}^{\frac{{{\rm{i}}t}}{{1 - \alpha }}}}{\rm{d}}\alpha } . $ | (2) |
令y=1-α,则式(2)可化为
| $ \varphi \left( t \right) = \int_0^1 {{{\rm{e}}^{ - {\rm{i}}t}}{{\rm{e}}^{\frac{{{\rm{i}}t}}{y}}}{\rm{d}}y} . $ | (3) |
令z=1/y,式(3)可化为
| $ \varphi \left( t \right) = \int_1^{ + \infty } {{{\rm{e}}^{ - {\rm{i}}t}}\frac{{{{\rm{e}}^{{\rm{i}}tz}}}}{{{z^2}}}{\rm{d}}z} . $ |
根据欧拉公式,计算可得
| $ \varphi \left( t \right) = {{\rm{e}}^{ - {\rm{i}}t}}\left( {\cos t - \frac{{\rm{ \mathsf{ π} }}}{2}t + t{f_{\sin }}\left( t \right) + i\sin t - {\rm{i}}{f_{\cos }}\left( t \right)} \right). $ |
式中:fsin(t)=
假设不确定变量ξ服从正则不确定分布,则其特征函数φ(t),具有以下性质.
性质1 对于任意t,有|φ(t)|≤φ(0)=1.
证明 根据欧拉公式,可得
| $ \begin{array}{l} \left| {\varphi \left( t \right)} \right| = \left| {\int_0^1 {{{\rm{e}}^{{\rm{i}}t\mathit{\Phi } - 1\left( \alpha \right)}}{\rm{d}}\alpha } } \right| \le \int_0^1 {\left| {{{\rm{e}}^{{\rm{i}}t\mathit{\Phi } - 1\left( \alpha \right)}}} \right|{\rm{d}}\alpha } = \\ \;\;\;\;\;\;\;\;\;\;\;\int_0^1 {\left| {\cos t{\mathit{\Phi }^{ - 1}}\left( \alpha \right) + i\sin t{\mathit{\Phi }^{ - 1}}\left( \alpha \right)} \right|{\rm{d}}x} = \\ \;\;\;\;\;\;\;\;\;\;\;\int_0^1 {\sqrt {{{\cos }^2}t{\mathit{\Phi }^{ - 1}}\left( \alpha \right) + {{\sin }^2}t{\mathit{\Phi }^{ - 1}}\left( \alpha \right)} {\rm{d}}x} = \\ \;\;\;\;\;\;\;\;\;\;\;\int_0^1 {1{\rm{d}}x} = 1, \end{array} $ |
又φ(0)=
性质2 ξ、η分别为不确定变量,若ξ、η相互独立,则φξ+η(t)=φξ(t)·φη(t).
证明 根据文献[12],eitξ、eitη分别为不确定变量,且相互独立.于是,有
| $ \begin{array}{l} {\varphi _{\xi + \eta }}\left( t \right) = E\left( {{{\rm{e}}^{{\rm{i}}t\left( {\xi + \eta } \right)}}} \right) = E\left( {{{\rm{e}}^{{\rm{i}}t\xi \left( { + \eta } \right)}}{{\rm{e}}^{{\rm{i}}t\eta }}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;E\left( {{{\rm{e}}^{{\rm{i}}t\xi }}} \right)E\left( {{e^{{\rm{i}}t\eta }}} \right) = {\varphi _\xi }\left( t \right) \cdot {\varphi _\eta }\left( t \right), \end{array} $ |
证毕.
性质3 不确定变量ξ服从正则不确定分布Φ(x),其特征函数φ(t)在(-∞, +∞)上一致连续.
证明 对于任意实数t, h及0<a<1,有
| $ \begin{array}{l} \left| {\varphi \left( {t + h} \right) - \varphi \left( t \right)} \right| = \left| {\int_0^1 {{{\rm{e}}^{{\rm{i}}\left( {t + h} \right){\mathit{\Phi }^{ - 1}}\left( \alpha \right)}}{\rm{d}}\alpha } - \int_0^1 {{{\rm{e}}^{{\rm{i}}t{\mathit{\Phi }^{ - 1}}\left( \alpha \right)}}{\rm{d}}\alpha } } \right| = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {\int_0^1 {{{\rm{e}}^{{\rm{i}}t{\mathit{\Phi }^{ - 1}}\left( \alpha \right)}}\left( {{{\rm{e}}^{{\rm{i}}h{\mathit{\Phi }^{ - 1}}\left( \alpha \right)}} - 1} \right){\rm{d}}\alpha } } \right| \le \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int_0^1 {\left| {{{\rm{e}}^{{\rm{i}}t{\mathit{\Phi }^{ - 1}}\left( \alpha \right)}}} \right|\left| {\left( {{{\rm{e}}^{{\rm{i}}h{\mathit{\Phi }^{ - 1}}\left( \alpha \right)}} - 1} \right)} \right|{\rm{d}}\alpha } \le \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int_0^1 {\left| {\left( {{{\rm{e}}^{{\rm{i}}h{\mathit{\Phi }^{ - 1}}\left( \alpha \right)}} - 1} \right)} \right|{\rm{d}}\alpha } = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int_0^a {\left| {\left( {{{\rm{e}}^{{\rm{i}}h{\mathit{\Phi }^{ - 1}}\left( \alpha \right)}} - 1} \right)} \right|{\rm{d}}\alpha } + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int_a^1 {\left| {\left( {{{\rm{e}}^{{\rm{i}}h{\mathit{\Phi }^{ - 1}}\left( \alpha \right)}} - 1} \right)} \right|{\rm{d}}\alpha } , \end{array} $ |
对任意的ε>0,必存在一个a,使得
| $ \int_a^1 {\left| {\left( {{{\rm{e}}^{{\rm{i}}h{\mathit{\Phi }^{ - 1}}\left( \alpha \right)}} - 1} \right)} \right|{\rm{d}}\alpha } < \frac{\varepsilon }{2}, $ |
∀α∈[0, a],取δ=
| $ \begin{array}{l} \left| { {{{\rm{e}}^{{\rm{i}}h{\mathit{\Phi }^{ - 1}}\left( \alpha \right)}} - 1} } \right| = \left| {{{\rm{e}}^{{\rm{i}}\frac{h}{2}{\mathit{\Phi }^{ - 1}}\left( \alpha \right)}}\left( {{{\rm{e}}^{{\rm{i}}\frac{h}{2}{\mathit{\Phi }^{ - 1}}\left( \alpha \right)}} - {{\rm{e}}^{ - {\rm{i}}\frac{h}{2}{\mathit{\Phi }^{ - 1}}\left( \alpha \right)}}} \right)} \right| = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2\left| {\sin \frac{{h{\mathit{\Phi }^{ - 1}}\left( \alpha \right)}}{2}} \right| \le 2\left| {\frac{{h{\mathit{\Phi }^{ - 1}}\left( \alpha \right)}}{2}} \right| < \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {h{\mathit{\Phi }^{ - 1}}\left( \alpha \right)} \right| < \frac{\varepsilon }{2}. \end{array} $ |
对任意t∈(-∞, +∞),有
| $ \left| {\varphi \left( {t + h} \right) - \varphi \left( t \right)} \right| \le \int_0^a {\frac{\varepsilon }{2}{\rm{d}}\alpha } + \frac{\varepsilon }{2} = \frac{{\left( {1 + a} \right)}}{2}\varepsilon < \varepsilon , $ |
即φ(t)在t∈(-∞, +∞)上一致连续.证毕.
性质4 不确定变量ξ服从正则不确定分布Φ(x),其特征函数φ(t),对于任意的x1<x2,有
证明 对于任意的a≥0,根据性质1,有
| $ \left| {{{\rm{e}}^{{\rm{i}}a}} - 1} \right| = \left| {\int_0^a {{{\rm{e}}^{{\rm{i}}x}}{\rm{d}}x} } \right| \le \int_0^a {\left| {{{\rm{e}}^{{\rm{i}}x}}} \right|{\rm{d}}x} \le a, $ | (4) |
对于任意的a<0,有
| $ \begin{array}{l} \left| {{{\rm{e}}^{{\rm{i}}a}} - 1} \right| = \left| {{{\rm{e}}^{{\rm{i}}a}}\left( {{{\rm{e}}^{{\rm{i}}\left| a \right|}} - 1} \right)} \right| \le \left| {{{\rm{e}}^{{\rm{i}}a}}} \right|\left| {{{\rm{e}}^{{\rm{i}}\left| a \right|}} - 1} \right| \le \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left| {{{\rm{e}}^{{\rm{i}}\left| a \right|}} - 1} \right| \le \left| a \right|, \end{array} $ | (5) |
即|eia-1|≤|a|,于是
| $ \begin{array}{l} \left| {\frac{{{{\rm{e}}^{ - {\rm{i}}t{x_1}}} - {{\rm{e}}^{ - {\rm{i}}t{x_2}}}}}{{{\rm{i}}t}}} \right| = \left| {\frac{{{{\rm{e}}^{ - {\rm{i}}t{x_1}}}\left( {1 - {{\rm{e}}^{ - {\rm{i}}t\left( {{x_2} - {x_1}} \right)}}} \right)}}{{{\rm{i}}t}}} \right| = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {\frac{{{\rm{i}}t{{\rm{e}}^{ - {\rm{i}}t{x_1}}}\left( {1 - {{\rm{e}}^{ - {\rm{i}}t\left( {{x_2} - {x_1}} \right)}}} \right)}}{{ - t}}} \right| \le \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {\rm{i}} \right|\left| {{{\rm{e}}^{ - {\rm{i}}t{x_1}}}} \right|\left| {\left( {1 - {{\rm{e}}^{ - {\rm{i}}t\left( {{x_2} - {x_1}} \right)}}} \right)} \right| \le {x_2} - {x_1}, \end{array} $ |
特别的
| $ \mathop {\lim }\limits_{t \to 0} \left| {\frac{{{{\rm{e}}^{ - {\rm{i}}t{x_1}}} - {{\rm{e}}^{ - {\rm{i}}t{x_2}}}}}{{{\rm{i}}t}}} \right| = \mathop {\lim }\limits_{t \to 0} \left| {\frac{{{\rm{i}}t\left( {{x_2} - {x_1}} \right)}}{{{\rm{i}}t}}} \right| = {x_2} - {x_1}, $ |
证毕.
性质5 不确定变量ξ服从正则不确定分布Φ(x),其特征函数φ(t),对于任意的x1<x2,有
| $ \mathit{\Phi }\left( {{x_2}} \right) - \mathit{\Phi }\left( {{x_1}} \right) = \mathop {\lim }\limits_{T \to + \infty } \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - T}^T {\frac{{{{\rm{e}}^{ - {\rm{i}}t{x_1}}} - {{\rm{e}}^{ - {\rm{i}}t{x_2}}}}}{{{\rm{i}}t}}\varphi \left( t \right){\rm{d}}t} . $ |
证明 根据特征函数定义,有
| $ \begin{array}{*{20}{c}} {\mathop {\lim }\limits_{T \to + \infty } \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - T}^T {\frac{{{{\rm{e}}^{ - {\rm{i}}t{x_1}}} - {{\rm{e}}^{ - {\rm{i}}t{x_2}}}}}{{{\rm{i}}t}}\varphi \left( t \right){\rm{d}}t} = }\\ {\mathop {\lim }\limits_{T \to + \infty } \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - T}^T {\frac{{{{\rm{e}}^{ - {\rm{i}}t{x_1}}} - {{\rm{e}}^{ - {\rm{i}}t{x_2}}}}}{{{\rm{i}}t}}{{\rm{e}}^{{\rm{i}}tx}}{\rm{d}}\mathit{\Phi }\left( x \right){\rm{d}}t} .} \end{array} $ | (6) |
根据性质3、4,式(6)可交换积分次序,有
| $ \begin{array}{l} \mathop {\lim }\limits_{T \to + \infty } \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \infty }^{ + \infty } {\int_0^T {\left( {\frac{{{{\rm{e}}^{{\rm{i}}t\left( {x - {x_1}} \right)}} - {{\rm{e}}^{ - {\rm{i}}t\left( {x - {x_1}} \right)}}}}{{{\rm{i}}t}} - } \right.} } \\ \left. {\frac{{{{\rm{e}}^{{\rm{i}}t\left( {x - {x_2}} \right)}} - {{\rm{e}}^{ - {\rm{i}}t\left( {x - {x_2}} \right)}}}}{{{\rm{i}}t}}} \right){\rm{d}}t{\rm{d}}\mathit{\Phi }\left( x \right) = \\ \mathop {\lim }\limits_{T \to + \infty } \frac{1}{{\rm{ \mathsf{ π} }}}\int_{ - \infty }^{ + \infty } {\int_0^T {\left( {\frac{{\sin t\left( {x - {x_1}} \right)}}{t} - } \right.} } \\ \left. {\frac{{\sin t\left( {x - {x_2}} \right)}}{t}} \right){\rm{d}}t{\rm{d}}\mathit{\Phi }\left( x \right). \end{array} $ | (7) |
由于
| $ S\left( {T,x,{x_1},{x_2}} \right) = \frac{1}{{\rm{ \mathsf{ π} }}}\int_0^T {\left( {\frac{{\sin t\left( {x - {x_1}} \right)}}{t} - \frac{{\sin t\left( {x - {x_2}} \right)}}{t}} \right){\rm{d}}t} , $ |
则
因此,必存在M>0,使得|S(T, x, x1, x2)|<M,即S(T, x, x1, x2)有界.式(7)可交换积分符号和极限符号顺序,可得
| $ \begin{array}{l} \frac{1}{{\rm{ \mathsf{ π} }}}\int_{ - \infty }^{ + \infty } {\mathop {\lim }\limits_{T \to + \infty } \int_0^T {\left( {\frac{{\sin t\left( {x - {x_1}} \right)}}{t} - } \right.} } \\ \left. {\frac{{\sin t\left( {x - {x_2}} \right)}}{t}} \right){\rm{d}}t{\rm{d}}\mathit{\Phi }\left( x \right) = \\ \int_{ - \infty }^{ + \infty } {\mathop {\lim }\limits_{T \to + \infty } S\left( {T,x,{x_1},{x_2}} \right){\rm{d}}\mathit{\Phi }\left( x \right)} = \\ \int_{ - \infty }^{{x_1} - \delta } {\mathop {\lim }\limits_{T \to + \infty } S\left( {T,x,{x_1},{x_2}} \right){\rm{d}}\mathit{\Phi }\left( x \right)} + \\ \int_{{x_1} - \delta }^{{x_1} + \delta } {\mathop {\lim }\limits_{T \to + \infty } S\left( {T,x,{x_1},{x_2}} \right){\rm{d}}\mathit{\Phi }\left( x \right)} + \\ \int_{{x_1} + \delta }^{{x_2} - \delta } {\mathop {\lim }\limits_{T \to + \infty } S\left( {T,x,{x_1},{x_2}} \right){\rm{d}}\mathit{\Phi }\left( x \right)} + \\ \int_{{x_2} - \delta }^{{x_2} + \delta } {\mathop {\lim }\limits_{T \to + \infty } S\left( {T,x,{x_1},{x_2}} \right){\rm{d}}\mathit{\Phi }\left( x \right)} + \\ \int_{{x_2} + \delta }^{ + \infty } {\mathop {\lim }\limits_{T \to + \infty } S\left( {T,x,{x_1},{x_2}} \right){\rm{d}}\mathit{\Phi }\left( x \right)} , \end{array} $ | (8) |
式中δ为充分小的正数.易知:
| $ \int_{ - \infty }^{{x_1} - \delta } {\mathop {\lim }\limits_{T \to + \infty } S\left( {T,x,{x_1},{x_2}} \right){\rm{d}}\mathit{\Phi }\left( x \right)} = 0, $ |
| $ \int_{{x_1} - \delta }^{{x_1} + \delta } {\mathop {\lim }\limits_{T \to + \infty } S\left( {T,x,{x_1},{x_2}} \right){\rm{d}}\mathit{\Phi }\left( x \right)} = 0, $ |
| $ \int_{{x_2} - \delta }^{{x_2} + \delta } {\mathop {\lim }\limits_{T \to + \infty } S\left( {T,x,{x_1},{x_2}} \right){\rm{d}}\mathit{\Phi }\left( x \right)} = 0, $ |
| $ \int_{{x_2} + \delta }^{ + \infty } {\mathop {\lim }\limits_{T \to + \infty } S\left( {T,x,{x_1},{x_2}} \right){\rm{d}}\mathit{\Phi }\left( x \right)} = 0, $ |
则式(8)可化为
| $ \begin{array}{l} \frac{1}{{\rm{ \mathsf{ π} }}}\int_{ - \infty }^{ + \infty } {\mathop {\lim }\limits_{T \to + \infty } \int_0^T {\left( {\frac{{\sin t\left( {x - {x_1}} \right)}}{t} - } \right.} } \\ \left. {\frac{{\sin t\left( {x - {x_2}} \right)}}{t}} \right){\rm{d}}t{\rm{d}}\mathit{\Phi }\left( x \right) = \\ \int_{{x_1} + \delta }^{{x_2} - \delta } {\mathop {\lim }\limits_{T \to + \infty } S\left( {T,x,{x_1},{x_2}} \right){\rm{d}}\mathit{\Phi }\left( x \right)} = \\ \int_{{x_1} + \delta }^{{x_2} - \delta } {1{\rm{d}}\mathit{\Phi }\left( x \right)} = \mathit{\Phi }\left( {{x_2}} \right) - \mathit{\Phi }\left( {{x_1}} \right), \end{array} $ |
即
| $ \mathit{\Phi }\left( {{x_2}} \right) - \mathit{\Phi }\left( {{x_1}} \right) = \mathop {\lim }\limits_{T \to + \infty } \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - T}^T {\frac{{{{\rm{e}}^{ - {\rm{i}}t{x_1}}} - {{\rm{e}}^{ - {\rm{i}}t{x_2}}}}}{{{\rm{i}}t}}\varphi \left( t \right){\rm{d}}t} , $ |
证毕.
性质6 不确定变量ξ服从正则不确定分布函数Φ(x),其特征函数φ(t)唯一确定.
证明 由性质3及性质5,可得
| $ \begin{array}{*{20}{c}} {\mathop {\lim }\limits_{\Delta x \to 0} \mathit{\Phi }\left( {x + \Delta x} \right) - \mathit{\Phi }\left( x \right) = }\\ {\mathop {\lim }\limits_{\Delta x \to 0} \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \infty }^{ + \infty } {\frac{{{{\rm{e}}^{ - {\rm{i}}tx}} - {{\rm{e}}^{ - {\rm{i}}t\left( {x + \Delta x} \right)}}}}{{{\rm{i}}t\Delta x}}\varphi \left( t \right){\rm{d}}t} .} \end{array} $ | (9) |
由式(4)、(5),可得
| $ \begin{array}{*{20}{c}} {\left| {\frac{{{{\rm{e}}^{ - {\rm{i}}tx}} - {{\rm{e}}^{ - {\rm{i}}t\left( {x + \Delta x} \right)}}}}{{{\rm{i}}t\Delta x}}} \right| = \frac{1}{{\left| {t\Delta x} \right|}}\left| {{{\rm{e}}^{ - {\rm{i}}tx}} - {{\rm{e}}^{ - {\rm{i}}t\left( {x + \Delta x} \right)}}} \right| \le }\\ {\frac{{\left| { - t\Delta x} \right|}}{{\left| {t\Delta x} \right|}} = 1.} \end{array} $ |
考虑到
| $ \begin{array}{*{20}{c}} {\mathop {\lim }\limits_{\Delta x \to 0} \mathit{\Phi }\left( {x + \Delta x} \right) - \mathit{\Phi }\left( x \right) = }\\ {\frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \infty }^{ + \infty } {\mathop {\lim }\limits_{\Delta x \to 0} \frac{{{{\rm{e}}^{ - {\rm{i}}tx}} - {{\rm{e}}^{ - {\rm{i}}t\left( {x + \Delta x} \right)}}}}{{{\rm{i}}t\Delta x}}\varphi \left( t \right){\rm{d}}t} = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \infty }^{ + \infty } {{{\rm{e}}^{ - {\rm{i}}tx}}\varphi \left( t \right){\rm{d}}t} .} \end{array} $ | (10) |
根据式(10)可知,Φ(x)在x处的增量ΔΦ(x)=
| $ \mathit{\Phi }\left( x \right) = \mathit{\Phi }\left( { - \infty } \right) + \mathop {\lim }\limits_{N \to + \infty } \sum\limits_{i = 1}^N {\Delta \mathit{\Phi }\left( {{x_i}} \right)} . $ | (11) |
式中:x1>x2>…>xN,且x=x1,
进一步,根据性质5,对Φ(x)上每一个连续点x,当y沿着Φ(x)的连续点趋于-∞时,有
| $ \mathit{\Phi }\left( x \right) = \mathop {\lim }\limits_{y \to - \infty } \mathop {\lim }\limits_{T \to + \infty } \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - T}^T {\frac{{{{\rm{e}}^{ - {\rm{i}}ty}} - {{\rm{e}}^{ - {\rm{i}}tx}}}}{{{\rm{i}}t}}\varphi \left( t \right){\rm{d}}t} . $ | (12) |
综合考虑式(11)、(12),易知不确定分布函数Φ(x)在任意x处的取值由其连续点上的值x及其特征函数φ(t)决定,即不确定分布函数Φ(x)有唯一确定的特征函数φ(t),故结论成立.证毕.
3 分布拟合有效性检验假设拟合的不确定分布Φ(x)与经验不确定分布Ψ(x)的特征函数分别为φΦ(t)与φΨ(t).根据性质6可知,不确定分布函数与其特征函数一一对应,即如果特征函数φΦ(t)与φΨ(t)相同,则不确定分布函数Φ(x)与Ψ(x)也必然相同.
如果拟合的不确定分布与经验不确定分布的期望、方差等数字特征在数值上比较接近且两者形状上比较接近,即
|
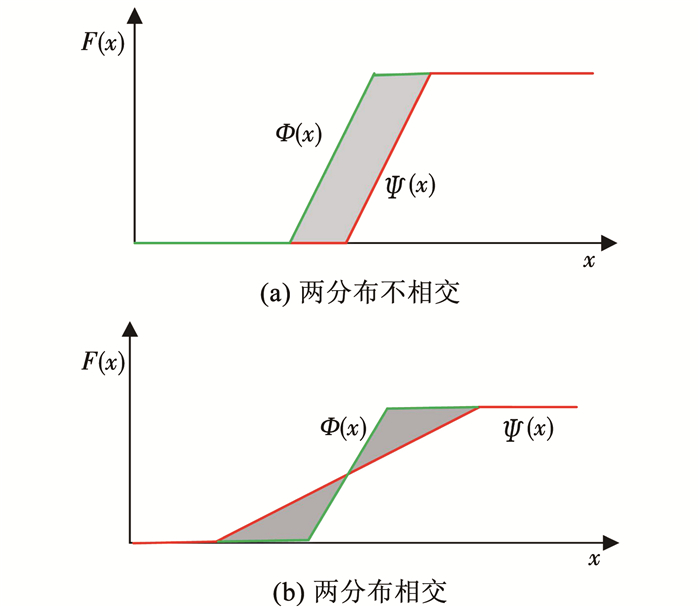
图 1 线性拟合分布与经验不确定分布示意 Fig. 1 Linear fitting distribution and its experimental uncertainty distribution |
图 1针对线性不确定分布给出了拟合分布及经验分布分别在相交和不相交的情况下所围成的面积.图 1中横轴表示x的取值范围,纵轴F(x)表示不确定分布函数,灰色部分表示Φ(x)、Ψ(x)两者围成的面积.从图 1中可以明显看出,对于线性不确定分布无论拟合效果好坏,总有
由于0≤Φ(x)≤1, 0≤Ψ(x)≤1,易知:
| $ 0 \le \Delta \mathit{\Phi }\left( x \right) = \mathit{\Phi }\left( {x + \Delta x} \right) - \mathit{\Phi }\left( x \right) \le 1, $ | (13) |
| $ 0 \le \Delta \mathit{\Psi }\left( x \right) = \mathit{\Psi }\left( {x + \Delta x} \right) - \mathit{\Psi }\left( x \right) \le 1, $ | (14) |
根据式(13)、(14),必存在正实数τ,使得
| $ \left| {\Delta \mathit{\Phi }\left( x \right) - \Delta \mathit{\Psi }\left( x \right)} \right| \le \tau , $ | (15) |
式中τ的取值与Δx有关,若Δx足够小,τ可取极小的正数.
由
| $ \begin{array}{l} \left| {\Delta \mathit{\Phi }\left( x \right) - \Delta \mathit{\Psi }\left( x \right)} \right| = \\ \left| {\frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \infty }^{ + \infty } {\mathop {\lim }\limits_{\Delta x \to 0} \frac{{{{\rm{e}}^{ - {\rm{i}}tx}} - {{\rm{e}}^{ - {\rm{i}}t\left( {x + \Delta x} \right)}}}}{{{\rm{i}}t\Delta x}}\left( {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right){\rm{d}}t} } \right| = \\ \left| {\frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - \infty }^{ + \infty } {{{\rm{e}}^{ - {\rm{i}}tx}}\left( {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right){\rm{d}}t} } \right| \le \tau , \end{array} $ | (16) |
根据式(12),在x处,有
| $ \begin{array}{l} \mathit{\Phi }\left( x \right) - \mathit{\Psi }\left( x \right) = \\ \mathop {\lim }\limits_{y \to - \infty } \mathop {\lim }\limits_{T \to - \infty } \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - T}^T {\frac{{{{\rm{e}}^{ - {\rm{i}}ty}} - {{\rm{e}}^{ - {\rm{i}}tx}}}}{{{\rm{i}}t}}\left( {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right){\rm{d}}t} , \end{array} $ | (17) |
根据积分中值定理,存在t0,使得
| $ \mathit{\Phi }\left( x \right) - \mathit{\Psi }\left( x \right) = \frac{{{{\rm{e}}^{ - {\rm{i}}{t_0}y}} - {{\rm{e}}^{ - {\rm{i}}{t_0}x}}}}{{{\rm{ \mathsf{ π} }}{t_0}}}\left( {{\varphi _\mathit{\Phi }}\left( {{t_0}} \right) - {\varphi _\mathit{\Psi }}\left( {{t_0}} \right)} \right)T. $ |
假设存在t1,使得
| $ \begin{array}{l} \mathit{\Phi }\left( x \right) - \mathit{\Psi }\left( x \right) = \\ \frac{{\mathop {\lim }\limits_{y \to - \infty } \mathop {\lim }\limits_{T \to - \infty } \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - T}^T {\frac{{{{\rm{e}}^{ - {\rm{i}}ty}} - {{\rm{e}}^{ - {\rm{i}}tx}}}}{{{\rm{i}}t}}\left( {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right){\rm{d}}t} }}{{{t_1}}}, \end{array} $ | (18) |
根据积分中值定理,存在t2,使得
| $ \mathit{\Phi }\left( x \right) - \mathit{\Psi }\left( x \right) = \frac{{{{\rm{e}}^{ - {\rm{i}}{t_2}y}} - {{\rm{e}}^{ - {\rm{i}}{t_2}x}}}}{{{\rm{ \mathsf{ π} }}{t_1}}}\left( {{\varphi _\mathit{\Phi }}\left( {{t_2}} \right) - {\varphi _\mathit{\Psi }}\left( {{t_2}} \right)} \right)T, $ | (19) |
根据式(17)及式(19),可得
| $ \begin{array}{l} \frac{{{{\rm{e}}^{ - {\rm{i}}{t_0}y}} - {{\rm{e}}^{ - {\rm{i}}{t_0}x}}}}{{{\rm{ \mathsf{ π} }}{t_0}}}\left( {{\varphi _\mathit{\Phi }}\left( {{t_0}} \right) - {\varphi _\mathit{\Psi }}\left( {{t_0}} \right)} \right)T = \\ \frac{{{{\rm{e}}^{ - {\rm{i}}{t_2}y}} - {{\rm{e}}^{ - {\rm{i}}{t_2}x}}}}{{{\rm{ \mathsf{ π} }}{t_1}}}\left( {{\varphi _\mathit{\Phi }}\left( {{t_2}} \right) - {\varphi _\mathit{\Psi }}\left( {{t_2}} \right)} \right)T, \end{array} $ |
进一步,可得
| $ {t_1} = {t_0}\frac{{\left( {{{\rm{e}}^{ - {\rm{i}}{t_2}y}} - {{\rm{e}}^{ - {\rm{i}}{t_2}x}}} \right)\left( {{\varphi _\mathit{\Phi }}\left( {{t_2}} \right) - {\varphi _\mathit{\Psi }}\left( {{t_2}} \right)} \right)}}{{\left( {{{\rm{e}}^{ - {\rm{i}}{t_0}y}} - {{\rm{e}}^{ - {\rm{i}}{t_0}x}}} \right)\left( {{\varphi _\mathit{\Phi }}\left( {{t_0}} \right) - {\varphi _\mathit{\Psi }}\left( {{t_0}} \right)} \right)}}, $ | (20) |
由于t1∈(-∞, +∞),等式(20)必成立.
由于式(16)对任意x成立,于是
| $ \left| {\frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_{ - T}^T {\left( {{{\rm{e}}^{ - {\rm{i}}ty}} - {{\rm{e}}^{ - {\rm{i}}tx}}} \right)\left( {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right){\rm{d}}t} } \right| \le 2\tau , $ | (21) |
根据式(18)及式(21),可得
| $ \left| {\mathit{\Phi }\left( x \right) - \mathit{\Psi }\left( x \right)} \right| \le \frac{{2\tau }}{{\left| {{t_1}} \right|}}, $ |
式中t1的取值与x的取值有关.当τ取极小的正数时,Φ(x)与Ψ(x)在x处的取值非常接近,进一步可将其推广到整个分布函数,即两个分布函数在任意处取值都很接近.
综上所述,可以给出不确定分布拟合有效性的定义.不妨假设Φ(x)的期望为EΦ(ξ),方差为VΦ(ξ),Ψ(x)的期望为EΨ(ξ),方差为VΨ(ξ).
定义4 如果拟合分布与经验不确定分布的特征函数存在正实数A,使得:
| $ \begin{array}{*{20}{c}} {\mathop {\lim }\limits_{t \to + \infty } {\varphi _\mathit{\Phi }}\left( t \right) = \mathop {\lim }\limits_{t \to - \infty } {\varphi _\mathit{\Psi }}\left( t \right),\mathop {\lim }\limits_{t \to + \infty } {\varphi _\mathit{\Phi }}\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } {\varphi _\mathit{\Psi }}\left( t \right),}\\ {\int_{ - \infty }^{ + \infty } {\left| {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right|{\rm{d}}t} \le A,} \end{array} $ |
且对于给定的σ(0<σ<1),拟合分布与经验不确定分布的期望与方差满足:
| $ \max \left\{ {\left| {\frac{{{E_\mathit{\Phi }}\left( \xi \right) - {E_\mathit{\Psi }}\left( \xi \right)}}{{{E_\mathit{\Psi }}\left( \xi \right)}}} \right|,\left| {\frac{{{V_\mathit{\Phi }}\left( \xi \right) - {V_\mathit{\Psi }}\left( \xi \right)}}{{{V_\mathit{\Psi }}\left( \xi \right)}}} \right|} \right\} < \sigma , $ |
则拟合的不确定分布Φ(x)是σ-有效的.
定义4是通过经验不确定分布检验拟合分布的有效性.如果对于给定的A和σ,定义4成立,则可认为拟合分布是有效的.
定理1 不确定变量ξ服从正则不确定分布Υ(x),若E(ξL)存在,则ξ的特征函数φ(t)可L次求导,且对于1≤k≤L,有φ(k)(0)=ikE(ξk).
证明 不确定变量ξ服从正则不确定分布,则ξL为不确定变量,不妨记其服从正则不确定分布ΥL(x),因为E(ξL)存在,有
| $ \int_{ - \infty }^{ + \infty } {{x^L}{\rm{d}}{\Upsilon _L}\left( x \right)} < + \infty . $ | (22) |
根据式(22)可知,广义积分
| $ {\varphi ^{\left( k \right)}}\left( t \right) = \int_{ - \infty }^{ + \infty } {{i^k}{x^k}{{\rm{e}}^{{\rm{i}}tx}}{\rm{d}}\Upsilon \left( x \right)} = {i^k}E\left( {{\xi ^k}{{\rm{e}}^{{\rm{i}}t\xi }}} \right). $ | (23) |
令t=0,式(23)可化为
| $ {\varphi ^{\left( k \right)}}\left( 0 \right) = {i^k}E\left( {{\xi ^k}} \right), $ |
证毕.
定理2 若存在实数C>0,使得特征函数满足
| $ \max \left\{ \begin{array}{l} \mathop {\lim }\limits_{t \to 0} \left| {\frac{{\left| {{{\varphi '}_\mathit{\Phi }}\left( t \right)} \right| - \left| {{{\varphi '}_\mathit{\Psi }}\left( t \right)} \right|}}{{\left| {{{\varphi '}_\mathit{\Psi }}\left( t \right)} \right|}}} \right|,\\ \mathop {\lim }\limits_{t \to 0} \left| {\frac{{\left| {{{\varphi ''}_\mathit{\Phi }}\left( t \right)} \right| - \left| {{{\varphi ''}_\mathit{\Psi }}\left( t \right)} \right| + {{\left| {{{\varphi '}_\mathit{\Psi }}\left( t \right)} \right|}^2} - {{\left| {{{\varphi '}_\mathit{\Phi }}\left( t \right)} \right|}^2}}}{{\left| {{{\varphi ''}_\mathit{\Psi }}\left( t \right)} \right| - {{\left| {{{\varphi '}_\mathit{\Psi }}\left( t \right)} \right|}^2}}}} \right| \end{array} \right\} \le \sigma , $ |
则称拟合的Φ(x)是σ-有效的.
证明 假设
| $ \left| {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right| > \delta . $ | (24) |
根据式(24),可得
| $ \begin{array}{l} \int_{ - \infty }^{ + \infty } {{{\left| {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right|}^2}{\rm{d}}t} = \\ \int_{ - \infty }^H {{{\left| {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right|}^2}{\rm{d}}t} + \\ \mathop {\lim }\limits_{T \to + \infty } \int_H^T {{{\left| {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right|}^2}{\rm{d}}t} = \\ \int_{ - \infty }^H {{{\left| {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right|}^2}{\rm{d}}t} + \delta \cdot \mathop {\lim }\limits_{T \to + \infty } \left( {T - H} \right). \end{array} $ |
由于
因为|φΦ(t)-φΨ(t) ≥0,且
根据定理1,可知φ′(0)=iE(ξ), φ″(0)= -E(ξ2).即E(ξ)=|φ′(0)|=
于是,有
| $ \begin{array}{l} \max \left\{ \begin{array}{l} \mathop {\lim }\limits_{t \to 0} \left| {\frac{{\left| {{{\varphi '}_\mathit{\Phi }}\left( t \right)} \right| - \left| {{{\varphi '}_\mathit{\Psi }}\left( t \right)} \right|}}{{\left| {{{\varphi '}_\mathit{\Psi }}\left( t \right)} \right|}}} \right|,\\ \mathop {\lim }\limits_{t \to 0} \left| {\frac{{\left| {{{\varphi ''}_\mathit{\Phi }}\left( t \right)} \right| - \left| {{{\varphi ''}_\mathit{\Psi }}\left( t \right)} \right| + {{\left| {{{\varphi '}_\mathit{\Psi }}\left( t \right)} \right|}^2} - {{\left| {{{\varphi '}_\mathit{\Phi }}\left( t \right)} \right|}^2}}}{{\left| {{{\varphi ''}_\mathit{\Psi }}\left( t \right)} \right| - {{\left| {{{\varphi '}_\mathit{\Psi }}\left( t \right)} \right|}^2}}}} \right| \end{array} \right\} = \\ \max \left\{ {\left| {\frac{{{E_\mathit{\Phi }}\left( \xi \right) - {E_\mathit{\Psi }}\left( \xi \right)}}{{{E_\mathit{\Psi }}\left( \xi \right)}}} \right|,\left| {\frac{{{V_\mathit{\Phi }}\left( \xi \right) - {V_\mathit{\Psi }}\left( \xi \right)}}{{{V_\mathit{\Psi }}\left( \xi \right)}}} \right|} \right\}, \end{array} $ | (25) |
若存在
| $ \max \left\{ \begin{array}{l} \mathop {\lim }\limits_{t \to 0} \left| {\frac{{\left| {{{\varphi '}_\mathit{\Phi }}\left( t \right)} \right| - \left| {{{\varphi '}_\mathit{\Psi }}\left( t \right)} \right|}}{{\left| {{{\varphi '}_\mathit{\Psi }}\left( t \right)} \right|}}} \right|,\\ \mathop {\lim }\limits_{t \to 0} \left| {\frac{{\left| {{{\varphi ''}_\mathit{\Phi }}\left( t \right)} \right| - \left| {{{\varphi ''}_\mathit{\Psi }}\left( t \right)} \right| + {{\left| {{{\varphi '}_\mathit{\Psi }}\left( t \right)} \right|}^2} - {{\left| {{{\varphi '}_\mathit{\Phi }}\left( t \right)} \right|}^2}}}{{\left| {{{\varphi ''}_\mathit{\Psi }}\left( t \right)} \right| - {{\left| {{{\varphi '}_\mathit{\Psi }}\left( t \right)} \right|}^2}}}} \right| \end{array} \right\} \le \sigma . $ | (26) |
根据式(25)、(26)可转换为
| $ \max \left\{ {\left| {\frac{{{E_\mathit{\Phi }}\left( \xi \right) - {E_\mathit{\Psi }}\left( \xi \right)}}{{{E_\mathit{\Psi }}\left( \xi \right)}}} \right|,\left| {\frac{{{V_\mathit{\Phi }}\left( \xi \right) - {V_\mathit{\Psi }}\left( \xi \right)}}{{{V_\mathit{\Psi }}\left( \xi \right)}}} \right|} \right\} \le \sigma . $ |
根据定义4,拟合的Φ(x)是σ-有效的.证毕.
4 算例分析算例1 不确定变量ξ服从某种不确定分布,根据文献[1]中的方法设计调查问卷,收集了一组专家经验数据:(2.0, 0),(2.3, 0.1),(2.9, 0.3),(3.2, 0.4),(3.4, 0.5),(3.8,0.6),(4.1, 0.7),(4.5, 0.8),(4.7, 0.9),(5.0, 1.0).采用最小二乘法,拟合不确定分布如下:
| $ \mathit{\Phi }\left( x \right) = \left\{ \begin{array}{l} 0,x < 2;\\ \frac{{\left( {x - 2} \right)}}{3},2 < x \le 5;\\ 1,x > 5, \end{array} \right. $ |
在σ=0.5的条件下,检验拟合分布的有效性.
根据文献[1],其逆分布为Φ-1(α)=3α+2.根据推论1,拟合不确定分布的特征函数φΦ(t)=
根据推论3,该拟合分布对应的经验不确定分布函数的特征函数为
| $ {\varphi _\mathit{\Psi }}\left( t \right) = \frac{{4{{\rm{e}}^{5{\rm{i}}t}} + 2{{\rm{e}}^{\frac{{47{\rm{i}}t}}{{10}}}} + {{\rm{e}}^{\frac{{41{\rm{i}}t}}{{10}}}} + 3{{\rm{e}}^{\frac{{17{\rm{i}}t}}{5}}} - 3{{\rm{e}}^{\frac{{9{\rm{i}}t}}{2}}} - {{\rm{e}}^{\frac{{19{\rm{i}}t}}{5}}} - 2{{\rm{e}}^{\frac{{16{\rm{i}}t}}{5}}} - 4{{\rm{e}}^{2{\rm{i}}t}}}}{{12{\rm{i}}t}}. $ |
根据拟合不确定分布和经验不确定分布函数的特征函数,有
| $ \begin{array}{l} \int_{ - \infty }^{ + \infty } {{{\left| {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right|}^2}{\rm{d}}t} = \\ \int_{ - \infty }^{ + \delta } {{{\left| {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right|}^2}{\rm{d}}t} + \int_{ - \delta }^\delta {{{\left| {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right|}^2}{\rm{d}}t} + \\ \int_\delta ^{ + \infty } {{{\left| {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right|}^2}{\rm{d}}t} \le \\ \int_{ - \infty }^{ - \delta } {{{\left| {\frac{{2{{\rm{e}}^{\frac{{47{\rm{i}}t}}{{10}}}} + {{\rm{e}}^{\frac{{41{\rm{i}}t}}{{10}}}} + 3{{\rm{e}}^{\frac{{17{\rm{i}}t}}{5}}} - 3{{\rm{e}}^{\frac{{9{\rm{i}}t}}{2}}} - {{\rm{e}}^{\frac{{19{\rm{i}}t}}{5}}} - 2{{\rm{e}}^{\frac{{16{\rm{i}}t}}{5}}}}}{{12{\rm{i}}t}}} \right|}^2}{\rm{d}}t} + \\ \int_{ - \delta }^\delta {{{\left( {\left| {{\varphi _\mathit{\Phi }}\left( t \right)} \right| - \left| {{\varphi _\mathit{\Psi }}\left( t \right)} \right|} \right)}^2}{\rm{d}}t} + \\ \int_\delta ^{ + \infty } {{{\left| {\frac{{2{{\rm{e}}^{\frac{{47{\rm{i}}t}}{{10}}}} + {{\rm{e}}^{\frac{{41{\rm{i}}t}}{{10}}}} + 3{{\rm{e}}^{\frac{{17{\rm{i}}t}}{5}}} - 3{{\rm{e}}^{\frac{{9{\rm{i}}t}}{2}}} - {{\rm{e}}^{\frac{{19{\rm{i}}t}}{5}}} - 2{{\rm{e}}^{\frac{{16{\rm{i}}t}}{5}}}}}{{12{\rm{i}}t}}} \right|}^2}{\rm{d}}t} . \end{array} $ |
根据性质1,有
| $ \begin{array}{*{20}{c}} {\int_{ - \infty }^{ + \infty } {{{\left| {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right|}^2}{\rm{d}}t} \le \int_{ - \infty }^{ - \delta } {{{\left| {\frac{{12}}{{12{\rm{i}}t}}} \right|}^2}{\rm{d}}t} + 8\delta + }\\ {\int_\delta ^{ + \infty } {{{\left| {\frac{1}{{{\rm{i}}t}}} \right|}^2}{\rm{d}}t} = 8\delta + \frac{2}{\delta }.} \end{array} $ |
因此,必存在实数M>0,使得
进一步,考虑两者的数字特征,由定理1,可得
| $ \begin{array}{*{20}{c}} {\mathop {\lim }\limits_{t \to 0} {{\varphi '}_\mathit{\Phi }}\left( t \right) = \mathop {\lim }\limits_{t \to 0} \frac{{\left( {5{\rm{i}}{{\rm{e}}^{5{\rm{i}}t}} - 2{\rm{i}}{{\rm{e}}^{2{\rm{i}}t}}} \right)3{\rm{i}}t - \left( {{{\rm{e}}^{5{\rm{i}}t}} - {{\rm{e}}^{2{\rm{i}}t}}} \right)3{\rm{i}}}}{{ - 9{t^2}}} = }\\ {\mathop {\lim }\limits_{t \to 0} i\frac{{\left( {5{\rm{i}}{{\rm{e}}^{5{\rm{i}}t}} - 2{\rm{i}}{{\rm{e}}^{2{\rm{i}}t}}} \right)t - {{\rm{e}}^{5{\rm{i}}t}} + {{\rm{e}}^{2{\rm{i}}t}}}}{{ - 3{t^2}}}.} \end{array} $ |
利用泰勒级数
| $ \begin{array}{l} \mathop {\lim }\limits_{t \to 0} {{\varphi '}_\mathit{\Phi }}\left( t \right) = \\ \mathop {\lim }\limits_{t \to 0} {\rm{i}}\frac{{5{\rm{i}}t\left( {1 + 5{\rm{i}}t - \frac{{25}}{2}{t^2} + o\left( {{t^3}} \right)} \right) - 2{\rm{i}}t\left( {1 + 2{\rm{i}}t - 2{t^2}} \right)}}{{ - 3{t^2}}} + \\ \;\;\;\;\;\;\;\;\frac{{\left( {1 + 5{\rm{i}}t - \frac{{25}}{2}{t^2} + o\left( {{t^3}} \right) - 1 - 2{\rm{i}}t + 2{t^2}} \right)}}{{3{t^2}}} = 3.5{\rm{i}}{\rm{.}} \end{array} $ |
同理,
| $ \begin{array}{l} \max \left\{ {\left| {\frac{{{E_\mathit{\Phi }}\left( \xi \right) - {E_\mathit{\Psi }}\left( \xi \right)}}{{{E_\mathit{\Psi }}\left( \xi \right)}}} \right|,\left| {\frac{{{V_\mathit{\Phi }}\left( \xi \right) - {V_\mathit{\Psi }}\left( \xi \right)}}{{{V_\mathit{\Psi }}\left( \xi \right)}}} \right|} \right\} = \\ \max \left\{ {\left| {\frac{{3.500 - 3.405}}{{3.405}}} \right|,\left| {\frac{{0.750 - 0.778}}{{0.778}}} \right|} \right\} = \\ \max \left\{ {0.028,0.036} \right\} = 0.036 < 0.050, \end{array} $ |
即在给定α=0.050条件下,拟合的不确定分布是有效的.
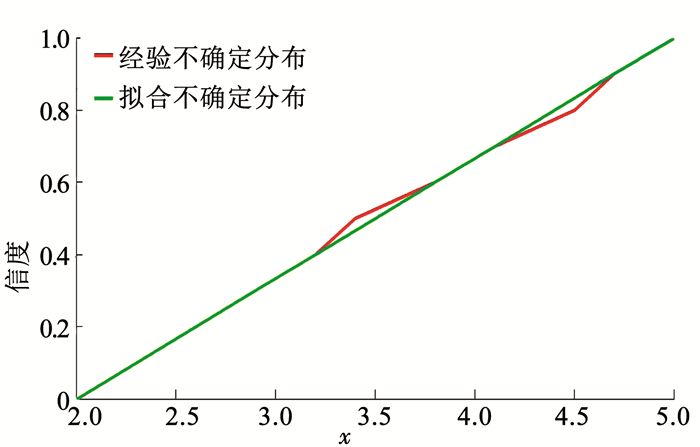
图 2中,横轴表示不确定变量的取值范围,纵轴表示相应的信度,从图 2中可以看出分布拟合的效果较好,与计算结果一致.
|
图 2 线性不确定分布拟合 Fig. 2 Linear uncertainty distribution fitting |
算例2 不确定变量η服从某种不确定分布,收集的专家经验数据如下:(1.00, 0),(1.90, 0.25),(3.00, 0.50),(4.00, 0.60),(5.10, 0.70),(6.00, 0.80),(8.00, 1.00).拟合的不确定分布如下:
| $ \mathit{\Phi }\left( x \right) = \left\{ \begin{array}{l} 0,x \le 1;\\ \frac{{x - 1}}{4},1 < x \le 3;\\ \frac{{x + 2}}{{10}},3 < x \le 8;\\ 1,x > 5, \end{array} \right. $ |
在σ=0.500的条件下,检验拟合分布的有效性.
根据文献[1],其逆分布为
| $ {\mathit{\Phi }^{ - 1}}\left( \alpha \right) = \left\{ \begin{array}{l} 4\alpha + 1,0 \le \alpha \le 0.5;\\ 10\alpha - 2,0.5 < \alpha \le 1.0. \end{array} \right. $ |
根据推论2,拟合不确定分布的特征函数为
| $ {\varphi _\mathit{\Phi }}\left( t \right) = \frac{{{{\rm{e}}^{3{\rm{i}}t}} - {{\rm{e}}^{{\rm{i}}t}}}}{{4{\rm{i}}t}} + \frac{{{{\rm{e}}^{8{\rm{i}}t}} - {{\rm{e}}^{3{\rm{i}}t}}}}{{10{\rm{i}}t}}. $ |
根据推论3,该拟合分布对应的经验不确定分布函数的特征函数为
| $ \begin{array}{l} {\varphi _\mathit{\Psi }}\left( t \right) = \\ \frac{{99{{\rm{e}}^{8{\rm{i}}t}} + 11{{\rm{e}}^{6{\rm{i}}t}} - 20{{\rm{e}}^{\frac{{51{\rm{i}}t}}{{10}}}} + 9{{\rm{e}}^{4{\rm{i}}t}} + 126{{\rm{e}}^{3{\rm{i}}t}} + 50{{\rm{e}}^{\frac{{19{\rm{i}}t}}{{10}}}} - 275{{\rm{e}}^{{\rm{i}}t}}}}{{990{\rm{i}}t}}. \end{array} $ |
根据拟合不确定分布和经验不确定分布函数的特征函数,有
| $ \begin{array}{l} \int_{ - \infty }^{ + \infty } {{{\left| {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right|}^2}{\rm{d}}t} = \\ \int_{ - \infty }^{ - \delta } {{{\left| {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right|}^2}{\rm{d}}t} + \int_{ - \delta }^\delta {{{\left| {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right|}^2}{\rm{d}}t} + \\ \int_\delta ^{ + \infty } {{{\left| {{\varphi _\mathit{\Phi }}\left( t \right) - {\varphi _\mathit{\Psi }}\left( t \right)} \right|}^2}{\rm{d}}t} \le \\ \int_{ - \delta }^\delta {{{\left| {\frac{{14}}{{99{\rm{i}}t}}} \right|}^2}{\rm{d}}t} + 8\delta + \int_\delta ^{ + \infty } {{{\left| {\frac{{14}}{{99{\rm{i}}t}}} \right|}^2}{\rm{d}}t} = 8\delta + \frac{{1\;148}}{{9\;801\delta }} < \\ 8\delta + \frac{1}{{8\delta }}, \end{array} $ |
因此,
计算两者期望及方差,可得:
| $ \begin{array}{l} \mathop {\lim }\limits_{t \to 0} {{\varphi '}_\mathit{\Phi }}\left( t \right) = 3.750{\rm{i,}}\mathop {\lim }\limits_{t \to 0} {{\varphi ''}_\mathit{\Phi }}\left( t \right) = - 18.333\;3,\\ \mathop {\lim }\limits_{t \to 0} {{\varphi '}_\mathit{\Psi }}\left( t \right) = 3.735{\rm{i,}}\mathop {\lim }\limits_{t \to 0} {{\varphi ''}_\mathit{\Psi }}\left( t \right) = - 18.33{\rm{5}}\;{\rm{6}}. \end{array} $ |
根据定理1可得,EΦ(η)=3.750,VΦ(η)=4.270 8,EΨ(η)=3.735,VΨ(ξ)=4.385 4.
于是,有
| $ \begin{array}{l} \max \left\{ {\left| {\frac{{{E_\mathit{\Phi }}\left( \eta \right) - {E_\mathit{\Psi }}\left( \eta \right)}}{{{E_\mathit{\Psi }}\left( \eta \right)}}} \right|,\left| {\frac{{{V_\mathit{\Phi }}\left( \eta \right) - {V_\mathit{\Psi }}\left( \eta \right)}}{{{V_\mathit{\Psi }}\left( \eta \right)}}} \right|} \right\} = \\ \max \left\{ {\left| {\frac{{3.750 - 3.735}}{{3.735}}} \right|,\left| {\frac{{4.270\;8 - 4.385\;4}}{{4.385\;4}}} \right|} \right\} = \\ \max \left\{ {0.004\;0,0.026\;1} \right\} = 0.026\;1 < 0.050\;0, \end{array} $ |
即在给定α=0.050 0条件下,拟合的不确定分布是有效的.
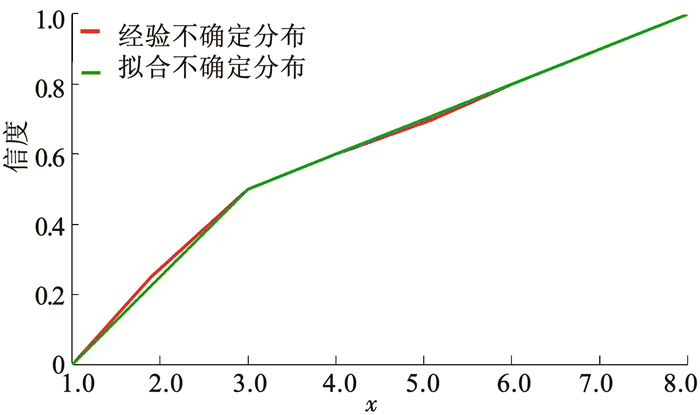
图 3中,横轴表示不确定变量的取值范围,纵轴表示相应的信度,表示之字形不确定分布拟合效果,从图 3中可以看出分布拟合效果较好,与计算结果一致.
|
图 3 之字形不确定分布拟合 Fig. 3 Zigzag uncertainty distribution fitting |
1) 本文从特征函数的角度出发提出了不确定分布拟合的有效性检验方法.根据不确定分布函数的定义及其性质,给出了不确定分布拟合有效性的定义及其判定定理.通过对线性不确定分和之字形不确定分布的拟合检验,验证了所提方法的正确性和可行性.
2) 该方法是通过分析不确定分布特征函数的关系来判断分布拟合的有效性,因此该方法不仅适用于检验利用专家给出一组经验数据拟合的不确定分布,同样可用于群决策时不确定分布的拟合检验.
3) 本文所提方法是通过对比经验不确定分布和拟合不确定分布的差异来分析拟合的效果,因此该方法具有一定的主观性.
| [1] |
LIU Baoding. Uncertainty theory[M]. 5th ed. Berlin: Springer-Verlag, 2016.
|
| [2] |
Peng Zixiong, IWAMURA K. A sufficient and necessary condition of uncertainty distribution[J]. Journal of Interdisciplinary Mathematics, 2010, 13(3): 277. DOI:10.1080/09720502.2010.10700701 |
| [3] |
LIU Baoding. Toward uncertain finance theory[J]. Journal of Uncertainty Analysis and Applications, 2013, 1: 1. DOI:10.1186/2195-5468-1-1 |
| [4] |
LIU Baoding. Membership functions and operational law of uncertain sets[J]. Fuzzy Optimization and Decision Making, 2012, 11(4): 387. DOI:10.1007/s10700-012-9128-7 |
| [5] |
CHEN Xiaowei. Uncertain calculus with finite variation processes[J]. Soft Computing, 2015, 19(10): 2905. DOI:10.1007/s00500-014-1452-0 |
| [6] |
GE Xintong. Neutral uncertain delay differential equations[J]. Wit Transactions on Information & Communication Technologies, 2014, 54: 1005. DOI:10.2495/GCN131342 |
| [7] |
LIU Baoding, CHEN Xiaowei. Uncertain multi-objective programming and uncertain goal programming[J]. Journal of Uncertainty Analysis and Applications, 2015, 3: 10. DOI:10.1186/s40467-015-0036-6 |
| [8] |
LIU Baoding, YAO Kai. Uncertain multilevel programming: Algorithm and applications[J]. Computers & Industrial Engineering, 2015, 89: 235. DOI:10.1016/j.cie.2014.09.029 |
| [9] |
PENG Jin. Risk metrics of loss function for uncertain system[J]. Fuzzy Optimization and Decision Making, 2013, 12(1): 53. DOI:10.1007/s10700-012-9146-5 |
| [10] |
LIU Baoding. Extreme value theorems of uncertain process with application to insurance risk model[J]. Soft Computing, 2013, 17: 549. DOI:10.1007/s00500-012-0930-5 |
| [11] |
JI Xiaoyu, ZHOU Jian. Option pricing for an uncertain stock model with jumps[J]. Soft Computing, 2015, 19(11): 3323. DOI:10.1007/s00500-015-1635-3 |
| [12] |
LIU Baoding. Uncertainty theory: a Branch of mathematics for modeling Human uncertainty[M]. Berlin: Springer-Verlag, 2010. DOI:10.1007/978-3-642-13959-8
|
| [13] |
GUO Haiying, WANG Xiaosheng, WANG Lili, et al. Delphi method for estimating membership function of uncertain set[J]. Journal of Uncertainty Analysis & Applications, 2016, 4: 1. DOI:10.1186/s40467-016-0044-1 |
| [14] |
WANG Xiaosheng, PENG Zixiong. Method of moments for estimating uncertainty distributions[J]. Journal of Uncertainty Analysis & Applications, 2014, 2: 5. DOI:10.1186/2195-5468-2-5 |
| [15] |
LI Runyu, LIU Gang. An uncertain goal programming model for machine scheduling problem[J]. Journal of Intelligent Manufacturing, 2017, 28(3): 689. DOI:10.1007/s10845-014-0982-8 |
| [16] |
NING Yufu, CHEN Xiumei, WANG Zhiyong, et al. An uncertain multi-objective programming model for machine scheduling problem[J]. International Journal of Machine Learning and Cybernetics, 2017, 8(5): 1493. DOI:10.1007/s13042-016-0522-2 |
| [17] |
GUO Jiansheng, WANG Zutong, ZHENG Mingfa, et al. Uncertain multi-objective redundancy allocation problem of repairable systems based on artificial bee colony algorithm[J]. Chinese Journal of Aeronautics, 2014, 27(6): 1477. DOI:10.1016/j.cja.2014.10.014 |
| [18] |
LIU Liying, ZHANG Bo, MA Weimin. Uncertain programming models for fixed charge multi-item solid transportation problem[J]. Soft Computing, 2017(1): 1. DOI:10.1007/s00500-017-2718-0 |
| [19] |
DALMAN H. Uncertain programming model for multi-item solid transportation problem[J]. International Journal of Machine Learning and Cybernetics, 2018, 9(4): 559. DOI:10.1007/s13042-016-0538-7 |
| [20] |
王族统.基于不确定理论的多目标规划方法及其应用研究[D].西安: 空军工程大学, 2015 WANG Zutong. Research on multi-objective programming and apply based on uncertainty theory[D]. Xi'an: Air Force Engineering University, 2015 |
 2019, Vol. 51
2019, Vol. 51


