2. 解放军95910部队,甘肃 酒泉 735000;
3. 空军工程大学 空管领航学院, 西安 710051
2. Unit 95910 of PLA, Jiuquan 735000, Gansu, China;
3. College of Air Traffic Control and Navigation, Air Force Engineer University, Xi'an 710051, China
蛇形机动是战斗机飞机飞行员在隐蔽接敌、机动规避及协同探测等战术动作中经常采用的战术机动类型[1-2].在一定的空战态势下,飞行员进行蛇形机动反映了其战术意图,因此在空战中如何快速而又准确地识别出目标的蛇形机动模式对于判明其战术意图以及评估当前的战场态势具有十分重要的意义[2-3].转弯角速度是识别蛇形机动模式最为关键的运动参量,通过精确辨识出机动目标的转弯角速度,可以进一步提高蛇形机动模式的识别率,然而,在实际空战过程中,由于机动目标的非合作特性,导致蛇形机动目标的转弯角速度无法被探测方直接获取,这也就为精确辨识蛇形机动目标的转弯角速度提出了迫切要求[2].
目前,机动目标转弯角速度辨识的问题已经得到了许多学者的关注.文献[4-7]将转弯角速度作为额外的状态变量,从而对状态进行扩维处理,然后使用非线性滤波方法辨识角速度和估计状态变量.缺点是角速度估计的精度依赖于目标初始状态及协方差、过程噪声和量测噪声等因素[2];文献[8-10]分别根据转弯角速度与目标速度方向角、速度、加速度之间的物理关系,首先采用非线性滤波算法估计出目标速度方向角、速度、加速度等状态量,而后间接辨识出转弯角速度.Yuan等[11]通过引入距离变化率量测,采用Cmin方法[12]并结合航向角的变化估计出两个可能的转弯角速度的值,基于此设计包含匀速模型和两个匀速转弯模型的IMM算法进行状态估计.Frencl等[13]通过引入距离变化率量测估计转弯角速度,并根据速度矢量在距离方向上的投影与距离变化率估计量之间的差异,对转弯角速度进行进一步修正以提高估计精度,然后依据最优线性无偏估计准则,利用粒子滤波进行状态估计.缺点是没有考虑角速度与目标状态之间相互耦合关系,增大了辨识风险[14].
上述文献在估计目标状态和辨识转弯角速度时,都假设量测数据能够实时到达数据处理中心,但是,在实际的目标跟踪过程中,由于通信信道带宽的限制导致量测抵达数据处理中心时不可避免地存在随机延迟现象,从而造成用于估计与辨识的量测无法及时更新[15-16],并且在经典的估计理论当中,一般假设量测噪声与系统噪声为相互独立或相关的高斯白噪声,但是,在实际的空战过程中,由于复杂的作战环境以及目标本身所存在的散射现象,使得雷达的量测噪声不再服从高斯分布,而是尾部较长的“闪烁”噪声[17-18].在实际空战中,由于蛇形机动目标的非合作特性,导致了蛇形机动目标的转弯角速度是未知且时变的,并且与目标状态相互耦合、彼此影响,一方面目标状态估计性能的提升有利于转弯角速度的辨识,另一方面转弯角速度辨识性能的提升有利于目标状态估计精度的提高,但是上述文献中所提到的转弯角速度辨识方法均没有考虑转弯角速度与目标状态之间的耦合关系以及这种耦合关系所带来的影响,并且均采取的是开环序贯处理方式,没有形成闭环反馈[2].
针对上述问题,本文通过将目标状态估计与转弯角速度辨识联合考虑,基于EM算法框架,通过充分考虑量测随机延迟特性和“闪烁”噪声条件,重构了量测随机延迟下的粒子滤波器的似然函数,同时,为了避免采样粒子多样性丧失现象的发生,采用粒子群算法进一步优化采样过程,并结合后向模拟粒子平滑相关理论,设计了一步量测随机延迟条件下具有提前终止条件的后向模拟粒子平滑器用以计算后验平滑概率密度和联合分布密度,并采用牛顿迭代法的优化思想,不断迭代求得目标状态与转弯角速度闭环形式的联合优化解,并将滑窗思想引入到EM算法框架当中以降低算法的整体运行时间.该算法主要包括:E-step基于当前的角速度并采用粒子群优化的粒子滤波器与后向模拟粒子平滑器获得的后验平滑概率密度和联合分布密度,近似计算完整的对数函数似然函数的期望;M-step通过极大化似然函数进而更新获得下一次迭代的角速度估计量.
1 问题描述蛇形机动可以分解成若干具有不同转弯角速度的圆弧转弯机动,因此蛇形机动目标转弯角速度的辨识问题相应地转化为圆弧转弯机动的角速度辨识问题.在量测一步随机延迟以及非高斯噪声背景下,假设目标在二维平面中运动,转弯机动模型状态方程为:
| $ {\mathit{\boldsymbol{x}}_k} = {\mathit{\boldsymbol{f}}_{k - 1}}\left( {{\mathit{\boldsymbol{x}}_{k - 1}},{\mathit{\Omega }_{k - 1}}} \right) + {\mathit{\boldsymbol{w}}_{k - 1}}, $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{f}}_{k - 1}}\left( {{\mathit{\boldsymbol{x}}_{k - 1}},{\mathit{\Omega }_{k - 1}}} \right) = \\ \;\;\;\left[ {\begin{array}{*{20}{c}} 1&{\frac{{\sin \left( {{\mathit{\Omega }_{k - 1}}T} \right)}}{{{\mathit{\Omega }_{k - 1}}}}}&0&{\frac{{\cos \left( {{\mathit{\Omega }_{k - 1}}T} \right) - 1}}{{{\mathit{\Omega }_{k - 1}}}}}\\ 0&{\cos \left( {{\mathit{\Omega }_{k - 1}}T} \right)}&0&{ - \sin \left( {{\mathit{\Omega }_{k - 1}}T} \right)}\\ 0&{\frac{{1 - \cos \left( {{\mathit{\Omega }_{k - 1}}T} \right)}}{{{\mathit{\Omega }_{k - 1}}}}}&1&{\frac{{\sin \left( {{\mathit{\Omega }_{k - 1}}T} \right)}}{{{\mathit{\Omega }_{k - 1}}}}}\\ 0&{\sin \left( {{\mathit{\Omega }_{k - 1}}T} \right)}&0&{\cos \left( {{\mathit{\Omega }_{k - 1}}T} \right)} \end{array}} \right] \cdot {\mathit{\boldsymbol{x}}_{k - 1}}. \end{array} $ |
式中:xk∈Rn为状态变量; Ωk-1为待辨识的转弯角速度; xk=
一步随机延迟量测模型[19]为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{z}}_k} = {\mathit{\boldsymbol{h}}_k}\left( {{\mathit{\boldsymbol{x}}_k}} \right) + {\mathit{\boldsymbol{v}}_k},\\ {\mathit{\boldsymbol{y}}_k} = \left( {1 - {\gamma _k}} \right){\mathit{\boldsymbol{z}}_k} + {\gamma _k}{\mathit{\boldsymbol{z}}_{k - 1}},k > 1,{\mathit{\boldsymbol{y}}_1} = {\mathit{\boldsymbol{z}}_1}. \end{array} \right. $ |
式中:k∈{1, 2, …},zk∈Rm为理想的量测向量; yk∈Rm为实际的量测向量; hk(·)为非线性量测函数; vk∈Rm为闪烁噪声并与过程噪声wk相互独立,即E[wkvkT]=0;{γk∈R, k > 1}为已知的服从Bernoulli分布的随机变量,取值范围在0和1之间且满足:
| $ \left\{ \begin{array}{l} p\left( {{\gamma _k} = 1} \right) = E\left[ {{\gamma _k}} \right] = \lambda ,\\ p\left( {{\gamma _k} = 0} \right) = 1 - E\left[ {{\gamma _k}} \right] = 1 - \lambda ,\\ E\left[ {\left( {{\gamma _k} - {p_k}} \right)2} \right] = \left( {1 - \lambda } \right)\lambda , \end{array} \right. $ |
初始状态x0与过程噪声{wk, k≥0},{vk, k≥1}以及{γk, k≥2}相互独立.λ为量测随机延迟概率,一般假设已知.
与高斯噪声相比,闪烁噪声具有“厚尾”特征,噪声分布尾部较长.雷达跟踪的闪烁噪声统计模型可由一个高斯分布噪声和一个附加残余噪声加权和表示,附加的残余噪声可由拉普拉斯分布、t分布、均匀分布、大方差的高斯分布等替代.
在本文当中采用两个高斯分布噪声的加权和表示雷达的闪烁噪声,其概率密度函数可表示为[18]
| $ p\left( v \right) = \left( {1 - \varepsilon } \right)N\left( {v;{\mu _1},{\mathit{\boldsymbol{P}}_1}} \right) + \varepsilon N\left( {v;{\mu _2},{\mathit{\boldsymbol{P}}_2}} \right). $ |
式中:ε∈[0, 1]为闪烁效应的强弱; N(ω; μt, Pt)为均值为μt、方差为Pt的高斯分布在v处的概率密度.则闪烁噪声的一、二阶距为:
| $ \begin{array}{*{20}{c}} {\mu = E\left( v \right) = \left( {1 - \varepsilon } \right){\mu _1} + \varepsilon {\mu _2},}\\ {P = E\left( {\left( {v - \mu } \right){{\left( {v - \mu } \right)}^{\rm{T}}}} \right) = \left( {1 - \varepsilon } \right){P_1} + \varepsilon {P_2} + \tilde P,} \end{array} $ |
式中
为了解决量测一步随机延迟和非高斯条件下蛇形机动目标的未知转弯角速度辨识和目标状态估计问题,本文通过将角速度辨识与目标状态估计联合考虑,提出了基于PSOPF-EM的联合估计与辨识算法.为了降低算法的整体运行时间成本,本文通过对后向模拟粒子平滑算法设置终止条件来进行算法优化,从而降低了粒子平滑算法的时间消耗,同时又引入了滑窗思想,窗口长度为l,其长度大小可依据辨识与估计精度的实际需求自行设定,用于均衡运算时间成本与精度之间的“博弈”.具体的算法框架如图 1所示.
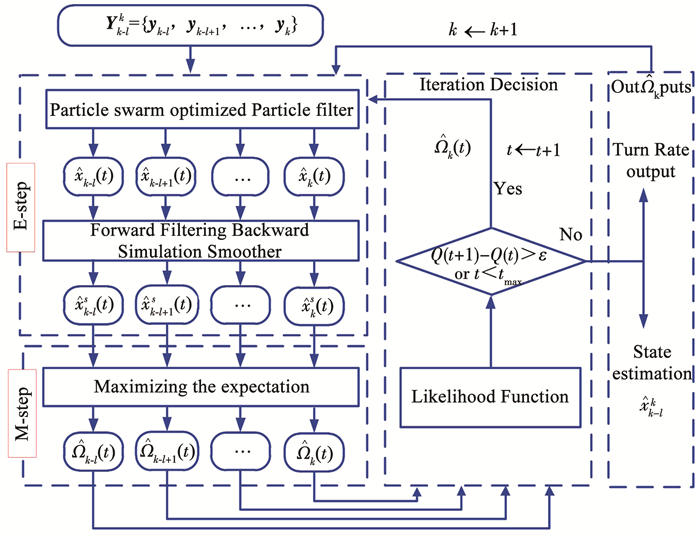
|
图 1 联合估计与辨识 Fig. 1 The joint estimation and identification |
EM算法通过极大化对数似然函数LΩ(Yk-lk|Y1k-l-1),求得角速度的估计值
| $ \begin{array}{*{20}{c}} {\mathit{\hat \Omega } = \arg \max {L_\Omega }\left( {\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right) \buildrel \Delta \over = }\\ {\arg \max \log {p_\Omega }\left( {\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right),} \end{array} $ |
式中, Y1k={y1, y2, …, yk}为实际的延迟量测.
由于一步随机延迟量测取决于未知的状态向量,因此直接极大化不完备数据的对数似然函数LΩ(Yk-lk|Y1k-l-1)是不可能实现的.为了解决这个问题,EM算法将缺失状态向量Xk-l-1k引入到对数似然函数`中,构成完备数据的对数似然函数LΩ(Xk-l-1k, Yk-lk|Y1k-l-1),其中Xk-l-1k={xk-l-1, xk-l, …, xk}.
依据贝叶斯准则可知
| $ \begin{array}{*{20}{c}} {{p_\Omega }\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^k,\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right) = }\\ {{p_\Omega }\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right){p_\Omega }\left( {\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right),} \end{array} $ |
则完备数据的对数似然函数可表示为[20]
| $ \begin{array}{l} {L_\Omega }\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^k,\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right) = \\ \log \left( {{p_\Omega }\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^k,\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right)} \right) = \\ \log \left( {{p_\Omega }\left( {\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right)} \right) + \log \left( {{p_\Omega }\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^k\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right)} \right) = \\ {L_\Omega }\left( {\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right) + \log \left( {{p_\Omega }\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^k\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right)} \right). \end{array} $ |
给定第t次迭代时角速度的参数估计值
| $ \begin{array}{l} Q\left( {\mathit{\Omega },{{\mathit{\hat \Omega }}_t}} \right) \buildrel \Delta \over = {E_{{{\hat \Omega }_t}}}\left\{ {{L_\Omega }\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^k,\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right)\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right\} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{L_\Omega }\left( {\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right) + \int {\log \left( {{p_\Omega }\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^k\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right)} \right)} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{p_{{{\hat \Omega }_t}}}\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^k\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right){\rm{d}}\mathit{\boldsymbol{X}}_{k - l - 1}^k, \end{array} $ |
则
| $ \begin{array}{*{20}{c}} {{L_\Omega }\left( {\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right) - {L_{{{\hat \Omega }_t}}}\left( {\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right) = }\\ {Q\left( {\mathit{\Omega },{{\mathit{\hat \Omega }}_t}} \right) - Q\left( {{{\mathit{\hat \Omega }}_t},{{\mathit{\hat \Omega }}_t}} \right) + }\\ {\int {\log \frac{{{p_{{{\hat \Omega }_t}}}\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^k\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right)}}{{{p_\Omega }\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^k\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right)}}{p_{{{\hat \Omega }_t}}}\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^k\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right){\rm{d}}\mathit{\boldsymbol{X}}_{k - l - 1}^k,} } \end{array} $ |
上式最右边的积分被称为Kullback-Leibler散度[21],其值非负.
则可知
| $ \begin{array}{*{20}{c}} {{L_\Omega }\left( {\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right) - {L_{{{\hat \Omega }_t}}}\left( {\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right) \ge }\\ {Q\left( {\mathit{\Omega },{{\mathit{\hat \Omega }}_t}} \right) - Q\left( {{{\mathit{\hat \Omega }}_t},{{\mathit{\hat \Omega }}_t}} \right).} \end{array} $ | (1) |
从式(1)可以看出如果选择Ω的一个合适值
根据贝叶斯准则可知
| $ \begin{array}{l} {p_\Omega }\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^k,\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right) = \\ \left( {\prod\limits_{i = 0}^l {{p_\Omega }\left( {{\mathit{\boldsymbol{y}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i}},{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.} \right)p\left( {{\mathit{\boldsymbol{x}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.} \right)} } \right).\\ {p_\Omega }\left( {{\mathit{\boldsymbol{x}}_{k - l - 1}}\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right) = \left( {\prod\limits_{i = 0}^l {\left( {1 - \lambda } \right){p_\Omega }\left( {{\mathit{\boldsymbol{z}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i}}} \right.} \right)} + } \right.\\ \left. {\lambda {p_\Omega }\left( {{\mathit{\boldsymbol{z}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.} \right)} \right) \times \left( {\prod\limits_{i = 0}^l {p\left( {{\mathit{\boldsymbol{x}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.} \right)} } \right).\\ {p_\Omega }\left( {{\mathit{\boldsymbol{x}}_{k - l - 1}}\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right), \end{array} $ | (2) |
其中
| $ \begin{array}{l} {p_\Omega }\left( {{\mathit{\boldsymbol{y}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i}},{x_{k - i - 1}}} \right.} \right) = \\ {p_\Omega }\left( {{\mathit{\boldsymbol{y}}_{k - i}}\left| {{\gamma _{k - i}} = 0,{\mathit{\boldsymbol{x}}_{k - i}},{x_{k - i - 1}}} \right.} \right)p\left( {{\gamma _{k - i}} = 0} \right) + \\ {p_\Omega }\left( {{\mathit{\boldsymbol{y}}_{k - i}}\left| {{\gamma _{k - i}} = 1,{\mathit{\boldsymbol{x}}_{k - i}},{x_{k - i - 1}}} \right.} \right)p\left( {{\gamma _{k - i}} = 1} \right) = \\ \left( {1 - \lambda } \right){p_\Omega }\left( {{\mathit{\boldsymbol{y}}_{k - i}} - {\mathit{\boldsymbol{h}}_{k - i}}\left( {{\mathit{\boldsymbol{x}}_{k - i}}} \right)} \right) + \\ \lambda {p_\Omega }\left( {{\mathit{\boldsymbol{y}}_{k - i}} - {\mathit{\boldsymbol{h}}_{k - i - 1}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right)} \right) = \\ \left( {1 - \lambda } \right){p_\Omega }\left( {{\mathit{\boldsymbol{z}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i}}} \right.} \right) + \lambda {p_\Omega }\left( {{\mathit{\boldsymbol{z}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.} \right), \end{array} $ |
则完备数据对数似然函数可以分解成如下
| $ \begin{array}{l} {L_\Omega }\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^k,\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right) = \\ \log {p_\Omega }\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^k,\mathit{\boldsymbol{Y}}_{k - l}^k\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right) = \\ \log {p_\Omega }\left( {{\mathit{\boldsymbol{x}}_{k - l - 1}}\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right) + \sum\limits_{i = 0}^l {\log {p_\Omega }\left( {{\mathit{\boldsymbol{x}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.} \right)} + \\ \sum\limits_{i = 0}^l {\log \left[ {\left( {1 - \lambda } \right){p_\Omega }\left( {{\mathit{\boldsymbol{z}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i}}} \right.} \right) + \lambda {p_\Omega }\left( {{\mathit{\boldsymbol{z}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.} \right)} \right]} , \end{array} $ |
则Q(Ω,
| $ Q\left( {\mathit{\Omega },{{\mathit{\hat \Omega }}_t}} \right) = {I_1} + {I_2} + {I_3}, $ |
其中:
| $ {I_1} = \int {\log {p_\Omega }\left( {{\mathit{\boldsymbol{x}}_{k - l - 1}}\left| {\mathit{\boldsymbol{Y}}_1^{k - l - 1}} \right.} \right){p_{{{\mathit{\hat \Omega }}_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - l - 1}}\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right){\rm{d}}{x_{k - l - 1}}} , $ | (3) |
| $ \begin{gathered} {I_2} = \sum\limits_{i = 0}^I {\iint {\log {p_\Omega }\left( {{\mathit{\boldsymbol{x}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.} \right){p_{{{\mathit{\hat \Omega }}_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}},{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right)}} \times \hfill \\ \;\;\;\;\;\;{\text{d}}{\mathit{\boldsymbol{x}}_{k - i}}{\text{d}}{\mathit{\boldsymbol{x}}_{k - i - 1}}, \hfill \\ \end{gathered} $ | (4) |
| $ \begin{gathered} {I_3} = \sum\limits_{i = 0}^I {\iint {\log \left[ {\left( {1 - \lambda } \right){p_\Omega }\left( {{\mathit{\boldsymbol{z}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i}}} \right.} \right) + } \right.}} \hfill \\ \;\;\;\;\;\;\left. {\lambda {p_\Omega }\left( {{\mathit{\boldsymbol{z}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.} \right)} \right] \times \hfill \\ \;\;\;\;\;\;{p_{{{\mathit{\hat \Omega }}_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}},{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right){\text{d}}{\mathit{\boldsymbol{x}}_{k - i}}{\text{d}}{\mathit{\boldsymbol{x}}_{k - i - 1}}. \hfill \\ \end{gathered} $ | (5) |
式中:当l=k-1时,I1为一个常数,与待辨识量θ无关;当0≤l<k-1时,I1与θ相关性较弱,而且,为了满足实时性的要求,辨识算法应尽量关注当前时刻的数据或者邻近时刻的数据[2],与此同时,由于蛇形机动目标的转弯角速度耦合在系统状态转移矩阵当中,即转弯角速度只与先验概率分布pΩ(xk-i|xk-i-1)有关,故可知在辨识转弯角速度时,只需要考虑条件期望函数的I2部分即可.
EM算法通过不断迭代求得Q(Ω,
E-step的主要任务是在给定第t次迭代时的角速度估计值
依据贝叶斯准则,联合平滑密度分布可表示成如下形式:
| $ \begin{array}{l} {p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}},{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right) = {p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i}}} \right.,\mathit{\boldsymbol{Y}}_1^k} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}}\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right). \end{array} $ | (6) |
根据文献[21]可知
| $ {p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i}}} \right.,\mathit{\boldsymbol{Y}}_1^k} \right) = {p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i}}} \right.,\mathit{\boldsymbol{Y}}_1^{k - i}} \right), $ | (7) |
其中
| $ \begin{array}{l} {p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i}}} \right.,\mathit{\boldsymbol{Y}}_1^{k - i}} \right) = \\ \frac{{{p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}},{\mathit{\boldsymbol{x}}_{k - i}},{\mathit{\boldsymbol{y}}_{k - i}}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right)}}{{{p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}},{\mathit{\boldsymbol{y}}_{k - i}}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right)}} = \\ \frac{{{p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{y}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.,{\mathit{\boldsymbol{x}}_{k - i}}} \right){p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.} \right){p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right)}}{{{p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}},{\mathit{\boldsymbol{y}}_{k - i}}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right)}}. \end{array} $ | (8) |
将式(7)~(8)带入式(6)中可得
| $ \begin{array}{l} {p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}},{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right) = {p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right) \times \\ \frac{{{p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{y}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.,{\mathit{\boldsymbol{x}}_{k - i}}} \right){p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.} \right){p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right)}}{{{p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}},{\mathit{\boldsymbol{y}}_{k - i}}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right)}}, \end{array} $ |
其中
| $ \begin{array}{l} {p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}},{\mathit{\boldsymbol{y}}_{k - i}}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right) = \\ \int {{p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}},{\mathit{\boldsymbol{x}}_{k - i}},{\mathit{\boldsymbol{y}}_{k - i}}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right){\rm{d}}{\mathit{\boldsymbol{x}}_{k - i - 1}}} = \\ \int {{p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{y}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.,{\mathit{\boldsymbol{x}}_{k - i}}} \right){p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.} \right)} \cdot \\ {p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}}\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right){\rm{d}}{\mathit{\boldsymbol{x}}_{k - i - 1}}. \end{array} $ | (9) |
式中:
滤波概率密度
| $ \begin{array}{*{20}{c}} {{p_{{{\hat \Omega }_t}}}\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^{k - i - 1}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right) \approx {{\hat p}_{{{\hat \Omega }_t}}}\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^{k - i - 1}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right) = }\\ {\sum\limits_{j = 1}^N {\bar w_{k - l - 1}^{k - i - 1,j}\delta \left[ {\mathit{\boldsymbol{x}}_{k - l - 1}^{k - i - 1} - \mathit{\boldsymbol{x}}_{k - l - 1}^{k - i - 1,j}} \right]} .} \end{array} $ | (10) |
式中:N为采样粒子数量; {xk-l-1k-i-1, j}j=1N为采样粒子集合, i∈[0, l]; wk-l-1k-i-1, j为采样粒子对应的归一化权重.wk-l-1k-i-1, j为重要性权重,并且满足:
| $ w_{k - l - 1}^{k - i - 1,j} = \frac{{{p_{{{\hat \Omega }_t}}}\left( {\mathit{\boldsymbol{X}}_{k - l - 1}^{k - i - 1,j}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right)}}{{q\left( {\mathit{\boldsymbol{x}}_{k - l - 1}^{k - i - 1,j}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right)}},\tilde w_{k - l - 1}^{k - i - 1,j} = \frac{{w_{k - l - 1}^{k - i - 1,j}}}{{\sum\limits_{j = 1}^N {w_{k - l - 1}^{k - i - 1,j}} }}. $ | (11) |
依据贝叶斯准则可知
| $ \begin{array}{*{20}{c}} {q\left( {\mathit{\boldsymbol{x}}_{k - l - 1}^{k - i - 1,j}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right) = }\\ {q\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {\mathit{\boldsymbol{x}}_{k - l - 1}^{k - i - 2},\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right) \cdot q\left( {\mathit{\boldsymbol{x}}_{k - l - 1}^{k - i - 2}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right).} \end{array} $ | (12) |
依据贝叶斯准则和Markov性可知
| $ \begin{array}{l} {p_{{{\hat \Omega }_t}}}\left( {\mathit{\boldsymbol{x}}_{k - l - 1}^{k - i - 1}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right) = {p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{y}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}},{\mathit{\boldsymbol{x}}_{k - i - 2}}} \right.} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{p_{{{\mathit{\hat \Omega }}_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 2}}} \right.} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{p_{{{\mathit{\hat \Omega }}_t}}}\left( {\mathit{\boldsymbol{x}}_{k - l - 1}^{k - i - 2}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 2}} \right.} \right), \end{array} $ | (13) |
则将式(12)~(13)带入到式(11)中可得
| $ \begin{array}{l} {w_{k - i - 1}} = \\ \frac{{{p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{y}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.,{x_{k - i - 2}}} \right){p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 2}}} \right.} \right)}}{{\mathit{\boldsymbol{q}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {\mathit{\boldsymbol{x}}_{k - l - 1}^{k - i - 2},\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right)}}{w_{k - i - 2}}. \end{array} $ | (14) |
为了便于重要性权重的计算,在此选择先验转移密度作为建议密度,即
| $ q\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {\mathit{\boldsymbol{x}}_{k - l - 1}^{k - i - 2},\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right) = {p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 2}}} \right.} \right), $ | (15) |
将式(15)带入式(14)中可得
| $ {w_{k - i - 1}} = {w_{k - i - 2}}{p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{y}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.,{x_{k - i - 2}}} \right). $ | (16) |
将式(2)带入式(16)中可知粒子xk-i-1j对应的权重为
| $ \begin{array}{l} w_{k - i - 1}^j = {w_{k - i - 2}}\left[ {\left( {1 - \lambda } \right){p_\Omega }\left( {{\mathit{\boldsymbol{z}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i}}} \right.} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {\lambda {p_\Omega }\left( {{\mathit{\boldsymbol{z}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i - 1}}} \right.} \right)} \right]. \end{array} $ | (17) |
将采样粒子xk-i-1j以及相应的归一化权重wk-i-1j带入到式(10)中可得滤波概率密度
| $ \begin{array}{l} {p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {\mathit{\boldsymbol{Y}}_1^{k - i - 1}} \right.} \right) \approx {{\hat p}_{{{\mathit{\hat \Omega }}_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {Y_1^{k - i - 1}} \right.} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^N {\bar w_{k - l - 1}^j\delta \left[ {{\mathit{\boldsymbol{x}}_{k - i - 1}} - \mathit{\boldsymbol{x}}_{k - l - 1}^j} \right]} . \end{array} $ | (18) |
由于传统的基于序贯重要性采样的粒子滤波算法采用了次优的重要性函数[23],所以,存在以下两个缺陷:1)粒子贫乏问题;2)为了确保状态估计精度需要大量采样粒子,造成算法的运行时间成本较高.为解决上述问题,本文将粒子群优化算法引入到粒子滤波算法当中,使得粒子群在权重值更新之前更加趋向高似然区域,从而缓解粒子匮乏现象,可以减少滤波所需的粒子数量.粒子群算法与粒子滤波算法的结合主要是利用粒子所经历过的最优状态值pbest和粒子群中的最优粒子的状态值gbest,通过下式进行更新[23]:
| $ V_k^i = \left| {{\rm{randn}}} \right|\left( {{\rm{pbest}} - \mathit{\boldsymbol{x}}_k^i} \right) + \left| {{\rm{Randn}}} \right|\left( {{\rm{gbest}} - \mathit{\boldsymbol{x}}_k^i} \right), $ | (19) |
| $ \mathit{\boldsymbol{x}}_k^i = \mathit{\boldsymbol{x}}_k^i + V_k^i. $ | (20) |
式中:|randn|、|Randn|分别为正的高斯分布的随机数,可由abs[N(0, 1)]产生;pbest为当前粒子所经历的状态值中适应度函数最大的粒子的状态值;gbest为粒子群中适应度函数值最大的粒子的状态值[24].当粒子群的最优值符合某阈值ε时,则表明粒子群中的粒子已经分布在真实状态附近,那么粒子群算法将停止优化.此时再对粒子集依据式(17)进行权重更新并依据式(11)进行归一化处理.具体的算法过程,见图 2.

|
图 2 量测随机延迟下基于粒子群优化的粒子滤波算法 Fig. 2 Particle filter algorithm based on particle swarm optimization with measuring random delay |
考虑到后向模拟粒子平滑器的在滤波效果不好的条件下仍能收敛的良好的性质[25],故本文拟采用该平滑器近似计算平滑概率密度
将式(18)带入到式(8)、(9)可得:
| $ \begin{array}{*{20}{c}} {{p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i - 1}}\left| {{\mathit{\boldsymbol{x}}_{k - i}}} \right.,\mathit{\boldsymbol{Y}}_1^{k - i}} \right) \approx }\\ {\sum\limits_{j = 1}^N {\bar w_{k - i - 1\left| {k - i} \right.}^j\delta \left[ {{\mathit{\boldsymbol{x}}_{k - i - 1}} - \mathit{\boldsymbol{x}}_{k - l - 1}^j} \right]} .} \end{array} $ | (21) |
式中
| $ \begin{array}{l} \bar w_{k - i - 1\left| {k - i} \right.}^j = \\ \frac{{\bar w_{k - i - 1}^j{p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{y}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i}}} \right.,\mathit{\boldsymbol{x}}_{k - i - 1}^j} \right){p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}}\left| {\mathit{\boldsymbol{x}}_{k - i - 1}^j} \right.} \right)}}{{\sum\limits_{r = 1}^N {\bar w_{k - i - 1}^r{p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{y}}_{k - i}}\left| {{\mathit{\boldsymbol{x}}_{k - i}}} \right.,\mathit{\boldsymbol{x}}_{k - i - 1}^r} \right){p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}}\left| {\mathit{\boldsymbol{x}}_{k - i - 1}^r} \right.} \right)} }}. \end{array} $ | (22) |
假设已经从平滑分布
| $ {p_{{{\hat \Omega }_t}}}\left( {\mathit{\boldsymbol{x}}_{k - l - 1}^k\left| {\mathit{\boldsymbol{Z}}_1^k} \right.} \right) \approx \frac{1}{M}\sum\limits_{m = 1}^M {\delta \left( {\mathit{\boldsymbol{x}}_{k - l - 1}^k - \mathit{\boldsymbol{\tilde x}}_{k - l - 1}^{k,m}} \right)} . $ |
则平滑概率密度
| $ {p_{{{\hat \Omega }_t}}}\left( {{\mathit{\boldsymbol{x}}_{k - i}}\left| {\mathit{\boldsymbol{Y}}_1^k} \right.} \right) \approx \frac{1}{M}\sum\limits_{m = 1}^M {\delta \left( {{\mathit{\boldsymbol{x}}_{k - i}} - \mathit{\boldsymbol{\tilde x}}_{k - i}^m} \right)} . $ |
标准的后向模拟粒子平滑算法过程见图 3.

|
注:Cat({pi}i=1n)为从离散数据集合{1, 2, …, n-1, n}中进行多项分布采样获得n个采样数据,其中第i个值被选中的概率为pi,且 |
从图 3中可以明显看出,在进行多项分布采样时,每采样得到一个粒子索引值,就需要繁琐地计算采样粒子的平滑权重,导致算法的计算量呈二次方式增加.为了避免粒子平滑权重的复杂计算,降低运算时间成本,Douc等[28]通过将拒绝采样(RS)方法引入到标准的后向模拟平滑算法中来,进行粒子索引值的采样,降低了时间复杂度,提升了算法运行效率.
假设系统状态转移密度函数存在上界,即pΩ(xk-i|xk-i-1)≤ρ.基于这个假设,直接将粒子滤波得到的粒子权重作为多项分布采样的采样概率,即依据该概率
| $ \frac{{\tilde w_{k - i - 1\left| {k - i} \right.}^{I\left( m \right),m}}}{{w_{k - i - 1}^{I\left( m \right)}}} \propto {p_\Omega }\left( {\mathit{\boldsymbol{\tilde x}}_{k - i}^m\left| {\mathit{\boldsymbol{x}}_{k - i - 1}^{I\left( m \right)}} \right.} \right) \le \rho , $ |
也就是说,通过建议分布采样得到的粒子如果满足pΩ(
将通过图 3计算得到的联合平滑概率分布函数
| $ {{\hat I}_1} \approx \frac{1}{M}\sum\limits_{j = 1}^M {\log {p_\Omega }\left( {\mathit{\boldsymbol{\tilde x}}_{k - l - 1}^j} \right)} , $ | (23) |
| $ {{\hat I}_2} \approx \sum\limits_{i = 0}^l {\frac{1}{M}\sum\limits_{j = 1}^M {\log {p_\Omega }\left( {\mathit{\boldsymbol{\tilde x}}_{k - i}^j\left| {\mathit{\boldsymbol{\tilde x}}_{k - i - 1}^j} \right.} \right)} } , $ | (24) |
| $ \begin{array}{l} {{\hat I}_3} \approx \sum\limits_{i = 0}^l {\frac{1}{M}\sum\limits_{j = 1}^M {\log \left[ {\left( {1 - \lambda } \right){p_\Omega }\left( {{\mathit{\boldsymbol{z}}_{k - i}}\left| {\mathit{\boldsymbol{\tilde x}}_{k - i}^j} \right.} \right) + } \right.} } \\ \;\;\;\;\;\;\left. {\lambda {p_\Omega }\left( {{\mathit{\boldsymbol{z}}_{k - i - 1}}\left| {\mathit{\boldsymbol{\tilde x}}_{k - i - 1}^j} \right.} \right)} \right]. \end{array} $ | (25) |

|
图 4 带终止条件的拒绝采样后向模拟粒子平滑 Fig. 4 Backward simulation particle smoothing algorithm with rejection sampling and early stopping |
将式(23)~(25)代入式(2)即可得到
M-step的主要任务是解决Q(Ω,
| $ {{\mathit{\hat \Omega }}_{t + 1}} = \arg \mathop {\max }\limits_\mathit{\Omega } Q\left( {\Omega ,{{\mathit{\hat \Omega }}_t}} \right). $ |
本文采用梯度下降法求取
| $ \frac{\partial }{{\partial \mathit{\Omega }}}\hat Q\left( {\mathit{\Omega },{{\mathit{\hat \Omega }}_t}} \right) = \frac{\partial }{{\partial \mathit{\Omega }}}{{\hat I}_1} + \frac{\partial }{{\partial \mathit{\Omega }}}{{\hat I}_2} + \frac{\partial }{{\partial \mathit{\Omega }}}{{\hat I}_3}, $ | (26) |
| $ \frac{\partial }{{\partial \mathit{\Omega }}}{{\hat I}_1} = \frac{1}{M}\sum\limits_{j = 1}^M {\frac{{\partial \log {p_\Omega }\left( {\mathit{\boldsymbol{x}}_{k - l - 1}^j} \right)}}{{\partial \mathit{\Omega }}}} , $ | (27) |
| $ \frac{\partial }{{\partial \mathit{\Omega }}}{{\hat I}_2} = \frac{1}{M}\sum\limits_{i = 0}^l {\sum\limits_{j = 1}^M {\frac{{\partial \log {p_\Omega }\left( {\mathit{\boldsymbol{x}}_{k - i}^j\left| {\mathit{\boldsymbol{x}}_{k - i - 1}^j} \right.} \right)}}{{\partial \mathit{\Omega }}}} } , $ | (28) |
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial \mathit{\Omega }}}{{\hat I}_3} = \frac{1}{M}\sum\limits_{i = 0}^l {\sum\limits_{j = 1}^M {} } }\\ {\frac{{\partial \log \left[ {\left( {1 - \lambda } \right){p_\Omega }\left( {{\mathit{\boldsymbol{z}}_{k - i}}\left| {\mathit{\boldsymbol{\tilde x}}_{k - i}^j} \right.} \right) + \lambda {p_\Omega }\left( {{\mathit{\boldsymbol{z}}_{k - i - 1}}\left| {\mathit{\boldsymbol{\tilde x}}_{k - i - 1}^j} \right.} \right)} \right]}}{{\partial \mathit{\Omega }}}.} \end{array} $ | (29) |
本文采用的是滞后窗口,即辨识k-l时刻的转弯角速度Ω的值需要使用[k-l, k]时刻的量测.
可将本文算法总结如下,见图 5.

|
图 5 基于PSOPF-EM的联合估计与辨识算法 Fig. 5 Joint estimation and identification algorithm based on PSOPF-EM |
本文利用水平方向上的转弯机动非线性动态模型,仿真出一条蛇形机动轨迹[3].假设机动目标在1~80 s以Ω1=-1.5°/s作转弯运动,在k=81 s时转弯角速度突变为Ω2=2°/s作转弯运动,并持续到200 s.设置转弯角速度初始值为Ω0=-0.5°/s,采样周期T=1,q1=0.1 m2/s3,wk是零均值高斯白噪声,其协方差为Q.
| $ \mathit{\boldsymbol{Q}} = {\rm{diag}}\left( {{q_1}\mathit{\boldsymbol{M}},{q_1}\mathit{\boldsymbol{M}}} \right),\mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {{T^3}/3}&{{T^2}/2}\\ {{T^2}/2}&T \end{array}} \right], $ |
载机雷达的非线性量测方程为
| $ {\mathit{\boldsymbol{z}}_k} = \mathit{\boldsymbol{h}}\left( {{\mathit{\boldsymbol{x}}_k}} \right) + {\mathit{\boldsymbol{v}}_k} = \left[ \begin{array}{l} \sqrt {x_k^2 + y_k^2} \\ \arctan \left( {{y_k}/{x_k}} \right) \end{array} \right] + {\mathit{\boldsymbol{v}}_k}. $ |
量测噪声vk是采用两个高斯分布的加权和合成的闪烁噪声,具体参数设置如下:两个高斯分布均值均为0, 协方差分别为R1, k=[σ1, r2σ1, φ2],R2, k=[σ2, r2σ2, φ2]σ1, r=10 m,σ1, φ=
本文所提出的基于EM框架的联合估计与辨识算法和扩维法的初始状态以及协方差分别设置为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_0} = {{\left[ {\begin{array}{*{20}{c}} {10\;{\rm{km}}}&{0.3\;{\rm{km/s}}}&{10\;{\rm{km}}}&{0.3\;{\rm{km/s}}} \end{array}} \right]}^{\rm{T}}},}\\ {{\mathit{\boldsymbol{P}}_0} = {\rm{diag}}\left[ {\begin{array}{*{20}{c}} {100\;{{\rm{m}}^2}}&{10\;{{\rm{m}}^2}/{{\rm{s}}^2}}&{100\;{{\rm{m}}^2}}&{10\;{{\rm{m}}^2}/{{\rm{s}}^2}} \end{array}} \right].} \end{array} $ |
扩维法初始状态和协方差的设置如下:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}_0^a = {{\left[ {10\;{\rm{km}}\;{\rm{0}}{\rm{.3}}\;{\rm{km/s}}\;{\rm{10}}\;{\rm{km}}\;{\rm{0}}{\rm{.3}}\;{\rm{km/s}}\; - {\rm{0}}{\rm{.}}{{\rm{5}}^ \circ }{\rm{/s}}} \right]}^{\rm{T}}},}\\ {P_0^a = {\rm{diag}}\left[ {100\;{{\rm{m}}^2}\;10\;{{\rm{m}}^2}/{{\rm{s}}^2}\;100\;{{\rm{m}}^2}\;10\;{{\rm{m}}^2}/{{\rm{s}}^2}100\left( {{\rm{mrad/s}}} \right)} \right],} \end{array} $ |
为了评估分析本文提出的算法性能,首先将本文提出的算法与传统的扩维法进行对比分析.本文提出的联合估计与辨识算法采用采取滑动滞后窗口策略,即使用未来几拍的量测估计与辨识当前目标状态和转弯角速度,出于目标跟踪实时性的要求,在保证辨识和估计精度的基础上应选择较小的滑动滞后窗口长度,一般滑动滞后窗口选择为5,其最大迭代次数为5次,粒子数为100,标准的粒子滤波算法、带一步任意量测的PF算法以及带一步任意量测的PSO-PF算法粒子数均为1 000,量测任意延迟概率均为0.3,各执行50次蒙特卡洛仿真.图 6、7分别显示了上述两类方法对角速度辨识和目标状态估计的效果,从图 6、7中可以看出,本文提出的联合估计与辨识算法在角速度辨识和目标状态估计上比传统的扩维法误差小、精度高,也就是说本文提出的算法在使用了很少的粒子情况下仍然能够保证目标状态估计与角速度辨识的收敛性,确保估计与辨识的精度,究其原因主要有:1)本文提出的一步量测随机延迟条件下基于粒子群改进的粒子滤波与后向模拟粒子平滑算法的良好的收敛性使然.本文首先通过采用粒子群算法改进粒子采样过程,充分保持了采样粒子的多样性,改善了粒子滤波的估计效果,其次,后向模拟粒子平滑器本身具有优良的特性,即使在滤波效果较差的时候依然能够保持一定的收敛性和估计精度,这两点也就确保了在使用低粒子数条件下仍能维持一定的收敛性.从图 5可以看出,本文提出的PSOPF-EM算法主要包括粒子平滑和极大似然估计两个方面,极大似然估计的数据来源于粒子滤波与平滑的输出,稳定收敛的粒子滤波与平滑输出对与极大似然估计值的收敛性影响很大,在此次仿真当中,可以明显看出,本文提出的算法在粒子数量很少的情况下依然能够保持收敛且精度很高,反之,粒子平滑在使用了很少的粒子条件下仍然是收敛的,这间接验证了本文提出的粒子滤波与后向模拟粒子平滑算法的优越性;2)采用了闭环反馈的处理方式,通过E-step和M-step的反复迭代不断修正角速度辨识与目标状态估计的误差,从而提高了辨识与估计的精度.从图 6、7中还可以看出,当量测延迟概率为0.3时,基于粒子滤波的算法整体辨识与估计精度整体较带一步任意延迟量测的CKF算法高,但是,在闪烁噪声条件下,带一步任意延迟量测的CKF算法并没有发散,只是估计效果变差了,这主要是因为,本文采取的闪烁噪声是由两个零均值的高斯白噪声加权组成的,依然符合高斯分布,所以该算法才不至于发散,依然保持一定的收敛性.从图 6、7中依然可以看出本文提出的PSO-PF算法估计精度明显高于标准的粒子滤波算法和带一步任意量测延迟的粒子滤波算法,并且,带一步任意量测延迟的粒子滤波算法的估计精度远高于标准的粒子滤波,并且这种精度优势会随着延迟概率的增加越发明显,而标准的粒子滤波在量测延迟条件下会存在发散现象,并不适合该条件下的目标状态估计与角速度的辨识.
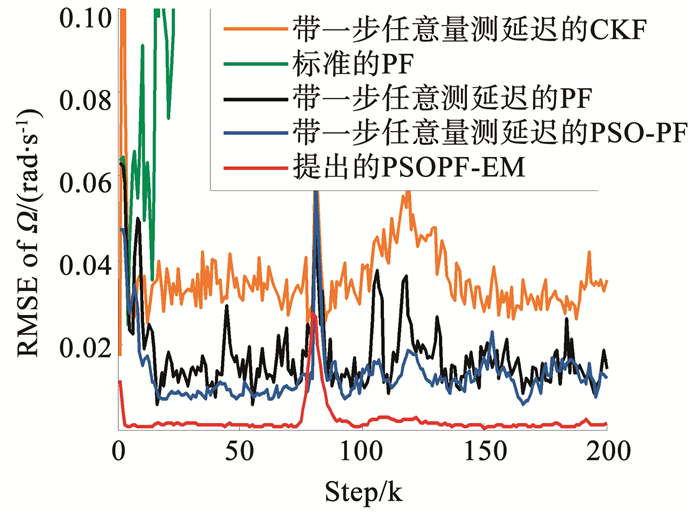
|
图 6 角速度辨识均方根误差 Fig. 6 RMSE of turn rate identification |
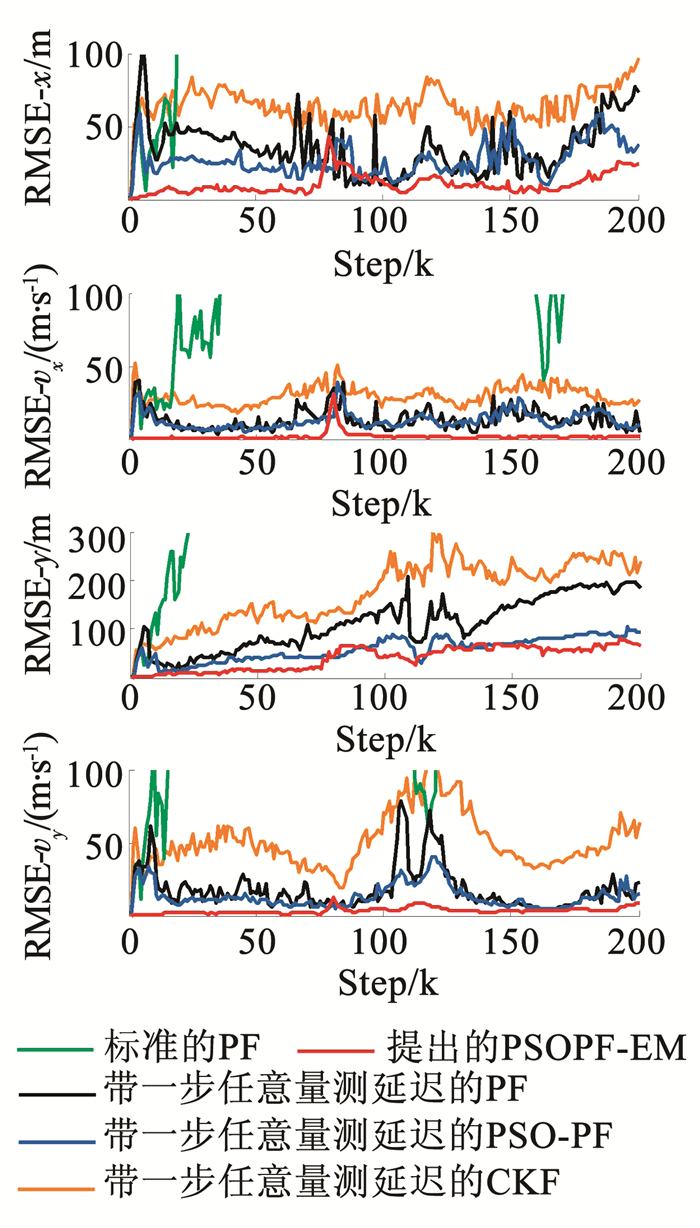
|
图 7 位置和速度估计均方根误差 Fig. 7 RMSE of position and velocity estimation |
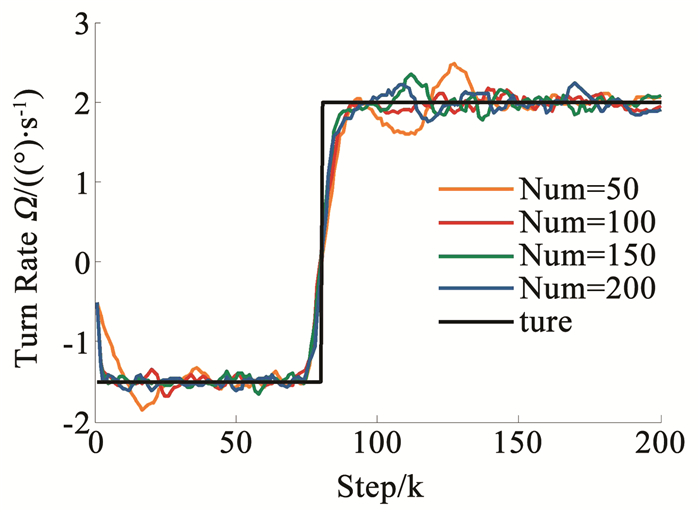
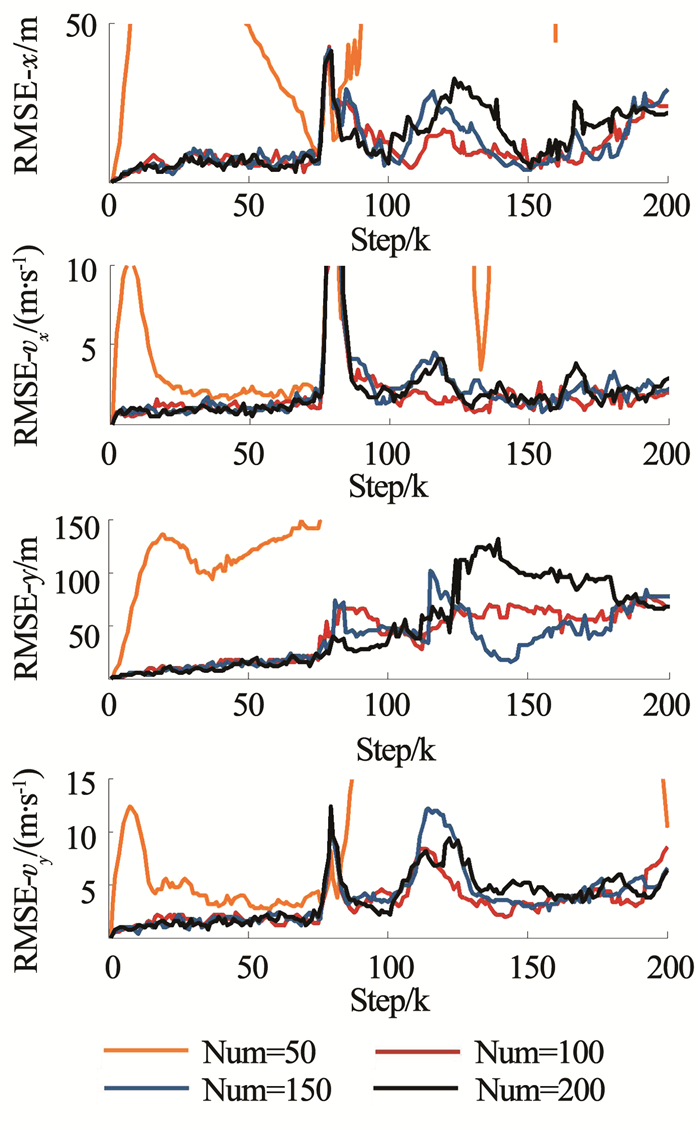
其次,从该算法的本身结构着手,对该算法进行评估分析.该算法主要包括:粒子滤波与粒子平滑算法以及极大似然估计的迭代寻优两个方面,也就是说本文提出的算法服从双收敛性,因此本文主要从粒子数量和EM算法最大迭代次数两个方面对该算法的性能进行评估分析.首先分析粒子数对算法性能的影响,粒子数分别为50、100、150、200,采取控制变量法的思想,最大迭代次数均为5次,滑动窗口均为5,各执行50次蒙特卡洛仿真如图 8所示.图 9为一次蒙特卡洛仿真转弯角速度的辨识结果,从图 9中可以看出,在蛇形机动第1阶段,当粒子数量100以上时,粒子数量对于转弯角度的辨识的收敛性以及辨识的精度影响不大,当角速度发生突变后,粒子数100以上的辨识结果也较为平稳,整体看来,当最大迭代次数为5,滞后窗口长度为5时,粒子数量维持在100以上,可以确保角速度辨识的精度以及稳定性.从图 9、10中可以发现当粒子数量低于100时,转弯角速度的辨识结果不稳定,存在发散的趋势,转弯角速度辨识与目标状态估计风险较大,图 11关于状态变量估计的均方根误差更能说明这一点.从图 11中可更加直观的看出粒子数位50时目标状态估计发散,当粒子数大于100时状态估计效果收敛且在蛇形机动第1阶段,粒子数量在目标状态估计精度方面的优势并没有体现出来,精度相差不大,当角速度发生突变后,发现粒子数量越大,状态估计的波动就越大,尤其在位置量y方向的均方根误差较为明显突出,但从整体看来,当粒子数量大于100时,发现粒子数量对于目标状态估计的精度影响不大,这是因为当粒子数量大于100时,本文提出的算法就已经能够保证辨识与估计收敛了,所以粒子数量对于精度的整体影响不大,但是从表 1还可以看出,粒子数越多,消耗的时间越长,从算法的时间成本以及估计与辨识的精度两方面综合考虑粒子数为100效果较好.
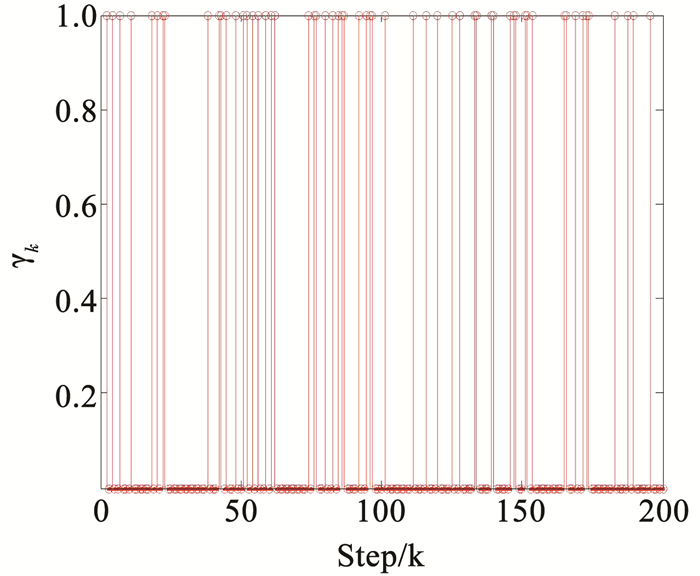
|
图 8 一次蒙特卡洛仿真随机变量γk的分布 Fig. 8 Distribution of random variables in a Monte Carlo simulation γk |
|
图 9 不同粒子数下角速度辨识结果 Fig. 9 The result of turn rate identification with different numbers of particles |

|
图 10 不同粒子数下角速度辨识均方根误差 Fig. 10 RMSE of turn rate identification with different numbers of particles |
|
图 11 不同粒子数下位置和速度估计均方根误差 Fig. 11 RMSE of position and velocity estimation with different numbers of particles |
| 表 1 计算k=60 s时的角速度和状态所耗费的时间 Tab. 1 Time cost for calculating the turn rate and states when k=60 s |
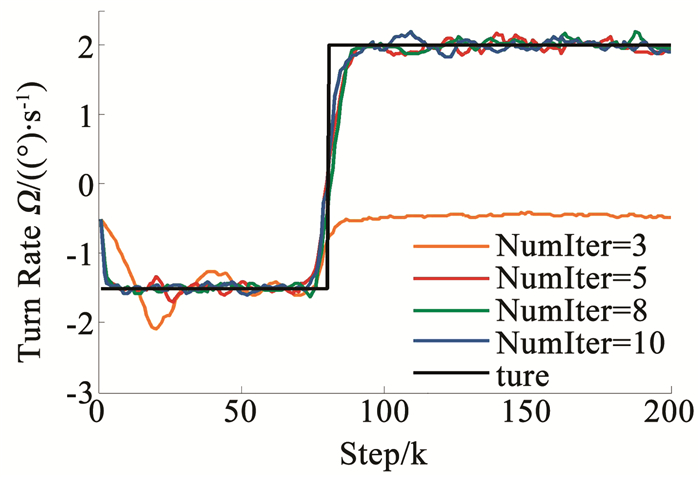
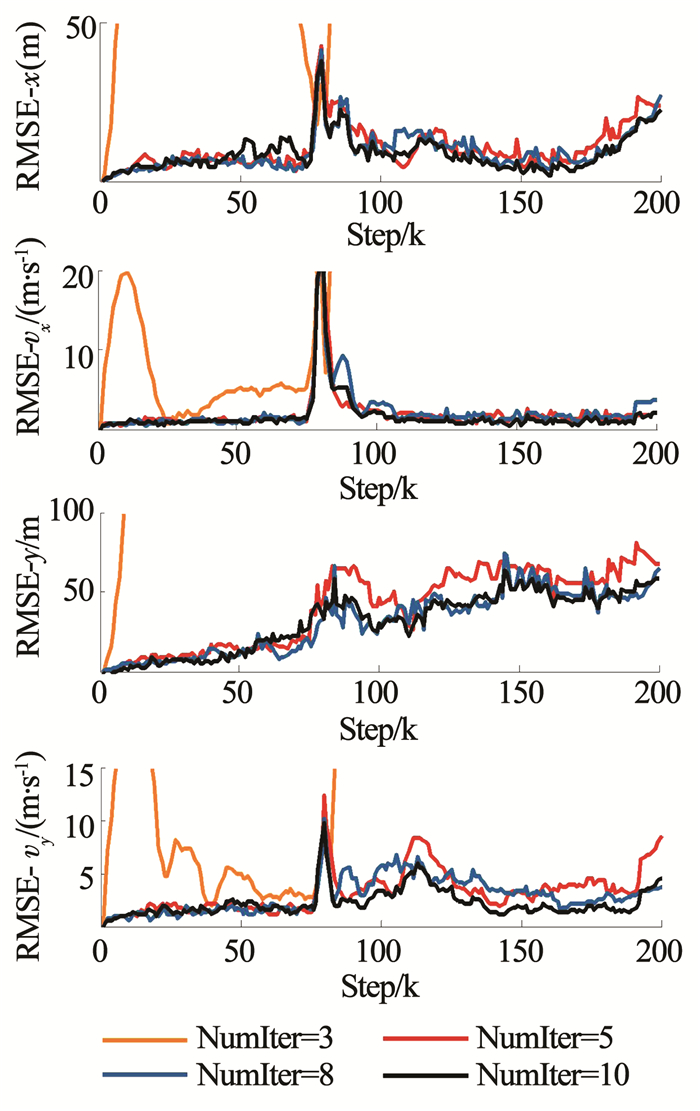
对于迭代次数而言,将窗口长度设置为5,最大迭代次数分别设置为3、5、8、10,各执行50次蒙特卡洛仿真.图 12为一次蒙特卡洛仿真转弯角速度的辨识结果,从图 12中可以看出,当迭代次数低于5时,该算法并不能保证转弯角速度辨识收敛,当迭代次数大于5时,随着迭代次数的增加,转弯角速度辨识的精度较高并且稳定,这一点在图 13中也得到了证实.从图 14还可以看出,目标状态4个分量的均方根误差随着迭代次数增加,逐渐减少,即该算法估计的目标状态整体精度就越高,尤其是当角速度发生突变之后,效果更加明显.但是从表 2显示的不同迭代次数下计算k=30 s时的角速度和状态所耗费的时间来看,随着迭代次数的增加,该算法的运算时间相应地就越长,结合图 13、14转弯角速度以及目标状态的均方根误差来看,当迭代次数大于5时,通过增加迭代次数带来的精度收益与算法运算时间成本来讲性价比不高,即当迭代次数大于5时,由迭代次数带来的精度效益远远比不上时间带来的损耗,降低该算法的实时性.
|
图 12 不同迭代次数下角速度辨识结果 Fig. 12 Result of turn rate identification with different iterations |

|
图 13 不同迭代次数下角速度辨识的均方根误差 Fig. 13 RMSE of turn rate identification with different iterations |
|
图 14 不同迭代次数下位置和速度估计均方根误差 Fig. 14 RMSE of position and velocity estimation with different iterations |
| 表 2 计算k=30 s时的角速度和状态所耗费的时间 Tab. 2 Time cost for calculating the turn rate and states when k=30 s |
1) 在E-step,通过充分考虑量测一步随机延迟特性及非高斯量测噪声,重构了粒子滤波算法中的粒子权重更新公式,并将拒绝采样思想引入到后向模拟粒子平滑器当中,并相应地设置拒绝采样终止条件,进一步优化了后向模拟粒子平滑器算法,提高了平滑算法的执行效率,然后采用改进的粒子滤波器与后向模拟粒子平滑器进一步获取目标状态的平滑估计.
2) 在M-step,通过采用数值优化算法极大化条件似然函数,从而获得转弯角速度的估计量,用于下一次算法迭代.通过E-step和M-step的不断迭代,进而获得转弯角速度的闭环形式的优化解,降低了辨识风险,提高了状态估计精度.
3) 仿真实验表明,在量测随机延迟及非高斯量测噪声条件下,本文提出的联合估计与辨识算法性能优于传统的扩维法.
| [1] |
郑昌艳, 梅卫, 冯小雨. 基于多时间窗口的空中目标机动模式提取及识别方法[J]. 探测与控制学报, 2016, 38(5): 81. ZHENG Changyan, MEI Wei, FENG Xiaoyu. Maneuvering pattern extraction and identification of air target based on multi-time-windows[J]. Journal of Detection & Control, 2016, 38(5): 81. |
| [2] |
卢春光, 周中良, 刘宏强, 等. 带异步相关噪声的战斗机蛇形机动跟踪算法[J]. 航空学报, 2018, 39(8): 322071. LU Chunguang, Zhou Zhongliang, Liu Hongqiang, et al. Algorithm for fighter zigzag maneuver target tracking with correlated noises at one epoch apart[J]. Acta Aeronautica ET Astronautica Sinica, 2018, 39(8): 322071. DOI:10.7527/S1000-6893.2018.22071 |
| [3] |
武华, 苏秀琴. 基于群广义直觉模糊软集的空袭目标威胁评估方法[J]. 控制与决策, 2015, 30(8): 1462. WU Hua, SU Xiuqin. Threat assessment of aerial targets based on group generalized intuitionistic fuzzy soft sets[J]. Control and Decision, 2015, 30(8): 1462. DOI:10.13195/j.kzyjc.2014.0529 |
| [4] |
ROTH M, HENDEBY G, GUSTAFSSON F. EKF/UKF maneuvering target tracking using coordinatd turn models with polar/Cartesian velocity[C]//Proceedings of the 17th International Conference on Information Fusion (FUSION). Salamanca, Spain: IEEE, 2014: 4 https://ieeexplore.ieee.org/document/6916122/
|
| [5] |
ARASARATNAM I, HAYKIN S. Cubature Kalman smoother[J]. IEEE Transaction on Automatic Control, 2009, 54(6): 1254. DOI:10.1109/TAC.2009.2019800 |
| [6] |
JIA Bin, XIN Ming, CHENG Yang. High-degree cubature Kalman filter[J]. Automatica, 2013, 49(2): 510. DOI:10.1016/j.automatica.2012.11.014 |
| [7] |
HUANG Yulong, ZHANG Yonggang. Design of high-degree student's t-based cubature filters[J]. Circuits Systems, and Signal Processing, 2018, 37(5): 2206. DOI:10.1007/s00034-017-0662-y |
| [8] |
黄伟平, 徐毓, 王杰. 基于改进"当前"统计模型的转弯机动跟踪算法[J]. 控制与决策, 2011, 26(9): 1412. HUANG Weiping, XU Yu, WANG Jie. Algorithm based on modified current statistic mode fo turn maneuver[J]. Control and Decision, 2011, 26(9): 1412. DOI:10.13195/j.cd.2011.09.135.huangwp.015 |
| [9] |
ZHU Lihua, CHENG Xianghong. High maneuver target tracking in coordinated turns[J]. IET Radar, Sonar & Navigation, 2015, 9(8): 1078. DOI:10.1049/iet-rsn.2014.0533 |
| [10] |
EFE M, ATHERTON D P. Maneuvering target tracking using adaptive turn rate models in the interacting multiple model algorithm[C]//Proceedings of the 35th IEEE Conference on Decision and Control. Piscataway, NJ: IEEE Press, 1996: 3151. DOI: 10.1109/CDC.1996.573613 https://ieeexplore.ieee.org/document/752274
|
| [11] |
YUAN Xianghui, HAN Chongzhao, DUAN Zhansheng, et al. Adaptive turn rate estimation using range rate measurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(4): 1532. DOI:10.1109/TAES.2006.314594 |
| [12] |
LIU Hongqiang, ZHOU Zhongliang, LU Chunguang, et al. Maneuvering detection using multiple parallel CUSUM detector[J]. Mathematical Problems in Engineering, 2018(5): 1. DOI:10.1155/2018/5062184 |
| [13] |
FRENCL V B, do Val JOÃO B R, Mendes R S, et al. Turn rate estimation using range rate measurements for fast manoeuvring tracking[J]. IET Radar, Sonar & Navigation, 2017, 11(7): 1099. DOI:10.1049/iet-rsn.2016.0467 |
| [14] |
卢春光, 周中良, 刘宏强, 等. 基于HCKS-EM的战斗机蛇形机动目标跟踪算法[J]. 北京航空航天大学学报, 2018, 44(9): 2004. LU Chunguang, Zhou Zhongliang, Liu Hongqiang, et al. Fighter zigzag maneuver target tracking algorithm using HCKS-EM[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(9): 2004. DOI:10.13700/j.bh.1001-5965.2018.0047 |
| [15] |
SHEN Bo, WANG Zidong, SHU Huisheng, et al. H-infinite filtering for nonlinear discrete-time stochastic systems with randomly varying sensor delays[J]. Automatica, 2008, 44(4): 1035. DOI:10.1016/j.automatica.2008.11.009 |
| [16] |
WANG Xiaoxu, LIANG Yan, PAN Quan, et al. Measurement random latency probability identification[J]. IEEE Transactions on Automatic Control, 2016, 61(12): 4210. DOI:10.1109/TAC.2015.2514259 |
| [17] |
KOSTANTINOS N P, DIMITRIS H. Advanced signal processing handbook[M]. Boca Raton, FL: CRC Press LLC, 2000.
|
| [18] |
刘望生, 李亚安. 闪烁噪声下目标跟踪的改进粒子滤波算法[J]. 兵工学报, 2011, 32(1): 91. LIU Wangsheng, LI Yaan. Target tracking based on modified particle filter algorithm in glint noise envirnoment[J]. ACTA Armamentarii, 2011, 32(1): 91. |
| [19] |
WANG Xiaoxu, LIANG Yan, PAN Quan, et al. Gaussian filter for nonlinear systems with one-step randomly deayed measurements[J]. Automatica, 2013, 49(4): 977. DOI:10.1016/j.automatica.2013.01.012 |
| [20] |
WILLS A, SCHON T B, LJUNG L, et al. Identification of Hammerstein-Wiener models[J]. Automatica, 2013, 49(1): 70. DOI:10.1016/j.automatica.2012.09.018 |
| [21] |
SCHON T B, WILLS A, NINNESS B. System identification of nonlinear state-space models[J]. Automatica, 2011, 47(1): 39. DOI:10.1016/j.automatica.2010.10.013 |
| [22] |
ARULAM M S, MAKSKELL S, GORDON N, et al. A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking[J]. IEEE Trans on Signal Processing, 2002, 50(2): 175. DOI:10.1109/78.978374 |
| [23] |
方正, 佟国峰, 徐心和. 粒子群优化粒子滤波方法[J]. 控制与决策, 2007, 22(3): 273. FANG Zheng, TONG Guofeng, XU Xinhe. Particle swarm optimized particle filter[J]. Control and Decision, 2007, 22(3): 273. DOI:10.3321/j.issn:1001-0920.2007.03.007 |
| [24] |
陈志敏, 薄煜明, 吴盘龙, 等. 基于自适应粒子群优化的新型粒子滤波在目标跟踪中的应用[J]. 控制与决策, 2013, 28(2): 193. CHEN Zhimin, BO Yuming, WU Panlong, et al. Novel particle filter algorithm based on adaptive particle swarm optimization and its application to radar target tracking[J]. Control and Decision, 2013, 28(2): 193. DOI:10.13195/j.cd.2013.02.36.chenzhm.018 |
| [25] |
LINDSTEN F, SCHON T B. Backward simulation methods for monte carlo statistical inference[M]. Hanover, MA: Now Publishers Inc., 2013.
|
| [26] |
GODSILL S J, DOUCET A, WEST M. Monte Carlo smoothing for nonlinear times series[J]. Journal of the American Statistical Association, 2004, 99(465): 156. DOI:10.1198/016214504000000151 |
| [27] |
LINDSTEN F. Particle filters and Markov chains for learning of dynamical systems[D]. Linköping, Sweden: Linköping University, 2013: 50
|
| [28] |
DOUC R, GARIVIER A, MOULINES E, et al. Sequential Monte Carlo smoothing for general state space hidden Markov models[J]. The Annals of Applied Probability, 2011, 21(6): 2109. DOI:10.1214/10-AAP735 |
 2019, Vol. 51
2019, Vol. 51


