2. 西北工业大学 航天学院,西安 710072;
3. 哈尔滨工业大学 航天学院,哈尔滨 150080
2. School of Astronautics, Northwestern Polytechnical University, Xi'an 710072, China;
3. School of Astronautics, Harbin Institute of Technology, Harbin 150080, China
高超声速飞行器是指一类飞行速度超过5Ma的未来新型航天飞行器,由于具有飞行速度快、突防能力强、全球快速响应等优势,在未来军事、政治、经济上都具有十分重要的战略地位,是世界上各军事强国的关注焦点[1-2].由于高超声速飞行器具有快时变、强耦合、强非线性等特点,其飞行控制系统的设计极具挑战性,近些年在飞行器控制领域受到了广泛的关注[3-4].文献[5]采用高阶滑模技术和神经网络设计动态状态反馈控制器,对速度和高度的参考轨迹进行稳定跟踪,并基于Lyapunov定理验证闭环系统的稳定性和系统输出的收敛性.文献[6]提出了一类滑模观测器和动态面结合的控制律设计方法,用滑模观测器预测难以测量的攻角和航迹倾角,根据预测结果设计了基于反步法的动态面控制律,以避免因系统的阶次增加,对虚拟控制反复求导所造成的“计算膨胀”现象,使飞行器精确跟踪参考轨迹.文献[7]提出了一种自适应滑模容错控制方法,以解决高超声速飞行器在存在未知外部干扰下快速姿态跟踪问题,对故障系统分别设计外环、内环容错控制器,通过更新参数的自适应方法以实现内环控制.上述结果都是通过将滑模控制方法应用于飞行器稳定跟踪控制.但是,一般是针对无限时间进行的控制方法研究,并未考虑在一个限定的时间内收敛于指定的跟踪误差.但实际上,由于高超声速飞行器的飞行速度快,飞行时间有限,机动飞行时间很短,因此要求在短时间内尽快达到预期跟踪指标,故需进行有限时间控制方法研究.
文献[8]基于有限时间滑模控制技术提出了一种自适应的容错控制方法,采用自适应更新法估计不确定性的上限和执行器效率因子的最小值,在执行器发生故障的情况下,所提出的控制方法能够抑制系统的不确定性.文献[9]将速度控制和高度控制作为控制器设计的两个子系统,通过将非线性动态逆与有限时间控制技术结合应用于控制系统的设计,即首先设计有限时间控制器,使航迹倾角在有限时间内收敛到期望值,然后根据航迹倾角和高度的一一对应关系,使得高度迅速收敛到期望值.文献[10]在有限时间控制方法的基础上,考虑到大切换增益引起较大的抖动现象,提出了一种基于非线性扰动观测器的改进滑模控制方法,通过对前馈补偿的干扰估计,改进的滑模控制器可以在不牺牲干扰抑制性能的情况下使切换增益取较小的值.以上文献都对高超声速飞行器设计了有限时间的控制方法,控制效果较为明显,但是文献中所设计的滑动函数以及相应的控制律一般均较为复杂,且对于非线性系统,其相应公式的推导以及计算量较大,不易于控制系统实现.因此需要提出一类更为简单有效的高超声速飞行器有限时间控制器设计方法.
文献[11]将有限时间稳定性的概念扩展到LPV系统,通过设计参数依赖的状态反馈控制器,利用李雅普诺夫函数给出有限时间稳定性的充分条件.文献[12]基于线性时不变(LTI)系统的结果,将有限时间收敛的滑模控制方法推广至LPV系统,给出了使降阶滑模存在的线性矩阵不等式(LMI)约束的充分条件,并通过张量积变换求解LMI不等式.以上文献将LPV系统与有限时间控制相结合,通过LPV模型的转化,对系统的模型进行了简化,有效的降低了计算量.但是,文献中一般未考虑抖振现象对系统稳定性的影响.因此,需要对基于有限时间的LPV控制方法做进一步的研究.
文献[13]对一类二阶非线性高速飞行器提出了一种有限时间终端滑模控制方法,保证了跟踪误差在有限时间内趋近于原点,闭环系统对参数不确定具有较强的鲁棒性.本文对文献[13]中的方法进行了相应的改进,并将其应用于复杂的高超声速飞行器模型当中,同时针对以上文献中的主要问题,提出了一种基于有限时间时变滑模的LPV控制方法.首先,采用线性化的方法将高超声速飞行器的动力学非线性模型转化为一般化的LPV模型,为后续进行LPV控制奠定基础.然后,在不考虑存在外界扰动的情况下对飞行器进行状态反馈控制器设计,使得飞行器能够保持稳定飞行.再之,考虑到高超声速飞行器在机动飞行的过程中,易受到外界的扰动,单一状态反馈控制下系统振荡较强,通过选取一个特殊的滑动函数,提出了一种基于有限时间时变滑模的LPV控制方法.理论推导证明所提出的控制方法能够保证闭环系统中的所有信号都是有界的,且在预定的时间内可将状态量跟踪误差控制在零点的一个很小的领域范围内并有效降低系统的振荡.最后,仿真结果表明了所提出控制方法的有效性.
1 高超声速飞行器模型 1.1 高超声速飞行器的运动方程选取文献[14]中提出的高超声速飞行器的纵向飞行动态系统模型为本文的研究对象.在地面惯性坐标系下,高超声速飞行器的的纵向平面的运动方程表示如下:
| $ \left\{ \begin{array}{l} \dot v = \frac{{T\cos \alpha - D}}{m} - \frac{{\mu \sin \gamma }}{{{r^2}}},\\ \dot \gamma = \frac{{L + T\sin \alpha }}{{mV}} - \frac{{\left( {\mu - {v^2}r} \right)\cos \gamma }}{{vr}},\\ \dot \alpha = q - \dot \gamma ,\\ \dot h = v\sin \gamma ,\\ \dot q = \frac{{{M_{yy}}}}{{{I_{yy}}}}. \end{array} \right. $ | (1) |
式中:v、γ、h、α、q分别为高超声速飞行器的速度、航迹角、飞行高度、攻角和俯仰角速率;T、D、L、Myy分别为推力、阻力、升力、俯仰力矩;上述各力与力矩系数的表达式如下:
| $ \left\{ \begin{array}{l} L = \frac{1}{2}\rho {v^2}S{C_{\rm{L}}},\\ D = \frac{1}{2}\rho {v^2}S{C_{\rm{D}}},\\ T = \frac{1}{2}\rho {v^2}S{C_{\rm{T}}},\\ r = h + {R_{\rm{E}}},\\ {M_{yy}} = \frac{1}{2}\rho {v^2}S\bar c\left[ {{C_{\rm{M}}}\left( \alpha \right) + {C_{\rm{M}}}\left( {{\delta _{\rm{e}}}} \right) + {C_{\rm{M}}}\left( q \right)} \right]. \end{array} \right. $ | (2) |
式中:g、RE、ρ分别为万有引力常数,地球半径和大气密度;μ、m、Iyy分别为地球引力常量、飞行器质量、转动惯量;CL、CD、CT分别为升力系数、阻力系数与推力系数; CM(α)、CM(δe)、CM(q)分别为攻角力矩系数、升降舵力矩系数、俯仰力矩系数.
各气动力系数与力矩系数如下:
| $ \left\{ \begin{array}{l} {C_{\rm{L}}} = \alpha \left( {0.493 + \frac{{1.91}}{{{M_\alpha }}}} \right),\\ {C_{\rm{D}}} = 0.008\;2\left( {171{\alpha ^2} + 1.15\alpha + 2.0} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\left( {0.001\;2M_\alpha ^2 - 0.054{M_\alpha } + 1} \right),\\ {C_{\rm{T}}} = \left\{ \begin{array}{l} 38\left[ {1 - 164{{\left( {\alpha - \alpha o} \right)}^2}} \right]\left( {1 + \frac{{17}}{{{M_\alpha }}}} \right)\left( {10 + 0.15} \right)\eta ,\eta > 1;\\ 38\left[ {1 - 164{{\left( {\alpha - \alpha o} \right)}^2}} \right]\left( {1 + \frac{{17}}{{{M_\alpha }}}} \right)\left( {1 + 0.15} \right)\eta ,\eta < 1, \end{array} \right.\\ {C_{\rm{M}}}\left( \alpha \right) = {10^{ - 4}}\left( {0.06 - {{\rm{e}}^{ - {M_\alpha }/3}}} \right)\left( { - 2{\alpha ^2} + 120\alpha - 1} \right),\\ {C_{\rm{M}}}\left( q \right) = \frac{{\bar c}}{{2V}}q\left( { - 0.025{M_\alpha } + 1.37} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left( { - 0.002\;1{\alpha ^2} + 0.005\;3\alpha - 0.23} \right),\\ {C_{\rm{M}}}\left( {{\delta _{\rm{e}}}} \right) = 0.029\;2\left( {{\delta _{\rm{e}}} - \alpha } \right). \end{array} \right. $ | (3) |
式中,η、δe表示系统的输入量,分别为节流阀开度、升降舵偏角.
式(1)~式(3)中各力及其力矩系数和飞行器其他参数的详细信息详见文献[15].
1.2 建立LPV模型根据上述的高超声速飞行器运动方程和相关的力与力矩系数,采用雅可比线性化的方法,可以得到在平衡状态下的高超声速飞行器的LPV模型.
基于平衡状态工作点,对飞行器的动力学非线性模型(1)进行雅可比线性化,得到线性状态空间矩阵:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{\partial _v}{f_v}}&{{\partial _\gamma }{f_v}}&{{\partial _\alpha }{f_v}}&{{\partial _h}{f_v}}&{{\partial _q}{f_v}}\\ {{\partial _v}{f_\gamma }}&{{\partial _\gamma }{f_\gamma }}&{{\partial _\alpha }{f_\gamma }}&{{\partial _h}{f_\gamma }}&{{\partial _q}{f_\gamma }}\\ {{\partial _v}{f_\alpha }}&{{\partial _\gamma }{f_\alpha }}&{{\partial _\alpha }{f_\alpha }}&{{\partial _h}{f_\alpha }}&{{\partial _q}{f_\alpha }}\\ {{\partial _v}{f_h}}&{{\partial _\gamma }{f_h}}&{{\partial _\alpha }{f_h}}&{{\partial _h}{f_h}}&{{\partial _q}{f_h}}\\ {{\partial _v}{f_q}}&{{\partial _\gamma }{f_q}}&{{\partial _\alpha }{f_q}}&{{\partial _h}{f_q}}&{{\partial _q}{f_q}} \end{array}} \right], $ | (4) |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{\partial _\eta }{f_v}}&{{\partial _\delta }{f_v}}\\ {{\partial _\eta }{f_\gamma }}&{{\partial _\delta }{f_\gamma }}\\ {{\partial _\eta }{f_\alpha }}&{{\partial _\delta }{f_\alpha }}\\ {{\partial _\eta }{f_h}}&{{\partial _\delta }{f_h}}\\ {{\partial _\eta }{f_q}}&{{\partial _\delta }{f_q}} \end{array}} \right]. $ | (5) |
式中:$\partial y = \frac{\partial }{{\partial y}}, {\rm{ }}{f_y} = \dot y$.
由线性状态空间矩阵可得系统的LPV模型为:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot x}}\left( t \right) = \mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{\varphi }}\left( t \right)} \right)\mathit{\boldsymbol{x}}\left( t \right) + \mathit{\boldsymbol{B}}\left( {\mathit{\boldsymbol{\varphi }}\left( t \right)} \right)\mathit{\boldsymbol{u}}\left( t \right),}\\ {\mathit{\boldsymbol{y}}\left( t \right) = \mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{\varphi }}\left( t \right)} \right)\mathit{\boldsymbol{x}}\left( t \right).} \end{array} $ | (6) |
式中:x(t)∈ Rn为状态矢量;u(t)∈Rr为输入矢量;y(t)∈ Rm为输出矢量;φ(t) = [φ1(t), φ2(t), …, φN(t)]T∈ RN为时变的参数矢量.
存在外界扰动时,飞行器的LPV系统模型描述如下:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot x}}\left( t \right) = \mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{\varphi }}\left( t \right)} \right)\mathit{\boldsymbol{x}}\left( t \right) + \mathit{\boldsymbol{Bu}}\left( t \right) + \mathit{\boldsymbol{f}}\left( t \right),}\\ {\mathit{\boldsymbol{y}}\left( t \right) = \mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{\varphi }}\left( t \right)} \right)\mathit{\boldsymbol{x}}\left( t \right).} \end{array} $ | (7) |
注释1 加性干扰f(t)∈ Rn为考虑高超声速飞行器在机动飞行过程中受到某一外界扰动,满足|f(t)| < di,其中di为未知的标量,仅用于稳定分析.
2 控制器设计针对高超声速飞行器的状态空间模型(6),求解其零极点并进行分析.由于存在一个含有正实部的极点,为系统的不稳定极点,对应了飞行器的不稳定模态[16].如果没有控制器对系统进行反馈控制,系统状态将会发散.所以首先需要设计状态反馈控制器uc(t) = K(φ)x(t),以保证飞行器能够稳定飞行.
则在高超声速飞行器机动过程中,控制律为
| $ {\mathit{\boldsymbol{u}}_{\rm{c}}}\left( t \right) = \mathit{\boldsymbol{Kx}}\left( t \right). $ | (8) |
注释2 为验证本文所设计的有限时间时变滑模控制器的有效性,不考虑LPV系统因参数的变化而引起的控制律的改变.即计算飞行器在机动飞行过程中某一平衡点处的状态反馈控制律,并假设这一段飞行过程整体的控制律也不随参数的改变而发生变化.
将式(8)带入式(6)可得:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot x}}\left( t \right) = \left( {\mathit{\boldsymbol{A}}\left( {\mathit{\boldsymbol{\varphi }}\left( t \right)} \right) + \mathit{\boldsymbol{B}}\left( {\mathit{\boldsymbol{\varphi }}\left( t \right)} \right)} \right)\mathit{\boldsymbol{Kx}}\left( t \right),}\\ {\mathit{\boldsymbol{y}}\left( t \right) = \mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{\varphi }}\left( t \right)} \right)\mathit{\boldsymbol{x}}\left( t \right).} \end{array} $ | (9) |
但是,若飞行器在机动飞行过程中受到一个外界扰动,采用传统的状态反馈控制方法会使系统保持稳定,但是闭环系统一般会存在较大的振荡,且传统的状态反馈控制律考虑的是无限时间系统稳定的情况,这与高超声速飞行器快速机动飞行的实际情况不相符,因此需要对飞行系统做进一步的控制律设计.本文设计一种基于有限时间时变滑模的LPV控制律u = uc+ uk(如图 1所示),其中uk为设计的有限时间时变滑模控制律.通过所设计的控制器,使得高超声速飞行器能有效降低系统的抖振现象,并在预定的时间内以预先设定的精度跟踪参考指令信号,并使闭环系统的所有状态量有界.

|
图 1 控制系统设计框图 Fig. 1 Block diagram of control system design |
定义状态量跟踪误差为
| $ \mathit{\boldsymbol{e}}\left( t \right) = \mathit{\boldsymbol{x}}\left( t \right) - {\mathit{\boldsymbol{x}}_{\rm{d}}}\left( t \right). $ | (10) |
式中:x ∈ Rn为系统实际输出的状态量,xd∈ Rn为参考指令信号.
选取一个滑动函数s(t)为
| $ \mathit{\boldsymbol{s}}\left( t \right) = \mathit{\boldsymbol{Ge}}\left( t \right) + \mathit{\boldsymbol{H}}\int_0^t {e\left( \tau \right){\rm{d}}\tau } - \mathit{\boldsymbol{w}}\left( t \right). $ | (11) |
式中:函数$\mathit{\boldsymbol{w}}\left(t \right) = \mathit{\boldsymbol{G\dot v}}\left(t \right) + \mathit{\boldsymbol{H\nu }}\left(t \right)$.其中:G ∈ Rr×n、H ∈ Rr×n分别为设计的矩阵;vi(t)为需要设计的函数,用于消除状态量跟踪误差的积累项.
注释3 传统的滑模控制方法,大多都含有复杂的非线性滑动函数$\mathit{\boldsymbol{s}} = \mathit{\boldsymbol{\dot e}} + \mathit{\boldsymbol{c}}{\mathit{\boldsymbol{e}}^{m/n}}$,且存在着奇异值的问题[17].本文所提出的时变滑动函数较为简单,无需进行复杂的指数型函数运算,且不存在奇异值的问题,从而简化了计算的过程.
下面,给出有限时间控制设计方法的一般条件[13].
条件1
1) vi(t)∈ C2[0, ∞);
2) 存在一个有限时间Tf,当t>Tf时,$\mathit{\boldsymbol{\dot v}}$ = 0.
3)$\mathit{\boldsymbol{\dot v}}$, $\mathit{\boldsymbol{\ddot v}} \in \mathit{\boldsymbol{L}}_\infty ^5$.
4) ${\mathit{\boldsymbol{\dot v}}}$(0) = e(0),v(0) = 0.
注释4 由条件1可得,在初始时刻,系统位于滑动函数上[18-19],即
| $ \mathit{\boldsymbol{s}}\left( 0 \right) = \mathit{\boldsymbol{Ge}}\left( 0 \right) - \mathit{\boldsymbol{w}}\left( 0 \right) = 0, $ | (12) |
由注释4可知,高超声速飞行器在跟踪指令信号机动飞行前,LPV系统(7)处于稳定状态.
定理1 设计如下控制律
| $ {\mathit{\boldsymbol{u}}_k} = {\left( {\mathit{\boldsymbol{GB}}} \right)^{ - 1}}\left[ {\mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\dot x}}}_{\rm{d}}} - \mathit{\boldsymbol{GAx}} - \mathit{\boldsymbol{He}} + \mathit{\boldsymbol{G\ddot v}} + \mathit{\boldsymbol{H\dot v}} - \mathit{\boldsymbol{k}}{\mathop{\rm sgn}} \left( s \right)} \right], $ | (13) |
其中:$k > {\left\| {\mathit{\boldsymbol{Gf}}\left(t \right)} \right\|_2} > 0$,且
| $ {\rm sgn}\left( s \right) = {\left[ {{\mathop{\rm sgn}} \left( {{s_1}} \right),{\mathop{\rm sgn}} \left( {{s_2}} \right), \cdots ,{\mathop{\rm sgn}} \left( {{s_n}} \right)} \right]^{\rm{T}}}, $ |
| $ {\rm sgn}\left( {{s_i}} \right) = \left\{ \begin{array}{l} 1,{s_i} > 0;\\ 0,{s_i} = 0;\left( {i = 1,2, \cdots ,n} \right)\\ - 1,{s_i} < 0. \end{array} \right. $ |
在控制律作用下,LPV系统(7)始终位于滑动函数上,即对∀t≥0, s(t)=0.
证明 选取李雅普诺夫函数如下
| $ \mathit{\boldsymbol{v}}\left( t \right) = \frac{1}{2}\mathit{\boldsymbol{s}}{\left( t \right)^{\rm{T}}}\mathit{\boldsymbol{s}}\left( t \right) \ge 0. $ | (14) |
对式(14)左、右两边同时求导,并带入式(7)、式(11)可得
| $ \begin{array}{l} \mathit{\boldsymbol{\dot v}}\left( t \right) = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {\mathit{\boldsymbol{G\dot e}} + \mathit{\boldsymbol{He}} - \mathit{\boldsymbol{G\ddot v}} - \mathit{\boldsymbol{H\dot v}}} \right) = \\ \;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\left[ {\mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{\dot x}} - {{\mathit{\boldsymbol{\dot x}}}_{\rm{d}}}} \right) + \mathit{\boldsymbol{He}} - \mathit{\boldsymbol{G\ddot v}} - \mathit{\boldsymbol{H\dot v}}} \right] = \\ \;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\left[ {\mathit{\boldsymbol{G}}\left( {\mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{u}}_k} + \mathit{\boldsymbol{f}}\left( t \right)} \right) - \mathit{\boldsymbol{G}}{{\mathit{\boldsymbol{\dot x}}}_{\rm{d}}} + \mathit{\boldsymbol{He}} - } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{G\ddot v}} - \mathit{\boldsymbol{H\dot v}}} \right] = {\mathit{\boldsymbol{s}}^{\rm{T}}}\left[ {\mathit{\boldsymbol{Gf}}\left( t \right) - \mathit{\boldsymbol{k}}{\mathop{\rm sgn}} \left( s \right)} \right] \le \\ \;\;\;\;\;\;\;\;\;{\left\| \mathit{\boldsymbol{s}} \right\|_2}{\left\| {\mathit{\boldsymbol{Gf}}\left( t \right)} \right\|_2} - \mathit{\boldsymbol{k}}{\left\| s \right\|_2} \le 0, \end{array} $ | (15) |
则${\mathit{\boldsymbol{\dot v}}}$ < 0.因此可证得v为正定函数,${\mathit{\boldsymbol{\dot v}}}$为负定函数.因s(0) = 0,由式(14)可得v(0) = 0.由${\mathit{\boldsymbol{\dot v}}}$ < 0易知v(t)的取值随时间t的增加而减小,且v(t)≥0,则
| $ \mathit{\boldsymbol{v}}\left( t \right) \equiv 0, $ | (16) |
式(16)等同于
| $ \mathit{\boldsymbol{s}}\left( t \right) \equiv 0. $ |
因此通过选取适当的正实数k,矩阵G、H与函数v(t),满足k >‖Gf(t)‖2>0,可使得闭环系统始终位于滑动模态之内,则定理1成立.证毕.
注释5 由式(10)、式(16)可知:
| $ \mathit{\boldsymbol{Ge}}\left( t \right) + \mathit{\boldsymbol{H}}\int_0^t {\mathit{\boldsymbol{e}}\left( t \right){\rm{d}}\tau } \equiv \mathit{\boldsymbol{w}}\left( t \right),\forall t \ge 0. $ | (17) |
由式(17)可知,状态量跟踪误差e(t)可由函数w(t)表示,即可通过设计函数w(t)来消除跟踪误差.
定理2 针对式(9)所示的LPV系统,采用式(11)的滑动函数,若控制律为(13),跟踪误差e(t)在有限时间内趋近于零.
证明 由滑动函数s(t)可得
| $ \begin{array}{l} \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{Ge}} + \mathit{\boldsymbol{H}}\int_0^t {\mathit{\boldsymbol{e}}{\rm{d}}\tau } - \mathit{\boldsymbol{w}} = \\ \;\;\;\;\;\mathit{\boldsymbol{Ge}} + \mathit{\boldsymbol{H}}\int_0^t {\mathit{\boldsymbol{e}}{\rm{d}}\tau } - \mathit{\boldsymbol{G\dot v}} - \mathit{\boldsymbol{Hv}} = \\ \;\;\;\;\;\mathit{\boldsymbol{G\dot \mu }} + \mathit{\boldsymbol{H\mu }}. \end{array} $ | (18) |
式中:$\mathit{\boldsymbol{\mu }}\left(t \right) = \int_0^t {\mathit{\boldsymbol{e}}\left(t \right){\rm{d}}\tau-\mathit{\boldsymbol{v}}(t)} $.由条件1可得$\mathit{\boldsymbol{\dot \mu }}\left(0 \right) = \mathit{\boldsymbol{\mu }}\left(0 \right) = 0$.因∀t≥0,s(t) = 0故可得∀t≥0,μ(t) = 0.则
| $ \int_0^t {\mathit{\boldsymbol{e}}\left( t \right){\rm{d}}\tau } \equiv \mathit{\boldsymbol{v}}\left( t \right), $ |
即
| $ \mathit{\boldsymbol{e}}\left( t \right) \equiv \mathit{\boldsymbol{\dot v}}\left( t \right). $ |
由条件1可得∀t≥Tf, ${\mathit{\boldsymbol{\dot v}}}$(t)=0.则有
| $ \forall t \ge {T_f},\mathit{\boldsymbol{e}}\left( t \right) = 0, $ |
即跟踪误差e(t) = x(t)- xd(t)在Tf时间内趋近于0.证毕.
为有效缓解滑模运动的抖振,采用如下式所示的饱和函数sat(s)替换控制律(13)中的符号函数sgn(s),可得[20-21]
| $ {\rm{sat}}\left( {{\mathit{\boldsymbol{s}}_i}} \right) = \left\{ {\begin{array}{*{20}{c}} {{\mathop{\rm sgn}} \left( {{\mathit{\boldsymbol{s}}_i}} \right),}&{\left| {{\mathit{\boldsymbol{s}}_i}} \right| > {\mathit{\boldsymbol{\sigma }}_i};}\\ {\frac{{{\mathit{\boldsymbol{s}}_i}}}{{{\mathit{\boldsymbol{\sigma }}_i}}},}&{\left| {{\mathit{\boldsymbol{s}}_i}} \right| \le {\sigma _i},} \end{array}} \right. $ | (19) |
其中:
| $ {\rm{san}}\left( {{\mathit{\boldsymbol{s}}_i}} \right) = \left\{ \begin{array}{l} 1,{\mathit{\boldsymbol{s}}_i} > 0;\\ 0,{\mathit{\boldsymbol{s}}_i} = 0;\\ - 1,{\mathit{\boldsymbol{s}}_i} < 0, \end{array} \right. $ |
| $ {\sigma _i} > 0,i = 1,2, \cdots ,n. $ |
推论1 通过设计的控制器,可将LPV系统(7)的状态量跟踪误差|e(t)|在预定时间Tf内趋近于零点的一个很小的领域范围内,且状态量均有界.即当∀t≥Tf时:
| $ \left| {{e_i}\left( t \right)} \right| \le \frac{{{\mathit{\boldsymbol{\sigma }}_i}}}{{{\mathit{\boldsymbol{g}}_i}}}, $ |
| $ \left| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_{id}}} \right| < {\mathit{\boldsymbol{\varepsilon }}_i}, $ |
式中εi为任意一个常数,满足εi >0,且$\frac{{{\mathit{\boldsymbol{\sigma }}_i}}}{{{\mathit{\boldsymbol{g}}_i}}} < {\mathit{\boldsymbol{\varepsilon }}_i}$.
证明由式(15)、式(19)可知,当|si| ≥ σi时,${\mathit{\boldsymbol{\dot v}}}$ < 0.结合式(12)易得当t≥0时,|si(t)| ≤ σi.
由式(18)得${\mathit{\boldsymbol{s}}_i} = {\mathit{\boldsymbol{g}}_i}{{\mathit{\boldsymbol{\dot \mu }}}_i} + {\mathit{\boldsymbol{h}}_i}{\mathit{\boldsymbol{\mu }}_i}$,即
| $ {{\mathit{\boldsymbol{\dot \mu }}}_i} = - \frac{{{\mathit{\boldsymbol{h}}_i}}}{{{\mathit{\boldsymbol{g}}_i}}}\mathit{\boldsymbol{\mu }}\frac{{{\mathit{\boldsymbol{s}}_i}}}{{{\mathit{\boldsymbol{g}}_i}}} + \frac{{{\mathit{\boldsymbol{s}}_i}}}{{{\mathit{\boldsymbol{g}}_i}}}, $ |
故有
| $ \left| {{{\mathit{\boldsymbol{\dot \mu }}}_i}} \right| = \left| {\frac{{{\mathit{\boldsymbol{s}}_i}}}{{{\mathit{\boldsymbol{g}}_i}}}} \right| \le \frac{{{\mathit{\boldsymbol{\sigma }}_i}}}{{{\mathit{\boldsymbol{g}}_i}}}. $ |
当t>Tf时,${\mathit{\boldsymbol{\dot v}}}$(t) = 0,则
| $ {\mathit{\boldsymbol{e}}_i}\left( t \right) = {{\mathit{\boldsymbol{\dot \mu }}}_i}\left( t \right) + {{\mathit{\boldsymbol{\dot v}}}_i}\left( t \right) = {{\mathit{\boldsymbol{\dot \mu }}}_i}\left( t \right). $ | (20) |
由式(20)易知状态量误差e是有界的,则由式(11)、式(18)得s与w有界,故由式(10)易得
| $ \left| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_{id}}} \right| \le \frac{{{\mathit{\boldsymbol{\sigma }}_i}}}{{{\mathit{\boldsymbol{g}}_i}}} < {\mathit{\boldsymbol{\varepsilon }}_i}, $ |
即x与${\mathit{\boldsymbol{\dot x}}}$有界.证毕.
3 数值仿真对式(6)、(7)所示的高超声速飞行器模型,假设飞行器在5 s时接收到阶跃指令,做加速爬升机动飞行,由平衡状态v0 = 4 000 m/s,α0 = 0.978°,γ0 = 0°,h0 = 25 km, q0 = 0°/s,变化为平衡状态vd = 4 525.6 m/s,αd = 0.978°,γd = 0°,hd = 30 km,qd = 0°/s.
由式(4)、(5)解得其LPV系统状态空间矩阵为:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}\\ {{a_{21}}}&{{a_{22}}} \end{array}} \right], $ |
| $ {a_{11}} = \left[ {\begin{array}{*{20}{c}} { - 1.422\;5 \times {{10}^{ - 13}}}&{\frac{{ - 4.084\;5e + 14}}{{{{\left( {6\;401\;000 - {\varphi _2}} \right)}^2}}}}&{ - 16.64}\\ {9.734\;6 \times {{10}^{ - 7}}}&0&{\frac{{392.82}}{{4\;525.6 - {\varphi _1}}}}\\ { - 9.734\;6 \times {{10}^{ - 7}}}&0&{ - \frac{{392.82}}{{4\;525.6 - {\varphi _1}}}} \end{array}} \right], $ |
| $ {a_{12}} = \left[ {\begin{array}{*{20}{c}} \begin{array}{l} 0\\ 5.862\;5 \times {10^{ - 10}}\\ 5.862\;5 \times {10^{ - 10}} \end{array}&\begin{array}{l} 0\\ 0\\ 1 \end{array} \end{array}} \right],{a_{22}} = \left[ {\begin{array}{*{20}{c}} 0&0\\ 0&{ - 0.076\;3} \end{array}} \right], $ |
| $ {a_{21}} = \left[ {\begin{array}{*{20}{c}} \begin{array}{l} - 1.664\;5 \times {10^{ - 16}}\\ 1.221\;4 \times {10^{ - 6}} \end{array}&\begin{array}{l} 4\;525.6 - {\varphi _1}\\ 0 \end{array}&\begin{array}{l} 0\\ 0.780\;3 \end{array} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {16.219}&0\\ {6.118\;1 \times {{10}^{ - 5}}}&0\\ { - 6.118\;1 \times {{10}^{ - 5}}}&0\\ 0&0\\ 0&{3.661\;9} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0\\ 0&0&0&1&0 \end{array}} \right],\mathit{\boldsymbol{D}} = \left[ 0 \right]. $ |
式中:φ1、φ2分别为两个平衡位置处的速度与高度值.
采用文献[22]中的方法对高超声速飞行器在平衡点vd = 4 525.6 m/s,αd = 0.978°,γd = 0°,hd = 30 km,qd = 0°/s处设计模型参考控制器,保证飞行器能够稳定飞行.其计算得到控制器K的结果为
| $ \mathit{\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} {0.99}&{11.29}&{ - 0.76}&{0.010}&{ - 0.02}\\ { - 0.51}&{2\;024.17}&{39.21}&{0.998}&{4.71} \end{array}} \right]. $ |
注释6 考虑传统的滑动函数$\mathit{\boldsymbol{s}} = \mathit{\boldsymbol{\dot e}} + \mathit{\boldsymbol{ce}}$(c>0),对于一个典型的LPV系统,其状态量误差为e(t) = x(t)- xd(t),为证明构造的滑动模态存在且可达,需构建李雅普诺夫函数$\mathit{\boldsymbol{\dot v}}\left(t \right) = \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{s}} \ge 0$,等式左、右两边求导后,$\mathit{\boldsymbol{\dot v}}\left(t \right) = {\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\left({\mathit{\boldsymbol{\ddot e}} + \mathit{\boldsymbol{c\dot e}} + \mathit{\boldsymbol{v}}\left(t \right)} \right)$,其中v(t)为用于消除状态量跟踪误差的积累项而设计的函数.在此步骤中,需要求取$\mathit{\boldsymbol{\ddot e}} = \mathit{\boldsymbol{\ddot x}}\left(t \right)-{{\mathit{\boldsymbol{\ddot x}}}_{\rm{d}}}\left(t \right)$,而对于典型的LPV系统:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot x}}\left( t \right) = \mathit{\boldsymbol{A}}\left( {\varphi \left( t \right)} \right)\mathit{\boldsymbol{x}}\left( t \right) + \mathit{\boldsymbol{B}}\left( {\varphi \left( t \right)} \right)\mathit{\boldsymbol{u}}\left( t \right),}\\ {\mathit{\boldsymbol{y}}\left( t \right) = \mathit{\boldsymbol{C}}\left( {\varphi \left( t \right)} \right)\mathit{\boldsymbol{x}}\left( t \right),} \end{array} $ |
求取状态量x(t)的二阶微分是没有意义的.故本文考虑将设计的控制器与文献[22]中的控制方法进行对比仿真实验.
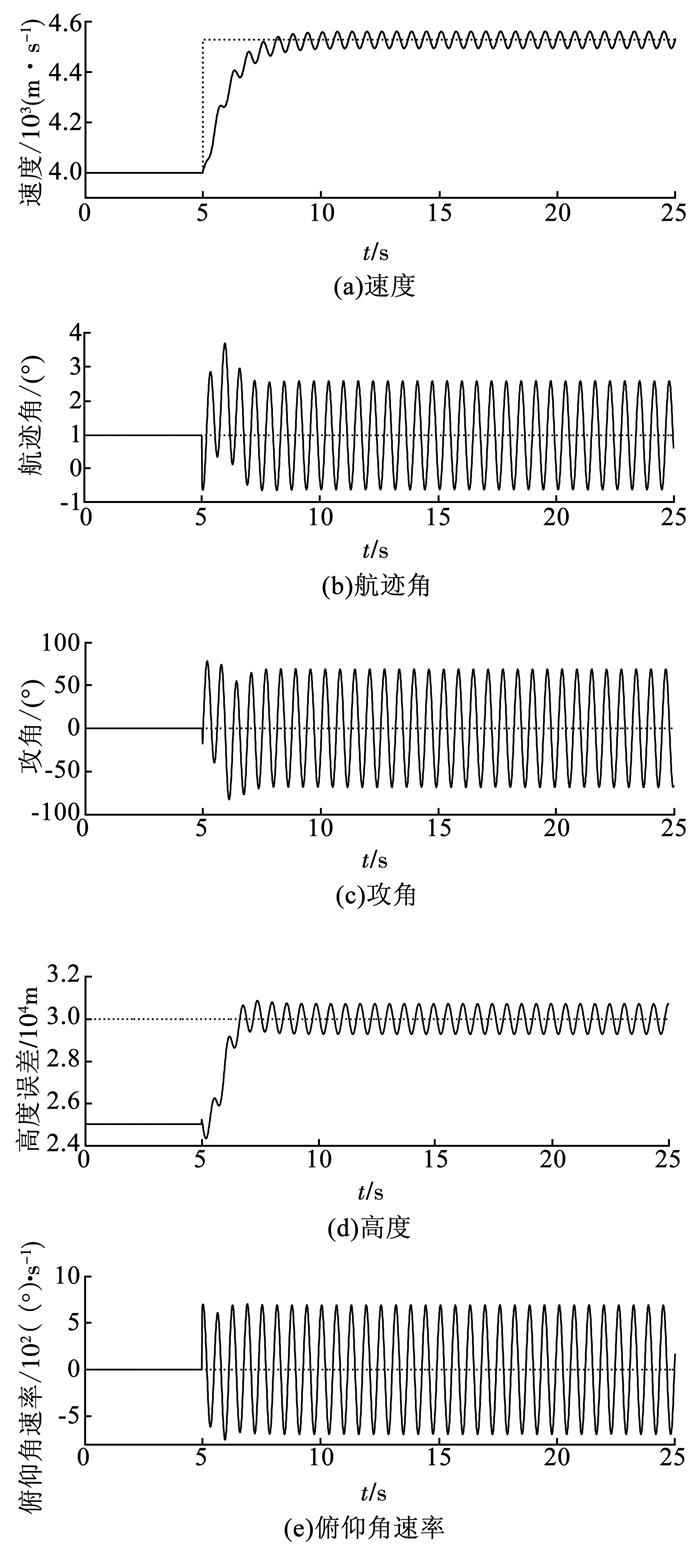
若飞行器在第5 s进行机动飞行,受到一个外界扰动信号f(t) = 10 sin(10t).此时指令信号的跟踪情况如图 2~3所示.
|
图 2 传统状态反馈下指令跟踪情况 Fig. 2 Instruction tracking under traditional state feedback |

|
图 3 传统状态反馈下控制量变化情况 Fig. 3 Change of control quantity under traditional state feedback |
由图 2、3中可以看出,在扰动信号作用下,系统仍旧可以保持稳定,但振荡非常严重,且控制输入超出了输入量的要求范围,(舵偏角:-25°≤δe≤25°,油门开度:0.1≤β≤1.0)即存在输入饱和,因此需要改进控制器设计方法.引入设计的有限时间时变滑模的控制方法来提高系统应对外界干扰的鲁棒性能,并引入饱和函数减小系统抖振.
现设计参数k = 500,$\mathit{\boldsymbol{G}} = \left[{\begin{array}{*{20}{c}} {25}&0&0&0&0\\ 0&0&0&0&{25} \end{array}} \right]$,$\mathit{\boldsymbol{H}} = \left[{\begin{array}{*{20}{c}} {{{10}^{-5}}}&0&0&0&0\\ 0&0&0&0&{{{10}^{-5}}} \end{array}} \right]$,σi = 1(i = 1, 2, …, 5),Tf = 5,
并将方程vi(t)设计为如下五次多项式的形式:
| $ {\mathit{\boldsymbol{v}}_i}\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {{a_{i0}} + {a_{i1}}t + {a_{i2}}{t^2} + {a_{i3}}{t^3} + {a_{i4}}{t^4} + {a_{i5}}{t^5},}&{0 \le t \le {T_f};}\\ {0,}&{t > {T_f},} \end{array}} \right. $ |
其中:
| $ {a_{i0}} = \int_0^t {{e_i}\left( 0 \right){\rm{d}}\tau } = 0,{a_{i1}} = {e_i}\left( 0 \right),{a_{i2}} = {{\dot e}_i}\left( 0 \right), $ |
| $ {a_{i3}} = - 4\left( {{e_i}\left( 0 \right)/T_f^2} \right) - 3\left( {{{\dot e}_i}\left( 0 \right)/{T_f}} \right), $ |
| $ {a_{i4}} = 3\left( {{e_i}\left( 0 \right)/T_f^3} \right) + 2\left( {{{\dot e}_i}\left( 0 \right)/T_f^2} \right), $ |
| $ {a_{i5}} = - 2\left( {{e_i}\left( 0 \right)/T_f^4} \right) - \left( {{e_i}\left( 0 \right)/T_f^3} \right). $ |
将高超声速飞行器机动飞行前平衡点处的初始状态量记为 x0,即
| $ {\mathit{\boldsymbol{x}}_0} = {\left[ {\begin{array}{*{20}{c}} {4\;000}&{0.978}&0&{25\;000}&0 \end{array}} \right]^{\rm{T}}}. $ |
将其机动飞行后平衡点处的状态量设为参考指令信号xd,即
| $ {\mathit{\boldsymbol{x}}_{\rm{d}}} = {\left[ {\begin{array}{*{20}{c}} {4\;525.6}&{0.978}&0&{30\;000}&0 \end{array}} \right]^{\rm{T}}}. $ |
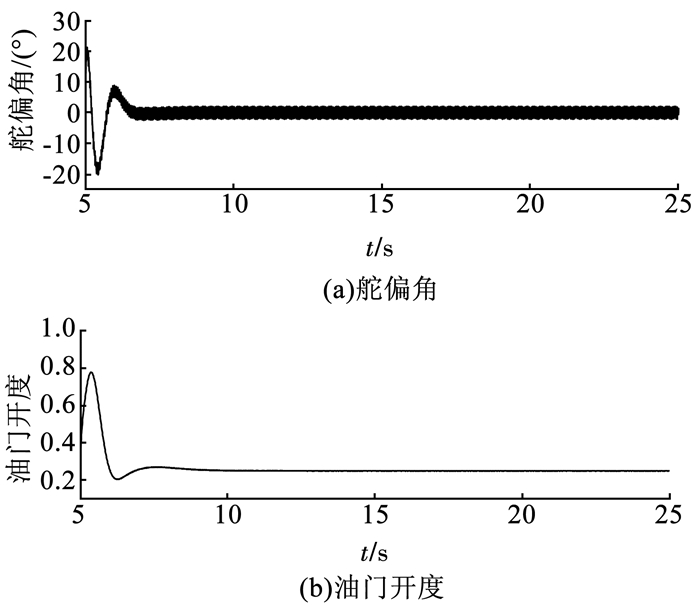
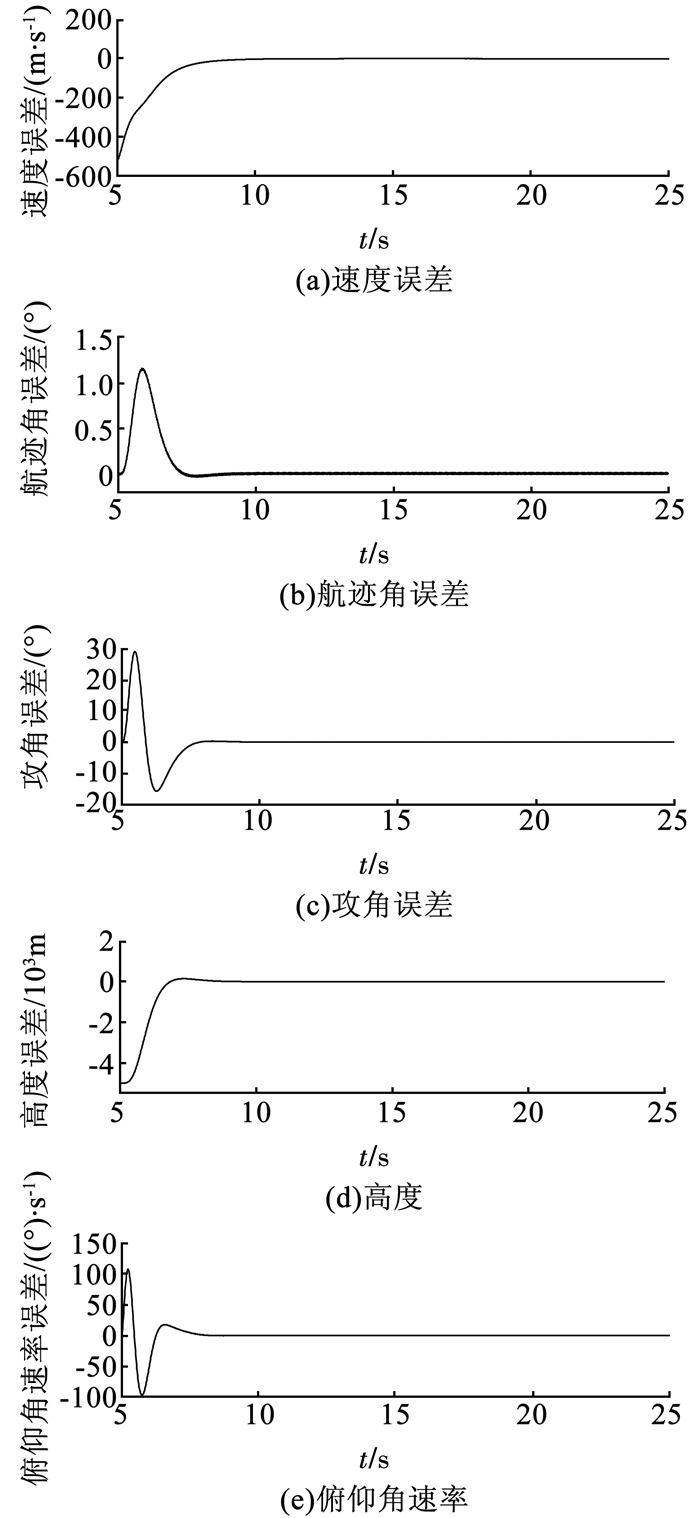
运用本文所设计的控制器,对高超声速飞行器在机动飞行过程中的指令跟踪情况进行数值仿真,仿真结果如图 4~6所示.

|
图 4 有限时间时变滑模控制器下指令跟踪情况 Fig. 4 Command tracking under a finite time variable sliding mode controller |
|
图 5 控制量变化情况 Fig. 5 Control quantity variation |
|
图 6 状态量误差变化情况 Fig. 6 Variation of state variable error |
图 4为在存在扰动时,采用本文所设计的控制方法,高超声速飞行器的指令信号跟踪情况.由图 4中可知,所有状态量均有界,能够克服外界的扰动保持稳定,具有较强的鲁棒性.在给定的有限时间Tf = 5内,系统的振荡被控制在较小的范围内,且能够稳定跟踪参考指令信号.图 5为高超声速飞行器控制量变化情况,执行器均在有效范围内.图 6为各状态量的跟踪误差变化情况,由图 6中可知,跟踪误差e(t)在给定的有限时间Tf = 5内趋于零点的一个很小的领域范围内.结合图 4~6可知,所设计的控制器能够有效克服外界的扰动,具有较强鲁棒性.可在有限时间内使系统保持稳定并降低系统的振荡,且具有良好的跟踪性能.
4 结论1) 设计了一种基于LPV系统的有限时间时变滑模的控制方法.通过选取一个平衡点建立高超声速飞行器的LPV模型,首先在不考虑外部扰动的情况下建立状态反馈控制器,保证飞行器稳定.当外部扰动存在的情况下,状态反馈控制器无法保证飞行器稳定的飞行,文中通过选取适当的滑动函数并设计控制律,建立了基于时变滑模方法的高超声速飞行器控制器.
2) 仿真结果表明,在存在外部干扰时,所设计的控制器能够抑制干扰,有效对指令信号进行稳定跟踪,具有较强的鲁棒性.并且闭环系统能够在预定的时间内收敛于指定的跟踪误差,使系统达到稳定.
3) 为验证所设计的有限时间时变滑模控制器的有效性,本文未考虑因参数的变化而引起的LPV系统控制律的改变.这对控制系统实现来说是不严谨的,在今后的工作中,拟考虑到因飞行参数的改变而引起的控制律的变化,进一步进行变参数的控制系统设计.
| [1] |
吴立刚, 安昊, 刘健行, 等. 吸气式高超声速飞行器控制的最新研究进展[J]. 哈尔滨工业大学学报, 2016, 48(10): 1. WU Ligang, AN Hao, LIU Jianxing, et al. Recent progress in control of air-breathing hypersonic vehicles[J]. Journal of Harbin Institute of Technology, 2016, 48(10): 1. DOI:10.11918/j.issn.0367-6234.2016.10.001 |
| [2] |
王勇, 张艳, 白辰, 等. 吸气式高超声速飞行器制导与控制方法综述[J]. 兵器装备工程学报, 2017, 38(4): 72. WANG Yong, ZHANG Yan, BAI Chen, et al. Review of guidance and control approaches for air-breathing hypersonic vehicle[J]. Journal of Ordnance Equipment Engineering, 2017, 38(4): 72. DOI:10.11809/scbgxb2017.04.016 |
| [3] |
刘鹏, 谷良贤. 高超声速飞行器动态输出反馈最优跟踪控制[J]. 哈尔滨工业大学学报, 2011, 43(7): 131. LIU Peng, GU Liangxian. Dynamic output feedback based optimal tracking for hypersonic flight vehicles[J]. Journal of Harbin Institute of Technology, 2011, 43(7): 131. DOI:10.11918/j.issn.0367-6234.2011.07.027 |
| [4] |
关欣, 赵静, 何友. 临近空间高超声速飞行器跟踪技术[J]. Journal of Sichuan Drdnance, 2011, 32(8): 4. GUAN Xin, ZHAO Jing, HE You. Track technology of hypersonic aircraft in near space[J]. Journal of Sichuan Ordnance, 2011, 32(8): 4. DOI:10.3969/j.issn.1006-0707.2011.08.002 |
| [5] |
ZHOU Hailiang, GAO Shun, RAN Yong, et al. Neural network high-order sliding mode control for a flexible air-breathing hypersonic flight vehicle[C]//Proceedings of the 30th Chinese Control and Decision Conference. Yinchuan, China: IEEE, 2016: 3035. DOI: 10.1109/CCDC.2016.7531502
|
| [6] |
GUO Yuyan, WANG Shixing, XU Bin, et al. Hypersonic vehicle longitudinal control based on sliding mode observer and dynamic surface control[C]//Proceedings of the 35th Chinese Control Conference. Chengdu, China: IEEE, 2016: 10926. DOI: 10.1109/ChiCC.2016.7555084
|
| [7] |
ZHAI Rongyu, QI Ruiyun, JIANG Bin. Adaptive sliding mode fault-tolerant control for hypersonic vehicle based on radial basis function neural networks[C]//Proceedings of the Chinese Control and Decision Conference (CCDC). Yinchuan, China: IEEE, 2016: 7531289. DOI: 10.1109/CCDC.2016.7531289.
|
| [8] |
WANG Jie, ZONG Qun, HE Xiao, et al. Adaptive finite-time control for a flexible hypersonic vehicle with actuator fault[J]. Mathematical Problems in Engineering, 2013, 2013(1): 1. DOI:10.1155/2013/920796 |
| [9] |
王钊, 李世华, 费树岷. 基于有限时间控制的高超声速飞行器控制律设计[J]. 东南大学学报(自然科学版), 2011, 41(5): 1024. WANG Zhao, LI Shihua, FEI Shumin. Control law design of hypersonic vehicle based on finite-time control[J]. Journal of Southeast University(Natural Science Edition), 2011, 41(5): 1024. DOI:10.3969/j.issn.1001-0505.2011.05.025 |
| [10] |
SUN Haibin, LI Shihua, SUN Changyin. Finite time integral sliding mode control of hypersonic vehicles[J]. Nonlinear Dynamics, 2013, 73(1/2): 229. DOI:10.1007/s11071-013-0780-4 |
| [11] |
HU Yanmei, DUAN Guangren, TAN Feng. Finite-time stability and stabilization of LPV systems[C]//Proceedings of the 35th Chinese Control Conference. Chengdu, China: IEEE, 2016: 1646. DOI: 10.1109/ChiCC.2016.7553327
|
| [12] |
WEN Nuan, LIU Zhenghua, SUN Yang, et al. Design of LPV-based sliding mode controller with finite time convergence for a morphing aircraft[J]. International Journal of Aerospace Engineering, 2017, 2017: 1. DOI:10.1155/2017/8426348 |
| [13] |
PARK K B, TSUJI T. Terminal sliding mode control of second-order nonlinear uncertain systems[J]. International Journal of Robust and Nonlinear Control: IFAC-Affiliated Journal, 1999, 9(11): 769. DOI:10.1002/(SICI)1099-1239(199909)9:11<769:AID-RNC435>3.0.CO;2-M |
| [14] |
PARKER J T, SERRANI A, YURKOVICH S, et al. Control-oriented modeling of an air-breathing hypersonic vehicle[J]. Journal of Guidance Control and Dynamics, 2016, 30(3): 856. DOI:10.2514/1.27830 |
| [15] |
SIGTHORSSON D O. Control-oriented modeling and output feedback control of hypersonic air-breathing vehicles[D]. Columbus: The Ohio State University, 2008
|
| [16] |
CAI Guangbin. Linear parameter-varying control for attitude control system of air-breathing hypersonic vehicle[D]. Xi'an: The Second Artillery Engineering University, 2012
|
| [17] |
PARK K B, LEE J J. Comments on "A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators"[J]. IEEE Transactions on Automatic Control, 1996, 41(5): 761. DOI:10.1109/9.489220 |
| [18] |
HOU Mingzhe, WANG Shitao, DUAN Guangren, et al. Practical finite-time control of missiles——a terminal sliding mode approach[C]//Proceedings of the 36th Chinese Control Conference. Dalian, China: IEEE, 2017: 1238. DOI: 10.23919/ChiCC.2017.8027519
|
| [19] |
CHOI S B, CHEONG C C, PARK D W. Moving switching surfaces for robust control of second-order variable structure systems[J]. International Journal of Control, 1993, 58(1): 229. DOI:10.1080/00207179308922999 |
| [20] |
CAI Ling, CHEN Fuyuan, Lu Feifei. Globe robust sliding mode tracking control for helicopter with input time delay[J]. Advanced Materials Research, 2014, 846: 434. DOI:10.4028/www.scientific.net/AMR.846-847.434 |
| [21] |
陈昌旭, 李洋, 祁琪, 等. 基于滑模变结构的导弹制导律设计[J]. 兵器装备工程学报, 2016, 37(12): 56. CHEN Changxu, LI Yang, QI Qi, et al. Missile guidance law design based on sliding mode[J]. Journal of Sichuan Ordnance, 2016, 37(12): 56. DOI:10.11809/scbgxb2016.12.014 |
| [22] |
ABDULLAH A, ZRIBI M. Model reference control of LPV systems[J]. Journal of the Franklin Institute, 2009, 346(9): 854. DOI:10.1016/j.jfranklin.2009.04.006 |
 2019, Vol. 51
2019, Vol. 51


