垂直/短距起降(vertical and/or short take-off and landing, V/STOL)飞机是对垂直起降(VTOL)和短距起飞/垂直降落(STOVL)固定翼飞机的统称.自20世纪40年代至今,诞生的各类V/STOL飞机型号达30余种[1-2].由于V/STOL飞机兼具旋翼和固定翼飞机的优势,既可以减少甚至摆脱对飞行跑道的依赖,又具备较大的飞行速度、航程、载荷和优异的机动性能;特别是近年来,随着美国第五代战斗机F-35B的陆续研发和服役,关于V/STOL飞机的研究越来越受到重视.
在确定V/STOL飞机总体设计方案的基础上,建立准确的飞机模型是对其飞行控制进行研究的基础和前提.鉴于V/STOL飞机设计与实现的技术复杂性[3],目前国内外关于其系统性建模方面的研究不多.早期,文献[4-5]针对一种“小角度偏转矢量发动机+升力喷管+升力风扇”方案的V/STOL飞机,分别建立了较为简单的矢量推力模型和空气动力模型,成为之后中国开展V/STOL飞机飞行控制研究的基础模型[6-7].文献[8]综合文献[4-5]的模型,给出了一种“小角度偏转矢量发动机+机腹喷管+引射器增升”方案的V/STOL飞机全状态动力学模型,并基于该模型开发了运动仿真器用于飞行控制研究.总的来说,上述模型考虑了V/STOL飞机特有的喷气诱导效应(jet-induced effect)和地面效应(ground effect)引起的空气动力学变化,一定程度上反映了V/STOL飞机的动力学特性,但却忽略了其在非常规飞行模式下可能出现的大迎角非线性和迟滞非定常特性,且在模型应用时往往将喷气诱导效应和地面效应的影响忽略,这在某些情况下是不得当的.
随着F-35B技术方案的日益成熟,近年来关于此类构型的V/STOL飞机研究不断增多.文献[9]在设计垂直起降控制律时,详细给出了此类飞机的推进系统模型,但模型中并没有反映出进气道气流量的变化对推进系统的影响问题;文献[10]则针对一种类似F-35B构型的V/STOL无人机,利用经验公式建立了悬停和过渡飞行模式的喷气诱导效应模型,但模型形式太过复杂,不易用于飞行控制的研究.文献[11]研究了一种梯形中单翼V/STOL无人机的大迎角非定常气动力特性,但忽略了其他非线性因素.此外,当前在研究V/STOL飞机的综合飞行控制问题时,通常采用的是类似CTOL(conventional take-off and landing)飞机的线性化六自由度数学模型[12-14],忽略的动力学特性更多.总之,现有的V/STOL飞机模型难以全面、准确地反映其在各种飞行模式下的动力学特点.
为此,本文针对现有V/STOL飞机模型的不足,以先进的“大范围偏转矢量发动机+升力风扇”型V/STOL飞机为研究对象,对其在推进系统和空气动力的联合作用下产生的力与力矩进行理论建模,推导其全状态六自由度非线性数学模型;然后对其特有的喷气诱导效应和地面效应所引起的动力学变化,及其非常规飞行模式下的迟滞非定常动力学特性进行仿真研究,为V/STOL飞机在不同飞行模式下的模型应用和飞行控制律设计提供依据.
1 V/STOL飞机概念模型本文研究的V/STOL飞机的气动布局为美国NASA某型STOVL验证机[4],采用单发动机、三角翼、鸭翼、双垂尾的布局形式,如图 1(a)所示.

|
图 1 升力风扇型V/STOL飞机概念方案 Fig. 1 Conceptual scheme of lift-fan V/STOL aircraft |
推进系统采用类似F-35B的设计方案,由一个轴驱动升力风扇和一个矢量发动机组成,具体形式如图 1(b)所示.矢量发动机尾喷管在飞机对称平面内可向下偏转0°~105°,同时可侧向偏转±12°,用于偏航控制;由发动机外涵道两侧引出两个姿态控制喷管至两翼根处,由压气机供气,用于滚转控制;由发动机低压涡轮驱动的升力风扇位于驾驶舱后方竖直安装,在对称平面内可偏转30°~105°,通过调节升力风扇与尾喷管之间的升力大小(偏转角度一定)可实现俯仰控制.因此,V/STOL飞机由常规气动舵面和推力矢量舵面共同操纵.
2 力与力矩模型 2.1 推进系统产生的力与力矩V/STOL飞机的推进系统可为非常规飞行模式提供直接升力和控制力矩,其产生的力除包含矢量尾喷管推力TCN、升力风扇推力TLF和左、右滚转控制喷管推力TLRN、TRRN外,还要考虑由主进气道、辅助进气道和升力风扇进气道的气体流量变化造成的推力损失TPI、TAI和TLFI,这在飞机飞行速度较快时影响显著.将上述各力在机体坐标系Oxbybzb下分解后叠加,可以得到由推进系统产生的纵向力Txb、侧向力Tyb和法向力Tzb表达式为
| $ \left\{ \begin{array}{l} {T_{{x_{\rm{b}}}}} = {T_{{\rm{C}}{{\rm{N}}_x}}} + {T_{{\rm{L}}{{\rm{F}}_x}}} + {T_{{\rm{P}}{{\rm{I}}_x}}} + {T_{{\rm{A}}{{\rm{I}}_x}}} + {T_{{\rm{LF}}{{\rm{I}}_x}}},\\ {T_{{y_{\rm{b}}}}} = {T_{{\rm{C}}{{\rm{N}}_y}}} + {T_{{\rm{P}}{{\rm{I}}_y}}} + {T_{{\rm{A}}{{\rm{I}}_y}}} + {T_{{\rm{LF}}{{\rm{I}}_y}}},\\ {T_{{z_{\rm{b}}}}} = {T_{{\rm{C}}{{\rm{N}}_z}}} + {T_{{\rm{L}}{{\rm{F}}_z}}} + {T_{{\rm{R}}{{\rm{N}}_z}}} + {T_{{\rm{P}}{{\rm{I}}_z}}} + {T_{{\rm{A}}{{\rm{I}}_z}}} + {T_{{\rm{LF}}{{\rm{I}}_z}}}, \end{array} \right. $ |
其中,各推力矢量产生的三轴分力分别为
| $ \left\{ \begin{array}{l} {T_{{\rm{C}}{{\rm{N}}_x}}} = {T_{{\rm{CN}}}}\cos {\delta _{{\rm{C}}{{\rm{N}}_y}}}\cos {\delta _{{\rm{CN}}}},\\ {T_{{\rm{C}}{{\rm{N}}_y}}} = {T_{{\rm{CN}}}}\sin {\delta _{{\rm{C}}{{\rm{N}}_y}}},\\ {T_{{\rm{C}}{{\rm{N}}_z}}} = - {T_{{\rm{CN}}}}\cos {\delta _{{\rm{C}}{{\rm{N}}_y}}}\sin {\delta _{{\rm{CN}}}},\\ {T_{{\rm{L}}{{\rm{F}}_x}}} = {T_{{\rm{LF}}}}\cos {\delta _{{\rm{LF}}}},\\ {T_{{\rm{L}}{{\rm{F}}_z}}} = - {T_{{\rm{LF}}}}\sin {\delta _{{\rm{LF}}}},\\ {T_{{\rm{R}}{{\rm{N}}_z}}} = - {T_{{\rm{LRN}}}} - {T_{{\rm{RRN}}}}, \end{array} \right. $ |
各进气道(XI∈{PI, AI, LFI})内、外流阻力造成的三轴推力损失分别为
| $ \left[ {\begin{array}{*{20}{c}} {{T_{{\rm{X}}{{\rm{I}}_x}}}}\\ {{T_{{\rm{X}}{{\rm{I}}_y}}}}\\ {{T_{{\rm{X}}{{\rm{I}}_z}}}} \end{array}} \right] = - {{\dot m}_{{\rm{XI}}}}\left\{ {\left[ {\begin{array}{*{20}{c}} u\\ v\\ w \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} p\\ q\\ r \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {{x_{{\rm{XI}}}}}\\ {{y_{{\rm{XI}}}}}\\ {{z_{{\rm{XI}}}}} \end{array}} \right]} \right\}. $ |
由各轴向力产生的滚转力矩lprop、俯仰力矩mprop和偏航力矩nprop的表达式分别为
| $ \left\{ \begin{array}{l} {l_{{\rm{prop}}}} = {l_{{\rm{RN}}}} + {l_{{\rm{PI}}}} + {l_{{\rm{AI}}}} + {l_{{\rm{LFI}}}},\\ {m_{{\rm{prop}}}} = {m_{{\rm{CN}}}} + {m_{{\rm{LF}}}} + {m_{{\rm{RN}}}} + {m_{{\rm{PI}}}} + {m_{{\rm{AI}}}} + {m_{{\rm{LFI}}}},\\ {n_{{\rm{prop}}}} = {n_{{\rm{CN}}}} + {n_{{\rm{PI}}}} + {n_{{\rm{AI}}}} + {n_{{\rm{LFI}}}}, \end{array} \right. $ |
其中,由各推力矢量偏转或推力转换而产生的控制力矩分别为
| $ \left\{ \begin{array}{l} {l_{{\rm{RN}}}} = - {T_{{\rm{RRN}}}}{y_{{\rm{RRN}}}} - {T_{{\rm{LRN}}}}{y_{{\rm{LRN}}}},\\ {m_{{\rm{CN}}}} = {T_{{\rm{C}}{{\rm{N}}_x}}}{z_{{\rm{CN}}}} - {T_{{\rm{C}}{{\rm{N}}_z}}}{x_{{\rm{CN}}}},\\ {m_{{\rm{LF}}}} = {T_{{\rm{L}}{{\rm{F}}_x}}}{z_{{\rm{LF}}}} - {T_{{\rm{L}}{{\rm{F}}_z}}}{x_{{\rm{LF}}}},\\ {m_{{\rm{RN}}}} = {T_{{\rm{LRN}}}}{x_{{\rm{RN}}}} + {T_{{\rm{RRN}}}}{x_{{\rm{RN}}}},\\ {n_{{\rm{CN}}}} = {T_{{\rm{C}}{{\rm{N}}_y}}}{x_{{\rm{CN}}}}, \end{array} \right. $ |
由各进气道推力损失引起的三轴力矩分别为
| $ \left\{ \begin{array}{l} {l_{{\rm{XI}}}} = - {T_{{\rm{X}}{{\rm{I}}_y}}}{z_{{\rm{XI}}}},\\ {m_{{\rm{XI}}}} = - {T_{{\rm{X}}{{\rm{I}}_z}}}{x_{{\rm{XI}}}} + {T_{{\rm{X}}{{\rm{I}}_x}}}{z_{{\rm{XI}}}},\\ {n_{{\rm{XI}}}} = {T_{{\rm{X}}{{\rm{I}}_y}}}{x_{{\rm{XI}}}}. \end{array} \right. $ |
式中:δCN、δCNy分别为矢量尾喷管纵向和侧向(左偏为正)偏转角; δLF为升力风扇偏转角;
相比于CTOL飞机,V/STOL飞机的气动力(即阻力D、侧力Y、升力L以及滚转力矩laero、俯仰力矩maero、偏航力矩naero)具有明显的非线性、非定常特性,主要原因在于:
1) V/STOL飞机在非常规飞行模式下以大迎角(α>10°)或低速飞行时,机体周围的复杂流场会使作用在飞机上的气动载荷呈现出较强的非线性、不对称、纵横向强耦合和时间迟滞等特性[11].
2) V/STOL飞机特有的大推力大范围偏转会产生喷气诱导效应[15-16],主要表现在:近地低速飞行时,向下的喷射气流会受到地面的阻隔,使矢量尾喷管和升力风扇之间的区域形成射流反射的“喷泉效应”,升力增加;其他区域受气流加速的影响形成“下吸效应”,造成较大的升力损失;过渡飞行时,喷射气流受对面来流的显著影响,会产生“射流卷积效应”,使飞机升力损失并产生抬头力矩.
3) V/STOL飞机在近地飞行时,除了推进系统的射流影响,地面还会影响空气绕飞机机体的流动特性,从而产生地面效应,其主要会对飞机的纵向通道造成扰动.
据此,可将气动力模型表示成如下的线性组合形式:
| $ \left\{ \begin{array}{l} D = {D_{{\rm{st}}}} + {D_{{\rm{unst}}}} + {D_{{\rm{GE}}}} = \bar qS\left( {{C_{{D_{{\rm{st}}}}}} + {C_{{D_{{\rm{unst}}}}}}} \right) + {D_{{\rm{GE}}}},\\ Y = {Y_{{\rm{st}}}} + {Y_{{\rm{unst}}}} = \bar qS\left( {{C_{{Y_{{\rm{st}}}}}} + {C_{{Y_{{\rm{unst}}}}}}} \right),\\ L = {L_{{\rm{st}}}} + {L_{{\rm{unst}}}} + {L_{{\rm{GE}}}} + {L_{{\rm{JIE}}}} = \bar qS\left( {{C_{{L_{{\rm{st}}}}}} + {C_{{L_{{\rm{unst}}}}}}} \right) + {L_{{\rm{GE}}}} + {L_{{\rm{JIE}}}}, \end{array} \right. $ | (1) |
| $ \left\{ \begin{array}{l} {l_{{\rm{aero}}}} = {l_{{\rm{st}}}} + {l_{{\rm{unst}}}} = \bar qSb\left( {{C_{{L_{{\rm{st}}}}}} + {C_{{L_{{\rm{unst}}}}}}} \right),\\ {m_{{\rm{aero}}}} = {m_{{\rm{st}}}} + {m_{{\rm{unst}}}} + {m_{{\rm{GE}}}} + {m_{{\rm{JIE}}}} = \bar qS\bar c\left( {{C_{{m_{{\rm{st}}}}}} + {C_{{m_{{\rm{unst}}}}}}} \right) + \\ \;\;\;\;\;\;\;\;\;{m_{{\rm{GE}}}} + {m_{{\rm{JIE}}}},\\ {n_{{\rm{aero}}}} = {n_{{\rm{st}}}} + {n_{{\rm{unst}}}} = \bar qSb\left( {{C_{{n_{{\rm{st}}}}}} + {C_{{n_{{\rm{unst}}}}}}} \right). \end{array} \right. $ | (2) |
式中:带有下标st、unst、GE和JIE的气动力分别为非线性定常、非线性非定常、地效诱导和喷气诱导气动力部分; C(省略下标)为各气动力定常/非定常系数; S为机翼面积; c、b分别为平均气动弦长和机翼展长; q = ρV2/2为空气动压,其中ρ为空气密度,V为空速.
2.2.1 非线性定常气动力模型考虑到V/STOL飞机的非线性气动力特性主要体现在其非常规飞行模式下,此时的飞行速度通常不大,因此可将式(1)、(2)中的定常气动力系数简化地表示成关于迎角α的非线性函数形式.这样,在仿真过程中这些非线性系数即可由α实时插值得到.即有
| $ \left\{ \begin{array}{l} {C_{{D_{{\rm{st}}}}}} = C_D^{{\delta _{\rm{c}}}}\left( \alpha \right){\delta _{\rm{c}}} + C_D^q\left( \alpha \right)\frac{{q\bar c}}{{2V}},\\ {C_{{Y_{{\rm{st}}}}}} = C_Y^{{\delta _{\rm{a}}}}\left( \alpha \right){\delta _{\rm{a}}} + C_Y^{{\delta _{\rm{r}}}}\left( \alpha \right){\delta _{\rm{r}}} + C_Y^p\left( \alpha \right)\frac{{pb}}{{2V}} + C_Y^r\left( \alpha \right)\frac{{rb}}{{2V}},\\ {C_{{L_{{\rm{st}}}}}} = C_L^{{\delta _{\rm{c}}}}\left( \alpha \right){\delta _{\rm{c}}} + C_L^q\left( \alpha \right)\frac{{q\bar c}}{{2V}} + + C_L^{\dot \alpha }\left( \alpha \right)\frac{{\dot \alpha \bar c}}{{2V}}, \end{array} \right. $ |
| $ \left\{ \begin{array}{l} {C_{{l_{{\rm{st}}}}}} = C_l^{{\delta _{\rm{r}}}}\left( \alpha \right){\delta _{\rm{r}}} + C_l^{{\delta _{\rm{a}}}}\left( \alpha \right){\delta _{\rm{a}}} + C_l^p\left( \alpha \right)\frac{{pb}}{{2V}} + C_l^r\left( \alpha \right)\frac{{rb}}{{2V}},\\ {C_{{m_{{\rm{st}}}}}} = C_m^{{\delta _{\rm{c}}}}\left( \alpha \right){\delta _{\rm{c}}} + C_m^q\left( \alpha \right)\frac{{q\bar c}}{{2V}} + C_m^{\dot \alpha }\left( \alpha \right)\frac{{\dot \alpha \bar c}}{{2V}},\\ {C_{{n_{{\rm{st}}}}}} = C_n^{{\delta _{\rm{r}}}}\left( \alpha \right){\delta _{\rm{r}}} + C_n^{{\delta _{\rm{a}}}}\left( \alpha \right){\delta _{\rm{a}}} + C_n^p\left( \alpha \right)\frac{{pb}}{{2V}} + C_n^r\left( \alpha \right)\frac{{rb}}{{2V}}, \end{array} \right. $ |
式中δc、δa、δr分别为鸭翼、副翼和方向舵偏转角.
2.2.2 地面效应和喷气诱导效应模型根据文献[5]给出的空气动力模型,经过简单变换可得地面效应模型:
| $ \left\{ \begin{array}{l} {D_{{\rm{GE}}}} = \bar qS{K_{{\rm{GE}}}}\left( h \right){C_{{D_{{\rm{GE}}}}}}\left( \alpha \right),\\ {L_{{\rm{GE}}}} = \bar qS{K_{{\rm{GE}}}}\left( h \right){C_{{L_{{\rm{GE}}}}}}\left( \alpha \right),\\ {m_{{\rm{GE}}}} = \bar qS\bar c{K_{{\rm{GE}}}}\left( h \right){C_{{m_{{\rm{GE}}}}}}\left( \alpha \right). \end{array} \right. $ | (3) |
式中:h为飞行高度; KGE(h)为地面效应洗出因子; CDGE(α)、CLGE(α)、CmGE(α)分别为地效诱导阻力、升力和俯仰力矩系数.
喷气诱导气动力的大小主要与喷管的大小、偏转角度、射流速度以及飞机的飞行速度和高度等因素有关.结合文献[5]的气动数据和文献[10]的经验公式,将上述影响因素融合并作归一化,统一地表示为喷气诱导气动力增量系数,进而可得喷气诱导效应模型:
| $ \left\{ \begin{array}{l} {L_{{\rm{JIE}}}} = T{C_{{L_{{\rm{JIE}}}}}},\\ {m_{{\rm{JIE}}}} = T{d_{\rm{e}}}{C_{{m_{{\rm{JIE}}}}}}, \end{array} \right. $ | (4) |
其中
| $ \left\{ \begin{array}{l} {C_{{L_{{\rm{JIE}}}}}} = {\left[ {{C_{{L_{{\rm{JIE}}}}}}\left( {{D_{\rm{e}}},{\delta _{{\rm{LF}}}},{V_{{\rm{e}},{\rm{LF}}}}} \right)} \right]_{{\rm{LF}}}} + \\ \;\;\;\;\;\;\;\;{\left[ {{C_{{L_{{\rm{JIE}}}}}}\left( {{D_{\rm{e}}},{\delta _{{\rm{CN}}}},{V_{{\rm{e}},{\rm{CN}}}}} \right)} \right]_{{\rm{CN}}}} + \\ \;\;\;\;\;\;\;\;{\left[ {{C_{{L_{{\rm{JIE}}}}}}\left( {{D_{\rm{e}}},{\delta _{{\rm{e}},{\rm{FT}}}},{V_{{\rm{e}},{\rm{FT}}}}} \right)} \right]_{{\rm{FT}}}},\\ {C_{{m_{{\rm{JIE}}}}}} = {\left[ {{C_{{m_{{\rm{JIE}}}}}}\left( {{D_{\rm{e}}},{\delta _{{\rm{LF}}}},{V_{{\rm{e}},{\rm{LF}}}}} \right)} \right]_{{\rm{LF}}}} + \\ \;\;\;\;\;\;\;\;{\left[ {{C_{{m_{{\rm{JIE}}}}}}\left( {{D_{\rm{e}}},{\delta _{{\rm{CN}}}},{V_{{\rm{e}},{\rm{CN}}}}} \right)} \right]_{{\rm{CN}}}} + \\ \;\;\;\;\;\;\;\;{\left[ {{C_{{m_{{\rm{JIE}}}}}}\left( {{D_{\rm{e}}},{\delta _{{\rm{e}},{\rm{FT}}}},{V_{{\rm{e}},{\rm{FT}}}}} \right)} \right]_{{\rm{FT}}}}. \end{array} \right. $ | (5) |
式中:CLJIE、CmJIE分别为量纲一的喷气诱导升力和俯仰力矩增量系数; T = TLF+TCN为升力风扇和矢量尾喷管的总推力; de为总的等效环流喷气直径; De = h/de为量纲一的高度; δe, FT为等效喷气角; Ve, LF、Ve, CN、Ve, FT分别为升力风扇、矢量尾喷管和“喷泉效应”的等效喷气速度比.
de、δe, FT、Ve, X(X∈{LF, CN, FT})可分别表示为
| $ \left\{ \begin{array}{l} {d_{\rm{e}}} = 2\sqrt {\left( {{A_{{\rm{LF}}}} + {A_{{\rm{CN}}}} + {A_{{\rm{FT}}}}} \right)/{\rm{ \mathsf{ π} }}} ,\\ {\delta _{{\rm{e}},{\rm{FT}}}} = \upsilon {\delta _{{\rm{LF}}}} + \left( {1 - \upsilon } \right){\delta _{{\rm{CN}}}},\\ {V_{{\rm{e,X}}}} = \sqrt {2{A_{\rm{X}}}\bar q/{T_{\rm{X}}}} . \end{array} \right. $ |
式中:AX、TX分别为相应喷气口的面积和推力; υ = TLF/T为推力比.
与文献[10]给出的模型相比,式(4)、(5)定义的喷气诱导效应模型结构形式简单,物理意义明确,可直观地表示成推力TCN和TLF(控制变量)的线性函数形式,便于飞行控制系统的设计.
2.2.3 非线性非定常气动力模型文献[11]已经给出了类似F-35B梯形翼的非定常气动力模型,本文借鉴其研究思路,以非定常升力系数CLunst为例,针对具有更强机动性能的三角翼V/STOL飞机,采用状态空间法来建立其非定常气动力模型.对于其他非定常气动力系数,同样可以采用如下类似方法得到.
文献[17]指出,三角翼飞机流场的非定常特性是由翼面前缘分离涡破裂点在翼弦上的位置变化所决定的,因此,可将非定常气动力系数表示成关于飞机运动状态和涡破裂点位置的函数.定义内部状态变量x∈[0, 1]为涡破裂点到机翼前缘的相对距离,x = 0对应于涡破裂点在机翼前缘,即完全破裂状态.该位置可用一个一阶微分方程来表征:
| $ {\tau _1}\frac{{{\rm{d}}x}}{{{\rm{d}}t}} + x = {x_0}\left( {\alpha - {\tau _2}\dot \alpha } \right). $ | (6) |
式中:τ1为表征非定常破裂发展过程的时间常数; τ2为表征由
| $ {x_0}\left( \alpha \right) = \frac{1}{{1 + {{\rm{e}}^{\sigma \left( {\alpha - {\alpha ^ * }} \right)}}}}. $ | (7) |
式中:σ为斜率因子,α*为定常状态下涡破裂点到达翼弦中点时的迎角.
然后利用考虑涡破裂的吸力比拟法,可将非定常升力系数写成
| $ {C_{{L_{{\rm{unst}}}}}}\left( {\alpha ,x} \right) = \frac{\lambda }{2}{\rm{ \mathsf{ π} }}\sin \alpha {\cos ^2}\alpha + {x^2}{\rm{ \mathsf{ π} si}}{{\rm{n}}^2}\alpha \cos \alpha , $ | (8) |
式中λ = b2/S为飞机展弦比.
式(6)~(8)即构成非定常气动力的封闭数学模型.
3 六自由度非线性数学模型为了得到符合客观事实又便于理论推导的V/STOL飞机六自由度非线性运动学和动力学模型,首先需要进行如下假设:
1) 地面为惯性坐标系Ogxgygzg,即忽略地球的自转运动以及地球质心的曲线运动;
2) 地面为平面,即忽略地球曲率;
3) 飞机为刚体,即忽略机身、机翼和尾翼的弹性自由度,且质量mF为常数;
4) 飞机关于xbOzb平面对称,有惯性积Ixy = Iyz = 0;
5) 重力加速度g、大气密度ρ不随飞行高度而变化;
6) 不考虑飞机上旋转部件(如发动机)产生的陀螺力矩.
3.1 动力学模型 3.1.1 飞机质心动力学方程假设飞机角速度矢量在Oxbybzb内的三轴分量表示为Ωb = [p q r]T,在气流坐标系Oxayaza内的三轴分量表示为Ωa = [pa qa ra]T,在航迹坐标系Oxkykzk内的三轴分量表示为Ωk = [pk qk rk]T,其中,Ωk为由绕地轴zg的航迹偏转角速度
| $ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{k}}} = \left[ {\begin{array}{*{20}{c}} {{p_{\rm{k}}}}\\ {{q_{\rm{k}}}}\\ {{r_{\rm{k}}}} \end{array}} \right] = \mathit{\boldsymbol{B}}_{\rm{g}}^{\rm{k}}\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {\dot \chi } \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ {\dot \gamma }\\ 0 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \dot \chi \sin \gamma }\\ {\dot \gamma }\\ {\dot \chi \cos \gamma } \end{array}} \right], $ | (9) |
式中Bij为从坐标系i到坐标系j的变换矩阵,下同.
在Oxkykzk下,飞机的质心运动矢量方程为
| $ {\mathit{\boldsymbol{F}}_{\rm{k}}} = {m_{\rm{F}}}\left( {\frac{{{\rm{d}}{\mathit{\boldsymbol{U}}_{\rm{k}}}}}{{{\rm{d}}t}} + {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_k} + {\mathit{\boldsymbol{U}}_{\rm{k}}}} \right), $ | (10) |
其中
| $ {\mathit{\boldsymbol{F}}_{\rm{k}}} = \left[ {\begin{array}{*{20}{c}} {{F_{{x_{\rm{k}}}}}}\\ {{F_{{y_{\rm{k}}}}}}\\ {{F_{{z_{\rm{k}}}}}} \end{array}} \right] = \mathit{\boldsymbol{B}}_{\rm{b}}^{\rm{k}}\left[ {\begin{array}{*{20}{c}} {{F_{{x_{\rm{b}}}}}}\\ {{F_{{y_{\rm{b}}}}}}\\ {{F_{{z_{\rm{b}}}}}} \end{array}} \right] + \mathit{\boldsymbol{B}}_{\rm{a}}^{\rm{k}}\left[ {\begin{array}{*{20}{c}} { - D}\\ Y\\ { - L} \end{array}} \right] + \mathit{\boldsymbol{B}}_{\rm{g}}^{\rm{k}}\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {{m_{\rm{F}}}g} \end{array}} \right], $ | (11) |
| $ {\mathit{\boldsymbol{U}}_{\rm{k}}} = {\left[ {\begin{array}{*{20}{c}} {{V_{\rm{k}}}}&0&0 \end{array}} \right]^{\rm{T}}}. $ | (12) |
将式(9)、式(11)和式(12)代入式(10),可推导出飞机质心动力学微分方程为
| $ \left\{ \begin{array}{l} {{\dot V}_{\rm{k}}} = \frac{1}{{{m_{\rm{F}}}}}\left( { - D + Y\sin \beta - {m_{\rm{F}}}g\sin \gamma } \right) + \frac{1}{{{m_{\rm{F}}}}}\left( {{T_{{x_{\rm{b}}}}}\cos \beta \cos \alpha + {T_{{y_{\rm{b}}}}}\sin \beta + {T_{{z_{\rm{b}}}}}\cos \beta \sin \alpha } \right),\\ \dot \chi = \frac{1}{{{m_{\rm{F}}}{V_{\rm{k}}}\cos \gamma }}\left( {L\sin \mu + Y\cos \mu \cos \beta } \right) + \frac{{{T_{{x_{\rm{b}}}}}}}{{{m_{\rm{F}}}{V_{\rm{k}}}\cos \gamma }}\left( {\sin \mu \sin \alpha - \cos \mu \sin \beta \cos \alpha } \right) + \\ \;\;\;\;\;\;\frac{{{T_{{y_{\rm{b}}}}}}}{{{m_{\rm{F}}}{V_{\rm{k}}}\cos \gamma }}\left( {\cos \mu \cos \beta } \right) - \frac{{{T_{{z_{\rm{b}}}}}}}{{{m_{\rm{F}}}{V_{\rm{k}}}\cos \gamma }}\left( {\sin \mu \cos \alpha + \cos \mu \sin \beta \sin \alpha } \right),\\ \dot \gamma = \frac{1}{{{m_{\rm{F}}}{V_{\rm{k}}}}}\left( {L\cos \mu - Y\sin \mu \cos \beta - {m_{\rm{F}}}g\cos \gamma } \right) + \frac{{{T_{{x_{\rm{b}}}}}}}{{{m_{\rm{F}}}{V_{\rm{k}}}}}\left( {\cos \mu \sin \alpha + \sin \mu \sin \beta \cos \alpha } \right) - \\ \;\;\;\;\;\;\frac{{{T_{{y_{\rm{b}}}}}}}{{{m_{\rm{F}}}{V_{\rm{k}}}}}\left( {\sin \mu \cos \beta } \right) + \frac{{{T_{{z_{\rm{b}}}}}}}{{{m_{\rm{F}}}{V_{\rm{k}}}}}\left( {\sin \mu \sin \beta \sin \alpha - \cos \mu \cos \alpha } \right). \end{array} \right. $ | (13) |
在Oxbybzb下,飞机的力矩矢量方程为
| $ {\mathit{\boldsymbol{M}}_{\rm{b}}} = \frac{{{\rm{d}}{\mathit{\boldsymbol{H}}_{\rm{b}}}}}{{{\rm{d}}t}} + {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{b}}} \times {\mathit{\boldsymbol{H}}_{\rm{b}}}, $ | (14) |
其中
| $ {\mathit{\boldsymbol{M}}_{\rm{b}}} = \left[ {\begin{array}{*{20}{c}} l\\ m\\ n \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{l_{{\rm{prop}}}}}\\ {{m_{{\rm{prop}}}}}\\ {{n_{{\rm{prop}}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{l_{{\rm{aero}}}}}\\ {{m_{{\rm{aero}}}}}\\ {{n_{{\rm{aero}}}}} \end{array}} \right]. $ | (15) |
角动量Hb取决于转动惯量矩阵I和角速度Ωb,即
| $ {\mathit{\boldsymbol{H}}_{\rm{b}}} = \mathit{\boldsymbol{I}} \cdot {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{b}}} = \left[ {\begin{array}{*{20}{c}} {{I_x}}&0&{ - {I_{xz}}}\\ 0&{{I_y}}&0\\ { - {I_{xz}}}&0&{{I_z}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} p\\ q\\ r \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{l_x}p - {I_{xz}}r}\\ {{l_y}q}\\ {{l_z}r - {I_{xz}}p} \end{array}} \right]. $ | (16) |
将式(15)、(16)代入式(14),可推导出飞机转动动力学微分方程为
| $ \left\{ \begin{array}{l} \dot p = {c_1}pq + {c_2}qr + {c_3}\left( {{l_{{\rm{prop}}}} + {l_{{\rm{aero}}}}} \right) + {c_4}\left( {{n_{{\rm{prop}}}} + {n_{{\rm{aero}}}}} \right),\\ \dot q = {c_5}pr + {c_6}\left( {{r^2} - {p^2}} \right) + {c_7}\left( {{m_{{\rm{prop}}}} + {m_{{\rm{aero}}}}} \right),\\ \dot r = {c_8}pq - {c_1}qr + {c_4}\left( {{l_{{\rm{prop}}}} + {l_{{\rm{aero}}}}} \right) + {c_9}\left( {{n_{{\rm{prop}}}} + {n_{{\rm{aero}}}}} \right), \end{array} \right. $ | (17) |
其中:
| $ {c_1} = \frac{{{I_{xz}}\left( {{I_x} - {I_y} + {I_z}} \right)}}{{{I_x}{I_z} - I_{xz}^2}},{c_2} = \frac{{{I_y}{I_z} - I_z^2I_{xz}^2}}{{{I_x}{I_z} - I_{xz}^2}}, $ |
| $ {c_3} = \frac{{{I_z}}}{{{I_x}{I_z} - I_{xz}^2}},{c_4} = \frac{{{I_{xz}}}}{{{I_x}{I_z} - I_{xz}^2}},{c_5} = \frac{{{I_z} - {I_x}}}{{{I_y}}}, $ |
| $ {c_6} = \frac{{{I_{xz}}}}{{{I_y}}},{c_7} = \frac{1}{{{I_y}}},{c_8} = \frac{{I_x^2 - {I_x}{I_y} + I_{xz}^2}}{{{I_x}{I_z} - I_{xz}^2}},{c_9} = \frac{{{I_x}}}{{{I_x}{I_z} - I_{xz}^2}}. $ |
通常,飞机的位置信息在Ogxgygzg下表示,假设飞机的位置为(xg, yg, zg),相应方向上的速度为(ug, vg, wg),根据运动学原理有
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {{x_{\rm{g}}}}\\ {{y_{\rm{g}}}}\\ {{z_{\rm{g}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{u_{\rm{g}}}}\\ {{v_{\rm{g}}}}\\ {{w_{\rm{g}}}} \end{array}} \right] = \mathit{\boldsymbol{B}}_{\rm{k}}^{\rm{g}}\left[ {\begin{array}{*{20}{c}} {{V_{\rm{k}}}}\\ 0\\ 0 \end{array}} \right], $ |
即
| $ \left\{ \begin{array}{l} {{\dot x}_{\rm{g}}} = {V_{\rm{k}}}\cos \gamma \cos \chi ,\\ {{\dot y}_{\rm{g}}} = {V_{\rm{k}}}\cos \gamma \sin \chi ,\\ {{\dot z}_{\rm{g}}} = - \dot h = - {V_{\rm{k}}}\sin \gamma . \end{array} \right. $ | (18) |
根据轴系之间的转换原理可知,Ωa与Ωb之间、Ωa与Ωk之间分别存在如下的对应关系:
| $ \left[ {\begin{array}{*{20}{c}} {{p_{\rm{a}}}}\\ {{q_{\rm{a}}}}\\ {{r_{\rm{a}}}} \end{array}} \right] = \mathit{\boldsymbol{B}}_{\rm{b}}^{\rm{g}}\left[ {\begin{array}{*{20}{c}} p\\ q\\ r \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {\dot \beta } \end{array}} \right] - \mathit{\boldsymbol{B}}_{\rm{b}}^{\rm{a}}\left[ {\begin{array}{*{20}{c}} 0\\ {\dot \alpha }\\ 0 \end{array}} \right], $ | (19) |
| $ \left[ {\begin{array}{*{20}{c}} {{p_{\rm{a}}}}\\ {{q_{\rm{a}}}}\\ {{r_{\rm{a}}}} \end{array}} \right] = \mathit{\boldsymbol{B}}_{\rm{k}}^{\rm{g}}\left[ {\begin{array}{*{20}{c}} {{p_{\rm{k}}}}\\ {{q_{\rm{k}}}}\\ {{r_{\rm{k}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\dot \mu }\\ 0\\ 0 \end{array}} \right]. $ | (20) |
联立式(19)、(20),并代入式(9)和式(13),可得到迎角α、侧滑角β和航迹滚转角μ的微分方程式(21).
式(13)、式(17)、式(18)和式(21)构成了V/STOL飞机的全状态六自由度非线性数学模型,与习惯在Oxbybzb下建立的飞机数学模型相比[8,12],更易直观反映V/STOL飞机在非常规飞行模式下的航迹变化情况,便于结合奇异摄动理论并应用非线性控制方法,进行飞行控制系统的设计与仿真.
| $ \left\{ \begin{array}{l} \dot \alpha = q - \tan \beta \left( {p\cos \alpha + r\sin \alpha } \right) + \frac{1}{{{m_{\rm{F}}}{V_{\rm{k}}}\cos \beta }}\left( { - L + {m_{\rm{F}}}g\cos \gamma \cos \mu } \right) + \frac{1}{{{m_{\rm{F}}}{V_{\rm{k}}}\cos \beta }}\left( { - {T_{{x_{\rm{b}}}}}\sin \alpha + {T_{{z_{\rm{b}}}}}\cos \alpha } \right),\\ \dot \beta = p\sin \alpha - r\cos \alpha + \frac{1}{{{m_{\rm{F}}}{V_{\rm{k}}}}}Y\cos \beta + \left. {{m_{\rm{F}}}g\cos \gamma \sin \mu } \right) + \frac{1}{{{m_{\rm{F}}}{V_{\rm{k}}}}}\left( { - {T_{{x_{\rm{b}}}}}\sin \beta \cos \alpha + {T_{{y_{\rm{b}}}}}\cos \beta - {T_{{z_{\rm{b}}}}}\sin \beta \sin \alpha } \right),\\ \dot \mu = \sec \beta \left( {p\cos \alpha + r\sin \alpha } \right) + \frac{L}{{{m_{\rm{F}}}{V_{\rm{k}}}}}\left( {\tan \gamma \sin \mu + \tan \beta } \right) + \frac{{\left( {Y + {T_{{y_{\rm{b}}}}}} \right)}}{{{m_{\rm{F}}}{V_{\rm{k}}}}}\left( {\tan \gamma \cos \mu \cos \beta } \right) - \\ \;\;\;\;\;\frac{g}{{{V_{\rm{k}}}}}\left( {\cos \gamma \cos \mu \tan \beta } \right) + \frac{{\left( {{T_{{x_{\rm{b}}}}}\sin \alpha - {T_{{z_{\rm{b}}}}}\cos \alpha } \right)}}{{{m_{\rm{F}}}{V_{\rm{k}}}}}\left( {\tan \gamma \sin \mu + \tan \beta } \right) - \frac{{\left( {{T_{{x_{\rm{b}}}}}\cos \alpha + {T_{{z_{\rm{b}}}}}\sin \alpha } \right)}}{{{m_{\rm{F}}}{V_{\rm{k}}}}}\left( {\tan \gamma \cos \mu \sin \beta } \right). \end{array} \right. $ | (21) |
针对地面效应和喷气诱导效应产生的动力学容易被忽略的问题,特对两者的作用效果进行定量分析.根据式(3)~(5)并结合文献[5]给出的试验数据计算可知,地面效应对V/STOL飞机气动力的影响远远小于喷气诱导效应,甚至可以忽略不计.原因在于:随着飞行高度的增加,地面效应逐渐减弱,当飞行高度h≥15 m时,KGE(h)≈0,如图 2所示;而在h < 15 m时,通常飞行速度很低(V≤15 m/s),导致DGE、LGE和mGE很小.

|
图 2 无动力作用下的地面效应洗出因子 Fig. 2 Power-off ground effect washout factor |
为了直观反映这一情况,在V = 10 m/s、α = 5°、δCN = δLF = 90°的典型条件下,仿真比较地效诱导升力增量LGE与喷气诱导升力增量LJIE的大小及其变化,如图 3所示.从图 3中可以明显看出:1)| LGE|

|
图 3 地效诱导与喷气诱导升力增量的比较 Fig. 3 Comparison between ground-effect-induced and jet-induced lift increment |

|
图 4 喷气诱导升力增量系数的比较 Fig. 4 Comparison of jet-induced lift increment coefficient |
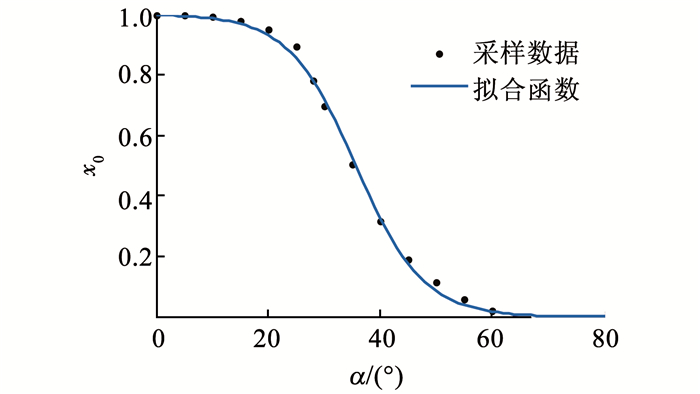
由于缺少必要的风洞试验数据,对式(7)直接采用文献[17]提供的数据进行拟合,如图 5所示,得到σ = 0.165 9,α* = 35.68;对时间常数近似取τ1 = 0.52(c /V),τ2 = 4.5(c /V).由此而导致的气动力系数误差,引入修正系数η,即将式(8)改为
| $ {C_{{L_{{\rm{unst}}}}}}\left( {\alpha ,x} \right) = \frac{\lambda }{2}\eta {\rm{ \mathsf{ π} sin}}\alpha {\rm{co}}{{\rm{s}}^2}\alpha + {x^2}\eta {\rm{ \mathsf{ π} si}}{{\rm{n}}^2}\alpha \cos \alpha , $ |
|
图 5 定常状态下的涡破裂点位置函数 Fig. 5 Position function of the vortex breakdown point in the steady state |
使之在小迎角区域(α≤10°)与文献[5]给出的气动力系数保持一致,式中η = 0.689 1.
假设迎角α的发展规律为
| $ \alpha = A - A\sin \left( {\frac{{\rm{ \mathsf{ π} }}}{{10}}t + \frac{{\rm{ \mathsf{ π} }}}{2}} \right),\left( {t \in \left[ {0,20} \right]} \right). $ |
首先令V = 10 m/s,A∈{15, 30}°,可以得到不同振幅下非定常气动力随迎角变化的曲线,如图 6所示;然后考虑V/STOL飞机在不同飞行模式下的飞行速度不同(低速悬停模式V≤15 m/s、过渡模式15 m/s < V < 60 m/s、高速巡航模式V≥60 m/s),令A = 30°,V∈{10, 30, 90}m/s,得到不同空速下非定常气动力随迎角变化的曲线,如图 7所示.

|
图 6 迎角振幅对非定常升力系数的影响 Fig. 6 Effect of α amplitude on the unsteady lift coefficient |

|
图 7 空速对非定常升力系数的影响 Fig. 7 Effect of airspeed on the unsteady lift coefficient |
从图 6、7中可以看出:1)在小迎角范围内,非定常气动力呈现出线性定常特性,且与文献[5]给出的数据相吻合;2)当迎角增大时,非定常气动力模型能够明显地表现出由翼面流场变化引起的非线性非定常特性.一方面,由于迎角的周期性变化(dα/dt≠0),使得流体流动迟于机体运动,进而使气动系数呈现出滞环效应,且滞环的形态与迎角变化的幅值密切相关,A越大,滞环表现得越明显.另一方面,飞行速度对气动系数的影响也十分显著,V越大,空气动力学动态越快,时延越小,非定常气动力特性越弱;当V增大至一定程度时,非定常气动力退化为准定常形式,并与常规大迎角下的非线性气动力特性相一致.
5 结论1) 建立了由矢量推力模型、多进气道推力损失模型、非线性定常/非定常气动力模型、地面效应和喷气诱导效应模型组成的V/STOL飞机动力学模型,模型各物理量意义明确,计算方便,能够较为全面的表征V/STOL飞机在不同飞行模式下的动力学特性.
2) 推导了能够直观反映V/STOL飞机状态与航迹变化的六自由度非线性数学模型,模型在理论上符合V/STOL飞机的机体动力学和运动学原理,可用于飞行控制系统的设计和仿真.
3) 仿真分析了地面效应和喷气诱导效应对V/STOL飞机动力学的影响效果,结果表明:地面效应的影响可以忽略不计,而近地飞行时喷气诱导效应的影响较为显著,在飞行高度为50 m时的升力损失为2.13%,而在2 m时的升力损失达46.42%.
4) 仿真研究了V/STOL飞机的三角翼非定常动力学特性,得到了由迎角变化率引起的气动力滞环效应及其与迎角幅值和空速的密切关系,比较已有的文献数据初步证实了非定常气动力模型的有效性.
5) 对于V/STOL飞机动力学模型及其特性的研究,还需要更多的风洞试验数据的支持,以进一步验证模型的准确性,并对模型进行合理修正.
| [1] |
HIRSCHBERG M J. An overview of the history of vertical and/or short take-off and landing(V/STOL) aircraft[EB/OL]. (2005-07-09)[2017-12-14]. http://www.vstol.org
|
| [2] |
索德军, 梁春华, 张世福, 等. S/VTOL战斗机及其推进系统的技术研究[J]. 航空发动机, 2014, 40(4): 7. SUO Dejun, LIANG Chunhua, ZHANG Shifu, et al. Technology of short/vertical takeoff and landing fighter and propulsion system[J]. Aeroengine, 2014, 40(4): 7. DOI:10.13477/j.cnki.aeroengine.2014.04.002 |
| [3] |
BEVILAQUA P M. Genesis of the F-35 joint strike fighter[J]. Journal of Aircraft, 2009, 46(6): 1825. DOI:10.2514/1.42903 |
| [4] |
FRANKLIN J A. Revised simulation model of the control system, displays, and propulsion system for a ASTOVL lift fan aircraft: NASA-TM-112208[R]. Washington: NASA, 1997
|
| [5] |
BIRCKELBAW L G, MCNEILL W E, WARDWELL D A. Aerodynamics model for a generic ASTOVL lift-fan aircraft: NASA-TM-110347[R]. Washington: NASA, 1995
|
| [6] |
金爱娟, 郭锁凤, 吴立浪. ASTOVL升力风扇飞机的纵向控制系统研究[J]. 哈尔滨工业大学学报, 2000, 32(5): 29. JIN Aijuan, GUO Suofeng, WU Lilang. Longitudinal control of ASTOVL lift-fan aircraft[J]. Journal of Harbin Institute of Technology, 2000, 32(5): 29. DOI:10.3321/j.issn:0367-6234.2000.05.008 |
| [7] |
金爱娟, 郭锁凤, 宋德风. 非线性动态逆控制律在ASTOVL升力风扇飞机侧向控制中的应用[J]. 电机与控制学报, 2000, 4(4): 239. JIN Aijuan, GUO Suofeng, SONG Defeng. Application of nonlinear dynamic inverse control low in lateral control for ASTOVL lift-fan aircraft control[J]. Electric Machines and Control, 2000, 4(4): 239. DOI:10.3969/j.issn.1007-449X.2000.04.013 |
| [8] |
王健, 王飞跃, 王家廞, 等. 先进短距起飞垂直着陆飞机的建模与仿真研究[J]. 系统仿真学报, 2003, 15(6): 760. WANG Jian, WANG Feiyue, WANG Jiaxin, et al. Modeling and simulation research on advanced short takeoff and vertical landing aircraft[J]. Journal of System Simulation, 2003, 15(6): 760. DOI:10.3969/j.issn.1004-731X.2003.06.002 |
| [9] |
刘超, 雒东超, 张文星, 等. 垂直/短距起降飞机的控制仿真技术[J]. 飞行力学, 2017, 35(5): 40. LIU Chao, LUO Dongchao, ZHANG Wenxing, et al. Control simulation technique of SVTOL aircraft[J]. Flight Dynamics, 2017, 35(5): 40. DOI:10.13645/j.cnki.f.d.20170602.001 |
| [10] |
WANG Xiangyang, ZHU Jihong, ZHANG Yijun. Dynamics modeling and analysis of thrust-vectored V/STOL aircraft[C]//Proceedings of the 32nd Chinese Control Conference. Xi'an: IEEE Xplore, 2013: 182
|
| [11] |
戴瀚苏.推力矢量垂直/短距起降飞行器动力学与控制研究[D].北京: 清华大学, 2010 DAI Hansu. Research on dynamics and control of thrust-vectored V/STOL aircraft[D]. Beijing: Tsinghua University, 2010 |
| [12] |
FAN Yong, ZHU Jihong, MENG Xianyu, et al. Intelligent method based coordinated integrated flight control of a tailless STOVL[C]//Proceedings of the 8th World Congress on Intelligent Control and Automation. Jinan: IEEE Xplore, 2010: 85
|
| [13] |
FAN Yong, MENG Xianyu, YANG Xili, et al. Control allocation for a V/STOL aircraft based on robust fuzzy control[J]. Science China, 2011, 54(6): 1321. DOI:10.1007/s11432-011-4257-0 |
| [14] |
WALKER G, WURTH S, FULLER D J. F-35B integrated flight-propulsion control development: AIAA-2013-4243[R]. Los Angeles: AIAA, 2013
|
| [15] |
BUCHHOLZ M D. Highlights of the JSF X-35 STOVL jet effects test effort: AIAA-2002-5962[R]. Williamsburg: AIAA, 2002
|
| [16] |
SADDINGTON A J, KNOWLES K. A review of out-of-ground-effect propulsion-induced interference on STOVL aircraft[J]. Progress in Aerospace Sciences, 2005, 41(3/4): 175. DOI:10.1016/j.paerosci.2005.03.002 |
| [17] |
GOMAN M, KHRABROV A. State-space representation of aerodynamic characteristics of an aircraft at high angles of attack[J]. Journal of Aircraft, 1994, 31(5): 1109. DOI:10.2514/3.46618 |
| [18] |
洪亮, 额日其太, 徐惊雷. 垂直起降飞行器升力突降动态过程的数值模拟研究[J]. 推进技术, 2015, 36(4): 527. HONG Liang, Eri qitai, XU Jinglei. Numerical simulation of STOVL aircraft dynamic process with lift loss[J]. Journal of Propulsion Technology, 2015, 36(4): 527. DOI:10.13675/j.cnki.tjjs.2015.04.007 |
 2019, Vol. 51
2019, Vol. 51


