网络化战争中,传感器调度通过实时分配战场的传感器资源,使得系统整体性能达到最优,其核心在于能够依据先验知识预测目标的未来状态.近年来,后验克拉美-罗下界PCRLB(posterior carmér-rao lower bound)被应用于传感器调度中,它表征了目标状态估计的理论下界.文献[1-2]提出基于PCRLB的无线传感器管理调度方法.进一步,考虑机动目标,文献[3-4]提出适用于机动目标的传感器调度策略,并给出基于最大模型概率的PCRLB预测方法.
实际上,有源传感器(如雷达)在探测目标时需要持续的向外辐射电磁波,因此如何隐蔽自身、提高自身生存能力显得尤为重要.文献[5-6]研究采用有源传感器开机次数衡量己方传感器辐射,当目标跟踪误差不满足要求则调度有源传感器,否则,不调度.对于多有源传感器系统,文献[7]提出基于空间的辐射控制方法.实际上,不同时刻不同传感器的辐射风险是不同的.为此,文献[8-9]提出采用截获概率熵量化传感器辐射风险,然而计算截获概率需要事先知道敌方窗函数参数,实际中不易获取.借鉴截获概率思想,文献[10-11]提出了辐射度影响ELI(emission level impact)的量化方法,之后文献[12]研究了面向跟踪任务需求的主动传感器调度方法.由于该方法仅以一步预测进行决策且没有考虑切换代价,系统辐射风险依然较大且存在频繁调度的缺陷,不利于实际应用.
针对上述问题,考虑跟踪任务需求,提出一种面向机动目标跟踪的传感器长时调度策略.仿真实验表明,所提策略有效降低了系统辐射、避免了频繁调度问题.
1 机动目标跟踪算法 1.1 机动目标模型在己方三维监视空间中,考虑一个敌方机动目标.不失一般性,假设目标以近似匀速直线和近似匀转弯(包含左转弯和右转弯)运动.则目标动态方程为
| $ \mathit{\boldsymbol{X}}_{k + 1}^j = {\mathit{\boldsymbol{F}}^j}\mathit{\boldsymbol{X}}_k^j + \mathit{\boldsymbol{v}}_k^j. $ | (1) |
式中:
| $ E\left[ {v_k^j{{\left( {v{{_k^j}^\prime }} \right)}^{\rm{T}}}} \right] = \left[ {\begin{array}{*{20}{c}} {{\tau ^3}/3}&{{\tau ^2}/2}\\ {{\tau ^2}/2}&\tau \end{array}} \right] \otimes {\mathit{\boldsymbol{I}}_{3 \times 3}}. $ |
式中:E、⊗分别为求期望和求Kronecker积;τ为采样间隔;I3×3为3×3的单位矩阵.
假设系统中有M个有源传感器(如雷达),则传感器m(m = 1, …, M)的观测方程为
| $ \mathit{\boldsymbol{Z}}_{{X_k}}^m = {h^m}\left( {{\mathit{\boldsymbol{X}}_k}} \right) + \mathit{\boldsymbol{w}}_k^m = {\left[ {r_k^m,\theta _k^m,\varphi _k^m} \right]^{\rm{T}}} + \mathit{\boldsymbol{w}}_k^m. $ | (2) |
式中:hm为传感器m的非线性观测方程;[rkm, θkm, φkm]为对应的目标状态观测值,包含斜距离、方位角和俯仰角;wkm为零均值白高斯量测噪声,对应的协方差矩阵为Rm.
1.2 多传感器IMMPDA为有效跟踪杂波环境下的机动目标,采用交互多模型和概率数据关联IMMPDA(interacting multiple model and probability data association)算法[13].同时,考虑到容积卡尔曼滤波CKF(cubature Kalman filter)在处理高维非线性系统的优越性[14],以CKF估计系统状态和协方差矩阵.算法具体步骤如下.
Step 1 初始化,计算混合概率和混合初始状态.
根据先验信息,假设k时刻模型j的模型概率为μkj,对应的状态估计和协方差矩阵分别为
Step 2 杂波环境下,模型条件滤波.
1) 状态预测和观测预测.
结合目标动态方程及各模型目标状态,计算其状态预测及对应的协方差矩阵,即:
| $ \mathit{\boldsymbol{\hat X}}_{k + 1\left| k \right.}^j = {\mathit{\boldsymbol{F}}^j}\mathit{\boldsymbol{\hat X}}_k^{0j}, $ |
| $ \mathit{\boldsymbol{P}}_{k + 1\left| k \right.}^j = {\mathit{\boldsymbol{F}}^j}\mathit{\boldsymbol{P}}_k^{0j}{\left( {\mathit{\boldsymbol{F}}_k^j} \right)^{\rm{T}}}. $ |
进一步,依据传感器m的观测方程,根据文献[14],计算容积点χk+1|kl, j(l = 1, …, 2L),其中L为状态维数.进一步,根据文献[14],计算k+1时刻模型j的预测观测
2) 观测确认.
判断观测
| $ \begin{array}{l} \left( {\mathit{\boldsymbol{Z}}_{{X_{k + 1}}}^m - \mathit{\boldsymbol{\hat Z}}_{{X_{k + 1}}\left| k \right.}^m} \right){\left( {\mathit{\boldsymbol{S}}_{k + 1}^l} \right)^{ - 1}}{\left( {\mathit{\boldsymbol{Z}}_{{X_{k + 1}}}^m - \mathit{\boldsymbol{\hat Z}}_{{X_{k + 1}}\left| k \right.}^m} \right)^{\rm{T}}} < {g^2},\\ \;\;\;\;\;l = \mathop {\max }\limits_j \left| {\mathit{\boldsymbol{S}}_{k + 1}^{m,j}} \right|. \end{array} $ | (3) |
式中:
如果观测满足式(3),则将该观测作为候选回波;否则,舍弃该观测.
3) 根据候选回波(假设共有nk+1m个),对模型j进行状态估计为
| $ \mathit{\boldsymbol{\hat X}}_{k + 1}^{m,j} = \mathit{\boldsymbol{\hat X}}_{k + 1\left| k \right.}^j + \mathit{\boldsymbol{K}}_{k + 1}^j\nu _{{X_{k + 1}}}^{m,j}. $ |
式中:Kk+1j为滤波增益;νXk+1m, j为组合新息,具体为
| $ \nu _{{X_{k + 1}}}^{m,j} = \sum\limits_{i = 1}^{n_{k + 1}^m} {\beta _{k + 1}^{m,i}\left( {\mathit{\boldsymbol{Z}}_{{X_{k + 1}}}^{m,i} - \mathit{\boldsymbol{\hat Z}}_{{X_{k + 1}}\left| k \right.}^{m,j}} \right)} , $ |
式中βk+1m, i为量测ZXk+1m, i来自于目标的概率,对于非参数模型,应用贝叶斯公式,有
| $ \beta _{k + 1}^{m,i} = \left\{ \begin{array}{l} b_{k + 1}^m{\left[ {b_{k + 1}^m + \sum\limits_{l = 1}^{n_{k + 1}^m} {\beta _{k + 1}^{m,l}} } \right]^{ - 1}},\;\;\;\;i = 0;\\ e_{k + 1}^{m,i}{\left[ {b_{k + 1}^m + \sum\limits_{l = 1}^{n_{k + 1}^m} {e_{k + 1}^{m,l}} } \right]^{ - 1}},\;\;\;\;\;其他. \end{array} \right. $ |
式中bk+1m、ek+1m, i(i = 1, …, nk+1m)可由文献[13]计算得到.
Step 3 更新模型概率.
依据nk+1m个新息的联合概率密度函数,结合文献[13],计算似然函数为
| $ \Lambda _{k + 1}^{m,j} = \left[ {b_{k + 1}^m + \sum\limits_{i = 1}^{n_{k + 1}^m} {e_{k + 1}^{m,l}} } \right]\frac{{{P_D}{P_G}}}{{n_{k + 1}^m}}{\left( {{c_{{n_z}}}{g^{{n_z}}}{{\left| {\mathit{\boldsymbol{S}}_{k + 1}^{m,j}} \right|}^{1/2}}} \right)^{ - n_{k + 1}^m + 1}}, $ |
则模型概率更新为
| $ \mu _{k + 1}^j = \frac{1}{c}\Lambda _{k + 1}^{m,j}\mathit{\boldsymbol{\pi }}_j^{\rm{T}}{\mathit{\boldsymbol{\mu }}_\mathit{k}}. $ |
式中:πj为列向量,表示其他模型转移到模型j的概率;μk为模型概率;c为归一化因子.
Step 4 滤波综合.
计算状态估计值和协方差矩阵为:
| $ {{\mathit{\boldsymbol{\hat X}}}_{k + 1}} = \sum\limits_{j = 1}^r {\mu _{k + 1}^j\mathit{\boldsymbol{\hat X}}_{k + 1}^{m,j}} , $ |
| $ {\mathit{\boldsymbol{P}}_{k + 1}} = \sum\limits_{j = 1}^r {\mu _{k + 1}^j\left[ \begin{array}{l} \mathit{\boldsymbol{P}}_{k + 1}^{m,j} + \left( {\mathit{\boldsymbol{\hat X}}_{k + 1}^{m,j} - {{\mathit{\boldsymbol{\hat X}}}_{k + 1}}} \right) \times \\ {\left( {\mathit{\boldsymbol{\hat X}}_{k + 1}^{m,j} - {{\mathit{\boldsymbol{\hat X}}}_{k + 1}}} \right)^{\rm{T}}} \end{array} \right]} , $ |
式中, Pk+1m, j为
以ELI量化传感器辐射,建立部分可观马尔可夫决策过程模型[15],其模型元素可由数组〈 a, E, T, ZE, O, b 〉表征,具体描述如下.
1) 调度动作a.
定义k时刻所有传感器的调度动作空间为ak = [ak1, …, akM]Τ,其中akm = 1为k+1时刻选择传感器m跟踪目标,否则,akm = 0.考虑到不同平台多传感器配准的困难性,假定每个时刻只有一个传感器跟踪目标,则存在
| $ \sum\limits_{m = 1}^M {a_k^m} = 1. $ |
2) 状态空间E及状态转移T.
| $ {\mathit{\boldsymbol{E}}_k} = {\left[ {E_k^1, \cdots ,E_k^m} \right]^{\rm{T}}}. $ |
式中Ekm为截止k时刻传感器m被敌方累积截获的辐射量[10],将其量化,记为{1, …, Ns},其中Ns为最大辐射量对应的量化值.
依据ELI理论,当akm = 1,即调度传感器m时,定义ELI状态转移矩阵为Tkm = Tm = (ti, j)Ns×Ns.其中,元素ti, j = p(Ek+1m = j|Ekm = i, akm)为k时刻在调度动作akm下传感器m从状态i转移到状态j的条件概率.否则,Tkm为Ns维单位矩阵INs×Ns.
3) 观测值ZE及观测矩阵O.
定义k时刻ELI状态观测值为ZEk,即
| $ {\mathit{\boldsymbol{Z}}_{{E_{\rm{k}}}}} = {\left[ {Z_{{E_{\rm{k}}}}^1, \cdots ,Z_{{E_{\rm{k}}}}^m} \right]^{\rm{T}}}, $ |
式中,ZmEk(m = 1, …, M)为调度传感器m时的瞬间威胁度观测值,将其量化,记为{1, …, Ms},其中Ms为最大瞬间威胁度观测值对应量化值.
同理,当ak-1m = 1,即调度传感器m时,定义不同ELI状态观测值的观测矩阵为Okm(l) = Om(l) = (qi, j, lm)Ns×Ns(l = 1, …, Ms).其中,qi, j, lm = p(ZEkm = l|Ek-1m = i, Ekm = j, ak-1m)表示在调度动作ak-1m下ELI前后状态分别为i和j时,瞬间威胁度观测值为l的条件概率.否则,Okm(l)为Ms维单位矩阵IMs×Ms.
4) 信念状态b.
为了有效描述ELI状态的后验分布,引入信念状态bk = [(bk1)Τ, …, (bkM)Τ]Τ. bk是依据初始状态、所有历史观测值及所有调度动作ηk = {E0, pE0, ZE1, …, ZEk, a0, …, ak-1},利用贝叶斯准则对ELI状态的后验估计,即bk = p(Ek|ηk).
因此,对于H时域内任意传感器调度序列Ak+H = [ak, …, ak+H-1],其辐射代价为
| $ \Re \left( {{\mathit{\boldsymbol{A}}_{k + H}}} \right) = \sum\limits_{h = 1}^H {\sum\limits_{m = 1}^M {a_{k + h - 1}^m{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{\tilde b}}_{k + h\left| k \right.}^m} } . $ |
式中: V为Ns×1维列向量,对应ELI状态量化值;
则信念状态估计为
| $ \begin{array}{l} \mathit{\boldsymbol{\tilde b}}_{k + 1\left| k \right.}^m\left( {E_k^{m + 1}} \right) = \\ p\left( {E_k^{m + 1}\left| {{\mathit{\boldsymbol{a}}_k},\mathit{\boldsymbol{b}}_k^m} \right.} \right) = \\ \sum\limits_{Z_{{E_{k + 1}}}^m = 1}^{{M_{\rm{s}}}} {p\left( {E_k^{m + 1}\left| {{\mathit{\boldsymbol{a}}_k},\mathit{\boldsymbol{b}}_k^m,\mathit{\boldsymbol{Z}}_{{E_{k + 1}}}^m} \right.} \right)} \times \\ p\left( {Z_{{E_{k + 1}}}^m\left| {{\mathit{\boldsymbol{a}}_k},\mathit{\boldsymbol{b}}_k^m} \right.} \right), \end{array} $ | (4) |
式中,ZEk+1m为k+1时刻瞬间威胁度观测值.
式(4)中
| $ p\left( {E_k^{m + 1}\left| {{\mathit{\boldsymbol{a}}_k},\mathit{\boldsymbol{b}}_k^m,\mathit{\boldsymbol{Z}}_{{E_{k + 1}}}^m} \right.} \right) = \frac{{\sum\limits_{i = 1}^{{N_{\rm{s}}}} {t_{i,E_k^{m + 1}}^mq_{i,E_k^{m + 1},Z_{{E_{k + 1}}}^m}^mb_k^m\left( i \right)} }}{{\sum\limits_{i = 1}^{{N_{\rm{s}}}} {\sum\limits_{k = 1}^{{N_{\rm{s}}}} {t_{i,w}^mq_{i,w,Z_{{E_{k + 1}}}^m}^mb_k^m\left( i \right)} } }}. $ | (5) |
进一步,
| $ \begin{array}{l} p\left( {Z_{{E_{k + 1}}}^m\left| {{\mathit{\boldsymbol{a}}_k},\mathit{\boldsymbol{b}}_k^m} \right.} \right) = \\ \sum\limits_{E_k^{m + 1}} {p\left( {{Z_{{E_{k + 1}}}},E_{k + 1}^m\left| {{\mathit{\boldsymbol{a}}_k},\mathit{\boldsymbol{b}}_k^m} \right.} \right)} = \\ \sum\limits_{E_k^{m + 1}} {p\left( {E_{k + 1}^m\left| {{\mathit{\boldsymbol{a}}_k},\mathit{\boldsymbol{b}}_k^m} \right.} \right)p\left( {{Z_{{E_{k + 1}}}}\left| {E_{k + 1}^m,{\mathit{\boldsymbol{a}}_k},\mathit{\boldsymbol{b}}_k^m} \right.} \right)} = \\ \sum\limits_{E_k^{m + 1}} {\sum\limits_{E_k^m} {\left\{ \begin{array}{l} p\left( {E_{k + 1}^m\left| {E_k^m,{\mathit{\boldsymbol{a}}_k}} \right.} \right)\\ \;\;\;\;\;\;\;p\left( {Z_{{E_{k + 1}}}^m\left| {E_{k + 1}^m,E_k^m,{\mathit{\boldsymbol{a}}_k}} \right.} \right)b_k^m\left( {E_k^m} \right) \end{array} \right\}} } = \\ \sum\limits_{i = 1}^{{N_{\rm{s}}}} {\sum\limits_{w = 1}^{{N_{\rm{s}}}} {t_{i,w}^mq_{i,w,Z_{{E_{k + 1}}}^m}^m\mathit{\boldsymbol{b}}_k^m\left( i \right)} } . \end{array} $ | (6) |
将式(5)、(6)代入式(4),并写为矩阵形式,可得
| $ \begin{array}{l} \mathit{\boldsymbol{\tilde b}}_{k + 1\left| k \right.}^m = \sum\limits_{Z_{{E_{k + 1}}}^m} {\left\{ {{{\left[ {{\mathit{\boldsymbol{O}}^m}\left( {Z_{{E_{k + 1}}}^m} \right)} \right]}^{\rm{T}}} \odot {{\left( {{\mathit{\boldsymbol{T}}^m}} \right)}^{\rm{T}}}\mathit{\boldsymbol{b}}_k^m} \right\}} = \\ \;\;\;\;\;\;\;\;\;\;{\left\{ {\left[ {\sum\limits_{Z_{{E_{k + 1}}}^m = 1}^{{M_{\rm{s}}}} {{\mathit{\boldsymbol{O}}^m}\left( {Z_{{E_{k + 1}}}^m} \right)} } \right] \odot {\mathit{\boldsymbol{T}}^m}} \right\}^{\rm{T}}}\mathit{\boldsymbol{b}}_k^m = {\left( {{T^m}} \right)^{\rm{T}}}\mathit{\boldsymbol{b}}_k^m, \end{array} $ |
式中,⊙为Hadamard积运算.
进一步,可得
| $ \tilde b_{k + h\left| k \right.}^m = {\left[ {{{\left( {{\mathit{\boldsymbol{T}}^m}} \right)}^{\sum\limits_{c = k}^{k + h - 1} {a_c^m} }}} \right]^{\rm{T}}}b_k^m, $ |
因此,H时域内辐射代价为
| $ \begin{array}{l} \Re \left( {{\mathit{\boldsymbol{A}}_{k + H}}} \right) = \sum\limits_{h = 1}^H {\sum\limits_{m = 1}^M {a_{k + h - 1}^mE\left( {\mathit{\boldsymbol{\tilde b}}_{k + h\left| k \right.}^m} \right)} } = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{h = 1}^H {\sum\limits_{m = 1}^M {a_{k + h - 1}^m{\mathit{\boldsymbol{V}}^{\rm{T}}}{{\left[ {{{\left( {{\mathit{\boldsymbol{T}}^m}} \right)}^{\sum\limits_{c = k}^{k + h - 1} {a_c^m} }}} \right]}^{\rm{T}}}\mathit{\boldsymbol{b}}_k^m} } . \end{array} $ | (7) |
传感器调度的核心在于能够依据先验知识预测目标的未来状态.理想条件下,文献[9,11]依据目标运动方程和量测方程预测了匀速运动目标未来一步[9]和多步[11]的协方差矩阵,并给出了基于协方差控制的传感器调度方法.显然,该方法不适用于本文场景.考虑PCRLB能够根据当前先验信息预测未来时刻目标状态估计的下界,为此给出一种基于PCRLB的跟踪精度预测方法.
对于任意时刻的目标状态估计,存在:
| $ {\mathit{\boldsymbol{P}}_k} = {\rm{E}}\left( {{{\mathit{\boldsymbol{\hat X}}}_k} - {\mathit{\boldsymbol{X}}_k}} \right){\left( {{{\mathit{\boldsymbol{\hat X}}}_k} - {\mathit{\boldsymbol{X}}_k}} \right)^{\rm{T}}} \ge \mathit{\boldsymbol{J}}_k^{ - 1}. $ |
式中:
目标状态转移先验概率密度函数[4]为
| $ \begin{array}{l} p\left( {{\mathit{\boldsymbol{X}}_{k + 1}}\left| {{\mathit{\boldsymbol{X}}_k}} \right.} \right) = \frac{1}{{\sqrt {{{\left( {2{\rm{ \mathit{ π} }}} \right)}^6}\left| {{\mathit{\boldsymbol{Q}}^{{j_{k + 1}}}}} \right|} }} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\exp \left\{ { - \frac{1}{2}\left( {{\mathit{\boldsymbol{X}}_{k + 1}} - {\mathit{\boldsymbol{F}}^{{j_{k + 1}}}}{\mathit{\boldsymbol{X}}_k}} \right){{\left( {{\mathit{\boldsymbol{Q}}^{{j_{k + 1}}}}} \right)}^{ - 1}} \cdot } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\left( {{\mathit{\boldsymbol{X}}_{k + 1}} - {\mathit{\boldsymbol{F}}^{{j_{k + 1}}}}{\mathit{\boldsymbol{X}}_k}} \right)}^{\rm{T}}}} \right\}. \end{array} $ | (8) |
进一步,结合式(8)和式(3),Fisher信息矩阵递推如下
| $ {\mathit{\boldsymbol{J}}_{k + 1}} = \mathit{\boldsymbol{D}}_k^{22} - \mathit{\boldsymbol{D}}_k^{21}{\left( {{\mathit{\boldsymbol{J}}_k} + \mathit{\boldsymbol{D}}_k^{11}} \right)^{ - 1}}\mathit{\boldsymbol{D}}_k^{12} + \sum\limits_{m = 1}^M {a_k^m\mathit{\boldsymbol{J}}_{k + 1}^m} , $ | (9) |
其中:
| $ \mathit{\boldsymbol{D}}_k^{11} = {\left( {{\mathit{\boldsymbol{F}}^{{j_{k + 1}}}}} \right)^{\rm{T}}}{\left( {{\mathit{\boldsymbol{Q}}^j}} \right)^{ - 1}}{\mathit{\boldsymbol{F}}^{{j_{k + 1}}}},\mathit{\boldsymbol{D}}_k^{12} = - {\left( {{\mathit{\boldsymbol{F}}^{{j_{k + 1}}}}} \right)^{\rm{T}}}{\left( {{\mathit{\boldsymbol{Q}}^j}} \right)^{ - 1}}, $ |
| $ \mathit{\boldsymbol{D}}_k^{21} = {\left( {\mathit{\boldsymbol{D}}_k^{12}} \right)^{{\rm{T}}}},\mathit{\boldsymbol{D}}_k^{22} = {\left( {{\mathit{\boldsymbol{Q}}^{{j_{k + 1}}}}} \right)^{ - 1}}, $ |
| $ \mathit{\boldsymbol{J}}_{k + 1}^m = {\left( {\mathit{\boldsymbol{H}}_{k + 1}^m} \right)^{\rm{T}}}{\left( {{\mathit{\boldsymbol{R}}^m}} \right)^{ - 1}}\mathit{\boldsymbol{H}}_{k + 1}^m. $ |
式中:Jk+1m为从传感器m获得的信息增益;H为雅可比矩阵;jk+1为k+1时刻目标的运动模型,在k时刻是未知的.
为了计算Jk+1,需要获知k+1时刻目标运动模型.依据当前先验信息,文献[3-4]提出以当前最大模型概率对应的模型作为未来时刻的运动模型,即
| $ {{\tilde j}_{k + 1}} = \arg \mathop {\max }\limits_{j \in \left\{ {1, \cdots ,r} \right\}} \mu _k^j. $ |
因此,算法具体流程见图 1.

|
图 1 基于PCRLB的跟踪精度预测流程 Fig. 1 Flow of tracking accuracy prediction by PCRLB |
考虑传感器辐射代价和切换代价,则基于代价函数和PCRLB的传感器长时调度问题可描述为:
| $ \begin{array}{l} \mathit{\boldsymbol{A}}_{k + H}^{{\rm{opt}}} = \arg \mathop {\max }\limits_{{A_k} + H} \left[ \begin{array}{l} \sum\limits_{h = 1}^H {\sum\limits_{m = 1}^M {a_{k + h - 1}^m{\mathit{\boldsymbol{V}}^{\rm{T}}}{{\left[ {{{\left( {{T^m}} \right)}^{\sum\limits_{c = k}^{k + h - 1} {a_c^m} }}} \right]}^{\rm{T}}}\mathit{\boldsymbol{b}}_k^m} } + \\ \sum\limits_{h = 1}^H {\sum\limits_{m = 1}^M {{c^m}{{\left( {a_{k + h - 1}^m - a_{k + h - 2}^m} \right)}^2}} } \end{array} \right] = \\ \;\;\;\;\;\;\;\;\;\;\arg \mathop {\max }\limits_{{A_k} + H} \left[ {\sum\limits_{h = 1}^H {{\mathit{\Gamma }_{k + h}}} + \sum\limits_{h = 1}^H {{\Upsilon _{k + h}}} } \right],\\ \;\;\;\;\;\;\;\;\;\;{\rm{s}}.{\rm{t}}\;\;\;\left\{ \begin{array}{l} \sum\limits_{m = 1}^M {a_{k + h - 1}^m} = 1,\\ {{\tilde \rho }_{k + h}} \le {\rho _{\rm{d}}}.\;\;\;h = 1, \cdots ,H \end{array} \right. \end{array} $ | (10) |
式中:cm为传感器m的切换代价(也称为启动/停止代价)[16];Γ、Υ分别为一步辐射代价和切换代价;ρd为任务需求对应的跟踪精度;
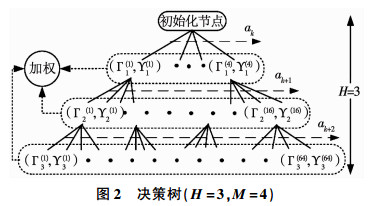
对于式(10),共有MH种传感器组合,且随着时域长度呈指数爆炸增长.为了求解最优传感器调度序列,将该问题建立为约束条件下决策树寻优问题.依据决策树原理,决策树深度和分支因子分别对应于调度序列长度H和传感器数目M,图 2为H = 3,M = 4的决策树.考虑到式(10)中的约束,不同深度的分支数是不同的.对于满足约束的分支,其权重即为式(10)中的代价函数.因此,求解最优传感器调度序列即为搜索具有最优代价函数的节点路径.
|
图 2 决策树(H = 3,M = 4) Fig. 2 Decision tree |
引入阈值剪支技术,给出基于阈值ε剪支的标准代价搜索UCS(uniform cost search)算法求解最优传感器调度序列,其步骤见图 3.

|
图 3 基于阈值剪支的UCS算法 Fig. 3 UCS algorithm based on threshold pruning |
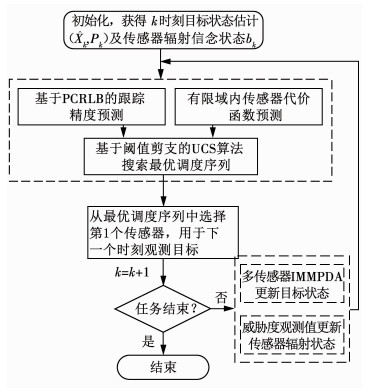
长时调度策略流程如图 4所示,具体步骤如下.
|
图 4 长时调度策略流程图 Fig. 4 Flow chart of non-myopic scheduling policy |
Step 1 初始化,获得k时刻目标状态估计(
Step 2 建立H时长决策树,由图 1预测每个节点的跟踪精度,式(10)预测传感器辐射代价和切换代价,并依据图 3搜索最优调度序列.
Step 3 从最优调度序列中选择第1个传感器,用于下一个时刻观测目标.
Step 4 k = k+1,若任务没有结束,则依据多传感器IMMPDA算法更新目标状态、结合威胁度观测值更新传感器辐射状态;否则,转到Step 5.
Step 5 任务结束.
2.5 复杂度分析本文长时调度策略的复杂度主要包括:目标状态及传感器辐射状态的更新、最优调度序列的计算.其中,传感器辐射状态更新只是简单的矩阵运算[12],而目标状态更新为滤波过程,其复杂度可参考文献[17].与其他调度策略相比,长时调度策略的复杂度主要体现在最优调度序列的计算.
由式(7)和图 1可知,每个节点的复杂度是相同的,则计算最优调度序列的复杂度取决于节点打开数.不失一般性,假设每个节点的复杂度为单位1,则对于给定的M和H,理论上需打开MH个节点,即其复杂度为O(MH).实际中,UCS以代价为顺序进行搜索,其复杂度要小于O(MH).进一步,引入阈值剪支技术,UCS依据阈值ε可以逐步的缩紧下界,从而降低算法复杂度.结合仿真实验,选择合适的阈值ε可以有效的减少节点打开数,并保证搜索正确率.以H = 3、ρd = 70 m为例,UCS(即ε = 0)节点打开率为68%,而本文方法取ε = 0.3,在保证传感器正确率不低于98%时,其节点打开率仅为31%.
3 实验及结果分析 3.1 仿真参数设置考虑M = 4个传感器在杂波环境下跟踪单个机动目标.目标的初始位置和速度分别为(15, 4, 5)km和(-280, -260, 0)m/s.采样间隔为τ = 1 s,仿真时长为100τ.不失一般性,假设目标运动模型为r = 3,即匀速直线运动、匀速左转弯和匀速右转弯.进一步,在26τ~50τ目标以角速度ω = 5°向右转弯,在51τ~74τ以角速度ω = 5°向左转弯,其余时间做直线运动.其中,模型切换概率为πij = 0.025(i≠j).假定杂波服从泊松分布,虚假量测密度为3×10-9/(m·mrad2),检测为1,波门参数为4,门概率为0.999 7.
传感器位置分别为(0, -5)、(-5, 0)、(5, 0)、(0, 5) km,其斜距离标准差分别为200、100、100、10 m,方位角标准差分别为0.010、0.005、0.005、0.001 rad,对应的俯仰角标准差与方位角一致.将传感器ELI状态量化为{1, 2, 3}(其中:1、2、3分别为低辐射、中辐射、高辐射);瞬间辐射的观测值量化为{1, 2, 3}(其中:1、2、3分别为小增量、中增量、高增量)[12].不失一般性,假定传感器1更易处于低ELI状态、传感器4更易处于高ELI状态.则ELI状态转移矩阵设为:
| $ {\mathit{\boldsymbol{T}}^1} = \left[ {\begin{array}{*{20}{c}} {0.8}&{0.1}&{0.1}\\ {0.5}&{0.3}&{0.2}\\ {0.4}&{0.3}&{0.3} \end{array}} \right],{\mathit{\boldsymbol{T}}^2} = \left[ {\begin{array}{*{20}{c}} {0.6}&{0.2}&{0.2}\\ {0.2}&{0.5}&{0.3}\\ {0.1}&{0.3}&{0.6} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{T}}^3} = \left[ {\begin{array}{*{20}{c}} {0.6}&{0.2}&{0.2}\\ {0.2}&{0.5}&{0.3}\\ {0.1}&{0.3}&{0.6} \end{array}} \right],{\mathit{\boldsymbol{T}}^4} = \left[ {\begin{array}{*{20}{c}} {0.5}&{0.3}&{0.2}\\ {0.2}&{0.5}&{0.3}\\ {0.1}&{0.2}&{0.7} \end{array}} \right]. $ |
此外,取切换代价为0.25,所有仿真结果均为200次蒙特卡洛仿真取平均.
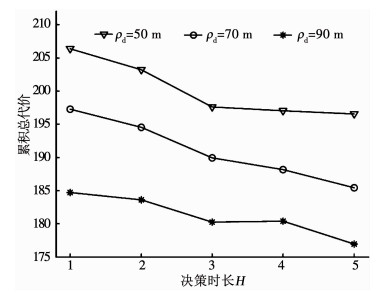
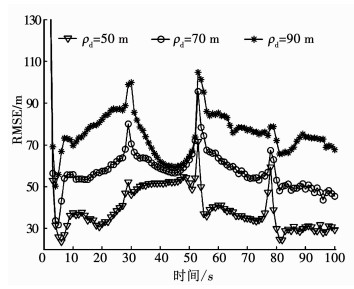
3.2 结果分析图 5为不同精度和决策时长下,系统累积总代价.由图 5可知,随着跟踪精度ρd降低,其跟踪需求逐渐升高,为了满足该需求,系统会频繁调度性能好、辐射风险高的传感器(如传感器4),因此其累积辐射总代价也逐渐升高.另一方面,对于给定跟踪精度ρd约束,随着决策时长增大,系统累积总代价总体下降,即能够获得更好地调度序列使得辐射代价和切换代价降低.进一步,以H = 3为例,图 6为不同精度下,目标均方根误差(root mean square error, RMSE).由图 6可知,本文滤波方法能够较好的估计杂波环境下机动目标状态.在不同跟踪精度ρd约束下,本文方法能够自适应的调度传感器满足精度约束.同时,由于目标机动,在模型切换过程中,目标RMSE可能会高于精度约束,符合实际情形.因此,不失一般性,考虑到计算复杂度,之后的实验中取H = 3、ρd = 70 m.
|
图 5 不同精度和决策时长下,累积总代价 Fig. 5 Cumulative total cost of different accuracies and decision steps |
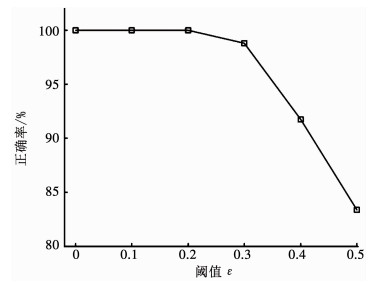
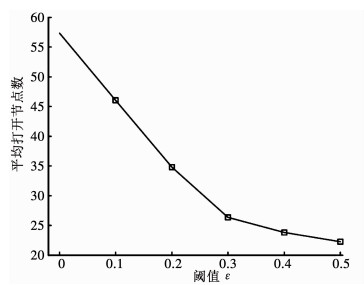
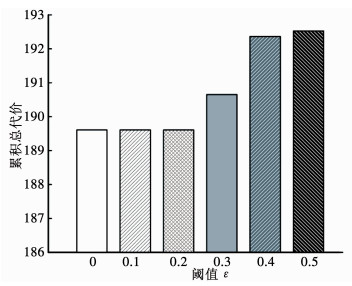
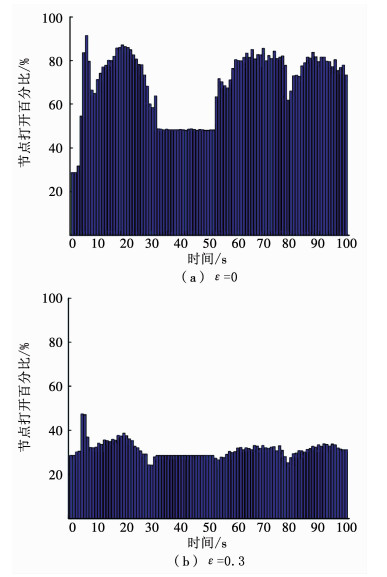
图 7为不同阈值ε下,传感器选择正确率.由图 7可知,随着阈值ε增大,传感器选择正确率逐渐下降,即系统有时不能获得最优的调度序列.图 8为对应的平均节点打开数,随着阈值ε增大,平均节点打开数逐渐减少,即加快了算法搜索速度.进一步,图 9为对应的累积总代价,随着阈值ε增大,其累积总代价逐渐提高,即系统的辐射代价和切换代价更大.综合上述因素,取阈值ε = 0.3较为适宜.图 10为ε = 0和ε = 0.3时,节点打开百分比对比.由图 10可知,在整个调度过程中,取阈值ε = 0.3能够显著地降低节点打开百分比,提高调度效率.
|
图 6 不同精度下,目标均方根误差 Fig. 6 RMSE of different accuracies |
|
图 7 不同阈值ε下,传感器选择正确率 Fig. 7 Accuracy rate versus threshold ε |
|
图 8 不同阈值ε下,平均节点打开数 Fig. 8 Average number of nodes opened versus threshold ε |
|
图 9 不同阈值ε下,累积总代价 Fig. 9 Cumulative total cost versus threshold ε |
|
图 10 节点打开百分比对比 Fig. 10 Comparison of the percentage of nodes opened |
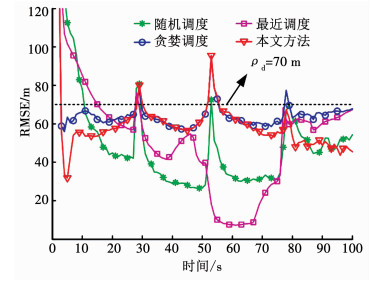
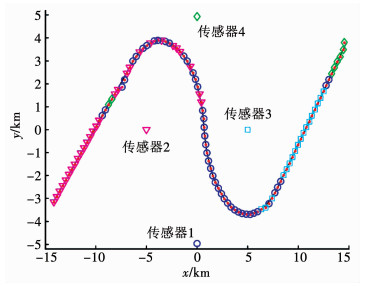
为了验证本文方法的有效性,选取随机调度[15]、最近调度[16]和贪婪调度(或短时调度)[12]3种调度策略进行对比.表 1为不同策略下,调度效果对比.图 11为不同调度策略下,目标RMSE.图 12为本文方法下,目标航迹、航迹估计及其传感器选择.为了显示清楚,将其投影到x-y平面,其中黑色实线为目标真实航迹、红色实点为航迹估计.由表 1可知,随机调度和最近调度由于不考虑传感器辐射风险和切换代价,其累积总代价较大.同时,这两种调度策略也不考虑跟踪精度ρd约束,其RMSE往往不能满足要求,由图 11可知,初始阶段随机调度(10 s内)和最近调度(15 s)的RMSE均高于ρd.相比而言,结合图 6,贪婪调度和本文方法能够依据ρd变化自适应的调度传感器以满足精度约束(由于目标机动,在模型切换过程中,可能不满足精度约束,符合实际情形).此外,贪婪调度和本文方法考虑传感器辐射风险和切换代价,其对应的累积总代价能够显著下降.进一步,由于本文方法以多步时长进行决策,相比于贪婪调度,其能够获得更优的调度序列.结合图 12和表 1,本文方法的累积切换次数更少,更易实现.同时,观察表 1,不同调度策略的累积辐射代价和累积ELI值近似相等,这也验证了目标优化函数的合理性.
| 表 1 不同策略下,调度效果对比 Tab. 1 Comparison of scheduling performance of different policies |
|
图 11 不同策略下,目标均方根误差 Fig. 11 RMSE of different scheduling policies |
|
图 12 本文方法下,目标航迹、航迹估计及其传感器选择 Fig. 12 Target trajectory, estimated trajectory, and sensor selection of the proposed method |
1) 以ELI量化传感器辐射风险,设计辐射代价函数,该函数能够有效衡量传感器真实ELI状态;以PCRLB预测目标跟踪精度,该方法能够有效控制跟踪误差、满足跟踪任务需求.
2) 提出基于阈值ε剪支的UCS快速搜索算法,与UCS搜索算法相比,该算法能够有效降低节点打开数、提高搜索实时性.
3) 与已有调度策略相比,本文方法能够在满足跟踪任务需求下,获得更优的调度序列,系统辐射代价更低.
4) 引入传感器切换代价,有效权衡了系统辐射代价和切换次数,避免了频繁调度问题.
| [1] |
杨小军, 马祥, 宋青松, 等. 基于条件后验克拉美-罗下界的目标跟踪传感器管理[J]. 控制理论与应用, 2013, 30(5): 543. YANG Xiaojun, MA Xiang, SONG Qingsong, et al. Sensor management for target tracking based on conditional posterior Craméér-Rao lower bounds[J]. Control Theory & Applications, 2013, 30(5): 543. DOI:10.7641/CTA.2013.20878 |
| [2] |
NAYEBI-ASTANEH A, PARIZ N, NAGHIBI-SISTANI M. Adaptive node scheduling under accuracy constraint for wireless sensor nodes with multiple bearings-only sensing units[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(2): 1547. DOI:10.1109/TAES.2014.130476 |
| [3] |
LIU Zhigang, WANG Jinkuan, XUE Yanbo. PCRLB-based sensor selection for maneuvering target tracking in range-based sensor networks[J]. Future Generation Computer Systems, 2013, 29(7): 1751. DOI:10.1016/j.future.2012.01.003 |
| [4] |
KESHAVARZ-MOHAMMADIYAN A, KHALOOZADEH H. Interacting multiple model and sensor selection algorithms for manoeuvring target tracking in wireless sensor networks with multiplicative noise[J]. International Journal of Systems Science, 2017, 48(5): 899. DOI:10.1080/00207721.2016.1177128 |
| [5] |
LIU Bin, JI Chunlin, ZHANG Yangyang, et al. Blending sensor scheduling strategy with particle filter to track a smart target[J]. Wireless Sensor Network, 2009, 1(4): 300. DOI:10.4236/wsn.2009.14037 |
| [6] |
吴卫华, 江晶, 高岚. 机载雷达辅助无源传感器对杂波环境下机动目标跟踪[J]. 控制与决策, 2015, 30(2): 277. WU Weihua, JIANG Jing, GAO Lan. Tracking maneuvering target in clutter with passive sensor aided by airborne radar[J]. Control and Decision, 2015, 30(2): 277. DOI:10.13195/j.kzyjc.2013.1781 |
| [7] |
吴巍, 王国宏, 双炜, 等. 多机载平台多目标跟踪与辐射控制[J]. 系统工程与电子技术, 2012, 34(3): 495. WU Wei, WANG Guohong, SHUANG Wei, et al. Multi-airborne-platform multi-target tracking and radiation control technology[J]. Systems Engineering and Electronics, 2012, 34(3): 495. DOI:10.3969/j.issn.1001-506X.2012.03.12 |
| [8] |
ZHANG Zining, SHAN Ganlin. Non-myopic sensor scheduling to track multiple reactive targets[J]. IET Signal Processing, 2015, 9(1): 37. DOI:10.1049/iet-spr.2013.0187 |
| [9] |
SHI Chengang, ZHOU Jianjiang, WANG Fei. Adaptive resource management algorithm for target tracking in radar network based on low probability of intercept[J]. Multidimensional Systems and Signal Processing, 2018, 29(4): 1203. DOI:10.1007/s11045-017-0494-8 |
| [10] |
KRISHNAMURTHY V. Emission management for low probability intercept sensors in network centric warfare[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(1): 133. DOI:10.1109/TAES.2005.1413752 |
| [11] |
SHAN Ganglin, ZHANG Zining. Non-myopic sensor scheduling for low radiation risk tracking using mixed POMDP[J]. Transactions of the Institute of Measurement and Control, 2015, 39(2): 230. DOI:10.1177/0142331215604211 |
| [12] |
乔成林, 单甘霖, 段修生, 等. 面向跟踪任务需求的主动传感器调度方法[J]. 系统工程与电子技术, 2017, 39(11): 2515. QIAO Chenglin, SHAN Ganlin, DUAN Xiusheng, et al. Scheduling algorithm of active sensors for tracking task requirement[J]. Systems Engineering and Electronics, 2017, 39(11): 2515. DOI:10.3969/j.issn.1001-506X.2017.11.18 |
| [13] |
HOULES A, BAR-SHALOMA Y. Multisensor tracking of a maneuvering target in clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25(2): 176. DOI:10.1109/7.18679 |
| [14] |
ARASARATNAM I, HAYKIN S. Cubature kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254. DOI:10.1109/TAC.2009.2019800 |
| [15] |
SONG H, XIAO M, XIAO J, et al. A POMDP approach for scheduling the usage of airborne electronic countermeasures in air operations[J]. Aerospace Science and Technology, 2016, 48: 86. DOI:10.1016/j.ast.2015.11.001 |
| [16] |
LI Y, KRAKOW L W, CHONG E K P, et al. Approximate stochastic dynamic programming for sensor scheduling to track multiple targets[J]. Digital Signal Processing, 2009, 19(6): 978. DOI:10.1016/j.dsp.2007.05.004 |
| [17] |
张召友, 郝燕玲, 吴旭. 3种确定性采样非线性滤波算法的复杂度分析[J]. 哈尔滨工业大学学报, 2013, 45(12): 111. ZHANG Zhaoyou, HAO Yanling, WU Xu. Complexity analysis of three deterministic sampling nonlinear filtering algorithms[J]. Journal of Harbin Institute of Technology, 2013, 45(12): 111. DOI:10.11918/j.issn.0367-6234.2013.12.020 |
 2019, Vol. 51
2019, Vol. 51


