2. 哈尔滨工业大学 深空探测基础研究中心,哈尔滨 150001
2. Deep Space Exploration Research Center, Harbin Institute of Technology, Harbin 150001, China
对地观测卫星利用星载传感器获取地球表面信息,广泛应用于土地资源普查、抗灾救援、军事侦察等多个领域.随着中国在轨运行和规划研制的对地观测卫星数量及种类越来越多,对航天观测任务提出了新的需求:1)重点区域巡查,快速加强对某重点区域的情报收集分析;2)热点区域应对,对周边海域舰船等突发事件针对性地应对.这些新的卫星应用需求与传统的卫星使用方式相比具有极强的突发、短暂等特性,因此卫星在轨任务的反应速度逐渐成为衡量空间系统性能的重要指标之一[1].
传统的卫星任务规划多依赖地面集中式管理,由于地面测控资源有限,易出现数据延迟,面对偶发目标等非预期情况响应速度较慢,难以保障日益增长的航天观测任务需求.随着对卫星运行智能化、精细化的要求程度不断提高,对遥感卫星自主任务规划能力的需求也日益凸显[2-3].因此,研究多星自主协同任务规划方法,减少对地面站点的依赖,实现卫星观测任务的自主规划和优化,对提高卫星管理水平和卫星观测数据质量具有重要意义.
多星自主任务规划问题是一个多约束、高冲突的复杂组合优化问题[4].即在满足星上资源约束和任务约束的前提下,怎样安排一组任务的执行顺序及具体执行时间,使得观测区域最大、成像数目最多、能量分配效率最高、任务收益最大等一个或多个目标函数达到最优[5].该问题一直备受各国学者的关注, 并进行了多角度的探索和研究.
Verfaillie等[6]提出了一种动态规划算法,可用于卫星在轨进行自主任务规划.刘嵩等[7]针对敏捷成像卫星自主规划问题,提出了基于时间线约束网络的问题模型及求解算法.赵萍等[8]面向高任务密度卫星任务规划问题,设计了一种改进的遗传算法,一定程度上提高了收敛速度.Luo等[9]提出了一种预调度策略和重调度策略组合的新型调度算法,有效提升了卫星任务规划问题的求解速度和精度.
由国、内外现阶段的研究成果可知,目前对多星任务规划问题的求解,多采用遗传算法[10-11]、模拟退火[12-13]、禁忌搜索[14]等智能算法.此类算法在求解星群协同任务规划这类含有复杂约束的多资源、大规模优化问题上取得了一定的成果,但依然存在收敛速度慢、易陷入局部最优等问题;同时考虑到卫星星上计算资源紧张,而智能算法通常较耗费时间和计算资源,因此寻找一种满足星上自主任务规划能力需求的优化算法,是本文研究的主要工作.
综合上述分析,本文面向非预期情况(主要包括新目标出现、目标消失、执行故障无法观测等突发情况),考虑卫星载荷异构条件下,针对多星自主协同任务规划问题的模型和求解算法进行研究,在充分考虑时间、载荷、能量等约束限制的前提下,提出了详细的求解算法流程及相应的约束检验规则,设计了合理的优化目标函数及相应的去量纲化方法,并通过仿真实验分析验证了算法的合理性、正确性和有效性.
1 多星自主协同任务规划问题模型 1.1 符号定义为了方便描述,首先给出相关符号定义,见表 1.
| 表 1 符号定义 Tab. 1 Symbol definition |
多星自主协同任务规划问题可描述为在一个规划周期内,M个卫星安排R个观测任务,使得目标函数最优.任务规划的最终输出结果主要是观测任务的分配方案,对某颗卫星来说,其分配结果可表示为如下的一个八元数组:
| $ \begin{array}{l} [m, {q_m}, r, {\rm{TaskTyp}}{{\rm{e}}_r}, {\rm{TaskS}}{{\rm{T}}_{rm}}, {\rm{TaskE}}{{\rm{T}}_{rm}}, \\ \;\;\;\;\;\;\;\;\;\;{\rm{TaskDuratio}}{{\rm{n}}_{rm}}, {\rm{Profi}}{{\rm{t}}_{rm}}]. \end{array} $ |
在考虑实际卫星系统的基础上,本文对星上自主协同任务规划问题做出如下合理简化和基本假设.
1) 观测目标为区域目标,观测活动具有一定的持续时间.
2) 假设一颗卫星只携带一个星载遥感器,考虑可见光、红外和合成孔径雷达(SAR)3种类型的星载遥感器,并假设卫星具备一定的自主运行能力和数据分析能力.
3) 假设各卫星间存在时时可用的星际链路,可满足任意时刻的通信需求,卫星在观测过程中产生的大量数据会及时进行数据下传,清空星上存储器容量.
1.3 约束条件 1.3.1 载荷能力任何时候每个星载遥感器只能执行一个观测任务:
| $ \sum\limits_{{r_1} \ne {r_2}} {\sum\limits_{1 \le m \le M} {x_{{r_1}, {r_2}}^m} } \le 1. $ |
若任务tr1和任务tr2都要占用卫星Sm,且tr1紧跟在tr2之后执行,则xmr1, r2 = 1;否则xmr1, r2 = 0.所有未定义的xmr1, r2值都为0.
1.3.2 可观测时间每个任务执行时只能占用一个可见时间窗口为
| $ \sum\limits_{1 \le d \le {N_{{r_1}m}}} {y_{{r_1}m}^d}-\sum\limits_{{r_1} \ne {r_2}} {x_{{r_1}, {r_2}}^m} = 0. $ |
卫星Sm执行任务tr时的时间窗口为SatWinrmd,则yrmd = 1;否则yrmd = 0.所有未定义的yrmd值都为0.
任务执行时间在相应的可见时间窗口内为:
| $ \begin{array}{l} \sum\limits_{1 \le m \le M} {\sum\limits_{1 \le d \le {N_{rm}}} {{\rm{WinST}}_{rm}^d} } *y_{rm}^d \le {\rm{TaskS}}{{\rm{T}}_{rm}}, \\ \sum\limits_{1 \le m \le M} {\sum\limits_{1 \le d \le {N_{rm}}} {\left( {{\rm{WinET}}_{rm}^d-{\rm{TaskDuratio}}{{\rm{n}}_{rm}}} \right)} } *y_{rm}^d \ge \\ {\rm{TaskE}}{{\rm{T}}_{rm}}. \end{array} $ |
执行后一个任务时,应保证从前一任务到该任务执行有足够的准备时间为
| $ {\rm{TaskS}}{{\rm{T}}_{rm}}-{\rm{TaskE}}{{\rm{T}}_{\left( {e-1} \right)m}} \ge {\rm{Preparetim}}{{\rm{e}}_{rm}}. $ |
本文主要考虑载荷运行、侧摆活动等与有效载荷密切相关的能量消耗.单圈所有任务执行过程中,卫星电池用电量不超过最大容量的20%.
| $ {\rm{Energ}}{{\rm{y}}_m} \le 0.2*{E_m}_{{\rm{max}}}. $ |
对于卫星任务规划问题,其优化目标可以有多种不同的形式,本文同时考虑完成任务的收益与成本,设置目标函数为寻找收益与成本之差的最大值,即保证完成任务的净收益最大化:
| $ F = {\rm{max}}\left( {{\rm{Profit}}-{\rm{Cost}}} \right) $ | (1) |
式中:Profit为任务完成的收益,与卫星载荷类型相关,其量纲一的单位为“1”;Cost为任务完成的成本,主要为卫星消耗的总能量(包括载荷能耗、卫星姿态机动能耗等),量纲一的单位为能量单位.由于各个指标的单位和量级(即计量指标的数量级)不同而无法直接进行评价,因此须对成本和收益进行去量纲化处理,然后再进行目标函数的计算和使用.本文采用线性比例法进行量纲化处理,线性比例法的公式如下:
| $ {x_{ij}}^* = \frac{{{x_{ij}}}}{{x{'_j}}}. $ |
式中:xij*为去量纲一之后的值; xij为去量纲一之前的原值; x′j为所有原值中的最小值,即
本文利用由博弈论思想延伸出的招投标案例,从招标、投标和评标3个方面构成一次完整的任务规划,从而获得求解自主任务规划数学模型的求解算法.
对于卫星星群中的每颗卫星在原观测任务中具有平等地位,在一次非预期协同任务规划过程中,发出非预期任务请求的卫星即为主星,其他卫星为从星.需要说明的是,卫星的角色并非固定,而是随着任务及环境的变化而发生改变,从而更好地适应对动态任务的响应和规划.
在算法设计中,本文根据卫星实际对地观测过程,考虑非预期情况中的“发现动目标”这一观测任务需求.一般来说,普查观测范围较大,有益于卫星对动目标进行“轨迹外推”,但普查的分辨率较低;详查观测范围较小,但其空间分辨率高,有助于对目标进行清晰全面地观测.据此,设定每一个观测总任务可合理分解为普查和详查两种类型的子任务,即每个观测任务可由若干个普查和详查子任务构成.
2.1.1 任务招标发现非预期目标的主星产生协作愿望,并将该目标任务分解为若干个子任务,即总观测任务代表的是一组观测子任务的集合.本文设定在一次招标过程中仅处理一个子任务,并采用最大优先级策略决定子任务的执行顺序,主星按任务优先级由高到低的顺序对相应的子任务进行招标.最大优先级策略表示如下:
| $ {\rm{PR}} = \mathop {{\rm{max}}}\limits_{1 \le r \le R} \{ {\rm{P}}{{\rm{R}}_r}\} . $ |
主星针对挑选出的子任务向各从星发出招标信息,招标信息可用一个七元数组表示为
| $ \begin{array}{l} [r, {\rm{Latitud}}{{\rm{e}}_r}, {\rm{Longitud}}{{\rm{e}}_r}, {\rm{TaskLE}}{{\rm{T}}_r}, {\rm{TaskDuratio}}{{\rm{n}}_r}, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{P}}{{\rm{R}}_r}, {\rm{TaskTyp}}{{\rm{e}}_r}]. \end{array} $ |
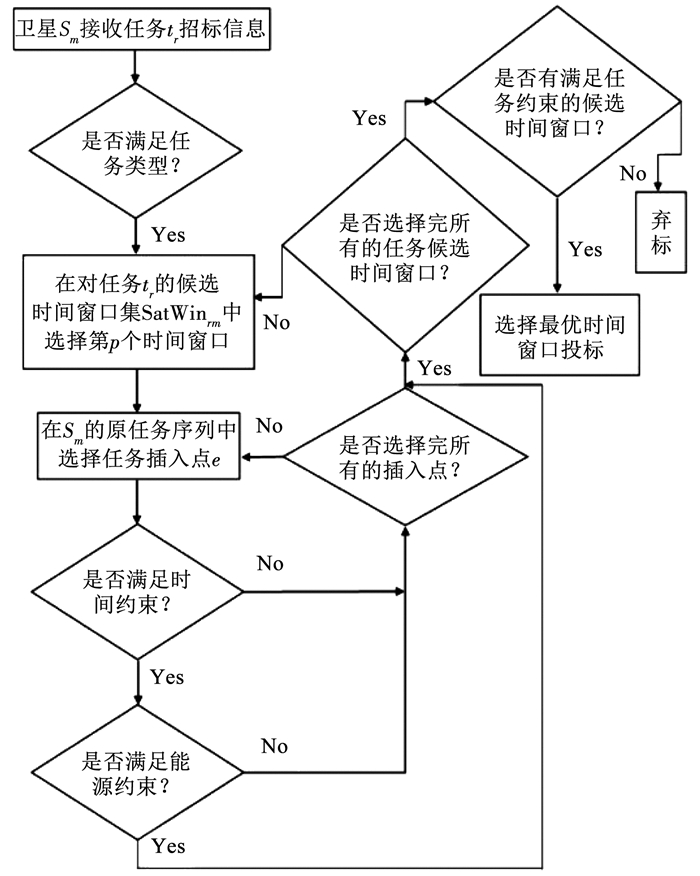
各从星收到招标信息后,根据自身现有能力或状况判断是否满足任务约束来决定是否投标[15],该过程称为任务的投标决策过程.本文主要考虑时间约束和能源约束,从星判断能否将任务tr无冲突地插入原任务集合中,由此从星自主决策是否投标.对某一从星Sm的任务投标决策过程如图 1所示.
|
图 1 卫星Sm对任务tr的投标决策过程 Fig. 1 Bidding decision process of satelliteSm to task tr |
满足任务约束的各从星分别向主星发出针对任务tr投标信息,包含执行任务的时间窗口、卫星完成该任务的成本和收益等,可由如下一个九元数组表示:
| $ \begin{array}{l} [m, {q_m}, r, {\rm{TaskTyp}}{{\rm{e}}_r}, {\rm{TaskS}}{{\rm{T}}_{rm}}, {\rm{TaskE}}{{\rm{T}}_{rm}}, \\ \;\;\;\;\;\;\;{\rm{TaskDuratio}}{{\rm{n}}_{rm}}, {\rm{Cos}}{{\rm{t}}_{rm}}, {\rm{Profi}}{{\rm{t}}_{rm}}]. \end{array} $ |
主星获得从星发出的投标信息,根据式(1)计算并比较各竞标从星完成任务的净收益,净收益最大的竞标从星将中标.其评标流程如图 2所示.

|
图 2 评标流程 Fig. 2 Bid evaluation process |
主星完成评标过程,将任务规划结果返回给执行任务的从星,任务规划结束,各从星生成新的任务规划方案.在此新任务方案的基础上可按招投标机制继续进行下一个子任务的安排.
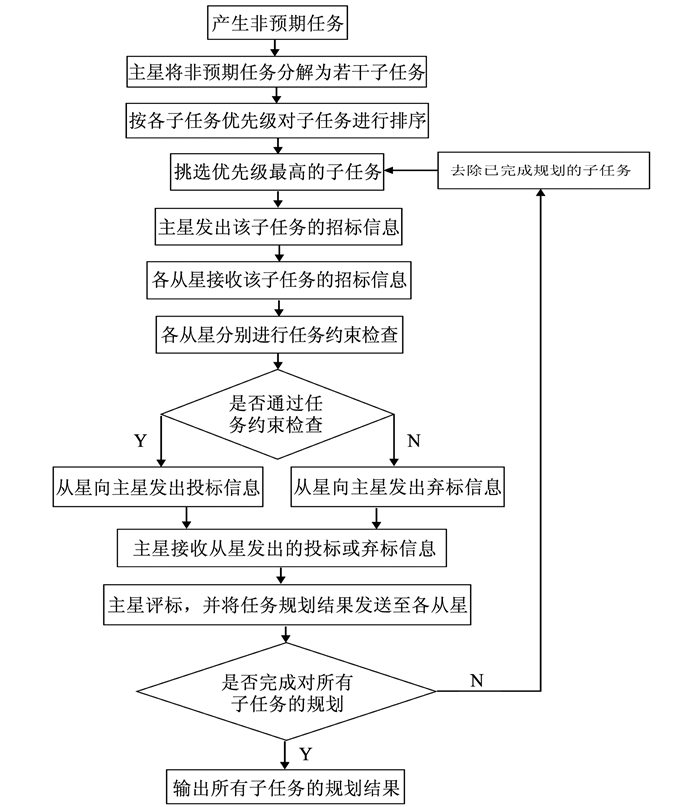
2.2 算法实现采用Matlab编程实现算法,算法流程如图 3所示.
|
图 3 基于招投标的星上自主任务规划求解算法 Fig. 3 On-board mission planning algorithm based on bidding |
Step1 当出现非预期任务时,主星发出非预期任务请求,并将该非预期任务分解为若干个子任务,组成子任务集合.
Step2 对子任务集合采用最大优先级策略决定子任务的执行顺序.
Step3 主星从子任务集合中挑选出优先级最高的子任务,向各从星发出招标信息.
Step4 各从星收到招标信息,进行子任务约束检查.
Step5 通过任务约束检查的从星向主星发出投标信息;否则从星发出空集投标信息,表示弃标.
Step6 主星接收投标信息,计算并比较各竞标从星完成任务的净收益,净收益最大的竞标从星将中标,主星完成评标过程,得到评标结果.
Step7 将评标结果返回给中标从星,中标从星执行该子任务规划方案.
Step8 主星判断是否完成对Step1所有子任务的规划安排,若是,则结束程序,输出任务规划方案;否则,继续进行下一子任务的安排,转Step2.
2.3 算法的时间复杂度分析假设可用工作卫星数目为m,每颗卫星的合同任务数量都为n,并考虑最坏的情况所有卫星都有k个候选时间窗口(k≥1).
针对一颗卫星和一个待判断的时间窗口,对应任务可能的插入点为(n+1)个.对第1个插入点,时间约束判断约需要3次计算,能源约束的判断约需要(n+1)次计算,因此总共需要计算(n+4)次,同理第2个插入点总共需要计算(n+3)次,这样直到最后一个插入点需要计算4次,总共需计算(n2+9n+8)/2,时间复杂度为O(n2).而针对k个时间窗口和m颗卫星而言,完成整个过程需要循环mk次.因而,算法结束共需的时间复杂度为多项式阶O(mkn2).由此可见,随着卫星的合同任务数n是算法时间复杂度的主要影响因素,随着卫星合同任务数n的增加,算法的时间复杂度加大.其中卫星数目m及各卫星的候选时间窗口数k也会在一定程度上影响算法的时间复杂度.
3 算例及分析 3.1 仿真环境在试验仿真中,所有算法和程序用MATLABR2014a编程软件实现,目标及卫星模型的建立、时间窗口的计算等均通过STK9.2仿真软件实现.仿真计算机环境为Intel Core i3-3220 CPU @ 3.30 GHz 3.30 GHz,8 GB RAM.
3.2 仿真场景说明本文设定10颗遥感卫星资源,构成卫星星座,如图 4所示.全球随机选择100个地面目标,先利用遗传算法给出各卫星的初始任务规划,然后随机选择一个目标作为发生非预期情况的目标,初始任务规划中负责观测该目标卫星则为星上自主任务规划时的主星,其余各星则为从星.设定星上自主规划周期为180 min,并考虑目标是在一定区域范围内实时移动和变化的.
|
图 4 卫星星群仿真模型 Fig. 4 Satellite constellation simulation model |
1) 招标过程.
设有突发任务T,将其分解为3个互相独立的子任务,即T = {t0, t1, t2},其中:t0、t1分别为普查任务; t2为详查任务.本文设定主星在发现非预期目标时算作已完成普查子任务t0,即主星只需对t1、t2进行招标.
本次算例中,主星S8发布招标信息见表 2.
| 表 2 子任务招标信息 Tab. 2 Subtask bidding information |
2) 投标过程.
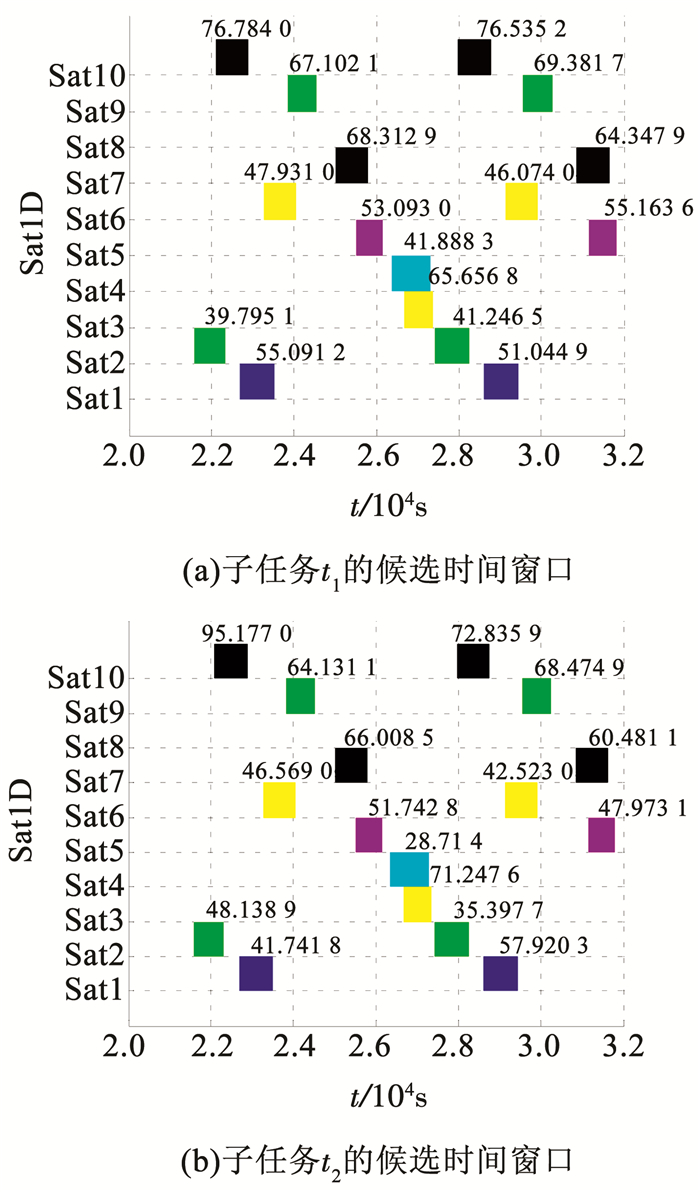
各从星收到招标信息,通过调用STK软件分别计算获得各星在一个规划周期(180 min)内对两个子任务对应动态目标的可见时间窗口集合,其候选时间窗口Gantt图如图 5所示.
|
图 5 各从星对子任务的候选可见时间窗口Gant图 Fig. 5 Candidate time window Gant graph for satellite to subtasks |
图 5中,横坐标为时间轴,纵坐标分别表示各卫星编号,每个矩形色块代表一个可见时间窗口,窗口旁的数字为选择在该时间窗口下执行相关子任务的收益值.
从图 5可以看出,在一个规划周期(180 min)内每颗从星对子任务t1、t2所对应的目标分别都至少有一个可见时间窗口.接下来各从星进行任务约束检查,以判断其在时间窗口内是否有“能力”完成招标子任务,从而自主决策投标或弃标.由此得到对子任务t1、t2的投标结果见表 3.
| 表 3 各从星对子任务的投标结果 Tab. 3 Bidding results of satellites to subtasks |
3) 评标过程.
主星接收投标信息,先对收益和成本进行去量纲化处理,见表 4.根据去量纲化结果,可以看出综合考虑收益与成本,对于子任务t1,从星S4优于卫从星S5,故从星S4中标,得到评标结果见表 5.
| 表 4 去量纲化过程 Tab. 4 De-dimensionalization process |
| 表 5 评标结果 Tab. 5 Bid evaluation result |
主星完成评标工作并将评标结果通知各从星,各星根据评标结果自主更新任务执行方案,得到一次非预期情况下的任务规划结果Gantt图如图 6所示.
|
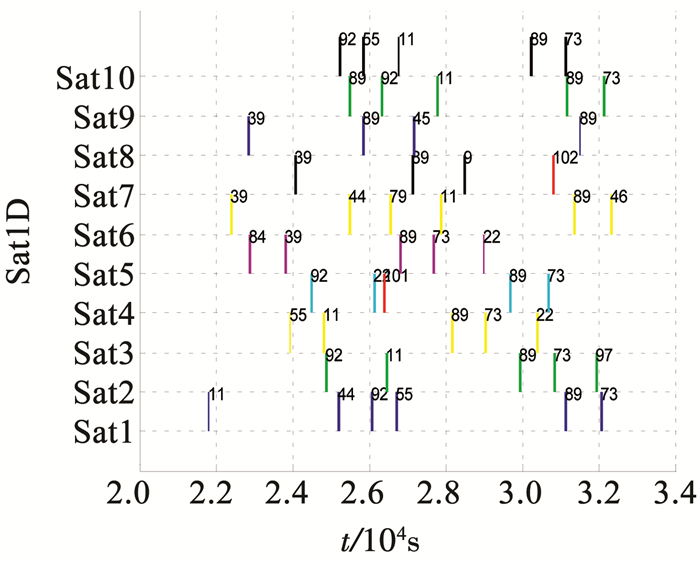
图 6 星上自主运行非预期任务规划结果Gantt图 Fig. 6 On-board autonomous mission planning Gantt diagram |
图 6中,横坐标为时间轴,纵坐标表示各卫星编号,每个矩形色块代表一个任务,其中红色矩形表示非预期子任务,其余矩形块为初始规划的任务.该算法完成了非预期情况下的任务规划.
3.3.2 算法性能对比与稳定性分析本文将招投标机制的多星任务规划算法与遗传算法这类典型智能进化算法比较,得到算法运行10次的时间数据见表 6,相应的数据函数图如图 7所示.
| 表 6 星上自主规划算法与智能进化算法运行时间数据比较 Tab. 6 Comparison of running time data between on-board autonomous planning algorithm and intelligent optinization algorithm |

|
图 7 星上自主规划算法与智能进化算法性能比较函数图 Fig. 7 Performance comparison between on-board autonomous planning algorithm and intelligent optincization algorithm |
上述结果表明,在条件完全相同的情况下,基于招投标机制的多星协同任务规划算法比遗传算法在计算速度上具有显著优势,可以满足星上计算的条件.
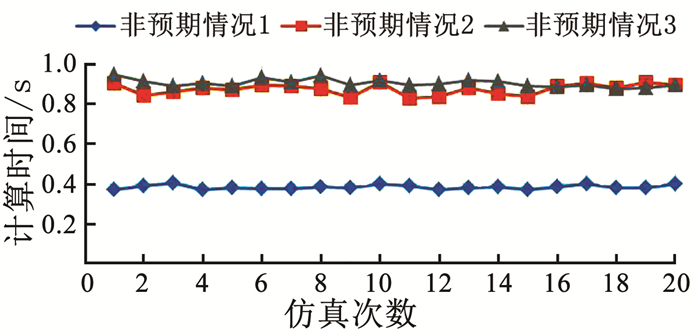
此外,本文针对3种不同的非预期情况,分别进行了20次星上自主任务规划仿真,得到计算时间函数图如图 8所示.
|
图 8 不同非预期情况下星上自主规划程序运行时间函数图 Fig. 8 Running time of on-board autonomous program under different unexpected conditions |
由图 8可知,对于同一种非预期情况,多次进行星上自主任务规划仿真,其运行时间较短、运行结果较稳定;针对不同的非预期情况,星上自主任务规划的仿真运行时间几乎无差异,其运行时间都在1 s以内.
综合上述分析,利用该算法对多星任务规划问题进行大规模求解时,可满足实际卫星星上计算能力较弱的特点,并能对非预期情况作出较快响应,表明该算法对实际应用具有一定的合理性、可行性及有效性.
3.3.3 有无星上自主规划对卫星快速响应能力影响有无星上自主规划对卫星快速响应能力影响见表 7.得到两类情况下的响应速度函数图如图 9所示.
| 表 7 有无星上自主规划对卫星在非预期情况下的响应策略 Tab. 7 Response strategy for satellites with/without on-board autonomous planning in unexpected situations |

|
图 9 有无星上自主规划卫星对非预期情况响应速度函数图 Fig. 9 Satellite response to unexpected situation with/without on-board autonomous planning |
由此说明,基于招投标机制的多星协同任务规划方法能够很好地实现对非预期情况的快速响应,充分发挥各卫星载荷能力,提高卫星遥感资源的利用效率.
4 结论1) 在充分考虑时间、载荷、能量等约束限制的前提下,构建了星上自主任务规划的数学模型.
2) 考虑在动态复杂的观测环境中,将一次完整的任务规划合理分解为招标、投标和评标3个过程,同时引入收益、成本等评价参数,详细设计了星上自主任务规划算法求解流程及相应的约束检验规则.
3) 通过仿真算例验证了算法的合理性、可行性及有效性,并通过仿真比较实验验证了该算法对非预期情况的快速响应能力,对提升卫星管理与规划水平提供一种有益的思路.
| [1] |
祝周鹏.面向任务的卫星平台载荷配置与应急规划技术[D].长沙: 国防科学技术大学, 2013: 13 ZHU Zhoupeng. Task-oriented satellite platform payloads configuration and contingency scheduling technology[D]. Changsha: National University of Defense Technology, 2013: 13 http://cdmd.cnki.com.cn/Article/CDMD-90002-1015958904.htm |
| [2] |
KARAPETYAN D, MITROVIC-MINIC S, MALLADI K T, et al. The satellite downlink scheduling problem: a case study of RADARSAT-2[M]//MURTY K G. Case Studies in Operations Research. New York: Springer, 2015: 497. DOI: 10.1007/978-1-4939-1007-6_21
|
| [3] |
ZHENG Zixuan, GUO Jian, GILL E. Swarm satellite mission scheduling & planning using Hybrid Dynamic Mutation Genetic Algorithm[J]. Acta Astronautica, 2017, 137: 243. DOI:10.1016/j.actaastro.2017.04.027 |
| [4] |
BARBULESCU L, HOWE A, WHITLEY D. AFSCN Scheduling: how the problem and solution have evolved[J]. Mathematic and Computer Modeling, 2006, 43(9/10): 1023. DOI:10.1016/j.mcm.2005.12.004 |
| [5] |
苗悦.编队飞行成像卫星的自主任务规划技术研究[D].哈尔滨: 哈尔滨工业大学, 2016: 12 MIAO Yue. Research on autonomous task planning of imaging satellite of formation flying[D]. Harbin: Harbin Institute of Technology, 2016: 12 |
| [6] |
VERFAILLIE G, BORNSCHLEGL E. Designing and evaluating an on-line on-board autonomous Earth observation satellite scheduling system[C]//Proceedings of the 2nd NASA International Workshop on Planning and Scheduling for Space. California: [s.n.], 2013: 122
|
| [7] |
刘嵩, 陈英武, 邢立宁, 等. 敏捷成像卫星时间依赖型调度问题、模型与算法[J]. 系统工程理论与实践, 2016, 36(3): 787. LIU Song, CHEN Yingwu, XING Lining, et al. Model and algorithm of the time-dependent agile imaging satellite scheduling problem[J]. Systems Engineering——Theory & Practice, 2016, 36(3): 787. DOI:10.12011/1000-6788(2016)03-0787-08 |
| [8] |
赵萍, 陈志明. 应用于卫星自主任务调度的改进遗传算法[J]. 中国空间科学技术, 2016, 36(6): 47. ZHAO Ping, CHEN Zhiming. An adapted genetic algorithm applied to satellite autonomous task scheduling[J]. Chinese Space Science and Technology, 2016, 36(6): 47. DOI:10.16708/j.cnki.1000-758x.2016.0064 |
| [9] |
LUO Kaiping, WANG Haihong, LI Yijun, et al. High-performance technique for satellite range scheduling[J]. Computers & Operations Research, 2017, 85: 12. DOI:10.1016/j.cor.2017.03.012 |
| [10] |
王钧.成像卫星综合任务调度模型与优化方法研究[D].长沙: 国防科学技术大学, 2007: 12 WANG Jun. Research on modeling and optimization techniques in united mission scheduling of imaging satellites[D]. Changsha: National University of Defense Technology, 2007: 12 http://cdmd.cnki.com.cn/Article/CDMD-90002-2008098680.htm |
| [11] |
XHAFA F, SUN Junzi, BAROLLI A, et al. Genetic algorithms for satellite scheduling problems[J]. Mobile Information Systems, 2012, 8(4): 351. DOI:10.1155/2012/717658 |
| [12] |
WU Guohua, LIU Jin, MA Manhao, et al. A two-phase scheduling method with the consideration of task clustering for earth observing satellites[J]. Computers & Operations Research, 2013, 40(7): 1884. DOI:10.1016/j.cor.2013.02.009 |
| [13] |
黄生俊, 邢立宁, 郭波. 基于改进模拟退火的多星任务规划方法[J]. 科学技术与工程, 2012, 12(31): 8293. HUANG Shengjun, XING Lining, GUO Bo. Multi-satellites mission scheduling technique based on improved simulated annealing[J]. Science Technology and Engineering, 2012, 12(31): 8293. DOI:10.3969/j.issn.1671-1815.2012.31.031 |
| [14] |
MOUW C B, GREB S, AURIN D, et al. Aquatic color radiometry remote sensing of coastal and inland waters: challenges and recommendations for future satellite missions[J]. Remote Sensing of Environment, 2015, 160(2): 15. DOI:10.1016/j.rse.2015.02.001 |
| [15] |
高黎.对地观测分布式卫星系统任务协作问题研究[D].长沙: 国防科学技术大学, 2007: 68 GAO Li. Resesrch on earth observation task cooperation for distributed satellites system[D]. Changsha: National University of Defense Technology, 2007: 68 |
 2019, Vol. 51
2019, Vol. 51


