2. 首钢集团有限公司矿业公司,河北 迁安 064400
2. Mining Corporation of Shougang Group Co., Ltd., Qian'an 064400, Hebei, China
中国铁矿石平均采出品位不足30%,需要将原矿加工富集成精矿才能用于冶炼,近年来中国年产铁矿石10~13亿t,破碎工作量大、单位能耗过高、且各破碎阶段能耗分布不合理,导致能源大量浪费,矿山生产成本较高.因此,降低铁矿石破碎加工的能量消耗对提升矿山经济效益和社会与环境效益有重要的意义.
破碎的目的在于降低矿石粒度,明确破碎能量与粒度的理论关系是降低矿石加工能耗的前提.很多学者致力于这方面的研究,并取得较为丰富的研究成果.在爆破方面,高应变率霍普金森(SHPB)压杆试验成为研究爆破冲击能量与矿石块度关系的重要方法.张文清等[1]通过霍普金森冲击破碎试验探究了煤岩冲击破碎的能量转化关系,分析了破碎能量与破碎粒度之间的相关关系.郭连军等[2]基于SHPB试验建立磁铁石英岩破碎块度与能耗关系模型,并揭示了有效能耗的变化机制.在机械破碎方面,一些学者通过多种破碎试验手段建立了破碎能量与破碎产品粒度模数、粒度分形维数、相对破碎率和Webull模数的关系模型,例如Tavares[3]和胡振中等[4]做的落锤冲击试验,Buhl等[5]做的弹射冲击破碎试验,Saeidi等[6]做的压缩加载破碎试验.Stamboliadis[7]使用以往相关试验数据对Gates-Gaudin-Schuhmann粒度分布模型和能量模型综合推导,得到了脆性材料破碎能与颗粒粒度之间理论关系.在磨矿方面,Tsiboukis[8]基于颗粒破碎能量与磨机消耗能量的比值为常数的假设,通过脆性材料的破碎和磨矿试验得到了颗粒尺寸模量与能量消耗的关系.LIU等[9]使用棒磨机对不同的煤块样品进行破碎,通过Rosin-Rammler分布分析破碎效果,发现破碎能量与入料粒度和破碎粒度正相关.Weerasekara等[10]使用离散元软件模拟磨机内部磨矿环境,通过改变入料粒度和磨机尺寸模拟研究二者对磨机能耗和平均颗粒碰撞能量的负相关关系,分析了磨机内不同区域的能量类型.
综上所述,现有的研究结果仍局限在各破碎阶段,难以描述整个破碎过程的能量与粒度的发展变化关系.李占金等[11]提出,明确铁矿石破碎能量在各阶段的分布规律,提高低能耗、高效率的阶段能量比例,可以降低高能耗、低效率的阶段能量比例,从而降低破碎系统能量.选择冀东—密云地区典型铁矿山为对象,将矿石从原矿破碎至精矿粒度的所有阶段作为一个破碎系统,分析铁矿石在各破碎阶段的能量分布和粒度分布特征,得到破碎系统能量与矿石粒度的关系,建立破碎能量理论模型拟合阶段破碎能量与入破粒度和破碎产物粒度的关系公式,验证理论模型的准确性与适用性,为铁矿山矿石破碎能量计算提供理论依据.
1 矿石破碎能量与粒度关系理论 1.1 破碎能量与粒度关系基础理论早期的矿石破碎能量与粒度关系理论主要包括Rittinger面积假说(1867年)和Kick体积假说(1885年),面积假说认为破碎能量与新生表面积呈函数关系, 模式公式为
| $ E = K\left( {1/{x_2} - 1/{x_1}} \right), $ | (1) |
式中:E为单位破碎能量; K为与材料性质相关的系数; x2破为破碎后的矿石粒度; x1为破碎前的矿石粒度.
体积假说认为能量促使物料颗粒体积减小,体积减小量与施加能量呈比例关系, 模式公式为
| $ E = - K\ln \left( {{x_2}/{x_1}} \right). $ | (2) |
Walker等[12]通过统计大量的磨矿数据,分析得出能量与破碎粒度关系的统一模型,并且给出了粒度指数的取值范围,模型公式为
| $ {\rm{d}}E = - K{\rm{d}}x/{x^n},1 < n < 2. $ | (3) |
式中:x为颗粒粒度; n为磨机指数,其余符号意义同前.
Bond[13]总结以往研究结果,并通过碎磨矿实验,提出破碎能量消耗与裂隙长度成正比,得出了著名的Bond能量公式,该公式成为矿物加工领域磨矿流程优化的指导依据.Bond能量公式为
| $ W = 2K\left( {1/\sqrt {{x_2}} - 1/\sqrt {{x_1}} } \right), $ | (4) |
式中W为单位破碎能量,其余符号意义同前.
Bond能量方程又称为“第三能量理论”,用于磨矿的能量粒度计算准确度较高.下式是相关学者和工程技术人员普遍接受和使用的Bond能量公式:
| $ W = {W_i}\left( {10/\sqrt P - 10/\sqrt F } \right). $ | (5) |
式中:Wi为功指数; P为通过率为80%的产品粒度; F为通过率为80%的供料粒度.
对Walker函数分析可得出,当n=2时,对应Rittinger公式;当n=1时,对应Kick公式;当x为80%累积质量分数粒度时,n=1.5的Walker函数对应Bond公式.根据实际生产验证,Rittinger公式适用于10~100 μm的细磨范围,Kick公式适用于大于1 mm的破碎范围,Bond公式适用于棒磨和球磨范围.
Hukki[14]在1962年通过破碎与磨矿实验,指出式(1)、(2)、(4)仅适用与相对较窄的粒度范围,式(3)的指数n与粒度有函数关系,即n=f(x),认为式(3)的正确形式应为
| $ {\rm{d}}E = - K{\rm{d}}x/{x^{f\left( x \right)}}. $ | (6) |
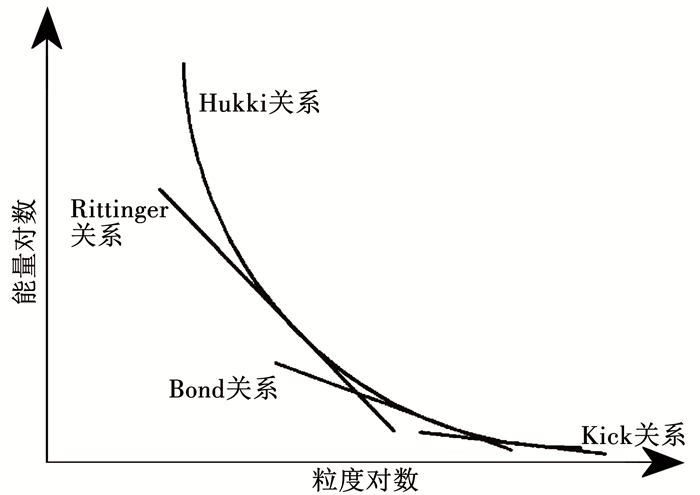
Thomas等[15]研究了Hukki能量指数与破碎颗粒尺寸之间的相关关系,绘制了破碎能量与粒度的关系图像,如图 1所示.
|
图 1 能量与粒度双对数关系 Fig. 1 Logarithmic relation between energy and particle size |
结合式(6),Morrell[16]根据磨矿试验结果对Bond功指数进行深入研究,得到指数n与粒度相关的新能量模型,取得较好的磨矿能量预测结果,如
| $ W = {M_i}{K_{\rm{t}}}\left( {x_2^{f\left( {{x_2}} \right)} - x_1^{f\left( {{x_1}} \right)}} \right), $ | (7) |
式中Kt为用于平衡方程单位的常数.
在此基础上,Morrell[17]分别就破碎和磨矿对能量模型进行了改进,得到适合于矿石辊磨和传统破碎的能量计算方法.
1.2 破碎系统中能量与粒度关系理论模型上述理论揭示了机械破碎与磨矿阶段的能量与粒度的变化关系,但式(1)~(7)试验条件与适用的粒度范围不同.为拓宽破碎能量计算的粒度范围,将各破碎阶段看做一个系统,整合以上能量与粒度理论关系,提出统一的矿石破碎能量理论模型为
| $ E = - {K_1}\ln \left( {{x_2}/{x_1}} \right) + {K_2}\left( {1/x_2^a - 1/x_1^b} \right) + t. $ | (8) |
式中:K1、K2分别为平衡方程单位的拟合系数; x1为破碎前矿石特征粒度; x2为破碎后矿石特征粒度;a、b分别为特征粒度指数;t为能量常数.
2 铁矿石破碎能量的分布特征 2.1 铁矿石样品性质冀东—密云地区赋存大量的沉积变质型铁矿,矿石类型主要为条带硅铁建造的磁铁石英岩(BIF型磁铁矿).采集该地区水厂铁矿、马兰庄铁矿和大石河铁矿矿石破碎能量数据,并在水厂铁矿和马兰庄铁矿选厂取样,统计矿石粒度分布特征.由于大石河铁矿选厂原矿来自多家矿山,矿石性质不统一,没有进行样品采集.
水厂铁矿、马兰庄铁矿的矿床由火山热液喷流与沉积形成[18].矿石以BIF型磁铁矿为主,条带状、条纹状、浸染状构造,粒状变晶结构,矿物成分主要包括石英、磁铁矿、辉石、角闪石.水厂铁矿标准圆柱体铁矿石试件平均强度为98 MPa,甘德清等[19]发现该矿山铁矿石中磁铁矿含量为15%~36%,石英含量为55%,其余辉石、角闪石、方解石含量分别为5%~20%.马兰庄铁矿标准圆柱体铁矿石试件平均强度为122 MPa,矿石中有用矿物磁铁矿平均含量为27.1%,脉石矿物以石英、辉石为主,包含少量的角闪石、黑云母和石榴子石.
2.2 能量参数采集与计算在水厂铁矿、马兰庄铁矿、大石河铁矿调研单位炸药消耗量、爆破平均块度、破碎设备和磨矿设备的型号与数量、生产功率、小时生产能力、产量比例等指标.为统一能量单位,根据矿山开采所用炸药的种类、炸药单耗和热值大小,将炸药单耗的单位kg/t换算为kWh/t,换算关系如
| $ {e_{\rm{b}}} = {q_{\rm{b}}}{Q_{\rm{e}}}/\left( {3.6 \times {{10}^6}} \right). $ | (9) |
式中:eb为单位爆破能量, kWh/t; qb为采场爆破单位质量矿石炸药消耗量, kg/t; Qe为炸药热值, J/kg.
根据机械破碎与磨矿设备的生产功率、小时生产能力和产量比例,按加权平均法计算矿山各破碎阶段的单位能量,如
| $ {e_{\rm{c}}} = \sum {{P_i}{\eta _i}} /{m_i}. $ | (10) |
式中:ec为某破碎阶段的单位破碎能量, kWh/t; Pi为某破碎阶段第i个设备的生产功率, kW; mi为某破碎阶段第i个设备的生产能力, t/h; ηi为某破碎阶段第i个设备的生产能力与总破碎能力的比值.
水厂铁矿平均炸药单耗0.201 5 kg/t,炸药类型为乳化铵油炸药,按式(10)换算后爆破单位能量消耗为0.08 kWh/t;马兰庄铁矿平均炸药单耗为0.212 6 kg/t,炸药类型为乳化炸药,换算后爆破单位能量消耗为0.085 kWh/t.根据矿山生产数据的调研结果,按式(9)计算各破碎阶段的单位能量,见表 1.大石河铁矿选厂的原矿来源于多家矿山,不同矿山爆破工艺有差异,没有采集爆破阶段的单位能量.
| 表 1 铁矿石破碎单位能量 Tab. 1 Comminution specific energy of iron ore |
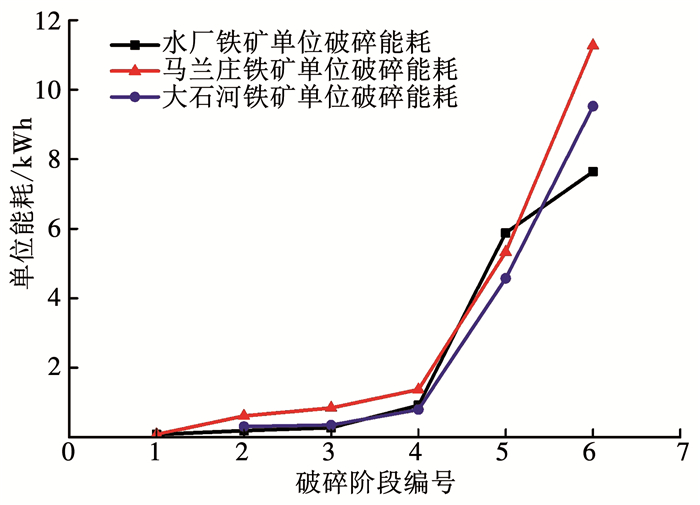
将爆破、粗碎、中碎、细碎、一段磨矿、二段磨矿看作铁矿石破碎系统,并对各破碎阶段进行编号,依次为1、2、3、4、5、6,绘制水厂铁矿、马兰庄铁矿和大石河铁矿的单位破碎能量在各阶段的变化曲线,如图 2所示.
|
图 2 铁矿山矿石破碎单位能量的变化曲线 Fig. 2 Curves of comminution specific energy in iron mine |
由图 2可知,在爆破至二段磨矿的过程中,铁矿石单位破碎能量指数增长.根据破碎能量与粒度关系理论,在矿山破碎系统的各阶段中,随着破碎阶段的变迁,矿石粒度的不断减小,新生表面积和新生裂隙数量急剧增加,颗粒体积急剧减小,需要的断裂表面能快速升高,单位能量消耗出现指数增大的变化规律,在矿山破碎系统中体现的单位能量变化特征符合破碎能量与粒度关系理论.
在爆破、粗破、中破、细破阶段,铁矿石破碎单位能量均小于1.5 kWh/t,且上升缓慢;在一段磨矿、二段磨矿阶段,单位能量均超过4.5 kWh/t,且上升速率较大.由此说明各阶段破碎能量差异较大,能量分布不合理,有必要把各破碎环节看做一个系统,实现铁矿石在破碎系统中不同破碎尺度下的能量计算,调节各阶段能量合理分布.
3 铁矿石破碎产品粒度分布特征从马兰庄铁矿选厂和水厂铁矿选厂采集粗碎、中碎、细碎、一段磨矿、二段磨矿的直接产品,粗碎与中碎样品在传输带上分段随机取样,细碎、一段磨矿、二段磨矿样品按四分法取样.
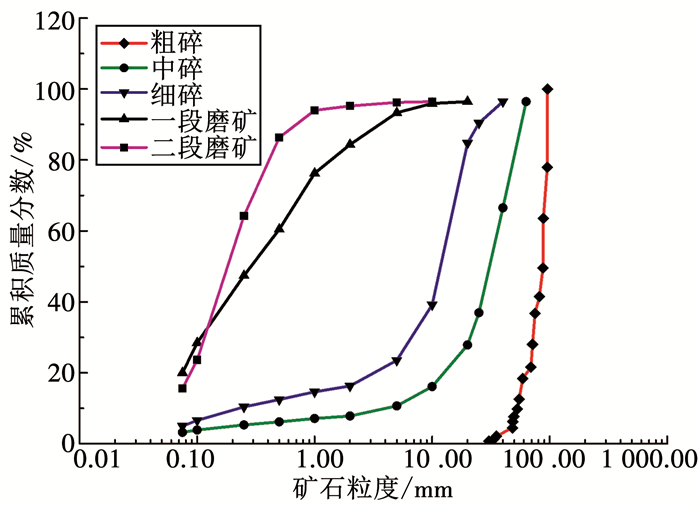
表 2为马兰庄铁矿与水厂铁矿的实际排矿粒度.由于粗碎和水厂铁矿中碎的矿石样品粒度偏大,不便于筛分,根据周仕学等[20]介绍的Heywood对不规则颗粒尺寸的测量方法,将此部分矿石样品以最大稳定度置于水平面上,用投影法测出矿石三维尺寸,计算不规则矿石的三轴调和平均径,然后用高精度电子秤测量矿石的质量,根据矿石三轴调和平均径与矿石质量,得到矿石粒度分布;其余矿石样品使用筛孔尺寸为0.075、0.100、0.250、0.500、1.000、2.000、5.000、10.000、20.000、25.000、40.000、63.000 mm的标准筛筛分得到等效粒度,用高精度电子秤测量筛上矿石质量.根据粒度测量、筛分和称重结果,绘制各破碎阶段铁矿石累积质量分布曲线,如图 3、4所示.
| 表 2 不同破碎阶段的排矿粒度范围 Tab. 2 Actual discharge scale in crushing stages |
|
图 3 马兰庄铁矿不同破碎阶段矿石累积质量分布曲线 Fig. 3 Cumulative mass distribution curves of different comminution stages of Malanzhuang Iron Mine |

|
图 4 水厂铁矿不同破碎阶段矿石累积质量分布曲线 Fig. 4 Cumulative mass distribution curves of different comminution stages of Shuichang Iron Mine |
拟合矿石累积质量分布曲线,得到各破碎阶段的累积质量分布函数,计算筛下累积质量分数为50%的中值粒度d50和累积质量分数为80%的特征粒度d80,见表 3.由表 3可知,矿石在粗碎至二段磨矿的破碎过程中,粒度分布经历了指数函数分布、多项式函数分布和朗缪尔幂函数分布的变化规律,磨矿阶段的矿石产品粒度均符合朗缪尔幂函数分布.
| 表 3 铁矿石样品累积质量分布函数与计算结果 Tab. 3 Cumulative mass distribution function and calculation result of the iron ore samples |
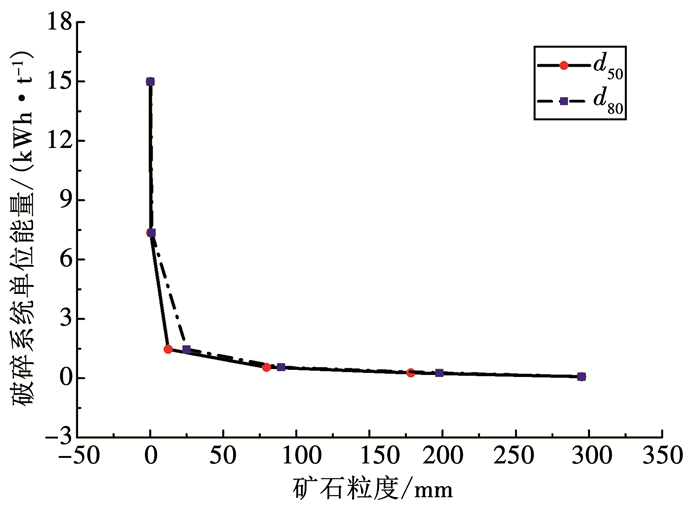
矿石破碎系统能量为原矿破碎至某种粒度时需要消耗的总能量.调研得到马兰庄铁矿平均爆破块度为333 mm,水厂铁矿平均爆破块度为295 mm.将表 1中各破碎阶段的单位能量依次累积,得到破碎系统单位能量,结合爆破平均块度与表 3的中值粒度d50和特征粒度d80,绘制原矿在破碎系统中单位能量与矿石粒度关系曲线,如图 5、6所示.由图 5、6可知,随着矿石粒度的降低,系统单位能量出现阶段性增长变化,在d50 > 12 mm或d80 > 25 mm的范围内系统单位能量增长缓慢,在d50 < 12 mm或d80 < 25 mm的范围内急剧增长,当d50为12 mm或d80为25 mm时破碎系统能量与粒度关系出现转折.

|
图 5 马兰庄铁矿破碎系统单位能量与产物粒度关系 Fig. 5 Relationship between the system specific energy and particle size of the Malanzhuang Iron Mine |
|
图 6 水厂铁矿破碎系统单位能量与产物粒度关系 Fig. 6 Relationship between the system specific energy and particle size of the Shuichang Iron Mine |
通过数值回归拟合得到破碎系统单位能量与矿石粒度的关系特征函数,以下各式分别为马兰庄铁矿破碎系统单位能量与矿石粒度函数、水厂铁矿破碎系统单位能量与矿石粒度函数.
| $ \left\{ \begin{array}{l} {E_0} = 212.789{{\rm{e}}^{\left( { - \frac{{{d_{50}}}}{{0.067}}} \right)}} + 80\;004.826d_{50}^{ - 1.034 \times {{10}^{ - 5}}} - 80\;000.17,\\ {r^2} = 0.995; \end{array} \right. $ | (11) |
| $ \left\{ \begin{array}{l} {E_0} = 42.304{{\rm{e}}^{\left( { - \frac{{{d_{80}}}}{{0.456}}} \right)}} + 80\;005.263d_{80}^{ - 1.227 \times {{10}^{ - 5}}} - 79\;999.137,\\ {r^2} = 0.995; \end{array} \right. $ | (12) |
| $ \left\{ \begin{array}{l} {E_0} = 20.819{{\rm{e}}^{\left( { - \frac{{{d_{50}}}}{{0.3}}} \right)}} + 6\;002.777d_{50}^{ - 7.362 \times {{10}^{ - 5}}} - 6\;000.22,\\ {r^2} = 0.999\;8; \end{array} \right. $ | (13) |
| $ \left\{ \begin{array}{l} {E_0} = 16.323{{\rm{e}}^{\left( { - \frac{{{d_{80}}}}{{0.889}}} \right)}} + 6\;004.106d_{80}^{ - 9.334 \times {{10}^{ - 5}}} - 6\;000.89,\\ {r^2} = 0.999\;2. \end{array} \right. $ | (14) |
式(11)~(14)的拟合度高,能较好的描述破碎系统能量与矿石粒度的关系,拟合系数差异较大可能是矿石强度性质、设备效率等因素导致的,铁矿山将原矿破碎至某种粒度的系统单位能量与粒度的关系模型为
| $ {E_0} = K{e^{\left( { - d/{t_0}} \right)}} + \alpha {d^{ - \beta }} - t. $ |
式中:E0为单位质量原矿破碎至某一粒度所需要的系统能量; K、t0、α、β分别为与矿石性质、设备效率有关的拟合系数; d为矿石粒度; t为能量常数.
4.2 阶段破碎能量与粒度关系阶段破碎能量为矿石从粒度x1降低至粒度x2时需要消耗的能量.根据调研结果,马兰庄铁矿矿石平均密度为3.4 t/m3,计算马兰庄铁矿1 t矿石的等球粒度为825.24 mm,爆破产物平均粒度为333 mm;水厂铁矿矿石平均密度为3.24 t/m3,计算水厂铁矿1 t矿石的等球粒度为838.6 mm,爆破产物平均粒度为295 mm.
铁矿石上一阶段的产品粒度为下一阶段的入破粒度,根据表 1中各破碎阶段的单位破碎能量、水厂铁矿和马兰庄铁矿爆破的入破粒度和产物平均粒度、表 3中的矿石中值粒度d50和特征粒度d80,利用式(8)进行拟合,建立破碎系统中阶段破碎能量与入破粒度和产品粒度的函数,如以下各式所示.
根据特征粒度d80得到的马兰庄铁矿阶段破碎单位能量与入破粒度、产物粒度的函数模型为
| $ \left\{ \begin{array}{l} E = 6.365 \times {10^{ - 4}}\ln \left( {{x_2}/{x_1}} \right) + 4.458\left( {x_2^{ - 1.003} - x_1^{0.071}} \right) + 7.278,\\ {r^2} = 0.999\;9. \end{array} \right. $ | (15) |
根据中值粒度d50得到的马兰庄铁矿阶段破碎单位能量与入破粒度、产物粒度的函数模型为
| $ \left\{ \begin{array}{l} E = - 0.131\ln \left( {{x_2}/{x_1}} \right) + 1.268\left( {x_2^{ - 2.111} - x_1^{0.291}} \right) + 1.85,\\ {r^2} = 0.995. \end{array} \right. $ | (16) |
根据特征粒度d80得到的水厂铁矿阶段破碎单位能量与入破粒度、产物粒度的函数模型为
| $ \left\{ \begin{array}{l} E = 1.178\ln \left( {{x_2}/{x_1}} \right) + 18.151\left( {x_2^{ - 0.24} - x_1^{ - 0.152}} \right) + 3.223,\\ {r^2} = 0.999\;9. \end{array} \right. $ | (17) |
根据中值粒度d50得到的水厂铁矿阶段破碎单位能量与入破粒度、产物粒度的函数模型为
| $ \left\{ \begin{array}{l} E = 0.825\ln \left( {{x_2}/{x_1}} \right) + 10.73\left( {x_2^{ - 0.271} - x_1^{ - 0.131}} \right) + 3.07,\\ {r^2} = 0.999\;9. \end{array} \right. $ | (18) |
由式(15)~式(18)可知,阶段破碎的单位能量与入破粒度和产品粒度高度拟合.使用式(15)、(16)计算马兰庄铁矿各阶段破碎单位能量,使用式(17)、(18)计算水厂铁矿各阶段的破碎单位能量,并与实际调研结果进行对比见表 4~7中,表 4~7中爆破阶段的入破粒度x1为1 t原矿的等球粒度,产物粒度x2为现场调研的爆破产物平均粒度.
| 表 4 根据d80计算马兰庄铁矿阶段破碎单位能量 Tab. 4 Calculation of specific energy in stage comminution of Malanzhuang Iron Mine with d80 |
| 表 5 根据d50计算马兰庄铁矿阶段破碎单位能量 Tab. 5 Calculation of specific energy in stage comminution of Malanzhuang Iron Mine with d50 |
| 表 6 根据d80计算水厂铁矿阶段破碎单位能量 Tab. 6 Calculation of specific energy in stage comminution of Shuichang Iron Mine with d80 |
| 表 7 根据d50计算水厂铁矿阶段破碎单位能量 Tab. 7 Calculation of specific energy in stage comminution of Shuichang Iron Mine with d50 |
由表 4~7可知,阶段破碎单位能量计算值与实际值吻合较好,式(8)描述的阶段破碎单位能量与粒度的函数关系具有较高的可靠性,可作为铁矿石破碎能量理论模型,为铁矿石破碎能量计算提供理论依据.
5 讨论能量是驱动矿石破碎的根本原因,破碎的目的是降低矿石粒度,因此研究破碎能量与粒度的关系有重要的意义.累积质量分数为80%的特征粒度(d80)是矿石破碎加工的常用指标,也是破碎能量计算的特征粒度.Martins [21]计算了不同破碎条件下入料与破碎产物的特征粒度,发现适用于三大能量理论的特征粒度基本小于d80.破碎过程中,矿石粒度越小,产生的比表面积越大,需要消耗的单位能量越大,在理论上中值粒度d50与破碎能量的相关性高于d80.因此,认为仅仅使用d80计算破碎能量是不可靠的,还需要用中值粒度d50进行验证.
LI等[22]认为矿石破碎的碎块粒度分布具有自相似性,Fuerstenau等[23]研究得出粒度分布自相似性的重要特征是粒度谱按中值粒度减小的方式向细粒级区间转移,中值粒度是衡量破碎产物细度的有效指标.因此,使用特征粒度d80和中值粒度d50分别建立矿山破碎系统单位能量和矿石粒度的关系曲线和关系函数,得到的能量变化规律一致.在建立马兰庄铁矿和水厂铁矿的阶段破碎单位能量与入破粒度和产物粒度关系函数时,分别使用了d80和d50,发现能量计算结果都达到很高的精度,说明破碎能量理论模型具有较好的可靠性.在各破碎阶段中,马兰庄铁矿和水厂铁矿的矿石粒度相差较大,但是使用矿石破碎能量理论模型拟合两家矿山的阶段破碎单位能量与粒度的关系时,均取得了很高的拟合度,说明所建立的破碎能量理论模型具有较强的适用性.需要说明的是:使用破碎能量理论模型计算阶段破碎单位能量时,破碎系统单位能量与粒度的关系模型是选择入破粒度与产物粒度的理论依据;反过来,将破碎能量理论模型的计算结果进行累加运算可得到新的破碎系统单位能量值,进而评价破碎系统能量分布的合理性,所计算的阶段破碎单位能量为破碎系统中能量调节与优化提供量化指导.
破碎能量理论模型把矿石破碎的各阶段看做一个整体,体现了系统工程的思想.根据文献[18]的研究,冀东—密云成矿带沉积变质型铁矿地质成矿作用一致,铁矿石类型主要为条带硅铁建造磁铁矿,矿石性质相近.通过该地区典型矿山生产调研数据对破碎能量理论模型加以应用和验证,目前认为式(8)所描述的破碎能量理论模型适用于冀东—密云地区沉积变质型铁矿石破碎能量计算,建议使用d80和d50作为入破粒度和产物粒度指标,对能量计算结果相互验证.适用于能量计算理论模型的d80和d50均是容易测试的粒度,便于通过实验检验工艺流程设计在能量优化环节的合理性,通过两种粒度指标的双重计算,可以提高矿山破碎能量成本核算的精度.
6 结论1) 将铁矿石从原矿破碎至精矿粒度的所有阶段作为一个矿石破碎系统,在破碎系统中随矿石粒度的减小,破碎单位能量指数升高;爆破与选厂破碎的单位能量均小于1.5 kWh/t,磨矿单位能量均大于4.5 kWh/t.
2) 铁矿石在选厂各阶段破碎中,矿石粒度依次呈现指数函数分布、多项式函数分布和朗缪尔幂函数分布的特征,磨矿产品的粒度分布均为朗缪尔幂函数分布.在破碎系统中,系统单位能量随产品粒度的减小呈阶段性的增长变化,在d50>12 mm或d80>25 mm的范围内增长缓慢,在d50 < 12 mm或d80 < 25 mm的范围内的范围内急剧增长,由此建立了破碎系统单位能量与产品粒度的关系模型.
3) 构建破碎系统中铁矿石破碎能量理论模型,扩大了破碎能量计算的粒度范围,拟合马兰庄铁矿和水厂铁矿各阶段破碎单位能量、入破粒度和产品粒度,得到矿石阶段破碎能量与入破粒度和产品粒度的关系函数,经验证,所建立的铁矿石破碎能量理论模型具有较高的可靠性,可以作为在铁矿山矿石破碎能量的计算依据.
| [1] |
张文清, 石必明, 穆朝民. 冲击载荷作用下煤岩破碎与耗能规律实验研究[J]. 采矿与安全工程学报, 2016, 33(2): 375. ZHANG Wenqing, SHI Biming, MU Chaomin. Experimental research on failure and energy dissipation law of coal under impact load[J]. Journal of Mining & Safety Engineering, 2016, 33(2): 375. DOI:10.13545/j.cnki.jmse.2016.02.029 |
| [2] |
郭连军, 杨跃辉, 张大宁, 等. 冲击荷载作用下磁铁石英岩破碎能耗分析[J]. 金属矿山, 2014(8): 1. GUO Lianjun, YANG Yuehui, ZHANG Daning, et al. Analysis on the fragmentation energy consumption of magnetite quartzite under impact loads[J]. Metal Mine, 2014(8): 1. |
| [3] |
TAVARES L M. Energy absorbed in breakage of single particles in drop weight testing[J]. Minerals Engineering, 1999, 12(1): 43. DOI:10.1016/S0892-6875(98)00118-6 |
| [4] |
胡振中, 庄亚明, 蔡天意, 等. 单颗粒煤岩冲击破碎能耗与粒度分布特性试验研究[J]. 煤炭学报, 2015, 40(S1): 230. HU Zhenzhong, ZHUANG Yaming, CAI Tianyi, et al. Experimental study on energy consumption and particle size distribution of single particle coal under impact crushing[J]. Journal of China Coal Society, 2015, 40(S1): 230. DOI:10.13225/j.cnki.jccs.2014.1179 |
| [5] |
BUHL E, SOMMER F, POELCHAU M H, et al. Ejecta from experimental impact craters: particle size distribution and fragmentation energy[J]. Icarus, 2014, 237: 131. DOI:10.1016/j.icarus.2014.04.039 |
| [6] |
SAEIDI F, TAVARES L M, YAHYAEI M, et al. A phenomenological model of single particle breakage as a multi-stage process[J]. Minerals Engineering, 2016, 98: 90. DOI:10.1016/j.mineng.2016.07.006 |
| [7] |
STAMBOLIADIS T H. A contribution to the relationship of energy and particle size in the comminution of brittle particulate materials[J]. Minerals Engineering, 2002, 15(10): 707. DOI:10.1016/S0892-6875(2)00185-1 |
| [8] |
TSIBOUKIS S J. Study on the crushing and grinding of brittle materials[D]. Chania: Technical University of Crete, 1995
|
| [9] |
LIU Xuemin, ZHANG Man, HU Nan. Calculation model of coal comminution energy consumption[J]. Minerals Engineering, 2016, 92: 21. DOI:10.1016/j.mineng.2016.01.008 |
| [10] |
WEERASEKARA N S, LIU L X, POWELL M S. Estimating energy in grinding using DEM modeling[J]. Minerals Engineering, 2016, 85: 23. DOI:10.1016/j.mineng.2015.10.013 |
| [11] |
李占金, 乔国刚, 米雪玉, 等. 冀东磁铁矿石粉碎过程节能降耗研究[J]. 中国矿业大学学报, 2008, 37(5): 625. LI Zhanjin, QIAO Guogang, MI Xueyu, et al. Energy savings during magnetite ore preparation in eastern Hebei province[J]. Journal of China University of Mining and Technology, 2008, 37(5): 625. DOI:10.3321/j.issn:1000-1964.2008.05.009 |
| [12] |
WALKER D R, SHAW M C. A physical explanation of the empirical laws of comminution[J]. AIME Trans, 1954, 199: 313. |
| [13] |
BOND F C. The third theory of comminution[J]. Transactions of AIME Mining Engineering, 1952, 193: 484. |
| [14] |
HUKKI R T. Proposal for a solomnic settlement between the theories of von Rittinger, Kick and Bond[J]. Transactions of the AIME, 1962, 220: 403. |
| [15] |
THOMAS A, FILIPPOV L O. Fractures, fractals and breakage energy of mineral particles[J]. International Journal of Mineral Process, 1999, 57(4): 285. DOI:10.1016/S0301-7516(99)00029-0 |
| [16] |
MORRELL S. An alternative energy-size relationship to that proposed by Bond for the design and optimisation of grinding circuits[J]. International Journal of Mineral Process, 2004, 74(1/2/3/4): 133. DOI:10.1016/j.minpro.2003.10.002 |
| [17] |
MORRELL S. Predicting the overall specific energy requirement of crushing, high pressure grinding roll and tumbling mill circuits[J]. Minerals Engineering, 2009, 22(6): 544. DOI:10.1016/j.mineng.2009.01.005 |
| [18] |
沈保丰. 中国BIF型铁矿床地质特征和资源远景[J]. 地质学报, 2012, 86(9): 1376. SHEN Baofeng. Geological characteristics and resource prospect of the BIF type iron ore deposits in China[J]. Acta Geological Sinica, 2012, 86(9): 1376. DOI:10.3969/j.issn.0001-5717.2012.09.005 |
| [19] |
甘德清, 李晶, 许英霞, 等. 水厂铁矿磁铁矿矿石工艺矿物学研究[J]. 金属矿山, 2015(12): 98. GAN Deqing, LI Jing, XU Yingxia, et al. Research of technological mineralogy of the magnetite ore of Shuichang iron deposit[J]. Metal Mine, 2015(12): 98. DOI:10.3969/j.issn.1001-1250.2015.12.022 |
| [20] |
周仕学, 张鸣林. 粉体工程导论[M]. 北京: 科学出版社, 2015. ZHOU Shixue, ZHANG Minglin. Powder engineering introduction[M]. Beijing: Science Publishing House, 2015. |
| [21] |
MARTINS S. Size-energy relationship in comminution, incorporating scaling laws and heat[J]. International Journal of Mineral Processing, 2016, 153: 29. DOI:10.1016/j.minpro.2016.05.020 |
| [22] |
LI Bo, LING Zongcheng, ZHANG Jiang, et al. Rock size-frequency distributions analysis at lunar landing sites based on remote sensing and in-situ imagery[J]. Planetary and Space Science, 2017, 146: 30. DOI:10.1016/j.pss.2017.08.008 |
| [23] |
FUERSTENAU D W, KAPUR P C. Newer energy-efficient approach to particle production by comminution[J]. Powder Technology, 1995, 82(1): 51. DOI:10.1016/0032-5910(94)02891-Q |
 2019, Vol. 51
2019, Vol. 51


