2. 寒地城乡人居环境科学与技术工业和信息化部重点实验室(哈尔滨工业大学), 哈尔滨 150090
2. Key Laboratory of Cold Region Urban and Rural Human Settlement Environment Science and Technology, Ministry of Industry and Information Technology(Harbin Institute of Technology), Harbin 150090, China
在宏观能源政策和经济利益的推动下,中国风电产业将继续保持快速平稳增长,预计总装机容量在2020年将突破200 GW,并在2030年达到总电力装机容量的20%,初步实现能源结构的转型升级[1].
然而,在风电迅猛发展的同时,三北地区部分风电场却出现了严重的弃风,全年总弃风率高达15~25%且主要发生在供热季夜间[2-3].由于承担系统的基础热负荷,热电联产机组的电力调峰能力严重受限,这是造成区域弃风的重要原因之一.配置蓄热设备和电热机组(电锅炉或热泵)能够解耦供热机组的热、电出力约束,促进风电消纳[4-7].同时也能扩大区域供热中清洁热能的比例,减少污染物排放,改善空气质量[8-9].
针对热电厂内集中配置的蓄热罐,于炎娟等[10]证明当蓄热容量确定时,优化调度策略能够有效发挥蓄热罐的蓄放热能力,提高弃风接纳量.针对某热电联供微网,孙杰等[11]提出一种基于经济调度的热电储能优化配置模型.通过比较微网在不同储能容量下的综合成本,该模型能够确定微网的最优储能容量.然而,当给定的储能容量有限时,该模型并不能保证所得结果一定为全局最优.Katulic等[12]研究了在峰谷电价市场中提升热电机组发电效益的蓄热罐最优容量计算方法,但该研究只能保证热电厂的经济效益,能源系统的宏观收益并未涉及.吕泉等[13-14]对蓄热、风电供热和抽水蓄能等弃风消纳方案进行了国民经济性评估,结果显示蓄热方案消纳单位弃风电量的投资最少、节煤量更高,但并未针对具体案例给出最优蓄热容量的计算方法.
在配置电热设备促进风电消纳方面,Hedegaard等[15-16]定量研究了分布式小型热泵在不同蓄热方式下对提升风电消纳和节约系统能耗的效果.郭宇航等[17]通过仿真算例证明在微电网中引入热泵能够有效减少系统弃风量和运行成本.崔杨等[18]提出一个包含蓄热设备、供热机组和电锅炉的系统优化调度模型,算例表明电锅炉在极限消纳弃风时经济性最优.然而,文献[17-18]均未给出电热设备最优容量的计算方法.
在配置蓄热或电热设备消纳风电的研究领域,现有成果多集中在确定配置条件下的短期优化调度层面,涉及系统优化规划的定量分析不足,无法针对具体的能源系统状况给出经济性最优的配置方案.同时,中国当前的风电供热试点项目中,电锅炉装机容量的确定仅依赖于风电场的历史弃风数据[19],并未考虑项目的经济性.针对上述问题,本文提出一种基于最大化“日内净收益”的双层优化配置模型.基于遗传算法和系统的短期优化调度,该模型可有效得到清洁供热设备的最优经济配置.
1 清洁供热改造项目的经济性优化 1.1 区域能源系统的建立区域能源系统宏观上由产能设备、输送系统和终端用户所组成,系统的热、电产能通过供热管网和区域电网实时满足用户的供热和用电需求.在中国弃风严重的三北地区,供热季的常规电源包括热电联产机组、纯凝火电机组和风电场(水电和灵活调峰电源的比例很小,本文不考虑);系统供热量一般由热电联产(分背压机和抽凝机两大类)和调峰供热锅炉提供.图 1为配置电热锅炉和蓄热系统后,区域能源系统的结构组成和能流关系.

|
图 1 区域能源系统的典型结构及清洁供热改造 Fig. 1 Typical structure and energy flow of the district energy system (DES) and clean heating project |
集中置换式蓄热罐是供热工程中常见的蓄热设备,冷热流体在浮力的作用下形成稳定的斜温层.斜温层的上、下移动对应系统的放、蓄热.蓄热罐的配置方式和工作原理如图 2、表 1所示.

|
图 2 集中式蓄热罐的配置方式 Fig. 2 Configuration of centralized heat storage system |
| 表 1 集中式蓄热罐的工作原理 Tab. 1 Operating principle of centralized displacement storage accumulator |
将区域能源系统看作利益共同体,不考虑系统内不同主体间(风电场、火电厂、供热企业等)的利益分配.清洁供热改造项目的整体收益体现在系统运行费用的降低(相对于“未改造”的项目),付出的代价则为配置电锅炉、蓄热罐和蓄放热设备的额外投资.
为定量分析清洁供热项目在整个生命周期内的经济效益,本文以改造项目的日内净收益(daily net benefits, DNB)作为评价指标,其表达式为
| $ {\rm{DNB}} = \left( {F{C_{{\rm{ref}}}} - F{C_{{\rm{new}}}}} \right) - {\rm{Cost}}. $ | (1) |
式中:FCref为区域能源系统的日内基准总煤耗费用,元;FCnew为清洁供热改造后系统的日内总煤耗费用,元;Cost为改造项目新增投资分摊到全生命周期每个采暖日内的费用(本文假设电锅炉和蓄热罐只在供热季运行),元.
1.3 清洁供热改造的决策变量在进行清洁供热改造后(配置一定容量的电热、蓄热设备),区域能源系统的煤耗费用FCnew需根据新的系统配置情况由短期优化调度得到.当电锅炉的装机容量、蓄热罐总蓄热能力、蓄(放)热能力及初始蓄热量不同时,改造系统的日内总煤耗费用不同.因此,FCnew的抽象表示式为
| $ F{C_{{\rm{new}}}} = f\left( {{\rm{CA}}{{\rm{P}}_{{\rm{eb}}}},{\rm{CA}}{{\rm{P}}_{{\rm{dsa}}}},{S_{\max }},{S_0}} \right). $ | (2) |
式中:f为能源系统的短期优化调度;CAPeb为新增电锅炉的装机容量,MW;CAPdsa为新增蓄热罐的蓄热容量,MWh;Smax为蓄热罐的最大蓄(放)热能力,MW;S0为蓄热罐的初始蓄热量,MWh.
供热工程中常用的置换式蓄热罐以显热的方式将系统的“超额供热量”储存在部分热媒中,因此系统的蓄热容量由罐体的有效容积和蓄热温差所决定,其表达式为
| $ {\rm{CA}}{{\rm{P}}_{{\rm{dsa}}}} = k' \cdot \rho c{V_{{\rm{dsa}}}}\Delta {T_{{\rm{dsa}}}}. $ | (3) |
式中:k′为单位换算系数(2.78×10-10);ρ为热煤密度,kg/m3;c为热煤的比热容,J/kg℃;Vdsa为蓄热罐的有效容积,m3;ΔTdsa为罐体的蓄热温差,由一次网的供回水温度决定.(本文假设供热系统在整个采暖季采用量调节,蓄热温差恒定),℃.
另外,蓄热系统的最大蓄(放)热能力由蓄热温差和蓄(放)热水泵的最大流量所决定,其表达式为
| $ {S_{\max }} = k'' \cdot c{G_{\max }}\Delta {T_{{\rm{dsa}}}}. $ | (4) |
式中:k″为单位换算系数(2.78×10-7);Gmax为蓄(放)热水泵的最大流量,t/h.
1.4 经济性优化配置的目标函数假设电锅炉、蓄热罐和蓄热水泵的初投资分别正比于电锅炉的装机容量、蓄热罐的有效容积和水泵的最大运行流量.考虑改造项目初投资的时间价值并结合式(1)~(4),组合优化模型的目标函数为
| $ \begin{array}{l} \max \;\;\;\;{\rm{DNB}} = F{C_{{\rm{ref}}}} - f\left( \begin{array}{l} {\rm{CA}}{{\rm{P}}_{{\rm{eb}}}}\\ k' \cdot \rho c{V_{{\rm{dsa}}}}\Delta {T_{{\rm{dsa}}}}\\ k'' \cdot c{G_{\max }}\Delta {T_{{\rm{dsa}}}}\\ {S_0} \end{array} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\left( {A/P,i,n} \right)}}{N} \cdot \left( {{K_{{\rm{eb}}}} \cdot {\rm{CA}}{{\rm{P}}_{{\rm{eb}}}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{K_{{\rm{dsa}}}} \cdot {V_{{\rm{dsa}}}} + {K_{{\rm{pump}}}} \cdot {G_{\max }}} \right). \end{array} $ |
式中:N为一年内的总供热天数;Keb为电锅炉单位装机容量的投资费用,元/MW;Kdsa为蓄热罐单位有效容积的投资费用,元/m3;Kpump为蓄(放)热水泵单位流量的投资费用,元/(t · h-1);(A/P, i, n)为工程经济中的“等额资金回收系数”,可展开为
| $ \left( {A/P,i,n} \right) = \frac{{i{{\left( {1 + i} \right)}^n}}}{{{{\left( {1 + i} \right)}^n} - 1}}. $ |
式中:i为社会折现率;n为经济性分析的计算周期(可取电锅炉或蓄热罐的预期使用寿命),年.
2 能源系统的短期优化调度由以上分析可知,清洁供热改造项目的日内净收益并没有简单的显式表达式,而必须调用能源系统的短期优化调度模型.
2.1 机组短期调度的目标函数区域能源系统的短期优化调度以最小化系统日内总煤耗费用(fuel cost)为目标,目标函数为
| $ \begin{array}{l} \min \;\;\;\;\;FC = {P_{{\rm{coal}}}} \cdot \Delta \tau \cdot \sum\limits_{t = 1}^{24} {\left[ {{P_{{\rm{bp}}}}\left( t \right) + {P_{{\rm{ec}}}}\left( t \right) + } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{P_{{\rm{hob}}}}\left( t \right) + {P_{\rm{c}}}\left( t \right)} \right]. \end{array} $ |
式中:Pcoal为燃煤锅炉单位发热量的煤耗费用,元/MWh;Pbp(t)、Pec(t)、Phob(t)、Pc(t)分别为背压机组、抽凝机组、调峰供热锅炉和纯凝火电机组在t时刻的能耗,MW;Δτ为短期优化调度计算的时间离散步长,1 h;机组能耗可由下式计算得到:
| $ \left\{ \begin{array}{l} {P_{{\rm{bp}}}}\left( t \right) = \frac{{{Q_{{\rm{bp}}}}\left( t \right)}}{{{\eta _{{\rm{boiler}}}}}}\left( {1 + \alpha } \right),\\ {P_{{\rm{ec}}}}\left( t \right) = \frac{{{E_{{\rm{ec}}}}\left( t \right) + {c_{\rm{v}}} \cdot {Q_{{\rm{ec}}}}\left( t \right)}}{{{\eta _{{\rm{co}}}} \cdot {\eta _{{\rm{boiler}}}}}},\\ {P_{{\rm{hob}}}}\left( t \right) = \frac{{{Q_{{\rm{hob}}}}\left( t \right)}}{{{\eta _{{\rm{boiler}}}}}},\\ {P_{\rm{c}}}\left( t \right) = \frac{{{E_{\rm{c}}}\left( t \right)}}{{{\eta _{{\rm{co}}}} \cdot {\eta _{{\rm{boiler}}}}}}. \end{array} \right. $ |
式中:Qbp(t)、Qec(t)、Qhob(t)分别为背压、抽凝供热机组和调峰供热锅炉t时刻的供热功率,MW;Eec(t)、Ec(t)分别为抽凝机和纯凝发电机组t时刻的发电功率,MW;ηboiler为燃煤锅炉的热效率;ηco为纯凝热力循环的发电效率;α为背压热力循环的电-热比(为常数);cv为抽凝机组的比发电损失.α、cv的表达式分别为
| $ \left\{ \begin{array}{l} \alpha = \frac{{{\eta _{{\rm{bp}}}}}}{{1 - {\eta _{{\rm{bp}}}}}},\\ {c_{\rm{v}}} = \frac{{{\eta _{{\rm{co}}}} - {\eta _{{\rm{bp}}}}}}{{1 - {\eta _{{\rm{bp}}}}}}, \end{array} \right. $ |
式中ηbp为背压热力循环的发电效率.
2.2 约束条件及决策变量 2.2.1 热、电平衡约束满足区域能源系统不同时刻的热、电供需平衡是短期优化调度最基本的要求,热、电平衡约束的表达式分别为:
| $ \begin{array}{l} {Q_{{\rm{bp}}}}\left( t \right) + {Q_{{\rm{ec}}}}\left( t \right) + {Q_{{\rm{hob}}}}\left( t \right) + {\eta _{{\rm{eb}}}} \cdot {E_{{\rm{eb}}}}\left( t \right) + S\left( t \right) = {Q_{{\rm{load}}}}\left( t \right),\\ \alpha \cdot {Q_{{\rm{bp}}}}\left( t \right) + {E_{{\rm{ec}}}}\left( t \right) + {E_{\rm{c}}}\left( t \right) + W\left( t \right) = {E_{{\rm{eb}}}}\left( t \right) + {E_{{\rm{load}}}}\left( t \right). \end{array} $ |
式中:ηeb为电锅炉的热效率;S(t)为能源系统t时刻的放热功率(S(t) < 0则为蓄热系统在t时刻内蓄热),MW;W(t)为风电场t时刻的并网发电量,MW;Eeb(t)为电锅炉t时刻的耗电功率,MW;Qload(t)、Eload(t)分别为能源系统t时刻的热、电负荷,MW.
2.2.2 背压、抽凝供热机组的热-电出力约束背压、抽凝供热机组的热-电出力约束分别为:
| $ \left\{ \begin{array}{l} {Q_{{\rm{bp}}}}\left( t \right) \cdot \left( {1 + \alpha } \right) \le {E_{{\rm{bp}},\max }},\\ {Q_{{\rm{bp}}}}\left( t \right) \cdot \left( {1 + \alpha } \right) \ge {E_{{\rm{bp}},\min }}; \end{array} \right. $ |
| $ \left\{ \begin{array}{l} {Q_{{\rm{ec}}}}\left( t \right) \ge 0,\\ {E_{{\rm{ec}}}}\left( t \right) \le {E_{{\rm{ec}},\max }} - {c_{\rm{v}}} \cdot {Q_{{\rm{ec}}}}\left( t \right),\\ {E_{{\rm{ec}}}}\left( t \right) \ge {E_{{\rm{ec}},\min }} - {c_{\rm{v}}} \cdot {Q_{{\rm{ec}}}}\left( t \right),\\ {E_{{\rm{ec}}}}\left( t \right) \ge {Q_{{\rm{ec}}}}\left( t \right) \cdot \alpha + K. \end{array} \right. $ |
式中:Ebp, min、Ebp, max分别为进入背压供热机组的最小、最大进汽量,MW;Eec, min、Eec, max分别为进入抽凝供热机组的最小、最大进汽量,MW.
2.2.3 蓄热系统容量及蓄放热能力约束在蓄热罐保温良好且布水装置设计合理的条件下,罐体的蓄热效率近似为1,相应的约束条件为
| $ \left\{ \begin{array}{l} 0 \le {S_0} - \sum\limits_{t = 1}^m {S\left( t \right)} \le {\rm{CA}}{{\rm{P}}_{{\rm{dsa}}}},\\ - {S_{\max }} \le S\left( t \right) \le {S_{\max }}. \end{array} \right.\left( {m = 1,2, \cdots ,24} \right) $ | (5) |
式中S0为蓄热罐的初始蓄热量,MWh.
另外,由于蓄热罐只起到平移系统热负荷的作用,因此每个优化调度周期内,蓄热罐的总蓄热量应等于总放热量(S0在不同优化周期内可恒定),因此下式成立:
| $ \sum\limits_{t = 1}^{24} {S\left( t \right)} = 0. $ |
风电场的逐时电出力约束为
| $ 0 \le W\left( t \right) \le {W_{\max }}\left( t \right), $ |
式中Wmax(t)为风电场t时刻的最大电出力,MW.
2.2.5 纯凝火电机组、调峰供热锅炉和电锅炉的容量约束纯凝火电机组、调峰供热锅炉和电锅炉的容量约束为
| $ \left\{ \begin{array}{l} {E_{{\rm{c,min}}}} \le {E_{\rm{c}}}\left( t \right) \le {E_{{\rm{c,max}}}},\\ {Q_{{\rm{hob}},\min }} \le {Q_{{\rm{hob}}}} \le {Q_{{\rm{hob}},\max }},\\ 0 \le {E_{{\rm{eb}}}}\left( t \right) \le {\rm{CA}}{{\rm{P}}_{{\rm{eb}}}}. \end{array} \right. $ |
式中:Ec, min、Ec, max分别为纯凝火电机组的最小、最大电出力,MW;Qhob, min、Qhob, max分别为调峰供热锅炉的最小、最大供热量,MW.
对清洁供热改造后的区域能源系统,短期优化问题的决策变量见表 2(由于热、电出力耦合,背压机组的逐时发电量并非独立的决策变量).
| 表 2 短期优化调度的决策变量 Tab. 2 Decision variables of short-term optimized dispatch |
遗传算法(genetic algorithm)作为一种高效、并行的全局搜索方法,能有效处理解空间维数较高,目标函数非线性的优化问题[20].为保证算法的稳定、可靠,本文利用MATLAB遗传优化工具箱(ga)对清洁供热改造项目的经济性优化问题进行求解.优化求解流程如图 3所示.

|
图 3 清洁供热改造项目的经济性优化流程 Fig. 3 Solving process of economical optimization for clean heating project |
如图 3所示,促进风电消纳清洁供热改造项目的经济性优化配置问题可看作两个独立优化模块的组合.内层优化模块用于计算特定配置条件下(CAPeb, Vdsa, Gmax, S0确定)能源系统的日内总煤耗费用;同时,外层优化模块根据内层的输出结果,对种群内个体进行遗传操作,当迭代终止时,得到清洁供热改造项目的经济性最优配置.
3.2 内层优化模块外部条件的确定能源系统运行优化调度的目的通常在于指导未来一段时间内(几小时或几天)各机组的运行调节,优化调度的实际效果依赖于热电负荷及可再生能源预测的准确性[21].然而,本文的主要目的在于确定能源系统的宏观最优配置方案,因此在调用短期优化调度模型时,外部计算条件(能源系统的逐时热、电负荷Qload(t)、Eload(t),风电场的逐时理论最大出力Wmax(t))要能够准确反映能源系统在整个供热季的一般状况.
为了有效解决热、电负荷及风电出力的随机性问题,本文提出一种基于历史观测数据的平均化方法,表达式为
| $ \left\{ \begin{array}{l} {Q_{{\rm{load}},{\rm{av}}}}\left( t \right) = \sum\limits_{i = 1}^N {\frac{{{Q_{{\rm{obs}}}}\left( {i,t} \right)}}{N}} ,\\ {E_{{\rm{load}},{\rm{av}}}}\left( t \right) = \sum\limits_{i = 1}^N {\frac{{{E_{{\rm{obs}}}}\left( {i,t} \right)}}{N}} ,\\ {W_{\max ,{\rm{av}}}}\left( t \right) = \sum\limits_{i = 1}^N {\frac{{{W_{{\rm{obs}}}}\left( {i,t} \right)}}{N}} . \end{array} \right.\left( {t = 1,2, \cdots ,24} \right) $ | (6) |
式中:Qload, av(t)、Eload, av(t)分别为区域能源系统的热、电负荷在供热季N天内同一时刻t的平均值,MW;Wmax, av(t)为风电场理论最大电出力在供热季N天内同一时刻t的平均值,MW;Qobs(i, t)、Eobs(i, t)分别为区域能源系统在供热季第i天、t时刻的实测热、电负荷,MW;Wobs(i, t)为风电场在供热季第i天、t时刻的实测最大电出力(由实时风速和风电机组的理论发电特性得到),MW.
4 案例计算本文以吉林省长春市某小型区域能源系统为例,对双层优化模型及遗传求解的有效性进行验证.并在特定的技术、经济参数下,得到清洁供热改造项目的最优配置方案.
4.1 外部计算条件与基准运行工况根据区域电网、集中供热系统和风电场2017年— 2018年供热季(共175 d)的逐时数据,调用式(6)得到日内优化调度的外部计算条件如图 4所示.

|
图 4 热、电逐时负荷及风电场的逐时最大电出力 Fig. 4 Hourly heat and power loads of the DES and the maximum hourly power output of the wind farm |
系统热负荷与室内外温差成正比,夜间高而白天低;另外,风电场的逐时理论最大出力与电网的逐时电负荷呈现相反的变化规律,这给风电的并网消纳造成巨大压力.
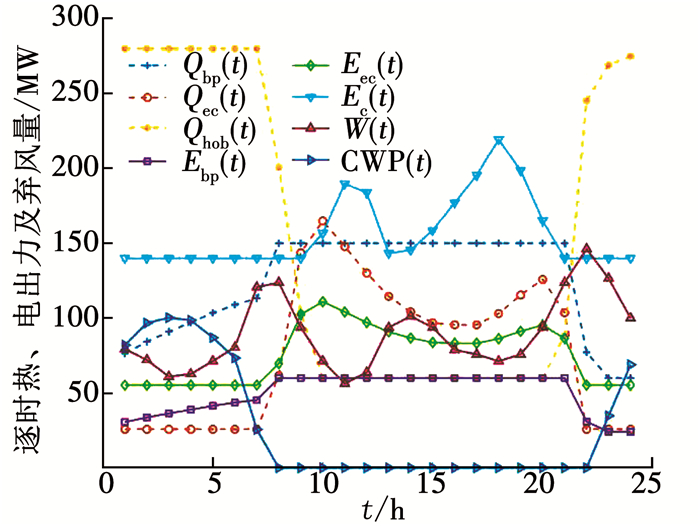
当未配置电锅炉和蓄热设备时,区域能源系统的基准运行工况如图 5所示,能源系统中相关设备的技术参数见表 3(在保温良好的情况下,短期蓄放热的能量损失很小,因此本文假设蓄热罐的蓄热效率为100%).
|
图 5 区域能源系统的基准运行工况 Fig. 5 Reference operating conditions of the DES |
| 表 3 能源设备的技术参数 Tab. 3 Technical parameters of different energy devices |
如图 5所示,为了尽可能的促进风电消纳并降低系统的总能耗费用,背压、抽凝供热机组在22: 00到次日7: 00之间降低自身的热、电出力,不足的供热量由调峰供热锅炉承担.另一方面,由于电网向下调峰的能力有限,风电场在23: 00到次日7: 00之间出现了弃风(日内总弃风电量667 MWh,弃风率23.8%).值得注意的是,出现弃风的时间段与调峰供热锅炉满负荷(280 MW)运行时间段高度重合,因此配置电热设备将部分弃风电能直接转化为供热量十分必要.
4.2 清洁供热项目的优化配置利用遗传算法对该区域能源系统清洁供热改造项目进行经济性优化,相关的经济性参数取值见表 4(表中Keb、Kdsa、Kpump根据已有的相似工程案例折算得到).表 5为多次独立遗传优化的计算结果(遗传计算的种群数量为200个,进化代数200代,其他参数取工具箱的默认值).
| 表 4 清洁供热项目的经济性参数 Tab. 4 Economic parameters of clean heating project |
从表 5可以看到,在本文的5次独立遗传搜索中,电锅炉装机容量CAPeb、蓄热罐有效容积Vdsa和蓄(放)热水泵设计流量Gmax的优化计算结果非常接近,变异系数(标准差与平均值之比)最大不超过2.7%;同时,每次优化计算所得到的日内净收益亦十分接近(变异系数仅为0.2%),虽然理论上的全局最优点并没有找到,但所得到的“局部最优解”已足够好,完全能满足工程应用的要求.
| 表 5 多次遗传优化的计算结果 Tab. 5 Results of several independent genetic calculations |
值得注意的是,作为能源系统短期优化调度的重要边界条件,蓄热罐的初始蓄热量S0(见式(5))在多次优化计算中存在显著差异,这可能是因为目标函数对不同决策变量变化的敏感性存在差异.
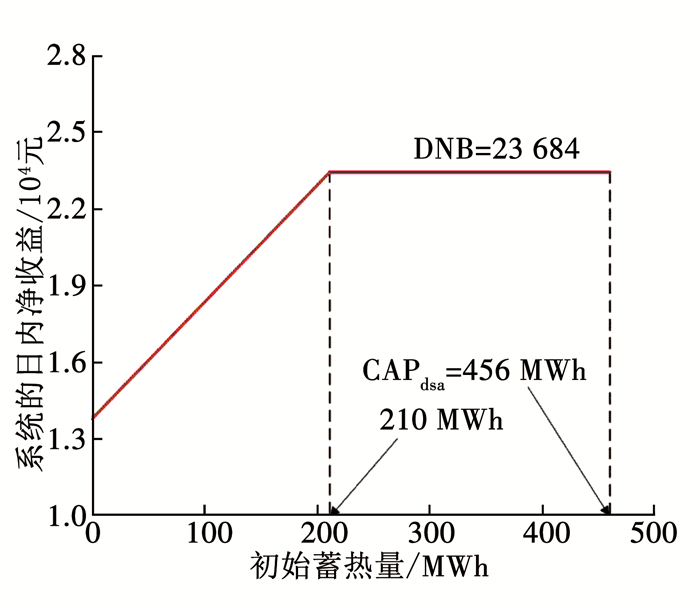
4.2.1 初始蓄热量的敏感性分析为分析蓄热罐的初始蓄热量S0对区域能源系统日内净收益的影响,将输入内层优化模型的CAPeb、Vdsa、Gmax分别固定为34.79 MW、6 548 m3和1 054 t/h(表 5中的第3次优化计算结果),同时S0从0逐渐增大到456 MWh(对应6 548 m3有效容积的最大蓄热量).系统日内净收益随S0的变化情况如图 6所示.
|
图 6 不同初始蓄热量对系统日内净收益的影响 Fig. 6 Daily net benefits of the reformed DES under different initial heat storage |
由图 6可见,当S0从0逐渐增大到“临界值(207 MWh)”时,系统的日内净收益随S0的增加而线性增大;当S0大于临界值后(直到最大蓄热量CAPdsa),日内净收益保持恒定.因此,S0在多次独立的遗传优化中出现了较大的差异.
4.2.2 清洁供热改造后系统的运行工况将表 5中第3次遗传优化的计算结果输入短期优化调度模型,得到清洁供热改造后,区域能源系统的运行情况(如图 7和表 6所示).

|
图 7 清洁供热改造后系统的运行工况 Fig. 7 Operating conditions of the DES after clean heating reformation |
| 表 6 区域能源系统的总弃风量和煤耗费用 Tab. 6 Total curtailed wind power and daily energy costs of the DES |
结合图 7(a)可知,新增电锅炉在23: 00到次日7: 00开机运行(该时段与基准工况下出现弃风的时间段完全一致),承担系统的部分热负荷.同时,蓄热罐在21: 00到次日9: 00之间对外放热(设备总蓄热量SE(t)在该时间段单调递减),在10: 00-20: 00时间段内蓄热(SE(t)单调递增,20: 00时达到罐体的最大蓄热量456 MWh).
从图 7(b)可以看到,在基准工况的弃风高发时段(23: 00到次日7: 00),背压、抽凝供热机组均以自身最低电出力运行(Ebp, min=24 MW,Eec, min=55.3 MW),因此引入电锅炉和蓄热罐能够有效解耦供热机组的热电约束,充分发挥其电力调峰能力,给风电的并网消纳提供更大的空间.
在本文案例中,经济性最优的清洁供热改造能够显著降低区域能源系统的总弃风量(弃风率由基准工况下的23.8%降低到10.1%);日煤耗费用亦可减少约2.8%.另外,已有的研究结果表明(篇幅所限详细内容略),随着室外平均温度的降低,区域能源系统的日煤耗费用和总弃风量将进一步增大.
4.3 设备投资费用变化对优化配置结果的影响由式(5)可知:Keb、Kdsa、Kpump分别为双层优化模型目标函数的重要参数.当电热设备和蓄热系统的初投资变化时(其他计算条件不变),优化得到的最优配置结果必然发生变化.对于本文案例,不同投资费用组合下经济性最优配置见表 7.
| 表 7 不同投资组合下的经济性最优配置 Tab. 7 Optimal economic configurations under different combinations of initial investment |
从表 7可以看到,最优经济性配置对电锅炉的成本增加比较敏感,当Keb增大到150万/MW时,优化计算得到的电锅炉经济性装机容量为0(CAPeb=0),说明该条件下配置电锅炉消纳风电不再具有经济性;另外,当Keb或Kpump增大时,对应的Vdsa、Gmax均减小;总体来看,当设备的投资费用升高后,系统的日内净收益会降低.
5 结论1) 遗传算法能够有效求解本文所提出的双层优化模型,虽然独立优化计算的结果之间存在一定的差异,但完全能够满足工程应用的需求.
2) 经优化配置的清洁供热项目能够显著降低系统的总弃风量,但由于投资项目边际收益递减,完全消除弃风并不经济.
3) 设备初投资显著影响到清洁供热改造项目的经济优化配置结果,须结合当地的社会经济状况合理选取.当系统热、电负荷及风电出力能够准确预测时,该模型亦可用于制定区域能源系统的短期运行计划.
| [1] |
CHEN Xinyu, MCELROY M B, KANG Chongqing. Integrated energy systems for higher wind penetration in China: formulation, implementation, and impacts[J]. IEEE Transactions on Power Systems, 2018, 33(2): 1309. DOI:10.1109/TPWRS.2017.2736943 |
| [2] |
舒印彪, 张智刚, 郭剑波, 等. 新能源消纳关键因素分析及解决措施研究[J]. 中国电机工程学报, 2017, 37(1): 1. SHU Yinbiao, ZHANG Zhigang, GUO Jianbo, et al. Study on key factors and solution of renewable energy accommodation[J]. Proceedings of the CSEE, 2017, 37(1): 1. DOI:10.13334/j.0258-8013.pcsee.162555 |
| [3] |
LUO Guoliang, LI Yanling, TANG Wenjun, et al. Wind curtailment of China's wind power operation: evolution, causes and solutions[J]. Renewable and Sustainable Energy Reviews, 2016, 53: 1190. DOI:10.1016/j.rser.2015.09.075 |
| [4] |
NUYTTEN T, CLAESSENS B, PAREDIS K, et al. Flexibility of a combined heat and power system with thermal energy storage for district heating[J]. Applied Energy, 2013, 104: 583. DOI:10.1016/j.apenergy.2012.11.029 |
| [5] |
LUND H. Large-scale integration of wind power into different energy systems[J]. Energy, 2015, 30(13): 2402. DOI:10.1016/j.energy.2004.11.001 |
| [6] |
MEIBOM P, KIVILUOMA J, BARTH R, et al. Value of electric heat boilers and heat pumps for wind power integration[J]. Wind Energy, 2007, 10(4): 321. DOI:10.1002/we.224 |
| [7] |
FITZGERALD N, FOLEY A M, MCKEOGH E. Integrating wind power using intelligent electric water heating[J]. Energy, 2012, 48(1): 135. DOI:10.1016/j.energy.2012.03.014 |
| [8] |
LUND H, MÖLLER B, MATHIESEN B V, et al. The role of district heating in future renewable energy systems[J]. Energy, 2010, 35(3): 1381. DOI:10.1016/j.energy.2009.11.023 |
| [9] |
LUND H, WERNER S, WILTSHIRE R, et al. 4th Generation District Heating (4GDH): integrating smart thermal grids into future sustainable energy systems[J]. Energy, 2014, 68: 1. DOI:10.1016/j.energy.2014.02.089 |
| [10] |
于炎娟, 陈红坤, 姜欣, 等. 促进风电消纳的蓄热罐运行策略[J]. 电力系统自动化, 2017, 41(7): 37. YU Yanjuan, CHEN Hongkun, JIANG Xin, et al. Operation strategy for heat storage tank to improve wind power accommodation[J]. Automation of Electric Power Systems, 2017, 41(7): 37. DOI:10.7500/AEPS20160510006 |
| [11] |
孙杰, 张炳达, 杨俊鹏. 微网热电储能容量配置优化[J]. 天津理工大学学报, 2017, 33(2): 1. SUN Jie, ZHANG Bingda, YANG Junpeng. Energy storage capacity optimization for micro grid including electricity and heat[J]. Journal of Tianjin University of Technology, 2017, 33(2): 1. DOI:10.3969/j.issn.1673-095X.2017.002.001 |
| [12] |
KATULIĆ S, ČEHIL M, BOGDAN Ž. A novel method for finding the optimal heat storage tank capacity for a cogeneration power plant[J]. Applied Thermal Engineering, 2014, 65(1/2): 530. DOI:10.1016/j.applthermaleng.2014.01.051 |
| [13] |
吕泉, 李玲, 朱全胜, 等. 三种弃风消纳方案的节煤效果与国民经济性比较[J]. 电力系统自动化, 2015, 39(7): 75. LYU Quan, LI Ling, ZHU Quansheng, et al. Comparison of coal-saving effect and national economic indices of three feasible curtailed wind power accommodation strategies[J]. Automation of Electric Power Systems, 2015, 39(7): 75. DOI:10.7500/AEPS20140125001 |
| [14] |
吕泉, 陈天佑, 王海霞, 等. 配置储热后热电机组调峰能力分析[J]. 电力系统自动化, 2014, 38(11): 34. LYU Quan, CHEN Tianyou, WANG Haixia, et al. Analysis on peak-load regulation ability of cogeneration unit with heat accumulator[J]. Automation of Electric Power Systems, 2014, 38(11): 34. DOI:10.7500/AEPS20130724002 |
| [15] |
HEDEGAARD K, MATHIESEN B V, LUND H, et al. Wind power integration using individual heat pumps analysis of different heat storage options[J]. Energy, 2012, 47(1): 284. DOI:10.1016/j.energy.2012.09.030 |
| [16] |
HEDEGAARD K, M NSTER M. Influence of individual heat pumps on wind power integration-Energy system investments and operation[J]. Energy Conversion and Management, 2013, 75: 673. DOI:10.1016/j.enconman.2013.08.015 |
| [17] |
郭宇航, 胡博, 万凌云, 等. 含热泵的热电联产型微电网短期最优经济运行[J]. 电力系统自动化, 2015, 39(14): 16. GUO Yuhang, HU Bo, WAN Lingyun, et al. Optimal economic short-term scheduling of CHP microgrid incorporating heat pump[J]. Automation of Electric Power Systems, 2015, 39(14): 16. DOI:10.7500/AEPS20141127011 |
| [18] |
崔杨, 陈志, 严干贵, 等. 基于含储热热电联产机组与电锅炉的弃风消纳协调调度模型[J]. 中国电机工程学报, 2016, 36(15): 4072. CUI Yang, CHEN Zhi, YAN Gangui, et al. Coordinated wind power accommodating dispatch model based on electric boiler and CHP with thermal energy storage[J]. Proceedings of the CSEE, 2016, 36(15): 4072. DOI:10.13334/j.0258-8013.pcsee.152406 |
| [19] |
王彩霞, 李琼慧, 谢国辉. 风电供热提高低谷风电消纳能力评估[J]. 中国电力, 2013, 46(12): 100. WANG Caixia, LI Qionghui, XIE Guohui. Evaluation of wind power heating in facilitating wind power integration capability during vally load period[J]. Electric Power, 2013, 46(12): 100. DOI:10.3969/j.issn.1004-9649.2013.12.021 |
| [20] |
王钤, 潘险险, 陈迎, 等. 基于实测数据的风电场风速-功率模型的研究[J]. 电力系统保护与控制, 2014, 42(2): 23. WANG Qian, PAN Xianxian, CHEN Ying, et al. Study of wind speed-active power model for wind farm based on measured data[J]. Power System Protection and Control, 2014, 42(2): 23. DOI:10.7667/j.issn.1674-3415.2014.02.004 |
| [21] |
郎斌斌, 穆钢, 严干贵, 等. 联网风电机组风速-功率特性曲线的研究[J]. 电网技术, 2008, 32(12): 70. LANG Binbin, MU Gang, YAN Gangui, et al. Research on wind speed vs output power characteristic curve of wind power generator interconnected with power grid[J]. Power System Technology, 2008, 32(12): 70. DOI:10.13335/j.1000-3673.pst.2008.12.008 |
 2019, Vol. 51
2019, Vol. 51



