目前, 大多数停车诱导系统向用户提供的可选择停车场及其路径的主要参考量是距离.单一的参考量往往会由于提供路径的拥堵, 建议选择的停车场规模过小等问题, 降低驾驶者在实际停车场转换中的体验.停车场网络是以停车场本身为节点, 停车场之间的连接作为连线的一种网络拓扑结构.停车场作为节点的单点信息量较大, 因此可以通过节点本身和节点间的线路连接对网络进行分析.
由于物联网概念的普及, 目前对停车场的研究以区域内的停车场诱导方法居多.Mangla等利用中央服务器处理动态信息, 确定停车场的停车有效性[1].Shin J H等通过动态多因子的权重分配算法实时控制最佳停车场的选择[2].Chen M基于无线传感器的原理提出了一种停车引导信息发布系统[3].但停车场诱导研究大多基于一组停车场之间线路的选择和比较, 而忽略了在停车场建设中的宏观网络调控.在交通复杂网络研究中, 学者们通过交通网络的无标度特性[4]和小世界特性[5]对其进行复杂性分析.最新的研究包括通过多层模型的动态研究创建和管理交通线网[6-7]以及利用传统的复杂网络参数对分析网络进行评价[8-11].目前交通复杂网络理论主要应用在公共交通, 轨道交通和海运交通网络中, 在停车场网络方向还没有相关研究.
基于以上问题, 本文利用改进的断裂点理论和停车生成率法, 同时考虑了停车场需求和影响范围在实际情况下的变化, 提出了吸引关系下的停车场网络连接方法, 分析其复杂网络并与现有的全局耦合网络及单边耦合网络进行参数对比.
1 参数计算 1.1 停车场需求确定停车场需求的影响因素很多, 包括停车场本身的泊位数和分类, 也包括停车场所处的地理位置, 用地类型以及所在区域的经济情况等.在计算停车场需求时的常用模型包括用地分析模型、车辆出行模型以及多元回归模型等.利用用地分析模型中的停车生成率法确定停车场停车需求量的公式为
| $ {S_i} = \alpha \mathop \sum \limits_{j = 1}^m {P_{ij}}{d_j}. $ | (1) |
式中:α为停车饱和度; Pij为需求点j的泊车者选择公共停车场i的概率; dj为点j的停车需求情况.
由于车辆停放特征会对停车场需求产生影响, 因此在该模型的基础上需考虑停放特征因素.常用的车辆停放特征包括周转率和利用率.周转率及利用率越高, 在同样停车位的情况下, 会产生更多次停车行为, 从而满足更多停车需求.因此, 在停车需求既定的情况下, 停车场的停车周转率及利用率均反作用于供应规模.考虑周转率和利用率参数对需求的影响的模型为
| $ {S_i} = \frac{{\alpha \mathop \sum \limits_{j = 1}^m {P_{ij}}{d_j}}}{{{U_i}{\omega _i}}}\left( {i = 1, 2, \ldots , n} \right). $ | (2) |
式中:ωi为该类型停车场的利用率, Ui为该停车场的周转率.
由于各地区的经济条件和城市规模不同, 因此只考虑停车场本身的参数限制无法得到相对于每个城市和地区的准确停车需求信息.中心性指中心地区的服务设施为其以外地区服务的相对重要性.停车场服务水平是停车场泊位数能够满足地区停车需求的比例.这两项指标的增长会提升停车人的泊车体验, 因此会增加停车需求.价格是另一个影响驾驶人停车需求的因素之一, 泊车费用反作用于停车需求.考虑这些影响因子, 本文得出如下的停车需求模型:
| $ {S_i} = \frac{{{\alpha _i}\mathop \sum \limits_{j = 1}^n {d_j}{P_{ij}}}}{{{U_i}{\omega _i}}}\varepsilon \delta \sigma . $ | (3) |
式中:ε为价格影响率, δ为服务水平影响率, σ为归一化后的地区中心性指数.
1.2 参数标定1) ε与停车场地理位置, 规模等有关.调整停车场费率是一种有效控制小汽车出行的手段.ε是一种对费率进行折算的方式, 其计算方式为
| $ \varepsilon = \frac{{{P_{\rm{r}}}}}{{{P_{\rm{e}}}}}. $ | (4) |
式中:Pe为实际泊车费用, Pr为驾驶人能够接受的最高泊车费用.当费率低于驾驶人期望值时, 会促进停车行为, 此时ε>1;当费率超过驾驶人的承受能力时, ε < 1.
2) 停车场服务水平是能够直接影响驾驶人停车体验的参数, 其计算公式为
| $ \delta = 1 + \frac{{A - {S_i}}}{A}. $ | (5) |
式中:A为停车场的实际泊位数.在停车场服务水平较高时, 能够吸引更多停车需求, 此时δ>1;服务水平较低时δ < 1, 服务水平对需求产生负影响.
3) 中心性强度是停车场对区域影响能力的综合要素, 是停车场划分服务范围和影响空间的依据.中心性强度可利用主成分分析法进行定量刻画, 其计算方法为
| $ \delta = \sum {V_i}{C_i}. $ | (6) |
式中:Vi为每个主成分的贡献率, ∑Vi=1, Ci为第i个成分的特征值.
4) ωi为在单位时间内, 单个停车位被使用的次数.当单个泊位使用次数较多时, 提供少量车位即可满足停车需求.其计算方式为
| $ {\omega _i} = \frac{{\sum t}}{{60A}}\left( {i = 1, 2, \cdots , n} \right). $ | (7) |
式中:∑t代表时间内停车场停车占用时间的和值, A为该停车场的泊位数.
5) 停车场周转率与停车时间及利用率有关.在一定情况下, 周转率越大, 停车需求越小.周转率的计算公式为
| $ {U_i} = \frac{{{L_{\rm{o}}}}}{{{L_i}}}\left( {i = 1, 2, \cdots , n} \right). $ | (8) |
式中:Lo为单位时间内出停车场的车辆数, Li为单位时间内进停车场的车辆数.
实际情况中若要对周转率参数进行预测, 用平均周转率代替.平均周转率的公式为
| $ {\mu _n} = \left\{ \begin{array}{l} {n^\mu }, n = 0, 1, 2, \cdots ;\\ {c^\mu }, n = {\rm{c}} + 1, {\rm{c}} + 2, \cdots . \end{array} \right. $ | (9) |
式中:n为停车需求, c为实际泊位数, μ为停车场的服务率.服务率参数通过对停车场的停车状态分析获得, 停车场的停车状态概率分布为
| $ {A_n} = \left\{ \begin{array}{l} \frac{{{c^n}{\mu ^n}}}{{n!(\mathop \sum \limits_{n = 0}^{c - 1} \frac{{{{\left( {\mu c} \right)}^n}}}{{n!}} + \frac{{{{\left( {\mu c} \right)}^c}}}{{c!\left( {1 - \mu } \right)}})}}, 0 \le n \le c;\\ \frac{{{c^n}{\mu ^n}}}{{c!(\mathop \sum \limits_{n = 0}^{c - 1} \frac{{{{\left( {\mu c} \right)}^n}}}{{n!}} + \frac{{{{\left( {\mu c} \right)}^c}}}{{c!\left( {1 - \mu } \right)}})}}, n \ge c. \end{array} \right. $ | (10) |
城市断裂点理论由P.D.Converse于1949年提出.由于其物理模型简单且易于接受, 因此被常用来划分城市的影响区域范围.该理论认为, 一个城市对周围地区的吸引力, 与它的规模成正比, 与距它的距离的平方成反比.断裂点即两城市的吸引力达到平衡的点.断裂点理论有3个关键性质[12] :
1) 相邻城市之间的欧氏距离等于断裂点到两个城市欧氏距离之和.公式表示为
| $ {d_{\rm{A}}} + {d_{\rm{B}}} = {D_{{\rm{AB}}}}. $ | (11) |
2) 断裂点到相邻两个城市的距离与这两个城市中心强度(规模)的平方根成正比.用公式表示为
| $ {d_{\rm{A}}} = {D_{{\rm{AB}}}}/(1 + \sqrt {{P_{\rm{B}}}/{P_{\rm{A}}}} ), $ | (12) |
| $ {d_{\rm{B}}} = {D_{{\rm{AB}}}}/(1 + {P_{\rm{A}}}/{P_{\rm{B}}}). $ | (13) |
式中:dA和dB为断裂点到城市的距离, DAB为两城市之间的直线距离, PA和PB分别为两城市的规模.
3) 每个城市的权重等于其中心性强度值的平方根.
通过断裂点理论的三条性质可以求得断裂点的准确位置.在确定断裂点后需要对节点范围进行划分确定, 广泛且有效的分割方法包括常规Voronoi图法, 加权Voronoi图法[13-14], 空间相互作用模型[15]等.Voronoi图是一种对空间区域进行完全划分的最短距离分割方法, 其具有最邻近、线性特性、局域动态性.在分类中按照图元的权值是否相等, 可分为常规Voronoi图和加权Voronoi图.常规Voronoi图由一组连接邻近节点的直线的垂直平分线组成的连续多边形构成.它的一个重要性质是位于常规Voronoi图网格中的每一个点到该网格中心的距离都小于到其它网格中心.加权Voronoi图在常规Voronoi图的基础上对城市节点进行加权, 并重新划分区域边缘.如果两个城市点的权重相同, 那么其吸引范围的分界线是这两个城市点连线的垂直平分线; 如果它们的权重不同, 那么其吸引范围的分界线是一个圆弧, 其圆心为((PBx1-PAx2)/(PB-PA), (PBy1-PAy2)/(PB-PA)), 且圆心位于两城市的连线, 半径为|(PAPB)0.5/(PB-PA)|×DAB.与城市相比, 停车场同样具有规模性质, 因此可用Voronoi图来计算停车场的影响范围.
2 吸引关系介绍当驾驶人在选择停车场时, 影响选择的因素较多, 例如驾驶员本身, 停车场费率, 停车场泊位数等.吸引度是来判断驾驶员对停车场选择统一的量化标准, 即该停车场对用户的吸引能力.吸引度越大, 则用户选择该停车场的可能性越大.通过类比断裂点理论, 可以认为两停车场之间的边权与起讫停车场的规模成正比, 与两停车场之间距离的平方成反比.因此列出如下的边权和停车场吸引度计算公式为
| $ {R_{{\rm{ab}}}} = {k_{{\rm{ab}}}}\frac{{{P_{\rm{a}}}{P_{\rm{b}}}}}{{{L^2}}}, $ | (14) |
| $ {K_{\rm{a}}} = \mathop \sum \limits_{b = 1}^n {R_{{\rm{ab}}}}. $ | (15) |
式中:Pa为起点停车场的规模, Pb为讫点停车场的规模, L为起讫点停车场之间的距离.Rab为起点为a, 讫点为b的线路的边权, kab为系数.
在实际网络计算中, 距离并不能完全表示出驾驶员在停车场转换过程中的驾驶感受, 因为不同的通行路径可能有不同的拥堵状况, 对用户的通行感受也不同.本文采用旅行时间替换距离.旅行时间参数可以一定程度上表达出该起讫点转换中道路的长度, 车况等, 利用该参数可以表示驾驶员的驾驶过程
| $ {R_{{\rm{ab}}}} = \sum k{'_{{\rm{ab}}}}\frac{{{P_{\rm{a}}}{P_{\rm{b}}}}}{{{T^2}}}. $ | (16) |
式中:T为在该行驶过程中的旅行时间, k'ab为修正系数.
由公式可知, 在确定停车场规模时, 停车需求量与规模呈正相关.当停车场规模已经既定时, 大的停车需求反而会造成额外的停车供给的减少, 从而降低驾驶人对该停车场的选择概率.通过停车需求分别对已有停车场和在建停车场的影响, 已建停车场对驾驶人的吸引能力公式为
| $ {T_{\rm{a}}} = {W_{\rm{a}}} - \frac{{{\alpha _{\rm{a}}}\mathop \sum \limits_{j = 1}^n {{\rm{d}}_j}{P_{{\rm{a}}j}}}}{{{U_{\rm{a}}}{\omega _{\rm{a}}}}}{\varepsilon _{\rm{a}}}{\delta _{\rm{a}}}{\sigma _{\rm{a}}}. $ | (17) |
式中Wa为起讫点停车场的实际停车能力.
以各停车场吸引能力为参数划分Voronoi图后得到每条连线的边权计算公式为
| $ {R_{{\rm{ab}}}} = \frac{{k'{'_{{\rm{ab}}}}{M_{\rm{a}}}{M_{\rm{b}}}}}{{{T^2}}}. $ | (18) |
式中:Ma为起点停车场的影响范围, Mb为讫点停车场的影响范围, k″ab为再次标准化后的系数.公式中的参数k″ab与断裂点与停车场之间的距离有关, 公式为
| $ k'{'_{{\rm{ab}}}} = \left\{ \begin{array}{l} 1, {l_{{\rm{ab}}}} \le {l_{\min }};\\ 1 - {(\frac{{{l_{{\rm{ab}}}} - {l_{\min }}}}{{{l_{\max }} - {l_{\min }}}})^\beta }, {l_{\min }} \le {l_{{\rm{ab}}}} \le {l_{\max }};\\ 0, {l_{\max }} \le {l_{{\rm{ab}}}}. \end{array} \right. $ | (19) |
式中:β代表敏感系数, lab代表断裂点与停车场之间的距离, lmin和lmax为距离的阈值.
3 实例解析由于停车场网络同样具有复杂网络的性质, 可以通过复杂网络理论对其进行拓扑结构描述.为了验证理论的正确性, 根据哈尔滨市交通设施的POI数据, 在哈尔滨市南岗区攫取了49个停车场的准确位置和关键参数, 并通过其停车场特点进行网络分析, 得出停车场网络和停车场转换方案, 再将该方案下的复杂网络参数与全局耦合网络及单边耦合网络下的复杂网络参数进行比较.
3.1 常用网络介绍全局耦合网络是任意两点都相连的网络形式, 其具有最大的平均路径长度和最大的聚类系数1.全局耦合网络可以反映很多实际网络的聚类性质, 但在停车场网络中, 由于用户的主观性和对停车换乘距离阈值的确定, 因此该网络在停车场分析中并不适用.
单边耦合网络的聚类系数是1/N, 每个节点与符合条件限制的另一节点相连.本文里使用最短路径对其进行确定.该方法可以确定的平均路径长度最短, 边数最少.但由于平均节点度仅为1, 因此可选择性小, 实际效果较差.
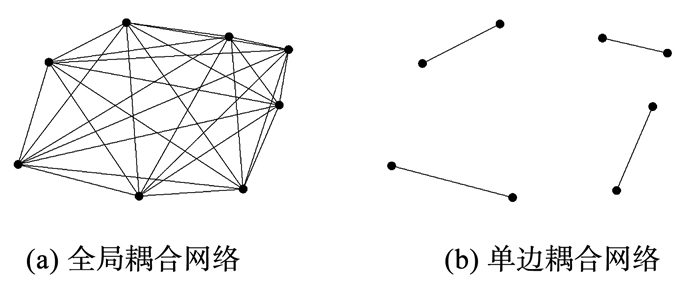
|
图 1 两种耦合网络制式 Fig. 1 Two coupling network formats |
若仅通过停车场规模对节点进行赋值, 并通过断裂点理论进行计算, 所获得的停车场的节点连接情况及其参数表如下:
| 表 1 规模赋值下的节点度(部分) Tab. 1 Node degree under the assignment of scale (part) |
在此情况下1、2、3、26、45、46、49号停车场无停车场连接.因此连接距离最短的连线.通过计算获得的停车场连接情况见图 2.
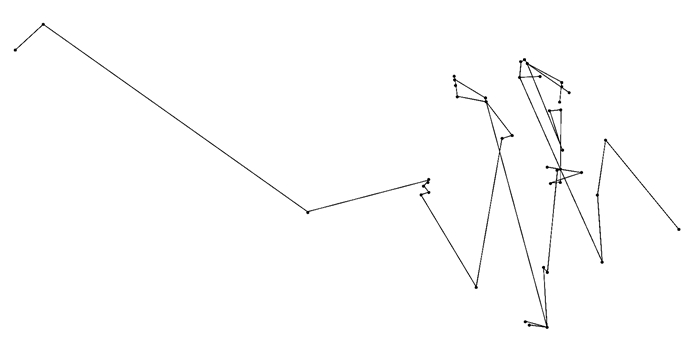
|
图 2 规模赋值下的停车场网络连接 Fig. 2 Parking network connection under the assignment of scale |
通过连接表中数据可以获得如下的停车场度分布公式和连接宏观参数为
| $ y = 15.221{x^{ - 0.707}}. $ | (20) |
| 表 2 规模赋值下的宏观参数 Tab. 2 Macro parameters under the assignment of scale |
在规模赋值条件中, 网络度分布符合幂律分布.该情况下有着较小的边数节点度和路径长度、较大的聚类系数和全局有效性.但由于平均节点度为1.29, 接近于1, 在实际情况中驾驶人在进行停车场选择时的选择余地较小, 因此需要进一步优化.
3.3 吸引关系下的停车场网络模型对规模赋值下的停车场网络模型进一步分析, 生成停车场的常规Voronoi图如图 3.Voronoi图中的面积实际上是每个停车场理论上的吸引范围, 其中包含的信息包括影响面积和影响范围边缘.通过影响面积计算出边权的结果如表 3:
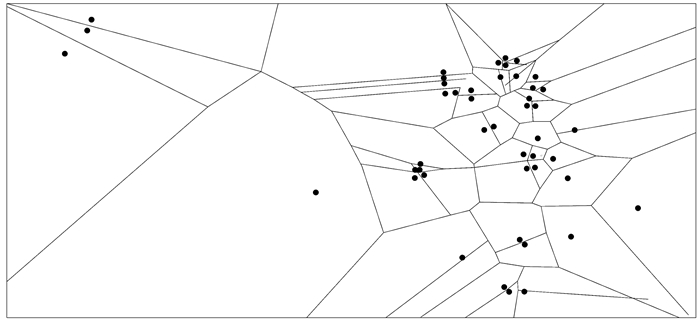
|
图 3 停车场常规Voronoi Fig. 3 The regular Voronoi diagram of the parking lot |
| 表 3 边权连接表格(部分) Tab. 3 Edge connection form (part) |
根据该地区实际情况, 设置阈值为0.1, 求得网络中连接线路如图 4所示.结果显示1、2、3、49号停车场不存在阈值内的连接线路, 因此选择权值最大的线路进行连接.由此筛选获得在吸引关系下的停车场网络连接宏观参数, 并将其与两种常见的网络模型进行比较如表 4.

|
图 4 吸引关系下的停车场网络连接 Fig. 4 Parking network connection under the attraction relationship |
| 表 4 三种连接关系宏观参数比较 Tab. 4 Comparison of macro parameters of three connection relationships |
通过吸引关系模型得到的停车场网络度分布为
| $ y = 24.892{x^{ - 0.648}}. $ | (21) |
符合幂律分布的分布特点, 因此该停车场网络为无标度网络.在吸引关系中, 网络度由规模赋值下的1.29增加到2.24, 驾驶人的停车场选择增加.相比较全局耦合网络, 网络的边数, 节点度和路径长度大大减小, 使得网络得到简化, 同时解决了单线耦合网络过于简单, 选择性小的缺点.
对表 5中的停车场微观参数分析可得, 34号停车场的节点度和规模为13和6.34, 均为49个停车场中最大.说明34号停车场在拥有较大的停车场泊位数的同时, 地理位置也较优越, 可以和多个停车场同时形成连接关系.
| 表 5 吸引关系下的微观参数(部分) Tab. 5 Micro parameters under the attraction relationship (part) |
本文通过分析停车场网络的特点和与其他交通网络的区别, 针对停车场网络独立性强, 无固定线路连接等特性, 利用复杂网络理论提出了基于吸引关系的停车场网络连接模型.
1) 确定了停车场之间的吸引度表达式, 并利用停车需求量确定停车场规模, 通过吸引度参数确定停车场之间是否进行连接, 从而构建停车场网络模型.
2) 提出了一种通过Voronoi图的面积划分确定停车场吸引度的停车场连接方式.通过引进服务水平影响率, 地区中心性指数等指标确定了新的停车场规模计算模型, 并将其代入改进的断裂点计算公式中, 评估每个停车场节点的吸引度及停车场之间的连接关系.
3) 通过哈尔滨市南岗区的停车场网络实例可以得出:在仅通过停车场规模确定停车场间连接关系时可以获得较为简洁有效的停车场网络, 但由于节点度较小造成了网络的选择性差.通过Voronoi图计算的停车场网络在拥有较大节点度的同时保证了路径长度, 聚类系数和全局有效性.
| [1] |
MANGLA M, GARG D. An automated parking guidance system for megacities[J]. International Journal of Information Technology & Computer Science, 2018, 10(1): 52. DOI:10.5815/ijitcs.2018.01.06 |
| [2] |
SHIN J H, JUN H B, KIM J G. Dynamic control of intelligent parking guidance using neural network predictive control[J]. Computers & Industrial Engineering, 2018. DOI:10.1016/j.cie.2018.04.023 |
| [3] |
CHEN M, CHANG T. A parking guidance and information system based on wireless sensor network[C] IEEE International Conference on Information and Automation. IEEE, 2011: 601. DOI: 10.1109/ICINFA.2011.5949065 https://www.researchgate.net/publication/238521388_A_parking_guidance_and_information_system_based_on_wireless_sensor_network
|
| [4] |
高自友, 吴建军, 毛保华, 等. 交通运输网络复杂性及其相关问题的研究[J]. 交通运输系统工程与信息, 2005, 5(2): 79. GAO Ziyou, WU Jianjun, MAO Baohua, et al. Research on complexity of transportation network and related problems[J]. Journal of Transportation Systems Engineering and Information, 2005, 5(2): 79. DOI:10.3969/j.issn.1009-6744.2005.02.013 |
| [5] |
冯佳, 许奇, 李夏苗, 等. 城市轨道交通系统网络复杂性研究[J]. 交通运输系统工程与信息, 2017, 17(6): 242. FENG Jia, XU Qi, LI Xiamiao, et al. Complex network study on urban rail rransit systems[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(6): 242. DOI:10.16097/j.cnki.1009-6744.2017.06.035 |
| [6] |
SOH H, LIM S, ZHANG T, et al. Weighted complex network analysis of travel routes on the Singapore public transportation system[J]. Physica A Statistical Mechanics & Its Applications, 2010, 389(24): 5852. DOI:10.1016/j.physa.2010.08.015 |
| [7] |
FENG J, LI X, MAO B, et al. Weighted complex network analysis of the Beijing subway system: Train and passenger flows[J]. Physica A, 2017(474): 213. DOI:10.1016/j.physa.2017.01.085 |
| [8] |
HOSSAIN M M, ALAM S. A complex network approach towards modeling and analysis of the Australian Airport Network[J]. Journal of Air Transport Management, 2017, 60: 1. DOI:10.1016/j.jairtraman.2016.12.008 |
| [9] |
ZHU L U, HAN Y P. Evaluation and optimization of urban rail transit network based on complex networks[J]. Railway Standard Design, 2016. DOI:10.4028/www.scientific.net/AMM.361.1891 |
| [10] |
YA Y H. Combinatorial network layout and optimization of urban rail transit[J]. Open House International, 2018, 43(1): 98. |
| [11] |
李振福, 姜书飞, 徐梦俏, 等. 面向北极航线通航的海运网络演化研究[J]. 复杂系统与复杂性科学, 2015, 12(4): 55. LI Zhenfu, JIANG Shufei, XU Mengqiao, et al. Study on the evolution of maritime networks facing the Arctic route navigation[J]. Complex Systems and Complexity Science, 2015, 12(4): 55. DOI:10.13306/j.1672-3813.2015.04.008 |
| [12] |
SALHI, SAID. Facility location: A survey of applications and methods[J]. Journal of the Operational Research Society, 1996, 47(11): 1421. DOI:10.1057/jors.1996.180 |
| [13] |
郭庆胜, 闫卫阳, 李圣权. 中心城市空间影响范围的近似性划分[J]. 武汉大学学报:信息科学版, 2003, 28(5): 596. GUO Qingsheng, YAN Weiyang, LI Shengquan. Approximate delimitation of influenced spatial regions of central cities[J]. Geomaties and Information Science of Wuhan University, 2003, 28(5): 596. DOI:10.3321/j.issn:1671-8860.2003.05.024 |
| [14] |
LIANG Z F, YUAN Y, CHEN W B, et al. A Study on suitability evaluation of rural residential areas and its consolidation division based on weighted Voronoi Diagram[J]. Acta Agriculturae Universitatis Jiangxiensis, 2017. |
| [15] |
OPENSHAW S, VENERIS Y. Numerical experiments with central place theory and spatial interaction modelling[J]. Environment & Planning A, 2003, 35(8): 1389. DOI:10.1068/a35295b |
 2019, Vol. 51
2019, Vol. 51


