随着对微波单片集成电路(MMIC, Microwave Monolithic Integrated Circuit)愈发严苛的尺寸限制和集成度要求, 越来越多的MMIC芯片如限幅器、开关等在版图设计中会采用非平衡的测试焊盘结构如GS(Ground Signal)或SG焊盘, 以替代芯片中部分尺寸较大的平衡式测试焊盘, 如GSG焊盘.对于该类MMIC芯片, 测试时需要同时采用文献[1-2]提及的平衡和非平衡两类射频探针.因射频传输电磁场分布模式的差异, 传统单一平衡式或非平衡式直通在片校准件无法同时满足平衡-非平衡混合射频探针的阻抗匹配要求, 导致校准精度大幅下降.
基于平衡-非平衡混合射频探针的测试属于异型结构测试, 针对异型结构, 研究人员提出了几种可行的解决方案.一是采用插损直减法, 通过标量运算去除射频探针等转接器的插损, 该方法未考虑矢量修正, 精度不高, 不适用于高频高精度测试.二是采用文献[3]中的OSL(Open Short Load)二阶去嵌法获得射频探针等转接器的S参数, 之后通过去嵌得到异型结构的S参数, 该方法的测量精度对校准件理想物理端面与实际校准端面之间的误差较为敏感.
本文对采用文献[4-6]中传统SOLR(Short Open Load Reciprocal)校准方式的平衡-非平衡混合射频探针测试的校准误差进行了评估计算, 并结合带误差修正的OSL二阶去嵌技术、文献[7-10]中的级联矩阵变换技术, 提出了一种基于平衡-非平衡混合射频探针的MMIC测试方法.该方法对校准件的实际校准端面与理想校准端面之间的误差进行修正, 进一步提高了射频探针的参数提取精度, 完成矢量修正和级联矩阵去嵌后, 校准参考平面可精确平移至探针尖端面, 显著提高了测试精度.为了提高测试效率, 结合文献[11]为该测试方案构建了自动测试系统, 实现了仪器控制、数据采集、结果修正、数据分析和图形化结果呈现的全自动操作.
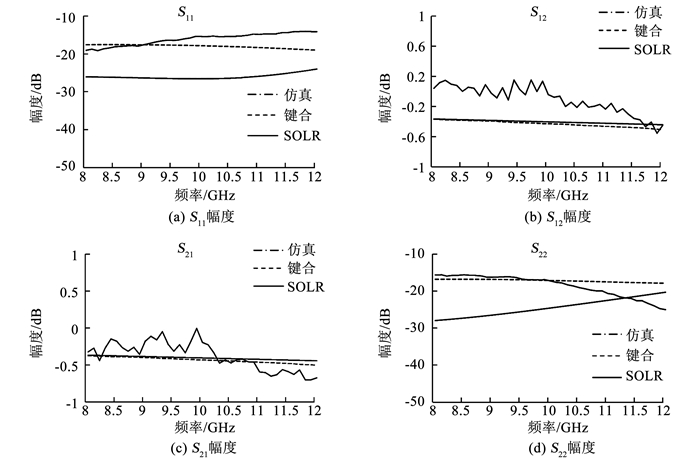
1 传统测试方案校准误差评估 随着对微波射频芯片愈发严苛的尺寸限制和集成度要求, 越来越多的芯片在版图设计中采用如图 1所示的平衡-非平衡(GSG-SG)测试焊盘结构.针对该异型结构, 对两种传统测试方案进行误差评估.第一种方案通过将下侧非平衡焊盘经金丝键合延伸到另一片测试用平衡GSG焊盘上, 使异型结构转换为两端均为GSG焊盘的可直接校准结构, 然后采用SOLT或者LRRM等传统校准方式进行双端口S参数测试.第二种方案直接采用SOLR方法对该异型结构进行在片校准.两种方案的测试结果与芯片仿真结果对比见图 2, 测试结果有明显差异.由图 2可知方案一测试与仿真结果吻合度较高, 但键合金丝等焊盘延伸转换结构引入的误差无法消除, 且芯片键合后无法非损取下, 只适用于少量样品评估测试, 不适用于大规模量产测试.方案二虽未破坏芯片但测试结果大幅偏离仿真结果, 故无法应用.
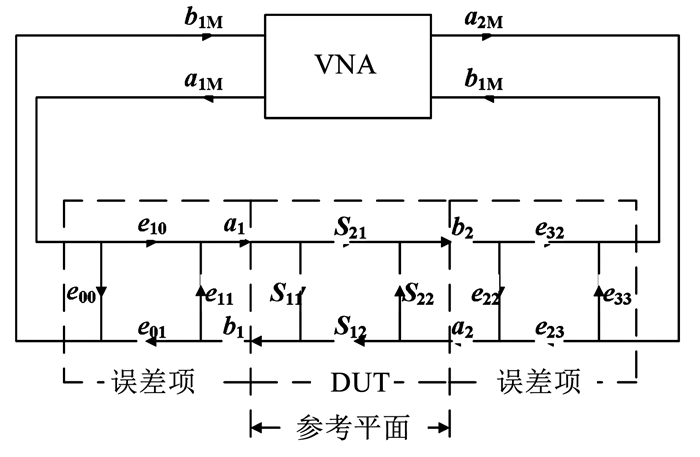
进一步分析方案二校准失效原因如下.SOLR校准方法采用8项误差模型, 其信号流图见图 3, 采用矢量网络分析仪(Vector Network Analyzer, VNA)进行测试.VNA收发机端面与待测件之间的传输矩阵采用二端口误差矩阵表示, 其中与Thru校准相关的乘积误差项方程如式(1)、(2)所示,
|
$
{e_{10}} \cdot {e_{32}} = \frac{{{E_{{\rm{RR}}}} \cdot {E_{{\rm{TF}}}}}}{{{E_{{\rm{RR}}}} + {E_{{\rm{DR}}}}({E_{{\rm{LF}}}} - {E_{{\rm{SR}}}})]}},
$
|
(1) |
|
$
{e_{01}} \cdot {e_{23}} = \frac{{{E_{{\rm{RF}}}} \cdot {E_{{\rm{TR}}}}}}{{{E_{{\rm{RF}}}} + {E_{{\rm{DF}}}}({E_{{\rm{LR}}}} - {E_{{\rm{SF}}}})]}}.
$
|
(2) |
式中:EDF为前向方向性误差、EDR为反向方向性误差、ESF为前向源失配误差、ESR为反向源失配误差、ERF为前向反射跟踪误差、ERR为反向反射跟踪误差可通过Open、Short、Load校准件校准获得.其它误差项ELF为前向负载失配误差、ELR为反向负载失配误差、ETF为前向传输跟踪误差、ETR为反向传输跟踪误差由Thru校准件测试获得, 文献[12-13]中给出了具体介绍.
式(3)中, SijMT(i=1, 2;j=1, 2)表示Open、Short、Load校准后测得Thru校准件S参数.对于无源互易器件, S12MT=S21MT, 忽略前向串扰误差EXF和反向串扰误差EXR.
|
$
{E_{{\rm{LF}}}} = \frac{{{S_{{\rm{11MT}}}} - {E_{{\rm{DF}}}}}}{{[{E_{{\rm{RF}}}} + {E_{{\rm{SF}}}}({S_{{\rm{11MT}}}} - {E_{{\rm{DF}}}})]}},
$
|
(3) |
|
$
{E_{{\rm{LR}}}} = \frac{{{S_{{\rm{22MT}}}} - {E_{{\rm{DR}}}}}}{{[{E_{{\rm{RR}}}} + {E_{{\rm{SR}}}}({S_{{\rm{22MT}}}} - {E_{{\rm{DR}}}})]}},
$
|
(4) |
|
$
{E_{{\rm{TF}}}} = ({S_{{\rm{21MT}}}} - {E_{{\rm{XF}}}})(1 - {E_{{\rm{SF}}}} \cdot {E_{{\rm{LF}}}}),
$
|
(5) |
|
$
{E_{{\rm{TR}}}} = ({S_{{\rm{12MT}}}} - {E_{{\rm{XR}}}})(1 - {E_{{\rm{SR}}}} \cdot {E_{{\rm{LR}}}}).
$
|
(6) |
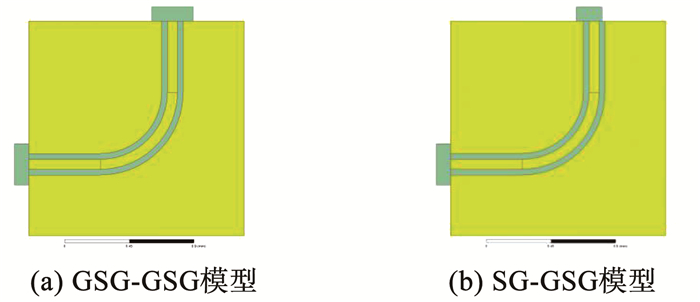
对不同类型探针进行全波电磁仿真, 模型见图 4, 参考文献[14].仿真结果与实际测得SijMT结果吻合, 将该Thru校准件的二端口S参数代入误差模型(3)~(6)中, 计算得到各误差项见图 5.可明显看出采用SG-GSG探针进行SOLR校准时, 如图 4 (b)所示, 端口阻抗不匹配会对误差模型参数以及实测结果产生显著影响; 而采用SG-GS探针进行SOLR校准时, 为满足端口匹配条件, 需修改校准片S与G之间缝隙的间距, 采用标准GSG Thru校准件无法满足SG射频端口匹配需求.因此, 若采用标准GSG Thru校准件, 上述方式均无法获得正确的ELF、ELR、ETR、ETF误差模型参数, 导致乘积项e10·e32、e01·e23误差进一步扩大, 从而产生不可靠的测试结果, 如图 2中SOLR校准测试结果所示.
综合分析比较上述两种方案, 传统基于单一平衡结构的直通在片校准件无法同时满足平衡-非平衡混合射频探针的阻抗匹配要求, 校准精度大幅下降, 无法获得准确可靠的测试结果, 键合方案也无法用于晶圆级MMIC量产测试, 亟需寻求新方案.
2 异型结构在片测试方案 为解决传统测试方案在测试精度与效率上无法满足晶圆级MMIC量产测试的需求问题.本文结合了带误差修正的OSL二阶去嵌技术、级联矩阵变换技术, 提出了一种基于平衡-非平衡混合射频探针的MMIC测试方法, 通过矢量修正将校准端面精准延伸至探针端面.
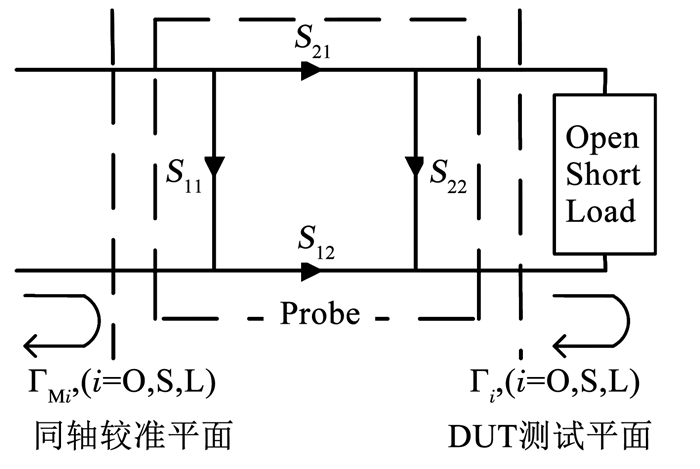
OSL二阶去嵌的信号流图见图 6.首先, 在同轴端面进行校准; 然后通过射频探针测量3个已知校准件物理端面反射系数Γi(i=O, S, L)的在片校准件Open、Short、Load, 得到探针同轴端面反射系数ΓMi, 如式(7)所示.假设Load校准件匹配良好, 则ΓL=0, 可得文献[3]中简化后射频探针的二端口S参数, 如式(8)~(10)所示.
|
$
{\Gamma _{{\rm{M}}i}} = \frac{{{b_1}}}{{{a_1}}} = {S_{11}} + \frac{{{S_{21}}{S_{12}}{\Gamma _i}}}{{1 - {S_{22}}{\Gamma _i}}},
$
|
(7) |
|
$
{S_{11}} = {\Gamma _{{\rm{ML}}}},
$
|
(8) |
|
$
{S_{22}} = \frac{{{\Gamma _{\rm{S}}}({\Gamma _{{\rm{ML}}}} - {\Gamma _{{\rm{MO}}}}) + {\Gamma _{\rm{O}}}({\Gamma _{{\rm{MS}}}} - {\Gamma _{{\rm{ML}}}})}}{{{\Gamma _{\rm{S}}}{\Gamma _{\rm{O}}}({\Gamma _{{\rm{MS}}}} - {\Gamma _{{\rm{MO}}}})}},
$
|
(9) |
|
$
{S_{21}}{S_{12}} = \frac{{({\Gamma _{\rm{S}}} - {\Gamma _{\rm{O}}})({\Gamma _{{\rm{MS}}}} - {\Gamma _{{\rm{ML}}}})({\Gamma _{{\rm{MO}}}} - {\Gamma _{{\rm{ML}}}})}}{{{\Gamma _{\rm{S}}}{\Gamma _{\rm{O}}}({\Gamma _{{\rm{M}}S}} - {\Gamma _{{\rm{MO}}}})}}.
$
|
(10) |
其中Open、Short、Load校准件一般采用电容、电感的三阶多项式模型分别表征, 由式(11)~(13)可以计算得到校准件物理端面反射系数ΓO、ΓS、ΓL.
|
$
\begin{array}{l}
{C_{\rm{O}}} = {C_0} + {C_1} \times f + {C_2} \times {f^2} + {C_3} \times {f^3}\\
{L_{\rm{S}}} = {L_0} + {L_1} \times f + {L_2} \times {f^2} + {L_3} \times {f^3}, \\
{L_{\rm{L}}} = {L_0} + {L_1} \times f + {L_2} \times {f^2} + {L_3} \times {f^3}
\end{array}
$
|
(11) |
|
$
\begin{array}{*{20}{c}}
{{Z_{\rm{O}}} = \frac{1}{{{\rm{j}}2{\rm{ \mathsf{ π} }}f{C_{\rm{O}}}}}}\\
{{Z_{\rm{S}}} = {\rm{j}}2{\rm{ \mathsf{ π} }}f{L_{\rm{S}}}}\\
{{Z_{\rm{L}}} = {\rm{j}}2{\rm{ \mathsf{ π} }}f{L_{\rm{L}}}}
\end{array},
$
|
(12) |
|
$
{\Gamma _i} = \frac{{{Z_i} - {Z_0}}}{{{Z_i} + {Z_0}}}.
$
|
(13) |
实际非理想校准件的理想物理端面与实际校准端面间存在一定偏差, 该偏差引入的衰减和相移可基于传输线模型进行等效, 并可进一步结合式(14)~(17)的修正算法予以消除, 等效模型见图 7, 式中Γi为已知校准件理想物理端面的反射系数, Γi'为经过误差修正后的校准件实际校准端面的反射系数, e-γl为修正因子.式中α和β为传输线的衰减常数和相位常数, Loffset和Doffset为传输线的插损和延时, 一般由校准件生产厂家如文献[15]提供, Z0, offset为传输线的特性阻抗, 通常为50 Ω.
|
$
al = \left[ {\frac{{{L_{{\rm{offset}}}} \cdot {D_{{\rm{offset}}}}}}{{2{Z_{0, {\rm{offset}}}}}}} \right]\sqrt {\frac{f}{{{{10}^9}}}} ,
$
|
(14) |
|
$
\beta l = 2{\rm{ \mathsf{ π} }}f \cdot {D_{{\rm{offset}}}} + \alpha l,
$
|
(15) |
|
$
{e^{ - \gamma l}} = {e^{ - \left( {\alpha + {\rm{j}}\beta } \right)l}},
$
|
(16) |
|
$
\Gamma {'_i} = {\Gamma _i}{e^{ - 2\gamma l}}.
$
|
(17) |
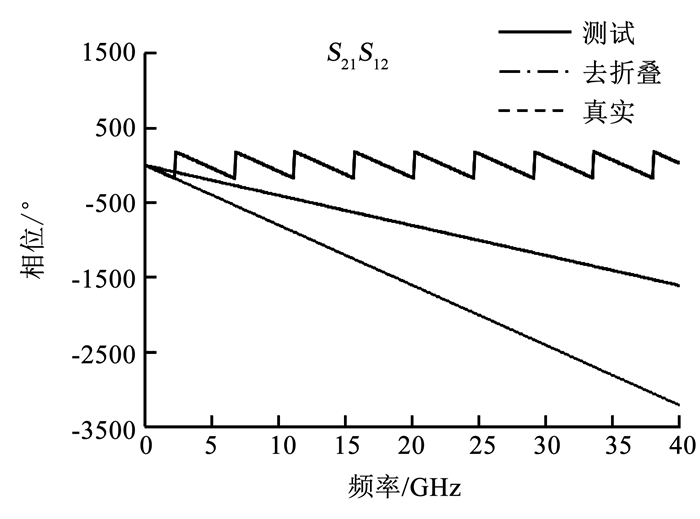
将修正后的校准件反射系数Γi'代入式(8)~(10)中, 可提取出修正后射频探针的S11、S22、S21S12.射频探针为无源非互易器件, 由式(10)可得$ {S_{12}} = {S_{21}} = \pm \sqrt {{S_{21}}{S_{12}}} $, 其具有文献[16]提及的相位不确定性问题, 可引入相位(Phase)连续性和Phase|0 Hz=0°补充条件进行相位分支选择, 见图 8.首先将测得S21S12原始相位数据(实线)基于相位连续性原则进行去折叠化(点划线), 而后沿纵轴进行180°周期延拓, 在其中选择零频相位为0°的分支(点划线), 将该相位分支的相频响应除以2, 便可得到S21真实的相频响应(虚线).
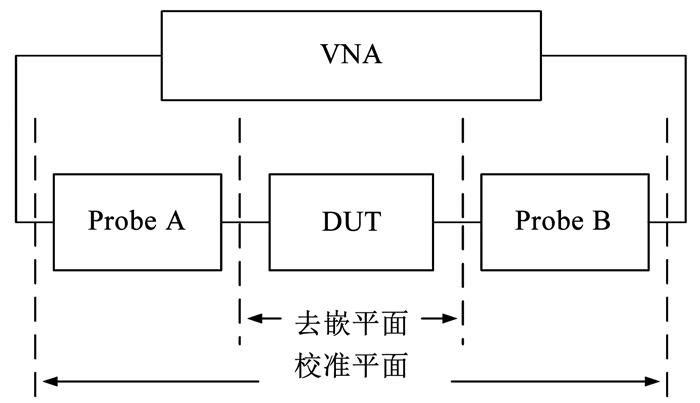
在依次获得平衡和非平衡射频探针的S参数(SA、SB)后, 用平衡-非平衡混合射频探针对待测MMIC芯片进行同轴端面的整体S参数(SM)测量, 并利用级联矩阵变换对SM进行矢量修正, 去嵌掉SA和SB, 从而得到待测MMIC的S参数(SD).测试系统框图见图 9.
级联矩阵变换首先利用式(18)将散射参数矩阵SM、SA、SB转换为传输参数矩阵TM、TA、TB, TM、TA、TB和待测件的传输参数矩阵TD满足式(19)关系.之后通过式(20)的矩阵逆运算得到TD, 最后由式(21)得到待测MMIC的散射参数SD.
|
$
\left[ {\begin{array}{*{20}{c}}
{{T_{i11}}}&{{T_{i12}}}\\
{{T_{i21}}}&{{T_{i22}}}
\end{array}} \right] = \left( {\frac{1}{{{S_{i21}}}}} \right)\left[ {\begin{array}{*{20}{c}}
{{S_{i12}}{S_{i21}} - {S_{i11}}{S_{i22}}}&{{S_{i11}}}\\
{ - {S_{i22}}}&1
\end{array}} \right], i = M, A, B.
$
|
(18) |
|
$
\left[ {{T_{\rm{M}}}} \right] = \left[ {{T_{\rm{A}}}} \right]\left[ {{T_{\rm{D}}}} \right]\left[ {{T_{\rm{B}}}} \right],
$
|
(19) |
|
$
\left[ {{T_{\rm{D}}}} \right] = {\left[ {{T_{\rm{A}}}} \right]^{ - 1}}\left[ {{T_{\rm{M}}}} \right]{\left[ {{T_{\rm{B}}}} \right]^{ - 1}},
$
|
(20) |
|
$
\left[ {\begin{array}{*{20}{c}}
{{S_{D11}}}&{{S_{D12}}}\\
{{S_{D21}}}&{{S_{D22}}}
\end{array}} \right] = \left( {\frac{1}{{{T_{D22}}}}} \right)\left[ {\begin{array}{*{20}{c}}
{{T_{D12}}}&{{T_{D11}}{T_{D22}} - {T_{D12}}{T_{D21}}}\\
1&{ - {T_{D12}}}
\end{array}} \right].
$
|
(21) |
3 测试结果与分析 基于异型结构在片测试方案, 本文设计了以矢量网络分析仪(Keysight PNA N5224A)、SG与GSG射频探针(Cascaded ACP-A-SG-150, ACP-A-GSG-150)、微波探针台(Cascaded Summit 11000BS)组成的在片测试系统来验证方案可行性.待测MMIC样片选择了如图 10 (a)所示的限幅器芯片, 基于GSG-SG混合射频探针的在片测试照片如图 10(b)所示.
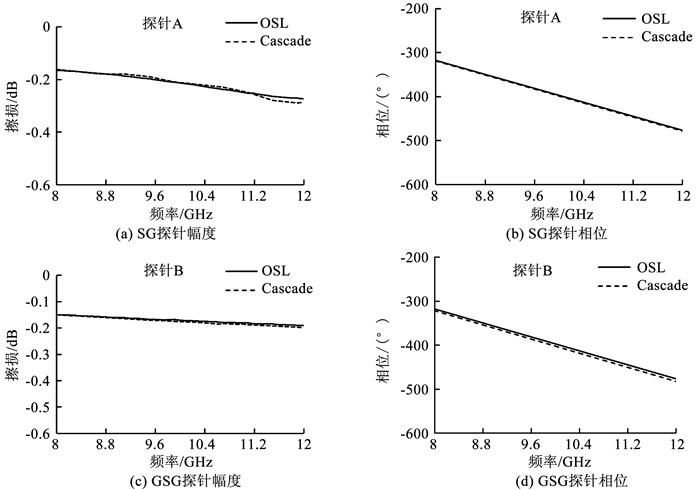
采用本文带误差修正的OSL二阶去嵌方法提取的SG与GSG两个探针的S参数与Cascade公司提供的出厂参数相吻合, 见图 11.
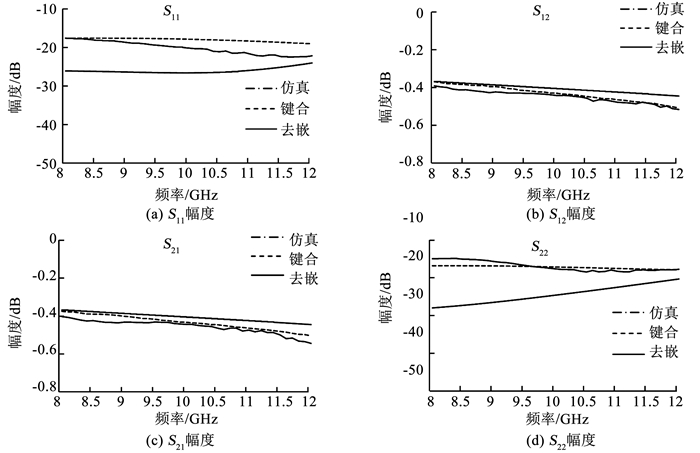
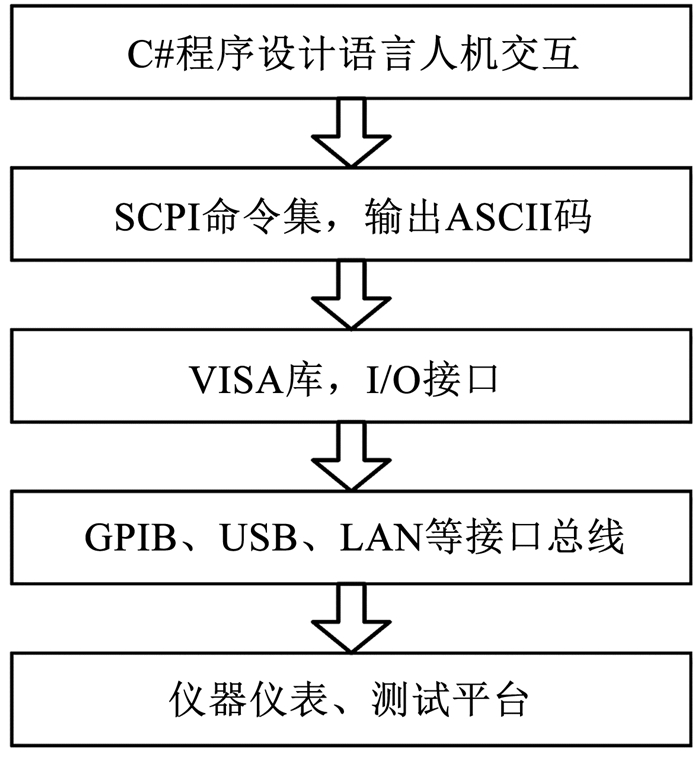
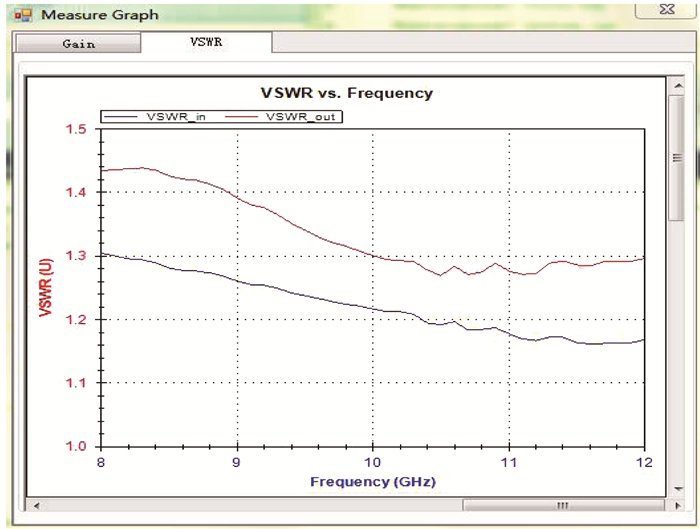
对限幅器芯片仿真结果、如图 1所示用于少量样品评估的键合方案测试结果以及本文提出的可用于大规模量产的方案测试结果进行了对比.对比结果见图 12, 本文方案测试结果与键合方案测试结果非常接近, S21误差小于0.1 dB, 具体对比见表 1.本文测试方案求解过程需要大量复数与矩阵运算, 采用C#面向对象语言, 借助程控仪器标准指令集(SCPI)和虚拟仪器软件结构(VISA), 通过调用标准I/O库内的指令集, 控制GPIB或者USB等接口总线将计算机与硬件仪器连接, 再通过仪器规定的控制代码实现对仪器的操作.测试程序框架见图 13, 测试结果界面见图 14.通过该程序实现了仪器控制、数据采集、结果修正、数据分析和图形化结果呈现的全自动操作, 避免了人为因素的干扰, 解决了晶圆级量产测试面临的效率问题.
表 1

表 1 传统方案与本文方案效率对比
Tab. 1 Comparison of traditional method and the method proposed in this paper
|
测试精度/dB |
测试速度/s |
| S11 |
S22 |
S21 |
S12 |
键合
(参考) |
-19.093~ |
-17.936~ |
-0.515~ |
-0.519~ |
600 |
| -17.594 |
-16.842 |
-0.386 |
-0.380 |
| 传统 |
-19.201~ |
-25.073~ |
-0.702~ |
-0.557~ |
600 |
| -14.126 |
-15.612 |
-0.007 |
0.150 |
| 本文 |
-22.511~ |
-18.506~ |
-0.565~ |
-0.537~ |
30 |
| -17.582 |
-14.900 |
-0.424 |
-0.412 |
|
|
表 1 传统方案与本文方案效率对比
Tab. 1 Comparison of traditional method and the method proposed in this paper
|
4 结论 本文对采用传统SOLR校准方式的平衡-非平衡混合射频探针测试的校准误差进行了评估计算, 并提出了一种基于平衡-非平衡混合射频探针的MMIC测试方法.该方法结合了带误差修正的OSL二阶去嵌技术、级联矩阵变换技术, 实现了射频探针S参数的精确提取和去嵌, 将校准参考平面从同轴端面精确平移至探针尖端面, 有效保证了待测MMIC芯片的测试精度, 并结合C#面向对象语言为该测试方案构建了自动测试系统, 可有效应用于MMIC产品晶圆级量产测试.




 2019, Vol. 51
2019, Vol. 51


