2. 多媒体与智能软件技术北京市重点实验室(北京工业大学),北京 100124
2. Beijing Municipal Key Laboratory of Multimedia and Intelligent Software Technology, Beijing University of Technology, Beijing 100124, China
蛋白质相互作用(Protein-protein Interaction,PPI)网络是一个生命有机体内所有蛋白质之间相互作用组成的生物分子关系网络,可用一个无向图G(V,E)表示,其中V为节点集合,E为边的集合.功能模块是指PPI网络中一定时空范围内通过相互作用完成某一特定分子功能的蛋白质集合.在PPI网络中检测蛋白质功能模块是蛋白质组学研究的一个重要内容,它不但有助于探索生命活动过程中某些未知蛋白质的功能,而且对于疾病诊断和研发新药具有十分重要的意义[1].
生物实验的方法是检测PPI网络功能模块最传统的方法,但它在检测质量、检测费用等方面存在局限性,已经无法满足后基因时代人们对于生命科学研究的实际需要[2].而近年来随着机器学习、数据挖掘等计算方法的兴起,人们开始利用各种聚类方法[3-6]来检测PPI网络中的功能模块,其中基于群智能的聚类方法在PPI网络功能模块检测中脱颖而出,表现出很好的效果.Pizzuti等[7]提出一种基于遗传算法的PPI网络GA-PPI聚类方法,该方法主要通过交叉操作和变异操作实现PPI网络的聚类.Ji等[8]提出一种基于蚁群聚类的PPI网络功能模块ACC-FMD检测方法,该方法采用拾起和放下概率模型对网络中的节点进行聚类.Yang等[9]提出一种基于细菌觅食机理的PPI网络功能模块BFO-FMD检测方法,该方法利用趋向、接合、繁殖和迁徙4个生物机制划分功能模块.综上,已有研究表明群智能聚类方法是目前进行PPI网络功能模块检测最具有竞争力的方法之一,但是由于其是通过种群的迭代进化来完成功能模块的检测,运行时间长已成为阻碍其在PPI网络功能模块检测中应用的主要瓶颈,所以发展更加高效的群智能功能模块检测方法仍然是该领域中一个值得深入研究的问题.
烟花算法(Fireworks Algorithm,FWA)是一种模拟烟花爆炸过程的群智能算法,具有平衡局部搜索和全局搜索的自调整机制,寻优能力较强,在求解全局优化问题上表现出快速收敛性,因此本文提出一种基于烟花算法的蛋白质相互作用网络功能模块检测方法FWA-FMD.该方法首先基于标签传播思想初始化种群中的每个烟花个体.其次在每一代进化过程中,利用具有局部搜索和全局搜索自调整能力的爆炸操作对每个烟花个体进行优化,并同时采用精英保留和轮盘赌策略选择下一代烟花种群.最后通过将适应度值最好的烟花个体中标签相同的节点划分到同一功能模块,完成PPI网络功能模块检测.在4个公共PPI网络数据集上的对比实验表明:FWA-FMD方法不仅具有求解时间快的优点,而且在检测质量上也具有一定的竞争性.
1 烟花算法受到烟花爆炸时产生火花并照亮夜空这一自然现象的启发,北京大学学者Tan和Zhu于2010年在首届国际群体智能大会上提出了一种新型的群体智能算法—烟花算法[10].在烟花算法中,每个烟花或者火花表示解空间中的一个可行解.算法的搜索过程如下:首先随机初始化N个烟花个体作为初始种群,其次在每代进化过程中,烟花种群通过爆炸操作和变异操作产生一定数量的火花,并应用选择策略从候选解集合(烟花和火花)中选择N个个体作为下一代种群.在选择过程中,为使当前种群中优秀的信息能够传递到下一代种群中,候选解集合中适应度值最好的个体会依据精英保留策略确定性地进入到下一代烟花种群,而剩下N-1个个体根据轮盘赌策略在候选解集合中选择.这样不断进化,使得种群对环境的适应性变得越来越好,从而求得问题的全局最优解.
2 FWA-FMD方法 2.1 基本思想FWA-FMD方法的基本思路为:首先基于标签传播思想初始化烟花种群,种群中的每个烟花个体被表示为一个候选的功能模块划分,即PPI网络功能模块检测问题的一个解.其次在每一代进化过程中,利用烟花算法的核心优化机制爆炸操作对每个烟花个体进行优化,并同时采用精英保留和轮盘赌策略选择下一代烟花种群.最后得到种群中适应度值最好的烟花个体,通过将其中标签相同的节点划分到同一功能模块,完成PPI网络功能模块检测.
在优化过程中,该方法利用模块密度函数来评价种群中烟花个体的适应度值.烟花个体的模块密度值越大表示适应度值越高,相应PPI网络功能模块检测的结果也越好.烟花个体Xi的适应度为
| $ f\left( {{X_i}} \right) = \sum\limits_{u = 1}^m {\frac{{2{l_u} - {{\bar l}_u}}}{{{n_u}}}} . $ | (1) |
式中:m为检测到的蛋白质功能模块个数; lu为第u个功能模块中所包含节点之间存在边的数目;
每个烟花个体Xi采用字符串编码的方式表示,算法基于标签传播思想将种群中的每个烟花个体初始化为一种候选的功能模块划分.在初始化过程中,算法首先根据PPI网络对应的图G(V,E)对所有蛋白质节点进行编号,建立蛋白质节点的邻居有序表.然后每个节点依照选择概率在其邻居节点集合中选择其中一个节点,假设节点k根据选择概率从其邻居节点集合中选择了邻居节点h,则将节点k和节点h分配相同的标签,有以下三种情形:
1) 节点k和节点h都还没有被分配标签,则将节点k和节点h分配一个相同且新的标签;
2) 节点k和节点h其中只有一个节点已经被分配标签,则将该标签分配给两者中没有被分配标签的节点;
3) 节点k和节点h都已经被分配标签,如果标签
最终形成一个烟花个体的编码,并将此个体存入初始种群中.图 1给出了一个烟花个体初始化过程的例子.

|
图 1 烟花个体的初始化过程 Fig. 1 Initialization process of firework individual |
图 1(a)为含有8个蛋白质节点的PPI网络,节点编号从1~8.图 1(b)为建立的邻居有序表.图 1(c)为初始化一个烟花个体的编码.其中标签相同的节点属于同一功能模块,图 1(d)对应的是图 1(c)中烟花个体的功能模块划分结果.
在烟花个体Xi中节点k选择邻居节点h的选择概率计算公式为
| $ P_k^h = \frac{{{C_{kh}}}}{{\sum\limits_{r \in {\rm{\Gamma }}\left( k \right)} {{C_{kr}}} }}. $ | (2) |
式中:Γ(k)为节点k的邻居节点集合; Ckh为节点k与节点h之间的相似性.由于在PPI网络中普遍存在大量的噪声数据,也并不完整,如果仅使用拓扑结构信息作为蛋白质节点之间相似性的度量标准存在较大的局限性.因此,本研究还将基因本体(Gene Ontology,GO)的功能注释信息作为蛋白质节点相似性度量的依据,可有效弥补PPI网络中数据的不完整和噪声的存在.基因本体主要通过分子功能、细胞组件和生物过程3个方面对基因和蛋白质功能进行了限定和描述,对于了解蛋白质在生命活动中所起的作用提供了更底层的信息.Ckh的计算公式见式(3),它综合了节点k和节点h的拓扑结构和功能注释信息.
| $ {C_{kh}} = \frac{{{s_{kh}} + {F_{kh}}}}{2}. $ | (3) |
式中:skh为节点k与节点h之间的结构相似性,Fkh为节点k与节点h之间的功能相似性,它们的计算公式分别如下:
| $ {s_{kh}} = \frac{{\left| {{\rm{\Gamma }}\left( k \right) \cap {\rm{\Gamma }}\left( h \right)} \right|}}{{\sqrt {\left| {{\rm{\Gamma }}\left( k \right)} \right|\left| {{\rm{\Gamma }}\left( h \right)} \right|} }}, $ | (4) |
| $ {F_{kh}} = \frac{{\left| {{g^k} \cap {g^h}} \right|}}{{\left| {{g^k} \cup {g^h}} \right|}}. $ | (5) |
式中:|Γ(k)|为节点k的邻居节点个数,即节点k的度数; gk为节点k的GO功能注释信息集合.
2.3 爆炸操作种群中的烟花个体爆炸产生爆炸火花,爆炸火花主要负责对烟花个体邻近区域的可行解空间进行搜索.适应度值越好的烟花个体爆炸产生的火花数越多,爆炸半径越小,体现了局部搜索过程; 而适应度值越差的烟花个体爆炸产生的火花数越少,爆炸半径越大,体现了全局搜索过程.每个烟花个体的爆炸半径和爆炸产生的爆炸火花数是根据其相对于当前种群中其他烟花个体的适应度值计算得到的.对于烟花个体Xi,其爆炸半径Ai和爆炸火花数Si的计算公式为
| $ {A_i} = \hat A \times \frac{{{f_{\max }} - f\left( {{X_i}} \right) + \varepsilon }}{{\sum\limits_{i = 1}^N {\left( {{f_{\max }} - f\left( {{X_i}} \right)} \right) + \varepsilon } }}, $ | (6) |
| $ {S_i} = M \times \frac{{f\left( {{X_i}} \right) - {f_{\min }} + \varepsilon }}{{\sum\limits_{i = 1}^N {\left( {f\left( {{X_i}} \right) - {f_{\min }}} \right) + \varepsilon } }}. $ | (7) |
式中:N为种群规模; fmax、fmin分别为当前种群中的适应度最大值、最小值;
原始烟花算法中的爆炸操作和变异操作用来产生火花,即烟花个体变异在可行解空间中进行搜索.这两种操作最初是为处理连续值设计的,然而蛋白质相互作用网络功能模块检测是一个离散优化问题,无法直接使用.本文利用一种离散的爆炸变异操作来产生爆炸火花,提高种群的多样性.烟花个体Xi中每个节点的标签经过爆炸操作产生爆炸火花Xs中与其对应节点的标签,其中爆炸火花Xs中节点k的标签产生方式见式(8)所示[11].
| $ X_s^k = \left\{ \begin{array}{l} X_i^k,\;{\rm{if}}\;{\rm{rand}} \ge {\rm{sigmoid}}\left( {{A_i}} \right);\\ U_{{\rm{Nbest}}}^k,\;\;{\rm{otherwise}}{\rm{.}} \end{array} \right. $ | (8) |
| $ {\rm{sigmoid}}\left( x \right) = \frac{1}{{1 + {{\exp }^{ - x}}}}. $ | (9) |
首先在0~1之间随机产生一个服从均匀分布的随机数rand,如果该随机数大于或者等于sigmoid(Ai),则爆炸火花Xs中节点k的标签与烟花个体Xi中节点k的标签保持一致; 否则,UNbestk为从烟花个体Xi中选择节点k的邻居节点标签集合中出现频率最高的标签,然后进行更新.图 2给出了烟花个体Xi中节点5的标签爆炸操作示意图,由图 1(b)中的邻居有序表可知,节点5的邻居节点有4、6、7,其中节点4的标签是1,节点6和7的标签都是3,可以看出标签3在节点5的邻居节点标签集合中出现的频率最高,所以将爆炸火花Xs中节点5的标签更新为3.
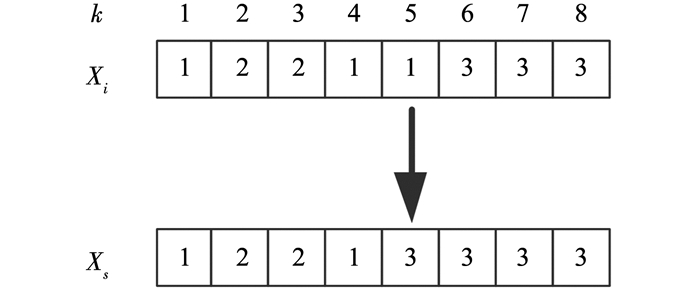
|
图 2 爆炸操作示意 Fig. 2 Sketch map of explosion operation |
烟花爆炸产生爆炸火花后,算法在烟花和火花候选解集合中按照如下方式选择N个个体作为下一代烟花种群:首先基于精英保留策略选择候选解集合中适应度值最大的个体; 然后采用轮盘赌策略在候选解集合中选择剩余N-1个个体[12].每个候选解Xi的选择概率为
| $ p\left( {{X_i}} \right) = \frac{{R\left( {{X_i}} \right)}}{{\sum\limits_{j \in K} {R\left( {{X_j}} \right)} }}, $ | (10) |
| $ R\left( {{X_i}} \right) = \sum\limits_{j \in K} {d\left( {{X_i},{X_j}} \right)} = \sum\limits_{j \in K} {\left| {f\left( {{X_i}} \right) - f\left( {{X_j}} \right)} \right|} . $ | (11) |
式中:K为候选解集合,包含当前种群中的烟花个体以及爆炸产生的火花; d(Xi, Xj)为候选解Xi与Xj之间的距离; R(Xi)为候选解Xi与其他候选解之间的距离之和.
2.5 算法描述与分析FWA-FMD算法的核心思想是利用具有局部搜索和全局搜索自调整能力的爆炸操作对每个烟花个体进行优化,通过将适应度值最好的烟花个体中标签相同的节点划分到同一功能模块,过滤掉节点数小于2的功能模块,最后得到PPI网络功能模块检测结果.FWA-FMD算法的伪代码如算法1:
算法1. FWA-FMD
输入:PPI网络对应的图G(V,E),|V|=n; GO基因本体功能注释信息;
输出:蛋白质功能模块集合;
1) 初始化参数:种群规模N; 最大迭代次数T; 控制爆炸半径大小的常数
2) for i=1 to N do
3) for k=1 to n do
4) 根据式(2)从节点k的邻居节点集合中选择一个邻居节点,将烟花个体Xi的节点k和选择的邻居节点分配相同的标签;
5) endfor
6) 计算烟花个体Xi的适应度值;
7) endfor
8) for t=1 to T do
9) for i=1 to N do
10) 根据式(6)计算烟花个体Xi的爆炸半径Ai;
11) 根据式(7)计算烟花个体Xi的爆炸火花数Si;
12) for j=1 to Si do
13) for k=1 to n do
14) 根据式(8)分配烟花个体Xi第j个爆炸火花的第k个节点的标签;
15) endfor
16) 计算烟花个体Xi第j个爆炸火花的适应度值;
17) endfor
18) endfor
19) 基于精英保留策略选择候选解集合(烟花和火花)中适应度值最好的个体;
20) 采用轮盘赌策略在候选解集合中选择剩余N-1个个体组成下一代烟花种群;
21) endfor
22) 算法运行结束,输出种群中适应度值最好的烟花个体对应的功能模块检测结果.
基于算法1的描述,假设PPI网络中节点度的最大值为dmax,对FWA-FMD算法的时间复杂度和空间复杂度做一个简单的分析:种群初始化的时间复杂度为
实验运行环境:Windows 8.1操作系统,Intel Core i5 - 6500 3.20 GHz CPU,12.0 GB内存,Eclipse运行平台.
实验中使用4个较新的公共PPI网络数据集,包括两个酵母菌(Saccharomyces cerevisiae)PPI网络数据集Gavin[13]和KroganCore[14],以及两个人类(Homo sapiens)PPI网络数据集DIPCore[15]和DIPFull[15].其中两个酵母菌PPI网络数据集使用Hernandez等[16]整理的数据,而两个人类PPI网络数据集通过网址(http://dip.doe-mbi.ucla.edu/dip/)下载,版本是Hsapi20170205.4个公共PPI网络数据集的详细信息见表 1.
| 表 1 实验使用的PPI网络数据集 Tab. 1 PPI network datasets in our experiment |
为评价算法的效果,实验中使用4个公共的标准功能模块数据集,包括两个酵母菌标准功能模块数据集SGD[17]和CYC2008[18],以及两个人类标准功能模块数据集PCDq[19]和CORUM[20].4个公共标准功能模块数据集的详细信息见表 2.
| 表 2 实验使用的标准功能模块数据集 Tab. 2 Gold standard datasets in our experiment |
实验用目前广泛使用的两组评价指标来度量功能模块检测算法的性能.
3.2.1 精度、召回率和F度量精度(Precision)、召回率(Recall)和F度量(F-measure)是目前PPI网络功能模块检测问题中常用的一组评价指标.精度和召回率的定义分别为:
| $ {P_{{\rm{precision}}}} = \frac{{{N_{{\rm{cp}}}}}}{{\left| P \right|}}, $ | (12) |
| $ {R_{{\rm{recall}}}} = \frac{{{N_{{\rm{cb}}}}}}{{\left| B \right|}}. $ | (13) |
式中:P为算法预测的功能模块集合,B为标准的功能模块集合,则P中至少和一个标准功能模块相匹配的模块数为
| $ N_{{\rm{NA}}}^{pb} = \frac{{{{\left| {{V_p} \cap {V_b}} \right|}^2}}}{{\left| {{V_p}} \right| \times \left| {{V_b}} \right|}}. $ | (14) |
式中:
F度量是精度和召回率的综合评价指标,定义为精度和召回率的调和平均数
| $ {F_{{\rm{f - measure}}}} = \frac{{2 \times {P_{{\rm{precision}}}} \times {R_{{\rm{recall}}}}}}{{{P_{{\rm{precision}}}} + {R_{{\rm{recall}}}}}}. $ | (15) |
灵敏度(Sensitivity,Sn)、正预测率(Positive Predictive Value,PPV)和准确度(Accuracy,Acc)是另一组用来度量功能模块检测算法的评价指标.灵敏度和正预测率的定义分别为:
| $ {S_{{\rm{sn}}}} = \frac{{\sum\limits_{i = 1}^n {\mathop {\max }\limits_j \left\{ {{T_{ij}}} \right\}} }}{{\sum\limits_{i = 1}^n {{N_i}} }}, $ | (16) |
| $ {P_{{\rm{ppv}}}} = \frac{{\sum\limits_{j = 1}^m {\mathop {\max }\limits_i \left\{ {{T_{ij}}} \right\}} }}{{\sum\limits_{j = 1}^m {{T_{.j}}} }}. $ | (17) |
式中:m=|P|,n=|B|; Tij为标准功能模块bi与预测功能模块pj共有的蛋白质数量; Ni为第i个标准功能模块中蛋白质的数量;
准确度是灵敏度和正预测率的综合评价指标,定义为灵敏度和正预测率的几何平均数
| $ {A_{{\rm{acc}}}} = \sqrt {{S_{{\rm{sn}}}} \times {P_{{\rm{ppv}}}}} . $ | (18) |
为给FWA-FMD算法选择一组相对合理的参数值,对FWA-FMD算法中用到的参数进行了实验.每种参数在其他参数固定不变的情况下,以精度、召回率、F度量、灵敏度、正预测率和准确度作为评价依据,取10次算法独立运行的平均结果,最后综合比较6种指标确定参数值为:种群规模N=40,最大迭代次数T=30,控制爆炸半径大小的常数A ^ =90,控制爆炸火花数的常数M=50.对比算法中的参数与原论文保持一致.
本文将提出的FWA-FMD算法与7种代表性算法MCODE[3]、CFinder[4]、NEMO[5]、FAG-EC[6]、GA-PPI[7]、ACC-FMD[8]和BFO-FMD[9]在4个数据集上进行了实验比较.FWA-FMD算法与其他三种群智能功能模块检测算法GA-PPI、ACC-FMD和BFO-FMD在4个数据集上时间性能的比较见表 3.
| 表 3 4种群智能算法在不同PPI网络数据集上的运行时间对比s Tab. 3 Running time comparison of four swarm intelligent algorithms in different PPI network datasets |
不难发现,FWA-FMD算法在4个数据集上的运行时间相比其他三种群智能算法GA-PPI、ACC-FMD和BFO-FMD都是最短的,具有绝对的优势.以Gavin和DIPCore数据集为例,具体说明一下算法的时间性能,在Gavin数据集上,GA-PPI、ACC-FMD和BFO-FMD算法的运行时间分别是FWA-FMD算法的1.3倍、28.5倍和3.9倍.在DIPCore数据集上,GA-PPI、ACC-FMD和BFO-FMD算法的运行时间分别是FWA-FMD算法的2.6倍、14.7倍和20.1倍.这主要是因为GA-PPI算法的收敛速度较慢,ACC-FMD和BFO-FMD在后处理阶段采用了功能模块合并策略,造成了各自求解时间过长的缺陷.而FWA-FMD算法采用字符串编码的方式表示烟花个体,方便对个体进行编码和解码,降低了计算复杂度,并且基于标签传播思想优化初始烟花种群,从而加快了算法的收敛速率,也无需后处理操作,因此FWA-FMD算法与其他3种群智能算法相比具有良好的时间性能,是一种高效快速的功能模块检测方法.
表 4~7分别给出8种算法在4个数据集上预测模块数、模块平均大小、至少与一个标准模块相匹配的预测模块数Ncp和至少与一个预测模块相匹配的标准模块数Ncb的对比结果.
| 表 4 8种算法在Gavin数据集上的实验结果 Tab. 4 Experimental results of eight algorithms in Gavin dataset |
| 表 5 8种算法在KroganCore数据集上的实验结果 Tab. 5 Experimental results of eight algorithms in KroganCore dataset |
| 表 6 8种算法在DIPCore数据集上的实验结果 Tab. 6 Experimental results of eight algorithms in DIPCore dataset |
| 表 7 8种算法在DIPFull数据集上的实验结果 Tab. 7 Experimental results of eight algorithms in DIPFull dataset |
以FWA-FMD算法在Gavin数据集上的检测结果为例说明一下表 4~7中各个数据的含义,算法在Gavin数据集上检测到了175个功能模块,模块的平均大小为10.59,其中用SGD标准功能模块数据集作为基准评价的结果为,有77个预测模块和126个标准模块相匹配,用CYC2008标准功能模块数据集作为基准评价的结果为,有94个预测模块和119个标准模块相匹配.总体来看,在Ncp指标上,FWA-FMD算法在Gavin和KroganCore数据集上的检测结果用SGD标准功能模块数据集作为基准来评价分别排在第4、第3,用CYC2008标准功能模块数据集作为基准来评价都排在第4;在DIPCore和DIPFull数据集上的检测结果用PCDq标准功能模块数据集作为基准来评价都排在第1,用CORUM标准功能模块数据集作为基准来评价分别排在第2、第3.在Ncb指标上,FWA-FMD算法在Gavin和KroganCore数据集上的检测结果不论用SGD标准功能模块数据集作为基准来评价,还是用CYC2008标准功能模块数据集作为基准来评价都排在第2;在DIPCore和DIPFull数据集上的检测结果用PCDq标准功能模块数据集作为基准来评价都排在第1,用CORUM标准功能模块数据集作为基准来评价都排在第2.由此可以看出FWA-FMD算法检测到的功能模块与标准功能模块匹配的模块数较多,反映了FWA-FMD算法的性能较优.
为更进一步展现FWA-FMD算法的整体性能,图 3~10分别给出8种算法在4个数据集上精度、召回率、F度量、灵敏度、正预测率和准确度6个评价指标的对比结果.
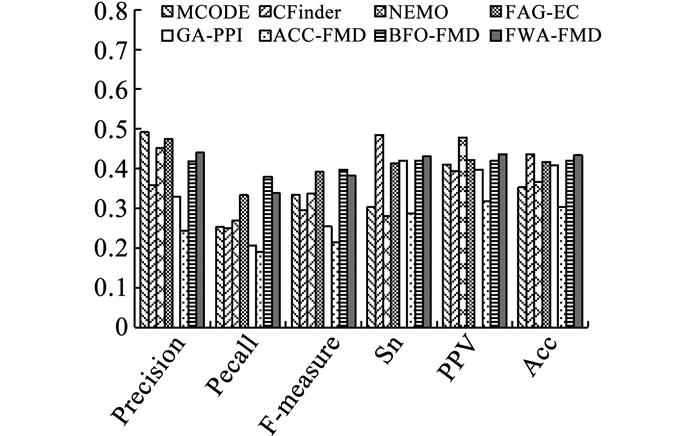
|
图 3 8种算法在Gavin数据集上用SGD作为标准数据集的对比结果 Fig. 3 Results comparison of eight algorithms in Gavin dataset using SGD gold standard |

|
图 4 8种算法在Gavin数据集上用CYC2008作为标准数据集的对比结果 Fig. 4 Results comparison of eight algorithms in Gavin dataset using CYC2008 gold standard |
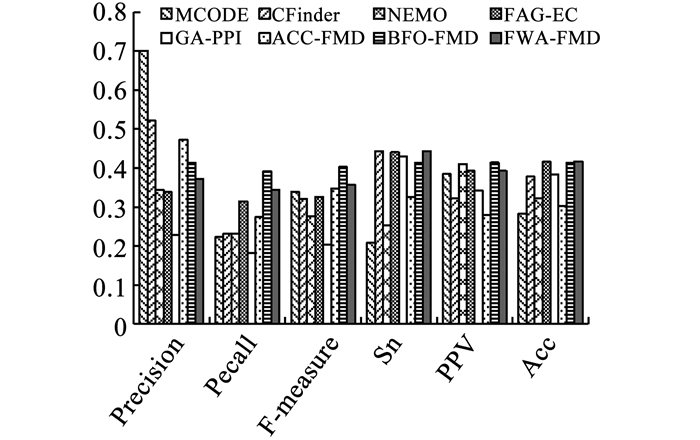
|
图 5 8种算法在KroganCore数据集上用SGD作为标准数据集的对比结果 Fig. 5 Results comparison of eight algorithms in KroganCore dataset using SGD gold standard |
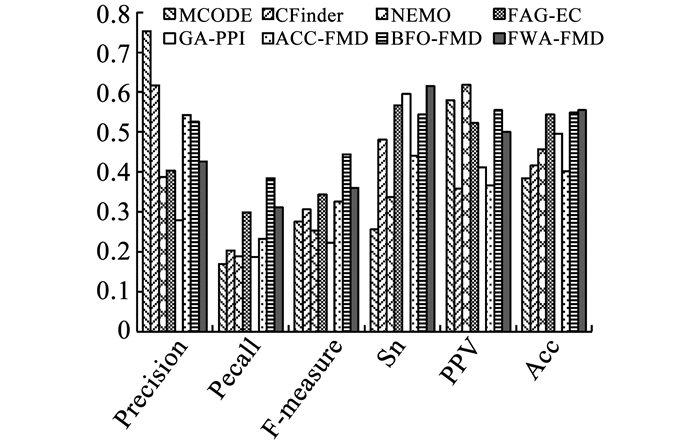
|
图 6 8种算法在KroganCore数据集上用CYC2008作为标准数据集的对比结果 Fig. 6 Results comparison of eight algorithms in KroganCore dataset using CYC2008 gold standard |

|
图 7 8种算法在DIPCore数据集上用PCDq作为标准数据集的对比结果 Fig. 7 Results comparison of eight algorithms in DIPCore dataset using PCDq gold standard |
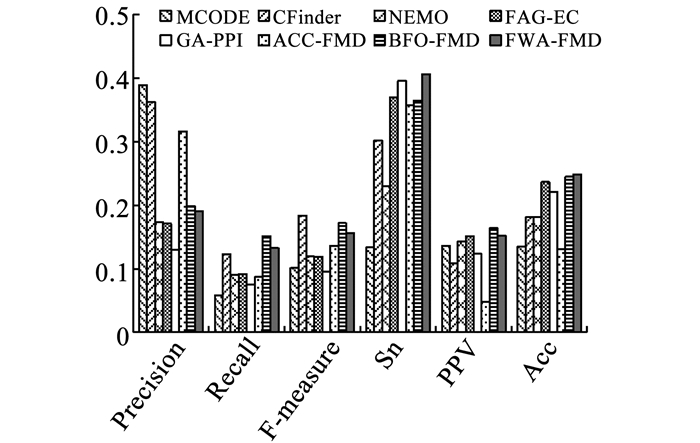
|
图 8 8种算法在DIPCore数据集上用CORUM作为标准数据集的对比结果 Fig. 8 Results comparison of eight algorithms in DIPCore dataset using CORUM gold standard |

|
图 9 8种算法在DIPFull数据集上用PCDq作为标准数据集的对比结果 Fig. 9 Results comparison of eight algorithms in DIPFull dataset using PCDq gold standard |
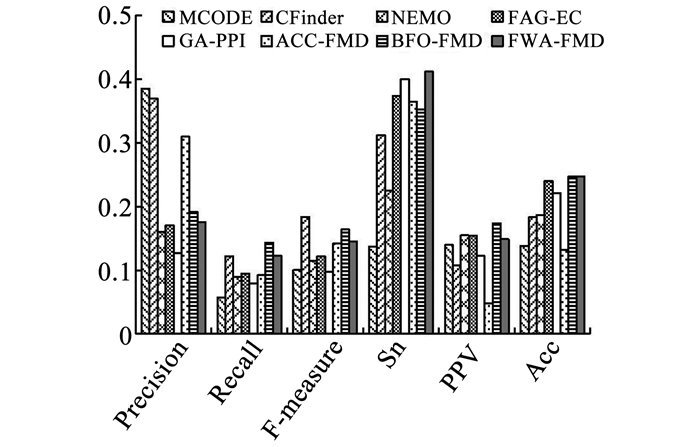
|
图 10 8种算法在DIPFull数据集上用CORUM作为标准数据集的对比结果 Fig. 10 Results comparison of eight algorithms in DIPFull dataset using CORUM gold standard |
在Gavin数据集上,用SGD标准功能模块数据集作为基准评价8种算法的检测结果见图 3,FWA-FMD算法在召回率、灵敏度、正预测率和准确度4个评价指标上都取得了第2的结果,F度量和精度分别排在第3、第4;用CYC2008标准功能模块数据集作为基准评价8种算法的检测结果见图 4,FWA-FMD算法在灵敏度和准确度两个评价指标上都取得了1的结果,召回率和F度量取得了第2的结果,正预测率和精度分别位于第3、第4.
在KroganCore数据集上,不论用SGD还是用CYC2008标准功能模块数据集作为基准评价8种算法的检测结果,由图 5和6可以看出,FWA-FMD算法在灵敏度和准确度两个评价指标上都取得了第1的结果,召回率和F度量取得了第2的结果,精度排在第5,正预测率分别位于第4、第5.
在DIPCore数据集上,用PCDq标准功能模块数据集作为基准评价8种算法的检测结果见图 7,FWA-FMD算法在召回率、F度量、灵敏度和准确度4个评价指标上都取得了第1的结果,正预测率和精度分别排在第2、第3;用CORUM标准功能模块数据集作为基准评价8种算法的检测结果见图 8,FWA-FMD算法在灵敏度和准确度两个评价指标上都取得了第1的结果,召回率和正预测率取得了第2的结果,F度量和精度分别位于第3、第5.
在DIPFull数据集上,用PCDq标准功能模块数据集作为基准评价8种算法的检测结果见图 9,FWA-FMD算法在召回率、F度量和灵敏度3个评价指标上都取得了第1的结果,正预测率和准确度取得了第2的结果,精度排在第3;用CORUM标准功能模块数据集作为基准评价8种算法的检测结果见图 10,FWA-FMD算法在灵敏度和准确度两个评价指标上都取得了第1的结果,召回率取得了第2的结果,F度量、正预测率和精度分别位于第3、第4和第5.
综合分析以上在酵母菌和人类两个物种的4个公共PPI网络数据集上的功能模块检测结果,分别用两种标准功能模块数据集作为基准来评价的实验表明:FWA-FMD算法与其他7种代表性算法相比,在两个综合评价指标F度量和准确度上具有较强的竞争力,这是因为FWA-FMD算法通过爆炸操作对每个烟花个体进行优化,适应度值好的烟花个体爆炸产生的火花数多且节点标签改变少,而适应度值差的烟花个体与之正好相反,较好地平衡了局部搜索和全局搜索,使得算法能够获得更优的烟花个体,从而更准确地刻画了PPI网络中的功能模块划分.另外FWA-FMD算法检测到的功能模块与标准功能模块匹配度较高,因而召回率和灵敏度的表现也不错,都排在前两名的位置.但是由于FWA-FMD算法检测到的功能模块总数比较多,使得精度和正预测率的表现一般,然而相比其中一些算法仍然具有一定的优势.由此可见,FWA-FMD算法不论是在酵母菌还是在人类物种PPI网络中都能够更好地识别功能模块,所以FWA-FMD是一个有效的功能模块检测方法.
4 结论本文提出一种基于烟花算法的蛋白质相互作用网络功能模块FWA-FMD检测方法,该方法首先基于标签传播思想将每个烟花个体初始化为一种候选的功能模块划分.其次在每一代进化过程中,利用具有局部搜索和全局搜索自调整能力的爆炸操作对每个烟花个体进行优化,并同时采用精英保留和轮盘赌策略选择下一代烟花个体.最后通过将最优烟花个体中标签相同的节点划分到同一功能模块,完成PPI网络功能模块检测.综合在酵母菌和人类两个物种的4个公共PPI网络数据集上的功能模块检测结果,分别用两种标准功能模块数据集作为基准来评价的实验表明:FWA-FMD方法不但具有良好的时间性能,而且在多项评价指标上都具有明显的优势,能够更好地识别功能模块.
FWA-FMD算法的提出,为快速进行PPI网络功能模块检测提供了一种新途径,是群集智能思想在PPI网络功能模块检测问题上的一个新探索.虽然FWA-FMD算法在运行时间上有很好的表现,但在检测精度上还存在一定的提升空间,这可能是由于烟花算法中的每一代个体都是独立的进化,没有考虑到不同烟花个体之间的相互联系和学习,使得进化过程中产生的有用信息没有得到充分利用,如何解决该问题,进一步优化算法的检测结果将是下一步工作的研究重点.
| [1] |
JI Junzhong, ZHANG Aidong, LIU Chunnian, et al. Survey: functional module detection from protein-protein interaction networks[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(2): 261. DOI:10.1109/TKDE.2012.225 |
| [2] |
冀俊忠, 刘志军, 刘红欣, 等. 蛋白质相互作用网络功能模块检测的研究综述[J]. 自动化学报, 2014, 40(4): 577. JI Junzhong, LIU Zhijun, LIU Hongxin, et al. An overview of research on functional module detection for protein-protein interaction networks[J]. Acta Automatica Sinica, 2014, 40(4): 577. DOI:10.3724/SP.J.1004.2014.00577 |
| [3] |
BADER G D, HOGUE C W. An automated method for finding molecular complexes in large protein interaction networks[J]. BMC Bioinformatics, 2003, 4(1): 2. DOI:10.1186/1471-2105-4-2 |
| [4] |
ADAMCSEK B, PALLA G, FARKAS I J, et al. CFinder: locating cliques and overlapping modules in biological networks[J]. Bioinformatics, 2006, 22(8): 1021. DOI:10.1093/bioinformatics/btl039 |
| [5] |
RIVERA C G, VAKIL R, BADER J S. Nemo: network module identification in cytoscape[J]. BMC Bioinformatics, 2010, 11(Suppl 1): S61. DOI:10.1186/1471-2105-11-S1-S61 |
| [6] |
LI Min, WANG Jianxin, CHEN Jian'er. A fast agglomerate algorithm for mining functional modules in protein interaction networks[C]//International Conference on Biomedical Engineering and Informatics. Sanya, China: IEEE, 2008: 3. DOI: 10.1109/BMEI.2008.121
|
| [7] |
PIZZUTI C, ROMBO S. Experimental evaluation of topological-based fitness functions to detect complexes in PPI networks[C]//Genetic and Evolutionary Computation Conference. Philadelphia, USA: ACM, 2012: 193. DOI: 10.1145/2330163.2330191
|
| [8] |
JI Junzhong, LIU Hongxin, ZHANG Aidong, et al. ACC-FMD: ant colony clustering for functional module detection in protein-protein interaction networks[J]. International Journal of Data Mining and Bioinformatics, 2015, 11(3): 331. DOI:10.1504/IJDMB.2015.067323 |
| [9] |
YANG Cuicui, JI Junzhong, ZHANG Aidong. BFO-FMD: bacterial foraging optimization for functional module detection in protein-protein interaction networks[J]. Soft Computing, 2018, 22(10): 3395. DOI:10.1007/s00500-017-2584-9 |
| [10] |
TAN Ying, ZHU Yuanchun. Fireworks algorithm for optimization[C]//International Conference on Swarm Intelligence. Berlin, Heidelberg: Springer, 2010: 355. DOI: 10.1007/978-3-642-13495-1_44
|
| [11] |
GUENDOUZ M, AMINE A, HAMOU R M. A discrete modified fireworks algorithm for community detection in complex networks[J]. Applied Intelligence, 2017, 46(2): 373. DOI:10.1007/s10489-016-0840-9 |
| [12] |
ZHENG S, JANECEK A, TAN Y. Enhanced fireworks algorithm[C]//IEEE Congress on Evolutionary Computation. Cancún, México: IEEE, 2013: 2069. DOI: 10.1109/CEC.2013.6557813
|
| [13] |
GAVIN A C, ALOY P, GRANDI P, et al. Proteome survey reveals modularity of the yeast cell machinery[J]. Nature, 2006, 440(7084): 631. DOI:10.1038/nature04532 |
| [14] |
KROGAN N J, CAGNEY G, YU H, et al. Global landscape of protein complexes in the yeast Saccharomyces cerevisiae[J]. Nature, 2006, 440(7084): 637. DOI:10.1038/nature04670 |
| [15] |
SALWINSKI L, MILLER C S, SMITH A J, et al. The database of interacting proteins: 2004 update[J]. Nucleic Acids Research, 2004, 32: D449. DOI:10.1093/nar/gkh086 |
| [16] |
HERNANDEZ C, MELLA C, NAVARRO G, et al. Protein complex prediction via dense subgraphs and false positive analysis[J]. Plos One, 2017, 12(9): e0183460. DOI:10.1371/journal.pone.0183460 |
| [17] |
CHERRY J M, ADLER C, BALL C, et al. SGD: saccharomyces genome database[J]. Nucleic Acids Research, 1998, 26(1): 73. DOI:10.1093/nar/26.1.73 |
| [18] |
PU S, WONG J, TURNER B, et al. Up-to-date catalogues of yeast protein complexes[J]. Nucleic Acids Research, 2009, 37(3): 825. DOI:10.1093/nar/gkn1005 |
| [19] |
KIKUGAWA S, NISHIKATA K, MURAKAMI K, et al. PCDq: human protein complex database with quality index which summarizes different levels of evidences of protein complexes predicted from H-Invitational protein-protein interactions integrative dataset[J]. BMC Systems Biology, 2012, 6(S2): S7. DOI:10.1186/1752-0509-6-S2-S7 |
| [20] |
RUEPP A, WAEGELE B, LECHNER M, et al. CORUM: the comprehensive resource of mammalian protein complexes—2009[J]. Nucleic Acids Research, 2010, 38(1): D497. DOI:10.1093/nar/gkp914 |
 2019, Vol. 51
2019, Vol. 51


