2. 华北水利水电大学 土木与交通学院,郑州 450046;
3. 华北理工大学 建筑工程学院,河北 唐山 063009
2. School of Civil Engineering and Communication, North China University of Water Resources and Electric Power, Zhengzhou 450046, China;
3. College of Civil and Architectural Engineering, North China University of Science and Technology, Tangshan 063009, Hebei, China
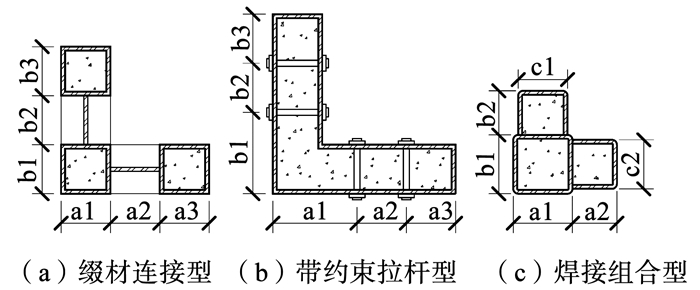
方钢管混凝土(CFSST)柱具有承载力高、无弱轴、形状规则易连接等优点而被广泛使用,但直接用于多层钢框架结构住宅中易在室内产生棱角,影响美观和实用.多位学者展开了对方钢管混凝土异形截面柱的研究.陈志华团队[1-2]提出一种由CFSST柱和缀材焊接而成的组合异形柱(见图 1(a)),并通过试验研究了其受压性能和抗震性能.蔡健等[3-4]通过试验研究了带约束拉杆的“L”形钢管混凝土柱(见图 1(b))的轴压、偏压性能.柳杨青等[5]提出一种用冷弯槽钢和冷弯方钢管焊接而成的闭口截面异形柱(见图 1(c)),并进行了轴压稳定性分析.
|
图 1 三种异形柱的截面型式 Fig. 1 Three types of special-shaped column |
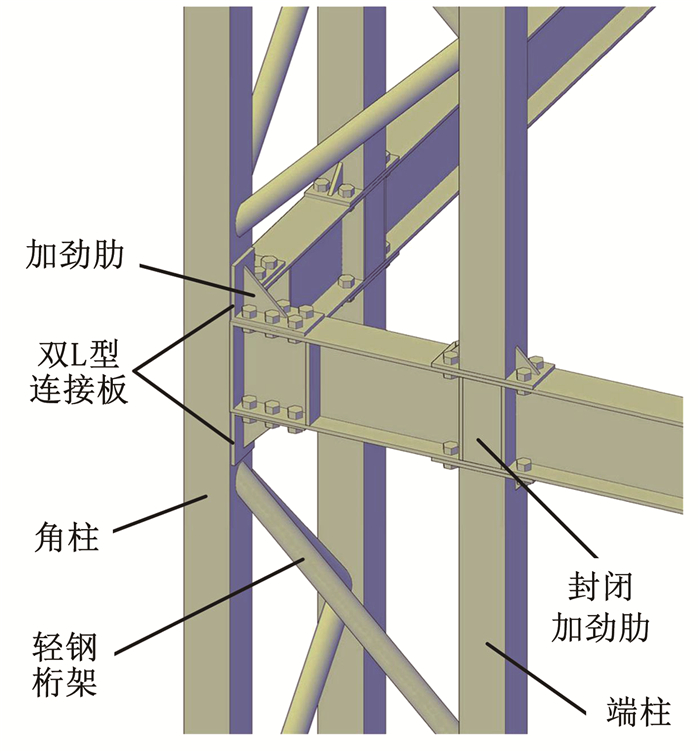
以上异形柱的肢高肢厚比一般是定值,而且普遍不大于4[6],使得其适用性和抗侧刚度受到限制.在低层装配式CFSST柱框架结构住宅中,较大窗洞的窗边墙或门垛的水平长度一般为300~1 000 mm,传统做法是固定龙骨后用多孔材料填充,不仅费工费时且有安全隐患.为提高结构抗震性能,可将CFSST柱和窗边墙或门垛结合起来,设计为桁架式异形截面柱,见图 2,其肢高肢厚比可根据窗边墙或门垛尺寸灵活设计.为方便分层装配施工,端柱与梁连接处设计为梁贯通.肢高肢厚比的改变,使得桁架式“L”形柱和前述的组合异形柱在受力性能、破坏特征等方面有较大区别; 又由于是桁架式构件,其受力和普通的RC短肢剪力墙也不同,因此把这种由轻钢桁架式“L”形柱组成的框架结构称为轻钢框架-轻钢桁架结构.
|
图 2 桁架式“L”形柱构造 Fig. 2 Construction of truss-type L-shaped column |
图 2所示的Warren式桁架之前主要用于桥梁和屋架.刘永健等[7]进行了该类桁架平面内的受弯性能试验.黄政华、张其林等[8]对平面钢管Warren式桁架的面外稳定问题进行了试验和理论研究,提出节点面外转动刚度公式并建立了钢管桁架面外稳定分析模型.对于将Warren桁架用作竖向构件,目前尚无相关资料.为研究该桁架式“L”形柱在高抗震设防烈度地区罕遇地震动甚至极罕遇地震动[9]下的的受力性能和破坏机理,设计和制作了一幢两层的装配式轻钢框架-轻钢桁架结构住宅足尺模型,选取天然地震波和人工地震波,对模型展开多个加速度级别的模拟地震振动台试验.研究模型结构在各水准地震作用下的动力特性、加速度、位移、应变等响应的变化规律及结构破坏特征,校验设计方案的可行性,为装配式轻钢框架-轻钢桁架结构的力学分析和抗震计算提供依据.
1 试验概况 1.1 模型设计桁架式“L”形柱为单轴对称截面,剪心和形心不重合,在水平地震作用下既可能发生绕非对称主轴的弯曲屈曲,也可能发生绕对称主轴的弯扭屈曲.根据弹性屈曲理论推导出其在发生弯曲屈曲时的换算长细比λox和弯扭屈曲[10]时的换算长细比λoy, 该值由方钢管截面特性、桁架斜杆截面特性及角度等因素决定.综合考虑换算长细比及轴压比要求,确定角柱及端柱均采用100 mm×100 mm(壁厚4 mm)的方钢管内灌C40再生混凝土,“L”形截面肢高肢厚比取7,斜杆采用ϕ50 mm圆钢管,壁厚3.5 mm,与柱夹角为45°.
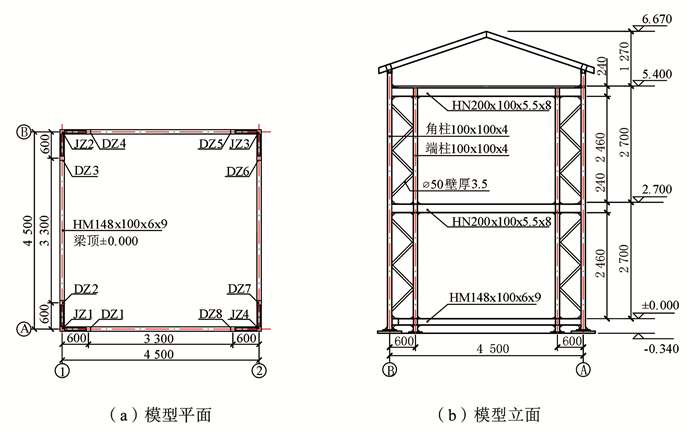
试验模型设计见图 3.主梁与角柱的连接采用双L型带加劲肋式节点[11],主梁与端柱连接处设计为梁贯通, 并在主梁连接区段设封闭加劲肋.在模型标高±0 m处设4根基础钢梁,标高2.7 m、5.4 m处各设4根主梁、7根次梁及1层楼板,楼板采用预制再生混凝土板,厚40 mm,配ϕ4@60 mm双层双向钢丝.在主、次梁顶面沿中心线均匀设置ϕ13 mm型栓钉,楼板上对应栓钉位置预留ϕ40 mm圆孔,装配时将楼板圆孔对准梁顶栓钉后落下,然后在圆孔中注入灌浆料并抹平.
|
图 3 模型平面图和立面(mm) Fig. 3 Floor plan and elevation of the model(mm) |
梁柱连接采用8.8级M16螺栓,屋架和柱顶连接采用8.8级M12螺栓.装配施工需要在螺栓孔、插接件等位置留出装配间隙,故模型所有钢板及钢梁上的螺栓孔直径均比设计螺栓公称直径大2 mm.所有螺栓均使用力矩扳手按《钢结构高强度螺栓连接技术规程》(JGJ82—2011)规定的扭矩和操作方法拧紧.模型主要材料的力学指标见表 1.制作过程的部分照片见图 4.
| 表 1 钢管与钢板材料性能 Tab. 1 Mechanical properties of steel and reinforcement |

|
图 4 模型制作过程 Fig. 4 The process of model construction |
试验通过配重来模拟楼面活荷载及墙体的影响.按《建筑结构荷载规范》(GB 50009—2012)确定活荷载取值,按《建筑抗震设计规范(2016年版)》 (GB 50011—2010)确定地震作用下结构荷载效应的组合值.固定在2.7 m标高楼面的配重为100 kg/m2,5.4 m标高楼面的配重为50 kg/m2.为模拟外挂墙板作用,将北京市某小区外挂轻质墙板的重力荷载换算为均布线荷载,按恒载考虑,沿钢梁纵向每米176 kg固定配重.模型结构共固定配重9.04 t,振动台控制端显示模型加配重总质量共22.5 t.
1.4 测点布置试验在中国地震局工程力学研究所地震工程与工程振动重点实验室的5 m×5 m振动台上实施,以实验室E-W向为X向,S-N向为Y向对模型输入地震波.
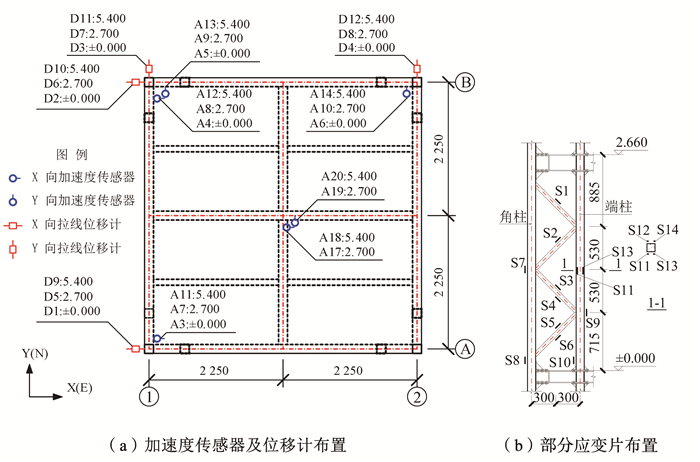
试验共布置加速度传感器20个,拉线式位移计18个,钢管管壁应变片34个,测点布置见图 5.主要量测内容如下:
|
图 5 测点布置(mm) Fig. 5 Details of measuring points layout(mm) |
1) 振动台台面中心沿X向、Y向的输出加速度时程;
2) 模型标高±0 m处、2.7 m处楼面和5.4 m处楼面的西南、西北、东北角部及楼面质心的加速度响应时程(图 5(a)中的A3~A14及A17~A20);
3) 屋架顶部X向、Y向的加速度响应时程;
4) 模型标高±0 m处、2.7 m处楼板和5.4 m处楼板的西南、西北、东北角点的绝对位移时程(图 5(a)中D1~D12);
5) 34个应变片分布在模型结构一层不同位置的角柱、端柱及圆钢管斜杆表面,以采集模型在地震波输入时的各构件表面的应变,见图 5(b).
1.5 加载工况设计试验共选取3条适合Ⅱ类场地的地震波进行加载,分别为El-Centro波、Taft波和一条人工合成地震波(简称HC波).加速度峰值从8度多遇地震的0.07g开始, 逐级增加到0.2g、0.3g、0.4g、0.51g、0.62g、0.9g等,大致相当于8度基本地震动、8.5度基本地震动、8度罕遇地震动、8.5度罕遇地震动、9度罕遇地震动、9度极罕遇地震动.加载时选取天然地震波的双向分量,先将结构第1阶自振周期处反应谱值较大的分量作为主方向,另一分量作为次方向,主方向和次方向的加速度峰值之比按照1: 0.85进行输入[12],然后再互换.每个加速度峰值加载后,输入双向白噪声来测定模型动力特性的变化.各个工况输入的地震波及加速度峰值如表 2所示.
| 表 2 各工况的加速度峰值 Tab. 2 Peak acceleration of all load cases |
地震波加速度峰值αp为0.07g和0.2g时,模型结构振动轻微,各工况后均未发现可见裂缝,振动台控制端显示模型自振频率无明显降低,说明模型处于弹性阶段.αp=0.3g时,工况16中模型振幅明显增大,加载时伴随有压紧钢板错动的响声,加载结束后在不同角柱、端柱与钢梁的连接钢板边缘发现有微量错动现象,此时模型结构表面仍未发现可见裂缝,但刚度有小幅下降.αp=0.4g时,振动较之前剧烈,工况23加载后在首层DZ5的下部K形节点处发现焊缝开裂,裂缝宽度为0.5 mm,见图 6(a),同时结构侧移增大.工况27加载后,在首层DZ8的下部K形节点焊缝处也发现了类似裂缝.数据采集系统显示,5.4 m标高X向位移测点处分别有3.6 mm(A轴)、2.4 mm(B轴)残余位移,说明结构已进入塑性阶段.αp=0.51g时,工况30加载后在模型首层各角柱、端柱下部的K形节点和Y形节点焊缝处共发现了7条类似裂缝,宽度也较之前增加,首层DZ5的下部K形节点处裂缝宽度已增至1 mm,见图 6(b).同时5.4 m标高Y向也出现了残余位移,分别为1.7 mm(①轴)和2.5 mm(②轴).αp=0.62g时,工况38加载后桁架各节点焊缝处的裂缝继续增多和变宽,首层DZ8的下部K形节点裂缝宽度增至3 mm,见图 6(c).工况40加载后在首层DZ7的下部K形节点焊缝处发现了宽约2 mm的裂缝,说明Y向桁架损伤也开始积累.工况42加载后,5.4 m标高X向残余位移增至6.1 mm(A轴),Y向残余位移也增至4.3 mm(②轴),说明模型塑性变形在加大.αp=0.7g时,工况44可听到明显的金属断裂响声,加载后桁架各节点焊缝处的裂缝已较为普遍,首层DZ5及DZ8下部K形节点和JZ1下部Y形节点焊缝已完全断开,见图 6(d)、(e),同时模型结构的侧移大幅增加.αp=0.8g时,工况48加载后在首层桁架各节点发现有6处焊缝完全断开,有4处端柱底部加劲肋出现掉漆和开裂,见图 6(f).同时模型结构的自振频率加速下降,角柱和端柱有明显弯曲.αp=0.9g时,模型结构上下层振动明显不同步,可观察到首层端柱DZ8和JZ4在桁架平面内弯曲变形加大,见图 6(g).此时二层破坏现象较轻微,有个别桁架下部K形节点处焊缝开裂,但未发现断开现象.控制端显示模型结构X向1阶自振频率已不足试验前的50%,试验结束.

|
图 6 模型的破坏现象 Fig. 6 Damage phenomenon of the model |
由试验现象可知,αp增大的过程中,模型结构刚度出现过两次明显下降.第一次出现在αp=0.3g时,刚度下降和螺栓连接处微量滑移有关; 第二次出现在裂缝快速发展阶段.最终在经历了αp=0.7g~0.9g的多次强震后,模型结构虽刚度严重退化,侧移大幅增大,但仍未倒塌,达到了“中震不坏,极罕遇地震不倒”的抗震设防新水准.
3 试验结果及分析 3.1 动力特性由模型结构各测点在白噪声激振下的加速度响应求出传递函数,通过传递函数曲线可确定试件的各阶自振频率、阻尼比、振型等动力特性,进而判断模型结构的工作状态.结构在各级加速度峰值地震波输入后X向、Y向前3阶自振频率的变化见图 7.
|
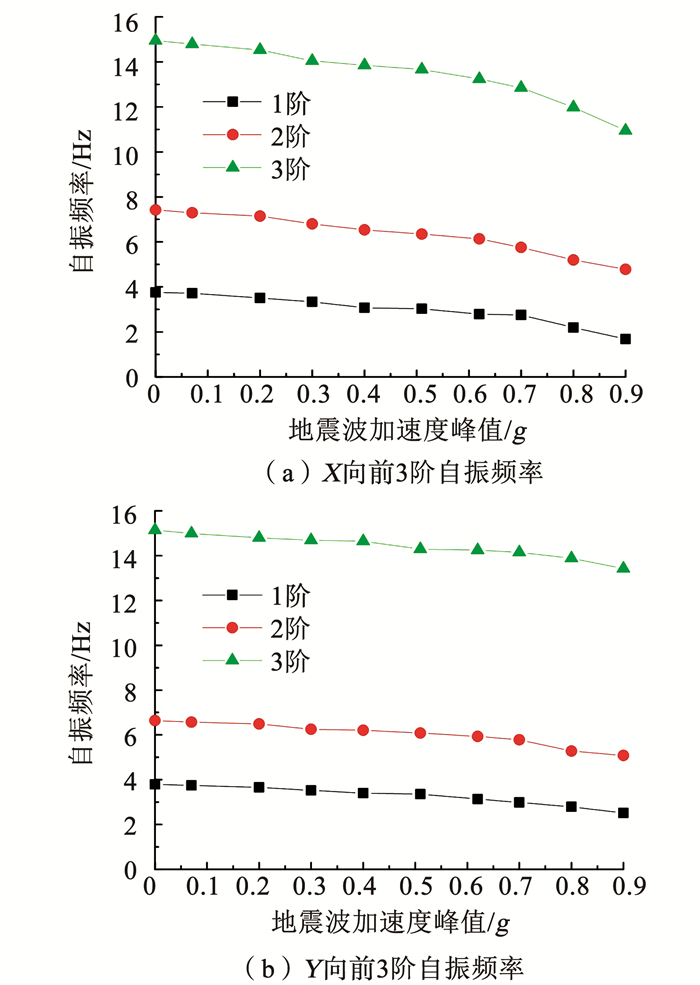
图 7 模型频率变化趋势 Fig. 7 Frequency variation trend of the model |
由图可知,模型结构的各阶自振频率随地震波加速度峰值的增大呈现下降趋势.模型初始阶段(WN1)X向前3阶自振频率分别3.76 Hz、7.42 Hz、14.95 Hz,经过αp=0.07g的地震波输入后,前3阶自振频率无明显下降,说明在8度小震时,结构损伤不明显.在αp=0.2g及αp=0.3g加载后,X向1阶自振频率分别比初始下降了6.7%和10.4%,说明结构刚度有所减小,结合试验现象分析,刚度减小和装配间隙处的微量错动有关.在αp=0.4g加载后,X向1阶自振频率比初始下降了18.3%,Y向1阶自振频率比初始下降了13.6%,降速增加,由试验现象可知,频率下降是模型结构局部开始开裂引起的.αp=0.51g加载后,结构自振频率下降幅度变大,说明随着地震波加速度峰值的增大,模型结构开始出现不可恢复的损伤和破坏,主要体现在角柱、端柱与圆钢管斜杆的焊缝处的裂缝逐渐增多和变宽,导致了结构刚度持续降低.
在αp增加到0.62g后,模型结构进入带损伤工作阶段.αp=0.7g时开始出现局部焊缝完全断开的现象,但模型结构的1阶自振频率并未快速下降,而是持续的缓慢下降,表现出延性破坏的特征.这是由于角柱、端柱和圆钢管斜杆组成的轻钢桁架是多次超静定结构,单个节点破坏失效只会降低超静定次数和抗侧刚度,不会导致轻钢桁架脆性破坏.Y向各阶自振频率的变化也具有同样的特点.最终在αp=0.9g的地震波加载后,由于X向和Y向焊缝发展程度的差异,X向1阶自振频率为1.69 Hz,比初始状态降低了55%,而Y向1阶自振频率为2.51 Hz,比初始状态降低了34%.
采用半功率点法[13]可在传递函数曲线峰值处近似求解模型结构的阻尼比ζ.模型在各个加速度峰值的地震波输入后第1阶振型的阻尼比变化曲线见图 8.
|
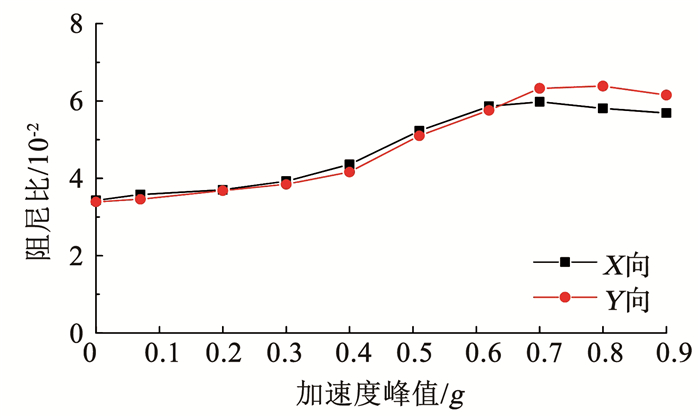
图 8 模型阻尼比变化趋势 Fig. 8 Variation trend of damping ratio of the model |
由图 8可知:1)模型结构X向及Y向的第1阶阻尼比初始值分别为0.034 3与0.033 9,随着地震波加速度峰值的增大,结构阻尼比整体上呈现出增长的趋势,说明结构内部出现损伤,在损伤发展的过程中不断耗散地震能量.2)最终模型结构X向及Y向的1阶阻尼比最高增长至0.06和0.063 8,分别比初始值增长了75.2%和88.6%,但由于模型结构为钢框架,总体来说阻尼比仍处于较低水平.3)由于模型结构及荷载在X向及Y向基本对称,αp=0.62g之前,两个方向的1阶阻尼比高度接近,之后随着αp的增加,由于模型结构局部开裂和断开现象的随机性和不对称性,X向及Y向的1阶阻尼比出现差异,但差异不大.4)模型结构X向阻尼比从αp=0.7g之前的上升趋势,变为之后的微幅下降趋势,说明随着部分节点处焊缝断开,节点裂缝面处的摩擦和错动变形有所减弱.
3.2 加速度响应在同一工况中,楼层最大加速度幅值与台面输入的同向最大加速度幅值的比值称为加速度放大系数Kmax,它是衡量结构动力响应的重要指标[14],采用每一楼层同方向两轴线的加速度平均值来计算,见图 9.图中数据点处的Y坐标分别对应振动台台面(-0.34 m)、基础钢梁顶面(±0 m)、二层楼面(2.7 m)、二层屋面(5.4 m)及屋顶(6.67 m).可知:1)加速度放大系数随测点高度增加而增加,各工况下加速度放大系数最大值都出现在屋顶测点,出现了明显的“鞭梢效应”.2)模型结构各楼层X向及Y向的加速度放大系数变化规律基本相同.3)随着地震波加速度峰值的增大,模型结构各楼层加速度放大系数虽在αp=0.62g时出现反复,但整体呈下降趋势.这说明随着地震波强度的提高,结构的损伤不断累积和加深,使得结构刚度减小,阻尼比逐渐增大,因而加速度放大系数表现出减小的趋势.

|
图 9 各地震波作用下的加速度放大系数 Fig. 9 Acceleration magnification factors of different earthquake waves |
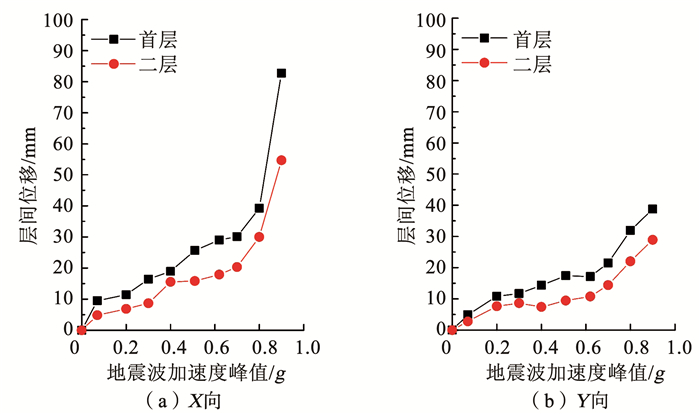
模型结构在三条地震波作用下的位移反应规律基本相同.各加速度峰值下模型结构首层及二层的最大层间位移见图 10.可知,随着地震波加速度峰值的增加,结构各楼层的层间位移也逐渐增加,其中首层的最大层间位移普遍大于二层,结构变形曲线呈现出典型的剪切型特征.X向及Y向最大层间位移均随加速度峰值的增长而增长,αp=0.8g之前,增速较为稳定; αp=0.8g后,X向层间位移剧增,刚度退化严重,而由于两个方向轻钢桁架节点破坏的差异,Y向层间位移尚处于较低水平.模型结构从αp=0.4g时出现裂缝到αp=0.9g时位移剧增而停止加载,经历了较长的塑性变形过程,表现出了较好的延性.
|
图 10 模型的最大层间位移 Fig. 10 Maximum inter-story drift of the model structure |
模型结构在各主要加速度峰值地震波作用下的最大位移数据如表 3所示.在8度多遇地震动、8度基本地震动作用下,模型结构最大层间位移角分别为1/294和1/268,低于多层钢结构的弹性层间位移角限值(1/250),满足8度“小震不坏、中震可修”的抗震设防要求; 在8度罕遇地震动、9度罕遇地震动作用下,模型结构最大层间位移角分别为1/164和1/93,远低于多层钢结构的弹塑性层间位移角限值(1/50);在9度极罕遇地震动作用时,最大层间位移角为1/33,仍可实现“极罕遇地震不倒”的目标,具有较宽的安全极限边界和韧性.
| 表 3 模型结构最大层间位移角 Tab. 3 Maximum inter-story drift ratio of the model structure |
由于模型结构对称布置,因此以首层JZ4、DZ7及其柱间斜杆为例,汇总各加速度级别下相应测点的最大应变值,以研究各构件关键截面的受力特性.
图 11(a)、(b)列出了桁架斜杆(圆钢管)表面最大应变数据,试验前其应变可忽略不计,工况1输入前对应变通道进行了清零操作,因此可认为加载时所采集数据为绝对应变.由图 11(a)可知,4个测点的最大应变随斜杆高度的降低依次增大.在αp=0.3g之前,S1、S2、S3、S5最大拉应变(拉为正,压为负)随着αp的增大而逐渐线性增加,表现出明显的弹性特征.在αp=0.51g~0.62g时,各应变增大的斜率普遍减小,与此同时角柱、端柱表面各应变最大值增速变大,说明随着桁架节点焊缝处开裂和变形,使得整个桁架各杆件之间出现了内力重分布,导致各斜杆应力增加趋缓,柱承担的水平力开始增加.在αp=0.8g时,各斜杆最大拉应变增幅突然变大,S5所在斜杆端部焊缝断开,断开前斜杆最大应变为1.674×10-3,折算拉应力为364 MPa.随后在αp=0.9g时,S5所在斜杆退出工作,其余斜杆最大应变继续增加,但增速略降.由于CFSST柱中混凝土的抗压作用,使得各斜杆表面最大压应变增幅相对不大,见图 11(b),但变化规律和最大拉应变类似.

|
图 11 各测点应变幅值分布 Fig. 11 Distribution of strain amplitude value on measuring points |
图 11(c)、(d)列出了角柱、端柱部分测点的应变数据,由于试验前在已固定配重的情况下对应变通道清零,因此采集的应变数据是应变增量,正应变表示压应力减小,负应变表示压应力增加.可知:1)受柱端约束条件影响,S7~S10的应变大小顺序是S8>S7>S9>S10;2)在斜杆两端焊缝开裂破坏前,角柱测点的最大应变呈线性增长; 当焊缝逐步破坏时,应变值增大的同时伴随着增速变大; 随着部分斜杆两端焊缝断开,应变曲线变陡.以上特点表明:在斜杆两端焊缝断开前,由于桁架抗侧刚度大,角柱和端柱受弯不明显,但下部斜杆失效后,桁架内部出现了应力重分布,角柱和端柱下部出现明显弯曲,这和试验现象相符.
和角柱相比,端柱在桁架平外受约束较弱,因此通过DZ5和DZ7的S11~S14位置应变考察其稳定性.做出两条时程曲线:1)C1=|(S11+S12)-(S13+S14)|; 2)|(S11+S13)-(S12+S14)|.C1和C2的峰值变化可反映端柱在桁架平面内及平面外的弯曲程度和稳定趋势.经对比,在αp=0.4g之前,C1和C2不足水平截面应变均值(S11~S14的平均值)的3%,说明在桁架斜杆的约束下端柱稳定性良好.在αp=0.62g之后,随着桁架节点开裂和裂缝发展,桁架斜杆对端柱约束变小,C1最大值为均值的12.4%,C2最大值为均值的7.8%,说明在部分桁架节点失效后部分端柱稳定性变差,但未能引起端柱失稳.端柱有平面内失稳和平面外失稳的趋势,但前者更明显.
试验前期结构以剪切变形为主.对桁架式“L”形柱来说,抗剪主要依靠斜杆.对比桁架斜杆应变和柱应变可知,随着αp的增加,斜杆应变增量普遍高于柱应变增量.这是由于在水平地震作用下结构的应力和变形集中于斜杆,使其充当了第一道抗震防线的作用,其特点是“刚度大,变形小”.随着部分斜杆端部焊缝拉伸断开后退出工作,桁架逐渐往框架过渡.其余斜杆的应变继续增加,同时端柱和角柱应变也急剧增加并伴随有弯曲变形,充当了第二道抗震防线的作用,特点是“刚度小,变形大”.虽然未做倒塌试验,但由于CFSST柱的弯曲破坏属延性破坏,所以经合理设计的轻钢框架-轻钢桁架结构的整体破坏可实现延性破坏模式.
4 结论1) 装配式轻钢框架-轻钢桁架结构模型在8度基本地震动下处于弹性状态; 在8度罕遇地震动作用下,进入塑性状态; 在9度罕遇地震动作用下,塑性变形加剧; 在9度极罕遇地震动作用下, X向、Y向第1阶自振频率比试验前分别下降55%和34%,刚度严重退化但未倒塌.
2) 在地震波加速度峰值从0.07g逐渐增加到0.9g的过程中,模型的1阶模态阻尼比分别由初始的0.034 3(X向)与0.033 9(Y向)分别增加到0.06(X向)和0.063 8(Y向),随后略有下降.建议后期采用简易阻尼墙增加结构耗能能力.
3) 模型中的桁架式“L”形柱在αp<0.4g的地震波作用时具有较好的抗侧刚度和稳定性; 在承受更大地震作用时,桁架下部K形节点和Y形节点的焊缝出现拉伸破坏,逐渐发展至焊缝断开.从αp=0.4g时桁架节点焊缝开裂到αp=0.9g时结构刚度严重退化,桁架式“L”形柱经历了较长的塑性变形过程,具有较好的延性.
4) 采用了小截面CFSST柱的装配式轻钢框架-轻钢桁架结构,在αp为0.07g、0.2g的地震波作用下能满足多层钢结构的弹性层间位移角限值; 在αp为0.4g、0.62g的地震波作用下能满足多层钢结构的弹塑性层间位移角限值,可在高设防烈度地区应用.
| [1] |
陈志华, 荣彬. L形方钢管混凝土组合异形柱的轴压稳定性研究[J]. 建筑结构, 2009, 39(6): 39. CHEN Zhihua, RONG Bin. Research on axial compression stability of L-shaped column composed of concrete-filled square steel tubes[J]. Building Structure, 2009, 39(6): 39. |
| [2] |
王亚雯, 陈志华, 周婷, 等. 反复荷载下方钢管混凝土组合异形柱参数分析[J]. 地震工程与工程振动, 2014, 34(3): 126. WANG Yawen, CHEN Zhihua, ZHOU Ting, et al. Parametric analysis of special-shaped column composed of concrete-filled square steel tubes under cyclic loading[J]. Earthquake Engineering and Engineering Dynamics, 2014, 34(3): 126. DOI:10.13197/j.eeev.2014.03.126.wangyw.017 |
| [3] |
蔡健, 孙刚. 轴压下带约束拉杆L形钢管混凝土短柱的试验研究[J]. 土木工程学报, 2008, 41(9): 14. CAI Jian, SUN Gang. Experimental investigation on L-shaped concrete-filled steel tube stub columns with binding bars under axial load[J]. China Civil Engineering Journal, 2008, 41(9): 14. DOI:10.3321/j.issn:1000-131X.2008.09.003 |
| [4] |
蔡健, 左志亮, 赵小芹, 等. 带约束拉杆L形钢管混凝土短柱偏压试验研究[J]. 建筑结构学报, 2011, 32(2): 83. CAI Jian, ZUO Zhiliang, ZHAO Xiaoqin, et al. Experimental research on eccentrically loaded L-shaped concrete-filled steel tubular stub columns with binding bars[J]. Journal of Building Structures, 2011, 32(2): 83. DOI:10.14006/j:jzjgxb.2011.02.013 |
| [5] |
柳杨青, 王恒华, 蔡建国, 等. 闭口截面异形柱轴心受压稳定系数[J]. 东南大学学报(自然科学版), 2015, 45(5): 923. LIU Yangqing, WANG Henghua, CAI Jianguo, et al. Stability coefficient of closed special-shaped column under axial compression[J]. Journal of Southeast University (Natural Science Edition), 2015, 45(5): 923. DOI:10.3969/j.issn.1001-0505.2015.05.018 |
| [6] |
混凝土异形柱结构技术规程: JGJ 149—2017[S].北京: 中国建筑工业出版社, 2017: 2 Technical specification for concrete structures with specially shaped columns: JGJ 149—2017[S]. Beijing: China Architecture & Building Press, 2017: 2 |
| [7] |
刘永健, 刘君平, 张俊光. 主管内填混凝土矩形和圆形钢管桁架受弯性能对比试验研究[J]. 建筑结构学报, 2010, 31(4): 86. LIU Yongjian, LIU Junping, ZHANG Junguang. Experimental research on RHS and CHS truss with concrete filled chord[J]. Journal of Building Structures, 2010, 31(4): 86. |
| [8] |
黄政华, 张其林, 杨宗林, 等. 平面钢管桁架的面外稳定分析模型研究[J]. 土木工程学报, 2011, 44(5): 49. HUANG Zhenghua, ZHANG Qilin, YANG Zonglin, et al. Study of model for out-of-plane stability of planar tubular trusses[J]. China Civil Engineering Journal, 2011, 44(5): 49. DOI:10.15951/j.tmgcxb.2011.05.015 |
| [9] |
中国地震动参数区划图: GB 18306—2015[S].北京: 中国标准出版社, 2015: 3 Seismic ground motion parameters zonation map of China: GB 18306—2015[S]. Beijing: Standard Press of China, 2017: 3 |
| [10] |
荣彬, 陈志华, 李黎明. L形截面方钢管组合异形柱的长细比计算[J]. 钢结构, 2006, 21(4): 8. RONG Bin, CHEN Zhihua, LI Liming. Calculation of slenderness ratio for L-shaped combined column of square steel tubes[J]. Steel Construction, 2006, 21(4): 8. DOI:10.3969/j.issn.1007-9963.2006.04.003 |
| [11] |
曹万林, 王如伟, 刘文超, 等. 装配式轻型钢管框架-轻墙共同工作性能[J]. 哈尔滨工业大学学报, 2017, 49(12): 61. CAO Wanlin, WANG Ruwei, LIU Wenchao, et al. Experimental study of joint work characteristic of assembly light steel tube frame with recycled concrete-thin wall[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 61. DOI:10.11918/j.issn.0367-6234.201612064 |
| [12] |
建筑抗震设计规范(2016年版): GB 50011—2010[S].北京: 中国建筑工业出版社, 2010: 342 Code for seismic design of buildings(2016 edition): GB 50011—2010[S]. Beijing: China Architecture & Building Press, 2010: 342 |
| [13] |
黄浩华. 地震模拟振动台的设计与应用技术[M]. 北京: 地震出版社, 2008: 317. HUANG Haohua. Design and application of seismic simulated shaking table[M]. Beijing: Seismological Press, 2008: 317. |
| [14] |
李国强, 李杰. 工程结构动力检测理论与应用[M]. 北京: 科学出版社, 2002: 24. LI Guoqiang, LI Jie. Theory and application of dynamic testing of engineering structure[M]. Beijing: Science Press, 2002: 24. |
 2019, Vol. 51
2019, Vol. 51


