脑效应连接网络是一种由节点和有向边构成的图模型,其中节点表示脑区,有向边表示脑区之间的效应连接.准确地从影像数据中学习脑效应连接网络,不仅能够加深研究人员对人脑功能复杂性的理解,而且有助于进行脑疾病的早期诊断以及病理研究[1-2].因此从影像数据中识别高质量的脑效应连接网络,已经成为近年来人脑功能网络研究的一个重要课题.
功能磁共振成像技术(functional magnetic resonance imaging,fMRI)是一种非介入的活体人脑功能成像技术,具有无创性、高时空分辨率等优势,自诞生以来迅速成为脑科学研究领域最主要的技术手段.迄今为止,研究人员已经提出了多种从fMRI数据中进行脑效应连接网络识别的方法.这些方法大致可分为两类:基于模型驱动的方法和基于数据驱动的方法[3].其中,基于模型驱动的方法是一种验证性方法,主要包括结构方程模型(structural equation modeling, SEM)[4]和动态因果模型(dynamic causal modeling, DCM)[5].已有研究表明,该类方法在缺少先验的情况下并不适用,而且仅能构建小规模的脑效应连接网络[3].基于数据驱动的方法不需先验知识和假设,能够直接从数据中得到脑区之间的因果关系,在神经影像技术不断发展和数据日益丰富的今天,该类方法逐渐成为主流方法.常用的数据驱动方法包括格兰杰因果模型(Granger Causality, GC)[6-7]、线性非高斯无环模型(Linear non-Gaussian acyclic model, LiNGAM)[8-9]、广义同步(Generalised synchronization, GS)[10]、Patel条件独立性方法(Patel)[11]和贝叶斯网方法[12-13]等.其中,格兰杰因果模型使用矢量自回归模型通常能够在广义平稳和零均值数据下实现脑区间脑效应连接的有效估计,已经被广泛地应用于脑效应连接网络的构建.但是该类方法存在对数据噪声和下采样过程比较敏感的缺陷[14].线性非高斯无环模型使用高阶分布统计和独立成分分析来估计网络的连接.但该方法的有效性高度依赖于如下3个假设:数据产生过程是线性的、不存在隐变量、干扰变量服从非零方差的非高斯分布.广义同步方法是通过分析脑区信号间的独立关系来评估脑区信号间的相互依赖性.该方法采用3种相关的非线性独立度量(Sk、Hk和Nk).虽然这些非线性独立度量是有方向的,但是不对称的方向判断有时会产生前后的矛盾[3].Patel的条件独立性方法首先计算两个脑区信号之间的条件依赖关系,然后从条件依赖关系中得到两个脑区连接方向的度量τ和连接强度的度量κ,最后利用τ和κ分别进行连接方向的识别以及连接强度的判断.该方法与已有方法相比,在连接方向识别上具有一定优势,但在连接强度的判断上具有灵敏度不高的缺陷.总之,尽管上述4种数据驱动的方法各自具有一定的适用性,但普遍存在对数据噪声敏感、识别准确率不高等缺陷.
近年来,基于贝叶斯网(Bayesian network,BN)的学习方法采用无监督的数据驱动方法构建脑效应连接网络,具有良好的灵活性和适应性,已经成为一个新的研究热点[12].文献[3]中对多种基于BN的脑效应连接网络学习方法进行了对比测试,发现贪婪等价类搜索(greedy equivalence search,GES)的性能相对较好,但是该方法采用贪婪搜索技术,容易陷入局部最优.为了克服上述缺陷,已有学者将全局随机搜索的群智能方法与贝叶斯网模型学习相结合来完成脑效应连接网络的学习.例如,文献[15]提出一种从fMRI数据中构建脑效应连接网络的人工免疫方法(AIAEC),该方法能够学习到较高精度的效应连接网络.文献[16]提出了一种基于蚁群算法的脑效应连接网络学习方法(ACOEC),该方法不仅能够准确识别网络的连接和方向,而且能够有效量化网络的连接强度.综上可见,脑效应连接网络识别的研究进行得如火如荼.虽然群智能算法已经在脑效应连接网络学习中进行了有效尝试,但探索脑效应连接网络学习新方法仍是该领域极具挑战性的研究问题.
萤火虫算法(Firefly algorithm,FA)作为一种新型的群智能算法在多个领域已经表现出了较好的效果[17-19],在脑效应连接网络学习问题上可能具有潜在的应用价值,故本文提出了一种带有繁殖机制的脑效应连接网络萤火虫学习方法(Firefly algorithm with reproductive mechanism for learning brain effective connectivity network, FAR-EC),新方法主要是通过萤火虫种群的迭代寻优机制,搜索最佳的脑效应连接网络结构.具体来说,新方法在种群的每次迭代中,每个个体通过定向移动和随机移动操作逐步完成脑效应连接网络的构建.在经过一定代数的寻优后,种群执行一次繁殖操作以进一步提高整体寻优的质量.最后,将最优个体所代表的网络结构作为学习到的脑效应连接网络.在模拟数据集上的实验证明了繁殖机制的有效性,而且与多个算法相比,新算法在多组数据上都能够得到质量更高的脑效应连接网络.在真实数据集上的实验结果也表明,新算法具有较好的实用性.
1 萤火虫算法萤火虫算法的核心思想是:绝对亮度低的萤火虫会被绝对亮度高的萤火虫吸引,根据位置更新公式更新原有位置,向高亮度位置移动,移动距离由吸引度大小决定,吸引度大小与相对亮度成比例.通常,把待求解问题的目标函数值作为萤火虫的绝对亮度.
萤火虫i在萤火虫j所在位置处的光强度为萤火虫i对萤火虫j的相对亮度,记作Iij.考虑到光传播过程中光的强度会随着距离的增加以及空气的吸收而减弱,故将其定义如下:
| $ {I_{ij}} = {I_i}{{\rm{e}}^{ - \gamma r_{ij}^2}}. $ | (1) |
式中:Ii为萤火虫i的绝对亮度,γ为光强度吸收系数,rij为萤火虫i到j的距离.
| $ {r_{ij}} = d\left( {{x_i} - {x_j}} \right) = \sqrt {\sum\limits_{k = 1}^d {{{\left( {{x_{i,k}} - {x_{j,k}}} \right)}^2}} } . $ | (2) |
假设萤火虫i被萤火虫j吸引且向j所处位置移动.吸引度的大小与相对亮度Iij成比例,相对亮度越大则吸引度越大,吸引度βij的公式为
| $ {\beta _{ij}} = {\beta _0}{{\rm{e}}^{ - \gamma r_{ij}^2}}. $ | (3) |
式中β0为最大吸引度.萤火虫i的位置更新公式为
| $ {x_i} = {x_i} + {\beta _{ij}}\left( {{x_j} - {x_i}} \right) + \alpha {\varepsilon _i}. $ | (4) |
式中:α为步长因子,εi为服从高斯分布或者均匀分布的随机数.
2 带有繁殖机制的脑效应连接网络萤火虫学习算法带有繁殖机制的脑效应连接网络萤火虫学习算法(FAR-EC)的大致思路如下:首先,将每个萤火虫个体初始化为仅含少量边的脑效应连接网络结构,并且使用K2评分作为目标函数来衡量萤火虫个体的绝对亮度大小; 然后,每个个体通过定向移动以及随机移动完成脑效应连接网络的构建; 接着,每隔一定代数,执行一次繁殖过程来对种群进行优化.最后,得到满足要求的脑效应连接网络.
2.1 绝对亮度评价方法K2评分是一种常用的贝叶斯网结构评分度量标准,它不仅能够评价候选网络结构与数据集的匹配程度,而且具有可分解性,即一个节点结构发生变化时,仅需重新计算该节点评分.由于本文是基于贝叶斯网络的学习方法,故使用K2评分作为目标函数来衡量萤火虫个体的绝对亮度,K2评分值越大,绝对亮度越高.萤火虫i的绝对亮度计算公式如下
| $ \begin{array}{*{20}{c}} {{I_i} = f\left( {{G_i},{D_{{\rm{data}}}}} \right) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^{{q_i}} {} } }\\ {\left( {\log \left( {\frac{{\left( {{r_i} - 1} \right)!}}{{\left( {{N_{ij}} + {r_i} - 1} \right)!}}} \right) + \sum\limits_{k = 1}^{{r_i}} {\log \left( {{N_{ijk}}} \right)} } \right).} \end{array} $ | (5) |
式中:Gi为萤火虫i所代表的脑效应连接网络,Ddata为fMRI数据集,n为网络中含有的脑区个数,qi是节点Bi的父节点可能取值的组合数,ri是节点Bi可能取值的数目,Nij是数据集中节点Bi取第j个值的实例数量,例如节点Bi可能取值为{0, 1},则Ni1代表数据集中节点Bi取值为第1个值(取值为0)的实例数量,Nijk是数据集中节点Bi取第j个值,Bi的父节点取第k个组合值时的实例数量.
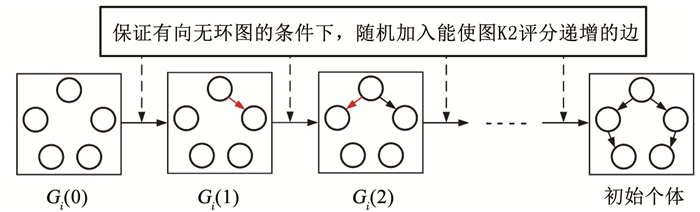
2.2 萤火虫种群的初始化萤火虫个体初始化过程见图 1,图中Gi(m)为萤火虫i所代表的网络结构中含有m条边.萤火虫i从空图Gi(0)开始,在保证有向无环图的条件下不断加入使得图K2评分增大的边,直到边数达到预先设定的边数为止,得到萤火虫i的初始个体.
|
图 1 萤火虫个体i初始化实例 Fig. 1 Example of initialization of the firefly individual i |
假设萤火虫i向萤火虫j所处位置移动,则萤火虫的位置更新方式具体可以描述为:首先,计算i与j之间的距离rij,即i与j所代表的脑效应连接网络中边不一致的数量; 然后,计算i与j之间的吸引度βij; 最后,将βij与移动阈值pm进行比较,若大于pm,i进行定向移动操作,反之,i进行随机移动操作.下面将具体介绍这两个操作.
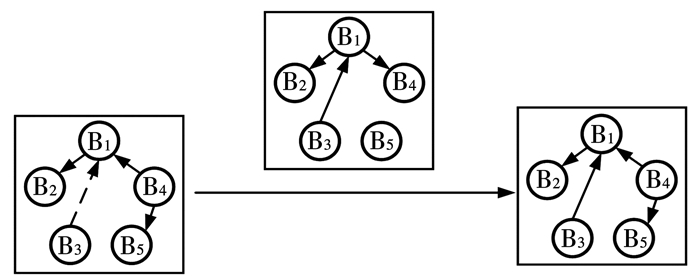
定向移动操作:见图 2,假设萤火虫i向j移动,在满足有向无环图的条件下,萤火虫i随机选择图Gi中一条边(虚线所标识边),将其变为与Gj一致,得到i的新位置Gi, new.
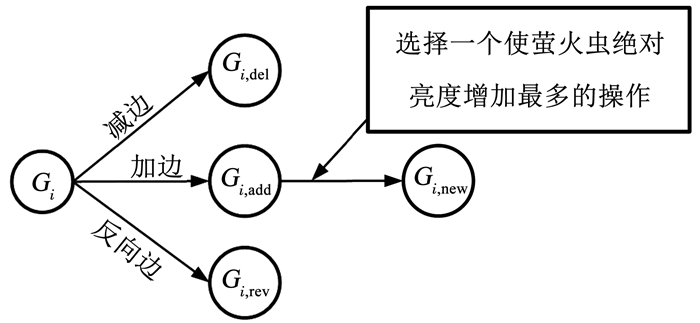
随机移动操作:见图 3,萤火虫i在满足有向无环图的条件下,随机进行减边、加边和反向边操作,分别得到图结构Gi, del、Gi, add和Gi, rev; 然后从中选择使萤火虫绝对亮度增加最多的操作,即加边操作; 将执行加边操作所得到的图结构Gi, add作为i的新位置Gi, new.
|
图 2 萤火虫个体i定向移动实例 Fig. 2 Example of directional movement of the firefly individual i |
|
图 3 i随机移动实例 Fig. 3 Example of random movement of the firefly individual i |
萤火虫成虫交配产生的幼虫只有成长为成虫后,才发出性别交流信号,进行下一代繁殖.本文受上述现象启发,提出了一种繁殖机制,以此加强萤火虫之间的信息交流,以及提高种群的多样性.繁殖机制主要由配偶选择、子代产生、子代成长和种群更新4个操作组成,下面将具体介绍这4个操作.
配偶选择:首先规定结为配偶的两萤火虫不再与种群中其余个体结对.从当前绝对亮度最大个体u开始,将距离u最远个体v作为u的配偶.
子代产生:结为配偶的萤火虫分别向对方所处位置进行一次定向移动,将移动后所处的新位置,作为产生的两个子代的初生位置,此时子代为初生子代.
子代成长:初生子代进行一定次数的随机移动后加入到萤火虫种群中.
种群更新:设萤火虫种群规模为a.首先,去除种群中网络结构重复的个体; 然后,判断去重后剩余个体数量,若大于a,则取绝对亮度最大的前a个个体作为下一代种群.反之,则按照初始化过程,重复加入新个体到种群中,直到种群规模达到a.
2.5 算法描述FAR-EC算法的核心思想是利用萤火虫个体的定向移动、随机移动和繁殖操作完成种群的进化.具体的伪代码见算法1.
算法1:FAR-EC
Input:fMRI数据集
Output:脑效应连接网络
1) 初始化参数:a(种群规模)、β0(最大吸引度)、γ(光传播系数)、lstep(隔代执行繁殖机制代数)、pm(移动阈值)
2) 产生初始萤火虫种群:每个萤火虫个体被初始化为仅含有少数条边的脑效应连接网络结构
3) While不满足终止条件
4) for i=1:a
5) for j=1:a
6) if Ii < Ij
7) 计算萤火虫i、j之间的距离rij以及吸引度βij
8) if βij>pm
9) 萤火虫i执行定向移动操作
10) else
11) 萤火虫i执行随机移动操作
12) end
13) end
14) 计算萤火虫i新位置的绝对亮度Ii
15) end
16) end
17) if当前迭代次数整除lstep
18) 执行繁殖机制
19) end
20) end
21) 输出最亮个体所代表的脑效应连接网络
基于算法1的描述,下面对FAR-EC算法的时间复杂度进行分析.种群初始化阶段时间复杂度为
在本文中使用通用的由Smith等人在文献[3]中所给出的模拟fMRI数据集(www.fmrib.ox.ac.uk/datasets/netsim/index.html).该数据集每组数据均包含50个被试,其具体设置见表 1.
| 表 1 模拟数据集的具体参数 Tab. 1 Specific parameters of the simulated dataset |
表 1中,nodes为节点数(脑区数); Session duration为扫描时间; TR为扫描重复时间; Noise为噪声占比; HRF.std.dev.为血氧动力学响应函数延迟时间标准差; Other factors为其他因素,主要包含:2-group test(两组测试); shared inputs(外部输入); backwards connections(反向连接); more connections(稠密连接).
3.1.2 真实数据集本文使用的真实fMRI数据来自于阿尔兹海默症神经影像学联盟(Alzheimer’s Disease neuroimaging Initiative,ADNI)数据集(www.loni.ucla.edu).主要选取了两组被试,分别是阿尔茨海默病(Alzheimer’s disease,AD)患者组和正常组,被试的基本信息见表 2.
| 表 2 被试的基本信息 Tab. 2 Information of the subjects |
本文使用解剖学标记模板(anatomical automatic labeling template,AAL)将每幅图像分割成116个感兴趣区域(region of interest,ROI)然后根据已有文献选择被认为与AD病较为相关的16个ROI,其主要分布在额叶、顶叶、颞叶.具体选择的ROI见表 3.
| 表 3 选择的感兴趣区域 Tab. 3 Selected regions of interest |
由于FAR-EC算法不能直接使用连续的fMRI数据,故需要对数据进行离散化的处理.对于被试每个脑区的时间序列,使用等频离散化方法将体素时间序列离散成若干部分,其中每个部分包含相同的数量的体素值.
3.2 评价标准本文中使用精度(Precision)、召回率(Recall)、F度量(Fmeasure)来评价学习到的脑效应连接网络的连接和方向.用LN表示学习到的网络,GN表示真实网络.连接的精度、召回率和F度量分别定义如下:
| $ {P_{\rm{c}}} = \frac{{{C_{\rm{s}}}}}{{{C_{\rm{s}}} + {C_{\rm{a}}}}}, $ | (6) |
| $ {R_{\rm{c}}} = \frac{{{C_{\rm{s}}}}}{{{T_{{\rm{tc}}}}}}, $ | (7) |
| $ {F_{\rm{c}}} = \frac{{2 \times {P_{\rm{c}}} \times {R_{\rm{c}}}}}{{{P_{\rm{c}}} + {R_{\rm{c}}}}}. $ | (8) |
式中:Pc为连接的精度,Rc为连接的召回率,Fc为连接的F度量,Cs为LN与GN中含有相同连接的数量,Ca为存在于LN但不存在于GN的连接数量,Ttc为GN含有的连接总数.
方向的精度、召回率和F度量分别定义如下:
| $ {P_{\rm{d}}} = \frac{{{D_{\rm{s}}}}}{{{D_{\rm{s}}} + {D_{\rm{w}}} + {D_{\rm{a}}}}}, $ | (9) |
| $ {R_{\rm{d}}} = \frac{{{D_{\rm{s}}}}}{{{T_{{\rm{td}}}}}}, $ | (10) |
| $ {F_{\rm{d}}} = \frac{{2 \times {P_{\rm{d}}} \times {R_{\rm{d}}}}}{{{P_{\rm{d}}} + {R_{\rm{d}}}}}. $ | (11) |
式中:Pd为方向的精度,Rd为方向的召回率,Fd为方向的F度量,Ds为LN与GN具有相同方向连接的数量,Dw为LN与GN中连接相同但方向不同的连接数量,Da为存在于LN但不存在于GN的方向连接的数量,Ttd为GN含有的方向总数.
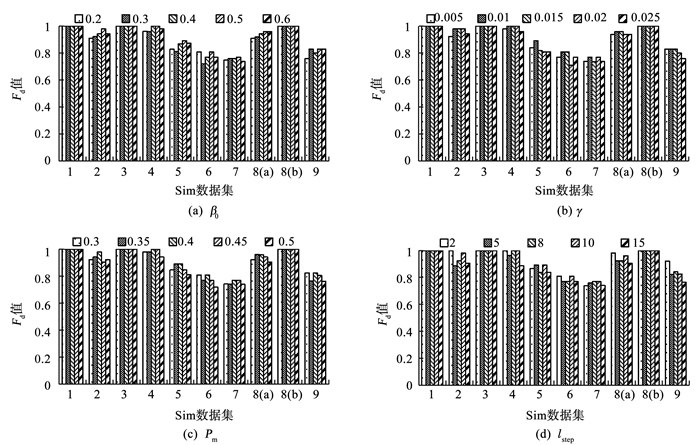
3.3 参数对算法影响本文在9个模拟数据集上主要测试了最大吸引度β0、光吸收系数γ、移动阈值pm和执行繁殖机制的隔代代数lstep对FAR-EC算法的影响.在测试过程中保持其余参数不变,种群规模设为20,仅变动待测试参数,测试结果见图 4.
|
图 4 参数发生变化时FAR-EC算法在Sim1~9上的Fd值比较 Fig. 4 Comparison of Fd by FAR-EC on Sim1~9 when parameters change |
总体来看,随着参数取值的变化FAR-EC算法的性能会发生相应的波动.究其原因,参数β0、γ、pm的变动会影响算法全局和局部搜索的平衡,参数lstep的变动会影响算法进行繁殖机制的次数.具体来看,当β0=0.5、γ=0.01、pm=0.04、lstep=2或10时算法对于方向的学习能力达到最强.但值得注意的是,参数lstep控制进行繁殖操作的频率,而进行过多次繁殖操作会降低算法的效率.
综上可得,FAR-EC算法最优参数设置如下:a=20,β0=0.5,γ=0.01,pm=0.04,lstep=10.
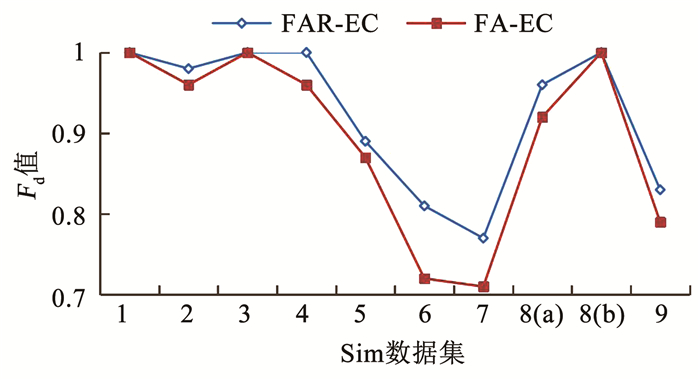
3.4 繁殖机制有效性检验为评价繁殖机制对FAR-EC算法性能的影响,本文在9组模拟数据上,将FAR-EC与FA-EC(不带繁殖机制的脑效应连接网络萤火虫学习方法)进行了对比,结果见图 5.
|
图 5 两种算法在Sim1~9上运行结果的Fd值比较 Fig. 5 Comparison of Fd by two algorithms on Sim1~9 |
由于两种算法均能准确地识别连接,故本文仅比较它们对于方向的识别能力.总的来看,FAR-EC算法在各组数据上的Fd值均不低于FA-EC算法,说明繁殖机制对网络质量的提升具有一定作用,特别是在脑区较多的Sim6、7上,两种算法的Fd值相差较大,说明随着脑区的增多,繁殖机制的提升效果愈发显著.
3.5 与其它算法的性能比较为展示FAR-EC算法的性能,本文将其与7个脑效应连接网络学习算法在12组模拟数据上进行了比较.下面,将具体分析不同实验条件下,FAR-EC算法的性能.
样本数量:Sim1~4中分别包含2 500、5 000、10 000、60 000条数据.在Sim1~4上,FAR-EC算法的Fd的值均保持相对稳定,说明算法具有较好的稳定性.在Sim1上,FAR-EC算法的Fd值高于其余7种算法,说明具有较强的小样本学习能力.在Sim4上,FAR-EC算法也能得到最优的结构,说明具有较强的大样本学习能力.
节点数量:Sim5~7分别包含10、15、50个节点.随着节点数量的增加,尽管FAR-EC算法对方向的识别能力有所下降,但其依然能够准确的识别连接.在Sim5、7上,FAR-EC算法的Fd值均取得了前3位的成绩.在Sim6上,由于在本组数据上出现了多个评分相同的候选网络结构,FAR-EC算法输出选择具有一定的随机性,故性能有所下降,但性能依然优于GES、GC算法.
连接强度:Sim8将50个被试分为两组.前25个为Sim8(a),后25个为Sim8(b).Sim8(b)将一条连接的连接强度值减半.FAR-EC算法在Sim8上Fc、Fd值均取得了第1位的成绩,说明在连接强度发生变化时FAR-EC算法能够准确的识别连接以及方向.
| 表 4 8种算法在Sim1~12上的结果 Tab. 4 Results of eight algorithms on Sim1~12 |
神经噪声:Sim9、10将一些可看作神经噪声的外部输入加入到网络中,这使得所有算法对于连接以及方向的识别能力下降.但在此情况下,FAR-EC算法性能优于其余算法,说明其具有较好的抗噪能力.
负向连接:Sim11随机使一条连接存在两个方向,此时8种算法的性能均有所下降,但FAR-EC算法对连接和连接方向的识别能力依然处于前两位,依然具有较好的性能.
稠密连接:Sim12在Sim3的基础上多加入了两条连接,使得网络到达一个连接稠密的状态.在Sim12上FAR-EC算法能够准确识别连接,对于方向的识别能力仅次于Patel.
由于多数算法对于边的识别能力较好,故本文仅给出了在5%显著水平下FAR-EC算法与对比算法关于Fd值的Friedman检验结果,具体见表 5.其中,yes表示存在显著性差异,no表示不存在显著性差异.由表 5得,FAR-EC算法对于方向的识别能力显著优于除AIAEC、ACOEC外的其余5种算法.以上可见,对比其它7种算法,FAR-EC算法具有优良的性能,是一种很具有竞争力的算法.
| 表 5 FAR-EC与对比算法在模拟数据集上关于Fd值的Friedman检验结果 Tab. 5 Friedman test results of Fd by FAR-EC and contrast algorithmon the Smith dataset |
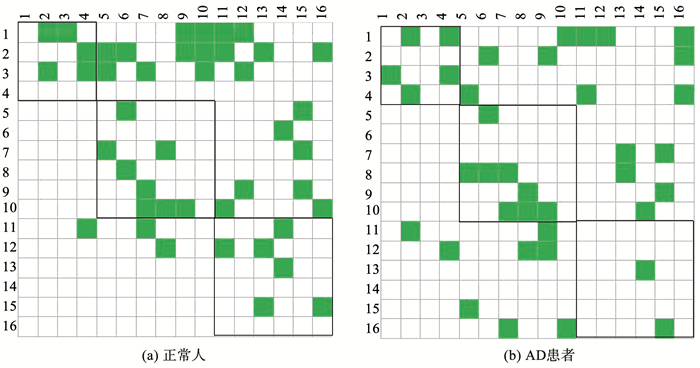
使用FAR-EC算法在真实数据集上学习到的脑效应连接网络见图 6,图 6(a)为正常人脑效应连接网络,图 6(b)为AD患者脑效应连接网络.
|
图 6 FAR-EC在真实数据集上构建的脑效应连接网络 Fig. 6 EC network constructed by FAR-EC on real dataset |
首先统计了两个脑效应连接网络的连接总数,得到AD患者连接数为38,正常人连接数为44,显然AD患者存在的连接数要小于正常人,这种失连接的现象与已有文献[13、20]得到的结果相似,可看作AD的病理生物学标记.进一步,已知认知以及记忆功能减弱是AD的症状之一,而海马区(图 6中13、14节点)主要负责信息的临时存储,同时还可将短时的程序性记忆转化为长时记忆,故海马对AD病情的发展有重大的影响.通过对比图 6中两个脑效应连接网络可得,AD患者的脑效应连接网络中海马与其它ROI之间的连接明显少于正常被试的数量,存在明显的失连接.另外,还可发现AD患者脑效应连接网络中后扣带回(图 6中5、6节点)与其它ROI与之间的连接数明显小于正常被试,而在静息态下后扣带回是新陈代谢最活跃的脑区,它参与情景记忆的提取,是AD最早发生新陈代谢降低的区域.上述研究结果表明,FAR-EC算法在真实数据集上可以学习到合理的脑效应连接网络,再次反映了算法的有效性.
4 结论针对脑效应连接网络学习问题,本文基于萤火虫算法及其繁殖机制提出了一种新方法,即FAR-EC.该方法使用K2评分衡量萤火虫的绝对亮度,通过萤火虫的吸引移动操作,逐步构建脑效应连接网络.同时,本文通过模拟萤火虫的繁殖行为提出了一种繁殖机制,以此来进一步优化种群的质量.在Simth数据集上的实验证实了繁殖机制的有效性,且与同类算法相比,FAR-EC算法具有一定优势.而在ADNI数据集上的实验表明,FAR-EC算法在AD病理研究中具有潜在的应用价值.
本文方法是基于群智能的脑效应连接网络学习的一个新探索,为构建高质量的脑效应连接网络提供了一个有效的方法,在多个模拟数据集的实验表明,本文方法求得的脑效应连接网络质量较其它算法有所提升,但当脑区数量增多时,求解精度有所下降,因此如何提高大规模脑效应连接网络求解精度,将是下一步研究的主要方向.
| [1] |
HEIN G, MORISHIMA Y, LEIBERG S, et al. The brain's functional network architecture reveals human motives[J]. Science, 2016, 351(6277): 1074. DOI:10.1126/science.aac7992 |
| [2] |
左西年, 张喆, 贺永, 等. 人脑功能连接组:方法学、发展轨线和行为关联[J]. 科学通报, 2012, 57(35): 3399. ZUO Xinian, ZHANG Zhe, HE Yong, et al. The human functional connectome: Its methodology, developmental trajectory and behavioral association (in Chinese)[J]. Chinese Science Bullitin (Chinese Version), 2012, 57(35): 3399. DOI:10.1360/972012-702 |
| [3] |
SMITH S M, MILLER K L, SALIMI K G, et al. Network modeling methods for FMRI[J]. Neuroimage, 2011, 54(2): 875. DOI:10.1016/j.neuroimage.2010.08.063 |
| [4] |
SAMDI S B, TING C M, OMBAO H, et al. A unified estimation framework for state-related changes in effective brain connectivity[J]. IEEE Transactions on Bbio-medical Engineering, 2016, 64(4): 844. DOI:10.1109/TBME.2016.2580738 |
| [5] |
FRASSLE S, LOMAKINA E I, RAZI A, et al. Regression DCM for fMRI[J]. NeuroImage, 2017, 155: 406. DOI:10.1016/j.neuroimage.2017.02.090 |
| [6] |
FAROKHZADI M, HOSSEIN Z G A, SOLTANIAN Z H. Nonlinear effective connectivity measure based on adaptive Neuro Fuzzy Inference System and Granger Causality[J]. NeuroImage, 2018, 181: 382. DOI:10.1016/j.neuroimage.2018.07.024 |
| [7] |
SETH A K. A MATLAB toolbox for Granger causal connectivity analysis[J]. Journal of Neuroscience Methods, 2010, 186(2): 262. DOI:10.1016/j.jneumeth.2009.11.020 |
| [8] |
XU L, FAN T, WU X, et al. A pooling-LiNGAM algorithm for effective connectivity analysis of fMRI data[J]. Frontiers in Computational Neuroscience, 2014, 8(8): 125. DOI:10.3389/fncom.2014.00125 |
| [9] |
LIU Y, WU X, ZHANG J, et al. Altered effective connectivity model in the default mode network between bipolar and unipolar depression based on resting-state fMRI[J]. Journal of Affective Disorders, 2015, 182: 8. DOI:10.1016/j.jad.2015.04.009 |
| [10] |
DAUWELS J, VIALATTE F, MUSHA T, et al. A comparative study of synchrony measures for the early diagnosis of Alzheimer's disease based on EEG[J]. Neuroimage, 2010, 49(1): 668. DOI:10.1016/j.neuroimage.2009.06.056 |
| [11] |
PATEL R S, BOWMAN D B, RILLING J K. A Bayesian approach to determining connectivity of the human brain[J]. Human Brain Mapping, 2010, 27(3): 267. DOI:10.1002/hbm.20182 |
| [12] |
IDE J S, ZHANG S, LI C S R. Bayesian network models in brain functional connectivity analysis[J]. International Journal of Approximate Reasoning Official Publication of the North American Fuzzy Information Processing Society, 2014, 55(1): 23. DOI:10.1016/j.ijar.2013.03.013 |
| [13] |
HUANG S, LI J, YE J, et al. A sparse structure learning algorithm for Gaussian Bayesian Network identification from high-dimensional data[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 35(6): 1328. DOI:10.1109/tpami.2012.129 |
| [14] |
GOEBEL R, ROEBROECK A, KIM D S, et al. Investigating directed cortical interactions in time-resolved fMRI data using vector autoregressive modeling and Granger causality mapping[J]. Magnetic Resonance Imaging, 2003, 21(10): 1251. DOI:10.1016/j.mri.2003.08.026 |
| [15] |
JI J, LIU J, LIANG P, et al. Learning effective connectivity network structure from fMRI data based on artificial immune algorithm[J]. PLOS ONE, 2016, 11(4). DOI:10.1371/journal.pone.0152600 |
| [16] |
LIU J, JI J, ZHANG A, et al. An ant colony optimization algorithm for learning brain effective connectivity network from fMRI data[C]//IEEE International Conference on Bioinformatics and Biomedicine(BIBM). Shenzhen: IEEE Press, 2016: 360. DⅡ: 10.1109/BIBM.2016.7822546
|
| [17] |
谢承旺, 肖驰, 丁立新, 等. HMOFA:一种混合型多目标萤火虫算法[J]. 软件学报, 2018, 29(4): 1143. XIE Chengwang, XIAO Chi, DING Lixin, et al. HMOFA: A hybrid multi-objective firefly algorithm[J]. Journal of Software, 2018, 29(4): 1143. DOI:10.13328/j.cnki.jos.005275 |
| [18] |
LEI X, WANG F, WU F X, et al. Protein complex identification through Markov clustering with firefly algorithm on dynamic protein-protein interaction networks[J]. Information Sciences, 2016, 329(6): 303. DOI:10.1016/j.ins.2015.09.028 |
| [19] |
田梦楚, 薄煜明, 陈志敏, 等. 萤火虫算法智能优化粒子滤波[J]. 自动化学报, 2016, 42(1): 89. TIAN Mengchu, BO Yuming, CHEN Zhimin, et al. Firefly algorithm intelligence optimized particle filter[J]. Acta Automatica Sinica, 2016, 42(1): 89. DOI:10.16383/j.aas.2016.c150221 |
| [20] |
WU X, LI R, FLEISHER A S, et al. Altered default mode network connectivity in Alzheimer's disease-A resting functional MRI and Bayesian network study[J]. Human Brain Mapping, 2011, 32(11): 1868. DOI:10.1002/hbm.21153 |
 2019, Vol. 51
2019, Vol. 51


