2. 陆军装备研究院,石家庄 050000
2. Army Equipment Research Institution, Shijiazhuang 050000, China
非晶态合金是指内部结构中原子呈长程无序排列的合金[1].Zr基非晶合金具有易成型、高强度、高硬度、低杨氏模量、高弹性极限、断裂韧性高等一系列优异的物理力学性能,因而得到广泛的研究和应用[2-3].尤其在军事领域,独特的物理力学性能使其具有光明的应用前景[4-6],因而,对Zr基非晶合金冲击压缩行为及其物态方程的研究显得尤为重要.
在非晶合金的物态方程及冲击压缩性能研究方面,Li Gong[7]研究了Ni77P23非晶合金的压缩行为,并计算了材料的布里希-默纳罕(Birch-Murnaghan)物态方程.Masaru[8]总结了多种非晶合金体积模量与压力间的关系,研究了高压材料的结构预弛现象.J.Q.Wang[9]研究了Yb基非晶合金的压缩性能,结果表明压力对该材料的摩尔比容、体积模量、泊松比等参数的影响显著大于它种非晶合金;对Zr基非晶合金的研究方面,Wei等[10-11]测量了多种Zr基非晶合金的热力学参数,并从热力学参数出发计算了材料的Murnaghan方程.Zhang[12],Pan[13]等依据材料的热力学参数,分别计算了两种Zr基非晶合金基于Debye模型的物态方程.Martin[14],Mashimo等[15]分别研究了Zr57Nb5Cu15.4Ni12.6Al10、Zr55Al10Ni5Cu30两种非晶合金的冲击压缩行为,并发现了Zr基非晶合金冲击压缩曲线的分区现象.目前,国内外学者对非晶合金的高压响应研究成果较为丰硕,但尚无针对Zr41Ti14Ni12.5Cu10Be22.5非晶态合金的冲击响应及其冲击物态方程的相关工作.
本文采用平板冲击实验,研究了Zr41Ti14Ni12.5Cu10Be22.5非晶合金5 GPa~10 GPa压力范围内的冲击压缩行为.求得了材料的雨贡纽(Hugoniot)参数及Hugoniot极限强度,并与理论分析结果对比,得出了理论计算结果的适用范围;提出了基于模拟退火算法计算材料格林艾森(Gruneisen)物态方程的方法,并与解析法计算结果、Birch-Murnaghan物态方程、三项式物态方程结果做了对比研究.
1 试验概况 1.1 材料制备实验对象为Zr41Ti14Ni12.5Cu10Be22.5非晶态合金,选用纯度高于99.5%的Zr,Ti,Ni,Cu,Be高纯金属,清除金属表面氧化膜后,按原子分数进行配置,分别在石油醚溶液,无水乙醇溶液中进行超声波清洗,以去除金属表面的油污以及在配料过程中附着的杂质.在高纯Ar气(99.99 mass%)气氛保护下,采用真空电弧炉熔炼,每个合金锭至少翻转熔炼4次,保证成分的均匀性良好,最终采用铜模喷铸法得到块体Zr基非晶合金,并利用线切割将材料制备成20 mm×20 mm×4 mm的长方体试样.图 1为制得试样的XRD图像,可以看到38°左右有一较宽的弥散峰且没有结晶峰,表明材料为典型的非晶结构.
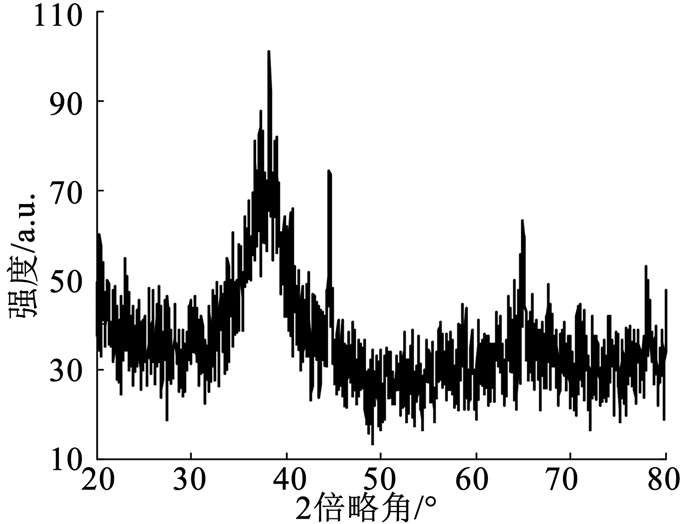
|
图 1 Zr41Ti14Ni12.5Cu10Be22.5非晶合金的XRD图像 Fig. 1 XRD pattern of Zr41Ti14Ni12.5Cu10Be22.5 |
平板冲击实验在中科院力学研究所的一级轻气炮上进行,见图 2(a).采用阻抗匹配法测量Zr基非晶合金的Hugoniot曲线,阻抗匹配法的基本原理为用冲击绝热线已知的材料做标准,将待测样品材料的冲击压缩特性与该标准材料进行比较,获得待测材料冲击绝热线.实验飞片材料为超导电无氧铜,其密度为8.93 g/cm3,Hugoniot参数C0为3.940 km/s,λ为1.489.Zr基非晶合金试样镶嵌在环氧树脂内,并与铝制靶环组成靶板,试验布置见图 2(b).
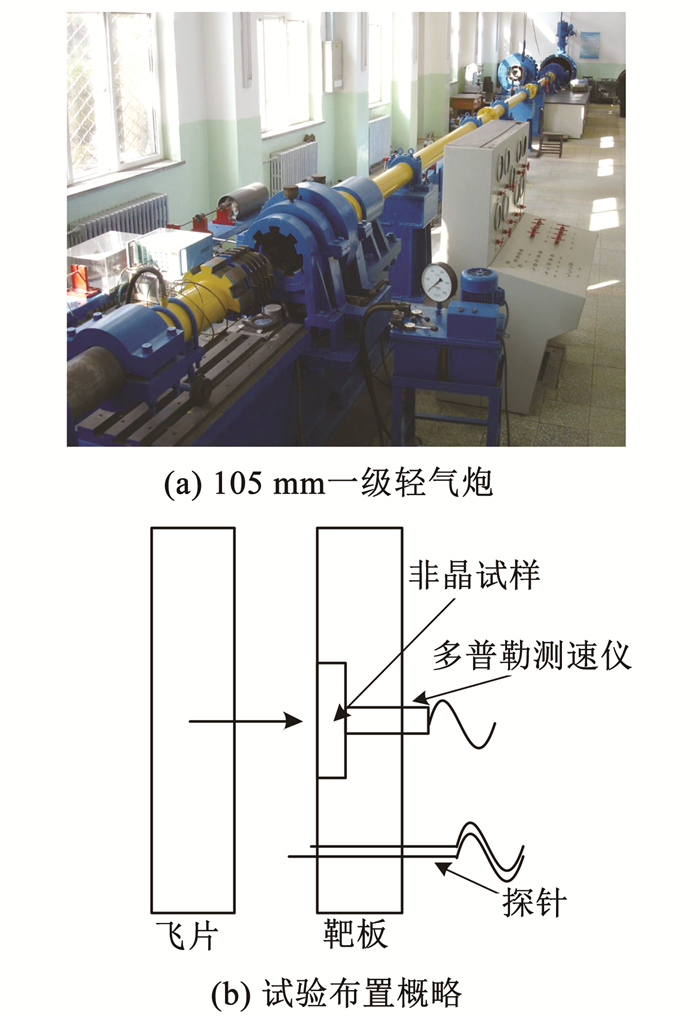
|
图 2 实验布置概略 Fig. 2 Schematic diagram of the experimental setup |
采用长短探针测量飞片的撞击速度V,长短探针头部距离与飞片撞击探针头部时间差的比值即为飞片速度.利用全光纤光子多普勒测速仪(PDV),根据多普勒频移效应测量试样自由面速度ufs.当被测物体向探头运动时,从被测物体表面反射回来的信号光fs,相对于激光器从探头发出的探测光fo,会有微小的多普勒频移fd
| $ {f_{\rm{d}}} = {f_{\rm{s}}} - {f_{\rm{0}}} = \frac{{2{u_{{\rm{fs}}}}}}{{{\lambda _0}}} = \frac{{2{f_0}}}{c}{u_{{\rm{fs}}}}. $ | (1) |
式中:λ0为探测光的中心波长,c为光速,通过对干涉光时频分析提取多普勒频移fd,代入式(1)即可求得试样自由面速度ufs.
2 实验结果与讨论 2.1 材料D-u曲线在流体模型近似下,冲击波从自由面反射的卸载过程为等熵过程,当冲击波加载过程不太高时,冲击波后粒子速度u与自由面粒子速度ufs的近似关系为[14]
| $ u \approx \frac{1}{2}{u_{{\rm{fs}}}}. $ | (2) |
式(2)的推导过程可见文献[16].对于大部分固体,尤其在中压条件下,其冲击波速D与粒子速度u呈线性关系,在波前静止坐标系中,D-u关系为[17]
| $ D = {C_0} + \lambda u. $ | (3) |
式中C0理论上等于固体的零压体积声速.
图 3为飞片撞击样品的p-u图,曲线OC为飞片(标准材料)的冲击绝热线,EAW为飞片冲击绝热线过速度W的镜像,待测样品的波直线OB与EAW相交于A点,波直线公式为[18]
| $ p = {\rho _0}Du. $ | (4) |
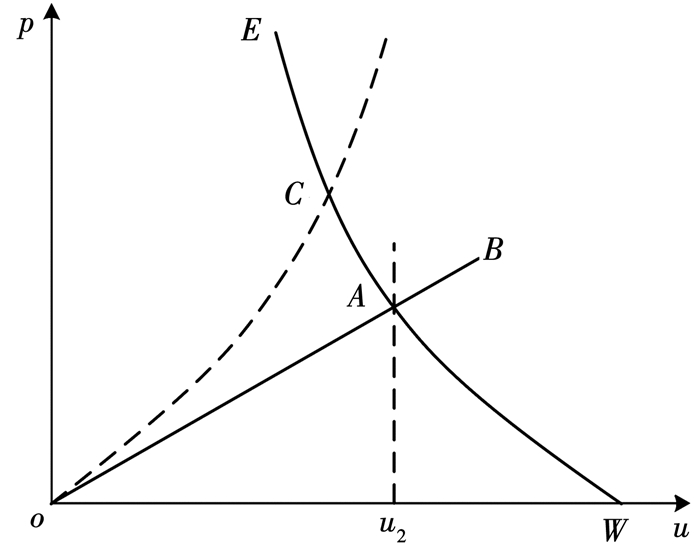
|
图 3 飞片撞击试样p-u Fig. 3 p-u diagram of flyer impacting sample |
已知飞片撞击非晶合金试样时压力平衡,根据图 2,由(3)(4)可得
| $ {D_2} = \frac{{{\rho _{01}}\left[ {{C_{01}} + {\lambda _1}\left( {W - {u_2}} \right)} \right]\left( {W - {u_2}} \right)}}{{{\rho _{02}}{u_2}}}. $ | (5) |
式中:下标1代表标准材料,下标2代表非晶合金.由冲击波阵面质量守恒关系[16],可得
| $ \rho = {\rho _0}D/\left( {D - u} \right). $ | (6) |
将标准材料的Hugoniot参数、测试数据代入式(4)~(6)即可得到压力p、冲击波速D及材料密度ρ,表 1为材料的实测及计算数据.
| 表 1 实测及计算数据 Tab. 1 Experimental and computational data |
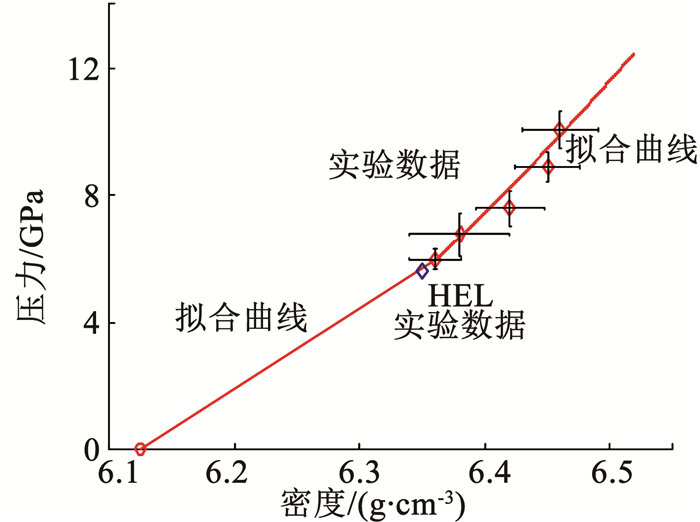
图 4为采用多普勒频移法测得的自由面速度曲线,可以看到材料明显的弹-塑性响应,曲线首先直线上升,到达材料的Hugoniot弹性极限时出现小波峰,随后塑性波到达,曲线继续上升一段高度后达到稳定.Hugoniot弹性极限(HEL)表示材料在单轴冲击载荷下的弹性响应极限,将弹性波波峰处的粒子速度代入式(4),即可求得Hugoniot弹性极限强度分别为5.59 GPa、5.65 GPa、5.66 GPa、5.51 GPa、6.75 GPa,舍弃最后一个明显偏大的值求平均,取材料的Hugoniot弹性极限强度σHEL为5.60 GPa.
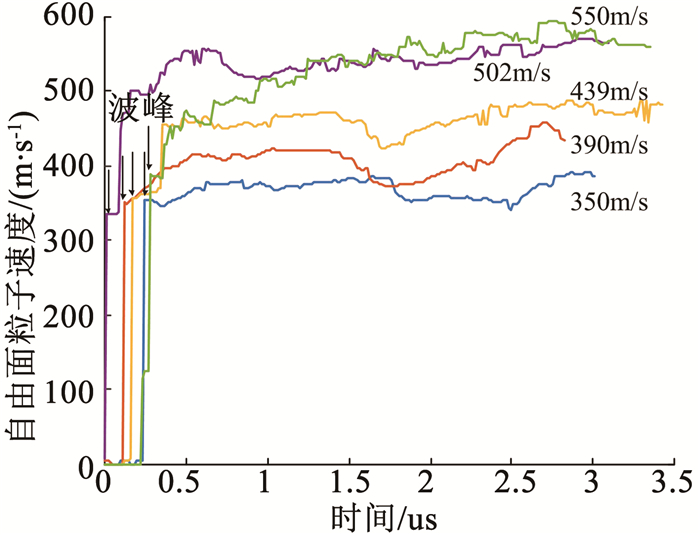
|
图 4 自由面速度 Fig. 4 Velocity of free surface |
图 5为最小二乘法拟合的Zr41Ti14Ni12.5Cu10Be22.5非晶态合金D-u曲线,在5~10 GPa压力范围内,材料的Hugoniot参数C0为4.267 km/s,λ0为4.376,远大于一般固体1.0~1.5的斜率值,Martin[14],Mashimo等[15]观测到Zr57Nb5Cu15.4Ni12.6Al10、Zr55Al10Ni5Cu30两种Zr基非晶合金也具有类似现象.图 6为材料的P-ρ曲线,已知Hugoniot弹性极限下为材料的弹性响应阶段[17],故可通过σHEL得到材料在0~6 GPa内的P-ρ响应.

|
图 5 材料的D-u曲线 Fig. 5 D-u curves of the material |
|
图 6 材料P-ρ的曲线 Fig. 6 P-ρ curves of the material |
假设Zr41Ti14Ni12.5Cu10Be22.5非晶态合金为理想混合物,由文献[18],当各组元的冲击波速度与粒子速度满足式(3)所示线性关系时,混合物的Hugoniot参数可由式(7)、(8)求得:
| $ \frac{1}{{C_0^2}} = \frac{1}{{V_0^2}}\sum\limits_i {\frac{{{x_i}V_{0i}^2}}{{C_{0i}^2}}} , $ | (7) |
| $ \frac{1}{{\lambda _0^2}} = \frac{1}{{V_0^2}}\sum\limits_i {\frac{{{x_i}V_{0i}^2}}{{\lambda _{0i}^2}}} . $ | (8) |
式中xi为组元i的质量分数,理论计算所需参数及计算结果见表 2.
| 表 2 计算参数及结果 Tab. 2 Parameters and computational results |
可见,理论计算所得Hugoniot曲线斜率远小于实验所得结果.Martin[14]对Zr57Nb5Cu15.4Ni12.6Al10非晶合金高压物态方程的研究结果表明,材料的冲击Hugoniot曲线为低压区、混合区、高压区三部分的组合,而低压区部分的冲击Hugoniot曲线斜率远大于一般材料,而高压区Hugoniot曲线斜率与一般金属材料类似,在1.0~1.5之间.因此,推测采用理想混合物模型的计算结果更接近非晶合金高压区Hugoniot参数,为验证该假设,采用相同方法计算Zr57Nb5Cu15.4Ni12.6Al10非晶合金Hugoniot参数,理论计算所需参数及计算结果见表 3(括号内为混合法理论计算结果).
由表 3可知,采用理想混合物模型计算高压区Zr57Nb5Cu15.4Ni12.6Al10非晶合金Hugoniot参数与实验结果相近,从而证实了假设,即Zr基非晶合金的高压区Hugoniot参数可通过理想混合物模型进行计算.对于Zr41Ti14Ni12.5Cu10Be22.5非晶态合金,其Hugoniot曲线低压区、混合区的拐点压力大于10 GPa,高压区Hugoniot参数约为C0=4.147 km/s,λ=0.925.
| 表 3 计算参数及结果 Tab. 3 Parameters and computational results |
在流体模型和谐振子模型近似下,忽略自由电子项的影响,由Gruneisen物态方程和Rankin-Hugoniot能量方程得出固体冲击物态方程计算模型[19].
| $ p = \frac{{\frac{V}{\gamma }{p_{\rm{C}}} - {E_{\rm{C}}}}}{{\frac{V}{\gamma } - \frac{1}{2}\left( {{V_0} - V} \right)}}. $ | (9) |
式中:pC为材料冷压,EC为材料冷能,γ为Gruneisen系数.为方便计算,通常利用波恩-迈耶势,冷能EC和冷压pC化为Q、q形式[20]:
| $ {E_{\rm{C}}} = \frac{{3Q}}{{{\rho _{{\rm{0K}}}}}}\left\{ {\frac{1}{q}\exp \left[ {q\left( {1 - {\delta ^{ - 1/3}}} \right)} \right] - {\delta ^{ - 1/3}} - \left( {\frac{1}{q} - 1} \right)} \right\}. $ | (10) |
| $ {p_{\rm{C}}} = Q{\delta ^{ - 2/3}}\left\{ {\exp \left[ {q\left( {1 - {\delta ^{ - 1/3}}} \right)} \right] - {\delta ^{ - 1/3}}} \right\}. $ | (11) |
式中:ρ0K为材料在0 K时的密度,
| $ {\gamma _{{\rm{D}} - {\rm{M}}}} = \frac{1}{6}\frac{{{q^2}{\delta ^{ - 1/3}} \cdot \exp \left[ {q\left( {1 - {\delta ^{ - 1/3}}} \right)} \right] - 6\delta }}{{q \cdot \exp \left[ {q\left( {1 - {\delta ^{ - 1/3}}} \right)} \right] - 2\delta }}. $ | (12) |
将式(10)~(12)代入式(9)即为材料物态方程的Q、q形式.波后比容可由式(6)导出,将实验得到的D-u形式的Hugoniot曲线代入式(4)(6)即可得到一组压力、比容值记为pfit-Vfit.将pfit-Vfit代入式(9)~(12),通过数学迭代可得到数值法的目标函数为
| $ f = \sqrt {\sum {{{\left[ {p\left( {Q,q} \right) - {p_{fit}}} \right]}^2}} } . $ | (13) |
式(13)将求材料物态方程参数的问题转化为非线性优化问题,模拟退火算法适合解决这类问题.
模拟退火算法(Simulated annealing algorithm, SA)是依据统计物理学原理,模仿固体退火过程的随机优化算法.模拟退火算法特别适用于求解组合优化问题,它的核心为Metropolis算法.Metropolis算法产生一个马尔可夫链,它的转移概率确实收敛到一个独立平稳的Gibbs分布,当温度时,系统能量将收敛到全局极小点.Metropolis算法如式(14)所示
| $ {X_{n + 1}} = \left\{ \begin{array}{l} {Y_n},\Delta E < 0;\\ {Y_n},\Delta E > 0,\xi < {{\rm{e}}^{\left( { - \Delta E/T} \right)}};\\ {X_n},\Delta E > 0,\xi \ge {{\rm{e}}^{\left( { - \Delta E/T} \right)}}. \end{array} \right. $ | (14) |
式中:Xn为n时刻状态,Yn为随机生成的新状态,ΔE为系统从状态Xn到Yn的能量差,T为当前温度,ξ为(0, 1)间的随机数.若ΔE为负,则新状态系统能量更低,该次转移被接受;若ΔE为正,则Yn以概率e(-ΔE/T)被接受,对于求解材料参数Q、q的问题,系统能量差即为目标函数(13)的新旧状态之差,算法的具体细节本文不再赘述.参数设置如下,其中Tini=1032为初始温度,Tend=10-20为终止温度,k=0.995为温差系数,温度依据式(15)进行迭代.
| $ {T_{n + 1}} = k{T_n}. $ | (15) |
图 7为退火过程,横坐标采用对数形式,可以看到,高温时,曲线波动范围较大,以此跳出局部最小值;低温时,曲线快速收敛,以提高计算速度.经多次试验,算法稳定性较高.

|
图 7 退火过程 Fig. 7 Annealing process |
将所求参数Q、q代入式(9),即得Zr41Ti14Ni12.5Cu10Be22.5非晶态合金的Gruneisen冲击物态方程.最终求得Q=6.829 6×109 GPa,q=2.047 8,所得物态方程数据与实验数据均方差为0.376 1 GPa,而通过解析法[20, 22]求得Q=7.869 5×109 GPa,q=44.846 7,代入实验数据解得负压力值,与事实不符,表明提出方法较适用于Zr基非晶合金Gruneisen物态方程的计算,而传统解析法误差较大.
2.4 多项式物态方程实际应用过程中,也常采用Birch-Murnaghan物态方程[7, 14]和三项式物态方程表示材料的p-V关系,Birch-Murnaghan物态方程为
| $ p = \frac{{3{K_0}}}{2}\left[ {{{\left( {\frac{{{V_0}}}{V}} \right)}^{\frac{7}{3}}} - {{\left( {\frac{{{V_0}}}{V}} \right)}^{\frac{5}{3}}}} \right]\left\{ {1 + 3\left( {\frac{{{{K'}_0}}}{4} - 1} \right)\left[ {{{\left( {\frac{{{V_0}}}{V}} \right)}^{\frac{2}{3}}} - 1} \right]} \right\}. $ | (16) |
式中:K0为材料的零压体积模量.Zr41Ti14Ni12.5Cu10Be22.5非晶态合金的K0为114.4 GPa,K′0为体积模量对p的导数,其解析式为[14]
| $ {{K'}_0} = 4{\lambda _0} - 1. $ | (17) |
三项式物态方程为
| $ p = {A_1}\mu + {A_2}{\mu ^2} + {A_3}{\mu ^3}. $ | (18) |
式中:A1为材料零体积应变下的体积模量,A2、A3为材料常数,μ=ρ/ρ0-1为材料的体应变,由最小二乘法得,A1=114.4 GPa,A2=705.2 GPa,A3=7 651 GPa.
材料三种形式的物态方程曲线见图 8,曲线与实验数据走势契合,在实验压力范围内,Gruneisen物态方程、Birch-Murnaghan物态方程、三项式物态方程均可较好地表现材料性质.三种物态方程计算结果与实验数据的均方差分别为0.376 1 GPa、0.363 5 GPa、0.980 8 GPa,表明在5~10 GPa冲击压力范围内,Gruneisen物态方程、三项式物态方程对材料性质的描述更为精准.

|
图 8 材料物态方程曲线 Fig. 8 EOS curves of the material |
1) 采用匹配阻抗法,利用长短探针、PDV等手段实验测定了Zr41Ti14Ni12.5Cu10Be22.5非晶合金的冲击Hugoniot曲线,得到了材料Hugoniot参数及Hugoniot曲线,在5 GPa~10 GPa范围内,曲线的斜率远大于一般固态金属及合金.
2) 采用理想混合物模型理论计算Zr基非晶合金的高压区Hugoniot参数,计算结果适应性较好,但该方法不适用于计算材料低压区Hugoniot参数.Zr41Ti14Ni10Cu12.5Be22.5非晶态合金Hugoniot曲线的低压区、混合区拐点压力大于10 GPa.
3) 提出了基于模拟退火算法计算材料Gruneisen物态方程的方法,并得到了Zr41Ti14Ni12.5Cu10Be22.5非晶合金的Gruneisen物态方程,该方法较传统解析法更适用于Zr基非晶合金Gruneisen物态方程的计算;与三项式物态方程、Birch-Murnaghan物态方程对比结果表明,在5~10 GPa冲击压力范围内,Gruneisen物态方程、三项式物态方程对材料性质的描述更为精准.
| [1] |
惠希东, 陈国良. 块体非晶合金[M]. 北京: 化学工业出版社, 2007: 1. HUI Xidong, CHEN Guoliang. Bulk amorphous alloy[M]. Beijing: Chemical Industry Press, 2007: 1. |
| [2] |
WANG G Y, LIAW P K, MORRISON M L. Progress in studying the fatigue behavior of Zr-based bulk-metallic glasses and their composites[J]. Intermetallics, 2009(17): 579. DOI:10.1016/j.intermet.2009.01.017 |
| [3] |
DAI L H, YAN M, LIU L F, et al. Adiabatic shear banding instability in bulk metallic glasses[J]. Applied Physics Letters, 2005(87): 14916. DOI:10.1063/1.2067691 |
| [4] |
CONNER R D, DANDLIKER R B, SCRUGGS V, et al. Dynamic deformation behavior of tungsten fiber/metallic glass matrix composites[J]. International Journal of Impact Engineering, 2000(24): 435. DOI:10.1016/S0734-743(99)00176-1 |
| [5] |
RONG G, HUANG D W, YANG M C. Penetrating behaviors of Zr-based metallic glass composite rods reinforced by tungsten fibers[J]. Theoretical and Applied Fracture Mechanics, 2012(58): 21. DOI:10.1016/j.tafmec.2012.02.003 |
| [6] |
KIM G S, SON C Y, LEE S B, et al. Ballistic impact properties of Zr-based amorphous alloy composites reinforced with woven continuous fibers[J]. Metallurgical and Materials Transactions A, 2012(43): 870. DOI:10.1007/s11661-011-0915-5 |
| [7] |
LI G, GAO Y P, SUN Y N, et al. Compression behavior and equation of state of Ni77P23 amorphous alloy[J]. Chinese Science Bulletin, 2007, 52(4): 440. DOI:10.1007/s11434-007-0067-6 |
| [8] |
MASARU A. Elastic constants, equation of state and mechanical relaxations of some metallic glasses at high pressure[J]. Materials Science Forum, 2012, 706: 1305. DOI:10.4028/www.scientific.net/MSF.706-709.1305 |
| [9] |
WANG J Q, BAI H Y. High-pressure behaviors of Yb-based bulk metallic glass[J]. Scripta Materialia, 2009, 61: 453. DOI:10.1016/j.scriptamat.2009.04.044 |
| [10] |
WANG W H, LI F Y, PAN M X, et al. Elastic property and its response to pressure in a typical bulk metallic glass[J]. Acta Materialia, 2004, 52: 715. DOI:10.1016/j.actamat.2003.10.008 |
| [11] |
WANG W H, WEN P, WANG L M, et al. Equation of state of bulk metallic glasses studied by an ultrasonic method[J]. Applied Physics Letters, 2001, 79(24): 3947. DOI:10.1063/1.1426272 |
| [12] |
ZHANG Y, PAN M X, WANG W H. Mie potential and equation of state of Zr48Nb8Cu14Ni12Be18 bulk metallic glass[J]. Chinese Physics Letters, 2001, 18(6): 805. DOI:10.1088/0256-307X/18/6/331 |
| [13] |
PAN M X, WANG W H, ZHAO D Q, et al. The equation of state and potential function of Zr41Ti14Cu12.5Ni10Be22.5 bulk metallic glass[J]. Journal of Physics: Condensed Matter, 2002, 14: 5665. DOI:10.1088.0953-8984/14/23/302 |
| [14] |
MARTIN M, SEKINE T, KOBAYASHI T, et al. High-pressure equation of the state of a zirconium-based bulk metallic glass[J]. Metallurgical and Materials Transactions, 2007, 38(11): 2689. DOI:10.1007/s11661-007-9263-x |
| [15] |
MASHIMO T, TOGO H, Zhang Y, et al. Hugoniot-compression curve of Zr-based bulk metallic glass[J]. Applied Physics Letters, 2006, 89: 241094-1. DOI:10.1063/1.2403931 |
| [16] |
经福谦. 实验物态方程导引[M]. 2版. 北京: 科学出版社, 1999: 209. JING Fuqian. Experimental state equation guidance[M]. Second Edition. Beijing: Science Press, 1999: 209. |
| [17] |
ROSENBERG Z, DEKEL E.终点弹道学[M].钟方平, 译.北京: 国防工业出版, 2012: 9 ROSENBERG Z, DEKEL E. Terminal ballistics[M]. ZHONG Fangping translate Beijing: National Defence Industry Press, 2012: 9 |
| [18] |
谭华. 实验冲击波物理导引[M]. 北京: 国防工业出版社, 2007: 15. TAN Hua. Experimental shockwave physics guidance[M]. Beijing: National Defence Industry Press, 2007: 15. |
| [19] |
史安顺, 张先锋, 乔良, 等. 多功能含能结构材料冲击压缩特性的理论计算[J]. 爆炸与冲击, 2013, 33(2): 148. SHI Anshun, ZHANG Xianfeng, QIAO Liang, et al. Theoretical calculation on shock compression characteristics of multifunctional energetic structural materials[J]. Explosion and Shock Waves, 2013, 33(2): 148. DOI:10.11883/1001-1455(2013)02-148-08 |
| [20] |
汤文辉, 张若棋. 物态方程理论及计算概论[M]. 北京: 高等教育出版社, 2008: 212. TANG Wenhui, ZHANG Ruoqi. Introduction to theory and computation of equations of state[M]. Beijing: Higher Education Press, 2008: 212. |
| [21] |
HAYKIN S.神经网络与机器学习[M].申富饶, 译.北京: 机械工业出版社, 2011: 374 HAYKIN S. Neural networks and learning machines[M]. Shen Furao, translate. Beijing: China Machine Press, 2011: 374 |
| [22] |
胡金彪, 经福谦. 用冲击压缩数据计算物质结合能的一个简便解析方法[J]. 高压物理学报, 1990, 4(3): 175. HU Jinbiao, JING Fuqian. A simplified analytical method for calculations of equation-of-state of materials from shock compression data[J]. Chinese Journal of High Pressure Physic, 1990, 4(3): 175. |
 2019, Vol. 51
2019, Vol. 51


