随着空间攻防态势不断升级,机载双基地雷达因其获取目标信息丰富,观测距离远,抗干扰能力强,安全性高等优点而备受关注[1].相比单基地雷达,双基地雷达收发分置,接收机不发射电磁波,因而接收机隐蔽性更好,生存能力更强;而相比地基雷达,机载雷达发射平台升空,雷达作用距离受地球曲率和地面遮挡的影响减弱,“高瞻远瞩”的优势明显[3-4].然而,收发分置将使得原本因为雷达平台运动而展宽的地面强杂波的多普勒频谱更加复杂[5-6],对双基地机载雷达杂波抑制及目标检测将造成严重影响,因此,研究机载双基地雷达杂波对雷达系统设计有着举足轻重的作用.
研究机载双基地雷达杂波,首先需要建立几何模型,得到双基距离和单元的数学表达式.Klem R[7]、Zhang Y H[8]和王永良[9]等分别建立了几类特殊双基场景的几何模型.王永良等[9]建立的机载双基地雷达几何模型以接收机为原点,基线为Y轴,且收发平台位于同一水平面;吴洪,彭晓瑞,魏民等[10-12]以接收机在水平面的投影点为原点,基线在水平面的投影为Y或X轴,收发平台飞行高度差没有限制;段锐等[13]给出的机载双基雷达几何模型是以接收机在水平面的投影点作为坐标系的原点,坐标轴可为水平面任一方向;王成浩等[14]建立的地心直角坐标系,模型以接收机、发射机和地心三者所在平面为坐标系XOY平面.在上述特殊场景中,其建立的几何坐标系均与收发平台所在位置相关,且场景限制较多,特殊场景的几何模型对于其他场景不适用;另外,上述模型的建立基于接收平台,以接收机平台作为坐标原点,而实际中平台位置时变则,模型也随时变化,杂波仿真过程较为复杂.
基于此,本文针对机载双基地雷达系统在时不变坐标系中建立一般场景的几何模型,利用欧拉坐标转换法推导双基距离和单元在地面固定坐标系中的解析表达式,建立精确的数学模型,通过数值仿真分析不同飞行配置情况下的机载双基雷达杂波特性.
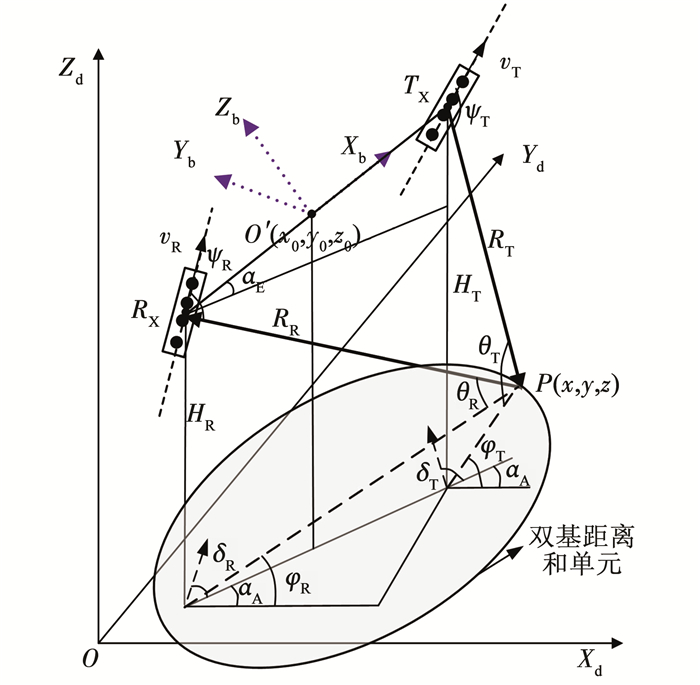
1 机载双基地雷达系统几何模型机载双基雷达系统包括一个发射机(以TX表示),一个接收机(以RX表示),假设雷达天线沿机身,以正侧视均匀线阵排布,具有N个阵元,在相干处理间隔内发射包含K个相干脉冲的脉冲串,其场景如图 1所示,建立几何关系模型.图 1中接收机平台距离地面高度为HR,发射机平台距离地面高度为HT,发射机与接收机连线为基线,长度为L,基线与地面夹角为αE,基线在地面投影与X轴夹角为αA.接收机平台飞行速度为vR,方向相对基线夹角为δR,发射机平台飞行速度为vT,方向相对基线的夹角为δT.发射机发出脉冲,经过地面固定点P反射后到达接收机,被接收机接收.收发波束指向与X轴之间的夹角分别为φRφT和,收发斜距与地面之间的夹角分别为θR和θT,杂波散射点P相对于雷达平台运动方向的空间锥角分别为ψR和ψT.点P到接收机和发射机的距离分别为RR和RT,收发双基距离和为Rsum=RR+RT,空间中到发射机TX和接收机RX的距离之和相等的所有点的集合为一个双基等距离和椭球面,双基等距离和椭球面与地平面XOY的交线即为双基距离和单元.
|
图 1 机载双基地雷达几何关系 Fig. 1 Geometry diagram of airborne bistatic radar |
从图 1中可以看到,场景中建立了两个笛卡尔坐标系,分别为大地坐标系O-XdYdZd和当地坐标系O′-XbYbZb.在大地坐标系O-XdYdZd中,原点O为接收机起始位置在地面的投影点,Z轴垂直地面向上,X轴和Y轴位于地平面,满足笛卡尔右手准则.该坐标系中接收机和发射机位于任意位置,与实际情况相符,可以表示任意双基场景.在当地坐标系O′-XbYbZb中,坐标原点O′位于接收机RX和发射机TX连线的中点位置,X轴指向发射机,Y轴垂直于X轴,且与地面平行,Z轴满足笛卡尔右手准则.
2 机载双基地雷达杂波模型为讨论问题方便,同时又不失一般性,对系统做如下假设:1)暂不考虑地球曲率影响,假设探测范围内地面为水平面;2)假设不考虑地球自转影响;3)暂不考虑大气折射效应,假设信号在发射机、地面固定点和接收机之间沿直线传播.
2.1 坐标系转换矩阵当地坐标系原点O′在大地坐标系中的坐标为(x0, y0, z0),假设任一点P在当地坐标系中的坐标为(xb, yb, zb),在大地坐标系中坐标为(xd, yd, zd),从当地坐标系到大地坐标系的转换矩阵为TBD.在不失一般性的情况下,为便于计算,可将转换阵扩展为方阵,坐标矢量增加一维常量,即可表示为[13]
| $ {\left[ {\begin{array}{*{20}{c}} {{x_{\rm{d}}}}&{{y_{\rm{d}}}}&{{z_{\rm{d}}}}&1 \end{array}} \right]^{\rm{T}}} = \mathit{\boldsymbol{T}}_{\rm{B}}^{\rm{D}} \cdot {\left[ {\begin{array}{*{20}{c}} {{x_{\rm{b}}}}&{{y_{\rm{b}}}}&{{z_{\rm{b}}}}&1 \end{array}} \right]^{\rm{T}}}. $ | (1) |
由几何知识可知,转换矩阵TBD包含平移和旋转两部分,定义平移转换阵为Tp(x0, y0, z0),将当地坐标系原点O′移动到大地坐标系原点O位置,得到新的坐标系O-X1Y1Z1,则有
| $ \left[ {\begin{array}{*{20}{c}} {{x_1}}\\ {{y_1}}\\ {{z_1}}\\ 1 \end{array}} \right] = {\mathit{\boldsymbol{T}}_{\rm{p}}}\left( {{x_0},{y_0},{z_0}} \right) \cdot \left[ {\begin{array}{*{20}{c}} {{x_{\rm{b}}}}\\ {{y_{\rm{b}}}}\\ {{z_{\rm{b}}}}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&0&{{x_0}}\\ 0&1&0&{{y_0}}\\ 0&0&1&{{z_0}}\\ 0&0&0&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{x_{\rm{b}}}}\\ {{y_{\rm{b}}}}\\ {{z_{\rm{b}}}}\\ 1 \end{array}} \right]. $ | (2) |
式中Tp(x0, y0, z0)为平移转换阵.
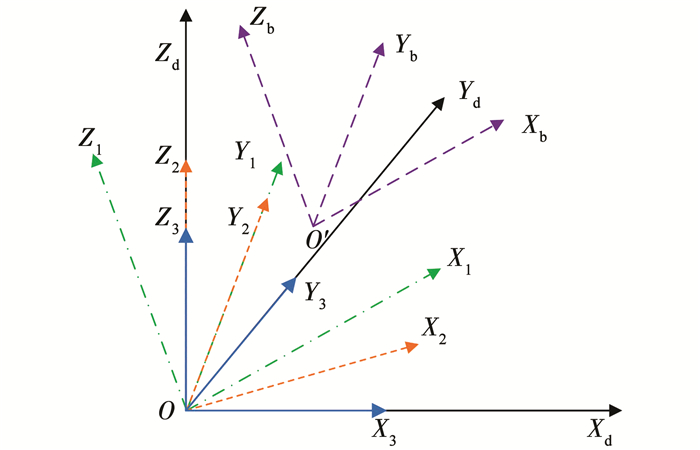
通过分析可知,使当地坐标系与大地坐标系重合需要进行两次旋转运算:1)绕固定轴OY1旋转角度αE,得到坐标系O-X2Y2Z2;2)绕固定轴OZ2旋转角度αA,得到坐标系O-X3Y3Z3.最终得到的坐标系O-X3Y3Z3即与大地坐标系O-XYZ重合,坐标系转换示意图如图 2所示.
|
图 2 坐标转换示意 Fig. 2 Coordinate transformation diagram |
第一次旋转绕固定轴OY1旋转角度αE的数学表达式为
| $ \begin{array}{*{20}{c}} {{{\left[ {\begin{array}{*{20}{c}} {{x_{\rm{2}}}}&{{y_{\rm{2}}}}&{{z_{\rm{2}}}}&1 \end{array}} \right]}^{\rm{T}}} = {\mathit{\boldsymbol{M}}_2}\left( {{\alpha _{\rm{E}}}} \right) \cdot {{\left[ {\begin{array}{*{20}{c}} {{x_{\rm{1}}}}&{{y_{\rm{1}}}}&{{z_{\rm{1}}}}&1 \end{array}} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{M}}_2}\left( {{\alpha _{\rm{E}}}} \right) = \left[ {\begin{array}{*{20}{c}} {\cos {\alpha _{\rm{E}}}}&0&{ - \sin {\alpha _{\rm{E}}}}&0\\ 0&1&0&0\\ {\sin {\alpha _{\rm{E}}}}&0&{\cos {\alpha _{\rm{E}}}}&0\\ 0&0&0&1 \end{array}} \right].} \end{array} $ | (3) |
式中M2(αE)为转换矩阵,且有M2(αE)·M2(-αE)=E.
第二次旋转绕固定轴OZ2旋转角度αA的数学表达式为
| $ \begin{array}{*{20}{c}} {{{\left[ {\begin{array}{*{20}{c}} {{x_{\rm{3}}}}&{{y_{\rm{3}}}}&{{z_{\rm{3}}}}&1 \end{array}} \right]}^{\rm{T}}} = {\mathit{\boldsymbol{M}}_3}\left( {{\alpha _{\rm{A}}}} \right) \cdot {{\left[ {\begin{array}{*{20}{c}} {{x_{\rm{2}}}}&{{y_{\rm{2}}}}&{{z_{\rm{2}}}}&1 \end{array}} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{M}}_3}\left( {{\alpha _{\rm{A}}}} \right) = \left[ {\begin{array}{*{20}{c}} {\cos {\alpha _{\rm{A}}}}&{\sin {\alpha _{\rm{A}}}}&0&0\\ { - \sin {\alpha _{\rm{A}}}}&{\cos {\alpha _{\rm{A}}}}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right].} \end{array} $ | (4) |
式中M3(αA)为其转换矩阵,且有M3(αA)·M3(-αA)=E.
根据上述运算,最终的变换表达式为
| $ {\left[ {\begin{array}{*{20}{c}} {{x_{\rm{d}}}}&{{y_{\rm{d}}}}&{{z_{\rm{d}}}}&1 \end{array}} \right]^{\rm{T}}} = \mathit{\boldsymbol{T}}_{\rm{B}}^{\rm{D}} \cdot {\left[ {\begin{array}{*{20}{c}} {{x_{\rm{3}}}}&{{y_{\rm{3}}}}&{{z_{\rm{3}}}}&1 \end{array}} \right]^{\rm{T}}}. $ | (5) |
从当地坐标系到大地坐标系的转换矩阵为
| $ \mathit{\boldsymbol{T}}_{\rm{B}}^{\rm{D}} = {\mathit{\boldsymbol{M}}_3}\left( {{\alpha _{\rm{A}}}} \right) \cdot {\mathit{\boldsymbol{M}}_2}\left( {{\alpha _{\rm{E}}}} \right) \cdot {\mathit{\boldsymbol{T}}_{\rm{p}}}\left( {{x_0},{y_0},{z_0}} \right). $ | (6) |
同理,从大地坐标系到当地坐标系的转换矩阵为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{T}}_{\rm{B}}^{\rm{D}} = {{\left( {\mathit{\boldsymbol{T}}_{\rm{B}}^{\rm{D}}} \right)}^{ - 1}} = \mathit{\boldsymbol{T}}_{\rm{P}}^{ - 1}\left( {{x_0},{y_0},{z_0}} \right) \cdot \mathit{\boldsymbol{M}}_2^{ - 1}\left( {{\alpha _{\rm{E}}}} \right) \cdot \mathit{\boldsymbol{M}}_3^{ - 1}\left( {{\alpha _{\rm{A}}}} \right)}\\ { = {\mathit{\boldsymbol{T}}_{\rm{P}}}\left( { - {x_0}, - {y_0}, - {z_0}} \right) \cdot {\mathit{\boldsymbol{M}}_2}\left( { - {\alpha _{\rm{E}}}} \right) \cdot {\mathit{\boldsymbol{M}}_3}\left( { - {\alpha _{\rm{A}}}} \right).} \end{array} $ | (7) |
通过分析,空间中到发射机TX和接收机RX的距离之和相等的所有点的集合为一个双基等距离椭球面,接收机和发射机位置为椭球的两个焦点,焦距为基线长度L,长半轴则为双基距离和的一半a=Rsum/2,两个短半轴相等,根据椭圆定义,短半轴可表示为b=c=
| $ \frac{{x_{\rm{b}}^2}}{{{a^2}}} + \frac{{y_{\rm{b}}^2}}{{{b^2}}} + \frac{{z_{\rm{b}}^2}}{{{c^2}}} = 1. $ | (8) |
其球坐标表示的参数方程为
| $ \left\{ {\begin{array}{*{20}{c}} {{x_{\rm{b}}} = a \cdot \cos \alpha \cdot \cos \beta ,}\\ {{y_{\rm{b}}} = b \cdot \cos \alpha \cdot \sin \beta ,}\\ {{z_{\rm{b}}} = c \cdot \sin \alpha .} \end{array}} \right.. $ | (9) |
式中α和β分别为引入的参数变量.
通过坐标转换后,其在大地坐标系中的坐标为(xd, yd, zd),则由式(6)有
| $ \begin{array}{*{20}{c}} {{{\left[ {\begin{array}{*{20}{c}} {{x_{\rm{d}}}}&{{y_{\rm{d}}}}&{{z_{\rm{d}}}}&1 \end{array}} \right]}^{\rm{T}}} = T_{\rm{B}}^{\rm{D}} \cdot {{\left[ {\begin{array}{*{20}{c}} {{x_{\rm{b}}}}&{{y_{\rm{b}}}}&{{z_{\rm{b}}}}&1 \end{array}} \right]}^{\rm{T}}} = }\\ {\left[ {\begin{array}{*{20}{c}} {\cos {\alpha _{\rm{A}}}\cos {\alpha _{\rm{E}}}}&{\sin {\alpha _{\rm{A}}}}&{ - \cos {\alpha _{\rm{A}}}\sin {\alpha _{\rm{E}}}}&0\\ { - \sin {\alpha _{\rm{A}}}\cos {\alpha _{\rm{E}}}}&{\cos {\alpha _{\rm{A}}}}&{\sin {\alpha _{\rm{A}}}\sin {\alpha _{\rm{E}}}}&0\\ {\sin {\alpha _{\rm{E}}}}&0&{\cos {\alpha _{\rm{E}}}}&0\\ 0&0&0&1 \end{array}} \right] \cdot }\\ {{{\left[ {\begin{array}{*{20}{c}} {{x_{\rm{b}}} + {x_{\rm{0}}}}&{{y_{\rm{b}}} + {y_{\rm{0}}}}&{{z_{\rm{b}}} + {z_{\rm{0}}}}&1 \end{array}} \right]}^{\rm{T}}}.} \end{array} $ | (10) |
由式(7)则有
| $ \begin{array}{*{20}{c}} {{{\left[ {\begin{array}{*{20}{c}} {{x_{\rm{b}}}}&{{y_{\rm{b}}}}&{{z_{\rm{b}}}}&1 \end{array}} \right]}^{\rm{T}}} = \mathit{\boldsymbol{T}}_{\rm{D}}^{\rm{B}} \cdot {{\left[ {\begin{array}{*{20}{c}} {{x_{\rm{d}}}}&{{y_{\rm{d}}}}&{{z_{\rm{d}}}}&1 \end{array}} \right]}^{\rm{T}}}}\\ {\mathit{\boldsymbol{T}}_{\rm{D}}^{\rm{B}} = \left[ {\begin{array}{*{20}{c}} {\cos {\alpha _{\rm{E}}}\cos {\alpha _{\rm{A}}}}&{ - \cos {\alpha _{\rm{E}}}\sin {\alpha _{\rm{A}}}}&{\sin {\alpha _{\rm{E}}}}&{ - {x_0}}\\ {\sin {\alpha _{\rm{A}}}}&{\cos {\alpha _{\rm{A}}}}&0&{ - {y_0}}\\ { - \sin {\alpha _{\rm{E}}}\cos {\alpha _{\rm{A}}}}&{\sin {\alpha _{\rm{E}}}\sin {\alpha _{\rm{A}}}}&{\cos {\alpha _{\rm{E}}}}&{ - {z_0}}\\ 0&0&0&1 \end{array}} \right].} \end{array} $ | (11) |
联立式(9)椭球面参数方程,则可以得到椭球面在大地坐标系中的参数方程为
| $ \left\{ \begin{array}{l} {x_{\rm{d}}} = \cos {\alpha _{\rm{A}}}\cos {\alpha _{\rm{E}}}\left( {a\cos \alpha \cos \beta + {x_0}} \right) + \\ \sin {\alpha _{\rm{A}}}\left( {b\cos \alpha \sin \beta + {y_0}} \right) - \\ \cos {\alpha _{\rm{A}}}\sin {\alpha _{\rm{E}}}\left( {c\sin \alpha + {z_0}} \right),\\ {y_{\rm{d}}} = - \sin {\alpha _{\rm{A}}}\cos {\alpha _{\rm{E}}}\left( {a\cos \alpha \cos \beta + {x_0}} \right) + \\ \cos {\alpha _{\rm{A}}}\left( {b\cos \alpha \sin \beta + {y_0}} \right) + \\ \sin {\alpha _{\rm{A}}}\sin {\alpha _{\rm{E}}}\left( {c\sin \alpha + {z_0}} \right),\\ {z_{\rm{d}}} = \sin {\alpha _{\rm{E}}}\left( {a\cos \alpha \cos \beta + {x_0}} \right) + \\ \cos {\alpha _{\rm{E}}}\left( {c\sin \alpha + {z_0}} \right). \end{array} \right. $ | (12) |
通过式(11)坐标转换关系式,可以得到
| $ \left\{ \begin{array}{l} {x_{\rm{b}}} = {x_{\rm{d}}}\cos {\alpha _{\rm{E}}}\cos {\alpha _{\rm{A}}} - {y_{\rm{d}}}\cos {\alpha _{\rm{E}}}\sin {\alpha _{\rm{A}}} + \\ {z_{\rm{d}}}\sin {\alpha _{\rm{E}}} - {x_0},\\ {y_{\rm{b}}} = {x_{\rm{d}}}\sin {\alpha _{\rm{A}}} + {z_{\rm{d}}}\cos {\alpha _{\rm{A}}} - {y_0},\\ {z_{\rm{b}}} = - {x_{\rm{d}}}\sin {\alpha _{\rm{E}}}\cos {\alpha _{\rm{A}}} + {y_{\rm{d}}}\sin {\alpha _{\rm{E}}}\cos {\alpha _{\rm{A}}} + \\ {z_{\rm{d}}}\cos {\alpha _{\rm{E}}} - {z_0}. \end{array} \right. $ | (13) |
将式(13)代入式(8)椭球面方程,可以得到在大地坐标系中的椭球面方程表达式
| $ \begin{array}{l} f\left( {{x_{\rm{d}}},{y_{\rm{d}}},{z_{\rm{d}}}} \right) = 1\\ = \frac{{{{\left( {{x_{\rm{d}}}\cos {\alpha _{\rm{E}}}\cos {\alpha _{\rm{A}}} - {y_{\rm{d}}}\cos {\alpha _{\rm{E}}}\sin {\alpha _{\rm{A}}} + {z_{\rm{d}}}\sin {\alpha _{\rm{E}}} - {x_0}} \right)}^2}}}{{{a^2}}} + \\ \frac{{{{\left( {{x_{\rm{d}}}\sin {\alpha _{\rm{A}}} + {z_{\rm{d}}}\cos {\alpha _{\rm{A}}} - {y_0}} \right)}^2}}}{{{b^2}}} + \\ \frac{{{{\left( { - {x_{\rm{d}}}\sin {\alpha _{\rm{E}}}\cos {\alpha _{\rm{A}}} + {y_{\rm{d}}}\sin {\alpha _{\rm{E}}}\sin {\alpha _{\rm{A}}} + {z_{\rm{d}}}\cos {\alpha _{\rm{E}}} - {z_0}} \right)}^2}}}{{{c^2}}}. \end{array} $ | (14) |
令zd=0,由式(14)可以得到水平面的椭圆双基距离和单元表达式为
| $ \begin{array}{l} f\left( {{x_{\rm{d}}},{y_{\rm{d}}}} \right) = 1\\ \;\; = \frac{{{{\left( {{x_{\rm{d}}}\cos {\alpha _{\rm{E}}}\cos {\alpha _{\rm{A}}} - {y_{\rm{d}}}\cos {\alpha _{\rm{E}}}\sin {\alpha _{\rm{A}}} - {x_0}} \right)}^2}}}{{{a^2}}} + \\ \;\;\frac{{{{\left( {{x_{\rm{d}}}\sin {\alpha _{\rm{A}}} - {y_0}} \right)}^2}}}{{{b^2}}} + \\ \;\;\frac{{{{\left( { - {x_{\rm{d}}}\sin {\alpha _{\rm{E}}}\cos {\alpha _{\rm{A}}} + {y_{\rm{d}}}\sin {\alpha _{\rm{E}}}\sin {\alpha _{\rm{A}}} - {z_0}} \right)}^2}}}{{{c^2}}}. \end{array} $ | (15) |
至此,建立了可直接表示的双基距离和单元方程的解析表达式.
2.3 杂波模型常用的反射率Morchin模型[15]对不同杂波都有较好的描述,其表示为
| $ {\sigma ^0}\left( r \right) = \frac{{A\sigma _{\rm{c}}^0\sin {\theta _{\rm{g}}}}}{\lambda } + u{\cot ^2}{\beta _0}\exp \left[ { - \frac{{{{\tan }^2}\left( {B - {\theta _{\rm{g}}}} \right)}}{{{{\tan }^2}{\beta _0}}}} \right]. $ | (16) |
式中λ为发射信号波长;式(16)中各参数在海杂波、沙漠、农田、丘陵、高山场景时的取值如表 1所示.
| 表 1 Morchin模型参数对照表 Tab. 1 Comparison of Morchin model parameters |
表 1中,s为海杂波的海情等级,有5级,取值为1~5;Re=6 370 km为地球曲率半径;θg为擦地角,对于双基地雷达,有sin θg=
雷达的有效接收功率密度可表示为
| $ \begin{array}{l} {\mathit{P}_{{\rm{st}}}}\left( {{\theta _{\rm{T}}},{\varphi _{\rm{T}}},{\theta _{\rm{R}}},{\varphi _{\rm{R}}}} \right) = \\ \;\;\;\;\frac{{{D_{\rm{u}}}{P_{\rm{t}}}{G_{\rm{T}}}\left( {{\theta _{\rm{T}}},{\varphi _{\rm{T}}}} \right){G_{\rm{R}}}\left( {{\theta _{\rm{R}}},{\varphi _{\rm{R}}}} \right){\lambda ^2}{\sigma _{\rm{c}}}\left( {{R_{\rm{T}}},{R_{\rm{R}}}} \right)}}{{{{\left( {4{\rm{ \mathsf{ π} }}} \right)}^3}R_{\rm{T}}^2R_{\rm{R}}^2\mathit{\Gamma }}}. \end{array} $ | (17) |
式中:Du为占空比,Pt为发射功率,Γ为系统损耗因子,σc(RT, RR)为散射点P处地面反射率,GT(θT, φT)为发射天线增益,GR(θR, φR)为接收天线增益,可表示为
| $ {G_{\rm{T}}}\left( {{\theta _{\rm{T}}},{\varphi _{\rm{T}}}} \right) = {G_{{\rm{T0}}}}{F^2}\left( {{\theta _{\rm{T}}},{\varphi _{\rm{T}}}} \right), $ | (18) |
| $ {G_{\rm{R}}}\left( {{\theta _{\rm{R}}},{\varphi _{\rm{R}}}} \right) = {G_{{\rm{R0}}}}{g^2}\left( {{\theta _{\rm{R}}},{\varphi _{\rm{R}}}} \right). $ | (19) |
式中:GT0为发射天线最大功率增益,F(θT, φT)为发射天线的方向性函数,GR0为接收天线的最大功率增益,g(θR, φR)为接收天线的方向性函数.
假设Cl(n, k)表示机载雷达第n列的第k个脉冲对第l个双基距离和单元杂波的采样数据(忽略噪声项),考虑等效阵元方向性及距离调制,不考虑距离模糊,则有第l个双基距离和单元的杂波表示为
| $ \begin{array}{*{20}{c}} {{C_{\rm{l}}}\left( {n,k} \right) = \sum\limits_{i = 1}^{{N_{{\rm{num}}}}} {{a_{{\rm{il}}}}\sqrt {{P_{{\rm{st}}}}} {\Phi _{{\rm{s,i}}}}\left( {{f_{\rm{s}}}} \right){\Phi _{{\rm{t,i}}}}\left( {{f_{\rm{d}}}} \right)} }\\ {n = 1, \cdots ,N,k = 1, \cdots ,K} \end{array}. $ | (20) |
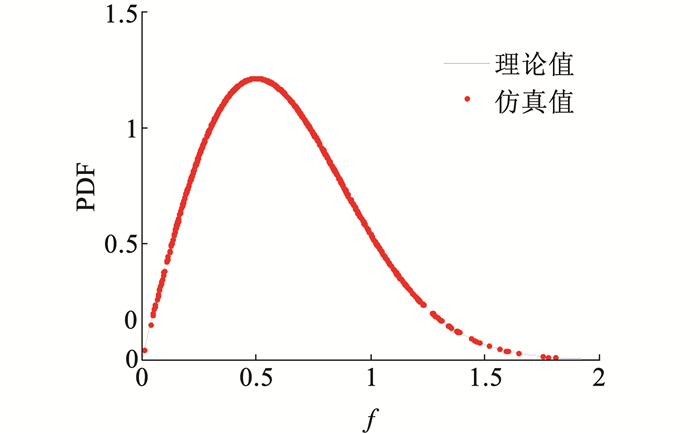
式中:Nnum为第l个双基距离和单元方位向的划分个数,N为接收天线阵元数,K为相干脉冲数,ail为杂波散射单元的随机幅度起伏值.常用的机载雷达地杂波统计分布模型为复高斯分布(或瑞利分布),其幅度分布的概率密度函数(probability dens ity function, PDF)为
|
图 3 瑞利分布PDF(σt=0.5) Fig. 3 PDF of Rayleigh distribution(σt=0.5) |
杂波回波表达式(19)中,Φs, i(fs)和Φt, i(fd)分别为对应杂波单元上的空时相位因子,表达式为
| $ {\mathit{\Phi }_{{\rm{s,i}}}}\left( {{f_{\rm{s}}}} \right) = \exp \left[ {{\rm{j}}2{\rm{ \mathsf{ π} }}\left( {n - 1} \right){f_{\rm{s}}}} \right], $ | (21) |
| $ {\mathit{\Phi }_{{\rm{t,i}}}}\left( {{f_{\rm{d}}}} \right) = \exp \left[ {{\rm{j}}2{\rm{ \mathsf{ π} }}\left( {k - 1} \right){f_{\rm{d}}}} \right]. $ | (22) |
地面固定散射点反射的回波的归一化多普勒频率和散射点杂波回波的归一化空间频率分别如下[13]
| $ {f_{\rm{d}}} = \frac{1}{{\lambda {f_{\rm{r}}}}}\left( {{v_{\rm{T}}}\cos {\psi _{\rm{T}}} + {v_{\rm{R}}}\cos {\psi _{\rm{R}}}} \right), $ | (23) |
| $ {f_{\rm{s}}} = \frac{d}{\lambda }\cos {\psi _{\rm{R}}}. $ | (24) |
式中:fr为脉冲重复频率,d=λ/2为天线子阵间隔,cos ψT=cosθTcos(δT+αA-φT)为发射锥角余弦,cos ψR=cos θRcos(δR+αA-φR)为接收锥角余弦.从式(23)中可看出,fd并不是关于cos ψR的线性函数,可以预计机载双基地雷达杂波呈现距离依赖性.
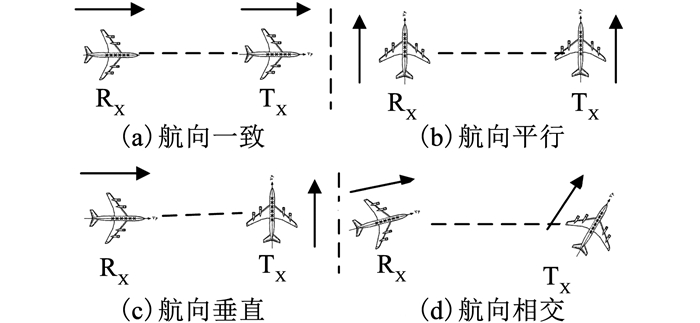
3 机载双基地雷达杂波仿真与特性分析 3.1 参数设置机载双基地雷达按正侧视阵配置,发射波束指向为阵列法线方向,其参数依据现有机载预警雷达的工作模式和工作参数范围等进行设置,具体参数如表 2所示.按照收发平台的航向关系可以将场景分为4类进行讨论,即航向一致、航向平行、航向垂直和航向交叉,如图 4所示,不同双基几何关系配置情况如表 3所示.
| 表 2 机载双基地雷达参数设置 Tab. 2 Parameters setting of airborne bistatic radar |
|
图 4 收发平台航向关系 Fig. 4 Direction diagram of transceiver platform |
| 表 3 双基地雷达几何关系配置 Tab. 3 Geometric relationship configuration of bistatic radar |
根据上述收发平台的初始参数进行数值仿真,图 5分别给出当地坐标系和大地坐标系中的双基距离和单元,其距离和均为30 km.从图中可以看出,两个坐标系中的仿真场景与实际场景相符,即仿真结果验证了上述建立的双基几何模型的正确性和有效性,该模型能精确的用数学解析表达.

|
图 5 不同坐标系中双基距离和单元(Rsum=30 km) Fig. 5 Representation of bistatic distance and unit in different coordinate systems(Rsum=30 km) |
根据双基地雷达收发平台的4种场景进行杂波特性仿真.
1) 收发平台航向一致.航向一致时,发射机远离基线中心运动,接收机靠近基线中心运动其等多普勒频率曲线(IsoDop迹,黑线)、等空间频率曲线(IsoBeam迹,白线)和双基距离和单元曲线(灰线)如图 6(a)所示.图 6(b)给出双基距离和分别为25 km、30 km、35 km、60 km、70 km和80 km时的杂波回波的角度多普勒迹,黑色点迹表示与发射波束扫描方向对应的各距离单元的杂波谱中心.双基距离和30 km处的空时二维杂波谱如图 6(c)所示.从图(a)中可看出,此时的IsoBeam迹为以基线为对称轴的双曲线族,且与IsoDop迹之间存在交点,这说明杂波空时特性与距离相关;从图中还可以看出位于收发平台基线延长线两端的多普勒频率变化较快,而平台之间的多普勒频率变化较缓慢.从图 6(b)和图(c)中可看出,杂波谱分布和多普勒曲线基本是一致的;杂波的空时分布随着双基距离和变化而变化,导致杂波空时分布不再满足独立同分布条件,有距离依赖性.从图 6(b)可发现,双基距离和越小,杂波的角度多普勒迹间隔越大,其多普勒频率随距离变化越大,距离相关性越强;随双基距离和增大,杂波的角度多普勒迹逐渐接近,且杂波谱中心逐渐重合,即随观测距离和增大,杂波特性的距离依赖性减弱.现将不同双基距离和杂波谱中心轨迹距离的数值列表如表 4,定量分析各场景中心距离,进一步说明随双基距离和增大,杂波的距离依赖性减弱.

|
图 6 航向一致时仿真 Fig. 6 Simulation diagram when the heading is consistent |
| 表 4 不同双基距离和杂波谱中心距离 Tab. 4 Different bistatic distances and clutter center distances |
2) 收发平台航向平行.航向平行时,收发平台均沿基线法线方向飞行,基线距离不变,其IsoDop迹、IsoBeam迹和双基距离和单元以及角度多普勒迹和空时二维杂波谱如图 7所示.从图 7(a)中可以看出,IsoDop迹以双基基线的垂直平分线为对称轴,成变形双曲线分布,由于基线方向上杂波点相对收发平台的径向速度为零,故其上各双基距离和单元杂波回波的多普勒频率为零;IsoBeam迹则为双曲线分布,其对称轴为接收机速度矢量.如图 7(b)和(c)中所示,由于IsoDop迹是关于基线的垂直平分线对称,关于接收机的航线非对称,使得前向和后向接收的杂波分布不一致,角度多普勒迹为封闭曲线,除在零多普勒频率外,杂波分布在距离维上扩散,双基距离和越小,分散越明显,随双基距离和增大,距离相关性减弱.

|
图 7 航向平行时仿真 Fig. 7 Simulation diagram when the heading is parallel |
3) 收发平台航向垂直.航向垂直时,接收平台沿基线飞行靠近发射机平台,发射机沿基线法线方向飞行,其IsoDop迹、IsoBeam迹和双基距离和单元以及角度多普勒迹和空时二维杂波谱如图 8所示.从图 8(a)中可以看出,IsoBeam迹为双曲线分布,其对称轴为基线;IsoDop迹非对称,且在发射机一侧与IsoBeam迹交点较多,则杂波特性与距离相关性较强.如图 8(b)和(c)中所示,杂波多普勒迹的前后瓣不对称,且曲线封闭,双基距离和越小,多普勒分散越明显,双基距离和越大,杂波谱中心越靠近,杂波特性的距离相关性减弱.

|
图 8 航向垂直时仿真 Fig. 8 Simulation diagram when heading is vertical |
4) 收发平台航向相交.航向相交时,接收平台与发射机平台航线相交,其IsoDop迹、IsoBeam迹和双基距离和单元以及角度多普勒迹和空时二维杂波谱如图 9所示.从图 9(a)中可以看出,IsoDop迹非对称,且在发射机一侧与IsoBeam迹交点较多,交点越多,则杂波特性与距离相关性越严重.如图 9(b)和(c)中所示,杂波多普勒迹曲线封闭,相互之间较为分散,随着双基距离和增大,杂波多普勒迹的分别越来越接近,杂波谱中心越靠近,杂波特性的距离相关性减弱.

|
图 9 航向相交时仿真 Fig. 9 Simulation diagram when heading intersects |
本文以机载双基地雷达系统的一般场景为研究对象,构建了场景的几何模型,利用欧拉坐标转换法推导了双基距离和单元的解析表达式,建立了实时的精确的数学模型,通过设置一般场景,进行数值仿真,得到双基距离和单元在大地固定坐标系水平面内成椭圆,验证了模型的正确性;通过分析了不同飞行配置情况下的机载双基雷达杂波特性,研究了杂波特性分布的距离依赖性,研究表明:四种飞行配置下,双基距离和越小,杂波的角度多普勒越分散,其多普勒频率随距离变化越快,距离相关性越强;而随双基距离和增大,杂波角度多普勒迹逐渐接近,杂波特性的距离依赖性相对减弱.本文建立的模型适用范围得到扩展,不仅限于特殊场景的应用,且相较时变坐标系,简化了运算过程,为机载双基地雷达杂波抑制的研究奠定了基础.
| [1] |
GELLI S, BACCI A, MARTORELLA M, et al. Clutter suppression and high resolution imaging of non-cooperative ground targets for bistatic airborne radar[J]. IEEE Transactions on Aerospace & Electronic Systems, 2018, 54(2): 932. DOI:10.1109/TAES.2017.2768918 |
| [2] |
杨予昊, 祝欢, 李思明. 高速机载雷达杂波特性分析与抑制方法研究[J]. 现代雷达, 2018, 40(3): 23. YANG Yuhao, ZHU Huan, LI Siming. Clutter properties analysis and suppression methods of high-speed airborne radar[J]. Modern Radar, 2018, 40(3): 23. DOI:10.16592/j.cnki.1004-7859.2018.03.006 |
| [3] |
JI Cunxiao, SHEN Mingwei, LIANG Chao, et al. An improved OMP application for airborne radar space-time clutter spectrum estimation[C]. International Conference on Intelligent Systems and Knowledge Engineering. Nanjing: IEEE, 2018: 24. DOI: 10.1109/ISKE.2017.8258837 10.1109/ISKE.2017.8258837
|
| [4] |
SUN Guohao, HE Zishu, TONG Jun, et al. Knowledge-aided covariance matrix estimation via Kronecker product expansions for airborne STAP[J]. IEEE Geoscience & Remote Sensing Letters, 2018, 15(4): 527. DOI:10.1109/LGRS.2018.2799329 |
| [5] |
MARTORELLA M, BERIZZI F, BACCI A, et al. Joint physical and virtual STAP for strong ground clutter suppression and imaging[C]//IEEE Radar Conference. Oklahoma, USA: IEEE, 2018: 0423. DOI: 10.1109/RADAR.2018.8378596 10.1109/RADAR.2018.8378596
|
| [6] |
BAI Gatai, TAO Ran, ZHAO Juan, et al. Fast FOCUSS method based on bi-conjugate gradient and its application to space-time clutter spectrum estimation[J]. Science China (Information Sciences), 2017, 60(8): 163. DOI:10.1007/s11432-015-1016-x |
| [7] |
KLEMM R. Comparison between monostatic and bistatic antenna configurations for STAP[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 596. DOI:10.1109/7.845248 |
| [8] |
ZHANG Yuhong, HIMED B. Effects of geometry on clutter characteristics of bistatic radars[C]. IEEE Radar Conference. Huntsville, Alabama, USA: IEEE, 2003: 417. DOI: 10.1109/NRC.2003.1203435 10.1109/NRC.2003.1203435
|
| [9] |
王永良, 魏进武, 陈建文. 双基地机载预警雷达空时二维杂波建模及杂波特性分析[J]. 电子学报, 2001(z1): 1940. WANG Yongliang, WEI Jinwu, CHEN Jianwen. Modelling and characteristics analysis of two-dimensional space-time clutter for bistatic airborne early warning radar[J]. Acta Electronica Sinica, 2001(z1): 1940. DOI:10.3321/j.issn:0372-2112.2001.z1.052 |
| [10] |
吴洪, 王永良. 双基地机载预警雷达杂波建模与分析[J]. 电子学报, 2006, 34(12): 2209. WU Hong, WANG Yongliang. Modeling and analysis of the ground clutter spectrum on bistatic airborne early warning radar[J]. Acta Electronica Sinica, 2006, 34(12): 2209. DOI:10.3321/j.issn:0372-2112.2006.12.018 |
| [11] |
彭晓瑞, 谢文冲, 王永良. 双基地机载雷达杂波建模及仿真分析[J]. 系统仿真学报, 2011, 23(2): 257. PENG Xiaorui, XIE Wenchong, WANG Yongliang. Modeling and simulation of clutter for bistatic airborne radar[J]. Journal of System Simulation, 2011, 23(2): 257. DOI:10.16182/j.cnki.joss.2011.02.005 |
| [12] |
魏民, 李小波, 黄中瑞. 机载双基地雷达杂波距离依赖补偿方法[J]. 信号处理, 2017, 33(1): 18. WEI Min, LI Xiaobo, HUANG Zhongrui. A compensation method for clutter range-dependence of airborne bistatic radar[J]. Journal of Signal Processing, 2017, 33(1): 18. DOI:10.16798/j.issn.1003-0530.2017.01.003 |
| [13] |
DUAN Rui, WANG Xuegang, JIANG Chaoshu, et al. Space-time clutter model for airborne bistatic radar with non-Gaussian statistics[J]. Journal of Systems Engineering and Electronics, 2009, 20(2): 283. |
| [14] |
王成浩, 廖桂生, 许京伟, 等. 超长基线双基机载雷达空时杂波建模与特性[J]. 系统工程与电子技术, 2016, 38(10): 2258. WANG Chenghao, LIAO Guisheng, XU Jingwei, et al. Modeling and characteristics analysis of space-time clutter for ultralong baseline bistatic airborne radar[J]. Systems Engineering and Electronics, 2016, 38(10): 2258. DOI:10.3969/j.issn.1001-506X.2016.10.06 |
| [15] |
MORCHIN W C. Airborne early warning radar[M]. London, Boston, USA: Artech House, 1990: 141.
|
 2019, Vol. 51
2019, Vol. 51


