2. 陆军步兵学院 基础部, 南昌 330000;
3. 陆军工程大学军械士官学校 基础部, 武汉 430075
2. Department of Basic Course, Army Infantry Academy, Nanchang 330000, China;
3. Department of Basic Course, Army Engineering University Ordnance Sergeant School, Wuhan 430075, China
随着材料制备工艺的不断完善,为了从本质上改进陶瓷材料的脆性,构成材料的基本组织从单相晶粒过渡到复合晶粒,这样在复合材料内出现了两类界面:一是复合晶粒之间的细观界面;二是复合晶粒内增强纤维与基体间的纳观界面.其中,复合晶粒之间的细观界面为物理连接的接触界面,复合晶粒内增强纤维和基体间的纳观界面为化学键结合界面.细观界面的物理连接特征使复相陶瓷具有较高的断裂韧性,纳观界面的化学键结合特性使复相陶瓷具有较高的高温和室温断裂强度[1-5].显然,复合材料的力学性能与两类界面密切相关,本文侧重分析纳观界面效应.
纳观界面具有强连接特性,计算复合晶粒弹性模量及平均应力场时可忽略应力集中的影响看作完全结合界面[6-7].但是分析复合晶粒断裂必须考虑应力集中效应.由于复合晶粒的破坏为垂直晶轴方向的断裂[8],类似于纤维增强复合材料的横向破坏,所以纤维增强复合材料在横向载荷作用下的界面处应力集中分析方法可以为本研究提供重要的参考.为了描述纤维增强复合材料内纤维与基体间界面的影响,有三类界面模型,其中线弹簧模型[9-10]和类位错模型[11-12]都认为界面处应力连续而位移不连续.线弹簧模型认为界面处位移的突变量与界面处应力成正比,比例系数类似于弹簧常数,很多研究者用此模型研究了界面切向自由滑动[13-14].类位错模型在界面处的应力边界条件与线弹簧模型相同,认为界面两侧的位移不等但是基体在界面处的位移与纤维在界面处的位移成正比,用此模型可研究复合材料内非完全结合界面的应力应变场.另一类界面应力模型认为界面上位移连续应力不连续[15],研究者用此模型预测了含有球形夹杂的非均匀材料的等效模量以及具有单向排列圆柱孔道的纳米介孔材料的弹性模量.黄争鸣等[16-17]计算了纤维增强复合材料内非完全结合界面产生的应力集中因子,并分析了横观各向同性纤维与各向同性基体之间的界面效应.上述分析应力集中因子的基本方法为研究复合晶粒的纳观界面行为奠定了基础.
但是将线弹簧模型和类位错模型应用于纳观界面存在两大问题:一是这两个模型认为基体的远场应力为复合材料的载荷,没有考虑纤维之间的相互作用;二是这两个模型认为界面处应力连续而位移不连续,是描述一般非完全结合界面的合适方法,但是对于具有强连接特性的纳观界面不能直接应用[18-20].而将界面应力模型用于复合晶体的纳观界面也出现了不合理现象,位移函数无法满足复合晶体的边界条件.其原因是纳观界面为完全结合界面,不仅位移连续应力也要保持连续.
为此,本文首先充分考虑纳米纤维间的相互作用,应用有效自洽法确定纳观界面模型的有效应力场,将有效应力作为复合晶粒内基体的远场应力.然后借鉴纤维复合材料承受横向载荷的位移函数,为保证强连接特性,假设纳观界面处基体和纤维的应力和位移均连续(应变不连续),确定纳观界面附近基体和纤维的应力应变场.最后基于界面附近基体应力场,计算纳观界面产生的应力集中因子,综合考虑复合晶粒内位错塞积和纳观界面的应力集中效应,建立复合晶粒的断裂应力预报模型.
1 复合晶粒内纳观界面应力场Al2O3-ZrO2共晶陶瓷是一类典型的含双尺度界面纤维增强复合材料,其在细观尺度上存在复合晶粒间弱连接的细观界面,而在纳观尺度上存在复合晶粒内增强纤维与基体间强连接的纳观界面[21-23],见图 1.为分析纳观界面效应,基于Al2O3-ZrO2共晶陶瓷微观结构特征,建立纤维增强复合材料中复合晶粒的理论结构模型.

|
图 1 共晶复合陶瓷显微结构扫描电镜 Fig. 1 SEM of eutectic multiphase ceramics |
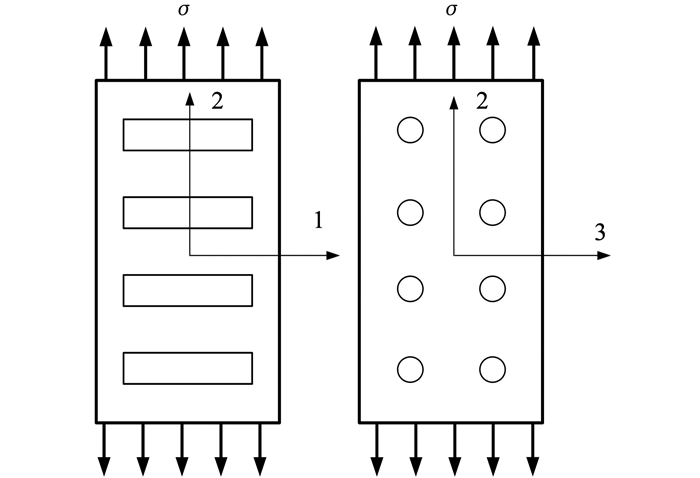
复合晶粒的主要破坏模式为垂直晶轴方向断裂,也就是使其破坏的主要因素为沿晶轴方向的拉应力,所以本文分析复合晶粒承受沿晶轴方向的拉应力作用时的纳观界面应力场.为研究方便,在复合晶粒处建立细观坐标系,见图 2,假设坐标轴1与增强纤维轴向平行,坐标轴2沿晶粒的晶轴方向,坐标轴3与坐标轴1和2垂直,则拉应力沿坐标轴2方向.
|
图 2 单向拉伸载荷作用下的复合晶粒 Fig. 2 Composite grain subjected to a uniaxial load |
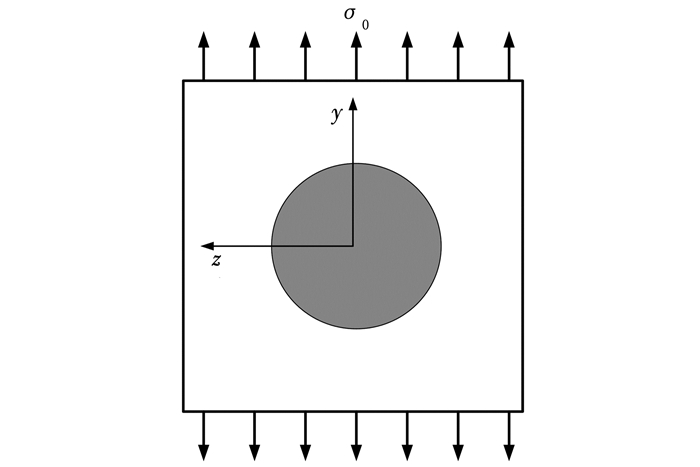
首先在复合晶粒内选取含单个增强纤维的纳观界面模型见图 3,其中增强纤维为具有纳米/亚微米尺度的各向同性体,增强纤维与基体间的界面为化学键连接的纳观界面.若将纤维看作具有一定体积分量的平行分布在基体内的夹杂,根据有效自洽法[24]可知,纤维对应的远场有效应力张量σ0与复合晶粒的外载应力张量σ关系为
|
图 3 单向拉伸应力状态下的纳观界面模型 Fig. 3 Nano-interface model subjected to a uniaxial tension |
| $ {\mathit{\boldsymbol{\sigma }}_0} = {\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{D}}}\mathit{\boldsymbol{H}}} \right)^{ - 1}}\mathit{\boldsymbol{\sigma }}. $ | (1) |
式中:I为单位张量,ΩD为有效介质(有效介质为横观各向同性体,具有复合晶粒的弹性性能)的本征刚度,H为有效介质相对复合晶粒基体的柔度增量张量,由文献[25]的公式计算.当复合晶粒承受单向拉伸载荷时,虽然有效应力场为复杂应力状态,但是主要应力为沿载荷方向的有效拉应力,其它应力分量与之相比小得多(相差3个数量级)[26],图 3中纳观界面模型可近似看作单向应力状态,其单向拉伸应力可表示为
| $ {\sigma _0} = {s_{22}}\mathit{\boldsymbol{\sigma }}. $ | (2) |
式中:比例系数s22与复合晶粒内基体、纤维和有效介质的弹性常数以及纤维的分布形式和体积分量有关[26].并且相对于纤维而言,σ0可看作无穷远处的应力.
纳观界面具有强约束化学键结合特性,可看作完全结合界面,即界面处位移和应力均连续.单向拉伸应力状态问题可以通过叠加法求解,即将单向拉伸应力状态分解为双向拉伸应力状态与纯剪切应力状态的组合.下面分别研究双向拉伸应力状态与纯剪切应力状态的纳观界面应力场.
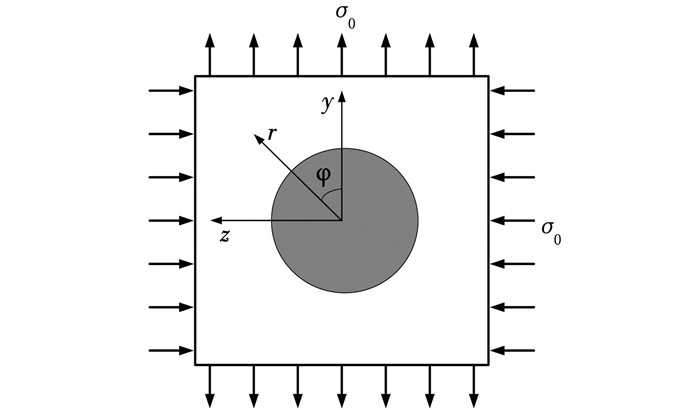
1.1 双向均匀拉伸应力状态下的纳观界面应力场如果纳观界面模型处于双向均匀拉伸应力状态见图 4,与纤维增强复合材料内含同向平行纤维的情况类似,可借鉴纤维增强复合材料承受横向载荷时的位移函数选取方法[25].若纤维中心为纳观坐标系原点,则在纳观柱坐标系下,纤维和基体内的纳观位移场可表示为:

|
图 4 双向拉伸应力状态下的纳观界面模型 Fig. 4 Nano-interface model subjected to a biaxial tension |
| $ \left\{ \begin{array}{l} u_x^{{\rm{f1}}} = x\varepsilon _x^0,\;\;\;\;u_r^{{\rm{f1}}} = {A_{{\rm{f1}}}}r,\;\;\;\;u_\varphi ^{{\rm{f1}}} = 0;\\ u_x^{{\rm{m1}}} = x\varepsilon _x^0,\;\;\;\;u_r^{{\rm{m1}}} = {A_{{\rm{m1}}}}r + \frac{{{B_{{\rm{m1}}}}}}{r},\;\;\;\;u_\varphi ^{{\rm{m1}}} = 0. \end{array} \right. $ | (3) |
式中:x为沿纤维轴线的坐标,r和φ为垂直纤维的平面极坐标;εx0为外载作用下复合晶粒沿纤维方向的线应变.Af1,Am1,Bm1为待定常数.
根据几何方程可得纤维和基体内的应变场,根据物理方程可得纤维和基体内的应力场(仅表示出非零项):
| $ \left\{ \begin{array}{l} \sigma _x^{{\rm{f1}}} = C_{11}^{\rm{f}}\varepsilon _x^0 + 2C_{12}^{\rm{f}}{A_{{\rm{f1}}}},\\ \sigma _r^{{\rm{f1}}} = C_{11}^{\rm{f}}{A_{{\rm{f1}}}} + C_{12}^{\rm{f}}\left( {\varepsilon _x^0 + {A_{{\rm{f1}}}}} \right),\\ \sigma _\varphi ^{{\rm{f1}}} = C_{11}^{\rm{f}}{A_{{\rm{f1}}}} + C_{12}^{\rm{f}}\left( {\varepsilon _x^0 + {A_{{\rm{f1}}}}} \right). \end{array} \right. $ | (4) |
| $ \left\{ \begin{array}{l} \sigma _x^{m1} = C_{11}^m\varepsilon _x^0 + 2C_{12}^m{A_{{\rm{m1}}}},\\ \sigma _r^{m1} = C_{12}^m\varepsilon _x^0 + \left( {C_{11}^{\rm{m}} + C_{12}^{\rm{m}}} \right){A_{{\rm{m1}}}} + \left( {C_{12}^{\rm{m}} - C_{11}^{\rm{m}}} \right)\frac{{{B_{{\rm{m1}}}}}}{{{r^2}}},\\ \sigma _\varphi ^{m1} = C_{12}^m\varepsilon _x^0 + \left( {C_{11}^{\rm{m}} + C_{12}^{\rm{m}}} \right){A_{{\rm{m1}}}} + \left( {C_{11}^{\rm{m}} - C_{12}^{\rm{m}}} \right)\frac{{{B_{{\rm{m1}}}}}}{{{r^2}}}. \end{array} \right. $ | (5) |
式中:Cijf和Cijm分别为纤维和基体的刚度矩阵分量,i=1,2,3分别代表x,r,φ.
根据在无穷远处的应力条件可知
| $ \sigma _r^{{\rm{m1}}}\left| {_{r \to \infty }} \right. = {\sigma _0}. $ | (6) |
纳观界面完全结合,位移和应力连续,则有
| $ u_r^{{\rm{m1}}}\left| {_{r = a}} \right. = u_r^{{\rm{f1}}}\left| {_{r = a}} \right., $ | (7) |
| $ \sigma _r^{{\rm{m1}}}\left| {_{r = a}} \right. = \sigma _r^{{\rm{f1}}}\left| {_{r = a}} \right.. $ | (8) |
根据式(6)~(8)得到如下方程组:
| $ \left\{ \begin{array}{l} \left( {C_{11}^{\rm{m}} + C_{12}^{\rm{m}}} \right){A_{{\rm{m1}}}} = {\sigma _0} - C_{12}^{\rm{m}}\varepsilon _x^0,\\ a{A_{{\rm{m1}}}} + \frac{1}{a}{B_{{\rm{m1}}}} - a{A_{{\rm{f1}}}} = 0,\\ \left( {C_{11}^{\rm{m}} + C_{12}^{\rm{m}}} \right){A_{{\rm{m1}}}} + \frac{1}{{{a^2}}}\left( {C_{12}^{\rm{m}} - C_{11}^{\rm{m}}} \right){B_{{\rm{m1}}}} - \\ \left( {C_{11}^{\rm{f}} + C_{12}^{\rm{f}}} \right){A_{{\rm{f1}}}} = C_{12}^{\rm{f}}\varepsilon _x^0 - C_{12}^{\rm{m}}\varepsilon _x^0. \end{array} \right. $ | (9) |
显然在外载确定的条件下,σ0和εx0很容易计算出来,进而根据方程组(9)计算出Af1,Am1和Bm1.将Af1,Am1和Bm1代入式(3)~(5)即可完全确定双向均匀拉伸应力作用下的纳观位移场和应力场.在双向均匀拉伸应力作用下,纤维内应力为常量,基体内平行纤维轴向的应力为常量、垂直纤维轴向的应力随点的位置而发生变化.
1.2 纯剪切应力状态下的纳观应力场纯剪切应力状态既是剪切载荷作用下常见形式,又是复杂应力状态的基本组成部分.对于图 5中纯剪应力状态,在纳观柱坐标系下,纤维和基体内的纳观位移场可表示为[17]:
|
图 5 纯剪切应力状态下的纳观界面模型 Fig. 5 Nano-interface model subjected to a pure shear stress |
| $ \left\{ \begin{array}{l} u_x^{{\rm{f2}}} = 0,\\ u_{\rm{r}}^{{\rm{f2}}} = \frac{{a{\sigma _0}}}{{4{G_{\rm{f}}}}}\left[ {{A_{f{\rm{2}}}}\left( {\frac{r}{a}} \right) + {B_{{\rm{f2}}}}\left( {{\eta _{\rm{f}}} - 3} \right){{\left( {\frac{r}{a}} \right)}^3}} \right]\cos 2\varphi ,\\ u_\varphi ^{{\rm{f2}}} = \frac{{a{\sigma _0}}}{{4{G_{\rm{f}}}}}\left[ { - {A_{f{\rm{2}}}}\left( {\frac{r}{a}} \right) + {B_{{\rm{f2}}}}\left( {{\eta _{\rm{f}}} + 3} \right){{\left( {\frac{r}{a}} \right)}^3}} \right]\sin 2\varphi . \end{array} \right. $ | (10) |
| $ \left\{ \begin{array}{l} u_x^{{\rm{m2}}} = 0,\\ u_{\rm{r}}^{{\rm{m2}}} = \frac{{a{\sigma _0}}}{{4{G_{\rm{m}}}}}\left[ \begin{array}{l} 2\left( {\frac{r}{a}} \right) + {A_{{\rm{m2}}}}\left( {{\eta _{\rm{m}}} + 1} \right)\left( {\frac{a}{r}} \right) + \\ {B_{{\rm{m2}}}}{\left( {\frac{a}{r}} \right)^3} \end{array} \right]\cos 2\varphi ,\\ u_\varphi ^{{\rm{m2}}} = \frac{{a{\sigma _0}}}{{4{G_{\rm{m}}}}}\left[ \begin{array}{l} - 2\left( {\frac{r}{a}} \right) - {A_{{\rm{m2}}}}\left( {{\eta _{\rm{m}}} - 1} \right)\left( {\frac{a}{r}} \right) + \\ {B_{{\rm{m2}}}}{\left( {\frac{a}{r}} \right)^3} \end{array} \right]\sin 2\varphi . \end{array} \right. $ | (11) |
式中:Af2、Bf2、Am2和Bm2为待定常数.ηf=3-4υf,ηm=3-4υm,υf和υm分别为纤维和基体的泊松比,Gf和Gm分别为纤维和基体的剪变模量.
根据几何方程可得纤维和基体内的应变场,根据物理方程可得纤维和基体内的应力场(仅给出非零项):
| $ \left\{ \begin{array}{l} \sigma _x^{{\rm{f2}}} = \frac{{C_{12}^{\rm{f}}{\sigma _0}}}{{4{G_{\rm{f}}}}}\left[ {{A_{{\rm{f2}}}} + {B_{{\rm{f2}}}}\left( {5{\eta _{\rm{f}}} - 9} \right)\left( {\frac{{{r^2}}}{{{a^2}}}} \right)} \right]\cos 2\varphi ,\\ \sigma _{\rm{r}}^{{\rm{f2}}} = \frac{{{\sigma _0}}}{{4{G_{\rm{f}}}}}\left[ {C_{11}^{\rm{f}}{A_{{\rm{f2}}}} + {B_{{\rm{f2}}}}\left\{ \begin{array}{l} \left( {2C_{12}^{\rm{f}} + 3C_{11}^{\rm{f}}} \right)\\ {\eta _{\rm{f}}} - 9C_{11}^{\rm{f}} \end{array} \right\}\left( {\frac{{{r^2}}}{{{a^2}}}} \right)} \right]\cos 2\varphi ,\\ \sigma _\varphi ^{{\rm{f2}}} = \frac{{{\sigma _0}}}{{4{G_{\rm{f}}}}}\left[ {C_{12}^{\rm{f}}{A_{{\rm{f2}}}} + {B_{{\rm{f2}}}}\left\{ \begin{array}{l} \left( {2C_{11}^{\rm{f}} + 3C_{12}^{\rm{f}}} \right)\\ {\eta _{\rm{f}}} - 9C_{12}^{\rm{f}} \end{array} \right\}\left( {\frac{{{r^2}}}{{{a^2}}}} \right)} \right]\cos 2\varphi ,\\ \tau _{{\rm{r}}\varphi }^{{\rm{f2}}} = \frac{{{\sigma _0}}}{4}\left[ { - {A_{{\rm{f2}}}} + {B_{{\rm{f2}}}}\left( {{\eta _{\rm{f}}} + 9} \right)\left( {\frac{{{r^2}}}{{{a^2}}}} \right)} \right]\sin 2\varphi . \end{array} \right. $ | (12) |
| $ \left\{ \begin{array}{l} \sigma _x^{{\rm{m2}}} = \frac{{{\sigma _0}}}{{4{G_{\rm{m}}}}}\left[ \begin{array}{l} \left. {2C_{12}^{\rm{m}} - {A_{{\rm{m2}}}}C_{12}^{\rm{m}}\left( {{\eta _{\rm{m}}} - 1} \right)} \right\}\\ \left( {\frac{{{a^2}}}{{{r^2}}}} \right) - {B_{{\rm{m2}}}}C_{12}^{\rm{m}}\left( {\frac{{{a^4}}}{{{r^4}}}} \right) \end{array} \right]\cos 2\varphi ,\\ \sigma _r^{{\rm{m2}}} = \frac{{{\sigma _0}}}{{4{G_{\rm{m}}}}}\left[ \begin{array}{l} 2C_{11}^{\rm{m}} + {A_{{\rm{m2}}}}\left\{ {2C_{12}^{\rm{m}} - C_{11}^{\rm{m}}\left( {{\eta _{\rm{m}}} + 1} \right)} \right\}\\ \left( {\frac{{{a^2}}}{{{r^2}}}} \right) + {B_{{\rm{m2}}}}\left( {2C_{12}^{\rm{m}} - 3C_{11}^{\rm{m}}} \right)\left( {\frac{{{a^4}}}{{{r^4}}}} \right) \end{array} \right]\cos 2\varphi ,\\ \sigma _\varphi ^{{\rm{m2}}} = \frac{{{\sigma _0}}}{{4{G_{\rm{m}}}}}\left[ \begin{array}{l} 2C_{12}^{\rm{m}} + {A_{{\rm{m2}}}}\left\{ {2C_{11}^{\rm{m}} - C_{12}^{\rm{m}}\left( {{\eta _{\rm{m}}} + 1} \right)} \right\}\\ \left( {\frac{{{a^2}}}{{{r^2}}}} \right) + {B_{{\rm{m2}}}}\left( {2C_{11}^{\rm{m}} - 3C_{12}^{\rm{m}}} \right)\left( {\frac{{{a^4}}}{{{r^4}}}} \right) \end{array} \right]\cos 2\varphi ,\\ \tau _{r\varphi }^{{\rm{m2}}} = \frac{{{\sigma _0}}}{4}\left[ { - 2 + {A_{{\rm{m2}}}}\left( {{\eta _{\rm{m}}} - 3} \right)\left( {\frac{{{a^2}}}{{{r^2}}}} \right) - 5{B_{{\rm{m2}}}}\left( {\frac{{{a^4}}}{{{r^4}}}} \right)} \right]\sin 2\varphi . \end{array} \right. $ | (13) |
应力场表达式(13)显然满足无穷远处的应力条件:
| $ \sigma _r^{{\rm{m2}}}\left| {_{\begin{array}{*{20}{c}} {r \to \infty }\\ {\varphi = 0} \end{array}}} \right.\frac{{C_{11}^{\rm{m}}}}{{2{G_{\rm{m}}}}}{\sigma _0} = {\sigma _0}, $ | (14) |
| $ \sigma _r^{{\rm{m2}}}\left| {_{\begin{array}{*{20}{c}} {r \to \infty }\\ {\varphi = \pi /2} \end{array}}} \right. = - \frac{{C_{11}^{\rm{m}}}}{{2{G_{\rm{m}}}}}{\sigma _0} = {\sigma _0}. $ | (15) |
根据纳观界面完全结合条件,则有:
| $ u_{\rm{r}}^{{\rm{m2}}}\left| {_{r = a}} \right. = u_{\rm{r}}^{{\rm{f2}}}\left| {_{r = a}} \right., $ | (16) |
| $ u_\varphi ^{{\rm{m2}}}\left| {_{r = a}} \right. = u_\varphi ^{{\rm{f2}}}\left| {_{r = a}} \right., $ | (17) |
| $ \sigma _r^{{\rm{m2}}}\left| {_{r = a}} \right. = \sigma _r^{{\rm{f2}}}\left| {_{r = a}} \right., $ | (18) |
| $ \tau _{r\varphi }^{{\rm{m2}}}\left| {_{r = a}} \right. = \tau _{r\varphi }^{{\rm{f2}}}\left| {_{r = a}} \right.. $ | (19) |
得到如下方程组:
| $ \left\{ \begin{array}{l} \frac{{{G_{\rm{m}}}}}{{{G_{\rm{f}}}}}{A_{{\rm{f2}}}} + \frac{{{G_{\rm{m}}}}}{{{G_{\rm{f}}}}}\left( {{\eta _{\rm{f}}} - 3} \right){B_{{\rm{f2}}}} - \left( {{\eta _{\rm{m}}} + 1} \right){A_{{\rm{m2}}}} - {B_{{\rm{m2}}}} = 2,\\ - \frac{{{G_{\rm{m}}}}}{{{G_{\rm{f}}}}}{A_{{\rm{f2}}}} + \frac{{{G_{\rm{m}}}}}{{{G_{\rm{f}}}}}\left( {{\eta _{\rm{f}}} + 3} \right){B_{{\rm{f2}}}} + \left( {{\eta _{\rm{m}}} - 1} \right){A_{{\rm{m2}}}} - {B_{{\rm{m2}}}} = - 2,\\ \frac{{{G_{\rm{m}}}}}{{{G_{\rm{f}}}}}C_{11}^{\rm{f}}{A_{{\rm{f2}}}} + \frac{{{G_{\rm{m}}}}}{{{G_{\rm{f}}}}}\left[ {\left( {2C_{12}^{\rm{f}} + 3C_{11}^{\rm{f}}} \right){\eta _{\rm{f}}} - 9C_{11}^{\rm{f}}} \right]{B_{{\rm{f2}}}} - \\ \left[ {2C_{12}^{\rm{m}} - C_{11}^{\rm{m}}\left( {{\eta _{\rm{m}}} + 1} \right)} \right]{A_{{\rm{m2}}}} - \left( {2C_{12}^{\rm{m}} - 3C_{11}^{\rm{m}}} \right){B_{{\rm{m2}}}} = 2C_{11}^{\rm{m}},\\ - {A_{{\rm{f2}}}} + \left( {{\eta _{\rm{f}}} + 9} \right){B_{{\rm{f2}}}} - \left( {{\eta _{\rm{m}}} - 3} \right){A_{{\rm{m2}}}} + 5{B_{{\rm{m2}}}} = - 2. \end{array} \right. $ | (20) |
根据方程组(20)计算出Am2、Bm2、Af2和Bf2.将Am2、Bm2、Af2和Bf2代入表达式(10)~(13)即可完全确定纯剪切应力状态下的纳观位移场和应力场.可以看出在纯剪切应力作用下,纤维和基体内的应力都随点的位置而发生变化.
1.3 单向拉伸应力状态下的纳观应力场显然双向均匀拉伸与纯剪切应力状态的叠加就是单向拉伸应力状态,所以单向拉伸应力状态下增强纤维和基体的应力场可表示为:
| $ \left\{ \begin{array}{l} \sigma _x^{\rm{f}} = \frac{1}{2}\left( {\sigma _x^{{\rm{f1}}} + \sigma _x^{{\rm{f2}}}} \right),\\ \sigma _r^{\rm{f}} = \frac{1}{2}\left( {\sigma _r^{{\rm{f1}}} + \sigma _r^{{\rm{f2}}}} \right),\\ \sigma _\varphi ^{\rm{f}} = \frac{1}{2}\left( {\sigma _\varphi ^{{\rm{f1}}} + \sigma _\varphi ^{{\rm{f2}}}} \right),\\ \tau _{r\varphi }^{\rm{f}} = \frac{{\tau _{r\varphi }^{{\rm{f2}}}}}{2}. \end{array} \right. $ | (21) |
| $ \left\{ \begin{array}{l} \sigma _x^{\rm{m}} = \frac{1}{2}\left( {\sigma _x^{{\rm{m1}}} + \sigma _x^{{\rm{m2}}}} \right),\\ \sigma _r^{\rm{m}} = \frac{1}{2}\left( {\sigma _r^{{\rm{m1}}} + \sigma _r^{{\rm{m2}}}} \right),\\ \sigma _\varphi ^{\rm{m}} = \frac{1}{2}\left( {\sigma _\varphi ^{{\rm{m1}}} + \sigma _\varphi ^{{\rm{m2}}}} \right),\\ \tau _{r\varphi }^{\rm{m}} = \frac{{\tau _{r\varphi }^{{\rm{m2}}}}}{2}. \end{array} \right. $ | (22) |
当复合晶粒内纤维为同向平行分布时,纤维方向与晶轴方向垂直,此时,σ0=s22σ,εx0=
因为复合晶粒内分布有多个纤维,每个纤维与基体连接的纳观界面都产生应力集中效应,所以需要综合考虑纳观界面对复合晶粒的应力集中影响,此影响用应力集中因子表示.
根据应力坐标转换公式,可知复合晶粒基体沿y方向的应力为
| $ \sigma _{\rm{y}}^{\rm{m}} = \sigma _{\rm{r}}^{\rm{m}}{\cos ^2}\varphi + \sigma _\varphi ^{\rm{m}}{\sin ^2}\varphi - \tau _{{\rm{r}}\varphi }^{\rm{m}}\sin 2\varphi . $ | (23) |
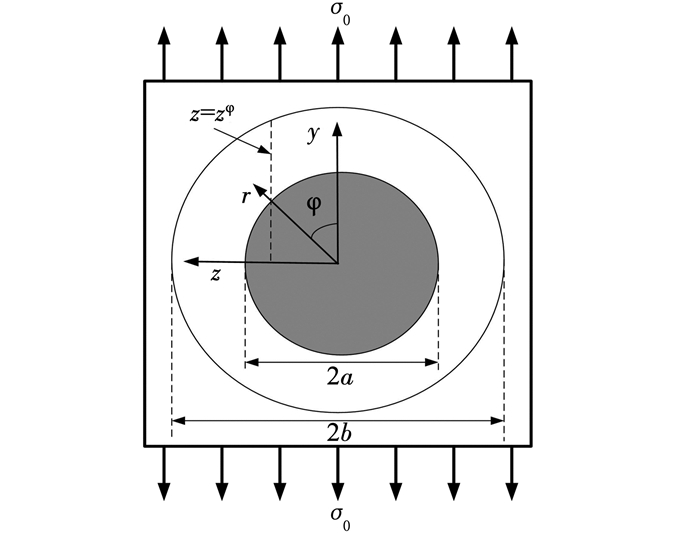
当复合晶粒沿晶轴方向承受单向拉伸载荷时,见图 6,与同向平行纤维复合材料承受横向拉伸载荷类似,采用类似的应力集中因子确定方法[17]
|
图 6 单向拉伸状态下的纳观界面模型 Fig. 6 Nano-interface model subjected to a uniaxial tension |
| $ K = {K^{\rm{I}}} \times {K^{{\rm{II}}}}. $ | (24) |
其中:
| $ {K^{\rm{I}}} = \max \left\{ {K_\varphi ^{\rm{I}},{0^ \circ } \le \varphi \le {{90}^ \circ }} \right\}, $ | (25) |
| $ K_\varphi ^{\rm{I}} = \frac{1}{{{y^{\rm{b}}} - {y^{\rm{a}}}}}\int\limits_{{y^{\rm{a}}}}^{{y^{\rm{b}}}} {\frac{{\sigma _{\rm{y}}^{\rm{m}}}}{{{\sigma _0}}}\left| {_{z = {z^\varphi }}} \right.{\rm{d}}y} , $ | (26) |
| $ {K^{{\rm{II}}}} = \frac{{{{\left( {\sigma _{\rm{y}}^{\rm{m}}} \right)}_{{\rm{avg}}}}}}{{{{\left( {\sigma _{\rm{y}}^{\rm{m}}} \right)}_{\rm{b}}}}} = \frac{{\frac{1}{{{\rm{ \mathsf{ π} }}\left( {{b^2} - {a^2}} \right)}}\int\limits_0^{2{\rm{ \mathsf{ π} }}} {\int\limits_a^b {\sigma _{\rm{y}}^{\rm{m}}r{\rm{d}}r{\rm{d}}\varphi } } }}{{{{\left( {\sigma _{\rm{y}}^{\rm{m}}} \right)}_{\rm{b}}}}}. $ | (27) |
式中:ya=acos φ, zφ=asin φ, yb=
考虑应力集中因子后,沿载荷方向的有效应力分量变为
| $ {\sigma _1} = K{s_{22}}\sigma . $ | (28) |
位错塞积是复合晶粒断裂的另一要素.由于纳观界面的应力集中效应,使复合晶粒内纳观界面附近的应力分量变成了原来的K倍;应力增加促使基体内产生更多的位错,而纳观界面阻止了位错的运动,随着外载应力的增加,位错数目不断增加,进而在纳观界面处构成一个位错塞积群,位错塞积群在纳观界面进一步产生应力集中,而纳观界面本身的应力集中反过来又增强了位错塞积群的作用效应,也就是纳观界面和位错塞积相互影响,加剧了应力集中效应,使复合晶粒更容易断裂.
由于位错塞积的数目与外加切应力成正比,而位错数目的增加会增强界面处应力集中效应,所以位错塞积群的应力集中效应也与外加切应力成正比.位错塞积产生的最大拉应力为[27]
| $ {\mathit{\boldsymbol{\sigma }}_{\max }} = \frac{2}{{\sqrt 3 }}{\left( {\frac{{2a}}{s}} \right)^{\frac{1}{2}}}\left( {\mathit{\boldsymbol{\tau }} - {\mathit{\boldsymbol{\tau }}_i}} \right). $ | (29) |
式中:s为最大应力所在位置与领先位错的距离,τ为外加切应力,τi为晶格对位错运动的阻力.若忽略晶格对位错运动的阻力,根据式(13)和(22)可知,在纳观界面处并且与晶轴相差45°角方向的切应力达到最大值,由此得到复合晶粒沿载荷方向的有效应力分量为σ0时,最大拉应力表达式如下
| $ \sigma _{\max }^0 = \frac{{{\sigma _0}}}{{2\sqrt 6 }}{\left( {\frac{a}{s}} \right)^{\frac{1}{2}}}\left[ { - 2 + {A_{{\rm{m2}}}}\left( {{\eta _{\rm{m}}} - 3} \right) - 5{B_{{\rm{m2}}}}} \right]. $ | (30) |
如果考虑纳观界面的应力集中与位错塞积的共同影响,则可用式(28)的σ1替换上式的σ0,则上式转换为
| $ \sigma _{\max }^1 = \sigma \frac{{K{s_{22}}}}{{2\sqrt 6 }}{\left( {\frac{a}{s}} \right)^{\frac{1}{2}}}\left[ { - 2 + {A_{{\rm{m2}}}}\left( {{\eta _{\rm{m}}} - 3} \right) - 5{B^{{\rm{m2}}}}} \right]. $ | (31) |
复合晶粒的理论断裂强度为
| $ {\sigma _{th}} = {\left( {\frac{{{E_m}{\gamma _m}}}{c}} \right)^{\frac{1}{2}}}. $ | (32) |
式中:Em和γm分别为复合晶粒基体的弹性模量和自由表面能,c为晶格常数.因为纳观界面处为强化学键连接,所以纳观界面连接键不会断裂,而靠近纳观界面处的基体将发生破坏,即s=2c处破坏.令:σmax1=σth,根据方程(31)和(32)得复合晶粒的断裂应力为
| $ {\sigma _{{\rm{eu}}}} = \frac{4}{{K{s_{22}}\left[ { - 2 + {A_{{\rm{m2}}}}\left( {{\eta _{\rm{m}}} - 3} \right) - 5{B_{{\rm{m2}}}}} \right]}}{\left( {\frac{{3{E_m}{\gamma _m}}}{a}} \right)^{\frac{1}{2}}}. $ | (33) |
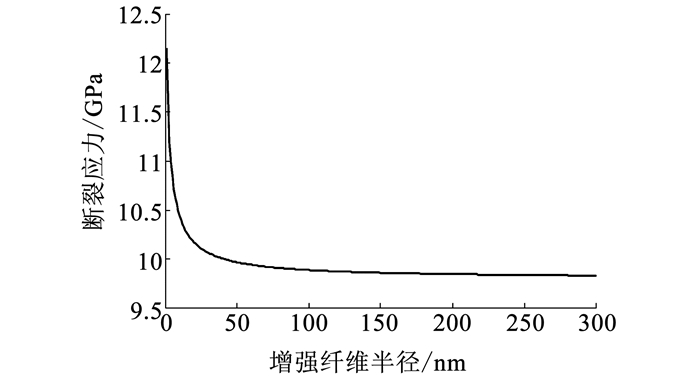
取纤维体积分数f=0.3,可得复合晶粒的断裂应力与增强纤维半径的关系见图 7.
|
图 7 断裂应力与纤维半径的关系 Fig. 7 Relationship between fracture stress and fiber radius |
图 7可看出,增强纤维半径较小时,复合晶粒的断裂应力随着纤维半径的增大迅速减小,当半径大于50 nm时,随着半径不断增大,复合晶粒的断裂应力变化趋于平缓.表明纤维半径越小,复合晶粒断裂应力越高,而纤维半径超过50 nm后,半径变化对复合晶粒断裂应力的影响较小.
取纤维半径a=50 nm,可得复合晶粒的断裂应力与增强纤维体积分数的关系见图 8.

|
图 8 断裂应力与纤维体积分数的关系 Fig. 8 Relationship between fracture stress and fiber volume fraction |
图 8可看出,复合晶粒的断裂应力随纤维体积分数的增大而不断减小.表明纤维体积分数较小时,复合晶粒强度更高,随着纤维体积分数不断增大,复合晶粒断裂应力减小,复合晶粒也越易发生破坏.
4 结论1) 充分考虑纳米纤维间的相互作用,应用有效自洽法,确定了纳观界面模型的有效应力场.将有效应力作为复合晶粒内基体的远场应力,参考纤维复合材料承受横向载荷的位移函数,应用纳观界面处的应力和位移连续性条件,确定了纳观界面附近基体和纤维的位移场、应变场和应力场.
2) 综合考虑了复合晶粒内位错塞积和纳观界面的应力集中效应,建立了复合晶粒的断裂应力预报模型并对断裂应力进行了定量分析,结果表明,纤维半径越小,复合晶粒强度越高,且纤维半径大于50 nm后,半径大小对复合晶粒断裂应力影响较小;纤维体积分数较小时,复合晶粒断裂应力更高,而纤维体积分数越大,复合晶粒越易发生破坏.
| [1] |
褚宗富, 翟慎秋, 丁锐, 等. 定向凝固氧化物共晶陶瓷的制备工艺与性能[J]. 中国陶瓷, 2017, 53(7): 8. CHU Zongfu, ZHAI Shenqiu, DING Rui, et al. Preparation technology and properties of directionally solidified oxides eutectic ceramics[J]. China Ceramics, 2017, 53(7): 8. DOI:10.16521/j.cnki.issn.1001-9642.2017.07.002 |
| [2] |
LIU Woye, ZHAO Zhongmin, ZHANG Long, et al. Microstructures and properties of large bulk Al2O3/ZrO2(Y2O3) prepared by SHS under high gravity[J]. International Journal of Self-Propagating High-Temperature Synthesis, 2009, 18(3): 180. DOI:10.3103/S106138620903008X |
| [3] |
ZHAO Zhongmin, ZHANG Long, SONG Yigang, et al. Al2O3/ZrO2(Y2O3) self-growing composites prepared by combustion synthesis under high gravity[J]. Scripta Materialia, 2008, 58(3): 207. DOI:10.1016/j.scriptamat.2007.09.051 |
| [4] |
付雪松, 孙胃涛, 韩文波, 等. 基于高温熔凝法Al2O3/ZrO2/YAG共晶陶瓷显微组织演变规律[J]. 材料工程, 2017, 45(2): 46. FU Xuesong, SUN Weitao, HAN Wenbo, et al. Microstructure evolution of melt-grown Al2O3/ZrO2/YAG eutectic ceramic by high temperature fused method[J]. Journal of Materials Engineering, 2017, 45(2): 46. DOI:10.11868/j.issn.1001-4381.2015.000555 |
| [5] |
YAO Bin, SU Haijun, ZHANG Jun, et al. Sintering densification and microstructure formation of bulk Al2O3/YAG eutectic ceramics by hot pressing based on fine eutectic structure[J]. Materials & Design, 2016, 92: 213. DOI:10.1016/j.matdes.2015.12.017 |
| [6] |
SHEN Lianxi, Takie Li. Effective elastic moduli of composites reinforced by particle or fiber with an inhomogeneous interphase[J]. International Journal of Solids and Structures, 2003, 40(6): 1393. DOI:10.1016/S0020-7683(02)00659-5 |
| [7] |
DUAN Huiling, WANG Jianxiang, HUANG Zhuping, et al. Stress concentration tensors of inhomogeneities with interface effects[J]. Mechanics of Materials, 2005, 37: 723. DOI:10.1016/j.mechmat.2004.07.004 |
| [8] |
HUANG Zhengmin, XIN Limin. In situ strengths of matrix in a composite[J]. Acta Mechanica Sinica, 2017, 33(1): 1. DOI:10.1007/s10409-016-0611-1 |
| [9] |
UPADHYAY P C. Stress concentration in the matrix with degraded fiber-matrix interfaces[J]. Journal of Composite Materials, 2006, 40(40): 1625. DOI:10.1177/0021998306060165 |
| [10] |
TAN Henry, HUANG Yingsheng, LIU Cheng, et al. The Mori-Tanaka method for composite materials with nonlinear interface debonding[J]. International Journal of Plasticity, 2005, 21(10): 1890. DOI:10.1016/j.ijplas.2004.10.001 |
| [11] |
YU H Y. A new dislocation-like model for imperfect interfaces and their effect on load transfer[J]. Composites Part A: Applied Science and Manufacturing, 1998, 29(9-10): 1057. DOI:10.1016/S1359-835X(98)00010-4 |
| [12] |
YU H Y, WEI Y N, CHIANG F P. Load transfer at imperfect interfaces-dislocation-like model[J]. International Journal of Engineering Science, 2002, 40(14): 1647. DOI:10.1016/S0020-7225(02)00028-9 |
| [13] |
HUANG J H, FURUHASHI R, MURA T. Frictional sliding inclusions[J]. Journal of the Mechanics and Physics of Solids, 1993, 41(2): 247. DOI:10.1016/0022-5096(93)90008-4 |
| [14] |
陈怀智, 仲政, 王旭. 反平面剪切作用下双材料滑动界面的细观力学模型[J]. 力学季刊, 2003, 24(2): 227. CHEN Huaizhi, ZHONG Zheng, WANG Xu. A mesomechanics model for sliding interface between bimaterials under antiplane shear[J]. Chinese Quarterly of Mechanics, 2003, 24(2): 227. DOI:10.15959/j.cnki.0254-0053.2003.02.012 |
| [15] |
段慧玲.非匀质材料力学中的界面效应[D].北京: 北京大学, 2005 DUAN Huiling. Interfacial effects in nonuniform material mechanics[D]. Beijing: Peking University, 2005 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y814153 |
| [16] |
HUANG Zhengming, LIU Ling. Predicting strength of fibrous laminates under triaxial loads only upon independently measured constituent properties[J]. International Journal of Mechanical Sciences, 2014, 79(1): 105. DOI:10.1016/j.ijmecsci.2013.08.010 |
| [17] |
YAO Zhan, HUANG Zhengming. Stress concentration factor in the matrix reinforced with fiber having an interface layer[J]. Journal of Reinforced Plastics & Composites, 2013, 32(2): 105. DOI:10.1177/0731684412453214 |
| [18] |
WANG Zhanjiang, YU Hao, WANG Qian. Layer-substrate system with an imperfectly bonded interface: coupled dislocation-like and force-like conditions[J]. International Journal of Solids & Structures, 2017, 122: 91. DOI:10.1016/j.ijsolstr.2017.06.004 |
| [19] |
TAN Henry, HUANG Young, LIU Cheng, et al. The uniaxial tension of particulate composite materials with nonlinear interface debonding[J]. International Journal of Solids & Structures, 2007, 44(6): 1809. DOI:10.1016/j.ijsolstr.2006.09.004 |
| [20] |
LI Donglong, WANG Zhanjiang, YU Hao, et al. Elastic?elds caused by eigenstrains in two joined half-spaces with an interface of coupled imperfections: Dislocation-like and force-like conditions[J]. International Journal of Engineering Science, 2018, 126: 22. DOI:10.1016/j.ijengsci.2018.01.003 |
| [21] |
XU Xiqing, HU Xiaoxia, REN Sue, et al. Fine grained Al2O3-ZrO2 (Y2O3) ceramics by controlled crystallization of amorphous phase[J]. Journal of the European Ceramic Society, 2016, 36(7): 1791. DOI:10.1016/j.jeurceramsoc.2016.01.049 |
| [22] |
HUANG Chinyu, CHEN Yuliang. Design and impact resistant analysis of functionally graded Al2O3-ZrO2 ceramic composite[J]. Materials & Design, 2016, 91: 294. DOI:10.1016/j.matdes.2015.11.091 |
| [23] |
任会兰, 龙波, 宁建国, 等. ZrO2增韧Al2O3陶瓷的力学性能和增韧机制[J]. 复合材料学报, 2015, 32(3): 776. REN Huilan, LONG Bo, NING Jianguo, et al. Mechanical properties and toughening mechanisms of ZrO2 toughened Al2O3 ceramics[J]. Acta Materiae Compositae Sinica, 2015, 32(3): 776. DOI:10.13801/j.cnki.fhclxb.20140620.001 |
| [24] |
ZHENG Quanshui, DU Danxu. An explicit and universally applicable estimate for the effective properties of multiphase composites which accounts for inclusion distribution[J]. Journal of the Mechanics and Physics of Solids, 2001, 49(11): 2765. DOI:10.1016/S0022-5096(01)00078-3 |
| [25] |
刘协权, 倪新华, 刘晶芝, 等. 纳米陶瓷材料弹性模量的尺度效应[J]. 稀有金属材料与工程, 2007, 36(s2): 131. LIU Xiequan, NI Xinhua, LIU Jingzhi, et al. The size effect in young's modulus of nano composite ceramics[J]. Rare Metal Materials and Engineering, 2007, 36(s2): 131. DOI:10.3321/j.issn:1002-185x.2007.z2.038 |
| [26] |
CHENG Zhaogang, NI Xinhua, LIU Xiequan. The mechanical stress field of matrix in eutectic ceramic composite[J]. Applied Mechanics and Materials, 2012, 121-126: 3607. DOI:10.4028/www.scientific.net/AMM.121-126.3607 |
| [27] |
倪新华, 郑坚, 刘协权, 等. 共晶基陶瓷复合材料的强度模型[J]. 固体力学学报, 2009, 30(2): 116. NI Xinhua, ZHENG Jian, LIU Xiequan, et al. Strength model of eutectic ceramic composites[J]. Acta Mechanica Solida Sinica, 2009, 30(2): 116. DOI:10.19636/j.cnki.cjsm42-1250/o3.2009.02.002 |
 2019, Vol. 51
2019, Vol. 51


