2. 西北工业大学 深圳研究院,广东 深圳 518057;
3. 西北工业大学 自动化学院,西安 710072
2. Research & Development Institute of Northwestern Polytechnical University in Shenzhen, Shenzhen 518057, Guangdong, China;
3. School of Automation, Northwestern Polytechnical University, Xi'an 710072, China
矩阵分解(matrix factorization, MF)是机器学习研究中最重要的工具之一[1].目前,国内外许多学者对矩阵中低维子空间的映射问题有一定的研究,但是主成分分析、奇异值分解、矢量量化等方法中各基向量中正负数的存在使得基向量的物理意义不明确.直到Lee和Seung在1999年的《Nature》杂志中提出了非负矩阵分解(Nonnegative Matrix Factorization,NMF)[2], 该方法分解出来的矩阵都是非负数,引起了广大学者的关注.但该算法存在初值敏感的问题,即在不同初始条件下对同一信号分解得到的基矩阵和系数矩阵并不唯一.虽然这种不唯一性可理解为特征子空间的不同表现形式,但是非负矩阵分解直接用于求解欠定盲信号分离时, 分解结果不唯一就很难正确分离源信号.为了保证分解结果的唯一性, 提高源信号分离性能,需要对算法的初值进行更好的确定.目前非负矩阵初始化方法除了随机初始化外,主要包括两大类方法,一是利用PCA、SVD等分解算法先进行分解,再将其分解结果作为非负矩阵分解的初值[3-4];二是使用聚类分析的方法提升随机初始化非负矩阵分解的性能,包括Fuzzy C-Means (FCM)聚类、Spherical K Means聚类、谱聚类等[5-6].这些方法都在一定程度上实现了一维非负矩阵分解的初值确定,但是二维卷积非负矩阵分解与一维非负矩阵分解一样存在分解结果不唯一的问题,然而,针对于二维卷积非负矩阵分解初始值的研究,国内外还未见报道.值得注意的是,通过初始化算法找到好的初始值可以提高整个分解算法的收敛速度,但是初始化算法太过复杂也会增加算法运行的整体时间.因此,初始化的好坏对算法的性能十分重要.
1 非负矩阵分解模型当源信号相互独立时,满足了盲源分离的基本假设和约束条件,可以实现混合信号的分离.在非负矩阵分解模型中,V=[v1, v2, …, vm]T∈Rm×n分解成两个矩阵W∈Rm×k与H∈Rk×n,公式如下:
| $ \mathit{\boldsymbol{V}} \approx \mathit{\boldsymbol{W}}\cdot\mathit{\boldsymbol{H}}. $ | (1) |
式中:V为待分解矩阵,W和H分别为基矩阵和系数矩阵,要求W和H中所有元素均为非负.
在实际应用环境中, 由于存在反射和延时, 观测到的信号往往是各源信号及其滤波和延迟信号的混迭,然而瞬时混合假设观测或接收到的信号为各源信号的加权混合形式,非负矩阵分解方法无法有效的刻画局部帧间相关[7].针对更为复杂但也更符合实际情况的卷积混合盲分离,卷积非负矩阵分解在保证分解结果非负性的前提下,使用了二维时频基代替原非负矩阵分解中的一维基向量[1].NMF中基矩阵与编码矩阵的点乘关系也由此扩展为时频二维基与编码矩阵的卷积关系,卷积非负矩阵分解公式即
| $ \mathit{\boldsymbol{V}}\approx \sum\limits_{t=0}^{T-1}{{{\mathit{\boldsymbol{W}}}_{t}}\cdot \overset{t\to }{\mathop{\mathit{\boldsymbol{H}}}}\,.}\text{ } $ | (2) |
式中
CNMF学习的每一个基矩阵描述了信号在某一时刻的频谱特征,故所有基矩阵共同描述了信号在某一段非常小的时间范围内的频谱特征.为更精细的描述出频谱关系,近年来发展起来的二维非负矩阵分解,除了扩展基矩阵外,还对系数矩阵进行了扩展,公式如下[8]
| $ \mathit{\boldsymbol{V}}\approx \mathit{\boldsymbol{ \varLambda}}\text{ }=\sum\limits_{\tau }{\sum\limits_{\varphi }{{{\overset{\varphi \downarrow }{\mathop{\mathit{\boldsymbol{W}}}}\,}_{\tau }}\cdot {{\overset{\tau \to }{\mathop{\mathit{\boldsymbol{H}}}}\,}_{\varphi }}\text{ }.}} $ | (3) |
式中
从式(3)看出,相比于一维非负矩阵分解V≈W·H来说,需要进一步确定初值包括时频基中的τ个W的列向量,系数矩阵中的φ个H的行向量.因此,二维卷积非负矩阵分解算法需要初始化的值更多,初始值的好坏对算法最终的结果更加重要.
和一维非负矩阵分解的目标函数(式(4))一致,二维卷积非负矩阵分解的目标函数为了使得Λ尽可能与V相等,见式(5).
| $ \begin{array}{l} \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{W}},\mathit{\boldsymbol{H}}} f\left( {W,H} \right) = \frac{1}{2}\left\| {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{WH}}} \right\|_{\rm{F}}^2,\\ \;\;\;\;s.t.\;\;\;\;\;\;\mathit{\boldsymbol{W}},\mathit{\boldsymbol{H}} \ge 0 \end{array} $ | (4) |
| $ \begin{align} &\underset{W,H}{\mathop{\text{min}}}\,f\left( \mathit{\boldsymbol{W}},\mathit{\boldsymbol{H}} \right)=\frac{1}{2}\left\| \mathit{\boldsymbol{A}}-\mathit{\boldsymbol{\varLambda }}\text{ } \right\|_{\text{F}}^{2} \\ &=\frac{1}{2}\left\| \mathit{\boldsymbol{A}}-\sum\limits_{\tau }{\sum\limits_{\varphi }{{{\overset{\varphi \downarrow }{\mathop{\mathit{\boldsymbol{W}}}}\,}_{\tau }}\cdot {{\overset{\tau \to }{\mathop{\mathit{\boldsymbol{H}}}}\,}_{\varphi }}}} \right\|_{\text{F}}^{2}\cdot \\ &s.t.\ \ \ \ \ \mathit{\boldsymbol{W}},\mathit{\boldsymbol{H}}\ge 0 \\ \end{align} $ | (5) |
虽然目标函数对W或H是凸函数,但当两者同时变化时则是非凸的,找不到可以取得上面两式全局最小值的优化算法.因此,初始值的选取直接关系到收敛结果.
2 NMF初始化方法非负矩阵分解求解中矩阵因子W和H的初始值设定仍然是尚待解决的重要问题[9].它们直接影响非负矩阵分解算法的收敛效果与分解性能,不同的初始值将使得矩阵分解结果存在较大差别.如果用随机值进行初始化,为了得到更好的结果通常需要用若干对随机取值,并多次执行算法,然后从得到的结果中选择一对相对较优的W和H作为分解结果.随机初始化方法在要求较高的实际工程应用中不适用.
2.1 奇异值分解初始化对观测信号矩阵做奇异值分解可得
| $ \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{U \boldsymbol{\varLambda} }}\;\mathit{\boldsymbol{V}}{^{\rm{T}}}. $ | (6) |
式中:U为M×M维酉矩阵,Λ为M×M维对角阵,Λ=diag([δ1, δ2, …, δM]),δi为矩阵X的奇异值,V为M×M维酉矩阵.根据式(6)可知
| $ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{XX}}{^{\rm{T}}} = \mathit{\boldsymbol{U \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{V \boldsymbol{\varLambda} U}}{^{\rm{T}}} = \mathit{\boldsymbol{U}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^2}\mathit{\boldsymbol{U}}{^{\rm{T}}}. $ | (7) |
式中:Λ2=diag([λ1, λ2, …, λM]), 根据矩阵的性质可知, λi=δi2,λi为矩阵Y的第i个特征值.
奇异值分解得到最大的b个特征值及其对应的最大特征行向量和特征列向量.文[4]将奇异值分解方法用于非负矩阵分解的初始化,取得了更快的收敛效果.
2.2 K均值聚类初始化在提前确定聚类数且选定初始聚类中心的前提下,K均值算法使各样本数据到其所属类别的聚类中心的聚类和达到最小.K均值算法步骤如下:
1) 针对n个样本{x1, x2, …, xn},随机选取k个样本点{z1, z2, …, zk}作为初始聚类中心;
2) 对每个样本xi,找到距离它最近的聚类中心zj,将其分配到zj对应的类uj;
3) 对分类后的各类样本取平均值,得到新的聚类中心zj′;
4) 计算
| $ D=\sum\limits_{i=1}^{n}{\text{min }\!\!~\!\!\text{ }\left\{ \text{distance}\left( {{x}_{i}},z_{1}^{'} \right),\ldots ,\text{distance}({{x}_{i}},z_{\text{k}}^{'}) \right\};} $ |
5) 如果D收敛,则返回z1′, z2′, …, zk′并停止;否则,转至步骤(3).
K均值聚类方法需要人为给定聚类数K, 聚类个数即为本文需要分解出的源信号个数.K均值算法由于简单高效而得到了广泛应用.文[10]将K均值算法用于非负矩阵分解的初始化,用聚类中心组成基矩阵W,系数矩阵H可以被看作是聚类的分配矩阵.第i个数据被分配到第j类,那么系数矩阵H中hij为1,否则为0.
2.3 主成分分析初始化主成分分析是数学上对数据降维的一种方法,其基本思想是设法将原来众多的具有一定相关性的指标,重新组合成一组较少个数的互不相关的综合指标来代替原来指标.算法步骤如下:
1) 计算相关系数矩阵.有m维随机矢量X=[x1, x2, …, xm]T的协方差Cx为
| $ {C_x} = E\left[ {\left( {X - E\left[ x \right]} \right){{\left( {X - E\left[ x \right]} \right)}^{\rm{T}}}} \right]. $ | (8) |
式中E[x]为均值.
2) 求出相关系数矩阵的特征值及相应的正交化单位特征向量.计算Cx的特征值λ1, λ2, …, λm和对应的归一化特征向量U1, U2, …, Um,不妨设特征值λ1≥λ2≥…≥λm.
3) 选择主成分.特征向量所对应的特征值越大,它在重构时的贡献也越大,而特征值越小,该特征向量在重构时的贡献就越小.λ1, λ2, …, λm中前L个(1≤L≤m)最大的特征值,X用这些特征向量决定的主分量来重构时,均方差可达到很小,可将前L个特征值对应的特征向量U1, U2, …, UL作为基矩阵W的初始化矩阵.
3 2-DCNMF初始化的混合算法 3.1 混合算法构成考虑对矩阵W和矩阵H同时初始化,实现算法最后得到唯一解的作用.但是只用一种初始化方法容易以收敛到不好的局部解为代价[8],本文结合多种非负矩阵分解初始值确定方法实现二维卷积非负矩阵分解的初始化方法.
首先,通过使用K均值聚类方法得到聚类中心作为H矩阵的初始值,避开了传统初始化不确定系数矩阵带来的分解结果不唯一问题;其次,考虑到相比一维卷积非负矩阵分解来说,二维卷积非负矩阵分解算法的W矩阵个数更多,利用奇异值分解和主成分分析方法交替产生W矩阵的初始值,克服了单个算法存在的误差问题.
3.2 混合算法步骤将奇异值分解和主成分分析方法与K均值聚类分别初始化矩阵W和矩阵H.混合算法主要包括以下步骤:
步骤1 选取初始聚类中心个数(K等于分解的源信号个数);
步骤2 使用K均值算法对原始矩阵的列进行聚类,将K均值算法的聚类中心结果作为矩阵H的初始值;
步骤3 对原始矩阵进行选取奇异值分解得到最大的b个特征值(b等于分解的源信号个数),及b个特征值对应的特征向量;
步骤4 对原始矩阵进行主成分分析,决定保留的主成分个数为C个(C等于分解的源信号个数),及对应的主成分得分;
步骤5 奇异值分解的特征向量与主成分分析的得分交替作为矩阵W的初始值.
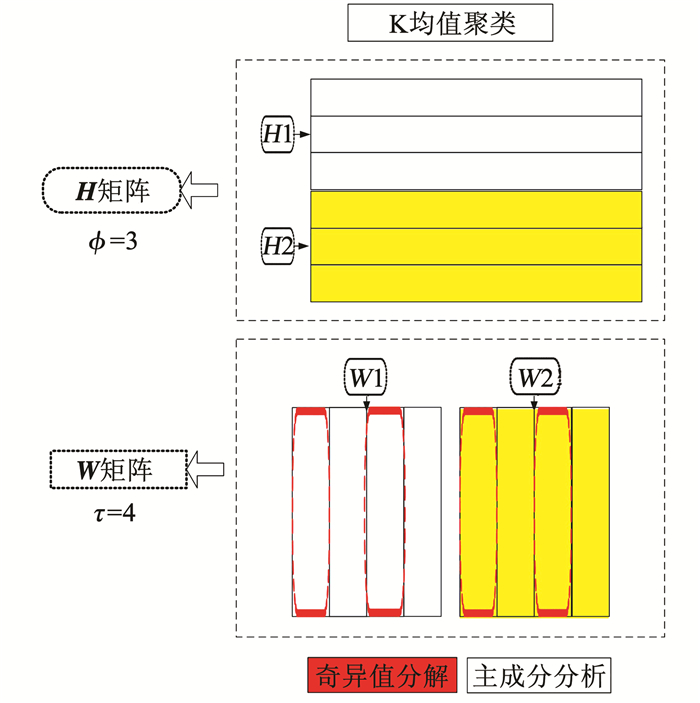
从本文提出的初始化算法步骤可看出,初始化算法主要包括3个经典算法的计算.与一维非负矩阵分解算法类似,二维卷积非负矩阵分解算法迭代占整个算法比例较高,算法时间复杂度为O(iter),其中iter为算法迭代次数.因此,经过本文算法的初始化确定,少量的增加了迭代前的计算复杂度,却可以大大减小整个算法的迭代次数.相比随机初始化二维卷积非负矩阵分解来说,运用本文算法初始化后的整体算法复杂度仍有减少.本文提出的混合算法逻辑见图 1.
|
图 1 算法逻辑 Fig. 1 Logic map of the algorithm |
从图 1可以看出,图中源信号个数为2.确定初值包括时频基中的τ个W的列向量,系数矩阵中的ϕ个H的行向量.本文混合算法通过奇异值分解和主成分分析交替产生W矩阵的τ个列向量,用K均值聚类产生H矩阵的ϕ个行向量,从而实现初始化.
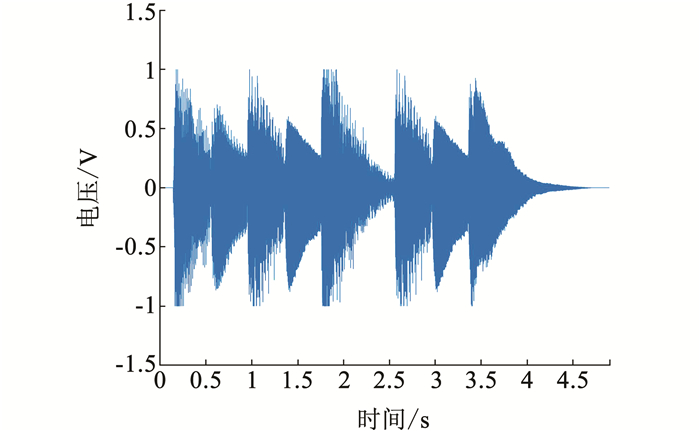
4 实验验证 4.1 算法有效性验证为验证本文算法的有效性,将随机初始化Random-2DCNMF、PCA初始化PCA-2DCNMF、SVD聚类初始化SVD-2DCNMF、K均值聚类初始化KMeans-2DCNMF和本文提出的混合算法Hybrid algorithm-2DCNMF进行比较.与其他窗函数相比,经汉明窗处理后可得到的相对纯净的频谱[11], 本文实验中的窗函数都选用汉明窗.本文对采集到的声信号进行实验[12].
|
图 2 混合信号 Fig. 2 Mixed signal |
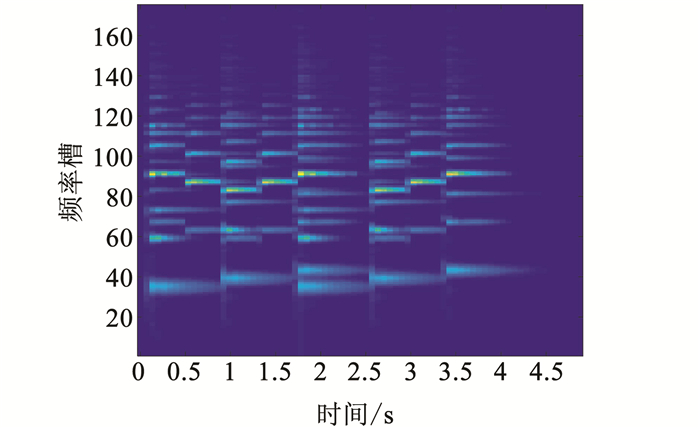
|
图 3 混合信号语谱图 Fig. 3 Spectrogram of mixed signal |
实验平台为:Intel Core 2Duo Q6600四核处理器, 工作频率为2.40 GHz, 内存为4.00 GB, 程序在Matlab2016b下运行.
本文将K均值聚类中心选为H的初始值,将PCA和SVD分解选为W的初始值,结果见图 4和表 1.

|
图 4 不同初始值确定算法重构语谱图 Fig. 4 Reconstruction of spectrogram with different initial value algorithms |
| 表 1 算法结果对比 Tab. 1 Comparison of different algorithms |
从结果可以看出,相对于随机初始化来说,算法效率提高的同时,避免收敛到相对不好的局部解.可见,由于PCA只提取了主成分,丢失了一定的信息.同时,相比只用奇异值分解这一种方法确定W的多个初始值来说,运用PCA和SVD交替产生W的初始值虽然算法的迭代次数有所增加(个人思考是由于初始值不同带来的必然问题),但是分解后与原矩阵V的相似度更高,也进一步说明,更能收敛到相对更好的局部最优解.更好的解决二维卷积非负矩阵分解随机初始化所引起的不稳定性问题.
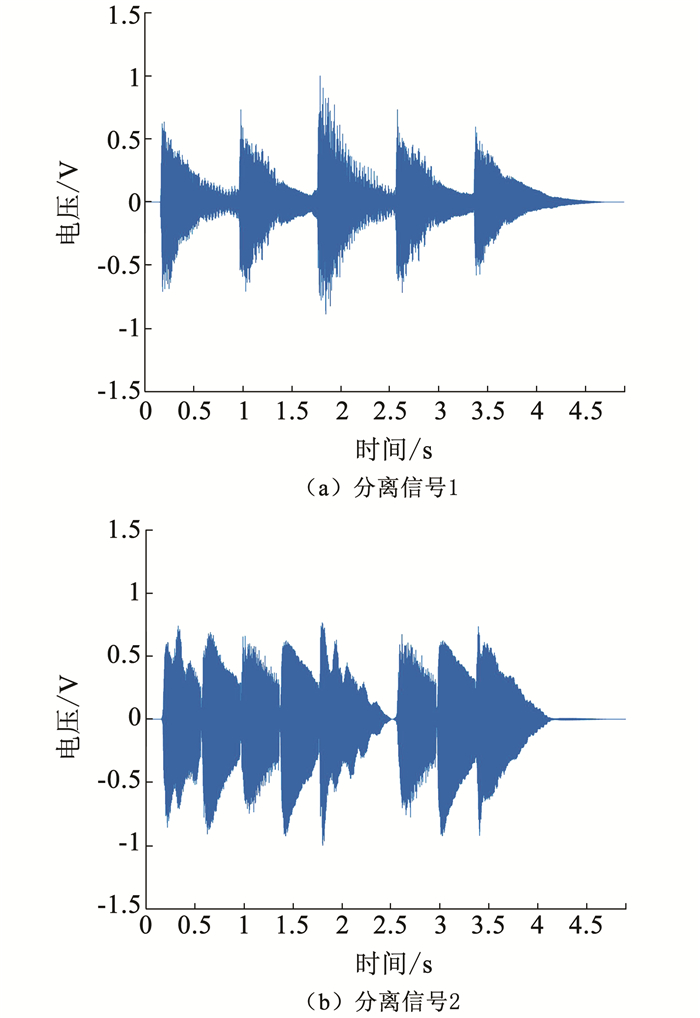
4.2 算法的鲁棒性分析进一步地,对原混合信号添加高斯白噪声进行分离实验.添加信噪比为10 dB的噪声后见图 6和图 7.
|
图 5 混合算法分解结果 Fig. 5 Matrix decomposition result of the proposed hybrid algorithm |

|
图 6 含噪混合信号 Fig. 6 Mixed signal with noise |
|
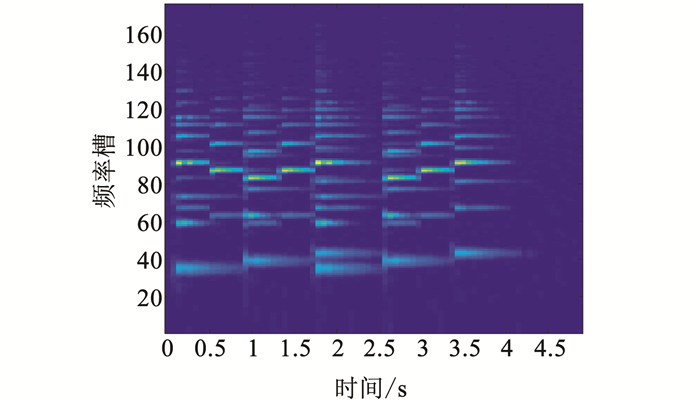
图 7 含噪混合信号语谱图 Fig. 7 Spectrogram of mixed signal with noise |
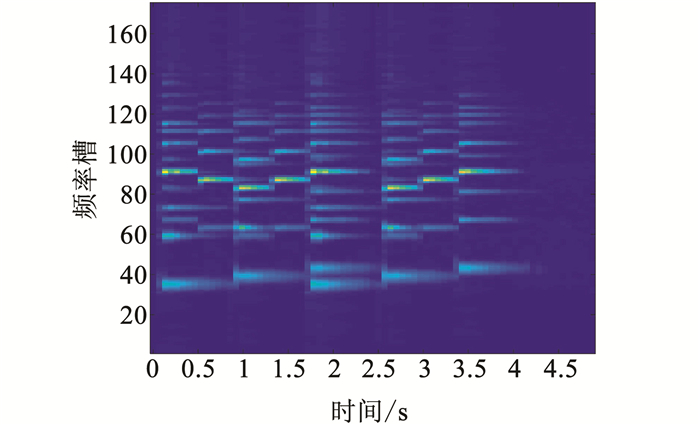
从图 8和图 9可以看出,经过本文算法确定初始值后,二维卷积非负矩阵分解可以在噪声环境下成功分离出信号.为了更好的验证算法的鲁棒性,算法在不同噪声下进行实验的迭代次数见表 2.
|
图 8 混合算法重构语谱图 Fig. 8 Reconstruction of spectrogram with different initial value algorithms |
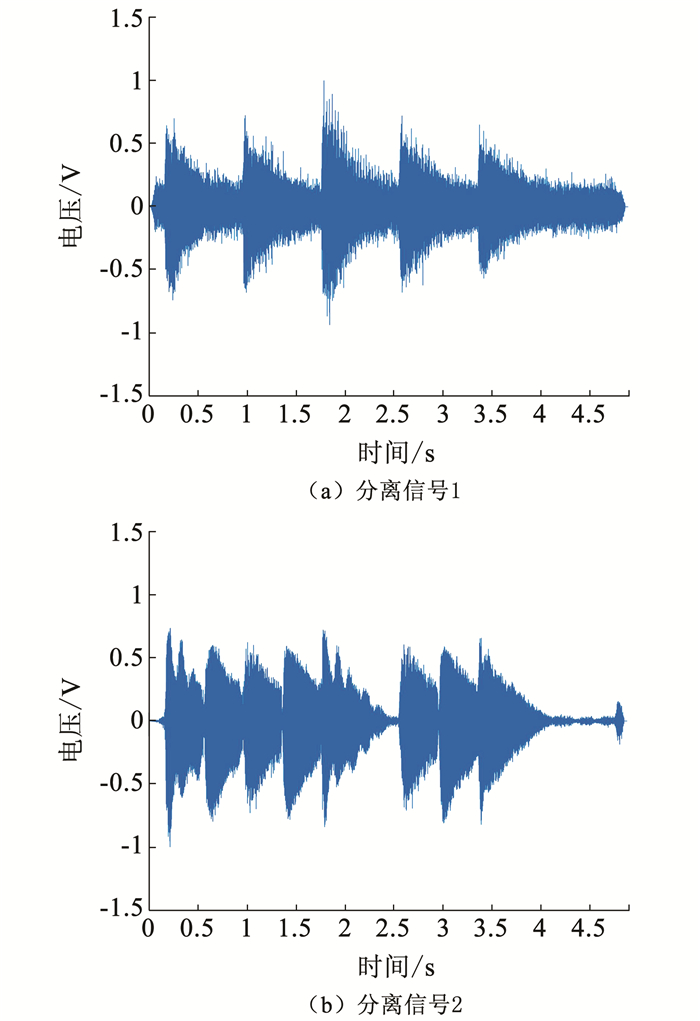
|
图 9 混合算法分解结果 Fig. 9 Matrix decomposition result of the proposed hybrid algorithm |
| 表 2 不同信噪比下算法迭代次数 Tab. 2 Iterative times of the algorithm under different RSNS |
从表中可以看出,在信噪比-1~10 dB之间都可以实现算法较快的收敛,保证了二维卷积非负矩阵分离算法在恶劣环境下实现较好的分离效果.因此,本文提出的算法对于噪声数据具有很强的鲁棒性.
5 结语国内对于二维卷积非负矩阵分解的初始化问题还未见研究报道,而初始化的好坏直接关系到最后分解的好坏.本文针对二维卷积非负矩阵分解(2-D CNMF)初值敏感问题,通过多种算法结合产生结构化初始值,提出了利用PCA+SVD交替初始化W矩阵,K均值初始化H矩阵的思路,在提高收敛效率的同时克服了陷入结果相对不好的局部最优值的问题,提升了2DCNMF收敛效果与分解性能,为二维卷积非负矩阵分解提供了一初始化和参数确定的新思路.
| [1] |
MENG Yang, SHANG Ronghua, JIAO Licheng, et al. Feature selection based dual-graph sparse non-negative matrix factorization for local discriminative clustering[J]. Neurocomputing, 2018, 290(5): 87. |
| [2] |
LEE D D, SEUNG H S. Learning the parts of objects by non-negative matrix factorization[J]. Nature, 1999, 401(6755): 788. DOI:10.1038/44565 |
| [3] |
谢昊.非负矩阵分解初始化及其应用[D].广州: 暨南大学, 2015 XIE Hao. Application and initialization of non-negative matrix factorization[D]. Guangzhou: Jinan University, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10559-1015978159.htm |
| [4] |
QIAO Hanli. New SVD based initialization strategy for non-negative matrix factorization[J]. Pattern Recognition Letters, 2015, 63(7): 71. |
| [5] |
XUE Yun, TONG Chongsze, CHEN Ying, et al. Clustering-based initialization for non-negative matrix factorization[J]. Applied Mathematics and Computation, 2008, 205(2): 525. DOI:10.1016/j.amc.2008.05.106 |
| [6] |
张焱, 汤宝平, 邓蕾. 基于谱聚类初始化非负矩阵分解的机械故障诊断[J]. 仪器仪表学报, 2013, 34(12): 2806. ZHANG Yan, TANG Baoping, DENG Lei. Mechanical fault diagnosis based on non-negative matrix factorization with spectral clustering initialization enhancer[J]. Chinese Journal of Scientific Instruments, 2013, 34(12): 2806. |
| [7] |
SMARAGDIS P. Convolutive speech bases and their application to supervised speech separation[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2007, 15(1): 1. DOI:10.1109/TASL.2006.876726 |
| [8] |
SCHMIDT M N, MORUP M. Nonnegative matrix factor 2-D deconvolution for blind single channel source separation[J]. International Conference on Independent Component Analysis and Blind Signal Separation, 2006, 3889(3): 700. |
| [9] |
WILD S, CURRY J, DOUGHERTY A. Improving non-negative matrix factorizations through structured initialization[J]. Pattern Recognition, 2004, 37(11): 2217. DOI:10.1016/j.patcog.2004.02.013 |
| [10] |
CURRY James, BETTERTON Meredith, ANNE Dougherty, et al. Seeding nonnegative matrix factorization with the spherical K-means clustering[D]. Colorado: University of Colorado, 2003
|
| [11] |
GAO Bin, WOO W L, DLAY S S. Adaptive sparsity non-negative matrix factorization for single-channel source separation[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(5): 989. DOI:10.1109/JSTSP.2011.2160840 |
| [12] |
GOTO M, HASHIGUCHI H, NISHIMURA T, et al. RWC music data-base: Music genre database and musical instrument sound database. Int. Symp. Music Inf. Retrieval (ISMIR)[C]//Baltimore, MD, 2003: 229
|
 2019, Vol. 51
2019, Vol. 51


