2. 中国人民解放军95507部队,贵阳 550025
2. The Chinese People's Liberation The 95507 troop, Guiyang 550025, China
网络病毒是实施网络入侵和达成网络行动目标的重要手段.在网络攻防博弈中,病毒的攻击感染表现出潜伏性,即感染目标前能利用免杀机制(如加壳、伪造数字签名等)潜伏在网络节点中,并于特定时机激活,迅速施效目标网络[1].近年来,陆续出现了“Regin”,“蓝色火焰”以及“狼人杀”木马等新型网络病毒,与传统蠕虫病毒相比,它们的技术手段和行动更为隐蔽高效[2-3].具体而言,潜伏型病毒在感染目标网络节点时,为实现特定战术目标,将其攻击感染的表征暂时隐藏起来;根据行动需求和前期设定的触发机制,攻击方会选择特定时机或采用特定手段激活启动该病毒[3-5].对这类新型网络病毒而言,“潜伏”特性更多表现为策略和操作层面的“潜伏”机制.
国内外目前对网络病毒传播的研究,主要基于传统网络病毒的扩散机理和特殊场景的需求.如Wang等[6-7]对无线传感和P2P的病毒传播进行研究,Li等[8]研究了小世界社团网络上的SI(Susceptible-Infected)病毒扩散模型,Qiu等[9]基于交通流量构建了SIS(Susceptible-Infected-Susceptible)修正扩散模型,Liu等[10]应用SIRS(Susceptible-Infected-Removed-Susceptible)病毒扩散模型研究了蠕虫病毒的传播机理,Guan等[11]研究了复杂网络上的SIQRS(Susceptible-Infected-Quarantined-Removed-Susceptible)病毒扩散模型及稳定性分析,Lu等[12]研究了自适应网络的病毒传播模型及其病毒传播阈值及稳态性分析.这些成果为开展病毒扩散建模和实际网络病毒传播研究提供了借鉴.但是,对于具有潜伏特性的新型网络病毒而言,病毒的快速演变和危害性的增强,客观上要求在病毒传播研究中综合考虑病毒的潜伏性及其影响.现有研究主要是通过考虑增加时延因素来实现,如Jackson等[13-14]构建了SIR(Susceptible-Infected-Removed)时滞扩散模型,并对其平衡点稳定性进行分析. Wang等[15]应用SIQR(Susceptible-Infected-Quarantined-Removed)病毒时滞扩散模型研究非线性接触率下的双时延病毒传播.这些研究将病毒的潜伏过程理解为感染前的一段时延,体现了网络和病毒的动态性.然而,从现实网络病毒传播过程看,由于病毒应用背景和目标的不同,时延的长短很难确定,具有典型的不确定性和不可预测性;其次,从潜伏阶段的病毒传播机理分析,还具有很多特有的属性,如潜伏周期、病毒激活时间以及潜伏状态向其它状态的转移过程等.显然,这些情况不是传统模型所能够解决的,同时仅靠时延因素也难以适应潜伏的多重属性及现实应用.
网络病毒传播研究需要解决潜伏性带来的新问题:一是新型网络病毒的“潜伏”特性引起了网络病毒传播机理和流程的改变,需要借鉴既有模型和研究方法,在SIQRS等传统模型基础上增加“潜伏”状态和相应的节点状态转移关系,建立与“潜伏”特性相一致的网络病毒传播模型;二是在“潜伏”机制下,节点状态间转移模式的改变会直接影响病毒传播效果和网络节点状态稳定性,如潜伏病毒的网络节点存在向易感节点、感染节点和免疫节点三种状态节点转化的可能,且不同的转移概率值将直接影响病毒扩散效果和系统的稳定性;三是新型网络病毒的潜伏特性,直接影响网络攻击防御策略和具体实践技术手段,尤其是对于防御方而言,现有的病毒查杀-隔离-免疫防御是否有效,如何结合集体防御、深度防御和动态目标防御方法,都建立在对新型网络病毒传播的深入研究基础上.为此,本文基于以上对病毒潜伏特性的认知,建立与潜伏机制相适应的SEIQRS(Susceptible-Escape-Infected-Quarantined- Removed-Susceptible)网络病毒传播模型,该模型在传统SIQRS(Susceptible-Infected-Quarantined-Removed- Susceptible)病毒扩散模型基础上增加了潜伏状态,并以模型为基础研究潜伏型病毒的传播机理和稳定性.
1 网络病毒传播模型Guan等[11]应用SIQRS经典病毒传播模型,研究了隔离状态对病毒传播的影响以及免疫节点功能退化问题,见图 1.其中,定义了4种节点状态:易感节点S,感染节点I,隔离节点Q,免疫节点R.总节点数为N,假设网络中节点平均度为k

|
图 1 网络病毒传播SIQRS模型 Fig. 1 SIQRS model of network virus spreading |
其中,S(t)、I(t)、Q(t)和R(t)分别表示t时刻易感节点、感染节点、隔离节点和免疫节点的数量.此处不考虑节点的增减情况[11],即总节点数恒定,N=S(t)+I(t)+Q(t)+R(t),对应的数学模型为
| $ \begin{align} &\frac{\text{d}S\left( t \right)}{\text{d}t}=-k\beta S\left( t \right)I\left( t \right)/N-vS\left( t \right)+bR\left( t \right), \\ &\frac{\text{d}I\left( t \right)}{\text{d}t}\text{ }=k\beta S\left( t \right)I\left( t \right)/N-\gamma I\left( t \right), \\ &\frac{\text{d}Q\left( t \right)}{\text{d}t}=\gamma I\left( t \right)-\varepsilon Q\left( t \right), \\ &\frac{\text{d}R\left( t \right)}{\text{d}t}=vS\left( t \right)+\varepsilon Q\left( t \right)-bR\left( t \right), \\ &N=S\left( t \right)+I\left( t \right)+Q\left( t \right)+R\left( t \right). \\ \end{align} $ | (1) |
基于以上模型,本文根据病毒传播时的潜伏特性,提出新的网络节点状态——潜伏状态,对其状态本身及转移规则进行研究.潜伏状态是指病毒传播过程中的网络节点隐蔽待激活状态,潜伏机制具体表现为网络节点在病毒扩散过程中存在潜伏状态和围绕潜伏状态的转移规则.考虑网络病毒攻防中的动态实时、自主免疫和自愈修复等情况,潜伏待激活状态的病毒的网络节点,可能会转化为以下三种状态:1)易感状态.基于自愈修复能力,潜伏病毒的网络节点在激活感染其他网络节点之前,通过自愈修复成为健康节点,但不具有抗病毒能力,易受病毒感染;2)感染状态.网络病毒/受病毒感染的节点在受激活启动后,直接感染其他网络节点;3)免疫状态.基于自主免疫特性,受病毒感染的网络节点在激活感染其他网络节点之前,进行免疫修复,具备抗病毒能力.
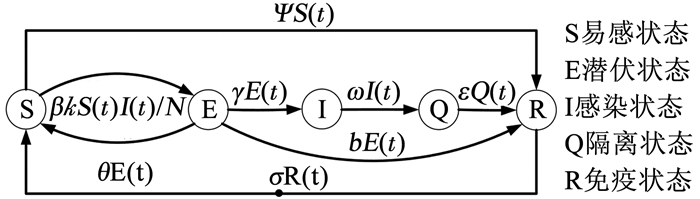
病毒传播过程中的潜伏状态E存在向易感状态S、感染状态I或免疫状态R等三种状态转移的可能,参照SIQRS模型[11, 16]给出网络病毒传播的SEIQRS模型,见图 2.其中:
|
图 2 SEIQRS网络病毒传播模型 Fig. 2 SEIQRS model of network virus spreading |
1) 易感状态S→潜伏状态E,部分易感节点被病毒潜伏进入潜伏状态,处于待激活状态,且暂时不具备攻击感染能力.假设网络中感染病毒的节点对易感节点的感染形式都是将其先感染为潜伏节点.感染节点与易感节点每次接触感染的概率为β1,单位时间内一个感染节点与其他易感节点接触的次数为U,则平均有效接触率为β1US(t)/N,即每个被潜伏型病毒感染的节点的感染率表达式为β1US(t)/N,其中N为网络节点总数.根据Guan等[11]研究得知,接触次数U与节点度k成正比,即U=β2k,从而得到单个感染节点的感染率为β1β2kS(t)/N,单位时间内所有被感染为潜伏节点的节点数量为β1β2kS(t)I(t)/N,记β=β1β2为潜伏型病毒的感染系数,则感染数可简化为βkS(t)I(t)/N.
2) 易感状态S→免疫状态R,部分易感节点自身具备抗病毒能力,不受网络病毒攻击感染,直接转移到免疫状态,转移参数ψ为网络节点具有抗病毒攻击感染能力的概率.
3) 潜伏状态E→感染状态I,潜伏节点中的病毒被激活,成为感染节点,可感染其它网络节点,转移参数γ为潜伏节点被激活的概率.
4) 潜伏状态E→感染状态S,潜伏的病毒具有一定的生命周期,在网络行动结束后依然未被激活的病毒,将失去潜伏的意义;攻击方预测到对方已经察觉或检测到潜伏病毒的特征,为了隐蔽核心目标,主动摧毁部分潜伏病毒.此时,可以认为潜伏节点再次转化为易感节点,转移参数θ表示潜伏的病毒未被激活的概率.
5) 潜伏状态E→感染状态R,在病毒潜伏期间,部分潜伏节点会具备对此种病毒的免疫能力,直接转化为免疫节点,转移参数b表示节点在病毒潜伏期具备免疫能力的概率.
6) 感染状态I→隔离状态Q,病毒防御中受感染节点断开通信连接进入隔离状态,转移参数ω为网络病毒/受病毒攻击感染的节点断开网络连接的概率.
7) 隔离状态Q→免疫状态R,受攻击感染后进入隔离状态的节点,通过自主免疫后具备抗病毒攻击感染的能力,进入免疫状态,转移参数ε为断开通信连接的网络节点进行免疫后具备抵御网络病毒攻击能力的概率;8)免疫状态R→易感状态S,由于病毒变异等原因,免疫状态节点抗病毒能力在安全防御过程逐渐减弱,最终不具备抗病毒能力,再次进入易感状态,转移参数δ为免疫节点抗病毒能力逐渐减弱的概率.其中:N为网络总节点数,k为网络节点平均度.S(t)、E(t)、I(t)、Q(t)和R(t)分别表示t时刻易感节点、潜伏节点、感染节点、隔离节点和免疫节点的数量.
根据系统动力学原理,参考文献[11, 16]给出的SIQRS模型,可得如下的SEIQRS模型数学表达式为
| $ \begin{align} &\frac{\text{d}S\left( t \right)}{\text{d}t}=-\beta kS\left( t \right)I\left( t \right)/N-\psi S\left( t \right)+\theta E\left( t \right)+\sigma R\left( t \right), \\ &\frac{\text{d}E\left( t \right)}{\text{d}t}=\beta kS\left( t \right)I\left( t \right)/N-\gamma E\left( t \right)-\theta E\left( t \right)-bE\left( t \right), \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\text{d}I\left( t \right)}{\text{d}t}=\gamma E\left( t \right)-\omega I\left( t \right), \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\text{d}Q\left( t \right)}{\text{d}t}=\omega I\left( t \right)-\varepsilon Q\left( t \right), \\ \end{align} $ | (2) |
| $ \frac{\text{d}R\left( t \right)}{\text{d}t}=\varepsilon Q\left( t \right)+\psi S\left( t \right)+bE\left( t \right)-\sigma R\left( t \right). $ |
令R(t)=N-S(t)-E(t)-I(t)-Q(t),式(2)可进一步表示为
| $ \begin{align} &\frac{\text{d}S\left( t \right)}{\text{d}t}=-k\beta S\left( t \right)I\left( t \right)/N-\psi S\left( t \right)+\theta E\left( t \right)+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \delta \left( N-S\left( t \right)-E\left( t \right)-I\left( t \right)-Q\left( t \right) \right), \\ &\frac{\text{d}E\left( t \right)}{\text{d}t}=k\beta S\left( t \right)I\left( t \right)/N-\left( \gamma +\theta +b \right)E\left( t \right), \\ &\frac{\text{d}I\left( t \right)}{\text{d}t}=\gamma E\left( t \right)-\omega I\left( t \right), \\ &\frac{\text{d}Q\left( t \right)}{\text{d}t}=\omega I\left( t \right)-\varepsilon Q\left( t \right). \\ \end{align} $ | (3) |
令
| $ \begin{align} &{{P}_{0}}\left( {{S}_{0}},{{E}_{0}},{{I}_{0}},{{Q}_{0}} \right)=\text{ }\left( \frac{\delta }{\psi +\delta }N,0,0,0 \right),{{P}_{1}}\left( {{S}_{1}},{{E}_{1}},{{I}_{1}},{{Q}_{1}} \right) \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\text{ }\left( \frac{\left( \gamma +\theta +b \right)\omega N}{k\beta \gamma }\text{ },{{E}_{1}},\text{ }\frac{\gamma }{\omega }{{E}_{1}},\text{ }\frac{\gamma }{\varepsilon }\text{ }{{E}_{1}} \right). \\ \end{align} $ |
式中
根据式(3)可得任意平衡点P*的Jacobi矩阵
| $ \begin{align} &\mathit{\boldsymbol{J }}\left( {{P}^{*}} \right)= \\ &\left( \begin{matrix} \frac{-kI\beta }{N}-\psi -\delta &\theta -\delta &\frac{-\text{ }kS\beta }{N}\text{ }-\delta &\text{ }-\delta \\ \frac{kI\beta }{N}&-\left( \gamma +\theta +b \right)&\frac{kS\beta }{\text{ }N}&0 \\ 0&\gamma &-\omega &0 \\ 0&0&\omega &-\varepsilon \\ \end{matrix} \right). \\ \end{align} $ | (4) |
定理1 当R0≤1时,无病毒平衡点P0局部渐近稳定;当R0>1时,平衡点P0不稳定.
证明 由式(4)可得平衡点P0处Jacobi矩阵为
| $ \begin{align} &\mathit{\boldsymbol{J }}\left( {{P}_{0}} \right)= \\ &\left( \begin{matrix} -\psi -\delta &\theta -\delta &k\beta \text{ }\frac{\delta }{\delta +\psi }-\delta &\text{ }-\delta \\ 0&-\left( \gamma +\theta +b \right)&k\beta \text{ }\frac{\delta }{\delta +\psi }&0 \\ 0&\gamma &-\omega &0 \\ 0&0&\omega &-\varepsilon \\ \end{matrix} \right). \\ \end{align} $ | (5) |
矩阵J(P0)的特征多项式为
| $ \begin{align} &\left( \lambda +\varepsilon \right)\left( \lambda +\psi +\delta \right)\left[ \left( \lambda +\gamma +\theta +b \right)\left( \lambda +\omega \right)- \right. \\ &\left. \beta \gamma \text{ }\frac{\delta }{\delta +\psi }\text{ }k \right]=0. \\ \end{align} $ | (6) |
其对应特征根
定理1表明,当网络病毒的攻击感染能力未达到网络病毒防御的给定门限时,防御方占据优势,网络中最终只存在易感节点和免疫节点,受病毒感染的网络节点均被隔离后修复.
定理2 当R0>1时,平衡点P1(S1, E1, I1, Q1)局部渐近稳定.
证明 由式(4)可得平衡点P1处的Jacobi矩阵为
| $ \begin{align} &\mathit{\boldsymbol{J }}\left( {{P}_{1}} \right)= \\ &\left( \begin{matrix} \frac{-k\text{ }\beta \text{ }{{I}_{1}}}{N}\text{ }-\psi -\delta &\theta -\delta &-\frac{\gamma +\theta +b}{\gamma }\omega -\delta &\text{ }-\delta \\ \frac{k\text{ }\beta \text{ }{{I}_{1}}}{N}&-\left( \gamma +\theta +b \right)&\frac{\gamma +\theta +b}{\gamma }\omega &0 \\ 0&\gamma &-\omega &0 \\ 0&0&\omega &-\varepsilon \\ \end{matrix} \right). \\ \end{align} $ | (7) |
对应的特征多项式λ4+μ1λ3+μ2λ2+μ3λ+μ4=0.
式中:
| $ \begin{align} &{{\mu }_{1}}=\gamma +\theta +b+\omega +\varepsilon +\psi +\delta +\frac{\text{ }k}{\beta {{I}_{1}}~}N\text{ };{{\mu }_{2}}= \\ &\left( \text{ }~\frac{k\beta {{I}_{1}}}{N}\text{ }+\psi +\delta \right)\text{ }\left( \gamma +\theta +b+\omega \right)\text{ }+\text{ }\frac{k\beta {{I}_{1}}~}{N}\text{ }\left( \delta -\theta \right)\text{ }+ \\ &\varepsilon \text{ }\left( \gamma +\theta +b+\omega \right)\text{ };{{\mu }_{3}}=\left( ~\frac{\text{ }k\beta {{I}_{1}}}{N}\text{ }+\psi +\delta \right)\text{ }\left( \gamma +\theta +b+\omega \right) \\ &\varepsilon +\text{ }\frac{k\beta {{I}_{1}}~}{N}\text{ }\left[ \left( \delta -\theta \right)\text{ }\left( \varepsilon +\omega \right)-\left( \gamma +\theta +b \right)\omega +\gamma \delta \right].\text{ }{{\mu }_{4}}= \\ &k\beta {{I}_{1}}~\left[ \left( \delta -\gamma -2\theta -b \right)\text{ }\varepsilon \omega +\gamma \omega \delta +\varepsilon \gamma \delta \right]\text{ }/N.~ \\ \end{align} $ | (8) |
式中μ1, μ2>0.根据劳斯稳定性判据[13, 16],计算得μ1μ2-μ3>0,μ1μ2μ3-μ32-μ4>0.因此,其对应的特征根全部位于坐标轴的左半平面,对应J(P1)的特征值实部为负.可得结论:当基本再生数R0>1时,感染源平衡点P1局部渐近稳定.证毕#.
定理2表明,当网络病毒的攻击感染能力超过网络安全防御门限时,网络中携带病毒信息的网络节点、受病毒信息感染的网络节点和断开通信连接的网络节点将以一定的比值持续稳定存在.
3 仿真分析为验证定理1和定理2的合理性,围绕基本再生数R0=kγβδ/[ω(δ+ψ)(γ+θ+b)],重点分析E-S转移概率θ、E-I转移概率γ和E-R转移概率b等3个参数对信息扩散的影响.运用Matlab组件Simulink求解网络病毒传播动力学模型的非线性微分方程组,分析3个参数对信息扩散的影响,进而验证模型的有效性及系统随时间的演进关系.仿真中的单位时间设置为1秒.参照文献[11, 12]设置变量的初值和相关参数,设置网络节点总数N=1 000,网络节点平均度为k=30,网络节点在初始时刻只存在易感状态和感染状态,对应节点数初值分别为S(0)=980和I(0)=20.同步给出其它参数的基本设置,δ=0.2,ψ=0.8,θ=0.78,β=0.2,γ=0.6,ω=0.5,ε=0.8,b=0.06.
3.1 E-S状态转移概率θ对病毒传播的影响运用控制变量的思想,保持其他参数值不变,调整E-S转移概率θ值并分析其对病毒传播的影响.根据基本再生数R0,可知E-S转移概率的阈值θlim=0.78.当θ≥θlim时,系统局部渐近稳定在无病毒平衡点P0处;当θ < θlim时,系统局部渐近稳定在感染源平衡点P1处,图 3(a)~(d)表示θ值为0.8和0.2的仿真结果.当θ=0.8>θlim时,系统在平衡点P0(200, 0, 0, 0)处局部渐近稳定,如图 3(a)所式,图 3(b)为状态E、I和Q的节点数变化放大曲线图;当θ=0.2 < θlim时,系统在平衡点P1(120, 65, 78, 48)处局部渐近稳定,如图 3(c)所示,图 3(d)为状态E、I和Q的节点数变化放大曲线图.

|
图 3 E-S状态转移概率仿真 Fig. 3 Simulation diagrams of E-S state transfer probability |
图 3(e)表示不同θ下感染状态I的节点数随时间的变化曲线.其中,θ在区间[0.2, 1]内取值,步长为0.2.当θ=0.8, 1>θlim时,系统局部渐近稳定在无病毒平衡点P0处;当θ=0.2, 0.4, 0.6 < θlim时,系统局部渐近稳定在感染源平衡点P1处.仿真结果与理论分析一致,随着θ的增大,感染状态I的节点数逐渐减少,表明受网络病毒攻击感染的网络节点进行自愈修复的能力越强,病毒节点/受感染节点越少,网络病毒防御能力越强.显然,通过合理调控θ,可以实现对网络病毒传播的有效控制.
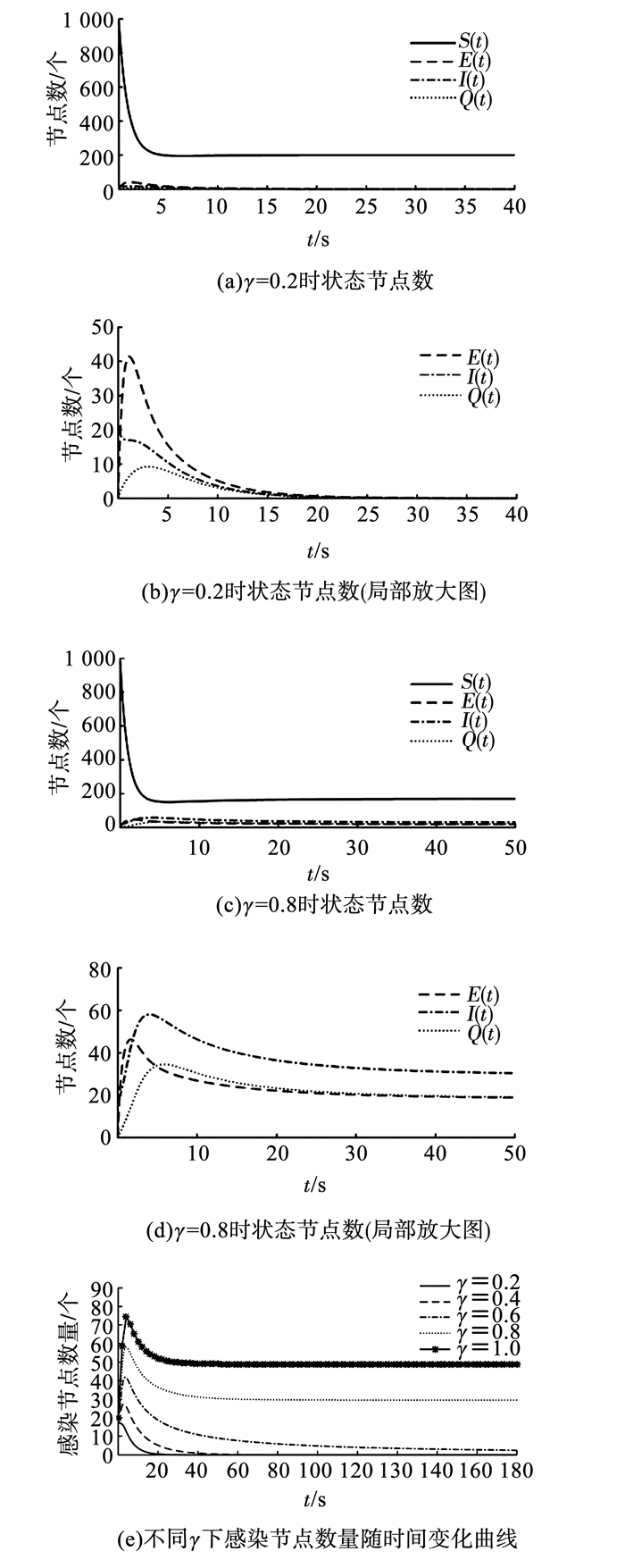
3.2 E-I状态转移概率γ对病毒传播的影响调整E-I转移概率γ值分析其对病毒传播的影响.由基本再生数R0计算可得E-I转移概率γ的阈值γlim=0.58.当γ≤γlim时,系统局部渐近稳定在无病毒平衡点P0处;当γ>γlim时,系统局部渐近稳定在感染源平衡点P1处,图 4(a)~(d)分别表示γ值为0.2和0.8的仿真结果.当γ=0.2 < γlim时,系统在平衡点P0(200, 0, 0, 0)处局部渐近稳定,如图 4(a)所式,图 4(b)为状态的节点数变化放大曲线图;当γ=0.8>γlim时,系统在平衡点P1(170, 18, 30, 18)处局部渐近稳定,如图 4(c)所示,图 4(d)为状态E、I和Q的节点数变化放大曲线图.
|
图 4 E-I状态转移概率仿真 Fig. 4 Simulation diagrams of E-I state transfer probability |
图 4(e)表示不同γ下感染状态I的节点数随时间的变化曲线.其中,γ在区间[0.2, 1]内取值,步长为0.2.当γ=0.2, 0.4 < γlim时,系统局部渐近稳定在无病毒平衡点P0处.当γ=0.6, 0.8, 1>γlim时,系统局部渐近稳定在感染源平衡点P1处.仿真结果与理论分析一致,随着γ的增大,感染状态I的节点数逐渐增多,表明病毒感染节点激活启动程度越强,病毒节点数量越多,网络病毒防御能力逐渐减弱,网络病毒传播速度逐渐下降.显然,通过合理调控γ,可以实现对网络病毒传播的有效控制.
3.3 E-R状态转移概率b对病毒传播的影响调整E-R状态转移概率b值分析其对病毒传播的影响.根据基本再生数R0,可得潜伏状态E—免疫状态R转移概率的阈值为blim=0.062.当b≥blim时,系统局部渐近稳定在无病毒平衡点P0处;当b < blim时,系统局部渐近稳定在感染源平衡点P1处,图 5(a)~(d)分别表示b值为0.18和0.02的仿真结果.当b=0.18>blim时,系统在平衡点P0(200, 0, 0, 0)处局部渐近稳定,如图 5(a)所式,图 5(b)为状态E、I和Q的节点数变化放大曲线图;当b=0.02 < blim时,系统在平衡点P1(195, 5, 6, 3)处局部渐近稳定,如图 5(c)所示,图 5(d)为状态E、I和Q的节点数变化放大曲线图.

|
图 5 E-R状态转移概率仿真 Fig. 5 Simulation diagrams of E-R state transfer probability |
图 5(e)表示不同b下感染状态I的节点数随时间的变化曲线.其中,b在区间[0.02, 0.18]内取值,步长为0.04.当b=0.1, 0.14, 0.18>blim时,系统局部渐近稳定在无病毒平衡点P0处.当b=0.02, 0.06 < γlim时,系统局部渐近稳定在感染源平衡点P1处.仿真结果与理论分析一致,随着γ的增大,感染状态I的节点数逐渐增多,表明病毒感染节点激活启动程度越强,病毒节点数量越多,网络病毒防御能力逐渐减弱,网络病毒传播速度逐渐下降.显然,通过合理调控γ,可以实现对网络病毒传播的有效控制.
仿真结果表明,在网络病毒防御过程中,通过优化潜伏状态E-易感状态S的转移概率θ、潜伏状态E-感染状态I的转移概率γ和潜伏状态E-免疫状态R的转移概率b,可有效控制病毒传播和维护网络安全.通过增大转移概率θ、减小转移概率γ和增大转移概率b,可减少网络病毒/受病毒攻击的节点,降低网络病毒攻击感染网络节点的概率.
4 结语本文构建了基于潜伏机制的网络病毒传播SEIQRS模型,系统分析了潜伏型病毒的传播特性.研究表明,在网络行动初始阶段,潜伏型病毒逐步入侵并潜伏到对手网络节点中,防御方尚未检测到潜伏病毒,潜伏病毒节点数逐渐增多,并在受激后攻击感染其他网络易感节点,一旦网络防御系统检测到节点被病毒感染并实施有效防御措施,网络病毒节点将被迅速消除,网络系统将稳定在无病毒平衡点;相反,如果网络防御系统的病毒检测和防御能力较弱,病毒感染节点将持续增加,最终网络系统将稳定在有病毒平衡点.可见,网络中最终是否存在病毒节点,取决于网络系统自身的防御能力与潜伏型病毒的扩散能力的相对大小.在网络安全防御行动中,防御方可通过增大潜伏状态到易感状态转移概率θ,减小潜伏状态到感染状态转移概率γ和增大潜伏状态到免疫状态转移概率b,将网络控制稳定在健康状态,维护网络安全.后期工作将考虑网络的动态性和时延因素,从理论层面的仿真验证向多条件/环境下的仿真拓展,开展集体防御和动态目标防御等新型网络安全防御技术和理论研究.
| [1] |
孙玺菁, 司守奎. 复杂网络算法与应用[M]. 北京: 国防工业出版社, 2016: 99. SUN Xijing, SI Shoukui. Complex network algorithms and applications[M]. Beijing: National Defense Industry Publishing House, 2016: 99. |
| [2] |
THOMAS G, KYPROS M, STEFANOS P, et al. The trojan horse reconstruction[J]. Mechanism and Machine Theory, 2015, 90(1): 261. DOI:10.1016/j.mechmachtheory.2015.03.015 |
| [3] |
YANG Xiuqing, WEI Kejin, MA Haiqiang, et al. Trojan horse attacks on counterfactual quantum key distribution[J]. Physics Letters A, 2016, 380(18): 1589. DOI:10.1016/j.physleta.2015.09.027 |
| [4] |
WANG Yinan, LIN Zhiyun, LIANG Xiao, et al. On modeling of electrical cyber-physical systems considering cyber security[J]. Journal of Zhejiang University Science C, 2016, 17(5): 465. DOI:10.1631/FITEE.1500446 |
| [5] |
WU Guangyu, SUN Jian, CHEN Jie. A survery on the security of cyber-physical systems[J]. Control Theory and Technology, 2016, 14(1): 2. DOI:10.1007/s11768-016-5123-9 |
| [6] |
WANG Yaqi, YANG Xiaoyuan. Virus spreading in wireless sensor networks with a medium access control mechanism[J]. Chinese Physical B, 2013, 22(4): 040206(1-5). DOI:10.1088/1674-1056/22/4/040206 |
| [7] |
冯朝胜, 秦志光, 袁丁. 移动P2P网络中的病毒传播建模[J]. 电子科技大学学报, 2012, 41(11): 98. FENG Chaosheng, QIN Zhiguang, YUAN Ding. Modeling of virus propagation in the mobile peer-to-peer networks[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(11): 98. DOI:10.3969/j.issn.1001-0548.2012.01.019 |
| [8] |
LI Chanchan, JIANG Guoping, SONG Yurong. Comparative effects of avoidance and immunization on epidemic spreading in a dynamic small-world network with community structure[J]. Wuhan University Journal of Natural Sciences, 2016, 21(4): 291. DOI:10.1007/s11859-016-1173-6 |
| [9] |
仇慎伟, 王开, 刘茜, 等. 基于交通流量的病毒扩散动力学研究[J]. 物理学报, 2012, 61(15): 1. QIU Shenwei, WANG Kai, LIU Qian, et al. Epidemic spreading on scale-free networks with traffic flow[J]. Acta Phys. Sin, 2012, 61(15): 1. |
| [10] |
刘启明. 一个蠕虫病毒传播SIRS模型的建立与分析[J]. 西南师范大学学报(自然科学版), 2010, 35(1): 168. LIU Qiming. Construction and analysis of a SIRS model for worm virus propagation[J]. Journal of Southwest China Normal University (Natural Science Edition), 2010, 35(1): 168. DOI:10.13718/j.cnki.xsxb.2010.01.047 |
| [11] |
关治洪, 亓玉娟, 姜晓伟, 等. 基于复杂网络的病毒传播模型及其稳定性[J]. 华中科技大学学报(自然科学版), 2011, 39(1): 114. GUAN Zhihong, QI Yujuan, JIANG Xiaowei, et al. Virus propagation dynamic model and stability on complex networks[J]. Huazhong University of Science and Technology (Natural Science Edition), 2011, 39(1): 114. DOI:10.13245/j.hust.2011.01.026 |
| [12] |
鲁延玲, 蒋国平, 宋玉荣. 自适应网络中病毒传播的稳定性和分岔行为研究[J]. 物理学报, 2013, 62(13): 130202(1-9). LU Yanling, JIANG Guoping, SONG Yurong. Stability and bifurcation of epidemic spreading on adaptive network[J]. Acta Phys Sin, 2013, 62(13): 130202(1-9). DOI:10.7498/aps.62.130202 |
| [13] |
MARK J, BENITO M. Modeling plant virus propagation with delays[J]. Journal of Computer and Applied Mathematics, 2017, 30(9): 611. DOI:10.1016/j.cam.2016.04.024 |
| [14] |
张晓潘, 袁凌云. 具有时滞-扩散作用的无线传感网络病毒传播模型的振荡动力学研究[J]. 计算机科学, 2017, 44(6): 390. ZHANG Xiaopan, YUAN Lingyun. Oscillatorybehaviors of malware propagation model in wireless sensor networks with time delays and reaction-diffusion terms[J]. COMPUTER SCIENCE, 2017, 44(6): 390. DOI:10.11896/j.issn.1002-137X.2017.6A.088 |
| [15] |
WANG Kai. Hopf bifurcation of a delayed SIQR epidemic model with constant input and nonlinear incidence rate[J]. Advances in Difference Equations, 2016, 2016(1): 168. DOI:10.1186/s13662-016-0899-y |
| [16] |
LI Tao, WANG Yuanmei, GUAN Zhihong. Spreading dynamics of a SIQRS epidemic model on scale-free networks[J]. Communications in Nonlinear Science and Numerical Simulation, 2014, 19(3): 686. DOI:10.1016/j.cnsns.2013.07.010 |
| [17] |
HADI M, GHADER R, SABER A. Stability and bifurcation analysis of an asymmetrically electrostatically actuated microbeam[J]. Journal of Computational and Nonlinear Dynamics, 2015, 10(2): 021002(1-8). DOI:10.1115/1.4028537 |
 2019, Vol. 51
2019, Vol. 51


