2. 中国人民解放军32147部队, 陕西 宝鸡 721000;
3. 中国人民解放军93786部队,河北 张家口 075000
2. Unit 32147 of PLA, Baoji 721000, Shanxi China;
3. Unit 93786 of PLA, Zhangjiakou 075000, Hebei, China
弹道目标识别技术是弹道导弹防御需要解决的核心技术难题之一.组网雷达与单部雷达相比,在获取目标信息、抗干扰、区域搜索等方面具有较大的优势,可以为弹道目标识别提供一个较好的解决途径[1-2].弹道导弹防御一般可分为助推段防御、中段防御和再入段防御.中段由于飞行时间长、弹道稳定,被认为是反导作战的关键阶段[3].在中段,不同的弹道目标常常伴随着不同形式的微动,这就为目标识别提供了可能.因此,利用雷达网对弹道目标进行微动提取具有一定的理论意义,可以为弹道目标识别提供一定的参考.
反导预警雷达网一般由窄带雷达和宽带雷达组成,窄带雷达主要应用于反导预警,其探测距离远,但分辨率有限;宽带雷达分辨率高,但作用距离有限且占用的信息处理资源较大,短时间内难以大量装备[4].目前同构组网雷达(同类型雷达进行组网)在提取弹道目标微动参数上存在一定的不足.因此,组建混合体制雷达网能够更有效的利用窄带雷达和宽带雷达的各自优势,获取目标更多的微动信息.美国林肯实验室就利用窄带雷达获取的RCS特征去评估宽带雷达对目标形成的ISAR像,实现了宽窄雷达的融合识别[5].文献[6]指出对于同一散射中心,其时频曲线与距离像序列存在前者是后者的导函数关系,这就给综合利用反导预警雷达网中宽窄带雷达信息提供了理论依据.
文献[7]根据不同散射中心频谱熵的差异实现了窄带雷达网散射中心的关联,并利用循环迭代的方法提取出了微动参数,但在信噪比较低时,频谱熵的关联方法鲁棒性较差,循环迭代法提取的参数精度也不高.文献[8-10]利用宽带雷达网多视角的特性,通过联立方程组求解出了微动参数和结构参数,提取出的参数精度较高,并分别对参数的CRB、鲁棒性和均方误差进行了分析.文献[11]构建混合体制雷达网,采用循环迭代的方法对宽带雷达和窄带雷达获取的微动信息进行了参数求取,参数提取的精度较文献[7]有了很大提高.文献[12-13]根据散射中心幅相参数信息对宽窄带雷达的微动信息进行了融合处理并对散射中心位置进行了空间重构,求得的参数精度高,重构的误差较小.然而以上文献在利用雷达网提取散射中心参数时均假设各雷达观测的散射中心数量一致,这在实际雷达布局中很难实现,尤其在利用宽窄带混合组网时,由于宽、窄带雷达作用距离的不同,得到散射中心数目一致的情况概率低.文献[11-13]考虑的情况较为理想,只对散射中心一致的情况进行了研究,缺乏适应性.
本文对混合体制雷达网如何进行弹道目标进动参数提取进行了研究,首先对目标进动进行了建模,分析其在窄带雷达和宽带雷达观测下的散射中心表达式,并对散射中心进行了关联.然后利用离散广义Radon变换对宽带雷达回波进行了参数提取,结合窄带雷达散射中心关联信息解出了进动角.最后利用进动角,结合雷达网多视角信息,求解出了雷达视线角和结构参数,并实现了三维锥旋矢量的求解.
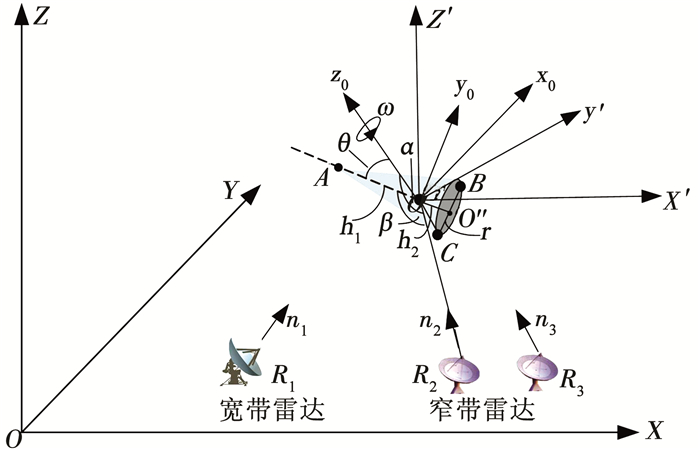
1 微动建模 1.1 目标进动建模进动锥体目标模型如图 1所示,锥体对称轴与锥旋轴交于O′点,高度为h,底面中心为O″,半径为r,锥顶A与O′距离为h1,O″与O′距离为h2,进动角为θ,旋转角速度为ω,半锥角为ε.雷达视线与锥体对称轴的夹角为β,与锥旋轴的夹角为α.当β∈(0, ε)∪(π/2, π-ε)[9]时,能观测到A、B、C 3个强散射中心,β∈(0,π/2-ε)[9],能观测到A和C两个强散射中心,O-XYZ为雷达网坐标系,O′-x0y0z0为弹体坐标系,z0轴为目标自旋轴的指向,O′-x′y′z′为相对坐标系,且O′-x′y′z′平行于O-XYZ.
|
图 1 混合体制雷达组网示意 Fig. 1 Sketch map of the hybrid-scheme radar network |
假设混合体制雷达网中有一部宽带雷达(雷达1)和两部窄带雷达(雷达2、3),考虑到宽、窄带雷达作用距离的差异,当弹道目标来袭时,混合体制雷达网一般会出现图 1所示的观测布局,此时宽带雷达由于遮挡效应能够观测到两个散射中心,窄带雷达能够观测到目标3个散射中心.
通过几何推导可得姿态角β(t)满足式(1),其中φi为初相.
| $ \cos \beta \left( t \right) = \cos \theta \cos {\alpha _i} + \sin \theta \sin {\alpha _i}\sin \left( {\omega t + {\varphi _i}} \right). $ | (1) |
则姿态角β(t)随t的变化规律为
| $ \beta \left( t \right) = \arccos \left( {\cos \theta \cos {\alpha _i} + \sin \theta \sin {\alpha _i}\sin \left( {\omega t + {\varphi _i}} \right)} \right). $ | (2) |
由上式可知,姿态角β(t)存在极大值和极小值,当sin(ωt+φi)=-1时,β(t)取极大值,记为βmax=θ+αi;当sin(ωt+φi)=1时,β(t)取极小值,记为βmax= θ-αi.
假设平动分量已补偿,设初始时刻雷达距O′点的距离为R0且满足远场条件.散射中心A、B和C到雷达的径向距离表达式为
| $ \left\{ \begin{array}{l} {R_{\rm{A}}} = {R_0} + {h_1}\cos \beta \left( t \right),\\ {R_{\rm{B}}} = {R_0} - {h_2}\cos \beta \left( t \right) + r\sin \beta \left( t \right),\\ {R_{\rm{C}}} = {R_0} - {h_2}\cos \beta \left( t \right) - r\sin \beta \left( t \right). \end{array} \right. $ | (3) |
其中散射中心A径向距离变化满足正弦规律,B和C径向距离变化不满足正弦规律,目标散射中心径向距离包含微动参数和结构参数,其中部分参数之间存在耦合.因此,为精确提取出目标微动参数和结构参数,需要考虑3个方面问题,一是如何准确提取出散射中心径向变化曲线参数,二是如何利用雷达网多视角特性对部分耦合参数进行解耦,三是如何充分发挥混合体制雷达网的优势,提高雷达网获取参数精度.
1.2 信号模型由文献[11]的窄带雷达和宽带雷达的信号模型,结合式(3)可得到目标各散射中心的微多普勒表达式如下:
| $ \left\{ \begin{array}{l} {f_{\rm{A}}} = 2\omega {h_1}\sin \theta \sin {\alpha _i}\cos \left( {\omega t + {\varphi _i}} \right)/\lambda ,\\ {f_{\rm{B}}} = 2\omega \left( { - {h_2} - r/\tan \beta \left( t \right)} \right)\sin \theta \sin {\alpha _i}\cos \left( {\omega t + {\varphi _i}} \right)/\lambda ,\\ {f_{\rm{C}}} = 2\omega \left( { - {h_2} + r/\tan \beta \left( t \right)} \right)\sin \theta \sin {\alpha _i}\cos \left( {\omega t + {\varphi _i}} \right)/\lambda ; \end{array} \right. $ | (4) |
| $ T = \sin {\alpha _i}/\sin {\alpha _j}. $ | (5) |
宽带雷达由于视角的限制能观测到A和C两个强散射中心,结合式(3)可得散射中心微距离变化表达式为
| $ \left\{ \begin{array}{l} {R_{\rm{A}}} = {h_1}\cos \beta \left( t \right),\\ {R_{\rm{C}}} = - {h_2}\cos \beta \left( t \right) - r\sin \beta \left( t \right). \end{array} \right. $ | (6) |
由于雷达网中各雷达观测到的散射中心位置不一致,因此在进行参数提取时,需要对同一类型的散射中心进行关联.由式(4)可知,锥顶散射中心A的调制系数仅与αi有关,多部窄带雷达获取的锥顶散射中心之间的比值L为定值,而其它散射中心之间的比值不满足这一条件,因此可通过提取散射中心调制系数来确定锥顶散射中心.同时在距离像中利用微多普勒信息还可以解决因散射中心距离像在最大值与最小值附近变化缓慢而难以确定相应时间的问题.
2 参数求解 2.1 进动角求解姿态角β∈(0,π/2-ε)时,散射中心A和C在雷达视线方向上投影长度的极大值和极小值分别为lAmax、lAmin和lCmax、lCmin,由文献[8]可得
| $ \left\{ \begin{array}{l} \left| {{l_{A\max }} - {l_{C\min }}} \right| = h\sec \varepsilon \cos \left( {{\beta _{\min }} + \varepsilon } \right),\\ \left| {{l_{A\min }} - {l_{C\max }}} \right| = h\sec \varepsilon \cos \left( {{\beta _{\max }} + \varepsilon } \right). \end{array} \right. $ | (7) |
令h1/h=k,则锥顶散射中心A的径向距离的极大值和极小值为
| $ \left\{ \begin{array}{l} {l_{A\max }} = h \cdot k\cos {\beta _{\min }},\\ {l_{A\min }} = h \cdot k\cos {\beta _{\max }}. \end{array} \right. $ | (8) |
由式(7)和式(8)可得:
| $ \frac{{\cos {\beta _{\min }}}}{{\cos {\beta _{\max }}}} = \left| {\frac{{{l_{A\max }}}}{{{l_{A\min }}}}} \right| \buildrel \wedge \over = a, $ | (9) |
| $ \frac{{\sin {\beta _{\min }}}}{{\sin {\beta _{\max }}}} = \left| {\frac{{\frac{1}{k}{l_{A\max }} - \left| {{l_{A\max }} - {l_{C\min }}} \right|}}{{\frac{1}{k}{l_{A\min }} - \left| {{l_{A\min }} - {l_{C\max }}} \right|}}} \right| = \hat b. $ | (10) |
由式(9)和式(10)可求出姿态角β的极大值和极小值为
| $ \left\{ \begin{array}{l} {\beta _{\max }} = \arccos \left( {\sqrt {\frac{{1 - {b^2}}}{{{a^2} - {b^2}}}} } \right),\\ {\beta _{\min }} = \arccos \left( {a\sqrt {\frac{{1 - {b^2}}}{{{a^2} - {b^2}}}} } \right). \end{array} \right. $ | (11) |
则目标进动角θ和视线角αi的估计值分别为:
| $ \hat \theta = \frac{{{{\hat \beta }_{\max }} - {{\hat \beta }_{\min }}}}{2}, $ | (12) |
| $ {{\hat \alpha }_1} = \frac{{{{\hat \beta }_{\max }} + {{\hat \beta }_{\min }}}}{2}. $ | (13) |
因此,可通过求出散射中心径向距离的极值达到对进动角的估计.其中参数k可k*=2h2/h1= |(fB+fC)/fA|和h1+h2=h两式联立求出.
本文采用广义Radon变换[15-16]对距离像序列图像中的散射中心位置变化曲线进行检测来获得散射中心径向距离极值.对散射中心A和C距离像正弦曲线进行建模
| $ \left\{ \begin{array}{l} {d_{\rm{A}}} = {m_{\rm{A}}} + {n_{\rm{A}}}\cos \omega t,\\ {d_{\rm{C}}} = {m_{\rm{C}}} + {n_{\rm{C}}}\cos \omega t. \end{array} \right. $ | (14) |
则曲线检测的参数空间为
| $ {G_{{\rm{CRT}}}}\left( {\rm{I}} \right) = \sum\limits_{i = 1}^N {\left| {Z\left( {i,\varphi \left( {i,{\rm{I}}} \right)} \right)} \right|} . $ | (15) |
式中:Z∈ZM×N表示距离像序列图像矩阵,φ(i, Ι)表示参数域Ι下的第i幅距离像上对应的径向距离单元.由于散射中心A、C在距离像序列中为两条曲线,因此GRT变换后会出现两个峰值,提取出峰值对应的坐标即可估计出散射中心极值点.
2.2 视线角和结构参数求解利用锥顶散射中心微多普勒fA和k*对雷达2和雷达3视角下的锥体底面散射中心B正弦频率分量进行补偿,利用补偿后的瞬时频率fb进行特征提取.当cos(ωt+φi)=1时,可得到的方程为
| $ \left\{ \begin{array}{l} A = \frac{{{f_{{\rm{b2}}}}}}{{{f_{{\rm{b3}}}}}} = \frac{{\cos {\alpha _2}\sin {\alpha _2}\sqrt {1 - {{\left( {\cos \theta \cos {\alpha _3}} \right)}^2}} }}{{\cos {\alpha _3}\sin {\alpha _3}\sqrt {1 - {{\left( {\cos \theta \cos {\alpha _2}} \right)}^2}} }},\\ \;\;\;\;\;\;\;\;\;B = \frac{{{f_{{\rm{A2}}}}}}{{{f_{{\rm{A3}}}}}} = \frac{{\sin {\alpha _2}}}{{\mathit{sin}\;{\alpha _3}}}. \end{array} \right. $ | (16) |
利用式(12)求出的进动角代入式(16)中,可实现视线角的求解.而文献[7]由于仅利用窄带雷达进行组网,进动角无法单独获取,根据进动角一般在5°~15°的先验知识,利用循环迭代的方法来实现对上述两个方程中的3个未知参数求解.但循环迭代方法运算量较大,易受噪声影响,而本文方法计算稳定性较好.
由雷达2视线角α2和进动角θ,利用下式即可计算出
| $ \left\{ \begin{array}{l} {{\hat r}_{ - 2}} = {\rm{mean}}\left( {\frac{{\left| {{f_{{\rm{b2}}}}} \right| \cdot \lambda \sqrt {1 - {{\left( {\cos \theta \cos {\alpha _2}} \right)}^2}} }}{{2\omega \cos \theta \cos {\alpha _2}\sin \theta \sin {\alpha _2}}}} \right),\\ {{\hat h}_{1 - 2}} = {\rm{mean}}\left( {\frac{{\left| {{f_{{\rm{A2}}}}} \right| \cdot \lambda }}{{2\omega \sin \theta \sin {\alpha _2}}}} \right);{{\hat h}_{2 - 2}} = \frac{{{{\hat h}_{1 - 2}} \cdot {k_ * }}}{2}. \end{array} \right. $ | (17) |
上式锥旋频率ω的求解,可参照文献[17]改进的自相关法.
同理利用雷达1和雷达3的微动信息也可求出
步骤1:以底面半径
步骤2:利用平均得到的r和h1对3部雷达各散射中心进行补偿并估计残余分量的幅度均值记为σ.
步骤3:对
步骤4:循环重复步骤2和步骤3.直到幅度均值σ变化范围小于10%或循环重复至10次时即停止循环.
步骤5:取幅值均值最小的r和h1作为最终估计值.
2.3 三维锥旋矢量求解设第i雷达在全局坐标系下的方位角和俯仰角为(α′i, β′i),ni(i=1, 2, 3)为雷达视线方向,满足
| $ {n_i} = {\left[ {\cos {\beta _i}\cos {\alpha _i},\cos {\beta _i}\sin {\alpha _i},\sin {\beta _i}} \right]^{\rm{T}}}. $ | (18) |
则雷达观测视角αi满足
| $ \left\{ \begin{array}{l} \sin {\alpha _i} = \left\| {\frac{{\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \omega } }}}}{\omega } \times {\mathit{\boldsymbol{n}}_i}} \right\|;\\ \;\;\;\;\omega = \left\| {\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \omega } }}} \right\|. \end{array} \right. $ | (19) |
式中:
仿真参数设置:假设目标为旋转对称锥体,参数设置为:h=2.5 m,h1=2 m,h2=0.6 m,r=0.5 m,θ=15°,φ=π/4.锥旋角速度ω=4πrad/s,锥旋矢量为
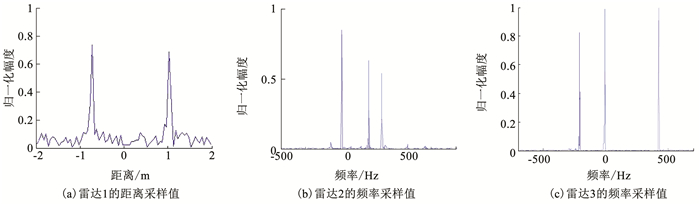
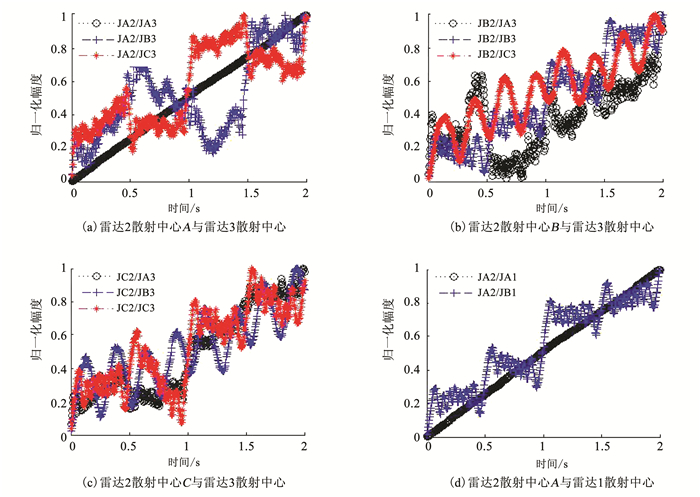
图 2(a)为雷达1获得的目标回波距离像序列,(b)和(c)为雷达2、3获得的目标回波微多普勒曲线,可以看出各散射中心曲线交织在一起,均呈现周期性变化.图 3(a)为雷达1采用ESPRIT超分辨算法[19]在t=0.3 s时对图 2(a)的采样结果.图 3(b)、(c)为雷达2、3利用峰值法在t=0.18 s、t=0.38 s时对图 2(b)和(c)进行采样的结果.根据采样得到的散射中心距离值和频率值可实现散射中心关联和k*的求解.在雷达观测时间2 s内均匀选取1 000个点,根据式(4)、式(5)和式(6)的关系,采用散射中心匹配算法对雷达网中各雷达观测到的散射中心进行匹配,得到如图 4所示的散射中心匹配关系图,图 4(a)~(c)为雷达2观测到的散射中心回波与雷达3观测到的散射中心回波随时间的比值.图 4(d)为在雷达2和雷达3匹配确定出散射中心A的基础上,雷达2散射中心A与雷达1散射中心匹配关系图.令雷达2散射中心A在ti时刻的频率采样值为fA2(ti),为克服某个时间点频率采样出现的偶然误差而导致频率比值变化范围较大的影响.采用对ti时刻前的频率比值进行求和减小偶然误差的方法.令

|
图 2 混合体制雷达网观测结果 Fig. 2 Observed results of the hybrid-scheme radar network |
|
图 3 雷达不同时刻采样结果 Fig. 3 Sampling results of radars at different time |
|
图 4 散射中心匹配关系 Fig. 4 Matching diagram of the scattering centers |
| $ \frac{{{J_{{\rm{A2}}}}\left( n \right)}}{{{J_{{\rm{A3}}}}\left( n \right)}} = \frac{{\sum\limits_{i = 1}^n {{f_{{\rm{A2}}}}\left( {{t_i}} \right)} }}{{\sum\limits_{i = 1}^n {{f_{{\rm{A3}}}}\left( {{t_i}} \right)} }} + \frac{{\sum\limits_{i = 1}^{n - 1} {{f_{{\rm{A2}}}}\left( {{t_i}} \right)} }}{{\sum\limits_{i = 1}^{n - 1} {{f_{{\rm{A3}}}}\left( {{t_i}} \right)} }} + \cdots + \frac{{\sum\limits_{i = 1}^1 {{f_{{\rm{A2}}}}\left( {{t_i}} \right)} }}{{\sum\limits_{i = 1}^1 {{f_{{\rm{A3}}}}\left( {{t_i}} \right)} }}. $ | (20) |
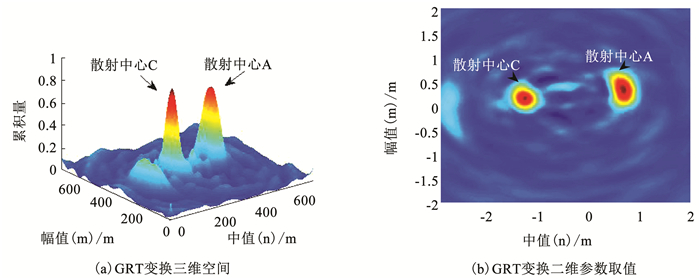
对不同雷达下的其余散射中心频率采样进行同样的频率求和比值再求和的处理方法.由式(4)可知fA2/fA3为定值,令比值为k,则JA2(n)/JA3(n)=k·tn/t1,在随时间变化的匹配关系图中呈现为一次函数,而其余的散射中心频率比值不满足此规律.同理可确定出雷达1的锥顶散射中心.图 5(a)为广义Radon变换对雷达1获取的距离像进行变换得到的三维空间图,可以看出图中有两个明显的峰值,表示的是两个回波散射中心.图 5(b)为广义Radon变换得到的回波距离像二维参数取值图,通过峰值检测可得到峰值所对应的坐标值,将峰值坐标代入式(8)中求出对应的极值点即可求解出进动角.该变换是在MATLAB软件上运行的,所用计算机为32位i5处理器,主频为3.10 GHz,内存为4 G,上述变换运行的时间为0.215 845 s.
|
图 5 GRT变换参数空间分布 Fig. 5 Space distribution of the GRT transformation parameters |
在利用广义Radon变换求出进动角的基础上,利用式(16)、式(17)和式(19)参数求解公式即可求出目标特征参数,如表 1和表 2所示.表 1为3部雷达3种组合求解得到的参数值.表 2为采用二分法对r和h1进行优化的结果.表 3为锥体弹头特征参数最后估计结果.利用表 3中雷达数据代入式(19)可得到锥旋矢量为
| 表 1 三种组合求解结果 Tab. 1 Solving results of three combinations |
| 表 2 二分法迭代结果 Tab. 2 Iteration results of dichotomy |
| 表 3 特征参数估计结果 Tab. 3 Estimation results of feature parameters |
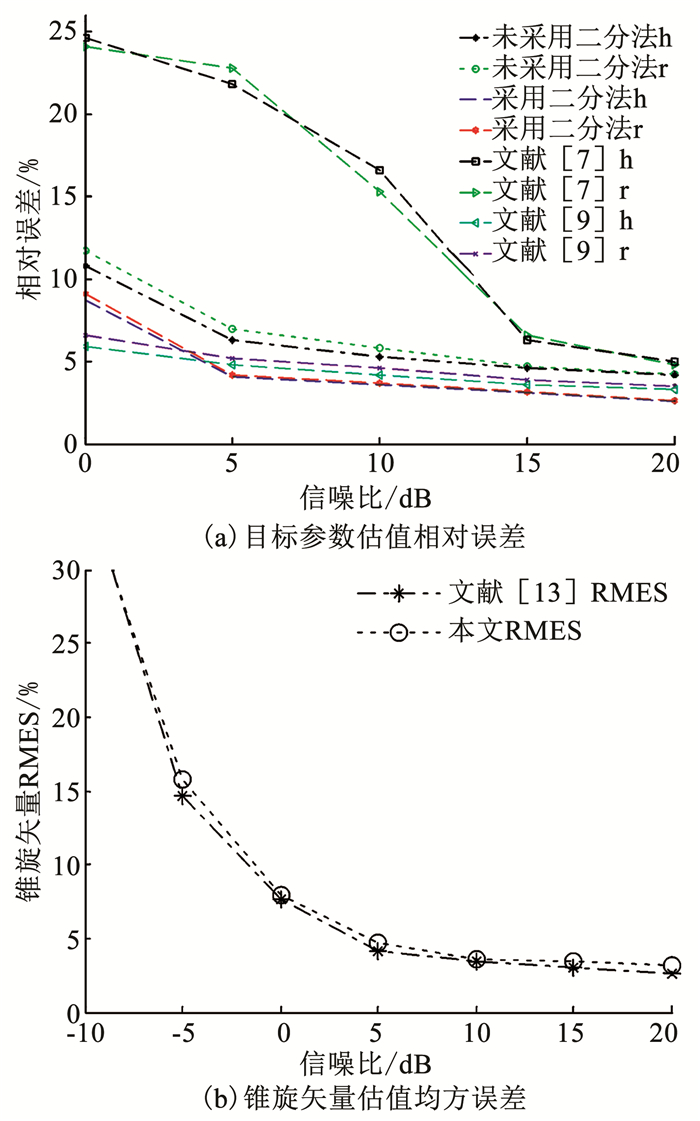
|
图 6 估计参数性能分析 Fig. 6 Performance analysis of the estimated parameters |
本文对进动目标在宽带、窄带混合雷达网下的微多普勒进行联合参数求解,实现了进动特征提取,并对不同类型同构组网雷达与异构组网雷达在参数估计性能上进行了对比.通过理论分析和仿真实验,表明:
1) 混合体制雷达网在参数估计性能上较窄带雷达网有很大改善,与宽带雷达网参数估计性能接近.在参数估计性能要求不苛刻的条件下,采用混合体制雷达网进行进动目标参数提取,符合当前国内雷达网的现状.
2) 雷达网观测目标时,各雷达很难得到相同数量的散射中心,在散射中心数量不一致的情况下进行参数提取,符合雷达网观测的实际情况.
3) 在求解进动角时,同时利用了宽带雷达和窄带雷达的观测信息,参数利用率较高.在求解结构参数时,充分利用宽带雷达的高分辨特性来提高估计精度.
4) 本文采用了两部窄带雷达和一部宽带雷达进行进动参数求取,并没有验证不同类型雷达数量对参数提取精度的影响.下一步将研究雷达数量和复杂环境下的目标参数估计性能.
| [1] |
CHEN V C. Advances in applications of radar micro-Doppler signatures[C]//Proceedings of 2014 IEEE Antenna Measurements & Applications (CAMA). Piscataway: IEEE, 2014: 1. DOI: 10.1109/CAMA.2014.7003362 10.1109/CAMA.2014.7003362
|
| [2] |
LIU Z, WEI X Z, LI X. Aliasing-free micro-Doppler analysis based on short-time compressed sensing[J]. IET Signal Processing, 2014, 8(2): 176. DOI:10.1049/iet-spr.2012.0403 |
| [3] |
FETTER S, SESSLER A M, CORNWALL J M, et al. Countermeasures: A technical evaluation of the operational effectiveness of the planned US National Missile Defense System[EB/OL]. http://www.fas.org, 2000
|
| [4] |
PAN X Y, WANG W, LIU J, et al. Modulation effect and inverse synthetic aperture radar imaging of rotationally symmetric ballistic targets with precession[J]. IET Radar, Sonar & Navigation, 2013, 7(9): 950. |
| [5] |
CAMP W W, JOSEPH T M, O'DONNELL R M. Wideband radar for ballistic missile defense and range-Doppler imaging of satellites[J]. Lincoln Laboratory Journal, 2000, 2(2): 267. |
| [6] |
张群, 罗迎. 雷达目标微多普勒效应[M]. 北京: 国防工业出版社, 2013: 22. ZHANG Qun, LUO Ying. Micro-Doppler effect of radar targets[M]. Beijing: National Defense Industry Press, 2013: 22. |
| [7] |
韩勋, 杜兰, 刘宏伟. 基于窄带雷达组网的空间锥体目标特征提取方法[J]. 电子与信息学报, 2014, 36(12): 2956. HAN Xun, DU Lan, LIU Hongwei. Feature extraction of space cone-shaped target based on narrow-band radar network[J]. Journal of Electronics & Information Technology, 2014, 36(12): 2956. |
| [8] |
贺思三, 赵会宁, 冯存前. 多视角距离像序列弹道目标的进动参数估计[J]. 信号处理, 2013, 29(8): 1027. HE Sisan, ZHAO Huining, FENG Cunqian. Precession parameter estimation for ballistic targets based on multi-aspect range-profile sequence[J]. Journal of Signal Procession, 2013, 29(8): 1027. DOI:10.3969/j.issn.1003-0530.2013.08.016 |
| [9] |
艾小锋, 邹小海, 李永桢, 等. 基于时间-距离像分布的锥体目标进动与结构特征提取[J]. 电子与信息学报, 2011, 33(9): 083. AI Xiaofeng, ZOU Xiaohai, LI Yongzhen, et al. Feature extraction of precession and structure of cone-shaped object based on time-HRRP distribution[J]. Journal of Electronics & Information Technology, 2011, 33(9): 2083. |
| [10] |
罗迎, 张群, 李松, 等. 基于分布式组网雷达的弹道目标三维进动特征提取[J]. 电子学报, 2012, 40(6): 1079. LUO Ying, ZHANG Qun, LI Song, et al. Three-dimensional precession feature extraction of ballistic targets in distributed radar networks[J]. Acta Electronica Sinica, 2012, 40(6): 1079. |
| [11] |
赵双, 鲁卫红, 冯存前, 等. 基于宽窄带微多普勒信息的进动目标特征提取[J]. 北京航空航天大学学报, 2016, 42(10): 2250. ZHAO Shuang, LU Weihong, FENG Cunqian, et al. Feature extraction of precession targets based on wideband and narrowband micro-Doppler information[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(10): 2250. |
| [12] |
陈蓉, 冯存前, 李靖卿, 等. 基于宽窄带微多普勒融合的锥体目标三维重构[J]. 空军工程大学校报(自然科学版), 2017, 18(2): 60. CHEN Rong, FENG Cunqian, LI Jingqing, et al. Three dimensional reconstruction of ballistic target based on micro-Doppler fusion[J]. Journal of Air Force Engineering University (Natural Science Edition), 2017, 18(2): 60. |
| [13] |
李靖卿, 冯存前, 孙宏伟, 等. 基于混合体制雷达网的弹道目标微特征及外形参数提取[J]. 航空学报, 2016, 37(6): 1963. LI Jingqing, FENG Cunqian, SUN Hongwei, et al. Micro-motion feature and shape parameters extraction based on hybrid-scheme radar network for ballistic targets[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1963. |
| [14] |
邹小海, 艾小锋, 李永祯, 等. 基于微多普勒的圆锥弹头进动与结构参数估计[J]. 电子与信息学报, 2011, 33(10): 2413. ZOU Xiaohai, AI Xiaofeng, LI Yongzhen, et al. Precession and structural parameter estimation of the cone-shaped warhead based on the micro-Doppler[J]. Journal of Electronics & Information Technology, 2011, 33(10): 2413. |
| [15] |
梁必帅, 张群, 娄昊, 等. 基于微动特征关联的空间自旋目标宽带雷达三维成像[J]. 电子与信息学报, 2013, 35(9): 2133. LIANG Bishuai, ZHANG Qun, LOU Hao, et al. Three-dimensional broadband radar imaging of space spinning targets based on micro-motion parameter correlation[J]. Journal of Electronics & Information Technology, 2013, 35(9): 2133. |
| [16] |
丁小峰, 范梅梅, 魏玺章, 等. 空间锥体目标窄带雷达成像算法[J]. 中国科学:技术科学, 2010, 40(6): 686. DING Xiaofeng, FAN Meimei, WEI Xizhang, et al. Narrowband imaging method for spatial precession cone-shaped targets[J]. Scientia Sinica (Technologica), 2010, 40(6): 686. |
| [17] |
肖立, 周剑雄, 何峻, 等. 弹道中段目标进动周期估计的改进自相关法[J]. 航空学报, 2010, 31(4): 812. XIAO Li, ZHOU Jianxiong, HE Jun, et al. Improved autocorrelation method for precession period estimation of ballistic target in midcourse[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(4): 812. |
| [18] |
高许岗, 苏卫民, 顾红. 一种基于最小熵准则的新的自聚焦优化算法[J]. 兵工学报, 2010, 31(12): 1659. GAO Xugang, SU Weimin, GU Hong. A novel autofocus optimization algorithm based on minimum entropy criterion[J]. Acta Armamentarii, 2010, 31(12): 1659. |
| [19] |
张贤达. 现代信号处理[M]. 北京: 清华大学出版社, 2002. ZHANG Xianda. Modern signal processing[M]. Beijing: Tsinghua University Press, 2002. |
 2019, Vol. 51
2019, Vol. 51


