2. 西北工业大学 电子信息学院, 西安710129;
3. 中国人民解放军95810部队, 北京100076
2. School of Electronics and Information, Northwestern Polytechnical University, Xi'an 710129, China;
3. Unit 95810 of the Chinese People's Liberation Army, Beijing 100076, China
飞蛾扑火优化算法[1](Moth-flame optimization algorithm, MFO)是澳大利亚Seyedali Mirjalili于2015年提出的一种新型智能优化算法[2-3],具有调节参数少、收敛较快、实现简单等优点,因此常被用于参数优化[4]、最优化计算[5].与改进遗传算法[5]、粒子群算法[6]、蝙蝠算法[6]相比,MFO收敛性能更优,但其在寻优过程中也存在一些不足,如每次迭代中都选取当前最优解导致容易陷入局部最优而早熟收敛、由于种群多样性低导致全局寻优性能较差等.针对此类问题,罗钧等[7]通过引入Logistic混沌序列初始化,提高了解的多样性,增强了算法的寻优性能;匡芳君等[8]结合混沌优化算法改进人工蜂群算法,改进了算法的收敛性能,避免陷入局部最优;薛永生等[9]提出用模拟退火算法改进粒子群算法,能够有效跳出局部最优解,得到近似全局最优解;李志明等[10]提出用Lévy飞行轨迹改进的飞蛾扑火优化算法,提高了收敛速度和寻优精度.
针对MFO算法存在的缺陷,本文借鉴Tent混沌优化、模拟退火算法和遗传算法中的算术交叉操作,提出Tent混沌和模拟退火改进的飞蛾扑火优化算法(Tent chaos and simulated annealing improved month-flame optimization algorithm, TCSA-MFO).该算法首先通过Tent混沌映射初始化种群,使初始种群尽可能地均匀分布于整个解空间,增加解的多样性;然后对每次迭代中当前最优解,通过模拟退火机制产生新解,并将当前最优解和新解按比例加权产生最终的新解,然后以一定的概率接受新解,提高其跳出局部最优的能力.仿真结果表明,该算法能够有效增加种群的多样性,寻优时能够跳出局部最优陷阱,与标准MFO相比,收敛速度更快,寻优精度更高.
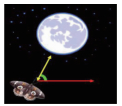
1 飞蛾扑火优化算法 1.1 仿生原理MFO的灵感源于飞蛾夜间飞行中的横向定位[1].飞蛾飞行时常常保持与月亮的夹角不变,由于与月亮距离很远,所以飞蛾与月亮不同时刻连线一直平行,使飞蛾可以沿直线飞行,见图 1所示[1].
|
图 1 横向定位飞行 Fig. 1 Lateral positioning flight |
然而在现实中,飞蛾与火焰距离很近,飞蛾仍然保持与火焰的夹角不变,使得飞蛾沿着等角螺线向火焰飞行,于是就有了“飞蛾扑火”,见图 2[1]所示.Mirjalili正是受到这个等角螺线函数的启发从而发明了MFO算法.

|
图 2 飞蛾扑火 Fig. 2 Moth to the flame |
MFO算法中,M为飞蛾矩阵,即搜索解的智能体,ZM为飞蛾适应度值矩阵,F为火焰位置矩阵,即当前最优解,ZF为火焰适应度值矩阵,如式(1)和(2)所示.初始时刻火焰矩阵和飞蛾矩阵维度相同.
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {{m_{1,1}}}&{{m_{1,2}}}& \cdots &{{m_{1,d}}}\\ {{m_{2,1}}}&{{m_{2,2}}}& \cdots &{{m_{2,d}}}\\ \vdots&\vdots &{}& \vdots \\ {{m_{n,1}}}&{{m_{n,2}}}& \cdots &{{m_{n,d}}} \end{array}} \right],{\mathit{\boldsymbol{Z}}_{\rm{M}}} = \left[ {\begin{array}{*{20}{c}} {{z_{m1}}}\\ {{z_{m2}}}\\ \vdots \\ {{z_{mn}}} \end{array}} \right]; $ | (1) |
| $ \mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {{f_{1,1}}}&{{f_{1,2}}}& \cdots &{{f_{1,d}}}\\ {{f_{2,1}}}&{{f_{2,2}}}& \cdots &{{f_{2,d}}}\\ \vdots&\vdots &{}& \vdots \\ {{f_{n,1}}}&{{f_{n,2}}}& \cdots &{{f_{n,d}}} \end{array}} \right],{\mathit{\boldsymbol{Z}}_{\rm{F}}} = \left[ {\begin{array}{*{20}{c}} {{z_{f1}}}\\ {{z_{f2}}}\\ \vdots \\ {{z_{fn}}} \end{array}} \right]. $ | (2) |
式中:n为飞蛾的个数,d为维度即待求变量的个数.
火焰位置根据适应度值从小到大排序,飞蛾分别围绕排序后的火焰,沿式(3)等角螺线飞行,并通过改变参数t更新其位置.
| $ {M_i} = {D_i}{{\rm{e}}^{bt}}\cos \left( {2{\rm{ \mathsf{ π} }}t} \right) + {F_j}. $ | (3) |
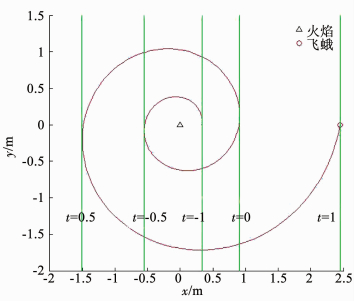
式中:Mi为第i只飞蛾新的位置,Di=|Mi-Fj|为第i只飞蛾与第j个火焰的距离,b为等角螺线参数,决定等角螺线的形状,t为[-1, 1]之间的随机数,控制飞蛾与火焰的距离,见图 3所示.t越小,飞蛾离火焰越近,通过改变t,飞蛾可以到达火焰周围的位置,增强了算法的局部寻优能力.
|
图 3 飞蛾位置随t变化 Fig. 3 Variation of the position of moth with t |
为提高算法的搜索效率,MFO采用火焰自适应减少机制,使得后期收敛更快,而不用在劣解周围继续寻优.火焰数量自适应减少公式为
| $ {N_{\rm{F}}} = {\rm{round}}\left( {{N_{\max }} - I \times \frac{{{N_{\max }} - 1}}{{{I_{\max }}}}} \right). $ | (4) |
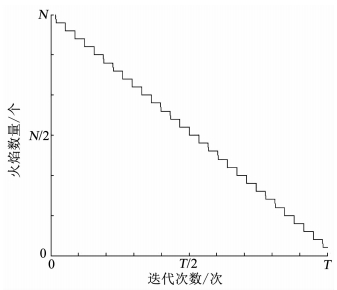
式中:NF为当前火焰数量,Nmax为最大火焰数量,I为当前迭代次数,Imax为最大迭代次数.火焰数量随迭代次数减少变化见图 4所示.
|
图 4 火焰数量自适应减少 Fig. 4 Decreases of the Number of flames with the number of iterations |
当火焰数量少于飞蛾数量时,飞蛾围绕适应度最差的火焰飞行.MFO算法流程如下:
1) 参数初始化.设置飞蛾数量为NM,最大迭代次数为Imax,求解问题维度为d,等角螺线参数为b.
2) 飞蛾位置初始化,即在搜索空间中随机生成飞蛾位置,迭代次数I=1.
3) 将飞蛾位置按适应度值从小到大排序,赋给火焰,作为排序火焰位置.
4) 根据式(3),未排序的飞蛾分别围绕排序后的火焰更新其位置.
5) 记录当前最优火焰适应度值.
6) 根据式(4)减少火焰数量,I=I+1.
7) 判断是否达到最大迭代次数,若达到则输出最优火焰位置和对应适应度值,否则转到3).
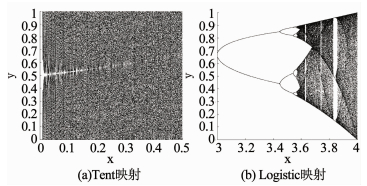
2 Tent混沌和模拟退火改进的飞蛾扑火优化算法 2.1 Tent混沌序列混沌序列具有遍历性和随机性,利用混沌序列可以使初始解分布更加均匀,有利于找到全局最优解.目前常用的混沌序列有Logistic映射和Tent映射两种.单梁等[11]通过研究证明Tent映射较Logistic映射遍历性更好,因此本文选用Tent映射优化初始种群.Tent映射和Logistic映射分布见图 5所示.
|
图 5 Tent和Logistic映射分布对比 Fig. 5 Comparison of tent map and logistic map |
Tent映射公式为
| $ {x_{{\rm{t}} + 1}} = \left\{ \begin{array}{l} 2{x_{\rm{t}}},\;\;\;\;\;\;\;\;\;\;\;0 \le {x_{\rm{t}}} \le 0.5;\\ 2\left( {1 - {x_{\rm{t}}}} \right),\;\;\;\;\;0.5 < {x_{\rm{t}}} \le 1. \end{array} \right. $ | (5) |
模拟退火算法是Metropolis发现物理中固体物质的退火过程与组合优化问题的相似性而提出的一种优化算法.物理退火过程根据温度变化可分为加温过程、等温过程和冷却过程3部分,其中,加温过程对应算法中的设置初始温度.等温过程对应算法中的Metropolis抽样,冷却过程对应减小算法的控制参数.物质的能量对应目标函数,能量最低态就是待求的目标函数最优值.Metropolis准则是模拟退火算法的核心,它以一定的概率接受当前的劣解,从而使算法具有能够跳出局部最优,收敛于全局最优解的能力.
模拟退火算法流程如下(以最小化问题为例):
1) 初始化:设置初始温度为T0,令T=T0,任取初始解S1,确定每个T时的迭代次数,即Metropolis链长L.
2) 对当前温度T和k=1, 2, …, L,重复步骤3)~6).
3) 给当前解S1一个随机扰动,得到新解S2;
4) 计算增量,df=f(S2)-f(S1)为S1的代价函数.
5) 根据Metropolis准则,公式为
| $ P = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\;\;{\rm{d}}f < 0;\\ {{\rm{e}}^{ - \frac{{{\rm{d}}f}}{T}}},\;\;\;\;{\rm{d}}f \ge 0. \end{array} \right. $ | (6) |
如果df < 0,则接受新解;否则,以
6) 判断是否达到终止条件,如果是则输出当前解S1为最优解,然后结束;否则减小温度T后返回步骤2).终止条件为:在连续多个Metropolis链中,都没有接受新解S2,或达到终止温度.
2.3 Tent混沌和模拟退火改进的飞蛾扑火优化算法流程TCSA-MFO算法通过引入Tent混沌映射初始化种群、按照模拟退火机制以一定概率接受劣解,借鉴遗传算法中的算术杂交操作,使算法具有一定的跳出局部最优的能力,从而避免早熟收敛.其中,杂交指对模拟退火产生的新解和旧解按比例杂交加权,得到最终新解.这样得到新解既有利于保留旧解的优点,又能减小扰动误差的影响.公式为
| $ {S_2} = a \times {S_2} + \left( {1 - a} \right) \times {S_1}. $ | (7) |
TCSA-MFO算法流程图见图 6所示,具体流程如下:

|
图 6 TCSA-MFO算法流程图 Fig. 6 TCSA-MFO flow diagram |
1) 参数初始化.设置飞蛾数量为NM,最大迭代次数为Imax,求解问题维度为d,等角螺线参数为b.
2) 飞蛾位置初始化,即在搜索空间中随机生成飞蛾位置后,根据式(5)进行Tent映射,迭代次数I=1,设置模拟退火初始温度T0,降温速率q.
3) 将飞蛾位置按适应度值从小到大排序赋给火焰,作为排序火焰位置.
4) 根据式(3),未排序的飞蛾分别围绕排序后的火焰更新其位置.
5) 对当前最优火焰位置S1根据式(8)产生扰动,即给当前最优火焰位置加上一个偏移量,该偏移量为当前温度与随机数映射到(-1, 1)区间的乘积,得到新的火焰位置S2,并根据式(7)加权得到最终新的火焰位置S2.
| $ {S_2} = {S_1} + T \times \frac{{{\rm{randn}}\left( {1,d} \right)}}{{{\rm{norm}}\left( {{\rm{randn}}\left( {1,d} \right)} \right)}}. $ | (8) |
6) 计算df=f(S2)-f(S1),根据式(6),如果df小于0,则接受S2,否则以
7) 记录当前最优火焰适应度值.
8) 根据式(4)减少火焰数量,T=q×T,I=I+1.
9) 判断是否达到最大迭代次数或终止温度,若达到则输出最优火焰位置和对应适应度值,否则转到3).
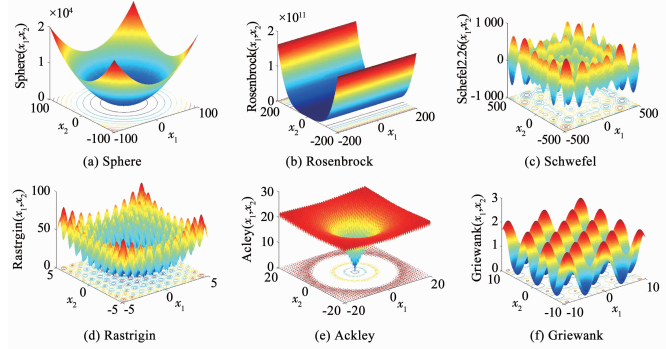
3 仿真实验与结果分析 3.1 基准测试函数本文选取CEC2010中的6个经典基准测试函数[12]来测试算法寻优性能,见图 7和表 1所示.其中,Sphere函数是平滑的单调函数,只有一个全局最小值,用于测试算法的收敛速度;Rosenbrock函数是非凸单峰函数,有多个局部极值,主要用于测试算法的收敛速度和寻优精度;Schwefel2.26、Rastrigin、Ackley和Griewank函数都是复杂的多峰函数,有多个局部极小值,主要用来测试算法的跳出局部极值、避免早熟收敛的全局寻优能力.这些函数可以较为全面地考察算法的寻优性能.
|
图 7 基准函数 Fig. 7 Benchmark functions |
| 表 1 基准测试函数 Tab. 1 Benchmark functions |
为了评价TCSA-MFO算法的有效性,本文用上述基准测试函数进行测试,并与MFO算法进行对比.采用MATLAB R2014a进行仿真,参数设置为:飞蛾种群数量为30,最大迭代次数为1 000,螺旋线参数为1,模拟退火初始温度为100,终止温度为0.001,退火系数为0.99,新解与旧解加权系数为0.5.为了减小误差,取连续运行50次得到的适应度均值作为测试结果.
10维基准函数测试的适应度收敛曲线见图 8~13所示;10维和50维基准函数测试的适应度均值、标准差、收敛时间和迭代次数见表 2所示.

|
图 8 Sphere寻优收敛曲线(10维) Fig. 8 Convergence curves of Sphere (10 dimensions) |
|
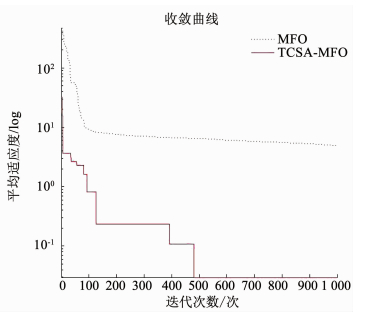
图 9 Rosenbrock寻优收敛曲线(10维) Fig. 9 Convergence curves of Rosenbrock (10 dimensions) |
|
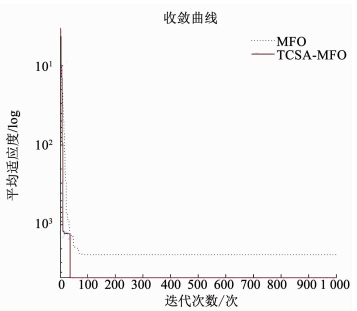
图 10 Schwefel寻优收敛曲线(10维) Fig. 10 Convergence curves of Schwefel (10 dimensions) |
|
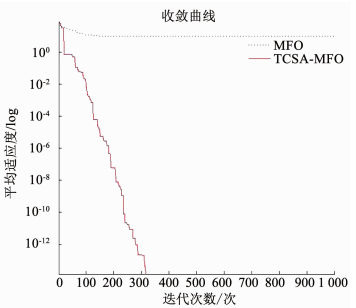
图 11 Rastrigin寻优收敛曲线(10维) Fig. 11 Convergence curves of Rastrigin (10 dimensions) |
|
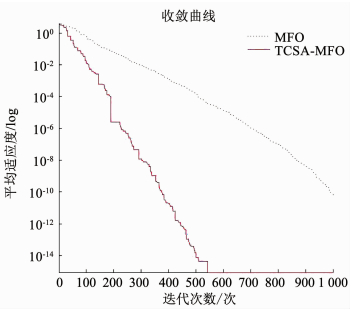
图 12 Ackley寻优收敛曲线(10维) Fig. 12 Convergence curves of Ackley (10 dimensions) |

|
图 13 Griewank寻优收敛曲线(10维) Fig. 13 Convergence curves of Griewank (10 dimensions) |
| 表 2 基准测试函数优化结果对比 Tab. 2 Comparison of optimization results of benchmark functions |
由图 8~13可知,对于单峰函数,TCSA-MFO算法比MFO算法收敛速度更快,寻优精度也更高;对于多峰函数,MFO算法基本都陷入局部最优值,收敛速度慢,而TCSA-MFO算法可以跳出局部最优陷阱,一直搜索最优解,具有良好的全局寻优性能,收敛速度更快.由表 2可知,TCSA-MFO算法的寻优的均值和标准差都比MFO算法的寻优均值和标准差小,证明了TCSA-MFO算法性能更优,且鲁棒性好.尤其是对于Schwefel函数和Rastrigin函数,MFO算法明显早熟收敛,提前停滞于局部最优,而TCSA-MFO几乎达到了全局最小值.
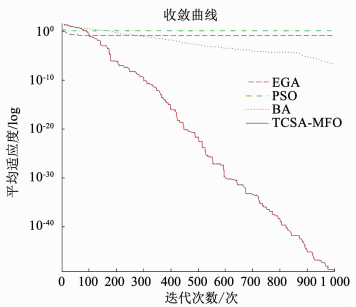
为进一步测试TCSA-MFO算法的性能,本文选取前文提到的改进遗传算法[5](EGA)、粒子群算法[6](PSO)、蝙蝠算法[6](BA)进行对比,用50维Sphere和Rastrigin函数测试,种群数量为30,最大迭代次数为1 000.4种算法寻优时的收敛曲线见图 14和15所示.
|
图 14 Sphere寻优收敛曲线(50维) Fig. 14 Convergence curves of Sphere (50 dimensions) |
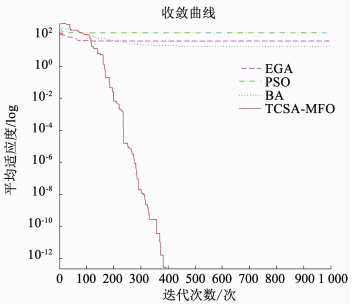
|
图 15 Rastrigin寻优收敛曲线(50维) Fig. 15 Convergence curves of Rastrigin (50 dimensions) |
由图 14和15可知,对于50维Sphere函数和Rastrigin函数寻优,TCSA-MFO相比其他三种智能优化算法,收敛速度更快,寻优精度更高.
综上可知,TCSA-MFO算法由于引进Tent混沌序列初始化和模拟退火中的跳出机制,在函数寻优中具有较好的跳出局部最优的能力,全局寻优性能更优.
3.2.2 航迹规划问题性能分析TCSA-MFO作为一种智能优化算法,可以用于解决多种优化问题,比如航迹规划、目标分配等.本文选择航迹规划问题对算法性能进一步测试.
航迹规划问题一般等效为在给定离散空间中,从起点到终点的一条可行路径的搜索问题.借鉴向祖全等[13]研究成果,建立航迹规划模型.选择适应度函数为航迹长度,函数值越小航迹越优,当航迹与禁飞区等交叉时函数值为无穷大.计算公式为
| $ P = {L_{{\rm{S}}{{\rm{P}}_1}}} + \sum\limits_{i = 1}^{n - 1} {{L_i}{L_{i + 1}}} + {L_{{P_{\rm{n}}}{\rm{G}}}} = \sum\limits_{i = 0}^n {{L_{{P_i}}}{L_{{P_{i + 1}}}}} , $ | (9) |
| $ F\left( i \right) = \left\{ \begin{array}{l} {L_{{\rm{SG}}}} = \sum\limits_{i = 0}^n {{L_{{P_i}}}{L_{{P_{i + 1}}}}} ,{L_{{P_i}}}{L_{{P_{i + 1}}}} \cap {D_{{\rm{NF}}}} = \emptyset ;\\ + \infty \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{L_{{P_i}}}{L_{{P_{i + 1}}}} \cap {D_{{\rm{NF}}}} \ne \emptyset . \end{array} \right. $ | (10) |
式中:S为起点,G为终点,LPiLPi+1为航迹点i和航迹点i+1之间的距离,DNF为禁飞区和威胁源(当飞机进入威胁源范围内时容易被击落,所以认为威胁源为不可进入区域).
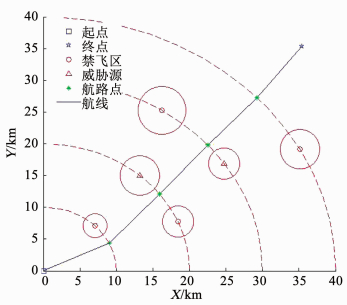
实验设置:以航迹起点为坐标原点,建立极坐标系,终点为(0.785 rad,50 km),禁飞区和威胁源位置参数见表 3所示.种群数量为30,搜索维度为4,最大迭代次数为1 000.TASA-MFO算法得到的最优航迹见图 16和17所示.
| 表 3 禁飞区和威胁源参数 Tab. 3 Parameters of no-fly zone and threat source |
|
图 16 TCSA-MFO算法规划最优航迹 Fig. 16 Optimal trajectory obtained by TCSA-MFO algorithm |
|
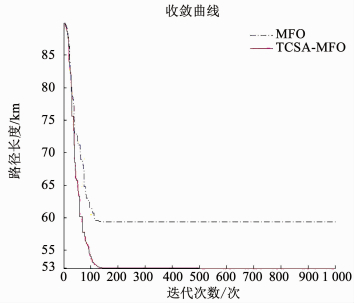
图 17 航迹长度收敛曲线 Fig. 17 Convergence curve of route length |
仿真结果表明,与标准MFO算法相比,TASA-MFO算法经过100代基本可以得到最优航迹长度为53 km,而MFO算法在60 km时基本陷入了局部最优值.因此,TCSA-MFO算法可以用于求解航迹规划问题,搜索精度较高,航迹较优.
4 结论针对标准MFO算法存在的问题,本文提出了一种改进的飞蛾扑火优化算法(TCSA-MFO),通过引入Tent混沌映射初始化和模拟退火中的Metropolis准则,改善了算法的寻优性能.该算法相比MFO算法主要有以下特点:
1) 引入Tent混沌映射初始化种群,使种群尽可能均匀分布在整个解空间.
2) 引入模拟退火机制,对迭代中的当前最优解产生扰动,生成新解,然后根据Metropolis准则判断是否接受该新解,即以一定的概率接受劣解,增强算法跳出局部最优能力.
3) 对扰动生成的新解和当前最优解杂交相加,得到最终的新解,既保留当前最优解的优势,又增加局部寻优的能力.
4) 6个基准函数寻优测试和航迹规划性能测试表明,TCSA-MFO算法在寻优过程中,因Tent初始化和模拟退火改进能防止早熟收敛,具备良好的全局寻优能力,收敛速度较快,精度较高,鲁棒性较好.
下一步研究如何将TCSA-MFO算法应用到更复杂的优化问题中去,并学习借鉴其他智能优化算法,提出性能更优的全局优化算法.
| [1] |
MIRJALILI S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm[J]. Knowledg-e-Based Systems, 2015, 89: 228. DOI:10.1016/j.knosys.2015.07.006 |
| [2] |
MIRJALILI S. The ant lion optimizer[J]. Advances in Engineering Software, 2015, 83(C): 80. DOI:10.1016/j.advengsoft.2015.01.010 |
| [3] |
MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69(3): 46. DOI:10.1016/j.advengsoft.2013.12.007 |
| [4] |
包义钊, 殷保群, 曹杰, 等. 基于飞蛾-烛火优化算法的贝叶斯网络结构学习[J]. 计算机工程, 2018, 44(1): 187. BAO Yizhao, YIN Baoqun, CAO Jie, et al. Bayesian network structure learning based on moth-flame optimization algorithm[J]. Computer Engineering, 2018, 44(1): 187. DOI:10.3969/j.issn.1000-3428.2018.01.032 |
| [5] |
王子琪, 陈金富, 张国芳, 等. 基于飞蛾扑火优化算法的电力系统最优潮流计算[J]. 电网技术, 2017, 41(11): 3641. WANG Ziqi, CHEN Jinfu, ZHANG Guofang, et al. Optimal power flow calculation with moth-flame optimization algorithm[J]. Power System Technology, 2017, 41(11): 3641. DOI:10.13335/j.1000-3673.pst.2017.0657 |
| [6] |
李志明, 莫愿斌, 张森. 一种新颖的群智能优化算法:飞蛾扑火优化算法[J]. 电脑知识与技术, 2016, 12(31): 172. LI Zhiming, MO Yuanbin, ZHANG Sen. A novel swarm intelligence optimization algorithm: Moth-flame optimization algorithm[J]. Computer Knowledge and Technology, 2016, 12(31): 172. DOI:10.14004/j.cnki.ckt.2016.4156 |
| [7] |
罗钧, 李研. 具有混沌搜索策略的蜂群优化算法[J]. 控制与决策, 2010, 25(12): 1913-1916. LUO Jun, LI Yan. Artificial bee colony algorithm with chaotic-search strategy[J]. Control and Decision, 2010, 25(12): 1913. DOI:10.13195/j.cd.2010.12.156.luoj.013 |
| [8] |
匡芳君, 徐蔚鸿, 金忠. 自适应Tent混沌搜索的人工蜂群算法[J]. 控制理论与应用, 2014, 31(11): 1502. KUANG Fangjun, XU Weihong, JIN Zhong. Artificial bee colony algorithm based on self-adaptive tent chaos search[J]. Control Theory & Applications, 2014, 31(11): 1502. DOI:10.7641/CTA.2014.31114 |
| [9] |
薛永生, 吴立尧. 基于模拟退火的改进粒子群算法研究及应用[J]. 海军航空工程学院学报, 2018, 33(2): 248. XUE Yongsheng, WU Liyao. Research and application of improved PSO algorithm based on simulated annealing[J]. Journal of Naval Aeronautical and Astronautical University, 2018, 33(2): 248. DOI:10.7682/j.issn.1673-1522.2018.02.012 |
| [10] |
李志明, 莫愿斌. 基于Lévy飞行的飞蛾扑火优化算法[J]. 计算机工程与设计, 2017, 38(3): 807. LI Zhiming, MO Yuanbin. Moth-flame optimization algorithm based on Lévy flights[J]. Computer Engineering and Design, 2017, 38(3): 807. DOI:10.16028/j.issn1000-7024.2017.03.046 |
| [11] |
单梁, 强浩, 李军, 等. 基于Tent映射的混沌优化算法[J]. 控制与决策, 2005, 20(2): 179. SHAN Liang, QIANG Hao, LI Jun, et al. Chaotic optimization algorithm based on tent map[J]. Control and Decision, 2005, 20(2): 179. DOI:10.3321/j.issn:1001-0920.2005.02.013 |
| [12] |
LIAO X, ZHOU J Z, OUYANG S, et al. An adaptive chaotic artificial bee colony algorithm for short-term hydrothermal generation scheduling[J]. Electrical Power and Energy Systems, 2013, 53(1): 34. DOI:10.1016/j.ijepes.2013.04.004 |
| [13] |
向祖权, 靳超, 杜开君, 等. 基于粒子群优化算法的水面无人艇分层局部路径规划[J]. 武汉理工大学学报, 2015, 37(7): 38. XIANG Zuquan, JIN Chao, DU Kaijun, et al. Local obstacle avoidance for unmanned surface vehicle using a hierarchical strategy based on particle swarm optimization[J]. Journal of Wuhan University of Technology, 2015, 37(7): 38. DOI:10.3963/j.issn.1671-4431.2015.07.008 |
| [14] |
PAN T S, DAO T K, PAN J S, et al. An unmanned aerial vehicle optimal route planning based on compact artificial bee colony[C]//Advances in Intelligent Information Hiding and Multimedia Signal Processing (IHMS). Kaohsiung, Taiwan: Springer, 2016: 361. DOI: 10.1007/978-3-319-50212-0_43
|
| [15] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of the IEEE International Conference on Neural Networks (ICNN). Piscataway, NJ: IEEE Press, 1995: 1942. DOI: 10.1109/ICNN.1995.488968
|
| [16] |
GAO W F, LIU S Y. A modified artificial bee colony algorithm[J]. Computer & Operations Research, 2012, 39(3): 687. DOI:10.1016/j.cor.2011.06.007 |
 2019, Vol. 51
2019, Vol. 51

 , 张一杰2, 于洋3, 张振兴1
, 张一杰2, 于洋3, 张振兴1