纤维增强复合材料由于其具有高比强度和比模量的性能特点,且具有抗疲劳性能好,可设计性能好等优势[1],被广泛的应用于各结构设计领域.潜艇耐压壳结构在深水环境下需要承受巨大的静水压力.传统的金属制潜艇耐压壳,通常采用环肋圆柱壳结构,通过间隔较密集的环肋结构提升金属圆柱壳的结构稳定性[2],其结构重量较大,较密集的环肋结构减小了舱室的可使用容积,且声隐身和磁隐身性能存在瓶颈.复合材料耐压壳结构具有优越的无磁、透波、轻质高强和结构具有可设计性的有点,且可以通过结构的合理设计提高整体结构的承载效率,从而进一步减轻结构重量[3].同时,复合材料耐压壳结构可以采用夹芯复合材料结构,通过增加壳体的厚度,增加壳体的耐压稳定性,提高了耐压壳的承载能力,且可以对芯材进行功能设计,使夹芯复合材料耐压壳具有优良的声隐身、磁隐身性能[4].
钢制环肋圆柱壳领域,已经有了很多较为成熟的研究,除了在结构设计问题外,还有在应力和稳定性问题[5],振动特性问题[6],带有初始缺陷的应力和稳定性问题[7],以及流固耦合下结构在冲击载荷下的动屈曲问题[8]等.在结构设计问题方面,目前的主要研究方向是环肋侧向屈曲问题[2, 9],长舱段肋骨的布置问题[10]和结构尺寸的多变量分析问题[11].从上述研究可以得到结论:钢制环肋圆柱壳的环肋通常采用T型截面.环肋的侧向屈曲机理为在肋骨腹板发生侧倾时,圆柱壳壳板对环肋根部存在转动约束作用,从而使肋骨腹板发生弯扭变形.肋骨型号对圆柱壳的整体临界屈曲载荷有较大的影响,既当肋骨强度刚度不足时,壳体的整体临界屈曲载荷会有大幅下降.此外,也有关于环肋对耐压壳的支撑能力研究[12],以及环肋损伤对耐压壳承载能力的影响研究[13].
目前,一些研究探讨了复合材料耐压壳和夹芯复合材料耐压壳的承载问题,李卓禹[14]使用了Abaqus仿真研究了刚性的MPC固定边界下的夹芯复合材料耐压壳承载问题;熊传志[15]的研究使用了ANSYS对复合材料耐压壳体进行了仿真计算,将纤维缠绕层作为层合板来处理,其仿真模型为长舱段模型,没有考虑整体成型的工艺可行性;程研雪[16]的研究使用了ANSYS软件对复合材料耐压壳的应力损伤进行了研究,而没有进行结构稳定性的研究.本文针对夹芯复合材料耐压壳在静水压力下的承载能力问题,以有限元仿真的方法,结合结构的成型工艺可行性,以在保证结构承载能力的前提下提高结构舱室的使用效率和降低结构重量为目的,进行了设计研究.
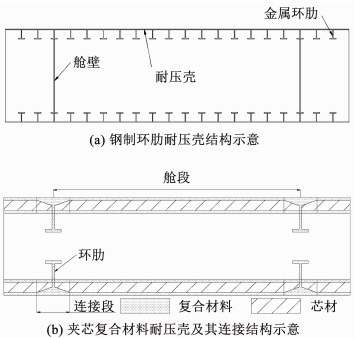
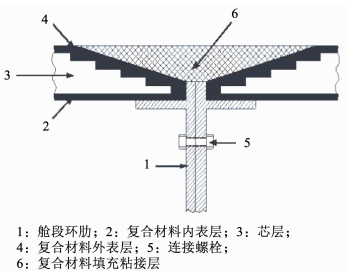
1 复合材料舱段环肋结构的提出以目前的发展趋势,潜艇结构向着大舱室、单壳耐压壳的结构形式发展.传统的钢制耐压壳结构通常采用间隔较密集的环肋提升结构稳定性,其结构形式见图 1(a).其结构设计中,环肋需要在满足自身不会产生侧向屈曲的情况下相邻环肋间的壳体不会在许用载荷下发生屈曲,舱段环肋或舱壁需要满足自身不会产生侧向屈曲的情况下分段不会在许用载荷下发生屈曲[2, 9-10].对于复合材料夹芯耐压壳结构而言,可以在复合材料表层厚度满足强度要求的前提下,通过增加芯材的厚度来达到增加耐压壳的整体刚度的目的.在现有的工程应用中,在航空航天领域,全复合材料环肋已经被应用于机翼骨架等结构中,全复合材料环肋和复合材料面板的粘接问题在工艺上是可靠的[17].考虑制造工艺的可行性,夹芯复合材料耐压壳可以采用分段缠绕技术进行加工,在芯层圆柱壳的内外表面上缠绕复合材料内外表层,并对分段进行固化成型.然后,使用坡口填充连接结构将分段拼接成整体,其局部结构见图 2.分段边缘的芯层削成坡口在缠绕内外复合材料表层并固化成型后与预制的复合材料环肋结构一起进行粘合拼接,最后在坡口位置的凹槽内通过复合材料缠绕技术或者预浸料铺设技术将凹槽填实后局部固化成型,从而完成分段的连接.使用此种技术方法制作的夹芯复合材料耐压壳单分段及其相邻连接结构的结构形式见下图 1(b).耐压壳体提供结构强度和一部分结构刚度,舱段环肋除了起到连接分段的作用外,也能给壳体提供支撑,提高结构的整体稳定性.图 1(a)、(b)两图为示意图,为方便显示,其构件的尺寸没有按照实际结构的尺寸比例.
|
图 1 钢制与复合材料耐压壳示意 Fig. 1 Diagrams of the steel made and sandwich composite made pressure shells structures |
|
图 2 连接结构示意 Fig. 2 Diagram of the connection structure |
由于夹芯复合材料耐压壳的可设计性与建造工艺的灵活性,其线型可以根据芯层的形状和铺层设计进行调整,所以这种结构形式可以满足潜艇单壳耐压壳结构形式的发展需求.另一方面,为了满足大舱室结构设计的需要,舱段环肋的结构形式可以在满足支撑壳体功能的情况下,尽可能占用较小的空间,从而不影响数个分段作为一个整体舱室的使用功能.在具有诸多优势的情况下,夹芯复合材料耐压壳在设计上仍然存在一些技术难点,包括耐压壳体复合材料铺层设计,壳体的夹芯功能性设计,舱段尺寸优化设计,以及舱段环肋结构的设计.本文针对舱段环肋结构的设计问题,通过基于Abaqus的有限元仿真方法,在夹芯复合材料耐压壳舱段结构一定的情况下,对舱段环肋的结构形式以及其对舱段起到的支撑作用进行了研究分析.
2 仿真计算方法与验证在Abaqus软件中使用实体单元对模型进行建模,对于夹芯圆柱壳的芯层部分,使用C3D8R单元进行模拟.对于结构中的复合材料部分,使用SC8R连续壳(Continuum Shell)单元,结合Property中的Composite Layup模块进行模拟.并在Composite Layup模块中设置复合材料的铺层属性,包括材料属性、铺层厚度.铺层角度,坐标系等.仿真计算使用的材料其基本材料属性见表 1和表 2.芯层使用一种轻质高强的浮体泡沫材料,复合材料使用的T300碳纤维增强的树脂基复合材料.
| 表 1 碳纤维增强复合材料材料属性 Tab. 1 Material properties of the carbon fiber enhanced composite |
| 表 2 浮体材料材料属性 Tab. 2 Float material properties |
因为上文所述的夹芯复合材料耐压壳结构为薄壳圆柱壳结构,在仿真计算研究中优先考虑结构的屈曲失效.使用Buckling分析步,计算结构的一阶屈曲,得到结构的一阶临界屈曲载荷和屈曲模态.然后,对结构在达到临界屈曲载荷之前是否发生了应力失效进行验证,使用Static分析步,对结构加载临界屈曲载荷,并通过导入节点文件的方法,将屈曲扰动添加到应力计算中.本文使用Hashin准则作为判定复合材料结构应力损伤的标准,Hashin理论中,平面应力状态单向纤维复合材料有纤维失效和基体失效两种失效模式.对于两种失效模式又分别存在拉伸和压缩两种应力状态,所以对于一个有限元单元,存在纤维拉伸、纤维压缩、基体拉伸、基体压缩4种损伤模式并对应4个判定标准值[18-19].在输出中添加4个Hashin准则和相关的输出项,当计算结果中结构中出现了某个Hashin标准值大于1时则认为结构在加载到临界屈曲载荷之前已发生了应力损伤,损伤方式与大于1的Hashin标准值相对应,且结构的损伤区域即为计算结果中Hashin标准值大于1的区域.若结构在临界屈曲载荷已发生应力损伤,则也可以通过仿真计算最大Hashin标准值等于1时的载荷进行预估,具有较高的准确性.Hashin准则针对结构中的复合材料部分,为参加强度计算,需要在复合材料的材料属性中添加强度属性见表 3.
| 表 3 复合材料强度材料属性 Tab. 3 Composite material strength properties |
在复合材料夹芯结构中,芯层的强度远小于复合材料层,主要通过提供厚度增加结构的整体刚度和稳定性,在应力计算中没有考虑芯层的损伤.
在之前本人的研究中,针对夹芯复合材料耐压壳单舱段模型进行了2个模型试验,并通过试验结果和仿真结果对比的方法验证了仿真方法的正确性.两个模型试验使用了模量相差很大的两种芯层材料,低模量模型发生了屈曲损伤,高模量模型发生了应力损伤,其试验结果与仿真结果的对比见表 4,上述仿真方法得到的计算结果与试验结果误差较小.
| 表 4 试验结果与仿真结果对照 Tab. 4 Comparison of the experimental and the simulated results |
本研究针对实尺度耐压壳舱段的承载能力进行仿真计算,按照现有潜艇的常用尺度建立模型,假设复合材料耐压壳分段的单段长度为8 m,直径为7 m,分段连接段长度为1.2 m,耐压壳总厚度为240 mm.夹芯复合材料圆柱壳部分,芯层厚200 mm,复合材料外表层和内表层厚度为20 mm,按照等强度设计,夹芯复合材料段的内外表层的复合材料铺层角度为±55°.分段连接段厚度与夹芯段相同,其中大部分结构为复合材料结构,由于连接段结构较复杂,且其部分结构的尺寸需要按照实际工艺需要进行调整,所以在仿真中将其考虑成完整的铺层方向为圆柱壳环向的全复合材料圆柱壳结构.此等效结构的实际强度和刚度略大于实际的连接段,因为研究对象是支撑连接段的舱段环肋,所以本研究中得到的仿真结果较实际结构的承载能力略微偏高.
为保证计算精度,将网格尺寸定为20 mm.为考虑实际的边界,在研究目标分段的两端各自再设置一个分段,各分段由连接段进行连接,并在外部分段的两端设置边界条件,一端设置为固支,另一端设置为可沿着圆柱壳轴向平移的固支.研究模型范围包括3段分段和夹在中间的2段连接段,5段模型各自与相邻的模型通过Tie相互连接.在实际工况中,圆柱壳体和两端的端部截面都需要承受静水压力,所以在整个模型的圆柱壳外壳上加载1 MPa的静水压力,然后将加载在圆柱壳两端截面上的1 MPa静水压力按照力等效加载在模型两端的圆柱壳的圆环截面上,大小为7.551 MPa.模型见图 3.

|
图 3 仿真模型示意 Fig. 3 Diagram of the simulation model |
为方便调整模型,环肋结构单独作为一个Part进行建模,使用Tie与连接段模型相连接.环肋结构采用T型筋截面,环肋的腹板与圆柱壳横截面方向垂直,环肋面板为环形板,方向与圆柱壳方向相同.由于复合材料的各向异性属性,铺层角度对环肋的支撑性能的影响很大.所以除了环肋腹板和面板的尺度,腹板和面板的铺层角度和铺层方法也是环肋的重要设计参数.根据模型尺寸结合相应的钢结构耐压壳强环肋的设计经验,将初始T型筋截面的尺寸定为腹板高度600 mm,厚度40 mm,面板宽度400 mm,厚度60 mm,并在此结构的基础上结合计算结果对结构进行修正.根据结构在静水压力下的应力状态分析,环肋面板主要承受圆柱壳环向的压缩载荷,结构整体存在环向的压应力,所以需要增强面板环向的强度.根据复合材料的特性,对于单向纤维复合材料,纤维方向的强度最大,所以将环肋面板的铺层方向定位环向,可以通过单向纤维布铺设或者纤维缠绕的工艺进行成型加工.环肋腹板除了产生环向压应力之外,考虑到圆柱壳变形时圆柱壳会给腹板根部施加一个正压力和侧向弯矩,所以环肋腹板还会受到圆柱壳直径的径向正应力和切向剪应力.所以在考虑腹板的铺层方向时需要考虑环向压应力外,还需要考虑腹板自身的侧向失稳问题.基于此,结合可行的成型工艺提出了两种腹板的铺层方案,一种是腹板使用正交纤维布进行铺层,对于腹板采用直角坐标系,铺层厚度为z方向,纤维方向为x方向和y方向交替铺层.第二种为使用纤维缠绕技术,将纤维方向定为按柱坐标系固定沿环向缠绕.
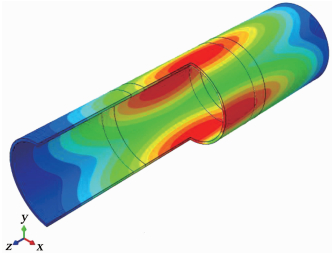
4 仿真计算结果对没有设置环肋的原始壳体模型进行计算,得到结构的极限屈曲载荷为2.856 2 MPa,屈曲模态见图 4.在没有环肋支撑的情况下,结构发生了整体的屈曲.可见,在没有环肋支撑的情况下,连接段的刚度不足以支撑各个分段.按照之前所述的建模方法和环肋设计方案进行了一系列仿真计算,其结果见表 5.
|
图 4 无环肋壳体屈曲模态 Fig. 4 Buckling mode of the model without rib-ring |
| 表 5 结构屈曲仿真计算结果 Tab. 5 Results of the buckling simulation model |
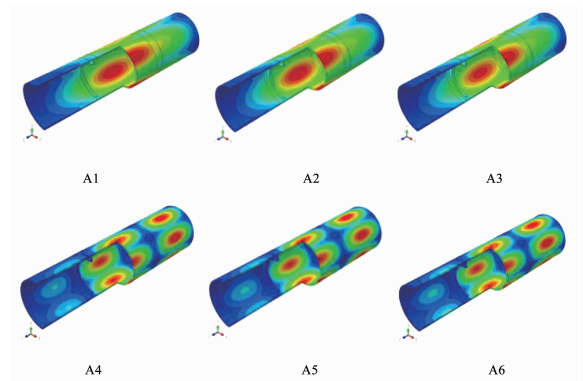
除了原始结构之外,仿真算例共分为3个系列,A系列为腹板正交铺层的环肋结构系列,环肋的尺寸和铺层数据见表 4.屈曲载荷随腹板高度的增高而增长.在腹板高度从600 mm增长到700 mm的区间,结构的屈曲载荷迅速增长,而当腹板高度达到750 mm时,屈曲载荷的增长趋势明显减缓,大约维持在7.09 MPa.A系列各个模型的屈曲模态见图 5.
|
图 5 A系列结构屈曲模态 Fig. 5 Buckling mode of series A |
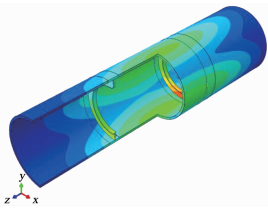
B系列中,当腹板高度从600 mm增加到800 mm时,结构的屈曲载荷骤然下降到2.945 9 MPa,略微大于没有环肋支撑的原始结构的屈曲载荷2.856 2 MPa.可见在B2模型中,环肋没有起到明显的支撑结构的作用.通过观察B2结构屈曲模态见图 6.所以,对于腹板环向铺层的环肋结构,由于腹板缺少径向纤维的支撑,当腹板高度增加到800 mm时,环肋腹板自身先于圆柱壳体发生了侧向屈曲.可以通过增加腹板厚度的方式防止环向铺层腹板发生侧向屈曲,从而利用这种铺层方式所得到的较强的环向强度和刚度.得到的模型系列即为C系列.
|
图 6 B2模型的屈曲模态 Fig. 6 Buckling mode of model B2 |
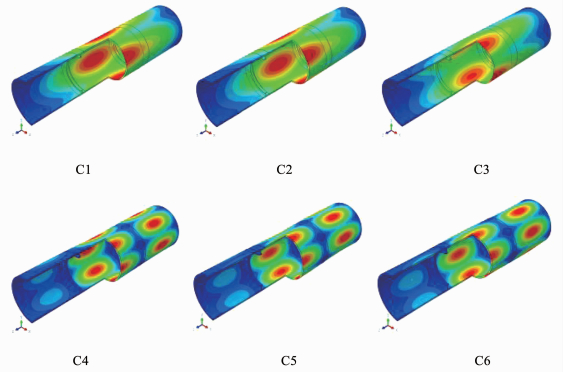
C系列的屈曲模态见7.C系列和A系列的计算结果有相似的规律,在腹板高度增加的第一阶段,结构的屈曲载荷快速上升,当腹板高度满足环肋的临界环肋高度后,腹板高度的增加对屈曲载荷的上升没有显著的影响.
|
图 7 C系列结构屈曲模态 Fig. 7 Buckling mode of series C |
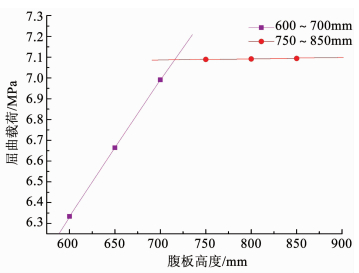
分析A系列的计算结果可见,从600 mm腹板到700 mm腹板模型,结构的屈曲模态呈模型的整体屈曲.而当腹板高度增加到750 mm以上时,结构的屈曲模态呈以连接段为界的以单个分段为单位的分段屈曲.所以当环肋的腹板升高到一定高度时,环肋所提供的刚度可完全支撑该区域的壳体不产生变形,从而将结构的屈曲限定在单个分段内.根据以上结果可以得到合理的推断,使结构达到单分段屈曲的腹板高度为图 8中两段趋势线的交点.计算的交点所对应的腹板高度为715.126 mm,向上取整为720 mm.对肋骨高为720 mm的A环肋结构进行屈曲计算,得到屈曲载荷为7.087 3 MPa,屈曲模态为单分段屈曲,所以两段趋势线的交点即为屈曲模态改变的拐点,称这个对应这个拐点对应的环肋高度为环肋有效支撑的临界环肋高度.为了考察该屈曲载荷下结构是否产生应力破坏,对腹板高度为720 mm的A模型在屈曲载荷下的应力状态进行计算,得到屈曲载荷下结构的Hashin标准值见表 6.可见在屈曲载荷下,此结构并没有发生应力损伤,结构在静水压力下的损伤方式为屈曲损伤.在Hashin标准值中,基体最大拉伸标准值为0.982 9,接近1,位置出现在环肋腹板和面板的连接处,是由于局部的三向应力状态较为复杂且由于外形突变产生了应力集中的现象.但是在屈曲载荷下,尚未出现应力破坏.在A系列中,当腹板高度到达720 mm满足临界环肋高度后,腹板高度的增加对结构屈曲载荷的影响不显著,720 mm为考虑工艺和安全余量后使结构达到单分段屈曲的最小腹板高度.
|
图 8 A系列屈曲载荷随腹板高度的增长趋势 Fig. 8 Growth trend of series A under buckling load |
| 表 6 A系列720 mm模型在屈曲载荷下的Hashin标准值 Tab. 6 Hashin results of 720 mm model in series A under buckling load |
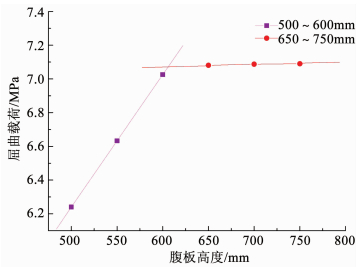
比较满足临界环肋高度后,A系列和C系列的计算结果发现当结构发生单分段屈曲后,两个系列的屈曲载荷非常相近.当结构发生单分段屈曲时,单个屈曲波形被限定在单个分段的范围内,此时包括环肋在内的连接段可以看成是屈曲分段的边界.所以可以推断当环肋满足临界环肋高度模型发生单分段屈曲时,模型的屈曲载荷与连接段和环肋的刚度没有显著的关系,屈曲载荷仅与夹芯复合材料圆柱壳自身的属性相关.与A系列相同,通过分析屈曲载荷上升趋势图 9,可以得到对应临界环肋高度的腹板高度为606.648 mm.向上取整腹板高度为610 mm的模型屈曲载荷为7.078 3 MPa,在屈曲载荷下的Hashin标准值计算结果如表 7所示,没有发生应力损伤.由于C系列中环肋腹板和面板连接部位局部结构较A系列结构更强,在这个局部的基体拉伸标准值并没有接近1.所以在C系列中,当腹板高度增加到610 mm后,环肋结构的支撑刚度满足临界环肋高度,腹板高度的增加对结构屈曲载荷的影响不显著,610 mm为使结构达到单分段屈曲的最小腹板高度.
|
图 9 C系列屈曲载荷随腹板高度的增长趋势 Fig. 9 Growth trend of series C under buckling load |
| 表 7 C系列610mm结构在屈曲载荷下的Hashin标准值 Tab. 7 Hashin results of 610 mm model in series C under buckling load |
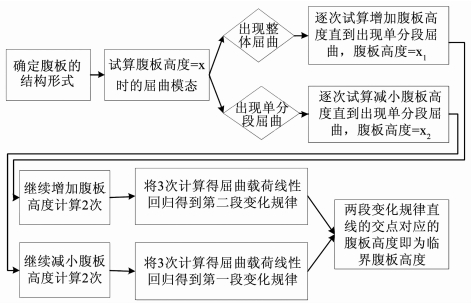
综上,环肋临界高度的确定方法为:首先通过仿真计算求得某种环肋的数个环肋高度对应的屈曲载荷,然后根据计算结果得到的屈曲模态确定临界环肋高度所在的高度区间,并计算达到临界环肋高度前和达到临界环肋高度后结构的屈曲载荷随环肋高度的变化趋势线.两条直线的交点所对应的位置即可确定为临界环肋高度.
6 结论根据上述研究结果可以得出以下结论:
1) 通过设置环肋可以有效地提高夹芯复合材料耐压壳长舱段的稳定性.
2) 当环肋的支撑高度增加到一定值时,长舱段的整体屈曲模态会被环肋边界限制转变为单个分段屈曲的多段屈曲模态,该环肋高度称为环肋有效支撑的临界环肋高度.在工程设计中,设计目标应为环肋高度大于临界环肋高度.
3) 本文给出的环肋有效支撑的临界环肋高度的确定方法可供工程设计时参考.
4) 当环肋高度大于临界环肋高度时,结构的临界屈曲载荷与环肋的属性关系不大,只与夹芯圆柱壳自身的尺寸与材料属性有关,称为分段屈曲载荷.
5) 当复合材料环肋的自身侧向稳定性不足时,环肋无法对圆柱壳体起到支撑作用,可以通过增加环肋腹板厚度增加环肋的自身侧向稳定性.
6) 本文所计算的夹芯复合材料耐压壳结构可以承载的静水压力大于7.0 MPa,在结构发生屈曲损伤之前,并不会产生应力破坏.
归纳得到的临界腹板高度计算流程图见图 10.本文的研究结果适用于各种使用环肋进行支撑的耐压壳结构.
|
图 10 临界环肋高度计算方法流程图 Fig. 10 Calculation flow chat of rib-ring critical height |
| [1] |
徐月明, 船用柴油机SCR催化剂选型及性能评价研究[D].武汉理工大学, 2012 XU Yueming. Study on marine engine SCR catalyst design and performance evaluation[D]. Wuhan: Wuhan University of Technology, 2012 |
| [2] |
王金, 吴梵, 张二, 等. 环肋圆柱壳肋骨侧向稳定性理论分析[J]. 船舶工程, 2015, 37(11): 10. WANG Jin, WU Fan, ZHANG Er, et al. Theoretical analysis of frame tripping of ring stiffened cylindrical shell[J]. Ship Engineering, 2015, 37(11): 10. |
| [3] |
蒋鞠慧. 复合材料加筋壳稳定性研究[J]. 玻璃钢/复合材料, 2001(3): 5. JIANG Juhui. Stability of composite stiffened cylindrical shells under external pressure[J]. Fiber Reinforced Plastics/Composites, 2001(3): 5. |
| [4] |
朱锡, 石勇, 梅志远. 夹芯复合材料在潜艇声隐身结构中的应用及其相关技术研究[J]. 中国舰船研究, 2007, 2(3): 34. ZHU Xi, SHI Yong, MEI Zhiyuan. Laminated compound material and technologies in the development of acoustic stealth structure in submarine[J]. Chinese Journal of Ship Research, 2007, 2(3): 34. DOI:10.3969/j.issn.1673-3185.2007.03.008 |
| [5] |
GOLMAKANI M E, EMAMI M. Buckling and large deflection behaviors of radially functionally graded ring-stiffened circular plates with various boundary conditions[J]. Applied Mathematics and Mechanics(English Edition), 2016, 37(9): 1131. DOI:10.1007/s10483-016-2122-6 |
| [6] |
王金朝, 曹贻鹏, 黄齐上, 等. 任意边界条件下环肋圆柱壳振动特性的建模与求解[J]. 固体力学学报, 2017, 38(3): 271. WANG Jinzhao, CAO Yipeng, HUANG Qishang, et al. Modelling and solution on vibration characteristics of ring-stiffened cylindrical shell with arbitrary boundary conditions[J]. Chinese Journal of Solid Mechanics, 2017, 38(3): 271. |
| [7] |
白雪飞, 郭日修. 带有损伤凹陷的环肋圆柱壳应力和稳定性分析[J]. 海军工程大学学报, 2010, 22(3): 76. BAI Xuefei, GUO Rixiu. Analysis of stress and stability of damaged ring-stiffened cylindrical shell[J]. Journal of Naval University of Engineering, 2010, 22(3): 76. |
| [8] |
袁建红, 朱锡, 张振华. 水下爆炸载荷作用下环肋加筋圆柱壳结构的弹塑性动力屈曲[J]. 爆炸与冲击, 2012, 32(6): 585. YUAN Jianhong, ZHU Xi, ZHANG Zhenhua. Dynamic bulking of a ring-stiffened cylindrical shell subjected to underwater explosive loading[J]. Explosion and Shock Waves, 2012, 32(6): 585. DOI:10.3969/j.issn.1001-1455.2012.06.005 |
| [9] |
吴梵, 王金, 刘勇, 等. 几何参数对环肋圆柱壳肋骨侧向稳定性的影响[J]. 中国舰船研究, 2015, 10(4): 59. WU Fan, WANG Jin, LIU Yong, et al. Effects of geometric parameters on frame tripping in the ring-stiffened cylinder[J]. Chinese Journal of Ship Research, 2015, 10(4): 59. DOI:10.3969/j.issn.1673-3185.2015.04.009 |
| [10] |
宋世伟, 张二, 吴梵. 基于Abaqus的环肋圆柱壳长舱段稳定性分析与结构优化[J]. 船海工程, 2011, 40(6): 79. SONG Shiwei, ZHANG Er, WU Fan. Buckling analysis and structural optimal design for Abaqus long ring-stiffened cylindrical shells[J]. Ship & Ocean Engineering, 2011, 40(6): 79. DOI:10.3963/j.issn.1671-7953.2011.06.021 |
| [11] |
梁来雨, 汪志强. 基于多变量分析的环肋圆柱壳结构特性研究[J]. 海洋技术学报, 2017, 36(3): 97. LIANG Laiyu, WANG Zhiqiang. Study on the structural characteristics of ring-stiffened cylindrical shell using multivariate analysis[J]. Journal of Ocean Technology, 2017, 36(3): 97. |
| [12] |
王小明. 纵骨对环肋圆柱壳肋间壳板稳定性的影响[J]. 舰船科学技术, 2017, 39(4): 35. WANG Xiaoming. Longitudinals influence on stability of shell between ribs for ring-stiffened cylindrical shell[J]. Ship Science and Technology, 2017, 39(4): 35. DOI:10.3404/j.issn.1672-7619.2017.04.007 |
| [13] |
马晓龙, 吴梵, 张二. 点蚀损伤对环肋圆柱壳极限强度的影响[J]. 船海工程, 2018, 47(1): 29. MA Xiaolong, WU Fan, ZHANG Er. Study on ultimate strength of ring-stiffened cylindrical shell under pitting corrosion damage[J]. Ship & Ocean Engineering, 2018, 47(1): 29. DOI:10.3963/j.issn.1671-7953.2018.01.007 |
| [14] |
李卓禹, 朱锡, 李华东. 静压作用下夹芯复合材料圆柱壳失效模式的有限元分析[J]. 中国舰船研究, 2015, 10(3): 45. LI Zhuoyu, ZHU Xi, LI Huadong. Finite element analysis of the failure mode of composite sandwich cylinders subjected to hydrostatic pressure[J]. Chinese Journal of Ship Research, 2015, 10(3): 45. DOI:10.3969/j.issn.1673-3185.2015.03.008 |
| [15] |
熊传志, 胡必文. 基于ANSYS的复合材料耐压壳体的有限元分析[J]. 水雷战与舰船防护, 2011, 19(3): 48. XIONG Chuanzhi, HU Biwen. Finite element analysis of composite overwrapped pressure vessels based on ANSYS[J]. Mine Warfare & Ship Self-Defence, 2011, 19(3): 48. |
| [16] |
程研雪, 庞永杰, 杨卓懿. 基于近似模型技术的复合材料耐压壳性能研究[J]. 船舶工程, 2015, 37(4): 74. CHENG Yanxue, PANG Yongjie, YANG Zhuoyi. Research on composite material pressure hulls based on approximation[J]. Ship Engineering, 2015, 37(4): 74. |
| [17] |
李河清, 陶华, 赵景丽, 等. 复合材料机翼环肋结构件的研制[J]. 工程塑料应用, 2005, 33(4): 35. LI Heqing, TAO Hua, ZHAO Jingli, et al. Studies on CFRP aerofoil rib parts[J]. Engineering Plastics Application, 2005, 33(4): 35. DOI:10.3969/j.issn.1001-3539.2005.04.010 |
| [18] |
HASHIN Z. Failure criteria for unidirectional fiber composites[J]. Journal of Applied Mechanics, 1980, 47(2): 329. DOI:10.1115/1.3153664 |
| [19] |
HASHIN Z. Fatigue failure criteria for unidirectional fiber composite[J]. Journal of Applied Mechanics, 1981, 48(4): 846. DOI:10.1115/1.3157744 |
 2019, Vol. 51
2019, Vol. 51


