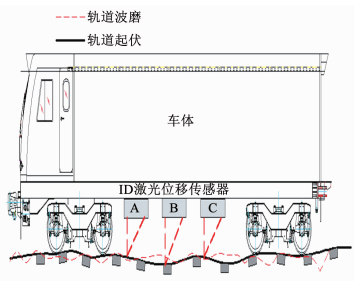
钢轨纵向波磨是指钢轨投入使用后,轨顶面出现的沿纵向分布的周期性类似波浪形状的不平顺现象,是轨道损伤的一种主要形式[1].如图 1所示,当车辆行驶至路基不匀的轨道或上下坡时,置于车体底部的激光位移传感器由于车体刚性不能实时跟踪轨道起伏的变化,导致测量的短周期波磨数据中含有轨道起伏引起的长周期趋势项,从而影响波磨测量的精度.因此,提取和消除信号中存在的趋势项在钢轨波磨检测领域扮演着一个重要的角色[2].
|
图 1 轨道起伏引起的趋势项 Fig. 1 Cause of the trend of track irregularity |
趋势项通常被认为是包含信号全局改变信息的加性平滑成分[3],是信号的“骨架”,和信号中其他成分相比具有典型的低复杂度、高幅特点.传统的趋势项去除方法普遍采用最小二乘原理,只能处理平稳且数据量小的信号,且需预先假定信号中趋势项的类型[4].而实际采集到的趋势项数据多为非平稳的随机信号,采用这种方法得到的结果是不准确的.
聚合经验模态分解(EEMD, ensemble empirical mode decomposition)以其自适应的多尺度分解特性[5-6],特别适合分析非线性、非平稳信号,目前已有的EEMD/EMD去趋算法主要从低频本征模式函数(IMF, Int Rinsicmode Function)分量中选取连续或间断的几个组合重构作为信号的趋势,如通过线性规划来选取相应IMF的EMD-SBP[7];通过分析相邻IMF边际谱的相关性找到信号与趋势项的分界点,然后选取后几个连续IMF进行组合的EMD-HHT等[8].这些方法都为EMD去趋提供了很好的思路,取得了较好的去趋效果.但忽视了一些潜在的问题:低频IMF分量中除了占据较大比例能量的趋势项成分外,还可能含有白噪声与信号的低频成分.这三种成分混合在一起,并没有完全隔离开来,因此直接选取低频IMF分量组合趋势是不精确的.
针对上述问题,本文提出一种EEMD-SVD-PE的IMF分量重构方法,其中,奇异值分解是一种信号的特征提取的技术[9].将IMF分量组成多维特征矩阵投影到奇异值分解(SVD, Singular Value Decomposition)得到的能量特征向量矩阵空间重构出新的奇异值分量,此时奇异值分量按照能量高低进行分布,同时引入的排列组合熵算法是一种衡量一维序列复杂度的平均熵参数[10],能够有效的提取出复杂度低的奇异值分量即钢轨波磨趋势项.它解决了传统EMD直接以低频IMF分量组合趋势时存在的信号混杂问题,有效提升了去趋效果.
1 基于PE选取低复杂度奇异值分量重构趋势的EEMD-SVD信号去趋方法由于钢轨波磨信息中的趋势项具有典型的低复杂度、高幅的特点,表明在提取钢轨波磨趋势项时应提取能量高且复杂度低的分解信号,本文提出的基于PE选取低复杂度奇异值分量重构趋势的EEMD-SVD信号去趋方法,详细步骤如下:
1.1 高斯平滑滤波与EEMD分解对长度为M的一维含噪时间序列s(t),首先对其进行高斯平滑,滤除部分随机脉冲噪声对后续分解的影响,得到平滑后的序列
1) 在目标数据中加入白噪声序列;
2) 将加入白噪声的序列分解为IMF;
3) 每次加入不同的白噪声序列,反复重复步骤1)、步骤2) N次;
4) 把分解得到的各个IMF对应求平均作为最终的结果.
得到
c1位于IMF最高频段,所占据的频带宽度最宽,拥有的噪声能量最多,所以将其舍去,其余N个长度为M的IMF分量组成一个多维特征信号矩阵XM×N=(c2T, c3T, …, cN+1T).将信号矩阵去均值
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;{{\bar X}_{{\rm{M}} \times {\rm{N}}}} = \left( {{{\mathit{\boldsymbol{\bar x}}}_1},{\mathit{\boldsymbol{x}}_2}, \cdots ,{{\mathit{\boldsymbol{\bar x}}}_{\rm{N}}}} \right) = \\ \left( {{x_1} - E\left( {{\mathit{\boldsymbol{x}}_1}} \right),{\mathit{\boldsymbol{x}}_2} - E\left( {{\mathit{\boldsymbol{x}}_2}} \right), \cdots ,{\mathit{\boldsymbol{x}}_N} - E\left( {{\mathit{\boldsymbol{x}}_{\rm{N}}}} \right)} \right). \end{array} $ | (1) |
同时,希望通过信号的能量对现有信号矩阵进行重构,信号的协方差矩阵的特征值往往可以用来表示信号强度[13],所以将原始信号的协方差矩阵CN×N=E((XT)N×M(X)M×N)作为转换矩阵,通过奇异值分解,
| $ {\mathit{\boldsymbol{C}}_{{\rm{N}} \times {\rm{N}}}} = {\mathit{\boldsymbol{U}}_{{\rm{N}} \times {\rm{N}}}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_{\rm{N}}}_{ \times {\rm{N}}}\mathit{\boldsymbol{U}}_{{\rm{N}} \times {\rm{N}}}^{\rm{T}}. $ | (2) |
其中: Λ=diag(λ1, λ2, …, λN)为对角矩阵,λ1≥λ2≥…≥λN为C的特征值,U=(u1, u2, …, uN)为特征值对应的特征向量组成的正交矩阵,去除特征值为0的特征向量项及原始数据向量,实现数据降维.降维后的奇异值分量个数K(K≤N).重构后的奇异值分量信号为
| $ {\mathit{\boldsymbol{P}}_{{\rm{M}} \times {\rm{K}}}} = {\left( {\mathit{\boldsymbol{\bar X}}} \right)_{{\rm{M}} \times {\rm{K}}}}{\mathit{\boldsymbol{U}}_{{\rm{K}} \times {\rm{K}}}} = \left( {{\mathit{\boldsymbol{p}}_1},{\mathit{\boldsymbol{p}}_2}, \cdots ,{\mathit{\boldsymbol{p}}_{\rm{K}}}} \right). $ | (3) |
降维重构的原始信号为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{\tilde X = }}{\mathit{\boldsymbol{P}}_{{\rm{M}} \times {\rm{K}}}}\mathit{\boldsymbol{U}}_{{\rm{K}} \times {\rm{K}}}^{\rm{T}} + {\mathit{\boldsymbol{E}}_{{\rm{M}} \times {\rm{K}}}}.\\ {\rm{式中:}}{\mathit{\boldsymbol{E}}_{{\rm{M}} \times {\rm{K}}}} = {\left( {\begin{array}{*{20}{c}} {E\left( {{x_1}} \right)}&{E\left( {{x_2}} \right)}& \cdots &{E\left( {{x_{\rm{K}}}} \right)}\\ {E\left( {{x_1}} \right)}&{E\left( {{x_2}} \right)}& \cdots &{E\left( {{x_{\rm{K}}}} \right)}\\ \vdots & \vdots & \vdots & \vdots \\ {E\left( {{x_1}} \right)}&{E\left( {{x_2}} \right)}& \cdots &{E\left( {{x_{\rm{K}}}} \right)} \end{array}} \right)_{{\rm{M}} \times {\rm{K}}}} \end{array} $ | (4) |
为M个样本的均值扩展矩阵.记为PM×K=(p1, p2, … pK)
1.3 基于排列组合熵选取低复杂度奇异值分量第i个奇异值分量pi的排列组合熵为
| $ H\left( {{\mathit{\boldsymbol{p}}_i}} \right) = - \sum\limits_{{\pi _j} \in {S_{\rm{D}}}} {{\mathit{\boldsymbol{p}}_i}\left( {{\pi _j}} \right){\rm{ln}}\left( {{\mathit{\boldsymbol{p}}_i}\left( {{\pi _j}} \right)} \right).} $ | (5) |
式中:πj是奇异值分量的任意一种排列组合方式,对各个奇异值分量pi(i=1, 2, …, K)的排列组合熵按从大到小排列得到矢量Η=(h1, h2, …, hK), h1≥h2≥…≥hK,由排列组合熵的定义可以看出:排列组合熵的大小反应序列的不规则程度,排列组合熵值越大,序列越不规则,值越小越规则.将得到的K个奇异值分量的排列组合熵进行k-means聚类,将聚类中的排列组合熵最小的一类作为选定的奇异值分量.由此可得所有奇异值分量的趋势项选取权系数矢量w=(w1, w2, …, wK).
1.4 依据选取的低复杂度奇异值分量重建趋势项依据趋势项选取权系数矢量来选取相应奇异值分量进行重构,再与扩展均值矩阵结合,得到原始信号的趋势项矩阵,即
| $ {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\rm{M}} \times {\rm{K}}}} = \sum\limits_{i\left| {{w_i} = 1} \right.} {{\mathit{\boldsymbol{p}}_i}{{\left( {{u_i}} \right)}^{\rm{T}}} + {\mathit{\boldsymbol{E}}_{{\rm{M}} \times {\rm{K}}}}.} $ | (6) |
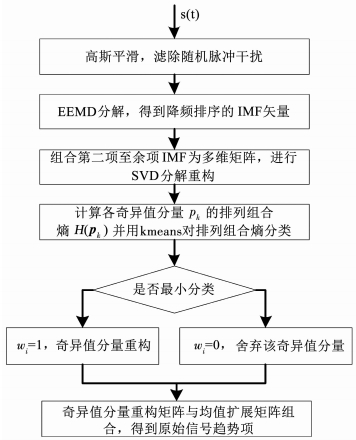
对趋势项矩阵按列求和,即得原始信号的一维趋势项.流程见图 2所示.
|
图 2 EEMD-SVD-PE信号去趋流程图 Fig. 2 Flowchart of the EEMD-SVD-PE de-trending algorithm |
为验证本文所提方法的有效性,参照文献[14]引入一种仿真信号进行测试,并分别采用无相位延迟的低通滤波法(LF)、与EMD结合的线性规划法(EMD-SBP)[7]、小波分解的方法(WD)[15]和本文提出的基于排列组合熵选取低复杂度奇异值分量重构趋势的EEMD-SVD法(EEMD-SVD-PE)进行对比.同时,使用均方根误差(RMSE),相对L2范数来定量分析各种方法的去趋效果[16],它的表达式为
| $ {\rm{RMSE = }}\sqrt {\sum\limits_{t = 1}^M {\frac{1}{M}{{\left( {T\left( t \right) - \Gamma \left( t \right)} \right)}^2}} } , $ | (7) |
| $ {L_2} = \frac{{\sqrt {\sum\limits_{t = 1}^M {{{\left( {\Gamma \left( t \right) - T\left( t \right)} \right)}^2}} } }}{{\sqrt {\sum\limits_{t = 1}^M {{{\left( {T\left( t \right)} \right)}^2}} } }}. $ | (8) |
式中:Γ(t)为算法提取出的趋势项,T(t)为原始信号的趋势项,M为测试采样长度.RMSE和相对L2范数越小,表示提取出的趋势越接近原始信号趋势,去趋效果越好.
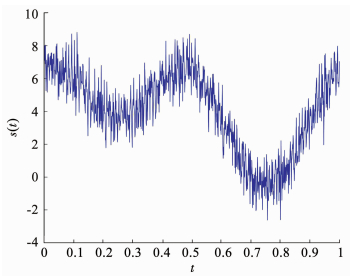
仿真信号为s(t)=y(t)+T(t)+n(t),式中y(t)=A1sin(2πf1t),A1=0.6,f1=100 Hz,T(t)=A2e-bt+A3sin(2πf2t)+A4cos(2πf3t),A2=4,b=0.02,A3=2,f2=1 Hz,A4=2.5,f3=2 Hz,n(t)为加性高斯白噪声成分,一段长为1 000的信号s(t)见图 3所示.为验证该方法在不同噪声环境下去趋效果的鲁棒性,分别进行单信噪比和多信噪比测试.
|
图 3 测试信号及其趋势项 Fig. 3 The test signal and its trend |
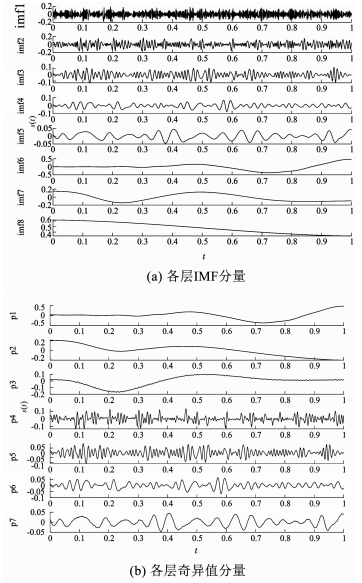
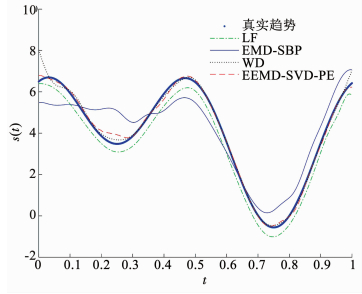
令信噪比(SNR, Signal-Noise Ratio)为5 dB,EEMD分解得到的各层IMF分量与SVD分解得到的奇异值分量分别见图 4(a)、(b)所示,各层奇异值分量的PE权系数见表 1所示.可看出,经过k-means分类后取最小排列组合熵的一类,作为趋势项的奇异值分量为p1、p2和p3.这4种方法提取出的趋势项与原趋势项对比效果见图 5所示,低通滤波法(通带截止频率取2 Hz,阻带截止频率取5 Hz)提取的趋势项信号幅度不足;与EMD结合的线性规划法(实线,选取第7层IMF作为趋势项) IMF成分选取不足,提取出的趋势项与原趋势项(粗点线)在峰值处相差较大;WD(细点线,小波分解后的第一项)在t=0.05与t=0.95信号边界处与原趋势相差较大;本文方法(虚线,选取第1、2、3项奇异值分量重构组合趋势)趋势提取的更为充分.表 2为4种方法提取出的趋势与原趋势的RMSE和相对范数比较,本文方法相对其他三种,RMSE分别约降低了0.183 4,0.254 9和0.055 1,相对范数分别约降低了0.112 6,0.127和0.028 3.
|
图 4 仿真信号分解到的IMF与奇异值分量 Fig. 4 IMF components and singular-value components decomposed from the simulation signal |
| 表 1 仿真信号各层奇异值分量的排列组合熵 Tab. 1 PE of singular-value components for simulation signal |
|
图 5 不同方法提取出的趋势项对比 Fig. 5 Comparison of trends extracted by different methods |
| 表 2 仿真信号不同方法去趋效果比较 Tab. 2 Trend extraction effect caused by different methods for simulation signal |
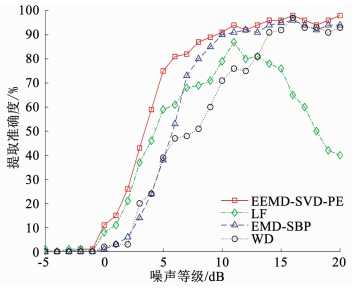
令RSN=-5~20 dB,步长1 dB,每个RSN等级执行1 000次试验,每次加入不同的白噪声序列,统计每个等级处的提趋准确率.4种方法的提趋准确率-噪声等级曲线见图 6所示.可以看出,随着信噪比增加,与EMD结合的线性规划法、直接选取小波分解项的WD法和本文方法提趋准确率均逐步增高,最高达到98%;低通滤波法在RSN=10 dB后准确率逐步下降,原因是低通滤波在复杂信号中效果较差.相比而言,本文所提方法提趋准确率保持稳步上升,总体性能优于其他三种,尤其在低信噪比情况下,准确率最大提高约30%.
|
图 6 不同信噪比下的各种方法提趋性能比较 Fig. 6 Comparison of trend extraction performance of each method at different SNR levels |
在不同噪声等级下4种方法的相对L2范数统计均值见表 3.由表 3可知,本文方法在不同噪声等级下的结果均优于其他方法,比低通滤波法(LF)平均降低约0.101,比与EMD结合的线性规划法(EMD-SBP)降低约0.115,比WD降低约0.015.
| 表 3 不同信噪比下各种方法相对L2范数均值统计 Tab. 3 Average relative L2-norm errors of different methods at different RSN levels |
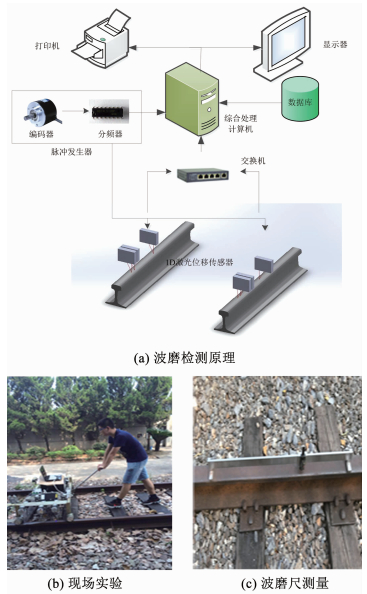
实验中采用三点弦测法对钢轨波磨进行检测[17],激光位移传感器的采样间隔设为2 mm.检测原理见图 7(a).
|
图 7 钢轨波磨动态测量系统及现场测试 Fig. 7 Dynamic track irregularity measurement system and field test |
检测流程如下:
1) 车轴转动带动光电编码器旋转输出触发信号,触发信号发给检测同一侧钢轨的3个1D激光位移传感器,完成同一时刻的钢轨波磨数据采集.
2) 数据经数据采集卡进行数据集中,然后传输给车载综合处理计算机.综合处理计算机利用三点弦测法将含有趋势的波磨信息提取、存储.
本文利用实验搭建的钢轨动态磨耗检测平台在实际50钢轨上进行现场实验见图 7(b)所示.实验中的钢轨由于长时间的使用,路基呈现出较大的起伏,十分适合本文的情况.通过三点弦测法最终得到17 m含有趋势的钢轨波磨数据.同时,为了得到标准的波磨信息,用波磨尺对同一路段的钢轨波磨进行测量,并以测得的数据作为去趋后的标准数据,见图 7(c).采集到的含有趋势项的钢轨波磨数据见图 8.
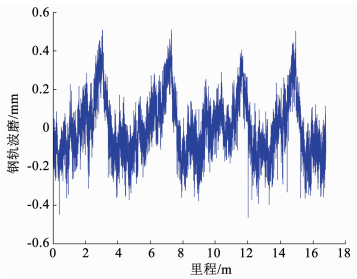
|
图 8 含有趋势项的钢轨波磨信号 Fig. 8 Track height irregularity signal containing trend |
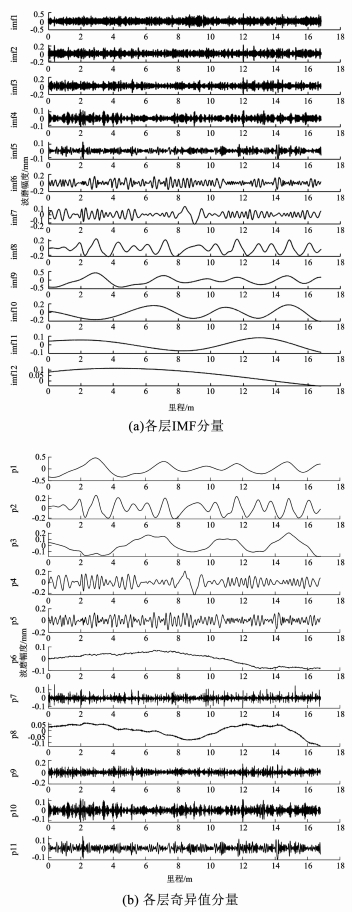
现场实验采集得到的波磨数据由于趋势项存在,轨道表面高低起伏很大,起伏范围达到±0.6 mm.EEMD分解得到的各层IMF分量与SVD分解得到的奇异值分量分别见图 9(a)、(b)所示,各层奇异值分量的PE权系数见表 4所示.此时选取p1、p3、和p6项奇异值分量来重构趋势,同时也可以看出组成趋势项的奇异值分量并未连续排列.
|
图 9 含趋钢轨波磨信号分解到的IMF与奇异值分量 Fig. 9 IMF components and singular-value components decomposed in real application |
| 表 4 不同信噪比下各种方法相对L2范数均值统计 Tab. 4 Average relative L2-norm errors of different methods at different RSN levels |
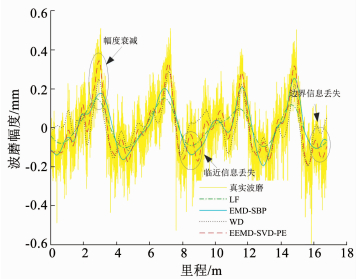
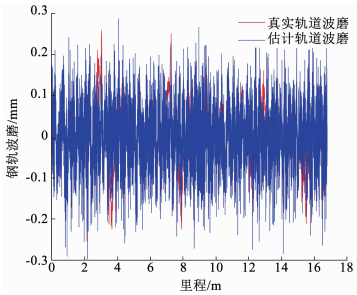
4种方法提取出的趋势对比见图 10所示,与EMD结合的线性规划法(EMD-SBP,实线)与WD(点线)提趋出的趋势项存在明显的邻近和边界信息丢失与峰值幅度衰减问题,低通滤波法(点划线)在复杂趋势项信号提取中效果较差.相比之下,EEMD-SVD-PE(虚线)提取出的复杂趋势成分更好地反映了信号走势,边界信息、临近信息和峰值信息得到了较好的保留.与其他3种方法相比的结果见表 5,本文方法的RMSE分别降低了0.086 0,0.069 1,0.042 8.应用本文所提方法去趋后的钢轨波磨效果见图 11所示,其中红色为由波磨尺测得的真实波磨值,测得的波磨与真实波磨的趋势相近,且最大误差在±0.2 mm的范围之内,符合实际需要.
|
图 10 不同方法提取出的趋势项对比 Fig. 10 Comparison of trends extracted by different methods |
| 表 5 含趋钢轨波磨信号不同方法去趋效果比较 Tab. 5 Relative L2-norm errors caused by different methods for track height irregularity signal containing trend |
|
图 11 EEMD-SVD-PE钢轨波磨去趋结果 Fig. 11 De-trended track height irregularity signal using EEMD-SVD-PE |
实验在matlabR2014a环境下进行,计算机内存为3.39 G,CPU主频为3.2 GHz.统计仿真信号的平均去趋时间开销:低通滤波法(LF)约为0.002 908 s,与EMD结合的线性规划法(EMD-SBP)为0.012 04 s,WD为0.010 528 s,本文提出的EEMD-SVD-PE为0.010 914 s,时间开销没有明显增加.
4 结论针对现有的EMD去趋方法直接选取低频IMF组合趋势项时存在的IMF中信号成分混杂问题,本文提出了一种基于排列组合熵选取低复杂度奇异值分量重构趋势的EEMD-SVD信号去趋新方法.首先对信号进行高斯平滑去噪和EEMD分解,然后选取第二项至余项IMF分量组成多维特征矩阵投影到SVD得到的能量特征向量矩阵空间重构出新的奇异值分量,最后基于排列组合熵自适应选取相应低复杂度奇异值分量组合成信号趋势项.为了验证所提算法的性能,引入了仿真趋势项信号,并选择了低通滤波法、与EMD结合的线性规划法、小波分解WD进行去趋效果比较.单信噪比和多信噪比的仿真实验,均表明所提算法的去趋效果总体优于其他三种,尤其在低信噪比情况下,提趋准确率最大提高约30%.然后对含趋轨道波磨数据进行的去趋实例应用,也进一步验证了本文方法的有效性.
| [1] |
GRASSIE S L. Rail corrugation: Advances in measurement, understanding and treatment[J]. Wear, 2005, 258(7-8): 1224. DOI:10.1016/j.wear.2004.03.066 |
| [2] |
MESSINA A R, VIRRAL V, HEYDT G T, et al. Nonstationary approaches to trend identification and de-noising of measured power system oscillations[J]. IEEE Transactions on Power Systems, 2009, 24(4): 1798. DOI:10.1109/TPWRS.2009.2030419 |
| [3] |
WU Zhaohua, HUANG N E, LONG S R, et al. On the trend, detrending, and variability of nonlinear and non-stationary time series[J]. National Academy of Sciences, 2007, 104(38): 14889. DOI:10.1073/pnas.0701020104 |
| [4] |
ALEXANDROV T, BIANCONCINI S, DAGUM E B, et al. A review of some modern approaches to the problem of trend extraction[J]. Econometric Reviews, 2012, 31(6): 32. DOI:10.1080/07474938.2011.608032 |
| [5] |
刘义艳, 贺栓海, 巨永锋, 等. 基于EEMD和SVR的单自由度结构状态趋势预测[J]. 振动与冲击, 2012, 31(5): 60. LIU Yiyan, HE Shuanhai, JU Yongfeng, et al. Trend prediction for a single-degree of freedom structure's state based on EEMD and SVR[J]. Journal of Vibration and Shock, 2012, 31(5): 60. DOI:10.3969/j.issn.1000-3835.2012.05.013 |
| [6] |
李利品, 党瑞荣, 樊养余. 改进的EEMD算法及其在多相流检测中的应用[J]. 仪器仪表学报, 2014, 35(10): 2365. LI Lipin, DANG Ruirong, FAN Yangyu. Modified EEMD de-noising method and its application in multiphase flow measurement[J]. Chinese Journal of Scientific Instrument, 2014, 35(10): 2365. DOI:10.3969/j.issn.0254-3087.2014.10.028 |
| [7] |
YANG Zhijing, LING B, BINGHAM C. Joint empirical mode decomposition and sparse binary programming for underlying trend extraction[J]. IEEE Transactions on Instrument and Measurement, 2013, 62(10): 2673. DOI:10.1109/tim.2013.2265451 |
| [8] |
梁兵, 汪同庆. 基于HHT的振动信号趋势项提取方法[J]. 电子测量技术, 2013, 36(2): 119. LIANG Bing, WANG Tongqing. Method of vibration signal trend extraction based on HHT[J]. Electronic Measurement Technology, 2013, 36(2): 119. DOI:10.3969/j.issn.1002-7300.2013.02.030 |
| [9] |
YANG Zhixin, ZHONG Jianhua. A hybrid EEMD-based SampEn and SVD for acoustic signal processing and fault diagnosis[J]. Entropy, 2016, 18(4): 112. DOI:10.3390/e18040112 |
| [10] |
袁明, 罗志增. 基于排列组合熵和聚类分析的SEMG识别方法[J]. 华中科技大学学报(自然科学版), 2011, 39(s2): 107. YUAN Ming, LUO Zhizeng. SEMG recognition based on permutation entroy and clustering analysis[J]. Journal of Huazhong University of Science and Technology (Nature Science), 2011, 39(s2): 107. |
| [11] |
聂永红, 程军圣, 张亢, 等. 基于EMD与响度的有源噪声控制系统[J]. 仪器仪表学报, 2012, 33(4): 801. NIE Yonghong, CHENG Junsheng, ZHANG Kang, et al. Active noise control system based on EMD and loudness[J]. Chinese Journal of Scientific Instrument, 2012, 33(4): 801. DOI:10.3969/j.issn.0254-3087.2012.04.013 |
| [12] |
WU Zhaohua, HUANG N E. Ensemble empirical mode decomposition: A noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1. DOI:10.1142/S1793536909000047 |
| [13] |
徐望, 丁琦, 王炳锡. 一种基于特征空间能量熵的语音信号端点检测算法[J]. 通信学报, 2003, 24(11): 125. XU Wang, DING Qi, WANG Bingxi. A speech endpoint detector based on eigenspace-energy-entropy[J]. Journal of China Institute of Communications, 2003, 24(11): 125. DOI:10.3321/j.issn:1000-436X.2003.11.018 |
| [14] |
MOGHTADERI A, FLANDRIN P, BORGNAT P. Trend filtering via empirical mode decompositions[J]. Computational Statistics and Data Analysis, 2013, 58: 114. DOI:10.1016/j.csda.2011.05.015 |
| [15] |
马子骥, 钟广超, 刘宏立, 等. 小波变换的稀疏最优化信号趋势项提取方法[J]. 传感器与微系统, 2017, 36(1): 27. MA Ziji, ZHONG Guangchao, LIU Hongli, et al. Sparse optimization methods for signal trend extraction based on wavelet wavelet transform[J]. Transducer and Microsystem Technologies, 2017, 36(1): 27. DOI:10.13873/J.1000-9787(2017)01-0027-04 |
| [16] |
FAWCETT T. An introduction to ROC analysis[J]. Pattern Recognition Letters, 2006, 27(8): 861. DOI:10.1016/j.patrec.2005.10.010 |
| [17] |
CHEN Liang, LI Yanfu, ZHONG Xiaoyun, et al. An automated system for position monitoring and correction of chord-based rail corrugation measuring points[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(1): 250. DOI:10.1109/TIM.2018.2840580 |
 2019, Vol. 51
2019, Vol. 51


