随着计算机技术的快速发展,对象与数据的关联性变得越来越复杂,随之衍生了很多结构复杂的大规模网络系统[1-2].在有限的时间内,通过对网络若干节点施加控制,如果网络系统的所有状态变量可以由任意初态迁移到任意终态,则称该网络系统是可控的[3-5].网络可控对于研究大规模网络问题具有重要的意义.文献[6]提出网络系统的结构能控性,大大降低传统方法中计算Kalman秩判据的复杂度.文献[6]通过引入图论的思想,将有向网络映射到二分图,从而确定图的最大匹配求得满足结构可控性的最少驱动节点数目.文献[7]基于PBH秩判据,通过计算网络系统矩阵的最大几何重数,来确定实现网络精确可控性所需的最少驱动节点的数目.文献[7]提出的精确可控性理论弥补了[6]的不足,可用于求解无向网络以及其他任意结构的加权网络的可控性,使网络系统可控性的理论更加完备.
现有的研究中,对于一个有向网络,关于确定其驱动节点的数目已经取得丰富的研究成果[6-8].但上述工作并不能保证受控网络在一定的时间内收敛到目标状态,这对大规模网络可控性研究具有理论和实际意义.文献[9]提出能控子网络的概念,对具有固定数量控制节点的有向网络的能控性指数进行优化,得出稠密的同质网络比稀疏的异质的网络具有更大的能控性指数的结论.文献[10]对带有时滞的线性系统的能控性指数进行研究,针对两种形式的能控性:Rn-controllability和R(
以上工作对于网络的控制节点的控制链长度没有施加限制,当网络规模较大时,节点之间的状态信息的传递会造成一定的控制延迟等问题[11].本文针对有向网络,对能控性指数的上下界进行研究.本文的主要工作有:首先通过对系统可控性进行分析,提出能控性指数的概念.然后根据Kalman秩判据的相关理论,提出能控性指数的下界算法(KMLA).最后结合最大匹配的原理,提出基于入度的能控性指数的最小上界算法(KMUA).结合具体的模型和实际的网络数据集对本文提出的算法进行验证,实验结果表明通过确定网络能控性指数的上下界,可以实现优化节点的控制链长度,为设计合理的使网络满足一定步数可控的控制方案提供依据.
1 问题描述对于一个由N个状态节点和M个控制节点组成的网络系统,可以将其近似的看成线性非时变系统[6],如下所示
| $ \mathit{\boldsymbol{\dot X}}\left( t \right) = AX\left( t \right) + Bu\left( t \right). $ | (1) |
式中: N维向量X(t)=(x1(t), x2(t), …xN(t))T表示网络在时间节点t的状态向量;A为N×N维的系统矩阵,描述了状态节点间边的连接情况以及边的连接强度;B为N × M维的输入矩阵,描述了网络的控制连线图,刻画了M个控制节点与N个状态节点的连接关系[12].
引理1[13] 对N维线性非时变系统(1),构造系统的可控性判别矩阵
| $ \mathit{\boldsymbol{C = }}\left[{B, AB, \cdots, {A^{{\rm{K-1}}}}B, {A^{\rm{K}}}B, \cdots, {A^{{\rm{N-1}}}}B} \right]. $ | (2) |
则系统完全可控的充分必要条件为
| $ {\rm{rank}}\left( \mathit{\boldsymbol{C}} \right) = \mathit{\boldsymbol{N}}{\rm{.}} $ | (3) |
事实上C矩阵所有列并不是完全线性无关的,可能某些列线性相关,则可能前(K+1)M列已经能够使C矩阵满秩,由此引出能控性指数的概念.定义一个N×(K+1)M维的K步可控性矩阵
| $ \mathit{\boldsymbol{C = }}\left[{B, AB, \cdots, {A^\mathit{K}}B} \right]. $ | (4) |
定义1 对于系统(1),定义系统的能控性指数为使下列等式成立的正整数K
| $ \begin{array}{l} {\rm{rank}}\left( {\mathit{\boldsymbol{Q = }}\left[{B, AB, \cdots, {A^K}B} \right]} \right) = N\;\;\;\;{\rm{且}}\\ \;\;\;\;\;\;\;\;{\rm{rank}}\left( {Q' = \left[{B, AB, \cdots, {A^K}B} \right]} \right) < N. \end{array} $ | (5) |
为表述的简洁性,用K步能控描述系统能控性指数为K这一性能.很明显,当K=N-1时,Q即为能控性判别矩阵.表明,当系统K步完全能控时,系统在K+1,K+2,…,步仍然满足完全能控的特性.
本文关于“K步能控”的表述在离散系统中具有特定的物理含义,指存在有限步的控制信号序列:u(0), u(1), …, u(K-1),使得系统当前状态X(0)能在第K步达到零状态.而连续系统在研究中不涉及到控制步数的概念,因此针对连续系统“K步能控”并不具有类似离散系统的实际物理含义.为了表述的一致性和简洁性,本文不再特别针对连续系统和离散系统进行区分说明.
2 能控性指数K的下界算法结合能控性指数的定义可知,需要从零开始不断的计算AB、A2B、…、AKB,直到满足K步可控的代数判据为止.控制输入矩阵B用N维方阵表示时,只有对角元素非零,为了简化,可将B转化成N×1维列向量形式
| $ {\mathit{\boldsymbol{B}}_{\rm{n}}} = \mathit{\boldsymbol{B}}{\rm{*}}{{\rm{1}}_{\rm{N}}}. $ | (6) |
式中:1N为N×1维元素都为1的列向量.计算AKBn时,向量中非零的元素表示控制输入可以在K步影响到该非零元素所映射的状态节点.能控性指数K的下界算法(KMLA)的步骤为
步骤1:将B矩阵转换成Bn形式的列向量;
步骤2:K从0开始取值,计算AKBn,并记录AKBn中非零元素所在的行索引集合为SR;
步骤3:令K=K+1,计算AKBn,若AKBn中存在非零元素,且非零元素所在的行索引不在集合SR中,则更新SR,将行索引添加到SR;
步骤4:若非零元素所在的行索引Rrow在集合SR中,将AKBn中行索引为Rrow的非零元素清零.若此时AKBn为零向量,则确定下界为K-1;否则,重复步骤3到步骤4.
如下所示的系统
| $ \mathit{\boldsymbol{A = }}\left[{\begin{array}{*{20}{c}} 0&0&0&0&0&0&0&0&0\\ 1&0&0&0&0&0&0&0&0\\ 1&0&0&0&0&0&0&0&0\\ 0&1&0&0&0&0&0&1&1\\ 0&0&0&1&0&0&0&0&0\\ 0&0&0&0&0&0&0&0&0\\ 0&0&0&0&0&1&0&0&0\\ 0&0&0&0&0&1&0&0&0\\ 0&0&0&0&0&0&0&1&0 \end{array}} \right]\mathit{\boldsymbol{B = }}\left[{\begin{array}{*{20}{c}} 1&0&0&0\\ 0&0&0&0\\ 0&1&0&0\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&1&0\\ 0&0&0&1\\ 0&0&0&0\\ 0&0&0&0 \end{array}} \right] $ |
将B矩阵转换成Bn形式的列向量:Bn=[101001100]T,则行索引集合SR={1, 3, 6, 7};ABn=[011000110]T,非零元素所在的行索引中,3和7位于SR中,故ABn=[010000010]T,更新行索引集合SR={1, 2, 3, 6, 7, 8};计算A2Bn=[000200001]T,更新行索引集合SR={1, 2, 3, 4, 6, 7, 8, 9};计算A3Bn=[000120000]T,4位于SR中,故A3 Bn=[000020000]T,更新行索引集合SR={1, 2, 3, 4, 5, 6, 7, 8, 9};计算A4Bn=[000010000]T,非零元素所在的行索引中,5位于SR中,故A4 Bn=[000000000]T为零向量,即网络系统在当前控制输入作用下,能控性指数K的下界为3,网络最快3步可控.
通过确定K值的下界,为设计合理的K步可控性方案提供理论依据.但是,在实际的K步可控网络中,当网络系统的规模较大时,可能导致控制输入的控制链过长,因此确定K值的上界对于K步可控的研究也是至关重要的.
3 能控性指数K的最小上界算法由可控性理论可知[1],有向网络的最少驱动节点的集合可由二分图的最大匹配算法得出.同时,研究结果表明网络的最少驱动节点的集合并不唯一,导致网络的最大可达路径的长度可能存在差别[8].如下图所示的系统
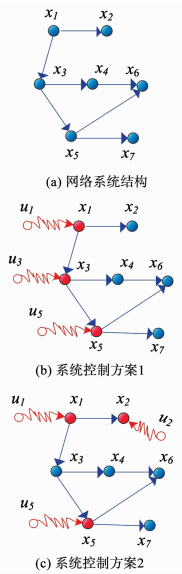
由图 1可知,图 1(b)中控制输入为u={u1, u3, u5},图 1(c)中控制输入为u={u1, u2, u5}.两种控制方案下,虽然最小控制输入集合的节点个数相同,但是控制输入的控制链长度并不一样.图 1(b)中,最大控制链长度为u3-x3-x4-x6.图 1(c)中,最大控制链长度为u1-x1-x3-x4-x6.表明两种控制方案下,能控性指数K的上界并不一样.
|
图 1 简单的有向网络的不同控制方案 Fig. 1 Simple directed networks with different control schemes |
对于一个有向无自环网络G=(V, E),基于入度的能控性指数K的最小上界算法(KMUA)的一般步骤如下
步骤1:令集合S={},随机查找未在S中并且入度为1的节点,记为vi,其中0≤i≤N,令S=S∪{vi};
步骤2:若存在vi,回溯一步可达vi的节点,记为vj,其中0≤j≤N;
步骤3:若vj的出度大于2,则只保留链路vj-vi,删除其他vj的一步可达链路,使vj的出度为1;
步骤4:若vj的入度大于2,回溯可达vj并以vj为终点的所有链路,只保留回溯链路长度最短的链路,删除其他一步可达vj的链路,使vj的入度为1;
步骤5:在剩余的网络中,重复步骤1~4,直到找不到未在集合S中并且入度为1的节点为止;
步骤6:将剩余网络中的入度为0的节点作为最小控制输入的节点集合,且剩余网络中控制输入的最大链路长度即为K值的最小上界.
上述步骤中,当初始网络不存在入度为1的节点时,需要对网络进行如下的初始化构造:随机查找网络中入度最小的节点,记为vs,其中0≤s≤N.按照上述步骤4的处理过程,使vs的出度为1.
3.2 算例分析以图 2(a)所示的网络系统,对KMUA算法进行简单的说明.
|
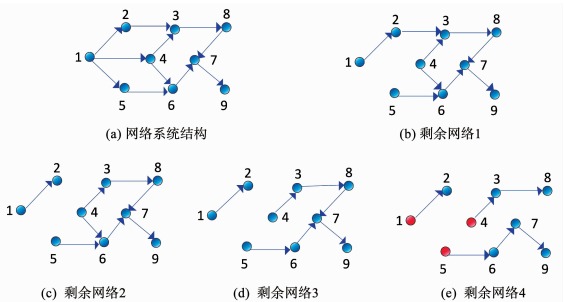
图 2 KMUA算法示意 Fig. 2 Schematic diagram for KMUA algorithm |
首先查找图 2(a)所示的网络中入度为1的节点,随机选择节点2为当前节点,更新集合S ={2}.一步可达2的节点为1,且节点1的入度为,出度大于2,则保留节点1~2的链路,删除其他链路,使节点1的出度为1,得到图 2(b)所示剩余网络.
查找图 2(b)所示的网络中入度为1的节点,得到节点8的入度为1,更新集合S ={2, 8}.一步可达8的节点为3,且节点3的入度大于2,回溯所有可达节点3并以节点3为终点的链路,并将较长的链路删除,只保留最短的一条链路,使节点3的入度为1,得到图 2(c)所示剩余网络.
对剩余的网络按照上述步骤继续查找,最终得到图 2(e)所示剩余网络,此时S ={2, 3, 6, 8, 7, 9}.剩余网络中的入度为0的节点为:1、4、5,即最小控制输入的节点集合{1, 4, 5}.剩余网络中控制输入的最大链路为:5—6—7—9,即K值的最小上界为3.
同时经过检验可知,传统最大匹配算法得到的K的最小上界值为5.本文提出的KMUA算法,不仅能够得到网络的最小控制输入集合,而且还能够使能控性指数K的上界尽量小.
4 仿真结果分析表 1为随机生成的ER随机网络仿真结果.其中N为网络节点的个数,L为网络的边,<k>为网络的平均度.令nD=ND/N来描述网络的控制输入情况,式中ND为网络达到可控状态的最小控制输入的数目.nDHP为传统最大匹配算法Hopcroft-Karp得到的值;nDKM为KMUA算法得到的值;KHPup为Hopcroft-Karp算法得到的控制输入的最大控制链路的长度;KKMup为KMUA算法得到的控制输入的最大控制链路的长度;KHP、KKM表示网络满足式(5)的最小正整数K;KLOW为KMLA算法得到值.
| 表 1 ER随机网络仿真结果 Tab. 1 Simulation results for ER random networks |
从表 1可以看出,本文提出的KMUA算法得到的nDKM值和nDHP值相等,表明在不额外添加控制输入的情况下,KMUA算法能够保证网络系统达到相应的可控状态.且当网络规模一致时,nD数目随着网络稠密程度的增加而减少,验证了网络的最小控制输入集合与网络的度序列相关的结论.当网络规模一致时,KKMup的值始终不大于KHPup,且有时KKMup的值是KKMup的数倍之多,表明传统算法求得的最小控制输入可能存在控制链特别长的情况,本文提出的KMUA算法可以很好的改善控制链的长度,使控制链尽量短.同时,当网络的最小控制输入数目相同时,KHP和KKM的值相等,表明两种算法得到的最小控制输入都能使网络满足K步可控,且KMUA算法得到的K值上界值更小,表明通过KMUA算法能够使网络的控制输入的控制链长度变短.
大规模网络系统中,在进行能控性指数K的秩判据的计算时,可能存在2N-1个组合的矩阵计算,同时对于真实网络的A、B矩阵的具体值并不能完全的确定,导致秩判据无法得到确定的K值[14].为了描述大规模真实网络的K步可控性,结合本文得到的K值的上下界来间接描叙K的变化范围.
表 2为几种不同领域的真实数据集,所有真实数据集的来源均来自文献[6]和互联网[15].对于每一种网络,给出网络的一些基本描述特征,其中TType表示网络的类型,NName为网络的名称,N为节点个数为,L为边数,<k>为网络的平均度.
| 表 2 真实网络数据集仿真结果 Tab. 2 Simulation results for real networks |
从表 2可以看出,对于真实网络,本文提出的KMUA算法可以保证得到的nDKM值和nDHP相同,且KKMup的值始终不大于KHPup.也就是说在保证不额外添加控制输入的情况下,KMUA算法能够使原始网络的控制链长度变短,使网络满足K步可控的上界更小.
5 结论本文通过对有向网络能控性指数的上下界的研究,结合Kalman秩判据提出KMLA算法,通过确定K值的下界,为设计合理的K步可控性方案提供理论依据.受到网络匹配节点的入度大小的启发,本文提出KMUA算法,发现当最小控制输入个数相同时,KMUA算法相较于传统的最大匹配算法能够使K的上界更小,表明通过KMUA算法得到的控制输入集合能够优化控制链的长度,避免出现控制链过长的情况.同时结合KMUA算法能够使K值的上界更加接近网络达到K步可控时的K值.在现实网络中,当无法忽略通信网络或者电力传感器网络信息传递过程中的链路延时带来的影响时,在保证网络可控的前提下,对控制输入的链路长度进行优化,使网络满足K步可控显得至关重要.
| [1] |
NEWMAN M E J. The structure and function of complex networks[J]. SIAM Review, 2003, 45(2): 167. DOI:10.1137/S003614450342480 |
| [2] |
TIAN Shaolin, LU Jinhu, CHEN Guanrong, et al. When structure meets function in evolutionary dynamics on complex networks[J]. IEEE Circuits & Systems Magazine, 2014, 14(4): 36. DOI:10.1109/MCAS.2014.2360790 |
| [3] |
HOPCROFTJ E, KARP R M. A n5/2 algorithm for maximum matchings in bipartite[C]// 12th Annual Symposium on Switching and Automata Theory. New York, USA: IEEE, 1971: 122. DOI: 10.1109/SWAT.1971.1
|
| [4] |
TASSA T. Finding all maximally-matchable edges in a bipartite graph[J]. Theoretical Computer Science, 2012, 423(423): 50. DOI:10.1016/j.tcs.2011.12.071 |
| [5] |
汪小帆, 李翔, 陈关荣. 复杂网络理论及其应用[M]. 北京: 清华大学出版社, 2006. WANG Xiaofan, LI Xiang, CHEN Guanrong. Complex network theory and its application[M]. Beijing: Tsinghua University Press, 2006. |
| [6] |
LIU Y Y, SLOTINE J J, BARABASI A L. Controllability of complex networks[J]. Nature, 2011, 473(7346): 167. DOI:10.1038/nature10011 |
| [7] |
YUAN Zhengzhong, CHEN Zhao, DI Zengru, et al. Exact controllability of complex networks[J]. Nature Communications, 2013, 4. DOI:10.1038/ncomms3447 |
| [8] |
ZHANG Xizhe, HAN Jianfei, ZHANG Weixiong. An efficient algorithm for finding all possible input nodes for controlling complex networks[J]. Scientific Reports, 2017, 7(1): 10677. DOI:10.1038/s41598-017-10744-w |
| [9] |
DING Jin, TAN Ping, LU Yongzai. Optimizing the controllability index of directed networks with the fixed number of control nodes[J]. Neurocomputing, 2016, 171: 1524. DOI:10.1016/j.neucom.2015.07.102 |
| [10] |
SENAME O, LAFAY J F, RABAH R. Controllability indices of linear systems with delays[J]. Kybernetika, 1995, 31(6): 559. |
| [11] |
JUNGERS R M, D'INNOCENZO A, BENEDETTO M D D. Controllability of linear systems with switching delays[J]. IEEE Transactions on Automatic Control, 2016, 61(4): 1117. DOI:10.1109/TAC.2015.2460711 |
| [12] |
SCHIZAS C, EVANS F J. APL and graph theory in dynamic systems analysis[J]. IEE Proceedings D (Control Theory and Applications), 1981, 128(3): 85. DOI:10.1049/ip-d.1981.0016 |
| [13] |
郑大钟. 线性系统理论[M]. 北京: 清华大学出版社, 2002. ZHENG Dazhong. Linear system theory[M]. Beijing: Tsinghua University Press, 2002. |
| [14] |
KALMAN R E. Mathematical description of linear dynamical systems[J]. Journal of the Society for Industrial and Applied Mathematics, Series A: Control, 1963, 1(2): 152. DOI:10.1137/0301010 |
| [15] |
BATAGELJ V, MRVAR A. Pajek-analysis and visualization of large networks[C]//International Symposium on Graph Drawing. Berlin, Heidelberg: Springer, 2001: 477. DOI: 10.1007/3-540-45848-4_54
|
 2019, Vol. 51
2019, Vol. 51


