2. 东莞理工学院 建筑工程系,广东 东莞 523808
2. Department of Civil Engineering, Dongguan University of Technology, Dongguan 523808, Guangdong, China
钢筋混凝土桥梁在服役过程中同时受到车辆荷载和外部环境作用,其抗力和可靠度随时间逐渐降低,一旦荷载超过其承载力将造成桥梁垮塌等重大事故.因此,对多因素影响下的桥梁时变可靠度进行准确评估具有重要意义.在桥梁可靠度分析方面前人做了大量工作[1-4].钢筋锈蚀是导致钢筋混凝土桥梁抗力和可靠度退化的主要原因[5].锈蚀主要由氯盐侵蚀或碳化引起,在已有研究中,只考虑氯盐侵蚀或碳化的研究成果较多,考虑二者耦合作用的成果较少,且主要集中在材料层次,关于它们对结构可靠性的影响缺乏重视[1, 6-7].氯盐侵蚀环境下,混凝土表面氯离子质量浓度会随时间的增长逐渐累积最后达到稳定,现有研究大多忽略了该累积效应,在计算时将氯离子质量浓度取为定值,如此处理虽简单易行,但与真实情况存在明显差异[8].
锈蚀导致抗力退化在时间上分为两个阶段:从建成至钢筋初锈,以及钢筋初锈之后的锈蚀扩展阶段.这两个阶段的发展受诸多因素影响,如混凝土表面氯离子质量浓度、氯离子扩散系数、氯离子临界质量浓度以及混凝土工程质量等,这些因素的随机性导致钢筋初锈时间具有随机性.在锈蚀发展阶段,由于腐蚀电流强度和混凝土质量的随机性,锈蚀速率也是随机的.综上,由于某一服役期对应的钢筋锈蚀率具有随机性,加之混凝土材性的时变性以及锈蚀钢筋的材性时变情况,桥梁的抗力和可靠度均为随机过程[9].因此,根据现有统计数据,采用概率方法对桥梁时变性能进行评估更具合理性.
将钢筋锈蚀发展理论模型进行整合,提出一种考虑碳化和氯离子累积效应的桥梁时变可靠度分析方法.分析碳化、荷载效应、裂缝以及混凝土表面氯离子累积效应对氯盐侵蚀过程的影响.应用路径概率模型和蒙特卡洛方法计算桥梁不同服役期时的抗力概率密度函数及可靠概率,并探究碳化和混凝土表面氯离子累积效应对抗力分布及可靠概率的影响.
1 氯盐侵蚀环境下钢筋锈蚀率计算钢筋表面的氯离子质量浓度达到一定限值时,氯离子能直接穿透钢筋表面钝化膜引起钢筋锈蚀.氯离子在混凝土中的传输主要包括扩散、对流和电迁移等,目前一般采用Fick第二定律来描述混凝土中氯离子的扩散过程[10],其表达式为
| $ \frac{{\partial C}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {D\frac{{\partial C}}{{\partial x}}} \right), $ | (1) |
一维状态下,其解析解为
| $ C(x, t) = {C_0} + \left( {{C_{\rm{s}}} - {C_0}} \right)\left[ {1 - {\mathop{\rm erf}\nolimits} \frac{x}{{2\sqrt {Dt} }}} \right]. $ | (2) |
式中:C(x, t)为距混凝土表面x处的氯离子质量浓度,C0为初始氯离子质量浓度,Cs为混凝土表面氯离子质量浓度,D为氯离子扩散系数,erf(z)为误差函数.氯离子扩散系数受温度、湿度及水灰比等因素的影响[11],其值宜根据实测数据或经验值确定.
钢筋锈蚀的发展与环境温湿度和混凝土工程质量密切相关,对于常见沿海地区环境(温度20℃,相对湿度75%),文献[5]给出的锈蚀率计算公式为
| $ \Delta D = \frac{{0.5249}}{c}{\left[ {1 - \frac{{27}}{{{f_{\rm{c}}} + 13.5}}} \right]^{ - 1.64}}t_{\rm{e}}^{0.71}, $ | (3) |
| $ {\eta _{\rm{s}}} = \sqrt {4{\rm{ \mathsf{ π} }}} \Delta D/\sqrt {{A_{\rm{s}}}} - {\rm{ \mathsf{ π} }}\Delta {D^2}/{A_{\rm{s}}}. $ | (4) |
式中:ΔD为锈蚀深度, mm; te为锈蚀发展时间, a; c为混凝土保护层厚度, mm; fc为混凝土标号; As为钢筋的初始截面积; ηs为钢筋锈蚀率.
钢筋初锈时间与混凝土强度、表面氯离子质量浓度、氯离子扩散系数、临界氯离子质量浓度等因素有关,这些因素都具有随机性.本文在后续分析中,假定混凝土表面氯离子质量浓度稳定时服从均值为3.5 kg/m3,变异系数为0.5的对数正态分布;氯离子扩散系数服从均值为2×10-6 mm2/s,变异系数为0.75的对数正态分布;临界氯离子质量浓度服从0.6~1.2 kg/m3的均匀分布[12].得到钢筋初锈时间概率分布后,根据式(4)进行锈蚀率计算.
2 多因素对氯盐侵蚀的影响分析氯离子在混凝土中的扩散受诸多因素影响,如碳化、荷载、裂缝以及混凝土表面氯离子累积效应.本节对这些因素的影响进行论述,并将所得结论作为后续分析时的参数取值依据.
碳化对氯离子侵蚀的影响方面,Yoon[13]认为:碳化和氯离子共同作用时的碳化速率低于单一碳化作用时,且碳化不是导致混凝土结构劣化的主要原因,但是碳化对氯离子扩散却有明显影响,主要是碳化后混凝土释放的自由氯离子会重新向混凝土内部扩散.进一步研究表明:碳化对氯离子扩散存在正反两方面影响,一方面碳化产物填充混凝土孔隙,阻止氯离子扩散,另一方面碳化增加混凝土的平均孔径和最可几孔径,促进氯离子扩散[6-7, 14].也有研究表明:碳化深度小的混凝土试件氯离子扩散系数有很大程度下降,而碳化深度大的或完全碳化的混凝土试件的氯离子扩散系数却略有升高[15].氯离子临界质量浓度还与钢筋周围的pH有关,碳化会导致混凝土pH降低,降低氯离子临界质量浓度[16].综上,碳化对氯离子侵蚀的影响主要有:碳化释放结合氯离子增加自由氯离子含量;碳化使临界氯离子质量浓度降低;碳化深度较小时碳化阻碍氯离子扩散,碳化深度较大时碳化促进氯离子扩散.
荷载对氯离子扩散的影响方面,蒋金洋等[17]将残余拉应变作为损伤变量,研究了疲劳荷载对氯离子扩散的影响.结果表明,当混凝土残余拉应变低于60×10-6时,氯离子扩散系数增加不明显,当残余拉应变增加到120×10-6时,氯离子扩散系数提高了一个数量级.考虑到普通混凝土开裂应变约为70×10-6[18],可认为,对于普通混凝土在混凝土未开裂时荷载对氯离子的扩散系数影响不大.
裂缝对氯离子扩散系数的影响方面,文献[19]研究了裂缝宽度在0.08~0.68 mm时对氯离子扩散的影响.结果表明:氯离子扩散与宏观裂缝的宽度和裂缝间的粗糙程度关系不大,宏观裂缝对氯离子扩散的影响主要是裂缝表面作为一种自由的混凝土表面,导致了氯离子的二维扩散,并极大地促进了氯离子的扩散.文献[20]研究了收缩裂缝对混凝土中氯离子扩散的影响,结果表明当收缩裂缝宽度小于0.1 mm时,氯离子扩散系数增加幅度很小,随着裂缝宽度的增加氯离子扩散系数快速增大.由于混凝土结构中肉眼可见的裂缝宽度一般为0.1 mm,因此当桥梁不存在肉眼可见的裂缝时,可认为微裂缝对氯离子扩散系数没有影响,当出现肉眼可见的宏观裂缝时可认为钢筋已经开始生锈.
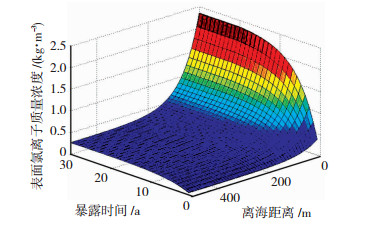
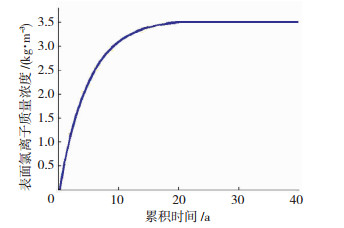
混凝土表面氯离子累积效应对氯离子扩散系数的影响方面,文献[8]根据实测数据对沿海地区混凝土表面氯离子的累积过程进行了研究.结果表明:当暴露时间为20 a时,表面氯离子质量浓度达到稳定值,其大小与结构位置到海的距离有关.文献[8]给出了混凝土表面氯离子质量浓度与结构暴露时间和离海距离的计算公式,相应关系见图 1.本文根据文献[13]认为表面氯离子质量浓度达到稳定时其值为3.5 kg/m3,表面氯离子随时间的累积见图 2.
|
图 1 表面氯离子质量浓度变化 Fig. 1 Change of the concentration of surface chlorine ions |
|
图 2 表面氯离子累积情况 Fig. 2 Accumulation of concrete surface chlorine ions |
梁跨中正截面抗弯承载力的功能函数为
| $ Z = {M_{\rm{R}}}(t) - {M_{\rm{G}}} - {M_{\rm{Q}}}(t), $ | (5) |
式中:MR(t)为截面弯矩抗力,MG为恒载效应,MQ(t)为车辆活荷载效应.
截面弯矩抗力按规范公式计算,对于第一类T梁截面,截面弯矩抗力可根据下式得到[21]:
| $ x(t) = {A_{\rm{s}}}(t){f_{\rm{y}}}(t)/\left[ {{f_{{\rm{cu}}}}(t){b^\prime }_{\rm{f}}} \right], $ | (6) |
| $ {M_{\rm{R}}}(t) = {A_{\rm{s}}}(t){f_{\rm{y}}}(t)\left[ {{h_0} - x(t)/2} \right]. $ | (7) |
式中:x(t)为混凝土受压区高度,As(t)为服役t年时受拉钢筋面积,fy(t)为服役t年时钢筋屈服强度,fcu(t)为服役t年时混凝土抗压强度,h0为截面有效高度,b′f为受压翼缘的有效宽度.
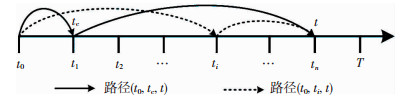
从上式可知,影响桥梁承载力的主要因素是钢筋面积As(t)和混凝土强度fcu(t),导致钢筋面积减小的主要因素是锈蚀.进行可靠度评估时首先要确定某一时间的钢筋锈蚀率分布,进而根据A0(1-ηs)得到相应的钢筋面积分布,其中A0为初始钢筋面积,ηs为钢筋锈蚀率.采用宋志刚等[5]提出的路径概率模型来计算钢筋锈蚀率分布.路径概率模型将锈蚀发展划分为一系列路径,在考虑了初锈阶段和锈蚀扩展阶段的诸多不确定性因素后,通过概率求和的方法获得钢筋锈蚀率的概率分布,其优点是将初锈阶段和锈蚀扩展阶段的概率特征进行了有效的结合.在应用路径概率方法时考虑了碳化和混凝土表面氯离子累积效应的影响,即:考虑了碳化释放结合Cl-和碳化降低临界Cl-质量浓度,并认为混凝土表面Cl-浓度是一个缓慢累积的过程,具体参数取值参见前文.路径概率模型的基本思路见图 3[5].
|
图 3 锈蚀路径概率 Fig. 3 Corrosion probability paths |
图 3中,tc为考虑碳化和Cl-累积效应后的钢筋起锈时间,t为结构评估时间,[0, tc, t]是评估期内锈蚀发展的一条随机路径.tc时刻钢筋起锈的条件下,t时刻钢筋锈蚀率ηs的条件概率密度函数为
| $ f\left( {{\eta _{\rm{s}}}, {t_{\rm{c}}}} \right) = f\left[ {{\eta _{\rm{s}}}/{t_{\rm{c}}}} \right]p\left( {{t_{\rm{c}}}} \right){\rm{d}}t, $ | (8) |
式中:f[ηs/tc]为钢筋tc时刻开始锈蚀条件下,钢筋锈蚀率的概率密度函数;p(tc)为tc时刻钢筋开始锈蚀的概率密度函数.定义n个锈蚀路径,只要n足够大就可覆盖所有的锈蚀发展路径,且所有这些路径是互斥的,根据概率求和公式可得t时刻钢筋锈蚀率ηs的无条件概率密度函数为
| $ \begin{array}{l} f\left( {{\eta _{\rm{s}}}} \right) = \sum\limits_{i = 1}^n f \left( {{\eta _{\rm{s}}}, {t_{{\rm{c}}i}}} \right) = \sum\limits_{i = 1}^n f \left( {{\eta _{\rm{s}}}/{t_{{\rm{c}}i}}} \right)p\left( {{t_{{\rm{c}}i}}} \right){\rm{d}}t\\ \;\;\;\;\;\;\;\;\; = \sum\limits_{i = 1}^n f \left( {{\eta _{\rm{s}}}/{t_{{\rm{c}}i}}} \right)\left[ {F\left( {{t_{{\rm{c}}i}}} \right) - F\left( {{t_{{\rm{c}}(i - 1)}}} \right)} \right], \end{array} $ | (9) |
式中F(tci)=p(t≤tci)=∫0tcip(t)dt为tci时发生初锈的累积概率,即根据Fick第二定律所得的tci时刻氯离子质量浓度大于临界氯离子质量浓度的概率.
由以上过程可得服役期t时的钢筋锈蚀率分布,进而得到钢筋面积分布,再根据钢筋屈服强度以及混凝土强度的时变概率分布,可得构件的抗力分布.
钢筋锈蚀后,屈服强度与锈蚀率相关,已知锈蚀率可通过下式计算钢筋的屈服强度[22]:
| $ {f_{\rm{y}}}(t) = \frac{{1 - 1.049{\eta _{\rm{s}}}(t)}}{{1 - {\eta _{\rm{s}}}(t)}}{f_{{\rm{y}}0}}, $ | (10) |
式中:fy(t)、fy0分别为锈蚀和未锈蚀钢筋的屈服强度,ηs(t)为钢筋锈蚀率.
混凝土抗压强度的时变概率分布方面,文献[23]研究表明,混凝土强度在某一服役期内仍服从正态分布,且随着时间的增长混凝土强度平均值先增大后减小,标准差逐渐增大.服役t年后,混凝土抗压强度平均值和标准差的经时变化模型为:
| $ {\mu _{{f_{{\rm{cu}}}}}}(t) = {\mu _{{f_{{\rm{cu}}0}}}}1.4529{{\rm{e}}^{ - 0.0246{{({\rm{ln}}\mathit{t} - 1.7154)}^2}}}, $ | (11) |
| $ {\sigma _{{f_{{\rm{cu}}}}}}(t) = {\sigma _{{f_{{\rm{cu}}0}}}}(0.0305t + 1.2368). $ | (12) |
式中:μfcu0和σfcu0分别为混凝土28 d强度的平均值和标准差,可根据下式计算[24]:
| $ {\mu _{{f_{{\rm{cu0}}}}}} = {\mu _{{K_{\rm{M}}}}}{f_{\rm{c}}}, $ | (13) |
| $ {\sigma _{{f_{{\rm{cu0}}}}}} = {\sigma _{{K_{\rm{M}}}}}{f_{\rm{c}}}, $ | (14) |
| $ {K_{\rm{M}}} = \frac{1}{{{\omega _0}}}\frac{{{f_{{\rm{ck}}}}}}{{{f_{\rm{c}}}}}. $ | (15) |
式中:KM为不定性无量纲参数,其统计参数见文献[24],fck为28 d混凝土强度实测值,fc为规范规定的混凝土强度设计值,1/ω0反映结构构件材料性能与试件材料性能的差异.
在桥梁荷载效应的计算方面,根据永久荷载效应标准值和文献[25]可得到永久荷载效应的概率分布.车辆荷载效应是一个与时间有关的量,应根据已服役时间内的荷载实测资料进行统计分析.由于缺乏相应的实测资料,本文选用的服役评估期t年内车辆荷载效应的分布函数为[12]
| $ {F_t}(x) = {{\rm{e}}^{ - {{\rm{e}}^{ - (x - \varepsilon )/\eta }}}}, $ | (16) |
式中:ε=u+vln(t/100),η=v,u=0.768 5SQK,υ=0.053 7SQK,SQK为按照规范荷载标准值计算的结构效应.车辆荷载效应的分布函数确定后,其对应的概率密度函数也可确定,进而可采用文献[26]中已知任意概率密度函数生成随机数的方法生成车辆荷载效应随机数.
由以上过程可得不同服役时间的抗力和荷载效应随机数.对于式(5)这样的功能函数,由于引入了时间因素,作用和抗力均为随机过程,这种考虑了抗力随时间变化的可靠性计算在实施时难度较大,常用的方法有等效抗力法[27]、最小抗力法[28]和公式递推法[29].其中最小抗力法计算简便,概念直观,且采用最小抗力法计算的可靠指标相对于另外两种方法要偏小一些,即偏安全一些.本文在计算目标可靠度时采用最小抗力法,其功能函数为
| $ Z = \min \left[ {{M_{\rm{R}}}(t)} \right] - {M_{\rm{G}}} - \max \left[ {{M_{\rm{Q}}}(t)} \right], $ | (17) |
式中:min[MR(t)]为服役评估期内的最小抗力,max[MQ(t)]为服役评估期内最大车载效应.
根据桥梁在服役过程中各参数的概率分布模型生成随机数,再结合式(17)应用蒙特卡洛方法进行可靠度分析.蒙特卡洛方法的优点在于不需具体考虑极限状态曲面的形状和复杂性,只需根据随机抽取的样本值计算功能函数的值,但计算量较大.工程结构的失效概率通常比较小,因此需要较大样本数才能给出正确估计,本文取样本数N=1×105[30].蒙特卡洛方法求失效概率的具体步骤:
1) 根据各变量的分布函数,随机生成每一个变量的样本值Xi(i=1, 2, …, n).
2) 根据生成的样本值计算功能函数的值Z.
3) 重复上述步骤N次,失效概率为
| $ {P_{\rm{f}}} \approx \frac{{n(Z < 0)}}{N}, $ | (18) |
式中n(Z < 0)是功能函数小于0的次数.
提出的基于路径概率的桥梁时变可靠度计算方法的实现流程为:选取功能函数→计算锈蚀率概率分布(路径概率模型)→选取参数概率分布→生成参数随机数→计算时变可靠度(蒙特卡洛法).
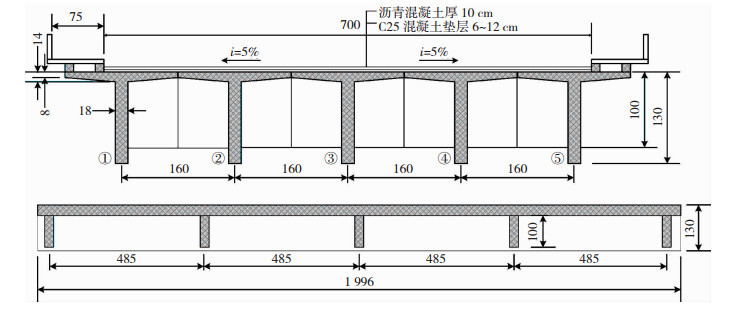
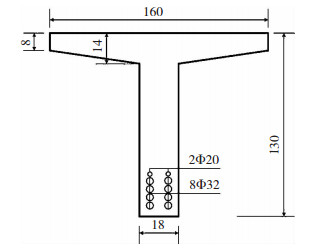
4 算例和分析为验证所提方法的合理性,分析碳化和氯离子累积效应对桥梁抗力和可靠性的影响,以文献[31]中的钢混简支T形梁桥中的一片梁为例进行计算分析.该桥的尺寸见图 4、5,混凝土强度等级为C30,主筋用HRB335钢筋.以弯矩效应最大的1号梁为例进行计算.永久荷载效应用随机变量描述,车辆荷载效应和截面抗力用随机过程描述.经计算永久荷载效应标准值为797.08 kN·m,根据文献[25]认为其服从均值μSG=808.88 kN·m,变异系数δSG=0.043 1的正态分布,车辆荷载效应标准值为783.96 kN·m,其时变概率分布可根据式(16)得到,截面抗力时变概率分布可根据式(7)并结合蒙特卡洛方法得到.
|
图 4 钢筋混凝土T梁桥尺寸(cm) Fig. 4 Size of reinforced concrete T beam bridge (cm) |
|
图 5 1号梁截面及配筋(cm) Fig. 5 Cross section of T type reinforced concrete beam (cm) |
为研究氯离子累积效应和碳化对钢筋起锈时间的影响,分别分析累积效应、碳化及它们共同作用时钢筋锈蚀概率随时间的变化.考虑累积效应时先从图 2中得到给定服役期下的表面氯离子质量浓度,再根据式(2)和蒙特卡洛方法计算该服役期时钢筋的锈蚀概率.由于混凝土表面的氯离子浓度是逐渐增加并趋于稳定的,这样的计算是偏于保守的.图 6为累积效应对钢筋锈蚀概率的影响.可看出,考虑累积效应后,同一服役期的钢筋锈蚀概率变小,在表面氯离子质量浓度达到稳定值之前差异最明显.服役5 a时,考虑累积效应时钢筋的锈蚀概率为11.90%,不考虑累积效应时对应的概率为21.74%.可见在计算钢筋起锈时间时,不应忽视累积效应.

|
图 6 累积效应对钢筋锈蚀概率的影响 Fig. 6 Effect of cumulative effect on corrosion of steel bar |
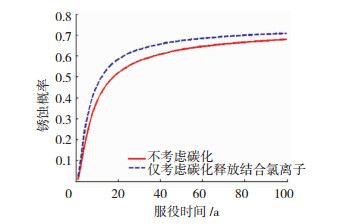
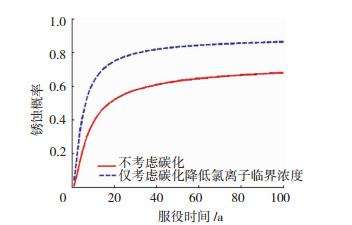
分析碳化对钢筋锈蚀概率的影响时,主要考虑碳化释放结合氯离子和碳化降低临界氯离子质量浓度的影响.研究表明碳化后混凝土将释放70%以上的结合氯离子[32-33],规范规定混凝土中初始氯离子含量不应超过胶凝材料的0.1%[34],假设混凝土中初始氯离子质量浓度为0.4 kg/m3,碳化后释放70%.文献[16]的结果表明临界氯离子质量浓度随pH减小而大幅降低,降幅可达50%,甚至更多.假设碳化后临界氯离子质量浓度降低50%.碳化释放结合氯离子和碳化降低临界氯离子质量浓度对钢筋锈蚀概率的影响结果见图 7、8.可看出,碳化释放结合氯离子和碳化降低临界氯离子质量浓度均会增加钢筋的锈蚀概率,其中碳化导致临界氯离子质量浓度降低的影响起主要作用.
|
图 7 碳化释放结合Cl-对钢筋锈蚀概率的影响 Fig. 7 Effect of carbonization release bound Cl- on corrosion probability of steel bar |
|
图 8 碳化降低临界Cl-浓度对钢筋锈蚀概率的影响 Fig. 8 Effect of reduced carbonization critical Cl- concentration on corrosion probability of steel bar |
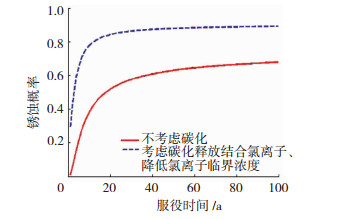
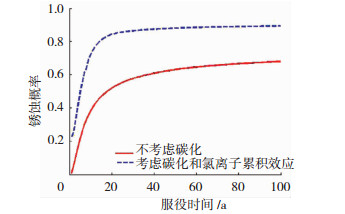
同时考虑碳化释放结合氯离子和碳化降低临界氯离子质量浓度的钢筋锈蚀概率计算结果见图 9.其中不考虑碳化时钢筋锈蚀概率为50%时对应服役期为18 a,而考虑碳化影响时对应服役期为3 a.可见碳化会大幅增加钢筋的锈蚀概率.对于某些实际工程,也存在钢筋表面氯离子质量浓度很低、碳化深度也不深的情况下发生钢筋大面积锈蚀的现象[16],因此分析钢筋锈蚀概率时不应忽视碳化的影响.图 10为同时考虑碳化和累积效应时的钢筋锈蚀概率时变情况,其中不考虑碳化和累积效应时锈蚀概率为50%时对应服役期为18 a,而考虑碳化和累积效应时,对应服役期为5 a.
|
图 9 同时考虑碳化释放结合Cl-和降低临界Cl-浓度的影响 Fig. 9 Effect of carbonization release bound Cl- and reduced critical Cl- concentration on corrosion probability of steel bar |
|
图 10 同时考虑碳化和累积效应的结果 Fig. 10 Effect of carbonization and Cl- accumulation on corrosion probability of steel bar |
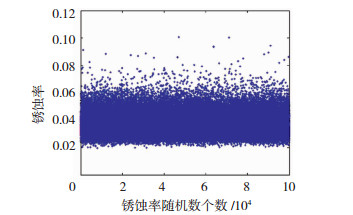
进行可靠性分析之前首先要根据式(9)得到给定服役期时钢筋的无条件锈蚀率概率密度函数,进而得到不同服役期时钢筋的锈蚀率随机数,图 11为服役10 a时的锈蚀率随机数分布.已知给定服役期时的锈蚀率分布,可根据式(10)~(12)得到混凝土和钢筋的强度概率分布,再应用蒙特卡洛方法结合式(6)、(7)得到给定服役期下桥梁的抗力分布情况.
|
图 11 服役10 a时的钢筋锈蚀率随机数 Fig. 11 Random number of steel bar corrosion rate at 10 years of service |
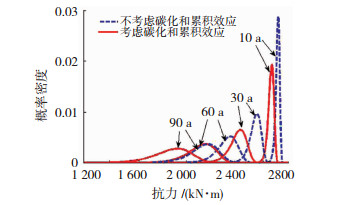
碳化和累积效应对抗力概率密度函数值的影响见图 12.由于混凝土表面的氯离子质量浓度是逐渐累积的,因此,计算时取评估期之前的平均浓度.从图 12可知,随服役时间的增加抗力逐渐减小,离散性逐渐增大,服役期90 a的抗力约为服役期10 a的72.55%.考虑碳化和累积效应后抗力加速衰减,离散性增大,抗力的差值随时间的增大逐渐变大.不考虑碳化和累积效应时,服役90 a的抗力分布与考虑碳化和累积效应时服役60 a的抗力分布接近,可见碳化和氯盐共同作用加速了抗力的退化过程.
|
图 12 时变抗力概率密度函数值 Fig. 12 Probability density function value of time-dependent resistance |
为探究桥梁服役过程中抗力的分布函数形式,对不同服役期的抗力概率密度函数值进行拟合.一般认为抗力服从对数正态分布[28, 35],本文研究发现抗力分布用三参数Burr Ⅻ分布拟合效果较好,Burr Ⅻ可以广泛地对经验数据进行拟合,很多常用的分布,如伽玛分布、对数正态分布等都可看作是Burr Ⅻ分布的特例.其概率密度函数为[36]
| $ f(x|\alpha , c, k) = \frac{{kc}}{\alpha }{\left( {\frac{x}{\alpha }} \right)^{c - 1}}/{\left( {1 + {{\left( {\frac{x}{\alpha }} \right)}^c}} \right)^{k + 1}}, $ | (19) |
式中:x>0, α>0, c>0, k>0, c和k是形状参数,α是尺度参数.
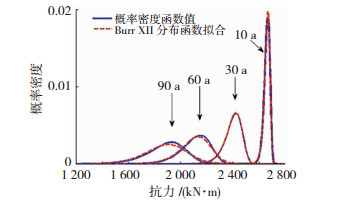
Burr Ⅻ分布函数的抗力拟合效果见图 13.值得指出的是,桥梁的抗力分布是一个随机过程,而不是随机变量,因此用同一个函数表示不同服役期的抗力分布是不合理的.表 1为不同服役期时,抗力分布拟合的具体结果,可以看出Burr Ⅻ分布中的参数值随服役时间的增加有减小的趋势.
|
图 13 抗力概率密度函数拟合效果 Fig. 13 Fitting effect of probability density function of resistance |
| 表 1 不同服役期对应的Burr Ⅻ分布参数值 Tab. 1 Distribution parameters of Burr Ⅻ at different service periods |
图 14为根据式(16)得到的荷载效应时变情况,荷载效应的时变性主要由车辆荷载引起,总荷载效应在服役初期增长较快,此后增长速率变缓.已知给定服役期的荷载效应和抗力分布后,可根据式(17)、(18)应用蒙特卡洛法计算可靠度.

|
图 14 荷载效应时变情况 Fig. 14 Time-dependent load effect |
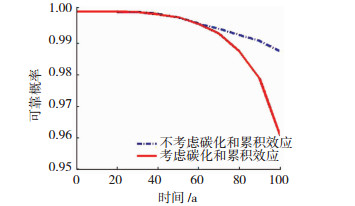
碳化和氯离子累积效应对该梁时变可靠度的影响见图 15.随着服役时间的增加该梁的可靠概率逐渐减小;碳化和氯离子累积效应对可靠概率的影响主要体现在服役后期,在服役的中前期影响较小.因此,在对老旧桥梁进行性能分析时,应重视碳化和氯离子累积效应的影响.
|
图 15 可靠度时变情况 Fig. 15 Time-dependent reliability of reinforced concrete beam |
1) 获得桥梁抗力概率分布和可靠度的实测结果非常困难,而结合已有理论和参数概率分布通过路径概率模型和蒙特卡洛方法进行演进模拟将是一种可行方法.
2) 考虑氯离子累积效应后钢筋的锈蚀概率降低,考虑碳化后钢筋的锈蚀概率增加.碳化对锈蚀的促进方面,碳化导致临界氯离子质量浓度降低的影响要大于碳化后释放结合氯离子的影响.同时考虑碳化和氯离子累积效应后,钢筋的锈蚀概率增加.
3) 随着服役时间的增加,梁的抗力逐渐减小,离散性逐渐增大,考虑碳化和累积效应后梁的抗力加速退化.不同服役期的抗力分布可用三参数Burr Ⅻ分布模型来描述.碳化和氯离子累积效应对可靠性的影响主要体现在服役后期,在服役的中前期影响较小.
| [1] |
ZHU X, ZI G, LEE W, et al. Probabilistic analysis of reinforcement corrosion due to the combined action of carbonation and chloride ingress in concrete[J]. Construction and Building Materials, 2016, 124: 667. DOI:10.1016/j.conbuildmat.2016.07.120 |
| [2] |
彭建新, 张建仁, 张克波, 等. 锈蚀RC桥梁弯曲抗力时变概率模型与试验研究[J]. 工程力学, 2012(6): 125. PENG Jianxin, ZHANG Jianren, ZHANG Kebo, et al. Probabilistic resistance model and experimental investigation for corroded RC bridges[J]. Engineering Mechanics, 2012(6): 125. DOI:10.6052/j.issn.1000-4750.2010.08.0614 |
| [3] |
LIU Y, SHI X. Stochastic modeling of service life of concrete structures in chloride-laden environments[J]. Journal of Materials in Civil Engineering, 2012, 24(4): 381. DOI:10.1061/(ASCE)MT.1943-5533.0000399 |
| [4] |
ZHU Jinsong, GAO Change. Probabilistic durability assessment approach of deteriorating RC bridges[J]. Journal of Southeast University (English Edition), 2011(1): 70. DOI:10.3969/j.issn.1003-7985.2011.01.015 |
| [5] |
宋志刚, 金伟良, 刘芳, 等. 钢筋锈蚀率概率分布的动态演进模拟[J]. 浙江大学学报(工学版), 2006, 40(10): 1749. SONG Zhigang, JIN Weiliang, LIU Fang, et al. Dynamic simulation method for probability evolution of reinforcement steel corrosion[J]. Journal of Zhejiang University (Engineering Science), 2006, 40(10): 1749. DOI:10.3785/j.issn.1008-973X.2006.10.019 |
| [6] |
许晨, 王传坤, 金伟良. 混凝土中氯离子侵蚀与碳化的相互影响[J]. 建筑材料学报, 2011(3): 376. XU Chen, WANG Chuankun, JIN Weiliang. Interaction effect of chloride attack and carbonization in concrete[J]. Journal of Building Materials, 2011(3): 376. DOI:10.3969/j.issn.1007-9629.2011.03.017 |
| [7] |
牛荻涛, 孙丛涛. 混凝土碳化与氯离子侵蚀共同作用研究[J]. 硅酸盐学报, 2013(8): 1094. NIU Ditao, SUN Congtao. Study on interaction of concrete carbonation and chloride corrosion[J]. Journal of the Chinese Ceramic Society, 2013(8): 1094. DOI:10.7521/j.issn.0454-5648.2013.08.11 |
| [8] |
徐田欣.滨海盐雾区非饱和混凝土中氯离子渗透机理[D].哈尔滨: 哈尔滨工业大学, 2014 XU Tianxin. The mechanism of chloride penetration in unsaturated concrete at coastal atmosphere zone[D]. Harbin: Harbin Institute of Technology, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10213-1014084569.htm |
| [9] |
ŠOMODÍKOVÁM, LEHKýD, DOLEŽELJ, 等. Modeling of degradation processes in concrete: Probabilistic lifetime and load-bearing capacity assessment of existing reinforced concrete bridges[J]. Engineering Structures, 2016, 119: 49. DOI:10.1016/j.engstruct.2016.03.065 |
| [10] |
International Federation for Structural Concrete (FIB). Fib model code for concrete structures 2010(2013)[S]. Lausanne, Switzerland: International Federation for Structural Concrete, 2013
|
| [11] |
SHAFEI B, ALIPOUR A, SHINOZUKA M. Prediction of corrosion initiation in reinforced concrete members subjected to environmental stressors: A finite-element framework[J]. Cement and Concrete Research, 2012, 42(2): 365. DOI:10.1016/j.cemconres.2011.11.001 |
| [12] |
卫璞, 肖汝诚. 氯离子侵蚀下预应力混凝土桥梁抗弯承载寿命函数[J]. 江苏大学学报(自然科学版), 2015(2): 233. WEI Pu, XIAO Rucheng. Bending bearing lifetime function of prestressed concrete bridges under chloride contaminated environment[J]. Journal of Jiangsu University (Natural Science Edition), 2015(2): 233. DOI:10.3969/j.issn.1671-7775.2015.02.020 |
| [13] |
YOON I S. Deterioration of concrete due to combined reaction of carbonation and chloride penetration: Experimental study[J]. Key Engineering Materials, 2007, 348/349: 729. DOI:10.4028/www.scientific.net/KEM.348-349 |
| [14] |
杨蔚为, 郑永来, 郑顺. 混凝土碳化对氯离子扩散影响试验研究[J]. 水利水运工程学报, 2014(4): 93. YANG Weiwei, ZHENG Yonglai, ZHENG Shun. Experimental studies of concrete carbonization impact on chloride diffusion[J]. Hydro-science and Engineering, 2014(4): 93. DOI:10.3969/j.issn.1009-640X.2014.04.015 |
| [15] |
王栋, 孙家瑛, 房信峰. 碳化作用对混凝土抗氯离子渗透性能的影响[J]. 四川建筑科学研究, 2014, 40(3): 212. WANG Dong, SUN Jiaying, FANG Xinfeng. Effect of carbonization on chloride penetration resistance of concrete[J]. Sichuan Buiding Science, 2014, 40(3): 212. DOI:10.3969/j.issn.1008-1933.2014.03.056 |
| [16] |
金伟良, 袁迎曙, 卫军, 等. 氯盐环境下混凝土结构耐久性理论与设计方法[M]. 北京: 科学出版社, 2011: 416. JIN Weiliang, YUAN Yingshu, WEI Jun, et al. Durability theory and design method for concrete structures under chloride attack[M]. Beijing: Science Press, 2011: 416. |
| [17] |
蒋金洋, 孙伟, 王晶, 等. 弯曲疲劳载荷作用下结构混凝土抗氯离子扩散性能[J]. 东南大学学报(自然科学版), 2010(2): 362. JIANG Jinyang, SUN Wei, WANG Jing, et al. Resistance to chloride ion diffusion of structural concrete under bending fatigue load[J]. Journal of Southeast University (Natural Science Edition), 2010(2): 362. DOI:10.3969/j.issn.1001-0505.2010.02.028 |
| [18] |
过镇海, 时旭东. 钢筋混凝土原理和分析[M]. 北京: 清华大学出版社, 2013: 217-228. GUO Zhenhai, SHI Xudong. Reinforced concrete theory[M]. Beijing: Tsinghua University Press, 2013: 217-228. |
| [19] |
RODRIGUEZ O G. Influence of cracks on chloride ingress into concrete[J]. Aci Materials Journal, 2003, 100(2): 120. |
| [20] |
金祖权, 侯保荣, 赵铁军, 等. 收缩裂缝对混凝土氯离子渗透及碳化的影响[J]. 土木建筑与环境工程, 2011(1): 7. JIN Zuquan, HOU Baorong, ZHAO Tiejun, et al. Influence of shrinkage cracks on chloride penetration and carbonation of concrete[J]. Journal of Civil, Architectural & Environmental Engineering, 2011(1): 7. DOI:10.3969/j.issn.1674-4764.2011.01.002 |
| [21] |
公路钢筋混凝土及预应力混凝土桥涵设计规范: JTG D62-2004[S].北京: 人民交通出版社, 2004 Code for design of highway reinforced concrete and prestressed concrete bridges and culverts: JTG D62-2004[S].Beijing: China Communications Press, 2004 |
| [22] |
张伟平, 商登峰, 顾祥林. 锈蚀钢筋应力-应变关系研究[J]. 同济大学学报(自然科学版), 2006(5): 586. ZHANG Weiping, SHANG Dengfeng, GU Xianglin. Stress-strain relationship of corroded steel bars[J]. Journal of Tongji University (Natural Science), 2006(5): 586. DOI:10.3321/j.issn:0253-374X.2006.05.004 |
| [23] |
牛荻涛, 王庆霖. 一般大气环境下混凝土强度经时变化模型[J]. 工业建筑, 1995(6): 36. NIU Ditao, WANG Qinglin. Models of concrete strength changing with time in general air environment[J]. Industrial Construction, 1995(6): 36. DOI:10.3321/j.issn:1000-8993.1995.06.008 |
| [24] |
李扬海, 鲍卫刚, 郭修武, 等. 公路桥梁结构可靠度与概率极限状态设计[M]. 北京: 人民交通出版社, 1997: 140-148. LI Yanghai, BAO Weigang, GUO Xiuwu, et al. Reliability and probability limit state design of highway bridge structure[M]. Beijing: China Communications Press, 1997: 140-148. |
| [25] |
公路工程结构可靠度设计统一标准: GB/T 50283-1999[S].北京: 中国计划出版社, 1999 Unified standard for reliability design of highway engineering structures: GB/T 50283-1999[S]. Beijing: China Planning Press, 1999 |
| [26] |
谢中华. MATLAB统计分析与应用: 40个案例分析[M]. 北京: 北京航空航天大学出版社, 2010: 134-140. XIE Zhonghua. Statistical analysis and application of MATLAB: Analysis of 40 cases[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2010: 134-140. |
| [27] |
贡金鑫, 赵国藩. 考虑抗力随时间变化的结构可靠度分析[J]. 建筑结构学报, 1998(5): 43. GONG Jinxin, ZHAO Guofan. Reliability analysis for deteriorating structures[J]. Journal of Building Structures, 1998(5): 43. DOI:10.14006/j.jzjgxb.1998.05.007 |
| [28] |
杨伟军. 服役结构可靠度理论及其应用[M]. 长沙: 中南工业大学出版社, 2000: 125-128. YANG Weijun. Reliability theory of service structure and its application[M]. Changsha: Central South University Press, 2000: 125-128. |
| [29] |
索清辉, 钱永久. 服役公路桥梁的时变可靠指标计算[J]. 交通运输工程学报, 2006(1): 69. SUO Qinghui, QIAN Yongjiu. Time-dependent reliability index calculation of existed highway bridge[J]. Journal of Traffic and Transportation Engineering, 2006(1): 69. DOI:10.3321/j.issn:1671-1637.2006.01.014 |
| [30] |
赵国藩, 金伟良, 贡金鑫. 结构可靠度理论[M]. 北京: 中国建筑工业出版社, 2000: 79-84. ZHAO Guofan, JIN Weiliang, GONG Jinxin. Structural reliability theory[M]. Beijing: China Architecture & Building Press, 2000: 79-84. |
| [31] |
易建国. 混凝土简支梁(板)桥[M]. 3版. 北京: 人民交通出版社, 2016: 72-97. YI Jianguo. Reinforced concrete simply supported girder (slab) bridges[M]. 3th ed. Beijing: China Communications Press, 2016: 72-97. |
| [32] |
龚傲龙, 郭万里, 孙朴, 等. 碳化作用下固化氯离子失稳特性研究[J]. 混凝土与水泥制品, 2012(8): 5. GONG Aolong, GUO Wanli, SUN Pu, et al. Study on the instability of chloride ions under carbonization[J]. China Concrete and Cement Products, 2012(8): 5. DOI:10.3969/j.issn.1000-4637.2012.08.002 |
| [33] |
李士彬, 孙伟. 疲劳、碳化和氯盐作用下混凝土劣化的研究进展[J]. 硅酸盐学报, 2013(11): 1459. LI Shibin, SUN Wei. Review on deterioration of concrete subjected to coupling effect of fatigue load, carbonation and chlorides[J]. Journal of the Chinese Ceramic Society, 2013(11): 1459. DOI:10.7521/j.issn.0454-5648.2013.11.01 |
| [34] |
混凝土结构耐久性设计与施工指南: CCES 01-2004[S].北京: 中国建筑工业出版社, 2004 Guide to durability design and construction of concrete structures: CCES 01-2004[S]. Beijing: China Architecture & Building Press, 2004 |
| [35] |
张建仁, 刘扬, 许福友, 等. 结构可靠度理论及其在桥梁工程中的应用[M]. 北京: 人民交通出版社, 2003: 115-119. ZHANG Jianren, LIU Yang, XU Fuyou, et al. Structure reliability theory and its application to bridge engineering[M]. Beijing: China Communications Press, 2003: 115-119. |
| [36] |
Mathworks. Burr type XII distribution[EB/OL].[2018-02-15].http://www.mathworks.com/help/stats/burr-type-xii-distribution.html
|
 2019, Vol. 51
2019, Vol. 51


