2. 岩土及地下工程教育部重点实验室(同济大学),上海 200092
2. Key Lab of Geotechnical and Underground Engineering (Tongji University), Ministry of Education, Shanghai 200092, China
中国西北地区存在大范围的盐渍土、盐湖,气候环境恶劣,服役于这些地区的桩基易遭受硫酸盐侵蚀破坏,对桩基结构性能和服役寿命造成严重影响[1].硫酸盐对混凝土腐蚀时发生复杂的化学-力学反应,由化学作用引起的膨胀应变和物理作用产生的结晶压力导致混凝土开裂破坏,微裂纹的产生同样加速了混凝土结构性能劣化[2-3].
目前腐蚀环境下的扩散理论模型基本以混凝土板、墙等为代表的直角坐标系为主,而缺乏以混凝土桩基、桥墩等为对象的柱坐标扩散理论研究[4].由于几何差异导致扩散方程的改变,有必要探讨硫酸盐在柱坐标下的扩散规律和计算方法.关于硫酸盐侵蚀机理,迄今已取得不少研究成果,主要探讨硫酸盐在扩散过程中由于化学-物理作用引起混凝土内部的微观结构改变,建立起化学-力学耦合模型并开展相关材料力学性能分析[5-7];诸多学者[8-10]对硫酸盐腐蚀下混凝土的损伤规律建立了不同的理论模型,然而当前的研究深度相当有限,仍缺乏较为完善的理论建立起硫酸盐侵蚀下由细观到宏观的侵蚀损伤模型,且不能定量反映侵蚀产物引起混凝土开裂与损伤破坏的全过程,这将直接导致相关结构耐久性和服役寿命预测出现困难.因此,正确建立硫酸盐侵蚀作用下混凝土损伤效应定量分析方法,是值得进一步深入研究的课题.
硫酸盐侵蚀将引起混凝土桩基结构性能退化,桩身承载力显著下降,当桩顶荷载大于桩身极限承载力时将引起桩身脆断破坏[11].由腐蚀引起桩身强度退化是导致腐蚀环境中桩基结构失效的主要原因,目前硫酸盐侵蚀引起的桩基损伤和承载力演变规律还有待更深入的研究.本文将以混凝土灌注桩为研究对象,建立柱坐标下硫酸根离子非稳态扩散的化学-力学模型并推导出相应的数值求解计算方法,通过引入损伤演化函数,确立桩基损伤度与桩身承载力之间的相关关系,对影响桩基损伤与桩身承载力的主要因素进行比较分析.
1 理论模型 1.1 扩散反应方程混凝土灌注桩遭受外部硫酸盐侵蚀时,硫酸根离子在混凝土中的侵蚀过程可等效为一维柱坐标系下的扩散-反应方程.以文献[3, 6]扩散理论模型为基础,根据Fick第二定律和化学反应动力学理论,建立硫酸根离子在一维柱坐标下的扩散反应方程式:
| $ \begin{array}{l} \frac{{\partial C}}{{\partial t}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left( {Dr\frac{{\partial C}}{{\partial r}}} \right) + \frac{{\partial {C_{\rm{d}}}}}{{\partial t}}, \\ \frac{{\partial {C_{\rm{d}}}}}{{\partial t}} = - k \cdot {C_{{\rm{CA}}0}} \cdot C\left( {1 - {h_\alpha } + 0.5\beta {h_\alpha } + \beta {h_\alpha } \cdot {{\rm{e}}^{ - \frac{1}{6}k \cdot c \cdot t}}} \right), \\ C(r, 0) = 0, x \in (0, R), \\ C(R, t) = {\varphi _0}{C_0}, \frac{{\partial C(0, t)}}{{\partial r}} = 0. \end{array} $ | (1) |
式中:C表示硫酸根离子浓度,D为硫酸根离子的有效扩散系数.将混凝土孔隙溶液视为电解溶液并考虑离子扩散,扩散系数可表示为孔隙率、硫酸根离子浓度和时间相关的函数[2],即D=φDm(C, t);t为扩散时间,r为侵蚀点的径向距离,R为桩半径,k为化学反应速率常数,Cd为化学反应过程中消耗的硫酸根离子浓度,CCA0为初始钙铝酸盐浓度,β为石膏质量分数,φ0为混凝土初始孔隙率.φ为混凝土侵蚀过程中的孔隙率[3]:
| $ \varphi = \max \left( {{f_{{\rm{cv}}}}\frac{{w/c - 0.39{h_\alpha }}}{{w/c + 0.32}}, 0} \right), $ | (2) |
式中:fcv为混凝土中水泥所占的体积分数,w/c为水灰比;hα表示水泥水化程度,其与水泥水化时间有关[2].
1.2 混凝土膨胀应变计算硫酸盐侵蚀引起混凝土的膨胀应变可通过化学-力学理论计算,在混凝土内部孔隙溶液中,硫酸根离子先与水泥水化产物氢氧化钙(CH)反应生成石膏(CSH2),而石膏作为中间相与水泥中水化铝酸钙(C3A、C4ASH12、C4AH13)反应生成膨胀产物钙钒石(C6AS3H32);当混凝土孔隙填充到一定程度时,膨胀产物与混凝土内部孔隙的孔壁接触并产生拉应力,此时由化学反应引起的体应变为[7]
| $ {\varepsilon _{\rm{v}}} = \sum\limits_{i = 1}^3 {\frac{{\Delta {V_i}}}{{{V_i}}}} \frac{{{M_i}}}{{{\rho _i}}}\frac{{{C_i}}}{{\sum {{C_i}} }}{C_{{\rm{CA}}}} - f\varphi , $ | (3) |
式右边第一项表示由化学反应引起的内膨胀应变,第二项fφ表示孔隙填充程度,f表示孔隙填充率;ΔVi/Vi表示各铝酸钙相C3A、C4ASH12和C4AH13参与反应时对应的体积变化,分别为:1.31、0.48、0.55[5];Mi/ρi和Ci/∑Ci对应各铝酸钙相的摩尔体积和浓度所占比例;CCA表示反应过程中消耗的铝酸钙总浓度[6]:
| $ {C_{{\rm{CA}}}} = {C_{{\rm{CA}}0}}\left( {1 - {{\rm{e}}^{\int_0^t {\frac{{kC}}{q}{\rm{dt}}} }}} \right), $ | (4) |
将桩身混凝土视为各向同性材料,钙矾石在混凝土内部孔隙中均匀生长,引起混凝土内膨胀应变在各方向相等,此时桩身结构的竖向应变ε为
| $ \varepsilon = \frac{{{\varepsilon _{\rm{v}}}}}{3}. $ | (5) |
外部硫酸根离子与混凝土水化产物发生化学反应生成的膨胀产物在初始孔隙填充阶段尚未与混凝土孔隙的孔壁接触,此时混凝土强度不发生改变;而当膨胀产物对孔壁产生的压应力大于混凝土极限拉应变εth时,孔隙内部裂纹开始生成,此时可认为混凝土内部细观单元发生损伤,宏观表现为混凝土的强度出现劣化.混凝土细观单元的应力-应变关系可通过改进的Mazars损伤模型[12]表示:
| $ \sigma = {E_0}(1 - \omega )\varepsilon , \varepsilon \ge {\varepsilon ^{{\rm{th}}}}. $ | (6) |
式中:E0为混凝土初始弹性模量,w为化学膨胀引起的细观单元损伤.为对硫酸盐侵蚀时混凝土内部是否发生损伤进行判定,需要引入损伤演变函数,而对于水泥基材料,一般假定损伤演变函数服从正态分布或Weibull分布[9, 13].杨卫忠等[13]将单轴受压下的混凝土等效为无数个细观单元的集合,且细观单元体的破坏强度服从正态分布.本文假设硫酸盐侵蚀引起的混凝土损伤同样由混凝土内部细观单元损伤引起,全部细观单元的破坏强度组成一个随机破坏场,对应的均值和方差分别为μ和η.内膨胀应变为ε时引起的细观单元损伤w为
| $ w = \int_0^\varepsilon {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} {\eta _{\cal E}}}}} \exp \left[ { - \frac{{{{(\ln \varepsilon - \mu )}^2}}}{{2{\eta ^2}}}} \right]{\rm{d}}\varepsilon , $ | (7) |
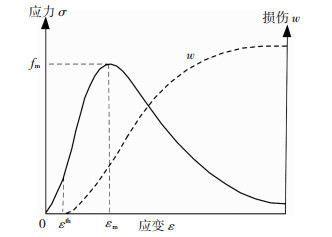
式中μ和η分别表示均值和方差,混凝土受压应力-应变曲线和损伤变量w分布形式见图 1.
|
图 1 混凝土应力-应变和损伤演化曲线 Fig. 1 Stress-strain and damage evolution curves of concrete |
混凝土受压应力-应变具有两个特征条件:1)受压应力-应变曲线过原点,即ε0=0;原点处的切线模量对应初始弹性模量,dσ/dε=E0;2)该曲线具有单峰值点,对应峰值应变εm和峰值强度σ=fm;该点处切线斜率为0,即dσ/dε=0;其中条件1)式(6)可以自然满足,将式(7)代入式(6),求导后结合条件2)可解得:
| $ \left\{ \begin{array}{l} \eta = \frac{\xi }{{\sqrt {2{\rm{ \mathsf{ π} }}} }}{{\rm{e}}^{ - 0.5{\mathit{\Phi }^{ - 1}}{{\left[ {1 - \frac{{{\sigma _{\rm{m}}}}}{{{E_0}}}{\varepsilon _{\rm{m}}}} \right]}^2}}}, \\ \mu = \ln {\varepsilon _{\rm{m}}} - \eta {\mathit{\Phi }^{ - 1}}(1 - 1/\xi ). \end{array} \right. $ | (8) |
式中:Φ-1(*)为标准正态分布函数的反函数,ξ=E0/Em,Em=fm/εm,所需确定参数为εm和ξ.考虑式(7)计算较为复杂,该式可等价为分布曲线相同的简便形式[13]:
| $ w(\varepsilon ) = 1 - \frac{1}{{1 + (\xi - 1){{\left( {\varepsilon /{\varepsilon _{\rm{m}}}} \right)}^{\xi /(\xi - 1)}}}}. $ | (9) |
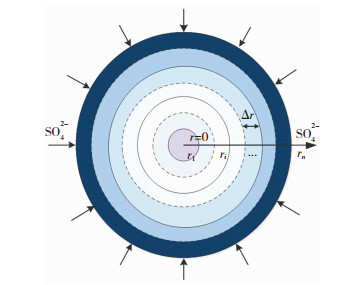
本文采用有限差分方法将桩基在横截面沿径向划分为n层,层厚均为Δr,对应每层损伤为wi,桩基横截面的分层损伤模型见图 2.
|
图 2 桩基横截面分层损伤模型 Fig. 2 Delamination damage model of pile cross section |
为进一步确定桩基的整体损伤,可将每层损伤度值加权平均得到桩身全截面的平均损伤度W:
| $ W = \frac{{\sum {{A_i}} {w_i}}}{A} = \frac{{\sum {{w_i}} (2i - 1)}}{{{n^2}}}, $ | (10) |
式中:wi为第i层对应的损伤,桩基横截面共分为n层,每层厚度为Δr,对应面积为Ai,截面总面积为A.
1.4 桩身承载力计算硫酸盐腐蚀主要引起桩基桩身的强度退化,为简化分析暂不考虑钢筋作用影响,根据JGJ 94—2008《建筑桩基技术规范》[14],混凝土轴心受压桩正截面受压承载力P为
| $ P = {\varphi _{\rm{c}}}{f_{\rm{c}}}{A_{{\rm{ps}}}}, $ | (11) |
式中:fc表示混凝土轴心抗压强度设计值;φc为成桩工艺系数,根据不同桩型取值范围为0.6~0.9;Aps表示桩基横截面面积.为建立桩基平均损伤度W与桩身承载力P之间的关系,由式(11)知,首先需建立桩基平均损伤度W与混凝土轴心抗压强度fc之间的关系.文献[15]通过混凝土受硫酸盐侵蚀试验拟合出损伤关系式,结合式(11)可得到混凝土受腐蚀的桩身承载力P:
| $ P = {\varphi _{\rm{c}}}{f_{\rm{c}}}\exp \left( { - 0.1683{W^2} - 1.5550W - 0.23732} \right)f_{{\rm{cu}}, {\rm{k}}}^{0.0704}{A_{{\rm{ps}}}}, $ | (12) |
式中:fc为混凝土初始抗压强度,fcu, k为混凝土立方体抗压强度.
2 计算方法与验证 2.1 数值求解由式(1)可得硫酸根离子扩散的时变规律,而扩散系数D是关于孔隙率、硫酸根离子浓度与时间的方程,导致式(1)具有非线性,无法得到其解析式,因此有必要采用数值方法.本文采用Crank-Nicolson有限差分格式,该格式具有无条件稳定性,并具有二阶精度.空间步长h=R/J,时间步长τ=T/N;t=tn=nτ (n=1, 2…N),Nτ=T;步长比λ=τ/h2.扩散系数D可通过迭代求解,为提高边界处的精度和稳定性,在r=0的初始条件处采用二阶向后的差分格式[16],最终通过离散得到扩散方程的差分格式:
| $ \begin{array}{l} \lambda D\left( {{r_{j + 1}} + {r_j}} \right)C_{j + 1}^{n + 1} - \lambda D\left( {{r_{j - 1}} + {r_j}} \right)C_{j - 1}^{n + 1} + \\ \left[ {4{r_j} + \lambda D\left( {{r_{j + 1}} + 2{r_j} + {r_{j - 1}}} \right) - 2{r_j}\tau K} \right]C_j^{n + 1}\\ = \lambda D\left( {{r_{j + 1}} + {r_j}} \right)C_{j + 1}^n + \lambda D\left( {{r_{j - 1}} + {r_j}} \right)C_{j - 1}^n + \\ \left[ {4{r_j} - \lambda D\left( {{r_{j + 1}} + 2{r_j} + {r_{j - 1}}} \right)} \right. + 2{r_j}\tau K]C_j^n, C(r, 0) = C_j^1 = 0, j = 0, 1, \cdots , J;\\ C(R, t) = C_J^n = {\varphi _0}{C_0}, n = 0, 1, \cdots , N;\\ \frac{{\partial C(0, t)}}{{\partial r}} = \frac{{ - 3C_j^0 + 4C_j^1 - C_j^2}}{{2\Delta r}} = 0. \end{array} $ | (13) |
试验采用上海海螺水泥公司生产的P · O 32.5R水泥,主要成分见表 1;试件尺寸为Ø100 mm×200 mm,混凝土设计强度等级为C30,混凝土配合比见表 2;粗骨料为人工碎石,粒径小于10 mm,细骨料为细度模数为2.6的河沙.
| 表 1 水泥主要组分 Tab. 1 Main components of the cements admixtures |
| 表 2 混凝土配合比 Tab. 2 Mix design of the concrete |
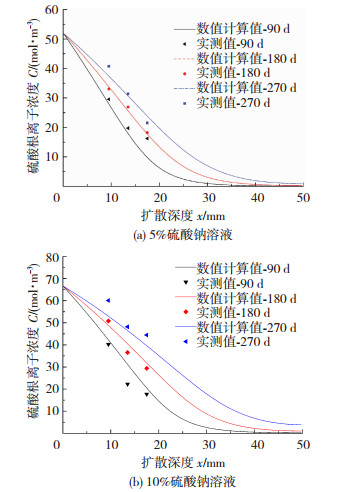
试件在浇筑24 h脱模后,试件底面和顶面用环氧树脂密封[17],最后将试件分别浸入质量分数为C0=5%(370.6 mol/m3)和C0=10%(782.4 mol/m3)的硫酸钠溶液中.采用钻孔取样法,每隔5 mm取一次粉末,并采用EDTA滴定法[10]测定样品浓度.选取浸泡时间为90、180和270 d,对应取样深度为9.5、13.5和17.5 mm试样浓度测定结果与数值计算结果进行对比,见图 3.相同侵蚀深度时对应的数值结果与实测值基本一致,表明该扩散理论模型和计算方法具有一定的准确性.
|
图 3 试验与数值计算对比 Fig. 3 Comparison between experimental and numerical values |
为模拟硫酸盐在桩基中的扩散反应过程和桩基损伤的时变规律,假定初始桩半径R=0.2 m,硫酸钠质量分数C0=5%(370.6 mol/m3),化学反应速率常数k=3.5×10-8/s[2];水泥体积分数fcv=0.3,C3A质量分数为CC3A=7%;石膏质量分数β=6%,孔隙填充系数f=0.3,混凝土水灰比w/c=0.485.为模拟相关因素对桩基损伤的影响,假设混凝土初始弹性模量E0=30 GPa,峰值抗压强度为fm=30 MPa,对应峰值应变为εm=0.001 64[18];极限拉应变εth=0.000 1;初始孔隙率φ0=0.14,空间增量Δr=h=0.001 m,时间增量Δt=τ=100 d.
3.1 扩散规律图 4为桩基中硫酸根离子的扩散规律,可由式(1)计算.从图 4可知,随扩散时间增加,硫酸根离子在桩身混凝土中的浓度和扩散深度逐渐增大;相等时间间隔内,侵蚀深度的增幅逐渐减小,说明截面表层的侵蚀速率较快(x < 0.1 m).内层扩散速率逐渐减小,其原因在于内层的扩散浓度梯度较小,反应消耗的硫酸根离子与扩散的硫酸根离子达到了动态平衡[6].当扩散时间达18 600 d(约50.9 a),扩散深度为0.2 m,对应混凝土内部的钙铝酸盐全部被消耗,此时桩基最内层浓度约为0.21 mol/m3.

|
图 4 硫酸根离子浓度随时间变化 Fig. 4 Changes of sulfate ion concentration over time |
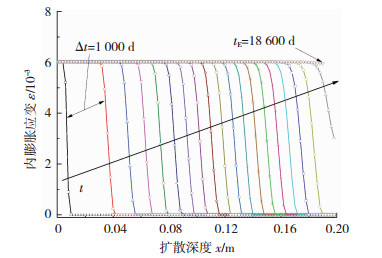
图 5为桩基截面内膨胀应变的时变规律,由式(3)可得.硫酸盐扩散过程中,随着钙铝酸盐不断消耗,内膨胀应变由表及里不断发展.由于化学反应所需时间很短,图 5对应内膨胀应变的曲线斜率较大[6-7].与扩散规律类似,内膨胀应变在表层发展速率较快;另外,内膨胀应变的发展深度小于硫酸盐的侵蚀深度,两者间存在滞后,其原因在于膨胀产物需填充孔隙且当内膨胀应力大于混凝土极限抗拉强度时,混凝土才产生内膨胀应变[3].另一方面,反应最大内膨胀应变值约为0.006,大于混凝土的极限拉应变,可引起混凝土开裂与损伤.
|
图 5 内膨胀应变随时间变化 Fig. 5 Changes of expansion strain over time |
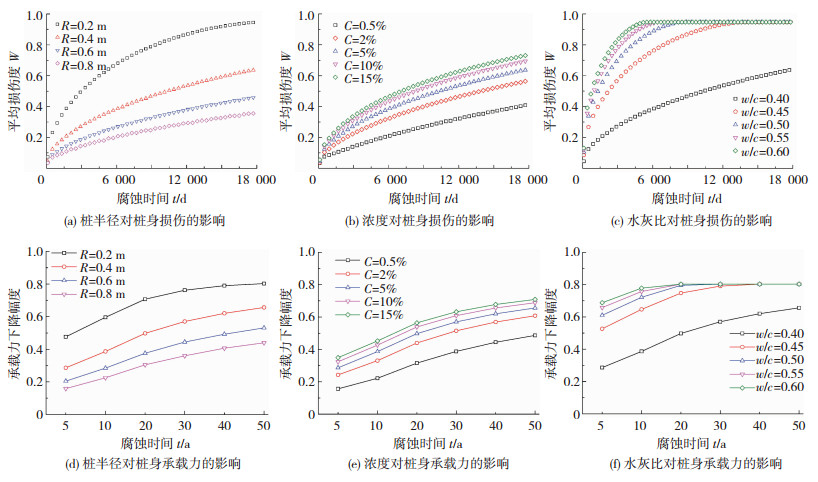
为进一步分析硫酸盐侵蚀下桩基损伤与桩身承载力的影响因素及发展规律,综合式(1)~(5),选取对桩基造成损伤影响的相关参数进一步分析,主要包括:桩半径(R=0.4 m),硫酸根离子浓度(硫酸钠质量分数C=5%)和水灰比(w/c=0.4),括号内为对应的初始参数值.腐蚀最大时间假定为18 000 d (约50 a).改变单一参数时,桩基的平均损伤度W和承载力P的数值计算结果见图 6.为反映桩身承载力劣化,选取腐蚀时间为5、10、20、30、40和50a对应的桩身承载力下降幅度值,用ΔP表示,ΔP= | P-P0 |/P0,其中P为当前承载力,P0为初始承载力.
由图 6(a)、(d)知,当桩半径为0.2 m时,桩基平均损伤度值和承载力下降幅度值最大,而当桩半径大于0.4 m时,平均损伤度和桩身承载力下降幅度显著减小,说明增大桩径可有效增大混凝土的抗腐蚀面积,提高腐蚀条件下的桩身承载力.
|
图 6 桩基平均损伤度影响因素分析 Fig. 6 Analysis of factors affecting the average damage degree of pile |
由图 6(b)、(e)知,硫酸钠质量分数(对应硫酸根离子浓度)较小(0.5%)时,桩基损伤增长幅度和承载力下降幅度最小;当硫酸钠质量分数增长至5%时,桩基损伤增长幅度和承载力下降幅度较大,而质量分数大于10%时,截面损伤和承载力下降幅度受浓度的影响减小.因此,硫酸根离子浓度的增大同样会加速桩基劣化.
由图 6(c)、(f)知,当水灰比为0.4时,腐蚀时间约为50 a对应的损伤程度和承载力下降幅度分别为0.64和0.66;而当水灰比大于0.4时,桩身承载力随着腐蚀时间增加急剧下降,且桩基在50 a之前桩横截面已全部腐蚀,达到最大损伤,对应水化铝酸钙全部反应,导致混凝土膨胀开裂,但仍有一定强度,桩基保持一定的承载能力[11].由于混凝土水灰比与孔隙率直接相关,水灰比越大时对应孔隙率越大,对应硫酸盐侵蚀速率越大,导致混凝土破坏速度增快,因此水灰比对桩基耐久性具有重要的影响,需选择较小的水灰比.
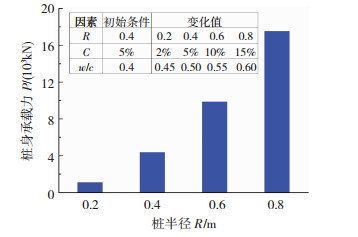
当桩基未腐蚀时,对应的初始条件及桩身承载力见图 7.当桩半径为0.4 m时对应桩身承载力为4 380 kN.桩基尚未遭受化学腐蚀,由式(12)知,对应各参数中仅桩径改变时对桩身承载力产生影响.由图 7可看出桩径变化对桩身承载力影响很大,说明桩径增加,可进一步提高桩身的承载力,而根据前述计算分析可知,桩径的增大还可显著降低腐蚀条件下桩身承载力的下降幅度.
|
图 7 桩身未腐蚀时的承载力 Fig. 7 Bearing capacity of un-corroded pile |
本文以混凝土灌注桩为研究对象,建立了柱坐标下硫酸盐侵蚀的化学-反应扩散模型,并引入了非稳态扩散理论的数值计算方法,通过试验验证了理论模型与计算方法的准确性.扩散反应结果分析表明,硫酸根离子在表层扩散和内膨胀应变发展更为迅速,混凝土桩基在表层更易遭受损伤.
给出了由化学-力学结合损伤演化方程计算桩基损伤和承载力的计算方法.通过损伤演变和桩身承载力的计算结果表明,增大桩径能显著提高桩基的耐久性,减小承载力的降低幅度;而水灰比大于0.4时,桩基损伤增长幅度最大,故硫酸盐腐蚀环境中的桩基设计应适当增大桩径并采用较小的混凝土水灰比.相对而言,桩径的增加对降低桩身承载力受硫酸盐腐蚀的影响和提升桩基耐久性的效果更为显著.
| [1] |
李镜培, 李林, 陈浩华, 等. 腐蚀环境中混凝土桩基耐久性研究进展[J]. 哈尔滨工业大学学报, 2017, 49(12): 1. LI Jingpei, LI Lin, CHEN Haohua, et al. Advances in concrete pile durability in corrosive environment[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 1. DOI:10.11918/j.issn.0367-6234.201708027 |
| [2] |
左晓宝, 孙伟. 硫酸盐侵蚀下的混凝土损伤破坏全过程[J]. 硅酸盐学报, 2009, 37(7): 1064. ZUO Xiaobao, SUN Wei. Full process analysis of damage and failure of concrete subjected to external sulfate attack[J]. Journal of the Chinese Ceramic Society, 2009, 37(7): 1064. |
| [3] |
TIXIER R, MOBASHER B. Modeling of damage in cement-based materials subjected to external sulfate attack. Ⅰ: formulation[J]. Journal of Materials in Civil Engineering, 2003, 15(4): 307. |
| [4] |
LI Jingpei, YAO Mingbo, SHAO Wei. Diffusion-reaction model of stochastically mixed sulfate in cast-in-situ piles[J]. Construction and Building Materials, 2016, 115: 662. DOI:10.1016/j.conbuildmat.2016.04.075 |
| [5] |
TAI I, CAVALARO S H P, SEGURA I, et al. Simplified methodology to evaluate the external sulfate attack in concrete structures[J]. Materials and Design, 2016, 89: 1147. DOI:10.1016/j.matdes.2015.10.084 |
| [6] |
ZUO Xiaobao, SUN Wei, YU Cheng. Numerical investigation on expansive volume strain in concrete subjected to sulfate attack[J]. Construction and Building Materials, 2012, 36(4): 406. |
| [7] |
SARKAR S, MAHADEVAN S, MEEUSSEN J C L, et al. Numerical simulation of cementitious materials degradation under external sulfate attack[J]. Cement and Concrete Composites, 2010, 32(3): 241. DOI:10.1016/j.cemconcomp.2009.12.005 |
| [8] |
YIN Guangji, ZUO Xiaobao, TANG Yujuan, et al. Numerical simulation on time-dependent mechanical behavior of concrete under coupled axial loading and sulfate attack[J]. Ocean Engineering, 2017, 142: 115. DOI:10.1016/j.oceaneng.2017.07.016 |
| [9] |
CHEN Jiankang, QIAN Chen, SONG Hui. A new chemo-mechanical model of damage in concrete under sulfate attack[J]. Construction and Building Materials, 2016, 115: 536. DOI:10.1016/j.conbuildmat.2016.04.074 |
| [10] |
SUN Chao, CHEN Jiankang, ZHU Jue, et al. A new diffusion model of sulfate ions in concrete[J]. Construction and Building Materials, 2013, 39(1): 40. |
| [11] |
李镜培, 李险峰, 李林, 等. 硫酸盐侵蚀损伤劣化基桩竖向承载特性[J]. 上海交通大学学报, 2016, 50(11): 1761. LI Jingpei, LI Xianfeng, LI Lin, et al. Axial bearing behavior of deteriorated foundation pile under sulfate attack[J]. Journal of Shanghai Jiao Tong University, 2016, 50(11): 1761. |
| [12] |
MAZARS J, PIJAUDIERCABOT G. Continuum damage theory application to concrete[J]. Journal of Engineering Mechanics, 1989, 115(2): 345. DOI:10.1061/(ASCE)0733-9399(1989)115:2(345) |
| [13] |
杨卫忠, 樊濬. 混凝土单轴受压本构模型及其应用[J]. 郑州大学学报(工学版), 2006, 27(1): 3. YANG Weizhong, FAN Jun. Uniaxial compression constitutive model of concrete and application[J]. Journal of Zhengzhou University (Engineering Edition), 2006, 27(1): 3. |
| [14] |
建筑桩基技术规范: JGJ 94-2008[S].北京: 中国建筑工业出版社, 2008 Technical code for building pile foundation: JGJ 94-2008[S]. Beijing: China Architecture and Building Press, 2008 |
| [15] |
钱春香, 徐亦冬. 混凝土结构材料的损伤特性及其本构模型[M]. 南京: 东南大学出版社, 2015. QIAN Chunxiang, XU Yidong. Damage characteristics and constitutive model of concrete structural materials[M]. Nanjing: Southeast University Press, 2015. |
| [16] |
MORI C N T, ROMÃO E C. Numerical simulation by finite difference method of 2D convection-diffusion in cylindrical coordinates[J]. Applied Mathematical Sciences, 2015, 9(123): 6157. |
| [17] |
ZAO Gaowen, LI Jingpei, SHAO Wei. Effect of mixed chlorides on the degradation and sulfate diffusion of cast-in-situ concrete due to sulfate attack[J]. Construction and Building Materials, 2018, 181: 49. DOI:10.1016/j.conbuildmat.2018.05.251 |
| [18] |
混凝结构设计规范: GB 5010-2011[S].北京: 中国建筑工业出版社, 2011 Code for design of concrete structure: GB 5010-2011[S]. Beijing: China Architecture and Building Press, 2011 |
 2019, Vol. 51
2019, Vol. 51


