近年来高速铁路快速发展，其运行引起地面振动日益影响到周边人们生活、工作以及精密仪器正常使用^[1]，合理评价高铁运行诱发地面振动对高铁建设具有重要意义.

学者们建立轨道-路基模型研究移动荷载下路基动力响应，最初将路基简化为单相弹性体并取得一系列成果^[2-6].Yang等^[7]、Takemiya等^[8]利用2.5D有限元，分别研究弹性均匀及成层弹性的单相路基在移动荷载下动力响应，并指出2.5D有限元方求解移动荷载作用下动力响应问题速度快，精度高.针对广泛分布的饱和土路基，继Biot^[9-10]建立饱和多孔介质波动方程后，Burke等^[11]首先给出忽略惯性项二维多孔饱和半平面在表面移动荷载作用下解析解.Theodorakopoulos等^[12-13]、Jin等^[14]使用半解析方法研究高速移动荷载作用下饱和多孔介质应力和超静孔压.Lefeuve-Mesgouez等^[15]采用Fourier变换分析竖向矩形简谐移动荷载引起的地面振动.蔡袁强等^[16-18]考虑路轨系统的影响，得到列车移动荷载下饱和半空间动力响应，并讨论荷载移动速度、土体物理参数和渗透系数对路面振动影响.高广运等^[19-25]利用2.5D有限元研究饱和均匀、层状及横观各向同性路基在高铁荷载下动力响应.

路基模型很大程度上决定着数值模拟准确性，以往研究中视土体为单相或者饱和介质，对分布更为广泛的非饱和路基则研究不多.在干旱和半干旱地区，文献[26]指出大量的蒸发和蒸腾作用使路基多处于非饱和状态，文献[27-29]指出非饱和土饱和度对其动力特性有显著影响，饱和度微小变化可以极大地影响土骨架动力位移和孔隙水压力，因此有必要对非饱和路基在移动荷载下地面振动进行深入研究.为此，将路基视为三相介质，开发一种非饱和路基2.5维有限单元方法，研究高速列车荷载引起的路面振动.用Euler梁模型模拟轨道系统，对控制方程时间进行Fourier变换并进行轨道方向波数变换，结合边界条件和Galerkin法推导出频域内2.5维有限元方程.通过快速Fourier逆变换将所得频域-波数域内解答转到时域-空间域，并数值模拟分析车速和路基饱和度对地面振动影响，得出一些有益结论.

1 非饱和路基2.5D FEM计算理论 1.1 非饱和路基2.5D有限元格式

定义对时间t和行车方向x的傅里叶变换为

$ \tilde {\bar u}\left( {{\varepsilon _x},y,z,\omega } \right) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } u } (x,y,z,t){{\text{e}}^{{\text{i}}{\varepsilon _x}x}}{{\text{e}}^{ - {\text{i}}\omega t}}{\text{d}}x{\text{d}}t. $

由土骨架质量守恒定律并考虑流体压力和体积变形对固体介质密度的影响^[30]，可得

$ \frac{{\partial n}}{{\partial t}} = \frac{{\alpha - n}}{{{K_{\rm{g}}}}}\frac{{\partial \left( {{S_{\rm{r}}}{p^{\rm{w}}} + \left( {1 - {S_{\rm{r}}}} \right){p^{\rm{a}}}} \right)}}{{\partial t}} + (\alpha - n)\nabla \cdot \dot u, $

(1)

式中：n为孔隙率，K_g为土体颗粒压缩模量，α=1-K_sk/K_g为Biot系数，K_sk为土骨架压缩模量，p^w、p^a为孔隙水和孔隙气压力，S_r为饱和度，u为土颗粒位移，▽为拉普拉斯算子，“·”表示对时间一阶导数.基质吸力s=p^a-p^w与S_r的关系可用水土特征曲线(SWCC)表示^[28]

$ {S_{\rm{r}}} = {S_{\rm{r}}}(s) = {S_{\rm{r}}}\left( {{p^{\rm{a}}} - {p^{\rm{w}}}} \right). $

(2)

由孔隙液、气相质量守恒定律^[30]以及式(2)，并考虑液相、气相密度与压力之间的关系^[28], 可得

$ \left\{ {\begin{array}{*{20}{l}} {{A_{11}}{{\dot p}^{\rm{w}}} + {A_{12}}{{\dot p}^{\rm{a}}} + {A_{13}}\nabla \dot u + {A_{14}}\nabla {{\dot u}^{\rm{w}}} = 0, }\\ {{A_{21}}{{\dot p}^{\rm{w}}} + {A_{22}}{{\dot p}^{\rm{a}}} + {A_{23}}\nabla \dot u + {A_{24}}\nabla {{\dot u}^{\rm{a}}} = 0.} \end{array}} \right. $

(3)

式中：${A_{11}} = \frac{{(\alpha - n)S_{\rm{r}}^2}}{{{K_{\rm{g}}}}} + \frac{{n{S_{\rm{r}}}}}{{{K_{\rm{w}}}}} - {A_{{\rm{ss}}}}\left( {n - \frac{{(\alpha - n){S_{\rm{r}}}s}}{{{K_{\rm{g}}}}}} \right)$, ${A_{12}} = \frac{{(\alpha - n){S_{\rm{r}}}\left( {1 - {S_{\rm{r}}}} \right)}}{{{K_{\rm{g}}}}} + {A_{{\rm{ss}}}}\left( {n - \frac{{(\alpha - n){S_{\rm{r}}}s}}{{{K_{\rm{g}}}}}} \right)$, ${A_{13}} = {S_{\rm{r}}}(\alpha - n)$, ${A_{14}} = n{S_{\rm{r}}}$, ${A_{21}} = \frac{{(\alpha - n){S_{\rm{r}}}\left( {1 - {S_{\rm{r}}}} \right)}}{{{K_{\rm{g}}}}} + {A_{{\rm{ss}}}}\left( {n + \frac{{(\alpha - n)\left( {1 - {S_{\rm{r}}}} \right)s}}{{{K_{\rm{g}}}}}} \right)$, ${A_{22}} = \frac{{(\alpha - n){{\left( {1 - {S_{\rm{r}}}} \right)}^2}}}{{{K_{\rm{g}}}}} + \frac{{n\left( {1 - {S_{\rm{r}}}} \right)}}{{{p^{\rm{a}}}}} - {A_{{\rm{ss}}}}\left( {n + \frac{{(\alpha - n)\left( {1 - {S_{\rm{r}}}} \right)s}}{{{K_{\rm{g}}}}}} \right)$, ${A_{23}} = \left( {1 - {S_{\rm{r}}}} \right)(\alpha - n)$, ${A_{24}} = n\left( {1 - {S_{\rm{r}}}} \right)$，${A_{{\rm{ss}}}} = \frac{{\partial {S_{\rm{r}}}}}{{\partial s}}$, K_w为液体压缩模量.

由广义Darcy定律，液相和气相渗流方程为^[28]

$ \left\{ \begin{array}{l} n{S_{\rm{r}}}\left( {\dot u_i^{\rm{w}} - {{\dot u}_i}} \right) = - \frac{{{k_{\rm{w}}}}}{{{\rho _{\rm{w}}}g}}\left( {p_{, i}^{\rm{w}} + {\rho _{\rm{w}}}\ddot u_i^{\rm{w}}} \right), \\ n\left( {1 - {S_{\rm{r}}}} \right)\left( {\dot u_i^{\rm{a}} - {{\dot u}_i}} \right) = - \frac{{{k_{\rm{a}}}}}{{{\rho _{\rm{a}}}g}}\left( {p_{, i}^{\rm{a}} + {\rho _{\rm{a}}}\ddot u_i^{\rm{a}}} \right). \end{array} \right. $

(4)

式中：ρ_w、ρ_a为液体和气体密度，u^w、u^a为液体和气体位移，k_w、k_a为水和气动力渗透系数，g为重力加速度“¨”表示对时间二阶导数.对式(4)进行傅里叶变换得频率域两相平均位移为

$ \left\{ {\begin{array}{*{20}{l}} {\tilde u_i^{\rm{w}} = \left( {{F_{\rm{w}}}{{\tilde u}_i} - \tilde p_{, i}^{\rm{w}}} \right)/\left( {{F_{\rm{w}}} - {\rho _{\rm{w}}}{\omega ^2}} \right), }\\ {\tilde u_i^{\rm{a}} = \left( {{F_{\rm{a}}}{{\tilde u}_i} - \tilde p_{, i}^{\rm{a}}} \right)/\left( {{F_{\rm{a}}} - {\rho _{\rm{a}}}{\omega ^2}} \right).} \end{array}} \right. $

(5)

式中：F_w=nS_rρ_wgωi/k_w，F_a=n(1-S_r)ρ_agωi/k_a，ω为振动圆频率，“~”代表频域内量.对式(3)傅里叶变换后，结合式(5)得频域内两相质量守恒方程为

$ \left\{ \begin{array}{l} \left( {{A_{13}} + \frac{{{A_{14}}{F_{\rm{w}}}}}{{{F_{\rm{w}}} - {\rho _{\rm{w}}}{\omega ^2}}}} \right){{\tilde u}_{i, i}} - \frac{{{A_{14}}}}{{{F_{\rm{w}}} - {\rho _{\rm{w}}}{\omega ^2}}}\tilde p_{, ii}^{\rm{w}} + \\ {A_{11}}{{\tilde p}^{\rm{w}}} + {A_{12}}{{\tilde p}^{\rm{a}}} = 0, \\ \left( {{A_{23}} + \frac{{{A_{24}}{F_{\rm{a}}}}}{{{F_{\rm{a}}} - {\rho _{\rm{a}}}{\omega ^2}}}} \right){{\tilde u}_{i, i}} - \frac{{{A_{24}}}}{{{F_{\rm{a}}} - {\rho _{\rm{a}}}{\omega ^2}}}\tilde p_{, ii}^{\rm{a}} + \\ {A_{21}}{{\tilde p}^{\rm{w}}} + {A_{22}}{{\tilde p}^{\rm{a}}} = 0. \end{array} \right. $

(6)

非饱和多孔介质动量守恒方程为^[30]

$ \begin{array}{l} \mu {u_{i, jj}} + (\lambda + \mu ){u_{i, ji}} - {S_{\rm{r}}}p_{, i}^{\rm{w}} - \left( {1 - {S_{\rm{r}}}} \right)p_{, i}^{\rm{a}} = \\ {{\bar \rho }_{\rm{s}}}{{\ddot u}_i} + {{\bar \rho }_{\rm{w}}}\ddot u_i^{\rm{w}} + {{\bar \rho }_{\rm{a}}}\ddot u_i^{\rm{a}}, \end{array} $

(7)

式中λ和μ为土体的Lame常数.采用复数形式的Lame常数λ =(1+2iη_s)λ，μ =(1+2iη_s)μ考虑土体阻尼的影响，η_s为阻尼系数；ρ_s=(1-n)ρ_s、ρ_w =nS_rρ_w、ρ_a = n(1-S_r)ρ_a为固相、液相和气相相对密度.对式(7)进行傅里叶变换，结合式(15)，并用几何方程消去应力项可得非饱和土体频域动力方程:

$ \begin{array}{l} \bar \mu {{\tilde u}_{i, jj}} + (\bar \lambda + \bar \mu ){{\tilde \mu }_{i, ji}} - {S_{\rm{r}}}\tilde p_{, i}^{\rm{w}} - \left( {1 - {S_{\rm{r}}}} \right)\tilde p_{, i}^{\rm{a}} + {\omega ^2}\left[ {(1 - n){\rho _{\rm{s}}}} \right.\\ + \frac{{n{S_{\rm{r}}}{\rho _{\rm{w}}}{F_{\rm{w}}}}}{{{F_{\rm{w}}} - {\rho _{\rm{w}}}{\omega ^2}}} + \frac{{n\left( {1 - {S_{\rm{r}}}} \right){\rho _{\rm{a}}}{F_{\rm{a}}}}}{{{F_{\rm{a}}} - {\rho _{\rm{a}}}{\omega ^2}}}]{{\tilde u}_i} - \\ \frac{{{\omega ^2}n{S_{\rm{r}}}{\rho _{\rm{w}}}}}{{{F_{\rm{w}}} - {\rho _{\rm{w}}}{\omega ^2}}}\tilde p_{, i}^{\rm{w}} - \frac{{{\omega ^2}n\left( {1 - {S_{\rm{r}}}} \right){\rho _{\rm{a}}}}}{{{F_{\rm{a}}} - {\rho _{\rm{a}}}{\omega ^2}}}p_{, i}^{\rm{a}} = 0 \end{array} $

(8)

可采用有限元法对非饱和多孔介质控制方式(6)和式(8)进行求解.引入虚位移δu_i^*和频域内有效应力${\tilde \sigma _{ij}}$，对式(8)和应力边界条件应用虚功原理可得多孔介质控制方程:

$ \begin{array}{l} \int {\left[ {\delta \varepsilon _i^*{{\tilde \sigma '}_{ij}} - \delta u_i^*{\omega ^2}\left[ {(1 - n){\rho _{\rm{s}}} + \frac{{n{S_{\rm{r}}}{\rho _{\rm{w}}}{F_{\rm{w}}}}}{{{F_{\rm{w}}} - {\rho _{\rm{w}}}{\omega ^2}}}} \right.} \right.} \\ + \frac{{n\left( {1 - {S_{\rm{r}}}} \right){\rho _{\rm{a}}}{F_{\rm{a}}}}}{{{F_{\rm{a}}} - {\rho _{\rm{a}}}{\omega ^2}}}]{{\tilde u}_i}]{\rm{d}}V + \int {\left( {\delta u_i^*\frac{{{\omega ^2}n{S_{\rm{r}}}{\rho _{\rm{w}}}}}{{{F_{\rm{w}}} - {\rho _{\rm{w}}}{\omega ^2}}}\tilde p_{, i}^{\rm{w}} - \delta \varepsilon _i^*{\delta _{ij}}{S_{\rm{r}}}\tilde p_{, i}^w} \right)} {\rm{d}}V + \\ \int {\left( {\delta u_i^*\frac{{{\omega ^2}n\left( {1 - {S_{\rm{r}}}} \right){\rho _{\rm{a}}}}}{{{F_{\rm{a}}} - {\rho _{\rm{a}}}{\omega ^2}}}\tilde p_{, i}^{\rm{a}} - } \right.} \delta \varepsilon _i^*{\delta _{ij}}\left( {1 - {S_{\rm{r}}}} \right)\tilde p_{, i}^a){\rm{d}}V = \int \delta u_i^*{f_i}{\rm{d}}S. \end{array} $

(9)

式中：ε_ij、σ_ij为土体应变和应力分量，δ_ij为Kronecker符号，f_i为边界处应力.对式(6)采用Galerkin法后进行x方向波数变换，用4节点等参单元离散并结合式(9)可得非饱和土2.5维有限元方程矩阵形式：

$ \mathit{\boldsymbol{KU = R, }} $

(10)

式中：$\mathit{\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}_{{\bf{up}}}^\prime - {\mathit{\boldsymbol{M}}_{{\bf{up}}}}}&{\mathit{\boldsymbol{Q}}_{{\bf{up}}}^\prime - {\mathit{\boldsymbol{Q}}_{{\rm{up}}}}}&{\mathit{\boldsymbol{G}}_{{\bf{up}}}^\prime - {\mathit{\boldsymbol{G}}_{{\bf{up}}}}}\\ {{\mathit{\boldsymbol{H}}_{{\bf{md}}}}}&{{\mathit{\boldsymbol{Q}}_{{\bf{md}}}} + \mathit{\boldsymbol{Q}}_{{\bf{md}}}^\prime }&{\mathit{\boldsymbol{G}}_{{\bf{md}}}^\prime }\\ {{\mathit{\boldsymbol{H}}_{{\bf{dw}}}}}&{\mathit{\boldsymbol{Q}}_{{\bf{dw}}}^\prime }&{\mathit{\boldsymbol{G}}_{{\bf{dw}}}^\prime + {\mathit{\boldsymbol{G}}_{{\bf{dw}}}}} \end{array}} \right]$, $ \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde {\bar u}}}}\\ {{{\mathit{\boldsymbol{\tilde {\bar p}}}}^{\bf{w}}}}\\ {{{\mathit{\boldsymbol{\tilde {\bar p}}}}^{\bf{g}}}} \end{array}} \right]$, $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde {\bar f}}}_{{\bf{up}}}^{\bf{s}}}\\ {{{\mathit{\boldsymbol{\tilde {\bar f}}}}^{\bf{w}}}}\\ {{{\mathit{\boldsymbol{\tilde {\bar u}}}}^{\bf{g}}}} \end{array}} \right]$，其中K_up^′、M_up、Q_up、G_up、f_up^s分别为刚度矩阵、质量矩阵、液体和气体贡献矩阵以及等效节点力矩阵，代表参数在波数域中的量，$\sum\limits_{\text{e}} {\iint {{{\left( {{\mathit{\boldsymbol{B}}^*}\mathit{\boldsymbol{N}}} \right)}^{\text{T}}}}} \mathit{\boldsymbol{D}}(\mathit{\boldsymbol{BN}})\left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, ${\mathit{\boldsymbol{M}}_{{\text{up}}}} = {\omega ^2}\left[ {(1 - n){\rho _{\text{s}}} + n{S_{\text{r}}}{\rho _{\text{w}}}} \right.\frac{{{F_{\text{w}}}}}{{{F_{\text{w}}} - {\rho _{\text{w}}}{\omega ^2}}} + n\left( {1 - {S_{\text{r}}}} \right){\rho _{\text{w}}}\frac{{{F_{\text{a}}}}}{{{F_{\text{a}}} - {\rho _{\text{a}}}{w^2}}}] \times \sum\limits_{\text{e}} {\iint {\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{N}}^{\text{T}}}}} \mathit{\boldsymbol{D}}(\mathit{\boldsymbol{BN}})\left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi , $, $\mathit{\boldsymbol{Q}}_{{\bf{up}}}^\prime = \frac{{{\omega ^2}n{S_{\text{r}}}{\rho _{\text{w}}}}}{{{F_{\text{w}}} - {\rho _{\text{w}}}{\omega ^2}}}\sum\limits_{\text{e}} {\iint {{{\bf{N}}^{\text{T}}}}} \mathit{\boldsymbol{\overline B}} \mathit{\boldsymbol{\overline N}} \left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, ${\mathit{\boldsymbol{Q}}_{{\bf{up}}}} = \alpha {S_{\text{r}}}\sum\limits_{\text{e}} {\iint {{{\left( {{\mathit{\boldsymbol{B}}^*}\mathit{\boldsymbol{N}}} \right)}^{\text{T}}}}} \mathit{\boldsymbol{m}}\mathit{\boldsymbol{\overline N}} \left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, $\mathit{\boldsymbol{G}}_{{\bf{up}}}^\prime = \frac{{{\omega ^2}n\left( {1 - {S_{\text{r}}}} \right){\rho _{\text{a}}}}}{{{F_{\text{a}}} - {\rho _{\text{a}}}{\omega ^2}}}\sum\limits_{\text{e}} {\iint {{\mathit{\boldsymbol{N}}^{\text{T}}}}} \mathit{\boldsymbol{\overline B}} \mathit{\boldsymbol{\overline N}} \left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, ${\mathit{\boldsymbol{G}}_{{\bf{up}}}} = \alpha \left( {1 - {S_{\text{r}}}} \right)\sum\limits_{\text{e}} {\iint {{{\left( {{\mathit{\boldsymbol{B}}^*}\mathit{\boldsymbol{N}}} \right)}^{\text{T}}}}} \mathit{\boldsymbol{m}}\mathit{\boldsymbol{\overline N}} \left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, ${\mathit{\boldsymbol{H}}_{{\bf{md}}}} = \left( {{A_{13}} + } \right.\frac{{{A_{14}}{F_{\text{w}}}}}{{{F_{\text{w}}} - {\rho _{\text{w}}}{\omega ^2}}})\sum\limits_{\text{e}} {\iint {{{\mathit{\boldsymbol{\overline N}} }^{\text{T}}}}} {\mathit{\boldsymbol{m}}^{\text{T}}}\mathit{\boldsymbol{BN}}\left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, ${\mathit{\boldsymbol{H}}_{{\text{dw}}}} = \left( {{A_{23}} + \frac{{{A_{24}}{F_{\text{a}}}}}{{{F_{\text{a}}} - {\rho _{\text{a}}}{\omega ^2}}}} \right)\sum\limits_{\text{e}} {\iint {{{\mathit{\boldsymbol{\overline N}} }^{\text{T}}}}} {\mathit{\boldsymbol{m}}^{\text{T}}}\mathit{\boldsymbol{BN}}\left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, ${\mathit{\boldsymbol{Q}}_{{\bf{md}}}} = \frac{{{A_{14}}}}{{{F_{\text{w}}} - {\rho _{\text{w}}}{\omega ^2}}}\sum\limits_{\text{e}} {\iint {{{\left( {\mathit{\boldsymbol{B}}_{\bf{s}}^*\mathit{\boldsymbol{\bar N}}} \right)}^{\text{T}}}}} \left( {{\mathit{\boldsymbol{B}}_{\bf{s}}}\mathit{\boldsymbol{\overline N}} } \right)\left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, $\mathit{\boldsymbol{Q}}_{{\bf{md}}}^\prime = {A_{11}}\sum\limits_{\text{e}} {{{\bar{\boldsymbol N}}^{\text{T}}}} \bar{\boldsymbol N}\left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, ${\mathit{\boldsymbol{G}}_{{\bf{dw}}}} = \frac{{{A_{24}}}}{{{F_{\text{a}}} - {\rho _{\text{a}}}{\omega ^2}}}\sum\limits_{\text{e}} {\iint {{{\left( {\mathit{\boldsymbol{B}}_{\bf{s}}^*\mathit{\boldsymbol{\bar N}}} \right)}^{\text{T}}}}} \left( {{\mathit{\boldsymbol{B}}_{\bf{s}}}\mathit{\boldsymbol{\overline N}} } \right)\left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, $\mathit{\boldsymbol{Q}}_{{\bf{dw}}}^\prime = {A_{21}}\sum\limits_{\text{e}} {\iint {{{\mathit{\boldsymbol{\bar N}}}^{\text{T}}}}} \mathit{\boldsymbol{\bar N}}\left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, $\mathit{\boldsymbol{G}}_{{\bf{md}}}^\prime = {A_{12}}\sum\limits_{\text{e}} {\iint {{{\mathit{\boldsymbol{\bar N}}}^{\text{T}}}}} \mathit{\boldsymbol{\bar N}}\left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, $\mathit{\boldsymbol{G}}_{{\bf{dw}}}^\prime = {A_{22}}\sum\limits_{\text{e}} {\iint {{{\mathit{\boldsymbol{\bar N}}}^{\text{T}}}}} \mathit{\boldsymbol{\bar N}}\left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, $\mathit{\boldsymbol{\tilde {\bar f}}}_{{\bf{up}}}^{\bf{w}} = - \sum\limits_{\text{e}} {\iint {\frac{{{F_{\text{w}}}{\rho _{\text{w}}}g{{\mathit{\boldsymbol{\widetilde v}}}_{\bf{n}}}}}{{{k_{\text{w}}}}}}} \left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, $ \mathit{\boldsymbol{\tilde {\bar f}}}_{{\bf{up}}}^{\bf{s}} = \sum\limits_{\text{e}} {\iint {{{\mathit{\boldsymbol{\bar N}}}^{\text{T}}}}} \mathit{\boldsymbol{\tilde {\bar f}}}\left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, $ \mathit{\boldsymbol{\tilde {\bar f}}}_{{\bf{up}}}^{\bf{g}} = - \sum\limits_{\text{e}} {\iint {\frac{{{\mathit{\boldsymbol{F}}_{\text{g}}}{\mathit{\boldsymbol{\rho }}_{\text{g}}}g{{\mathit{\boldsymbol{\tilde v}}}_{\bf{n}}}}}{{{k_{\text{g}}}}}}} \left| \mathit{\boldsymbol{J}} \right|{\text{d}}\eta {\text{d}}\xi $, N、N为时域和频域形函数矩阵，J为雅可比矩阵，D为应力矩阵，B为偏导矩阵，“*”代表矩阵共轭.

1.2 轨道系统模型

对轨道系统Euler梁动力方程进行时间域傅里叶变换和列车运行方向波数展开得波数-频率域方程：

$ \left( {EI\xi _x^4 - m{\omega ^4}} \right)u_r^{xt} = f_{IT}^{tt}\left( {{\xi _x}, \omega } \right) + p_0^{xt}\left( {{\xi _x}, \omega } \right). $

(11)

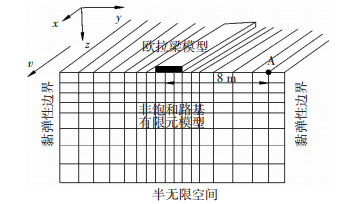
式中：EI为轨道的弯曲刚度，m为轨道和枕木的综合质量，f_IT^xt为路基接触反力，u_r^xt为轨道的位移，ξ_x为变量x对应波数，沿x正方向移动列车荷载频域表达式p₀^xt同文献[8].式(10)和(11)即为轨道-路基耦合控制方程，采用黏弹性边界^[26]降低外行波反射对计算结果的影响，边界处距离振源较远，非饱和路基边界处孔隙气压力忽略不计.轨道和非饱和地基2.5D有限元计算模型及边界示意见图 1.编制程序可求解方程得到在频域-波数域内解答，将结果通过快速傅里叶逆变换(IFFT)可得到时间-空间域内的解答.

1.3 模型验证和计算参数

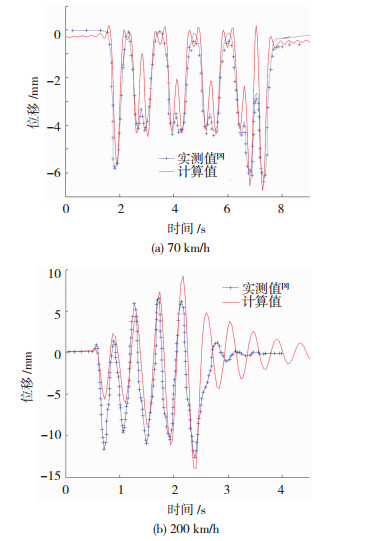
为便于验证，地基地层及参数采用瑞典国家铁路局X2000列车现场实测数据^[8]，地层、列车轴重和轨道参数同文献[8]，土体阻尼比η_s=0.05.取饱和度S_r=0进行退化验证，图 2给出两个速度下轨道中心地面竖向振动位移时程模拟与实测结果^[8]，两者相当一致说明计算模型可靠.

以下计算水土特征曲线采用V-G模型^[30]：S_e=[1+(α₁s)^k]^-m，流体渗透系数采用Mualem模型^[30]：${k_{\text{w}}} = \frac{{{\rho _{\text{w}}}{g^g}\kappa }}{{{\eta _{\text{w}}}}}\sqrt {{S_{\text{r}}}} {\{ 1 - {\left[ {1 - {{\left( {{S_{\text{e}}}} \right)}^{\frac{1}{m}}}} \right]^m}\} ^2}$, ${k_{\text{g}}} = \frac{{{\rho _{\text{g}}}g\kappa }}{{{\eta _{\text{g}}}}}\sqrt {1 - {S_{\text{r}}}} {\left[ {1 - {{\left( {{S_{\text{e}}}} \right)}^{\frac{1}{m}}}} \right]^{2m}}$式中α₁=1×10^-5，k=4，m=1-1/k=0.75，s为基质吸力，有效饱和度S_e=(S_r-S_wo)/(1-S_wo)，束缚饱和度S_wo=0.05，孔隙水和气的黏性系数η_w=1.0 mPa·s，η_g=0.015 mPa·s；固有渗透率κ=1.0 μm².计算过程中流体物理参数假定为常数，K_w=2.1×10⁹ N/m²，地面设为排水和排气边界，地层底边和两侧设置为不排水和不排气边界.中国高铁多分布于东南沿海地区，选取较高饱和度(100%、99%和90%)进行计算，分析饱和度与车速对地面振动与超静孔隙水压力影响.

2 不同车速下非饱和路基地面振动分析 2.1 轨道中心处路基地面振动分析

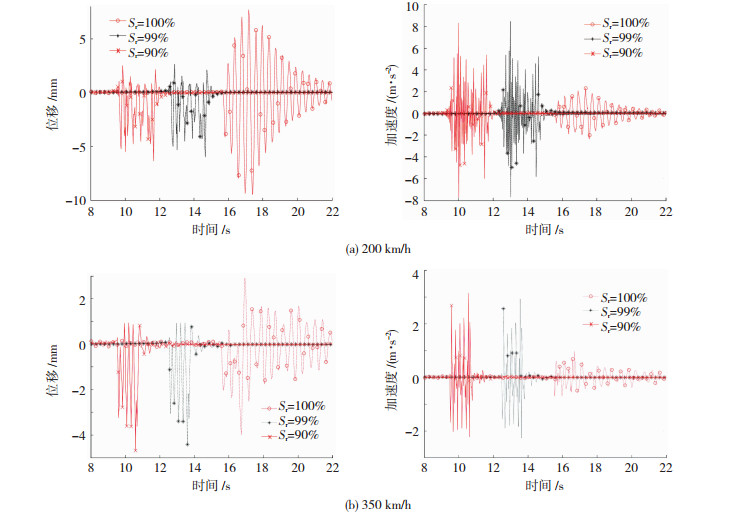
图 3为不同车速和饱和度下路基轨道中心处地面振动位移与加速度时程.图 3(a)在200 km/h时，饱和路基地面振动位移幅值明显大于非饱和土.饱和度从100%降为99%时，饱和土中进入极少量气体，土体从完全饱和变为准饱和状态，此时虽然孔隙气体含量改变量非常小，但是引起位移幅值大幅下降.这可能是由于在车速较低情况下，气相、液相的运动及其联合阻尼作用对土骨架位移产生了较大阻碍作用，使得非饱和土体位移低于饱和土体；而饱和度从99%降为90%，虽然气体含量改变量较大，但位移幅值降低可以忽略.可见土体由饱和变为准饱和时，会带来土体相状态的彻底改变(两相变为三相)，进而带来土体动力特性实质性改变.图 3(b)350 km/h时，饱和度的减小对地面振动位移幅值的影响有限，饱和与非饱和路基地面振动位移幅值相当.同一车速下相比于饱和路基，非饱和路基地面振动位移随时间衰减更快；随着速度增大，位移振动持时变短.图 3(a)、(b)，同一车速下，S_r=90%和99%非饱和路基地面振动加速度峰值相差不大，均大于饱和路基，可见非饱和路基中孔隙气的存在会增加振动波在轨道中心处产生的地面振动加速度.同一车速下，饱和地面振动加速度随时间衰减较非饱和地面更为缓慢.随速度增大，非饱和路基振动位移和加速度持时均变短.对比位移与加速度时程，低速时非饱和路基地面加速度幅值大于饱和路基，振动位移幅值则小于饱和路面；速度增为350 km/h，非饱和路基地面振动加速度幅值仍然大于饱和路基，振动位移幅值则与饱和路基相当.

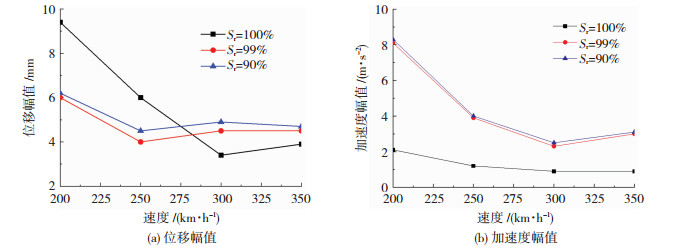
图 4为不同饱和度路基轨道中心处地面振动幅值随速度变化.图 4(a)，车速低于270 km/h时饱和路基轨道中心位移振幅大于非饱和路基；超过270 km/h后非饱和路基地面振动位移幅值略大于饱和路基.200~300 km/h范围内车速对饱和路基地面振动位移幅值影响很大，而超过250 km/h后车速对于非饱和地面位移幅值影响不甚明显.车速从200 km/h增加到250 km/h，路基地面振动位移幅值均减小，特别是饱和路基.速度继续增加，非饱和路基地面振动位移振动位移幅值几乎不变，而饱和路基位移幅值先继续减小后略微增大.为减少高饱和度地区(饱和度90%~100%)轨道中心处地面振动位移幅值，列车速度宜保持250~350 km/h(最好300 km/h).同时可见，同一速度下不同饱和度的非饱和路基振动位移幅值差别并不大.图 4(b)，同一车速下，S_r=90%和99%的非饱和路基地面振动加速度峰值几乎相等，且均大于同速度下饱和路基：200 km/h时非饱和路基地面振动加速度峰值远大于饱和路基(约为其4倍).随着车速增大，两者加速度呈不同速率的减小，非饱和路基地面振动加速度峰值减小更快，而饱和路基减小较慢，两者差距逐渐变小；300 km/h时，非饱和路基地面振动加速度峰值为2.3m/s²，饱和路基为1m/s²，前者为后者2.3倍；超过300 km/h后车速增大饱和路基地面振动加速度保持不变，非饱和路基地面振动加速度峰值稍有增大.为减少高饱和度区域轨道中心处地面振动加速度幅值，车辆行驶速度最好在300 km/h附近.

2.2 轨道中心8 m远处路基地面振动分析

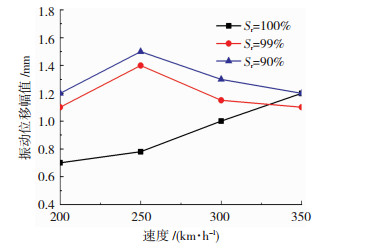
图 5为轨道中心8 m远处(图 1A点)不同饱和度路基地面振动位移幅值随速度变化曲线.饱和路基地面振动位移幅值随车速增加而增大，非饱和路基位移幅值先增大，250 km/h时达最大值后减小.相同速度下，随饱和度降低，非饱和路基地面振动位移幅值增大.300 km/h前同一速度下非饱和路基位移幅值大于饱和路基，超过300 km/h，两者大小趋于相等.

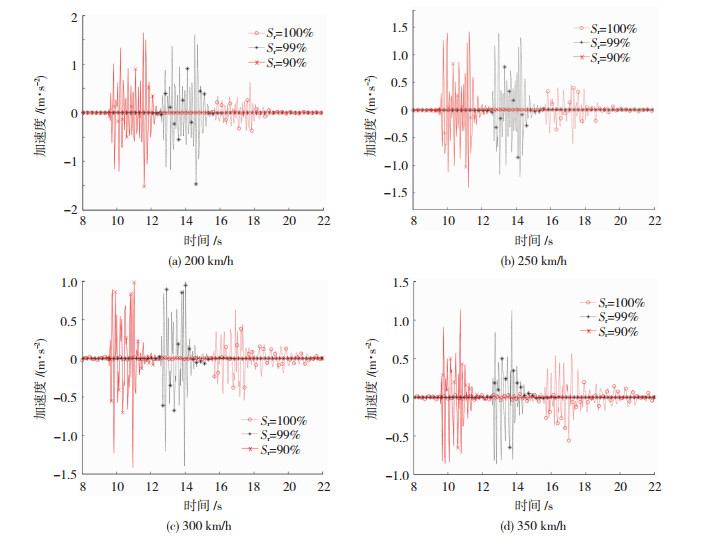
图 6为不同车速和饱和度路基轨道中心8 m处地面竖向振动加速度时程.各速度下非饱和路基地面振动加速度幅值明显大于饱和路基.与2.1节类似，饱和度从100%降低为99%时，相状态的彻底改变引起加速度幅值明显增大；饱和度从99%降低到90%，加速度幅值几乎不变.孔隙气体进入会放大向远处传播的振动波，引起轨道远处振动加速度幅值增大.从不同速度时程可见，轨道中心8 m远处饱和与非饱和路基地面振动加速度持时随速度增加变化不同：非饱和路基加速度持时不断减小，而饱和路基振动持时却稍有增加.这可能是由于孔隙水中剪切波使远处振动加速度增加且消散得慢.高速情况下(300~350 km/h)，非饱和路基地面振动加速度随时间衰减较饱和路基更快.

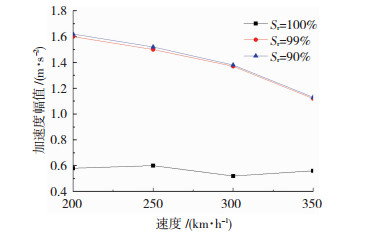
图 7为不同饱和度路基轨道中心8 m远处地面加速度幅值随速度变化曲线.同一车速下，非饱和路基地面振动加速度峰值几乎相等，均远大于饱和路基.这可能是由于非饱和路基中孔隙气的存在增加振动波在向轨道远处传播过程中的散射和折射，增大非饱和路基振动加速度.随车速提高非饱和路基地面振动加速度峰值不断降低，饱和路基地面振动加速度峰值则随速度增大变化较小.

图 8为不同车速和饱和度下轨道中心8 m远处地面振动加速度频谱.由于孔隙水和孔隙气体共同作用，距轨道中心8 m处非饱和路基振动加速度频谱成分复杂.车速为250 km/h时振动控制频率对应加速度谱值为非饱和路基远大于饱和路基，车速为350 km/h时饱和路基谱值大于非饱和路基.并且车速较低时，地面振动频率成分多小于10 Hz，而350 km/h时饱和与非饱和路基高于10 Hz地面振动加速度成分增多.

3 不同车速下非饱和土路基地面振动衰减特性

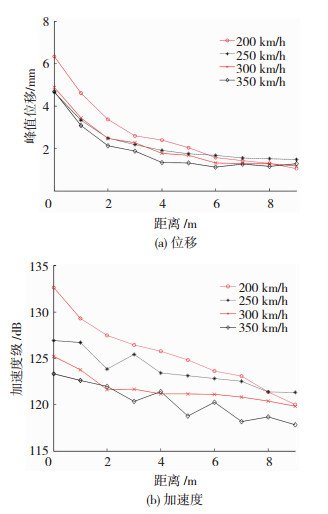
图 9为路基地面振动位移幅值和加速度级随距离衰减曲线.图 9(a)近轨道处(约5 m内)200 km/h时地面振动位移幅值大于其他速度，各种速度下均快速衰减且衰减速率相当；远轨道处(5 m外)地面振动位移振幅在200 km/h时衰减最快，其余车速下则大小相当且几乎不衰减.图 9 (b)加速度级低速时(200~250 km/h)随距离快速衰减，高速时衰减较慢.300 km/h时轨道中心2 m以外地面振动加速度衰减曲线平缓，200 km/h时地面振动加速度衰减最快.250 km/h时距轨道中心约3 m出现地面振动加速度反弹增大现象，350 km/h出现多次地面振动加速度反弹增大现象，距轨道中心约4、6和8 m.可见地面振动加速度级在某些车速下的衰减会出现反弹增大现象，其出现与否及其位置与车速密切相关.

4 不同车速下非饱和土路基孔隙水压力分析

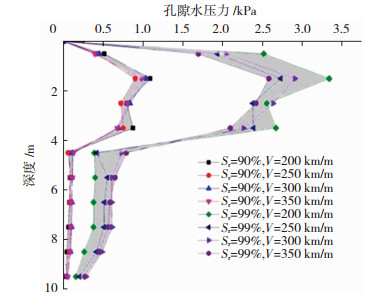
图 10为不同车速下轨道中心处地基超静孔隙水压力随深度变化曲线.可以发现饱和与非饱和路基超静孔隙水压力主要分布在浅层0~4.5 m，峰值出现在地表下1.8 m处左右，4.5 m以下路基超静孔隙水压力已经很小.同一车速下饱和度对超静孔隙水压力影响较大：轨道下4.5 m以内，饱和度90%路基超静孔隙水压力峰值约为1 kPa，99%饱和度路基超静孔隙水压力幅值明显大于90%饱和度，约为其3倍.饱和度为99%时随车速增大超静孔隙水压力幅值稍有减小.轨道下方4.5 m以下两者超静孔隙水压力亦有较大差别：不同速度下，99%饱和度地基5 m深处约0.6 kPa，10m深约0.2 kPa，而饱和度90%地基则分别约为0.1 kPa和0.02 kPa(分别为饱和度99%路基17%和10%).

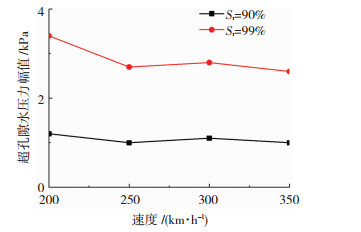
图 11为轨道下方不同饱和度路基超静孔隙水压力幅值随车速变化曲线.相同速度下，饱和度99%路基超静孔隙水压力幅值远大于90%饱和度路基.饱和度99%路基(准饱和)，速度从200 km/h增加到250 km/h时超静孔隙水压力幅值下降，而超过250 km/h后车速的影响有限.饱和度90%路基孔隙水压力幅值随车速增加变化不大.因此，为降低高饱和度地区轨道下超静孔压幅值，车辆行驶速度宜在250~350 km/h.

5 结论

利用非饱和路基2.5维有限单元方法研究高速列车移动荷载引起的非饱和路基地面振动，结论如下：

1) 路基从准饱和到饱和状态轨道中心处地面振动位移幅值显著增加.同一车速下非饱和路基地面振动位移和加速度随时间衰减较饱和路基更快；速度增大，非饱和路基振动持时变短.低速时非饱和路基地面振动加速度幅值大于饱和地面，位移幅值小于饱和地面；350 km/h时非饱和路面加速度幅值仍大于饱和路面，而位移幅值与饱和路面相当.

2) 为减少高饱和度地区轨道中心处地面振动位移幅值，列车速度宜保持250~350 km/h(最好300 km/h).为减少高饱和度地区轨道中心加速度幅值，列车行驶速度宜在300 km/h附近.

3) 轨道中心8 m远处：对饱和路基，位移幅值随车速增加而增大；对非饱和路基，位移幅值先增大，在250 km/h达最大值后减小，超过300 km/h两者大小趋于相等；随车速增加非饱和路基地面加速度持时不断减小，而饱和路基加速度持时有所增加；同一车速下，非饱和路基加速度峰值远大于饱和路基.

4) 轨道中心8 m远处，250 km/h时主频对应加速度谱值非饱和路基远大于饱和路基，350 km/h时饱和路基超过非饱和路基.车速较低时，地面振动以低频为主，而350 km/h时饱和与非饱和路基地面振动加速度高频成分增多.

5) 近轨道处200 km/h时地面振动位移幅值大于其他速度，各速度下均快速衰减且衰减速率相当；远轨道处地面振动位移振幅在200 km/h时衰减最快，其余车速下则大小相当且几乎不衰减.地面振动加速度级在某些车速下的衰减会出现反弹增大，反弹增大现象出现与否及其位置与车速密切相关.

6) 饱和与非饱和路基超静孔隙水压力主要分布在浅层0~4.5 m，峰值出现在地表下1.8 m处左右.同一车速下饱和度对超静孔隙水压力影响较大：饱和度为99%路基超静孔隙水压力幅值远大于饱和度90%路基.