裂隙介质中渗流现象广泛存在于自然界和人类活动中,而渗流往往伴随着溶质的运动迁移.关于裂隙介质中对流扩散过程的研究在工业工程、环境工程和岩土工程等领域中均有开展,其研究成果对水土污染治理、地热能源开发、盐碱地治理、临海工程施工、垃圾填埋场以及核废料处置库的安全性评估等关键问题具有重要意义[1].
考虑裂隙的多孔介质中溶质的运移规律与不考虑裂隙的多孔介质存在显著区别.首先,带有裂隙的多孔介质中易形成快速的渗流通道,即出现所谓的优势流; 优势流裹挟大量溶质快速穿透多孔介质,容易出现溶质穿透曲线中的早期穿透现象[2].其次,从数学模型上看,含裂隙的多孔介质由于其在不同区域处的渗流特性差异较大,不直接适用于包含介质均一化假定的模型.以传统对流扩散(CDE)方程为例:CDE方程已被广泛用于多孔介质内溶质输运规律的研究中,并有充分的实验结论证明其准确性[3],但由于其建立在物理域均质的框架内,因此无法考虑优势流流场内特殊的水动力学参数,也就无法描述穿透曲线中的早期穿透和拖尾等物理非平衡现象.后续学者在CDE方程基础上提出了进一步的修正和改进,Coats[4]考虑了土体中不动水体的存在,建立了可动水体-不动水体的两区模型; Skopp等[5]在此基础上提出两流区模型,两区流模型中考虑了渗流速度的不同,并根据流速的大小划分成两个计算区域.此后相继有学者提出了若干种能考虑优势流的数值模型,包括单孔隙模型、双重孔隙渗透模型和多重孔隙渗透模型等[2].
为仿真实现含裂隙多孔介质中孔隙水的真实运动过程,本文采用一种光滑粒子流体动力学(SPH)方法.SPH方法在流体力学领域应用广泛,可处理冲击作用、自由表面流动及流固耦合作用等水动力学问题[6-8].随着计算机运算能力的不断发展,采用SPH方法在细观尺度下模拟孔隙流动成为了可能.回归孔隙水运动的物理本质,重新认识多孔介质中的对流扩散规律,可进一步检验宏观模型的准确性.Zhu等[9]建立了孔隙尺度下周期多孔介质渗流计算的SPH模型,用于研究孔隙尺度的水动力弥散问题.Tartakovsky等[10]提出SPH孔隙多相流模型,研究了孔隙尺度下多孔介质的异质性和各向异性对多相流的影响以及反应性溶质运移过程.就方法本身而言,SPH是一种拉格朗日形式的粒子算法,在该框架内能够直观生成复杂的多孔介质边界,对流体质点的追踪也十分便捷.与基于网格的数值方法相比,SPH方法的粒子化格式有效地避免了因网格畸变、介质大变形、材料交界面等问题导致的数值误差或不收敛.因此,在处理动量驱动流及多孔介质等复杂几何计算域时,SPH方法有其天然优势.
因此,本文利用SPH方法在水动力学问题上的突出优势,旨在从孔隙尺度模拟裂隙多孔介质对流扩散的物理过程,探究不同裂隙张开度的多孔介质中溶质的运移规律,并提出一种两流区模型的简化方法对仿真实验结果进行描述.
1 SPH流动模型 1.1 SPH离散化格式在SPH中,计算域的材料由不同的粒子集合表示.对场函数的离散化主要包括两步,第一步,将点x处的场函数f表示为积分形式(核近似化)[11]:
| $ f\left( x \right) \approx \tilde f\left( x \right) = \int\limits_\Omega {f\left( {x'} \right)W\left( {\left| {x - x'} \right|,h} \right){\rm{d}}x'} , $ | (1) |
式中W(|x-x′|, h)为光滑函数,h为核函数的光滑长度.
式(1)中的核函数项可理解为点x′处的场函数值对x点的权重,因此核函数W(R, h)是SPH方法的关键点,这里选用一种在SPH中得到广泛应用的三次B-样条函数[7, 12]:
| $ W\left( {R,h} \right) = {\alpha _{\rm{d}}} \times \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 2/3 - {R^2} + {R^3}/2,\\ {\left( {2 - R} \right)^3}/6,\\ 0, \end{array}&\begin{array}{l} 0 \le R < 1;\\ 1 \le R < 2;\\ R \ge 2. \end{array} \end{array}} \right. $ | (2) |
式中:记
第二步为粒子近似化,将积分表达式(1)离散成求和公式,得到在粒子i处场函数的粒子近似形式[11]:
| $ f\left( {{x_i}} \right) \approx \sum\limits_{j = 1}^N {f\left( {{x_j}} \right)W\left( {{x_{ij}},h} \right)\frac{{{m_j}}}{{{\rho _j}}}} , $ | (3) |
式中:xij = xi-xj,xi和xj分别表示粒子点i和j对应的坐标,m和ρ表示粒子点的质量和密度.
1.2 SPH流动模型对密度函数直接使用SPH近似法,可得密度的SPH近似式[7-8]:
| $ {\rho _i} = \sum\limits_{j = 1}^N {{m_j}{W_{ij}}} . $ | (4) |
通过式(4)可直接建立密度的近似表达形式,且在整个问题的积分区域内严格满足质量守恒定律.
根据纳维斯托克斯公式,动量平衡方程可写为[13]
| $ \frac{{{\rm{d}}{u^\alpha }}}{{{\rm{d}}t}} = F_{{\rm{pre}}}^\alpha + F_{{\rm{vis}}}^\alpha + F_{{\rm{ex}}}^\alpha , $ | (5) |
上式等号右边第一项为单位质量流体微元受到的压力(pre),第二、三项分别为黏性力(vis)和外力(ex).这里不考虑外力作用,压力和黏性力可由下式确定:
| $ \left\{ \begin{array}{l} F_{{\rm{pre}}}^\alpha = - \frac{1}{\rho }\frac{{\partial \left( {p{\delta ^{\alpha \beta }}} \right)}}{{\partial {x^\beta }}},F_{{\rm{vis}}}^\alpha = \frac{1}{\rho }\frac{{\partial {\tau ^{\alpha \beta }}}}{{\partial {x^\beta }}};\\ {\tau ^{\alpha \beta }} = \mu {\varepsilon ^{\alpha \beta }},{\varepsilon ^{\alpha \beta }} = \frac{{\partial {u^\beta }}}{{\partial {x^\alpha }}} + \frac{{\partial {u^\alpha }}}{{\partial {x^\beta }}} - \frac{2}{3}\left( {\nabla \cdot u} \right){\delta ^{\alpha \beta }}. \end{array} \right. $ | (6) |
式中:上标α和β表示坐标方向,p为压强,δ为狄拉克函数,τ为黏性剪应力,μ为黏性系数,ε表示剪应变率.
采用的SPH离散化形式为[7]
| $ \begin{array}{*{20}{c}} {\frac{{{\rm{d}}u_i^\alpha }}{{{\rm{d}}t}} = - \sum\limits_{j = 1}^N {{m_j}\left( {\frac{{{p_i}}}{{\rho _i^2}} + \frac{{{p_j}}}{{\rho _j^2}}} \right)\frac{{\partial {W_{ij}}}}{{\partial x_i^\alpha }}} + }\\ {\sum\limits_{j = 1}^N {{m_j}\left( {\frac{{{\mu _i}\varepsilon _i^{\alpha \beta }}}{{\rho _i^2}} + \frac{{{\mu _j}\varepsilon _j^{\alpha \beta }}}{{\rho _j^2}}} \right)\frac{{\partial {W_{ij}}}}{{\partial x_i^\beta }}} .} \end{array} $ | (7) |
式(4)和式(7)中包含3个未知量(p、ρ和u),因此还需引入一个状态方程.不可压缩流体在数值计算时一般考虑为微可压缩流体,常采用一种人工压缩性状态方程[8, 10]:
| $ p = {c^2}\rho , $ | (8) |
式中c为人工速度[LT-1],一般选取为最大流速的10倍左右.
为避免相近粒子的相互穿透,保证粒子位置的相对齐整,采用XSPH方法[14]处理得到粒子的相对速度:
| $ \frac{{{\rm{d}}{x_i}}}{{{\rm{d}}t}} = {u_i} - \kappa \sum\limits_{j = 1}^N {\frac{{{m_j}}}{{{\rho _j}}}{x_{ij}}{W_{ij}}} , $ | (9) |
式中κ为常数,这里取0.3.XSPH方法可有效保持粒子的运动速度与相邻粒子的平均速度相近.
1.3 边界处理与时间步为处理多孔介质中复杂的固液边界,采用一种Lennard-Jones边界力模型[6, 15]:
| $ {F_{ab}} = \left\{ \begin{array}{l} {F_0}\left[ {{{\left( {\frac{{{r_0}}}{{\left| {{r_{ab}}} \right|}}} \right)}^{{n_1}}} - {{\left( {\frac{{{r_0}}}{{\left| {{r_{ab}}} \right|}}} \right)}^{{n_2}}}} \right]\frac{{{r_{ab}}}}{{{{\left| {{r_{ab}}} \right|}^2}}},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {{r_{ab}}} \right| < {r_0};\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {{r_{ab}}} \right| \ge {r_0}. \end{array} \right. $ | (10) |
式中:a、b分别指代边界固体粒子和流体粒子.n1、n2为常数,通常取12和4[15].r0为截止距离,液体粒子运动至边界粒子的r0范围内,将受到边界力的作用.
为保证数值计算的稳定性,时间步长的选取需满足以下条件[8]:
| $ \Delta t \le \min \left[ {0.25\frac{h}{c},0.25\min {{\left( {\frac{h}{f}} \right)}^{1/2}},0.125\frac{{{h^2}}}{v}} \right]. $ | (11) |
时间步迭代采用具有二阶精度的跳蛙法计算[10].具体做法为:计算的初始计算步结束时,密度、速度推进半个步长,位置推进一个步长; 在每个计算步开始前,密度、速度再向前预测半个时间步长.
2 考虑裂隙的对流扩散方程 2.1 对流-扩散方程在物理域均质的假定下,不考虑吸附和源项,饱和多孔介质中对流-扩散方程为[16]
| $ \frac{{\partial C}}{{\partial t}} = D{\nabla ^2}C - u\nabla C, $ | (12) |
式中:D是水动力弥散系数[L2T-1],D=Dde+Ddm,Dde和Ddm分别为分子弥散系数和机械弥散系数,u为平均流速[LT-1].在液体中常见溶质的分子弥散系数Dde的数量级一般在10-9 m2/s,因此这里不考虑分子弥散.
式(12)在推导的过程中,假定了流速u的方向与坐标轴方向相同,因此对单向流问题,可简化地使用一维对流扩散方程描述[3].若假定介质中初始质量浓度为0,注入流体的质量浓度为C0,则介质中任意时空分布下的无量纲浓度可由下列解析解求得:
| $ \frac{{C\left( {x,t} \right)}}{{{C_0}}} = \frac{1}{2}{\rm{Erfc}}\left( {\frac{{x - ut}}{{2\sqrt {Dt} }}} \right) + \frac{1}{2}{\rm{Exp}}\left( {\frac{{ux}}{D}} \right){\rm{Erfc}}\left( {\frac{{x + ut}}{{2\sqrt {Dt} }}} \right), $ | (13) |
两流区模型考虑整个流场中不同区域处有不同的流动状态,可将流场分为基质流动区(m)和裂隙流动区(f).两个区域中弥散度、含水量和流速可能有所不同.此外,引入相互作用系数表征区域间溶质的线性转移.饱和单向流动的两流区模型可写为[5]
| $ \left\{ \begin{array}{l} \frac{{\partial {C_{\rm{f}}}}}{{\partial t}} = {D_{\rm{f}}}\frac{{{\partial ^2}{C_{\rm{f}}}}}{{\partial {x^2}}} - {u_{\rm{f}}}\frac{{\partial {C_{\rm{f}}}}}{{\partial x}} - \frac{\alpha }{{\theta n}}\left( {{C_{\rm{f}}} - {C_{\rm{m}}}} \right),\\ \frac{{\partial {C_{\rm{m}}}}}{{\partial t}} = {D_{\rm{m}}}\frac{{{\partial ^2}{C_{\rm{m}}}}}{{\partial {x^2}}} - {u_{\rm{m}}}\frac{{\partial {C_{\rm{m}}}}}{{\partial x}} - \frac{\alpha }{{\left( {1 - \theta } \right)n}}\left( {{C_{\rm{m}}} - {C_{\rm{f}}}} \right). \end{array} \right. $ | (14) |
式中:下标f,m分别对应两流区中的物理量,α为质量交换系数[T-1],n为孔隙率,θ表示裂隙流动区在整个流场中的占比.总体的质量浓度可通过加权计算得到:
| $ \left\{ \begin{array}{l} C = \left[ {\left( {\theta {C_{\rm{f}}}{u_{\rm{f}}} + \left( {1 - \theta } \right){C_{\rm{m}}}{u_{\rm{m}}}} \right)} \right]/u,\\ u = \theta {u_{\rm{f}}} + \left( {1 - \theta } \right){u_{\rm{m}}}. \end{array} \right. $ | (15) |
由于两流区模型较为复杂,往往只能采用数值计算求解,而不便于进行参数拟合.因此,为推导得到解析解,这里简化认为两区之间的质量交换量很小,可忽略不计(α = 0).设定边界条件:C(0, t)=C0, C(∞, t)=0;则方程解析解为
| $ \begin{array}{l} \frac{{C\left( {x,t} \right)}}{{{C_0}}} = \frac{1}{{\left( {\theta {u_{\rm{f}}} + \left( {1 - \theta } \right){u_{\rm{m}}}} \right)}} \times \\ \left\{ {\frac{{\theta {u_{\rm{f}}}}}{2}\left[ {{\rm{Erfc}}\left( {\frac{{x - {u_{\rm{f}}}t}}{{2\sqrt {{D_{\rm{f}}}t} }}} \right) + {\rm{Exp}}\left( {\frac{{{u_{\rm{f}}}x}}{{{D_{\rm{f}}}}}} \right){\rm{Erfc}}\left( {\frac{{x + {u_{\rm{f}}}t}}{{2\sqrt {{D_{\rm{f}}}t} }}} \right)} \right] + } \right.\\ \left. {\frac{{\left( {1 - \theta } \right){u_{\rm{m}}}}}{2}\left[ {{\rm{Erfc}}\left( {\frac{{x - {u_{\rm{m}}}t}}{{2\sqrt {{D_{\rm{m}}}t} }}} \right) + {\rm{Exp}}\left( {\frac{{{u_{\rm{m}}}x}}{{{D_{\rm{m}}}}}} \right){\rm{Erfc}}\left( {\frac{{x + {u_{\rm{m}}}t}}{{2\sqrt {{D_{\rm{m}}}t} }}} \right)} \right]} \right\}. \end{array} $ | (16) |
定义无量纲量
| $ \begin{array}{l} \frac{{C\left( {L,{p_{\rm{v}}}} \right)}}{{{C_0}}} = \frac{{\theta {\lambda _{\rm{f}}}}}{2}\left[ {{\rm{Erfc}}\left( {\frac{{L - {\lambda _{\rm{f}}}L{p_{\rm{v}}}}}{{2\sqrt {{D_{\rm{f}}}L{p_{\rm{v}}}/u} }}} \right) + } \right.\\ \;\;\;\;\left. {{\rm{Exp}}\left( {\frac{{{\lambda _{\rm{f}}}uL}}{{{D_{\rm{f}}}}}} \right){\rm{Erfc}}\left( {\frac{{L + {\lambda _{\rm{f}}}L{p_{\rm{v}}}}}{{2\sqrt {{D_{\rm{f}}}L{p_{\rm{v}}}/u} }}} \right)} \right] + \\ \;\;\;\;\frac{{\left( {1 - \theta } \right){\lambda _{\rm{m}}}}}{2}\left[ {{\rm{Erfc}}\left( {\frac{{L - {\lambda _{\rm{m}}}L{p_{\rm{v}}}}}{{2\sqrt {{D_{\rm{m}}}L{p_{\rm{v}}}/u} }}} \right) + } \right.\\ \;\;\;\;\left. {{\rm{Exp}}\left( {\frac{{{\lambda _{\rm{m}}}uL}}{{{D_{\rm{m}}}}}} \right){\rm{Erfc}}\left( {\frac{{L + {\lambda _{\rm{m}}}L{p_{\rm{v}}}}}{{2\sqrt {{D_{\rm{m}}}L{p_{\rm{v}}}/u} }}} \right)} \right]. \end{array} $ | (17) |
对计算流场做假定:1)多孔介质饱和; 2)基质颗粒不可运动; 3)不考虑溶质质量; 4)忽略分子扩散.
3.1 计算模型一个含明显裂隙通道的二维多孔介质见图 1.左右两端为速度控制区域,中间为流场区域,上下边界为周期边界,从右端区域流出的粒子会被初始化后置于左端.设定原流场内流体粒子和新流入流体粒子的质量浓度分别为0和C0.
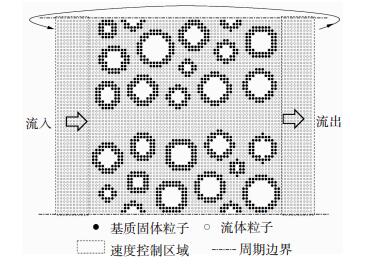
|
图 1 裂隙多孔介质流场物理模型 Fig. 1 Physical model of the fractured porous media flow field |
计算参数设定为:注入速度u = 0.04 m/s,初始粒子间距Δx = 0.000 2 m,多孔介质区域为正方形,长度为L = 0.012 m.固体粒子总计有1 068个,流体粒子1 987个,单个时间步长Δt = 2×10-5 s,光滑长度h等于1倍Δx.
图 2反映了裂隙多孔介质内部流体质点的速度分布.易知在贯通的裂隙区域,流速明显大于平均流速,而基质区域的流速基本在平均流速上下浮动,总体低于平均流速.
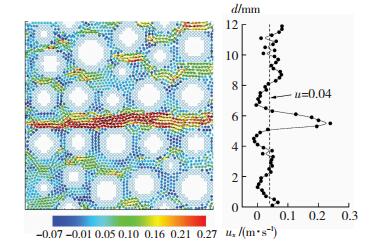
|
图 2 裂隙多孔介质水平流速分布 Fig. 2 Horizontal velocity of the fractured porous media |
图 3中,多孔介质A、B、C的孔隙率均为0.552,且中间均有一贯通裂隙,A、B、C中的最大裂隙宽度分别设定为2、1.4和1 mm,折算得到的θ值分别为0.167、0.117和0.083.在控制孔隙率和平均流速相同的情况下,不同裂隙介质中对流扩散演化规律的不同主要体现在:裂隙张开度越大,优势流效应越明显; 随着裂隙宽度增大,裂隙区域流速与基质区域流速差增大.

|
图 3 张开度不同的裂隙多孔介质中的对流弥散过程 Fig. 3 Process of convective diffusion in porous medias with different opening degrees |
图 4反映了多孔介质A、B、C在L位置处出流液的无量纲浓度随时间的演化过程(穿透曲线).可见在含裂隙的多孔介质中,注入溶质后不久穿透曲线即会出现陡增段,且裂隙宽度越大,陡增段越长,早期穿透略有提前,后期穿透则更为平缓.相应的物理过程为:大量溶质随着优势流快速穿透多孔介质,出现早期穿透现象,体现在穿透曲线中即为陡增段; 而分布在基质中的溶质由于整体迁移速度小于平均速度而出现拖尾现象,体现在穿透曲线中即为平缓段.
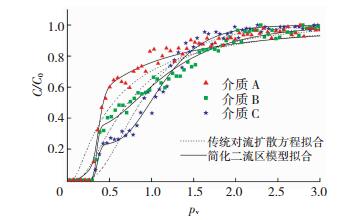
|
图 4 穿透曲线及其拟合曲线 Fig. 4 Penetration curves and the corresponding fitting curves |
为描述这一现象,图 4中分别采用了传统CDE方程(式(13))以及简化后的两流区模型(式(17))对孔隙尺度下裂隙多孔介质的仿真实验结果进行拟合.结果表明,简化两流区模型的拟合曲线(图 4中实线)与SPH仿真实验数据(图 4中散点)十分吻合,可准确地体现出穿透曲线中的早期穿透和后期拖尾现象.
对两流区模型,3个待拟合的参数为Df和Dm(单位m2/s)以及λf,其余参数可由模型参数直接得到或换算得到; 对流扩散方程中待拟合的参数为D(单位m2/s); 拟合结果见表 1和表 2.
| 表 1 两流区模型拟和参数 Tab. 1 Fitting parameters of the Two-Region Model |
| 表 2 传统CDE方程拟和参数 Tab. 2 Fitting parameters of the convection diffusion equation |
综上,两流区模型的拟合效果明显优于传统CDE方程,且文中对两流区模型的简化形式及其解析解的适用性也得到了有效验证.因此在研究裂隙多孔介质的对流扩散问题时,可以采用这种易于参数拟合的解析解形式,从而反演得到裂隙流中对流弥散的相关参数.
4 结论1) 建立孔隙尺度的SPH流动模型,采用Fortran语言编译程序,模拟得到孔隙水对流扩散的真实物理过程.并通过孔隙尺度下的仿真实验,检验了两流区模型的适用性.
2) 对两流区模型进行简化,给出了易于参数拟合的解析解形式.该解析式能够很好地描述裂隙多孔介质溶质运移过程中的早期穿透和拖尾现象,拟合效果明显优于传统CDE方程,有效性得到了有效验证,并可反演得到裂隙流中对流弥散的相关参数.
3) 仿真实验结果表明,在考虑裂隙的多孔介质中,裂隙张开度越大,优势流效应越明显.随着裂隙宽度增大,裂隙区域流速与基质区域流速差增大,穿透曲线中早期穿透和拖尾现象越明显,水动力弥散效应也更加显著.
| [1] |
李寻, 张土乔, 李金轩. 单裂隙介质中核素迁移模型的解析解及其应用[J]. 哈尔滨工业大学学报, 2010, 42(12): 1990. LI Xun, ZHANG Tuqiao, LI Jinxuan. Analytical solution and its application of modeling nuclide transport model in single fractured media[J]. Journal of Harbin Institute of Technology, 2010, 42(12): 1990. DOI:10.11918/j.issn.0367-6234.2010.12.030 |
| [2] |
解雪峰, 濮励杰, 朱明, 等. 土壤水盐运移模型研究进展及展望[J]. 地理科学, 2016, 36(10): 1565. XIE Xuefeng, PU Lijie, ZHU Ming, et al. Evolution and prospects in modeling of water and salt transport in soils[J]. Scientia Geographica Sinica, 2016, 36(10): 1565. |
| [3] |
BAI Bing, LONG Fei, RAO Dengyu, et al. The effect of temperature on the seepage transport of suspended particles in a porous medium[J]. Hydrological Processes, 2017, 31: 382. DOI:10.1002/hyp.11034 |
| [4] |
COATS K H. Dead-end pore volume and dispersion in porous media[J]. Society of Petroleum Engineers Journal, 1964, 4(4): 73. DOI:10.2118/647-PA |
| [5] |
SKOPP J, GARDNER W R, TYLER E J. Solute movement in structured soils: two-region model with small interaction[J]. Soil Science Society of America Journal, 1981, 45(5): 837. DOI:10.2136/sssaj1981.03615995004500050002x |
| [6] |
MONAGHAN J J. Simulating free surface flows with SPH[J]. Journal of Computational Physics, 1994, 110(2): 399. DOI:10.1006/jcph.1994.10340 |
| [7] |
LIU M B, LIU G R. Smoothed particle hydrodynamics (SPH): an overview and recent developments[J]. Archives of Computational Methods in Engineering, 2010, 17(1): 25. DOI:10.1007/s11831-010-9040-7 |
| [8] |
MORRIS J P, FOX P J, ZHU Y. Modeling low Reynolds number incompressible flows using SPH[J]. Journal of Computational Physics, 1997, 136(1): 214. DOI:10.1006/jcph.1997.5776 |
| [9] |
ZHU Yi, FOX P J. Simulation of pore-scale dispersion in periodic porous media using smoothed particle hydrodynamics[J]. Journal of Computational Physics, 2002, 182(2): 622. DOI:10.1006/jcph.2002.7189 |
| [10] |
TARTAKOVSKY A M, TRASK N, PAN K, et al. Smoothed particle hydrodynamics and its applications for multiphase flow and reactive transport in porous media[J]. Computational Geosciences, 2016, 20(4): 807. DOI:10.1007/s10596-015-9468-9 |
| [11] |
饶登宇, 白冰, 陈佩佩. 基于SPH方法的非饱和多孔介质相变耦合研究[J]. 岩土力学, 2018, 39(12): 4528. RAO Dengyu, BAI Bing, CHEN Peipei. Simulation of hydro-thermal coupling with phase-change in unsaturated porous media by SPH method[J]. Rock and Soil Mechanics, 2018, 39(12): 4528. DOI:10.16285/j.rsm.2017.0827 |
| [12] |
BAI Bing, RAO Dengyu, XU Tao, et al. SPH-FDM boundary for the analysis of thermal process in homogeneous media with a discontinuous interface[J]. International Journal of Heat & Mass Transfer, 2018, 117: 518. DOI:10.1016/j.ijheatmasstransfer.2017.10.004 |
| [13] |
夏维学, 王聪, 魏英杰, 等. 高速旋转小球入水空泡特性数值模拟[J]. 哈尔滨工业大学学报, 2018, 50(4): 139. XIA Weixue, WANG Cong, WEI Yingjie, et al. Numerical simulation investigation on water-entry cavity of high-speed spinning sphere[J]. Journal of Harbin Institute of Technology, 2018, 50(4): 139. DOI:10.11918/j.issn.0367-6234.201510024 |
| [14] |
MONAGHAN J J. On the problem of penetration in particle methods[J]. Journal of Computational Physics, 1989, 82(1): 1. DOI:10.1016/0021-9991(89)90032-6 |
| [15] |
李维仲, 赵月帅, 宋永臣. 多孔介质孔隙尺度下不可压缩流体流动特性SPH模拟[J]. 大连理工大学学报, 2013, 53(2): 190. LI Weizhong, ZHAO Yueshuai, SONG Yongchen. Simulation of incompressible fluid flow in porous media at pore scale via smoothed particle hydrodynamics[J]. Journal of Dalian University of Technology, 2013, 53(2): 190. DOI:10.7511/dllgxb201302006 |
| [16] |
BAI Bing, LI Huawei, XU Tao, et al. Analytical solutions for contaminant transport in a semi-infinite porous medium using the source function method[J]. Computers and Geotechnics, 2015, 69: 115. DOI:10.1016/j.compgeo.2015.05.002 |
 2019, Vol. 51
2019, Vol. 51


