2. 江苏省工程力学分析重点实验室(东南大学), 南京 210096
2. Jiangsu Key Lab of Engineering Mechanics (Southeast University), Nanjing 210096, China
工业厂房钢结构是土木工程一个常见结构形式,包括檩条、屋架、柱、吊车梁及各种支撑等构件,构件通过焊接、铆接等方式连接.在这些连接焊缝附近,不可避免地含有微、细观孔洞和裂纹,会加剧应力集中程度,导致结构性能衰退.已服役一定年限的既有工业厂房钢结构会存在某种程度的疲劳性能衰退,甚至在某些易损局部(如吊车梁的插板与封板连接焊缝处)发生疲劳失效[1-2].根据国际标准化组织的定义,金属材料在应力或者应变的反复作用下所发生的性能劣化叫做疲劳[3].疲劳机理是微观尺度上的缺陷(微孔洞、微裂纹)在外部荷载作用下萌生和扩展以致产生宏观尺度上的裂纹,裂纹继续扩展从而导致结构整体失效,甚至发生脆断,图 1描述了钢结构疲劳性能衰退过程.

|
图 1 钢吊车梁疲劳失效过程示意 Fig. 1 Process of fatigue deterioration of the crane runway girder |
疲劳性能预后是指对尚未且可能发生的疲劳衰退过程及其后果的预测,是在掌握疲劳性能衰退机理前提下,利用结构服役历程、当前运行状态、检测信息等,发展成结构中可能发生的疲劳及其后果的预测系统[4].结构疲劳预后分析需要理解结构疲劳损伤的诱因,确定合适的评估和量化损伤的方法及明确疲劳预后目标(预测结构启裂或剩余疲劳寿命).疲劳预后多用于航天、机械等领域,一些学者提出“治结构之未病”的学术理念用于土木工程领域[5-6].
现有研究多趋向于在单一尺度下,利用Miner准则分析工业厂房钢结构疲劳损伤演化过程[7-8],宏观裂纹出现后,则将疲劳裂纹简化为Ⅰ型裂纹进行分析[9].然而,疲劳损伤演化是多尺度问题,需要量化微、细观尺度上既有缺陷引起的初始损伤,并采用多尺度方法研究疲劳损伤跨尺度演化过程; Miner准则不能描述结构疲劳性能衰退的机理; 工业厂房钢结构的疲劳裂纹虽多为Ⅰ型裂纹主导,但通常是复合型裂纹.综上所述,现有工业厂房钢结构研究虽能解决部分疲劳问题,但不能准确描述结构当前运行状态以及疲劳性能衰退机理,因此,不能实现工业厂房钢结构疲劳预后的目标.
钢吊车梁是工业厂房钢结构核心构件,直接承受吊车来回运行引起的循环荷载,容易发生疲劳失效,导致整个工业厂房无法正常工作[8].为主动掌握结构疲劳性能衰退机理,更有效预防结构发生疲劳脆性断裂,发展了面向既有工业厂房钢结构疲劳性能预后分析的方法.基于跨尺度界面功平衡原理建立了工业厂房钢结构的疲劳损伤多尺度模型,分析了服役载荷的动态特征,量化了既有缺陷引起的损伤,研究了工业厂房钢结构的疲劳损伤演化以及复合型疲劳裂纹扩展过程及其影响.本文以直角式吊车梁(即插板与封板相互垂直)为研究对象,文中提出的疲劳性能预后方法亦适用于工程中常见的圆弧端式和等截面吊车梁乃至工业厂房的其他构件.
1 工业厂房钢结构疲劳损伤多尺度模型 1.1 钢吊车梁及既有缺陷的模拟方法繁重的生产任务和严苛的服役环境导致工业厂房钢吊车梁常未达到设计使用年限就发生了疲劳失效.以国内某钢结构电炉管坯连铸主厂房原料跨为例,结构的几何尺寸和材料属性均与报告[10]保持一致,平面布置见图 2,钢吊车梁的制材为Q345钢,材料属性见表 1[10].

|
图 2 某既有工业厂房钢结构平面布置(mm) Fig. 2 Floor plan of an existing steel industrial plant (mm) |
| 表 1 Q345钢的力学属性 Tab. 1 Mechanical properties of steel Q345 |
服役若干年的既有工业厂房钢结构难免存在某种程度上的微观缺陷(微裂纹、微孔洞),这些缺陷会导致结构含有损伤,从而影响结构的使用寿命,因此,需要引入损伤场表征钢结构的既有缺陷.材料的晶格内部通常存在微裂纹,含裂纹长ai的晶粒,其损伤Di可表示为
| $ D_{i}=\frac{a_{i}}{d}, $ | (1) |
式中d为晶格尺寸,材料损伤变量D可定义为代表性体元(representative volume element,RVE)中所有微损伤的平均值:
| $ D = \frac{{\sum\limits_i^n {{D_i}} }}{{{n_{{\rm{ total }}}}}}, $ | (2) |
式中ntotal为RVE中全部晶粒数目[11].
微裂纹尺寸一般为0~100 μm,考虑随机性,假定微裂纹尺寸在0~0.1 mm随机出现.建议采用均布随机数判断晶粒是否存在初始损伤:不存在初始微损伤的晶粒微裂纹尺寸为0,存在初始微损伤晶粒的微裂纹尺寸在0~0.1 mm随机选取,构件的既有损伤计算流程见图 3.

|
图 3 既有损伤量化流程图 Fig. 3 Flow chart of the existing damage calculation |
Q345钢的晶粒尺寸一般为0.1 mm,多尺度模型单元易损局部处单元尺寸为0.5 mm,则每单元所含全部晶粒数目为25.根据图 3流程图进行maltab编程,输入关键参数为d=0.1 mm和k=0, 1, …, 24(晶粒数量),从而得出钢吊车梁的易损局部的既有损伤为0.13.
1.2 含缺陷的结构疲劳损伤多尺度模型在结构服役过程中,易损局部的损伤会发生跨尺度演化,即损伤逐渐从小尺度域向大尺度域蔓延.传统宏观尺度模型不能准确表征结构性能衰退过程,细观尺度工业厂房钢结构模型计算代价过大.为兼顾精确度和计算代价要求,基于跨尺度界面功平衡原则(功平衡原理是指宏观尺度上的节点力在节点位移上做的功和细观尺度上的应力在应变上做的功平衡),运用ABAQUS进行建模:采用梁单元和实体单元连接方法实现跨尺度界面连接[12],即钢结构厂房及工字钢柱采用梁单元,牛腿与柱连接部位的工字柱采用实体单元,直角式钢吊车梁的焊缝区域则采用细观尺度的精细网格单元,建立了工业厂房钢结构的疲劳损伤多尺度模型,选取了宏观尺度(单元特征尺度量级100 m)和细观尺度(单元特征尺度量级10-3 m)进行建模,多尺度疲劳损伤模型见图 4.

|
图 4 既有工业厂房钢结构疲劳损伤多尺度模型 Fig. 4 Multi-scale fatigue damage model of the existing steel industrial plant |
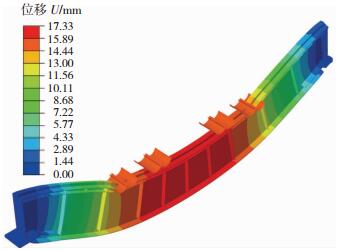
工业厂房钢结构检测通常以钢吊车梁跨中最大下挠度作为结构是否能继续服役的判据.本文通过采用荷载450 kN(最大轮压)进行模拟,结果见图 5.钢吊车梁跨中最大下挠度为17.33 mm.在相同工况下,工程实际检测挠度为11mm,考虑吊车梁起拱7 mm,即实测吊车梁下挠为18 mm[10].数值模拟结果与实测结果的相对误差为3.9%,说明本文建立的结构疲劳损伤多尺度模型是合理的.
|
图 5 直角式变截面钢吊车梁的位移分布 Fig. 5 Displacement distribution of the rectangular variable section steel crane girder |
工业厂房钢结构的服役荷载主要是吊车轮压荷载,本次研究的吊车为软钩桥式,其工作级别为A7,最大轮压值为450 kN[10],在吊车运行过程中,轮压值T通常在200 kN左右[13].为研究荷载动态效应,分别采用动态显式与静态隐式方法模拟吊车行驶引起的厂房结构力学响应,定义放大系数φ为同一单元采用动态显示与静态隐式的等效应力幅比.在ABAQUS中将吊车与钢吊车梁之间设置为无摩擦接触,采用刚体对吊车进行建模.
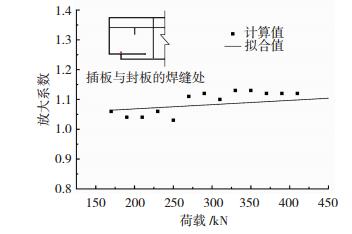
图 6描述了不同轮压值作用下的钢吊车梁插板与封板焊缝(部位B)的放大系数φ及其拟合曲线,见式(3).由图 6知:放大系数随轮压值增加而有逐渐上升趋势,最大可达1.13,相对误差值超过10%,与《钢结构设计规范》[14]动力系数为1.1~1.3倍的规定一致,说明需要考虑服役载荷的动力效应对易损局部的影响.
| $ \varphi=0.11324 T+0.00769. $ | (3) |
|
图 6 插板与封板焊缝处放大系数随荷载的变化 Fig. 6 Amplification factor of the weld between the insert plate and the seal plate along with load |
为主动掌握既有工业厂房钢结构损伤演化规律,需对其进行疲劳损伤预后分析.材料损伤演化曲线能反映其内部微观缺陷导致材料性能衰退过程,并可得到材料(结构)的疲劳寿命.采用经典Lemaitre损伤模型研究含缺陷结构在服役期间的疲劳损伤演化规律,Lemaitre模型可表示为[15]
| $ \frac{\mathrm{d} D}{\mathrm{d} N}=\left[\frac{\Delta \sigma}{2 B(1-D)}\right]^{\alpha}(1-D)^{-\beta}. $ | (4) |
对上式进行积分可得到损伤演化方程:
| $ D=1-\left(1-\frac{N}{N_{\mathrm{f}}}\right)^{\frac{1}{\alpha+\beta+1}}, $ | (5) |
| $ 其中~~ N_{\mathrm{f}}=\frac{1}{\alpha+\beta+1}\left[\frac{\Delta \sigma}{2 B}\right]^{-\alpha}. $ | (6) |
式中:D为损伤变量,Nf为疲劳寿命,N为循环次数,Δσ为应力幅, α、β、B均为材料参数,可通过纯疲劳试验获得.本次研究中,
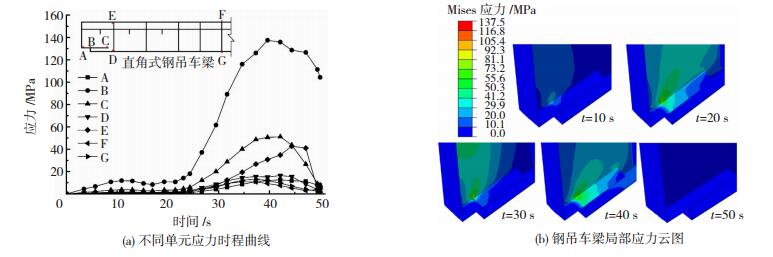
在插板与封板的连接焊缝及上、下翼缘与腹板的连接焊缝等易损区域选取了5个研究部位.图 7为从模拟结果中提取出的应力图,从而可得:部位B为钢吊车梁的危险部位.图 8描述了采用雨流计数法得到的危险部位等效应力幅值,可得出:经历的循环次数越多,则应力幅越大,其应力幅在0~55 MPa,等效应力幅为47.4 MPa.
|
图 7 钢吊车梁易损部位的应力分布(T=200 kN) Fig. 7 Stress distribution of the vulnerable positions of the steel crane runway girder (T=200 kN) |

|
图 8 易损部位B的应力幅(T=200 kN) Fig. 8 Stress amplitude of the vulnerable position B (T=200 kN) |
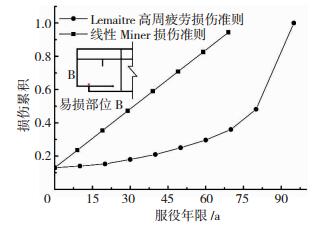
考虑了既有缺陷引起的损伤,疲劳损伤预后分析结果见图 9.直角式钢吊车梁损伤累积过程呈非线性上升趋势,在损伤演化初期,增长速率较为缓慢; 当损伤累积值达到0.4左右后,损伤增长速率显著加快,结构可能产生宏观裂纹; 与Lemaitre模型相比,基于线性Miner理论的工程评估方法过于保守.
|
图 9 易损部位B的疲劳损伤演化曲线 Fig. 9 Fatigue damage evolution curves of the vulnerable position B |
材料的损伤值达到某个临界值后,构件产生宏观裂纹,Q345钢的临界损伤值为0.407[18].宏观裂纹会使构件力学性能降低,但发生失稳之前,构件仍具有较高承载能力,需对疲劳裂纹扩展及其影响进行预后分析.钢吊车梁处插板与封板焊缝附近区域常会产生疲劳裂纹,裂纹形状通常近似为半椭圆表面裂纹[19-20].本次研究的钢吊车梁焊接为角焊缝与对接焊缝全焊透组合形式,焊脚尺寸为9 mm,腹板尺寸为18 mm,最大裂纹尺度
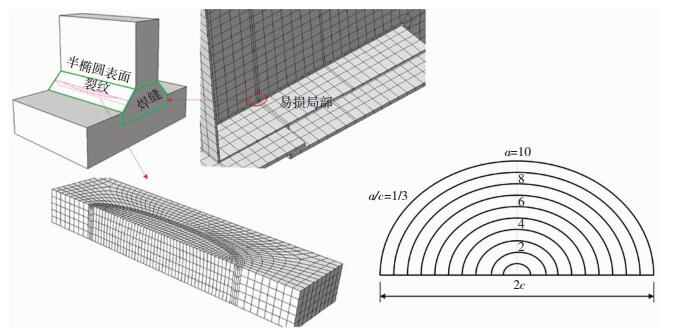
|
图 10 带裂纹的钢吊车梁有限元模型 Fig. 10 Finite model of the steel crane runway girder with a surface crack |
为防止结构发生疲劳脆性断裂,利用Paris疲劳理论对既有工业厂房钢结构的复合型疲劳裂纹扩展进行预后分析.Pairs模型利用裂纹尖端应力强度因子幅值ΔK来描述宏观裂纹扩展的规律[21]:
| $ \frac{\mathrm{d} a}{\mathrm{d} N}=C(\Delta K)^{m}, $ | (7) |
式中C和m均为材料常数.
从ABAQUS模拟结果中提取了部位B和中间加劲肋与腹板的连接焊缝(部位E)的应力强度因子幅ΔK值,见图 11.部位B的疲劳裂纹扩展由ΔKⅢ主导,为Ⅰ+Ⅲ型混合裂纹扩展模式,C取值为0.4×10-13,m取值为2.88[22-23]; 部位E的疲劳裂纹扩展则是由ΔKⅠ主导,是Ⅰ+Ⅱ型混合裂纹扩展模式,C取值为4×10-13,m取值为2.88[23].其中,Ⅰ型、Ⅱ型和Ⅲ型裂纹分别指张开型、滑开型和撕开型裂纹.
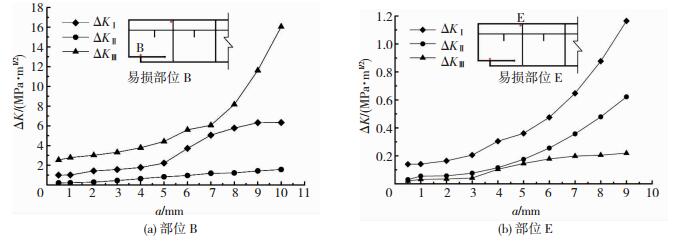
|
图 11 应力强度因子随裂纹深度变化的曲线(T=200 kN) Fig. 11 Changes of stress intensity factor along with crack length (T=200 kN) |
复合型裂纹的等效应力强度因子幅值可表示为[22]
| $ \Delta {K_{\rm{e}}} = {\left[ {\Delta K_{\rm{I}}^4 + 8 \cdot \Delta K_{{\rm{II}}}^4 + \frac{{8 \cdot \Delta K_{{\rm{III}}}^4}}{{(1 - v)}}} \right]^{0.25}}. $ | (8) |
结合式(8),通过拟合得到部位B和E处的等效应力强度因子幅值表达式,分别为式(9)和(10),对应的曲线见图 12.
| $ \Delta K_{\mathrm{eB}}=0.0184 a^{3}-0.084 a^{2}+0.4543 a+2.638, $ | (9) |
| $ \Delta K_{\mathrm{eE}}=0.0012 a^{3}+0.0013 a^{2}+0.0214 a+0.11881. $ | (10) |
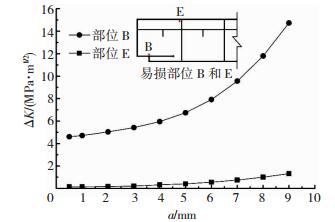
|
图 12 部位B和E处疲劳裂纹扩展曲线 Fig. 12 Fatigue crack propagation curves of the vulnerable positions B and E |
将式(9)和(10)分别代入式(7),并结合对应部位的Paris模型参数C和m,可得到部位B、E两处裂纹深度随循环次数变化的曲线,见图 13.由图 12、13描述预后分析结果可知:裂纹深度a超过5 mm后,裂纹迅速扩展,此时应对构件进行加固处理; 相同条件下,钢吊车梁的易损部位B处更容易发生疲劳失效,这也解释了工程实际中将此处焊缝列为检测重点的原因; 部位B裂纹扩展速率较大,且在N=2.5×106之后,裂纹扩展速率迅速增大.
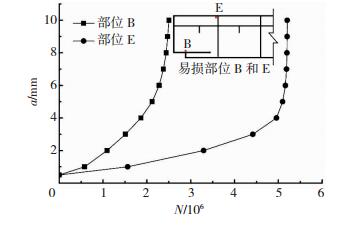
|
图 13 部位B和E处裂纹深度随循环次数变化的曲线 Fig. 13 Crack depth dependence on the number of cycles at positions B and E |
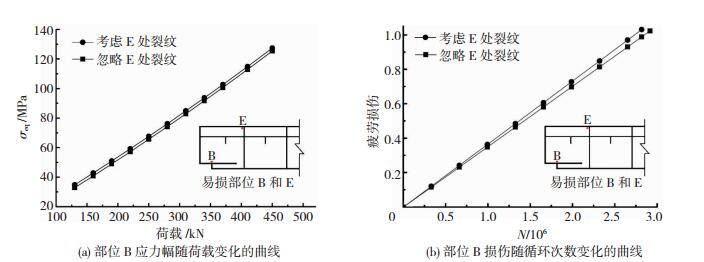
疲劳裂纹不仅会降低结构裂纹区域的承载能力,还会影响其他易损区域的应力状态,需要对疲劳裂纹的影响进行预后分析.虽然相对部位B而言,部位E是次要部位,但也是疲劳裂纹的多发区.因此,分别对部位B处裂纹对部位E的影响和部位E处裂纹对部位B的影响进行了预后分析,见图 14、15.可从预后分析结果得出:部位B处裂纹会导致部位E的等效应力幅值以及损伤值的增大,其中损伤值的变化尤为明显; 部位E处裂纹虽然也会引起部位B的等效应力幅值和损伤值的增长,但影响程度非常小.

|
图 14 部位B的裂纹对部位E损伤累积的影响(a=5 mm) Fig. 14 Influence of the crack of position B on the damage of position E (a=5 mm) |
|
图 15 部位E的裂纹对部位B损伤累积的影响(a=5 mm) Fig. 15 Influence of the crack of position E on the damage of position B (a=5 mm) |
1) 在工业厂房钢结构服役期间,载荷动力效应比较明显,其放大系数随荷载增加而增大,在疲劳预后分析中需要考虑其影响.
2) 疲劳损伤预后分析结果表明钢吊车梁焊缝区域的损伤在初始阶段增长率较为缓慢,后期急剧增加,论证了工程中常用的线性Miner损伤准则会导致评估结果过于保守.
3) 疲劳裂纹扩展预后分析结果表明变截面钢吊车梁的插板与封板连接处的焊缝区域最容易发生疲劳失效,且本次研究的钢吊车梁裂纹深度a超过5 mm后,裂纹迅速扩展,应对其进行加固处理.
4) 疲劳裂纹影响预后分析结果表明关键部位的裂纹对次要部位疲劳性能的影响较大,而次要部位的裂纹对关键部位的性能影响则很小.
| [1] |
王若林. 钢结构原理[M]. 南京: 东南大学出版社, 2016. WANG Ruolin. Principle of steel structure[M]. Nanjing: Southeast University Press, 2016. |
| [2] |
刘洪波, 谢礼立, 邵永松. 钢结构箱形柱与工字梁刚性节点有限元分析[J]. 哈尔滨工业大学学报, 2007, 39(8): 1211. LIU Hongbo, XIE Lili, SHAO Yongsong. Finite element analyses of the rigid connections with steel box columns and Ⅰ section beams[J]. Journal of Harbin Institution of Technology, 2007, 39(8): 1211. DOI:10.3321/j.issn:0367-6234.2007.08.007 |
| [3] |
SURESHS. 材料的疲劳[M]. 第2版. 北京: 国防工业出版社, 1993. SURESH S. Fatigue of materials[M]. 2nd ed. Beijing: National Defense Industrial Press, 1993. |
| [4] |
FARRAR C R, LIEVEN N A J. Damage prognosis: the future of structural health monitoring[J]. Philosophical Transactions, 2007, 365(1851): 623. DOI:10.1098/rsta.2006.1927 |
| [5] |
李兆霞. 大型土木结构多尺度损伤预后的现状、研究思路与前景[J]. 东南大学学报(自然科学版), 2013, 43(5): 1111. LI Zhaoxia. State of the art in multi-scale damage prognosis for major infrastructures[J]. Journal of Southeast University (Natural Science Edition), 2013, 43(5): 1111. DOI:10.3969/j.issn.1001-0505.2013.05.034 |
| [6] |
LI Z X, CHAN T H T, YU Y, et al. Concurrent multi-scale modeling of civil infrastructures for analyses on structural deterioration-Part Ⅰ: modeling methodology and strategy[J]. Finite Elements in Analysis & Design, 2009, 45(11): 782. DOI:10.1016/j.finel.2009.06.013 |
| [7] |
LIU H B, XING K T. Assessment of fatigue reliability of steel crane structures in service based on damage cumulative model[C]//Proceedings of the Fourth International Conference on Advances in Steel Structures. Shanghai, Holland: Elsevier, Volume Ⅱ 2005: 1121. DOI: 10.1016/B978-008044637-0/50165-7
|
| [8] |
常好诵.工业建筑钢结构疲劳测试、评估及加固研究[D].天津: 天津大学, 2014 CHANG Haosong. The research of fatigue test evaluation and strengthening for industrial steel buildings[D]. Tianjin: Tianjin University, 2014 http://cdmd.cnki.com.cn/Article/CDMD-10056-1015041417.htm |
| [9] |
郭春红, 弓俊青, 惠云玲, 等. 带裂纹钢吊车梁剩余寿命评估[J]. 钢结构, 2010, 25(11): 15. GUO Chunhong, GONG Junqing, HUI Yunling, et al. Assessment of crane girder fatigue life with initial crack[J]. Steel Construction, 2010, 25(11): 15. DOI:10.3969/j.issn.1007-9963.2010.11.005 |
| [10] |
幸坤涛.宝钢电炉管坯连铸主厂房原料跨(AB跨)吊车梁结构检测鉴定报告[R].北京: 国家工业建构筑物质量安全监督检验中心, 2015 XING Kuntao. The detection report of raw material span (AB span) crane girder of Baosteel electric furnace tube billet casting plant[R]. Beijing: China Nation Center Quality and Safety Supervision Testing of industrial structures, 2015 |
| [11] |
孙宾.损伤跨尺度演化致结构失效过程的模拟和分析方法[D].南京: 东南大学, 2016 SUN Bin. Simulation and analysis method of failure process of engineering structures due to trans-scale damage evolution[D]. Nanjing: Southeast University, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10286-1016328107.htm |
| [12] |
ZHENG Z Y, LI Z X, CHEN Z W. Adaptive multi-scale analyses on structural failure considering localized damage evolution on vulnerable joints[J]. Archives of Civil & Mechanical Engineering, 2014, 14(2): 304. DOI:10.1016/j.acme.2013.08.004 |
| [13] |
姚继涛, 谷慧. 工业厂房吊车荷载的概率模型和组合方法[J]. 建筑结构学报, 2016, 37(11): 1. YAO Jitao, GU Hui. Probability model and combination method of crane load of industrial building[J]. Journal of Building Structures, 2016, 37(11): 1. DOI:10.14006/j.jzjgxb.2016.11.020 |
| [14] |
中华人民共和国建设部.钢结构设计规范: GB 50017—2003[S].北京: 中国计划出版社, 2003 Ministry of Construction of China. Code for design of steel structures: GB 50017—2003[S]. Beijing: China Planning Press, 2003 |
| [15] |
LEMAITRE J. A course on damage mechanics[M]. Berlin: Springer Verlag, 1996.
|
| [16] |
LI Z X, CHAN T H T, KO J M. Determination of effective stress range and its application on fatigue stress assessment of existing bridges[J]. International Journal of Solids and Structures, 2002, 39(9): 2401. DOI:10.1016/S0020-7683(02)00120-8 |
| [17] |
李兆霞, 王莹. 在役桥梁结构疲劳监测与评估[M]. 北京: 科学出版社, 2002. LI Zhaoxia, WANG Ying. Fatigue analyses and evaluation of existing bridges with monitoring data[M]. Beijing: Science Press, 2002. |
| [18] |
SUN B, YANG L, GUO Y. A high-cycle fatigue accumulation model based on electrical resistance for structural steels[J]. Fatigue & Fracture of Engineering Materials & Structures, 2007, 30(11): 1052. DOI:10.1111/j.1460-2695.2007.01175.x |
| [19] |
KUNA M. Finite elements in fracture mechanics[M]. Berlin: Springer Netherlands, 2013.
|
| [20] |
American Society of Mechanical Engineers. Rules for inservice inspection of nuclear power plant components[S]. New York: American Society of Mechanical Engineers, 2013
|
| [21] |
PARIS P, ERDOGAN F. A critical analysis of crack propagation laws[J]. Transactions of the ASME, 1963, 85(4): 528. DOI:10.1115/1.3656900 |
| [22] |
BARSOUM Z. Residual stress analysis and fatigue assessment of welded stress structures[D]. Sweden: Kungliga Tekniska Hogskolan Stockholm, 2008
|
| [23] |
British Standards Institution. Steel, concrete and composite bridges: BSI 5400—Part 10[S]. London: BSI, 1980
|
 2019, Vol. 51
2019, Vol. 51


