2. 天津市土木建筑结构防护与加固重点实验室(天津城建大学),天津 300384;
3. 哈尔滨工业大学(深圳) 土木与环境工程学院,广东 深圳 518055
2. Engineering and Safety Management Department Key Lab of Urban Security and Disaster Engineering (Tianjin Chengjian University), Tianjin 300384, China;
3. School of Civil and Environmental Engineering, Harbin Institute of Technology(Shenzhen), Shenzhen 518055, Guangdong, China
根据大量的震害分析发现,空间钢结构震后多发生杆件损伤,节点损伤和支座损伤等损伤情况[1-4].震后如何快速识别出空间钢结构杆件损伤的具体位置成为空间结构健康监测体系研究中的重点内容之一.目前已建立比较完善的杆件损伤判别指标,其中基于小波包能量分析的损伤指标法相对比较成熟,得到了较好的数值分析结果,比仅依靠频率的改变识别损伤具有更好的精度和抗噪性能[5-6].但目前基于小波包分析的损伤识别研究多集中在识别损伤是否发生,而对损伤具体可能发生的位置识别研究较少,为了更好地对杆件损伤位置快速识别方法进行系统研究,本文对方法的工程应用开展了试验研究.通过建立的单层网壳结构试验模型,切断试验结构中单根杆件作为损伤杆件位置判别的目标,综合考虑结构特点,基于建立的试验结构有限元模型,模拟各种不同位置的杆件发生损伤,建立合适的损伤位置判别样本库,将实际工程中的监测数据与结构的有限元数值分析结果进行聚类分析,识别出杆件发生损伤可能区域.通过试验验证了提出的基于小波包能量分析的空间结构损伤杆件位置识别方法的有效性和工程可应用性.
1 试验概况 1.1 试验模型试验模型为K6型单层钢网壳,跨度6 m,矢跨比1/7, 具体参见图 1.杆件均采用Ф15×3圆钢管,钢材为Q235,网壳节点为焊接球节点,焊接球直径100 mm,壁厚6 mm,质量1.5 kg.选取最外环6个主肋处节点焊接在Q235b级钢板上,钢板尺寸为200 mm×200 mm×50 mm,钢板4个角处分别设置直径为18 mm的孔洞,通过膨胀螺栓将钢板与混凝土地面固定,具体形式见图 2.

|
图 1 试验结构 Fig. 1 Test Structure |

|
图 2 试验结构支座 Fig. 2 Support of test structure |
试验分别在结构的12个节点位置布置38.5 kg重的质量块,加载点现场图和位置示意图分别见图 3.在结构的顶点位置布置三向(x, y, z)加速度传感器,编号分别为1~3号,具体见图 4.考虑到试验中单层钢网壳结构的自振频率较高,拾振器采用加速度传感器,采样频率为512 Hz,采用东方所的DASP V2006数据采集系统.试验采用锤击法以获取结构的自由衰减信号,锤击点位置见图 5.

|
图 3 配重块位置 Fig. 3 Position of mass block |

|
图 4 加速度传感器布置 Fig. 4 Position of acceleration sensors |
|
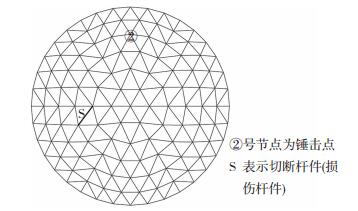
图 5 锤击点位置 Fig. 5 Location of the hammering point |
为模拟钢杆件的损伤,在试验结构的第三环杆处选择1号斜向杆件作为损伤杆件(切断杆件)的位置判别目标.杆件损伤具体位置见图 5,详图见图 6.

|
图 6 损伤杆件 Fig. 6 Damaged member |
试验结构加载后对结构完好时采用锤击法获得顶点处3个方向的加速度响应信号(x, y, z),在杆件损伤后,再采用锤击法获得损伤结构相同位置的振动响应信号.最终将通过采集系统获得的结构杆件损伤前后的3个加速度响应信号,作为后续损伤杆件位置判别的分析数据.
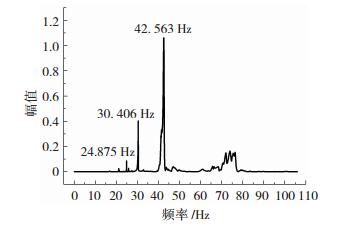
1.3 试验数据分析试验模型在无损状态下3个加速度传感器获得加速度传感器响应信息见图 7.选取有效时长的加速度响应信号的功率谱反应分析获得结构的频率,谱分析得到了3个主要参与振型的频率见图 8,分别为24.875、30.406和42.563 Hz.由于受试验条件的限制,试验结构模型只在顶点处布置了竖向加速度传感器,通过该处加速度响应数据的谱分析获得的结构主要参与振型频率与实际结构自振频率稍有偏差.

|
图 7 试验测试加速度响应信号(无损状态) Fig. 7 Testing acceleration result of test structure (no damage) |
|
图 8 加速度响应的谱分析 Fig. 8 Spectrum analysis of acceleration |
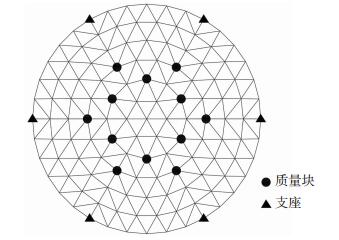
应用有限元软件ANSYS建立试验结构的数值分析模型,采用梁单元beam4模拟杆件,杆件弹性模量E=2.06×1011N/m2, 阻尼比取0.02.根据试验结构的频率分析结果,以有限元模型的节点质量分布为模型修正的调整参数,通过反复迭代和调整,获得修正后的有限元分析模型,见图 9.
|
图 9 试验结构的有限元模型 Fig. 9 Simulation model of test structure |
修正后有限元模型数值模拟分析,结构的3个主要参与振型分别为第7、17和31阶振型.对应的模态频率分别为24.657、30.701和48.664 Hz.均以竖向振动为主.将实际结构谱分析获得的主要参与振型的频率与模型修正后的有限元分析结果对比,最大误差为14.334%,见表 1.
| 表 1 实测频率与修正后有限元计算的频率对比 Tab. 1 Comparison of frequency between the measured and modified simulation models |
应用修正后的有限元分析模型,根据结构特点数值模拟不同环杆处杆件损伤,共计17个样本,作为杆件损伤识别的样本库,具体位置见图 10,其中Y1~Y6表示各主肋环杆件损伤,Y7~Y12表示各环杆件损伤,Y13~Y17表示各环斜向杆件损伤.应用有限元软件将圆钢管杆件的厚度减少一半,即杆件有效截面面积减小,模拟该处杆件发生损伤.

|
图 10 试验结构和样本库中损伤杆件位置 Fig. 10 Member damage position of the test structure and the sample database |
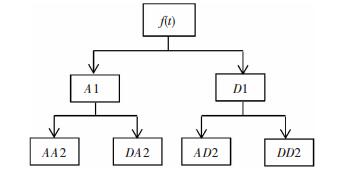
因小波包分析较传统小波分析在处理频率密集信号时有优势[7-9],对高频部分能够逐级分解,可自适应的选择相应频带,提高时频分辨率,小波包分解详图见图 11,图中f(t)表示加速度响应信号,进行j层(j=2)小波包分解后获得从低频到高频成分的信号分解系数,再对小波包各层分解系数重构,获得第j层第i个频带的重构系数fji(t)(i=1, …, 2j).应用式(1)获得小波包分解的各频带能量.
| $ \boldsymbol{E}_{i}=\int_{-\infty}^{\infty}\left[f_{j}^{i}(t)\right]^{2} \mathrm{d} t. $ | (1) |
|
图 11 小波包分解图 Fig. 11 Wavelet packet decomposition |
另外,根据已取得的研究成果,见文献[5],本文采用结构出现损伤前后的加速度响应信号的小波包能量频带分布的变化情况,通过归一化处理,获得杆件损伤位置判别的损伤判别指标,该损伤指标对于判别空间结构杆件损伤具有很好的灵敏性和抗噪性能.损伤指标计算公式为
| $ {\mathit{\boldsymbol{T}}_i} = \frac{{\left| {{\mathit{\boldsymbol{E}}_{{\rm{q}}i}} - {\mathit{\boldsymbol{E}}_{{\rm{h}}i}}} \right|}}{{\left( {\left| {{\mathit{\boldsymbol{E}}_{{\rm{q}}i}} - {\mathit{\boldsymbol{E}}_{{\rm{h}}i}}} \right|} \right)}}, $ | (2) |
式中:E=[E1, …, Ei](i=1, …, 2j), j为小波包分解层数; Eq和Eh分别表示杆件损伤前后结构加速度响应信号获得的小波包分解能量分布向量.
以杆件损伤样本库中Y1、Y7和Y13为例选取具有正交性,可以完全重构的Daubechies小波(Db21)小波,分解层数为6层,获得共计26=64阶频带能量.对3种不同杆件位置损伤的结构顶点竖向加速度响应信号进行小波包能量分析,其中前32阶频带能量分布情况见图 12,由于第33~64阶频带能量分布相对较小,图中未列出.

|
图 12 顶点竖向加速度的小波包能量分布 Fig. 12 Wavelet packet energy distribution of vertical acceleration on peak joint |
由图 12中频带分布可见,不同位置的杆件发生损伤,小波包频带分布都不尽相同.其中无损结构顶点竖向加速度响应信号的小波包能量分解以第1、26和28阶频带能量占优,而当Y1处杆件损伤,第1阶频带能量分布显著下降,仅以第26和28阶占优; 当Y7处环杆杆件损伤时以第26和28阶频带能量占优,但第1阶能量分布又有显著的升高; 当Y13处斜向杆发生杆件损伤时,表现为第1阶频带能量占优,而第11和15阶的频带能量又较无损结构的频带能量分布稍有降低.
3.2 杆件损伤位置判别在试验结构质量块布置后,对无损结构中的有效位置用锤击法获得结构加速度响应测试数据.然后切断一个斜向杆件,具体位置见图 10中S处杆件.对损伤结构再次用锤击法获得结构顶点加速度响应测试数据.对两次数据进行消噪处理后,进行小波包能量分解.选取Db21小波,分解层数为6层,获得共计64阶频带能量,应用式(2)得到实际试验结构杆件损伤时的损伤指标向量.
应用聚类分析法(见式(3)),将试验得到的损伤指标向量和样本库中各样本损伤指标向量进行聚类判别,研究结果表明[5],杆件位置判别指标越小,即实际损伤指标向量距离样本库某种位置发生杆件损伤的指标向量越接近,发生该处杆件损伤的可行性越大.
| $ {\mathit{\boldsymbol{P}}_{{\rm{S}}j}} = \sqrt {\left( {\sum\limits_{i = 1}^{2k} {{{\left( {{\mathit{\boldsymbol{T}}_{{\rm{S}}i}} - {\mathit{\boldsymbol{T}}_{{\rm{Y}}ji}}} \right)}^2}} } \right)} , $ | (3) |
式中:
将试验中S处杆件发生损伤前后结构的加速度响应数据进行小波包分解后,与样本库中17种不同位置的杆件损伤进行聚类分析,应用式(3)分别得到17个聚类分析损伤指标数值,具体结果见表 2.当Y14位置杆件发生损伤时,PS=27.81为最小值,判断试验中损伤杆件位置出现在Y14处,即第3环(由内到外)斜向杆件的可能性最大.另外,Y3和Y8的PS值也相对较小,分别为27.84和28.78.进一步分析发现,Y3为第3环与Y14杆件交汇同一节点的肋杆,Y8为第3环与Y14杆件交汇同一节点的环向杆,这也说明当Y14处杆件损伤时,杆件两端的节点也发生了一定程度的损坏,与该损伤节点相连的杆件也有可能被识别出损伤,这与实际结构损伤情况相符.所以在实际结构损伤判别中,应对Y3、Y8和Y14处损伤指标相对最小的杆件损伤位置进行检查和加固.
| 表 2 不同损伤位置下聚类分析后损伤指标Ps Tab. 2 Damage index of different positions |
本文提出的空间钢结构杆件损伤的位置识别方法能够有效判别空间钢结构杆件损伤的可能区域,并具有可操作性和工程应用价值,同时也完善了空间结构健康监测体系.该方法主要应用结构中布置的加速度传感器获得的结构在损伤前后两个重要阶段的响应数据,基于小波包能量分析建立损伤判别指标,通过聚类分析完成杆件损伤可能发生区域的最终识别.杆件损伤位置识别具体方法如下:
1) 获得实际结构损伤前后监测点的加速度响应数据,对加速度信号归一化处理后,进行小波包分解,选取具有正交性和可以重构的小波函数和合适的分解层数,层数越多精度越高,但计算时间越长.应用式(2)计算实际结构损伤指标向量.
2) 根据修正后结构有限元模型,获得完好结构和不同位置杆件损伤结构监测点的加速度响应信号,对加速度信号归一化处理后,应用式(1)、(2)计算损伤识别指标向量,作为损伤识别样本库的基础数据库.
3) 将前述1)中获得的实际结构的损伤指标向量,应用式(3)聚类分析方法,与前述2)计算得到的损伤识别样本库中的数据进行对比,获得聚类分析损伤识别指标,其中值越小判别其为损伤杆件的可能区域,完成最终的杆件损伤位置识别.
另外,本试验由于试验条件的限制,仅在结构顶点处布置了加速度传感器,如条件允许,根据结构特点,可以先划分子结构,在不同子结构处设置响应加速度传感器,先判别哪个子结构处发生杆件损伤,再进行杆件损伤的具体位置判别,这样可大大缩短判别时间和提高判别精度.
| [1] |
聂桂波, 戴君武, 张辰啸, 等. 芦山地震中大跨空间结构主要破坏模式及数值分析[J]. 土木工程学报, 2015, 48(4): 1. NIE Guibo, DAI Junwu, ZHANG Chenxiao, et al. Failure patterns of large span space structures in Lushan earthquake and numerical simulation[J]. China Civil Engineering Journal, 2015, 48(4): 1. DOI:10.15951/j.tmgcxb.2015.04.003 |
| [2] |
SHEN Shizhao. Recent advances on the fundamental research of spatial structures in China[J]. Journal of the International Association for Shell and Spatial Structures, 2006, 47(2): 93. |
| [3] |
曹正罡, 严佳川, 周传波. 80m球径螺栓球节点单层球面网壳强震失效机理[J]. 哈尔滨工业大学学报, 2017, 49(12): 39. CAO Zhenggang, YAN Jiachuan, ZHOU Chuanbo. Failure mechanism of an 80 meters span single-layer reticulated dome with bolt-ball joints subjected to severe earthquakes[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 39. DOI:10.11918/j.issn0367-6234.201603155 |
| [4] |
支旭东, 龚俊, 范峰. 正放四角锥平板网架楼盖地震易损性[J]. 哈尔滨工业大学学报, 2017, 49(12): 32. ZHI Xudong, GONG Jun, FAN Feng. Research on the seismic fragility of orthogonal pyramid space grid[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 32. DOI:10.11918/j.issn0367-6234.201705079 |
| [5] |
滕军, 姚姝. 基于小波包分析的地震作用下网壳结构的损伤判别方法[J]. 工程力学, 2011, 28(9): 183. TENG Jun, YAO Shu. A method of earthquake-induced latticed shell damage detection by wavelet packet analysis[J]. Engineering Mechanics, 2011, 28(9): 183. |
| [6] |
YAO Shu, TENG Jun, XIAO Yiqing, et al. Detection of the support damage spatial steel structures under earthquakes based on shaking table test[J]. Theoretical and Applied Mechanics Letters, 2011, 1(3): 5. |
| [7] |
TOUATI S, PESQUET J. Some results on the wavelet packet decomposition of nonstationary processes[J]. EURASIP Journal on Advances in Signal Processing, 2002, 2(11): 1289. |
| [8] |
魏玉明, 张永志, 王涛, 等. 基于小波包能量特征向量的结构动力响应损伤识别[J]. 地震工程学报, 2017, 39(6): 1157. WEI Yuming, ZHANG Yongzhi, WANG Tao, et al. Damage identification based on structural dynamic responses using wavelet packet energy eigenvector[J]. China Earthquake Engineering Journal, 2017, 39(6): 1157. |
| [9] |
SUN Z, CHANG C C. Structural damage assessment based on wavelet packet transform[J]. Journal of Structural Engineering, 2002, 128(10): 1354. DOI:10.1061/(ASCE)0733-9445(2002)128:10(1354) |
| [10] |
钢结构设计标准: GB 50017—2017[S].北京: 中国建筑工业出版社, 2018: 19 Standard for design of steel structures: GB 50017—2017[S]. Beijing: China Architecture & Building Press, 2018: 19 |
 2019, Vol. 51
2019, Vol. 51


