哈尔滨工业大学学报  2019, Vol. 51 Issue (6): 148-155  DOI: 10.11918/j.issn.0367-6234.201810039
0

引用本文 

苏鹏, 陈彦江, 闫维明. 近断层方向性效应地震作用下曲线梁桥试验[J]. 哈尔滨工业大学学报, 2019, 51(6): 148-155. DOI: 10.11918/j.issn.0367-6234.201810039.
SU Peng, CHEN Yanjiang, YAN Weiming. Experimental study on curved girder bridge under near-fault ground motion with directivity effect[J]. Journal of Harbin Institute of Technology, 2019, 51(6): 148-155. DOI: 10.11918/j.issn.0367-6234.201810039.

基金项目

国家自然科学基金(51378037)

作者简介

苏鹏(1986—)，男，博士研究生;
陈彦江(1963—)，男，教授，博士生导师;
闫维明(1960—)，男，教授，博士生导师

通信作者

陈彦江，cyjrlx@sina.com

文章历史

收稿日期: 2018-10-10
Abstract              Full text              Figures/Tables              PDF
近断层方向性效应地震作用下曲线梁桥试验
苏鹏, 陈彦江, 闫维明     
工程抗震与结构诊治北京市重点实验室(北京工业大学)，北京 100124
收稿日期: 2018-10-10
基金项目: 国家自然科学基金(51378037)
作者简介: 苏鹏(1986—)，男，博士研究生;
陈彦江(1963—)，男，教授，博士生导师;
闫维明(1960—)，男，教授，博士生导师
通信作者: 陈彦江，cyjrlx@sina.com
摘要: 为研究近断层方向性效应地震对曲线梁桥的影响，以一座曲线梁桥为研究对象，设计制作了缩尺比例为1: 10的全桥物理模型，选取破裂前方区域(forward region，FR)、破裂区域(middle region，MR)和破裂后方区域(backward region，BR)地震动，进行地震动模拟振动台试验。试验结果表明：FR地震动和MR地震动作用下曲线桥地震响应较BR地震动显著；单向激励时，MR地震动作用下结构响应明显，双向地震激励时，结构响应则和曲线桥与破裂方向相对位置有关；曲线桥垂直于破裂方向单向激励时，主梁绕固定墩产生水平转动，双向地震激励时，FR地震动和MR地震动作用下主梁的转动效应较BR地震动显著；相对于BR地震动作用，FR地震动和MR地震动对桥墩切向位移的放大作用大于径向位移的放大作用；曲线桥垂直于破裂方向时，主梁更容易产生转动，使得支座位移响应和梁端位移响应在低墩处显著，在抗震设计时，应合理分析避免支座脱落或落梁.
关键词: 曲线桥     振动台试验     近断层地震动     方向性效应     抗震分析    
Experimental study on curved girder bridge under near-fault ground motion with directivity effect
SU Peng, CHEN Yanjiang, YAN Weiming     
Beijing Lab of Earthquake Engineering and Structural Retrofit (Beijing University of Technology), Beijing 100124, China
Abstract: To study the influence of near-fault ground motion with directivity effect on curved girder bridges, a whole physical model of curved girder bridge with the scale ratio of 1: 10 was designed and manufactured, the ground motions in forward region (FR), middle region (MR), and backward region (BR) were selected, and seismic simulation shaking table test was carried out. Experimental results show that the seismic response of the curved bridge under the action of FR ground motion and MR ground motion was obviously higher than that of BR ground motion. In the case of unidirectional input, the structural response was greater under MR ground motion, while in bidirectional input, the structural response was related to the relative position of the curved bridge and the rupture direction. When the curved bridge was perpendicular to the rupture direction and the unidirectional input, the main girder rotated along the fixed pier. The rotational effect of the main girder under FR ground motion and MR ground motion was more obvious than that under BR ground motion in bidirectional input. The amplification effect of pier tangential displacement under FR ground motion and MR ground motion was greater than that of pier radial displacement. When the curved bridge was perpendicular to the rupture direction, the main girder was easier to rotate, making the displacement responses of the bearing and the beam end larger at the low pier. Therefore, in seismic design, rational analysis should be performed to avoid bearing shedding or girder falling.
Keywords: curved bridge     shaking table test     near-fault ground motion     rupture directivity     seismic analysis    

近些年来，全球发生了多次近断层地震，给人类的生命财产带来了重大损失，如1994发生在美国洛杉矶的Northridge地震，1995年发生在日本的Hyogo-Ken Nanbu地震，1999发生在台湾的Chi-Chi地震等，均造成了非常大的灾害和损失，因此近断层地震动也引起许多学者的关注[1-5].在多次近断层地震中发现，近断层地震动的空间分布特性与近断层的破裂方向性效应密切相关，近断层地震动在破裂方向上存在着方向性效应，沿破裂传播方向上具有更强的破坏性[6].方向性效应是在近断层地震发生破裂的过程中沿着破裂传播方向呈现多普勒效应，且在破裂的前方具有长周期、高能量等特点.

目前许多学者对近断层地震动的方向性效应进行了研究，文献[7-10]基于有限元软件分析了近断层方向性效应地震动的空间分布对结构的影响; 胡进军[11]对近断层地震动方向性效应及超剪切破裂进行了研究，分析了方向性效应的影响因素及分布特征; 文献[12-15]对全球各地近断层破裂方向性效应进行了研究，并对地震动频谱特性及成因进行了相关分析; Yazdani等[16]将破裂方向性效应纳入概率地震危险性分析，并建立危险性分析的方向性效应模型; 文献[17-18]通过格林函数对地震动方向性效应进行模拟，并验证了方法的有效性.以往的研究都通过数值模拟和理论分析讨论近断层地震的方向性效应，缺乏有效的试验验证.

本文以一座3跨曲线匝道桥为研究背景，设计了1: 10的曲线桥全桥物理模型，基于多子台阵系统展开地震动模拟振动台试验.研究了带有纵坡的曲线桥在近断层方向性效应地震动作用下结构动力特征，为近断层地震动作用下曲线梁桥抗震设计提供参考.

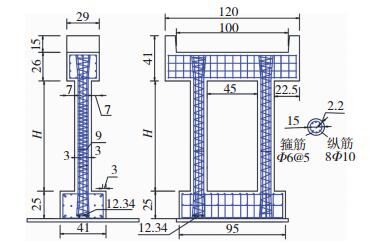
1 试验模型 1.1 试验模型设计与制作

以一座3跨曲线桥为原型桥，桥跨组合为3×40 m，曲率半径为R=50 m，在竖向存在5%的纵坡，主梁为单向双室的钢筋混凝土连续箱梁，采用C50混凝土浇筑，梁高2 m，梁底板宽度7.5 m，翼缘宽度为2.25 m，腹板高度为1.55 m.桥墩为直径1.5 m的双柱式桥墩，1#~4#桥墩高度依次为15、17、19、21 m.根据模型设计相似原理[19]，采用1: 10的相似比进行设计，相似关系见表 1.上部结构采用钢箱梁(图 3(c))，附加4.3 t人工配重来代替两种材料之间的质量差.桥墩使用与原结构相同材料进行制作，纵向钢筋与箍筋采用与原结构相同的配筋率，其中纵向钢筋配筋率为3.554%，箍筋体积配筋率为2.264%，桥墩钢筋布置见图 1，振动台试验模型见图 2.

表 1 振动台试验模型的相似关系 Tab. 1 Similitude relation of the shaking table test model
图 1 桥墩钢筋布置(cm) Fig. 1 Layout of the pier reinforcement (cm)
图 2 曲线桥振动台试验模型 Fig. 2 Shaking table test model for the curved bridge
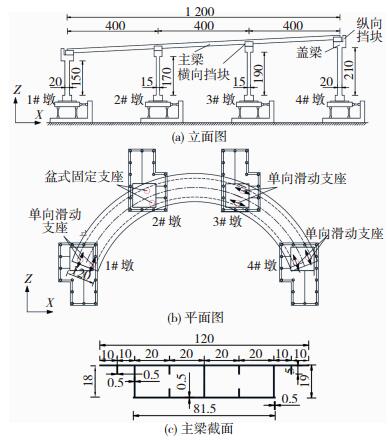
图 3 曲线桥振动台试验布置(cm) Fig. 3 Arrangement of the curved bridge shaking table test model(cm)
1.2 振动台与测点布置

本试验采用多子台阵系统展开，振动台参数见表 2.根据试验模型的线型进行振动台布置，见图 3.

表 2 振动台台阵系统性能参数 Tab. 2 Parameters of the shaking tables

在2#墩处安装盆式固定支座，在其他桥墩分别安装单向滑动支座.通过设置不同的墩高来实现曲线桥5%的纵坡.以两边墩连线方向作为X向(顺桥向)，与X垂直方向作为Y向(横桥向).

试验共布置了26个ICP加速度传感器，26个941B位移传感器，6个拉线位移计.分别对梁端、跨中、墩顶和墩底处的切向和径向加速度和位移进行测量.支座相对位移采用拉线位移计进行测量，在设有单向滑动支座的桥墩安装拉线位移计，传感器信号通过IMC动态系统进行采集.

2 地震波选取及加载方式 2.1 地震波的选取

1999年的台湾Chi-Chi地震位于一条南北走向的逆冲断层上，造成80 km的地表破裂带.Chi-Chi地震是个相对复杂的逆冲断层，断层运动在破裂的北端(末端)转变为以斜滑为主，由于地表破裂而引起方向性效应，使得位于断层破裂带两端区域的地震动差异较大，且破裂方向性效应很大程度影响了地震动强度及其空间分布，见图 4.根据近断层方向性效应的空间分布特点，将断层破裂带末端并且朝向破裂传播方向区域称为破裂前方区域(FR)，地表破裂区称为破裂区域(MR), 断层破裂开始传播并且与传播方向相反区域称为破裂后方区域(BR)，见图 5.选取上述3个不同区域的21条地震波，具体信息见表 3.

图 4 近断层破裂方向性效应 Fig. 4 Rupture directivity effect of near-fault
图 5 台湾Chi-Chi地震空间分布 Fig. 5 Spatial distribution of the Chi-Chi, Taiwan earthquake
表 3 近断层破裂方向性效应地震波参数 Tab. 3 Parameters of near-fault rupture directivity effect ground motions
2.2 地震波的频谱分析

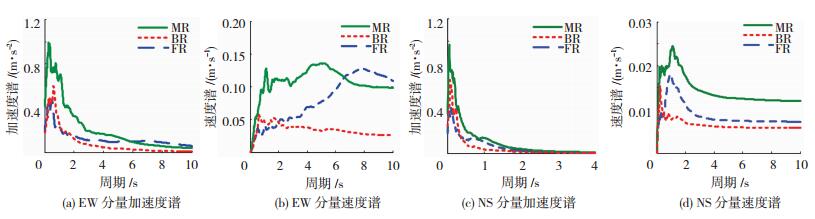
为分析近断层方向性效应地震的频谱特征，求得三组地震波在阻尼比为5 %单自由度弹性体系的反应谱均值.分别对比相互垂直的EW分量和NS分量地震动的加速度谱和速度谱.

由图 6(a)、(b)可知，EW分量在体系周期小于5.82 s时，MR地震动加速度谱最为显著; 当体系周期大于1.88 s时，FR地震动和MR地震动的加速度谱值依然较高.当体系周期大于1.93 s时，BR地震动速度谱明显低于FR地震动和MR地震动的速度谱.由图 6(c)、(d)可知，NS分量在MR地震动的反应谱最为显著; 体系周期大于0.35 s时，BR地震动加速度反应谱值最小; 当体系周期大于0.47 s时，FR地震动和MR地震动的速度谱值均高于BR地震动.

图 6 近断层方向性效应地震动加速度谱与速度谱 Fig. 6 Acceleration spectrum and velocity spectrum of rupture directivity effect of near-fault ground motion

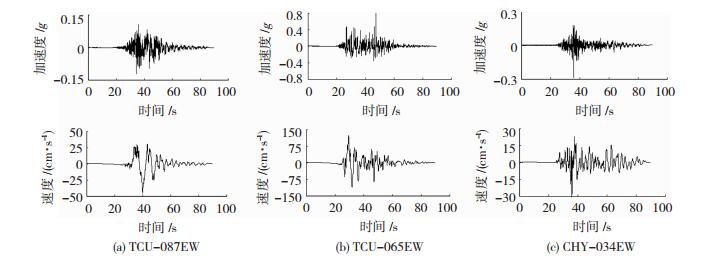
可以看出FR地震动和MR地震动EW分量具有显著的长周期特点，且部分伴随着速度脉冲，而BR地震加速度谱和速度谱在长周期范围内较小.由于篇幅有限，图 7给出了3个不同区域典型地震波的EW分量加速度和速度时程曲线.

图 7 方向性效应地震动加速度、速度时程 Fig. 7 Acceleration and velocity time history of rupture directivity effect ground motion
2.3 地震波的加载

假设原桥所处场地类型为Ⅱ类场地，按照7度设防，根据《公路桥梁抗震设计细则》[20]，将EW分量地震波峰值加速度调整到0.5 g，NS分量地震波根据与EW原始地震波实际比值进行调整.考虑到曲线桥相对于破裂方向的不同位置对结构响应产生的影响，通过以下两种布置方式进行分析，位置A：曲线桥与破裂方向相互垂直(图 8(a))，位置B：曲线桥与破裂方向相互平行(图 8(b))，分别进行水平单向加载和双向加载.

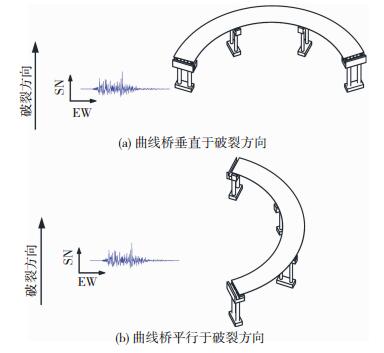
图 8 试验模型与破裂方向相对位置 Fig. 8 Relative position of test model and rupture direction
3 试验结果及分析 3.1 试验模型动力特性

采用随机子空间法(stochastic subspace identification)对模型桥在白噪声X向激励和Y向激励下的模态进行识别，随机子空间法频率稳定图见图 9.共识别出结构前四阶频率，其中一阶频率为2.55 Hz(纵向)，二阶频率为3.31 Hz(横向)，三阶频率为5.7 Hz(横向)，四阶频率为13.52 Hz(横向).试验过程中，模型桥未出现明显的裂缝及破损，结构未进入塑性阶段.

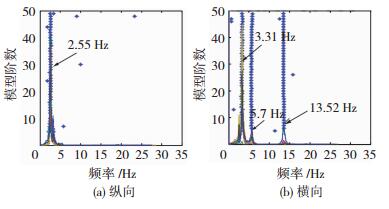
图 9 随机子空间法稳定图 Fig. 9 Stabilization diagram of the SSI method
3.2 主梁跨中位移响应

曲线桥与破裂方向相互垂直时，跨中位移响应见图 10.单向地震激励时，跨中位移响应在MR地震作用下最显著，相对于BR地震动放大系数的最大值分别为1.61(切向)和1.31(径向).双向地震激励时，跨中切向位移响应在MR地震作用下最显著，相对于BR地震动作用最大放大了1.68倍.跨中径向位移响应在FR地震动作用下最大，相对于BR地震动作用最大放大了1.45倍.单向地震激励时，主梁相对2#墩呈现非对称状态，主梁以2#固定墩为轴心产生转动，主梁与2#墩同步运动，承受桥墩传递的位移，使得1#跨中的切向位移响应较3#跨中显著.双向地震激励时，FR地震动和MR地震动作用下主梁的1#跨中切向位移较3#跨中显著，而BR地震动作用下则3#跨中切向位移响应较大，跨中径向位移响应在3#跨中均大于1#跨中.说明FR地震动和MR地震动在双向地震激励时激起的主梁的转动效应要大于BR地震动.

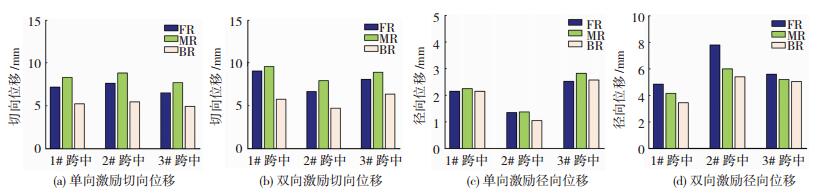
图 10 跨中位移响应(位置A) Fig. 10 Midspan displacement response of the main girder (Position A)

曲线桥与破裂方向相互平行时，主梁跨中位移响应见图 11.单向地震激励时，在MR地震动作用下跨中位移响应最大，相对于BR地震动放大系数的最大值分别为1.69(切向)和1.33(径向).双向地震激励时，在FR地震动作用下跨中切向位移响应最显著，相对于BR地震动作用最大放大了1.82倍.跨中径向位移响应在MR地震动作用下最大，相对于BR地震动作用最大放大了1.40倍.1#跨中位移响应小于3#跨中，可以看出地震波沿横桥向输入时，曲线桥以沿地震输入方向水平运动为主，FR地震动和MR地震动在平行于破裂方向输入时，激起的主梁转动效应明显小于垂直于破裂方向.

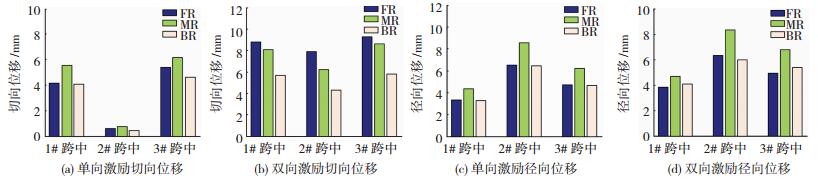
图 11 跨中位移响应(位置B) Fig. 11 Midspan displacement response of the main girder (Position B)
3.3 梁端位移响应

由于在梁端处沿切向设置了单向滑动支座，桥墩与主梁之间只产生切向位移，因此只需分析梁端的切向相对位移，梁端位移响应见表 4.

表 4 梁端位移响应峰值 Tab. 4 Displacement response of the beam end

曲线桥与破裂方向相互垂直时，梁端位移响应在MR地震动作用下最显著，BR地震作用下最小.地震动单向激励时，梁端位移响应在1#梁端显著大于4#梁端.双向地震激励时，FR地震动和MR地震动作用下，梁端位移响应在1#梁端比较显著，而BR地震动作用下则在4#梁端较大.这是由于双向激励时，FR和MR地震动激励时主梁产生的转动大于BR地震动，增大了1#梁端的位移响应.曲线桥与破裂方向相互平行时，梁端位移响应FR地震动和MR地震动作用下大于BR地震动，且在4#梁端比1#梁端显著.单向激励时，梁端位移响应在MR地震动作用下最大，而双向激励时则在FR地震作用下比较显著.

3.4 桥墩位移响应

曲线桥与破裂方向相互垂直时，桥墩相对位移响应见图 12.单向激励时，桥墩位移响应在MR地震动作用下最大，相对于BR地震动作用放大系数的最大值分别为1.61(切向)和1.31(径向).双向地震激励时，桥墩切向位移响应在MR地震动作用下最大，相对于BR地震动最大放大1.71倍，而桥墩径向位移响应则在FR地震动作用下最大，相对BR地震动最大放大1.48倍.2#墩切向位移响应大于其它各墩，4#墩墩顶位移响应较1#墩显著，3#墩墩顶径向位移响应在双向地震激励时大于2#墩.

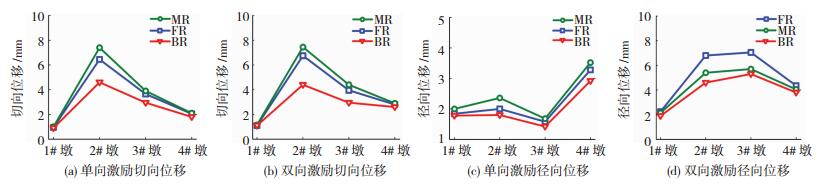
图 12 墩顶相对位移响应(位置A) Fig. 12 Relative displacement response of the pier (Position A)

曲线桥与破裂方向相互平行时，桥墩相对位移响应见图 13.单向激励时，桥墩位移响应在MR地震动作用下最大，相对于BR地震动作用放大系数的最大值分别为1.35(切向)和1.34(径向).双向激励时，桥墩切向位移响应在FR地震作用下最大，相对于BR地震动最大放大1.69倍，而桥墩径向位移响应则在MR地震动作用下最大，相对于BR地震动最大放大1.41倍.桥墩切向位移在2#墩处最显著，而径向位移则4#墩大于1#墩，3#墩大于2#墩.

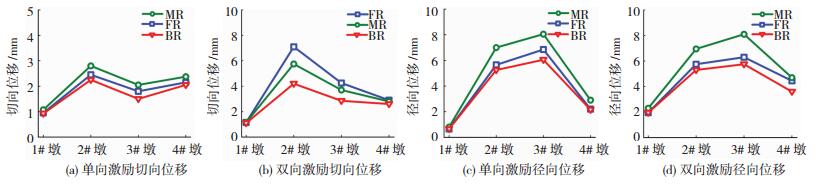
图 13 墩顶相对位移响应(位置B) Fig. 13 Relative displacement response of the pier (Position B)

可见，桥墩切向位移在2#墩处最显著.墩顶径向位移响应与墩高差有关，墩高越高，桥墩位移响应越显著.由于双柱墩的径向刚度大于切向刚度，使得FR地震动和MR地震动作用对桥墩切向位移放大作用大于径向位移的放大作用.

3.5 支座位移响应

支座位移响应见图 14.曲线桥与破裂方向相互垂直时(图 14(a)、图 14(b))，MR地震动激励时的支座位移响应最显著.单向地震激励时，支座位移响应在1#墩处显著大于4#墩处.双向地震激励时，FR地震动和MR地震动激励时的支座位移响应在1#墩处比较显著，而BR地震激励时的支座位移响应则在4#墩处较大，这是因为在FR地震动和MR地震动激励时主梁产生了转动，导致了支座位移响应在1#墩处显著增大.

图 14 支座位移响应 Fig. 14 Displacement response of the bearing

曲线桥与破裂方向相互平行时(图 14(c)、图 14(d))，MR地震单向激励时的支座位移响应最显著，而双向地震激励时的支座位移响应则FR地震作用下最大，且4#墩处支座位移响应均大于1#墩处，这是由于曲线桥平行于破裂方向时，主梁的转动小于垂直于破裂方向，而墩高差对桥墩位移响应具有放大作用，导致了支座相对位移在4#墩顶的显著增大.

4 结论

1) 相对于BR地震动，曲线桥结构动力响应在FR地震动和MR地震动作用下更加显著，因此，在进行近断层地震分析时，应考虑近断层地震动破裂方向性效应对结构响应的影响.

2) 曲线桥垂直于破裂方向单向激励时，主梁绕固定墩产生水平转动，双向地震激励时，FR地震动和MR地震动作用下主梁的转动效应较BR地震动显著，平行于破裂方向时，主梁转动效应相对较小.

3) 地震动单向激励时，桥墩位移响应在MR地震作用下最显著.地震动双向激励时，桥墩位移响应则和曲线桥与破裂方向的相对位置有关.相对于BR地震动作用，FR地震动和MR地震动作用对桥墩切向位移的放大作用高于径向位移的放大作用.

4) 曲线桥与破裂方向垂直时，主梁更容易产生转动，使得支座位移响应和梁端位移响应在低墩处更加显著.平行于破裂方向时，主梁的转动效应相对较小，高墩处支座位移响应和梁端位移响应更加显著，在抗震设计时，应合理分析避免支座脱落或落梁.

参考文献
[1]
赵金鑫.汶川地震近断层效应研究[D].哈尔滨: 中国地震局工程力学研究所, 2013
ZHAO Jinxin. Study on near-fault effects of Wenchuan earthquake[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2013
[2]
谢俊举, 李小军, 温增平, 等. 芦山7.0级地震近断层地震动的方向性[J]. 地球物理学报, 2018, 61(4): 1266.
XIE Junju, LI Xiaojun, WEN Zengping, et al. Variation of near-fault strong ground motion with directions during the 2013 Lushan Ms7.0 earthquake[J]. Chinese Journal of Geophysics, 2018, 61(4): 1266. DOI:10.6038/cjg2018K0686
[3]
曲哲, 师骁. 汶川地震和鲁甸地震的脉冲型地震动比较研究[J]. 工程力学, 2016, 33(8): 150.
QU Zhe, SHI Xiao. Comparative study on the pulse-like ground motions in the Wenchuan and the Ludian earthquakes[J]. Engineering Mechanics, 2016, 33(8): 150. DOI:10.6052/j.issn.1000-4750.2015.01.0039
[4]
江辉, 李新乐, 窦慧娟. 近断层长周期脉冲型地震动对竖向反应谱的影响研究[J]. 振动与冲击, 2012, 31(16): 56.
JIANG Hui, LI Xinle, DOU Huijuan. Influence of near-fault long-period pulse-type earthquake ground motions on vertical response spectra[J]. Journal of Vibration and Shock, 2012, 31(16): 56. DOI:10.13465/j.cnki.jvs.2012.16.007
[5]
杨永强, 谢礼立, 李明, 等. 汶川地震垂直和平行断层方向地震动特征差异[J]. 西南交通大学学报, 2011, 46(2): 235.
YANG Yongqiang, XIE Lili, LI Ming, et al. Differences between fault-normal and fault-parallel components of horizontal ground motion in Wenchuan earthquake[J]. Journal of Southwest Jiaotong Universiry, 2011, 46(2): 235. DOI:10.3969/j.issn.0258-2724.2011.02.010
[6]
胡进军, 谢礼立. 汶川地震近场加速度基本参数的方向性特征[J]. 地球物理学报, 2011, 54(10): 2581.
HU Jinjun, XIE Lili. Directivity in the basic parameters of the near-field acceleration ground motions during the Wenchuan earthquake[J]. Chinese Journal of Geophysics, 2011, 54(10): 2581. DOI:10.3969/j.issn.0001-5733.2011.10.015
[7]
李帅, 王景全, 颜晓伟, 等. 近断层地震动空间分布特征对斜拉桥地震响应影响[J]. 土木工程学报, 2016, 49(6): 94.
LI Shuai, WANG Jingquan, YAN Xiaowei, et al. Influence of spatial distribution characteristics of near-fault ground motions on seismic responses of cable-stayed bridges[J]. China Civil Engineering Journal, 2016, 49(6): 94. DOI:10.15951/j.tmgcxb.2016.06.011
[8]
颜晓伟.近断层地震动作用下大跨斜拉桥的复杂地震响应研究[D].南京: 东南大学, 2015
YAN Xiaowei. Study of the effects of near-fault ground motions on special seismic response of cable-stayed bridge[D]. Nanjing: Southeast University, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10286-1016755098.htm
[9]
双妙.风机结构在环境荷载激励下的损伤评估[D].北京: 北京科技大学, 2018
SHUANG Miao. Damage evaluation of wind turbines under environment loads[D]. Beijing: University of Science and Technology Beijing, 2018
[10]
GHAHARI S F, KHALOO A R. Considering rupture directivity effects, which structures should be named 'long-period buildings'[J]. The Structural Design of Tall and Special Buildings, 2013, 22(2): 165. DOI:10.1002/tal.667
[11]
胡进军.近断层地震动方向性效应及超剪切破裂研究[D].哈尔滨: 中国地震局工程力学研究所, 2009
HU Jinjun. Directivity effect of near-fault ground motion and super-shear rupture[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2009 http://cdmd.cnki.com.cn/article/cdmd-85406-2009173177.htm
[12]
KOKETSU K, MIYAKE H, GUO Y, et al. Widespread ground motion distribution caused by rupture directivity during the 2015 Gorkha, Nepal earthquake[J]. Scientific Reports, 2016, 6: 28536. DOI:10.1038/srep28536
[13]
HE X H, NI S D, LIU J. Rupture directivity of the August 3rd, 2014 Ludian earthquake (Yunan, China)[J]. Science China-Earth Sciences, 2015, 58(5): 795. DOI:10.1007/s11430-015-5053-2
[14]
LENGLINE O, GOT J L. Rupture directivity of microearthquake sequences near Parkfield, California[J]. Geophysical Research Letters, 2011, 38(8): 5. DOI:10.1029/2011gl047303
[15]
LUO Y, TAN Y, WEI S, et al. Source mechanism and rupture directivity of the 18 May 2009 MW 4.6 Inglewood, California, earthquake[J]. Bulletin of the Seismological Society of America, 2010, 100(6): 3269. DOI:10.1785/0120100087
[16]
YAZDANI A, NICKNAM A, DADRAS E Y, et al. Near-field probabilistic seismic hazard analysis of Metropolitan Tehran using region-specific directivity models[J]. Pure and Applied Geophysics, 2017, 174(1): 117. DOI:10.1007/s00024-016-1389-6
[17]
WANG H, WEN R, REN Y. Simulating ground-motion directivity using stochastic empirical green's function method[J]. Bulletin of the Seismological Society of America, 2017, 107(1): 359. DOI:10.1785/0120160083
[18]
WEN Y Y, MIYAKE H, YEN Y T, et al. Rupture directivity effect and stress heterogeneity of the 2013 Nantou blind-thrust earthquakes, Taiwan[J]. Bulletin of the Seismological Society of America, 2014, 104(6): 2933. DOI:10.1785/0120140109
[19]
王天稳. 土木工程结构试验[M]. 武汉: 武汉理工大学出版社, 2006: 16.
WANG Tianwen. Structure experiment of civil engineering[M]. Wuhan: Wuhan University of Technology Press, 2006: 16.
[20]
公路桥梁抗震设计细则: JTG/T B02-01—2008[S].北京: 人民交通出版社, 2008: 15
Guideline for seismic design for highway bridges: JTG/T B02-01—2008[S]. Beijing: China Communications Press, 2008: 15